1. Introduction
Coupled electron and proton transfer reactions play a key role in the mechanisms of biological energy transduction.1–3 Such reactions are also fundamental for artificial energy-related systems such as fuel cells, chemical sensors, and other electrochemical devices. Biological examples include, among others, cytochrome c oxidase,4,5 bc1 complex,6,7 and photosynthetic reaction centers.8,9 In such systems, electrons tunnel between redox cofactors of an enzyme, while the coupled protons are transferred either across a single hydrogen bond or between protonatable groups along special proton-conducting channels.
In this paper general theories and models of coupled electron transfer/proton transfer (ET/PT) reactions are discussed. Pure electron transfer reactions in proteins have been thoroughly studied in the past, both experimentally10–17 and theoretically.18–25 The coupled reactions are relatively new and currently are gaining attention in the field.6,8,26–43
Two types of coupled reactions can be distinguished. In concerted electron and proton transfer reactions (denoted PCET in Refs. 29,30,43–45, although this term is also used more generally), both the ET and PT transitions occur in one step. Such concerted processes occur in reactions in which proton transfer is typically limited to one hydrogen bond; however, examples with multiple hydrogen bond rearrangements are also known.46 In sequential reactions, the transitions occur in two steps: ET/PT or PT/ET. Typically each individual step is uphill in energy, while the coupled reaction is downhill.
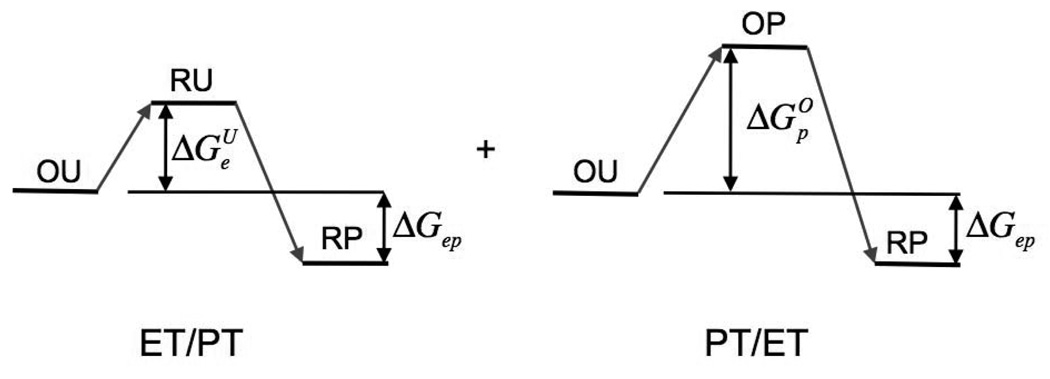
A sequential reaction can proceed along two parallel channels: ET then PT (EP) or PT then ET (PE). In each channel the reaction involves two sequential steps: uphill activation, and then downhill reaction to the final product state. The lifetime of the activated complex is limited by the back reaction. The general formula for the rate of such reactions can be easily developed. In the context of bioenergetics issues, however, it is interesting to analyze all of the possible cases separately because each corresponds to a different mechanism: for example, an electron can go first and pull out a proton; alternatively, a proton can go first and pull out an electron; or an electron can jump back and forth between donor and acceptor and gradually pull out a proton. In enzymes involving coupled proton and electron transport, the exact mechanism of the reaction is of prime interest.
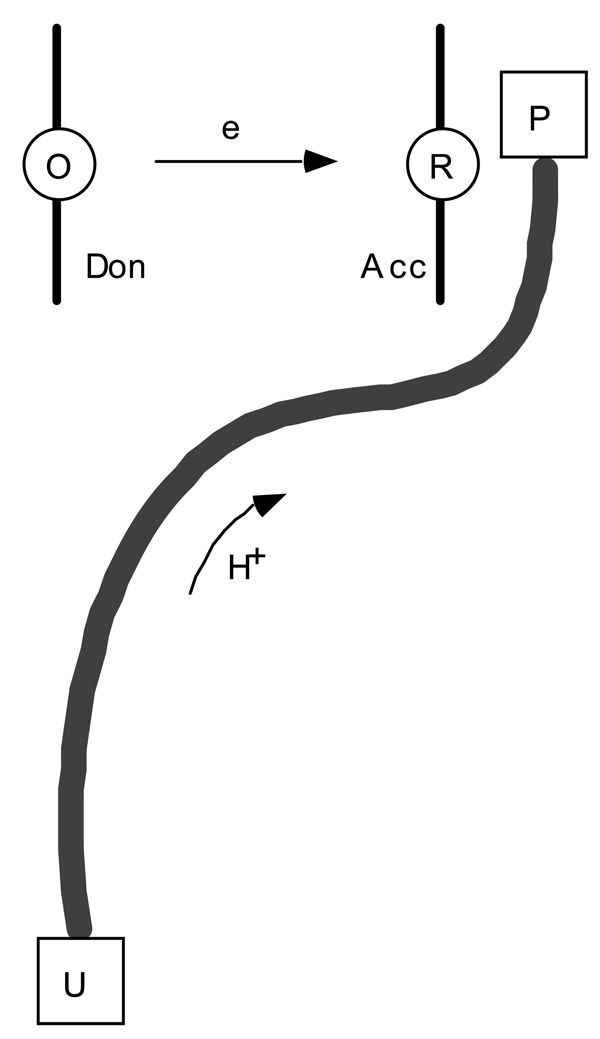
First we will consider a simple four-state model of reactions where the proton moves across a single hydrogen bond; both concerted and sequential reactions will be treated. Then we will consider models for long-distance proton transfer, also denoted proton transport or proton translocation. Typically, electron transfer coupled to proton translocation in proteins involves an electron tunneling over a long distance between two redox cofactors, coupled to a proton moving along a proton conducting channel in a classical, diffusion-like random walk fashion. Again, separately the electron and proton transfer reactions are typically uphill, while the coupled reaction is downhill in energy. The schematics of this process is shown in Fig. 1. The kinetics of such reactions can be much different from those involving proton transfer across a single hydrogen bond. In this paper, we will discuss the specifics of such long-distance proton-coupled reactions.
Fig. 1.
Schematics of the electron transfer reaction coupled to proton translocation. In the reaction, an electron is tunneling over a long distance between two redox cofactors, O and R, and a coupled proton is transferred over a proton conducting channel. The initial and final states of the proton are two protonatable groups of the protein, U and P. Separately, both electron and proton transfer are uphill in energy, however, the coupled reaction is downhill. Figure reprinted with permission from Ref. 42. Copyright 2003 World Scientific.
Following the review of theoretical concepts, a few applications will be discussed. First the phenoxyl/phenol and benzyl/toluene self-exchange reactions will be examined. The phenoxyl/phenol reaction involves electronically nonadiabatic proton transfer and corresponds to a proton-coupled electron transfer (PCET) mechanism, whereas the benzyl/toluene reaction involves electronically adiabatic proton transfer and corresponds to a hydrogen atom transfer (HAT) mechanism. Comparison of these two systems provides insight into fundamental aspects of electron-proton interactions in these types of systems. Next a series of theoretical calculations on experimentally studied PCET reactions in solution and enzymes will be summarized, along with general predictions concerning the dependence of rates and kinetic isotope effects (the ratio of the rate constants for hydrogen and deuterium transfer) on system properties such as temperature and driving force. The final application that will be discussed is cytochrome c oxidase (CcO). CcO is the terminal component of the electron transport chain of the respiratory system in mitochondria and is one of the key enzymes responsible for energy generation in cells. The intricate correlation between the electron and proton transport via electrostatic interactions, as well as the kinetics of the coupled transitions, appear to be the basis of the pumping mechanism in this enzyme.
2. Concerted reactions (PCET)
2.1. Theoretical Framework
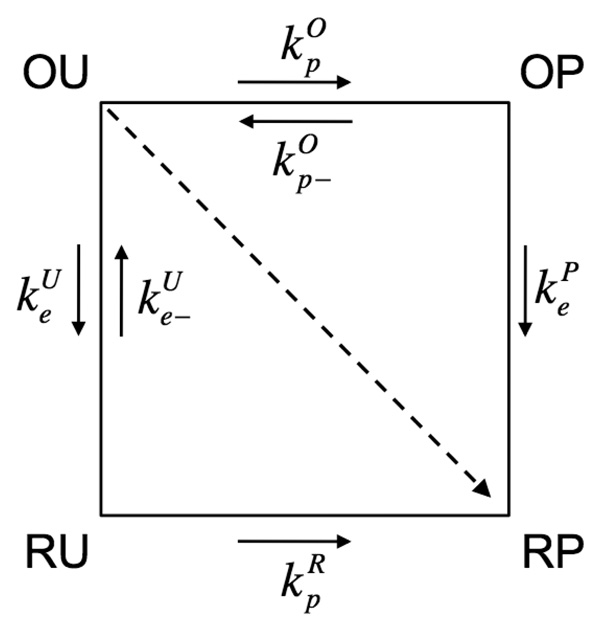
If one electron and one proton are transferred, the reaction can be described in terms of four diabatic electronic states, as depicted in Fig. 2:47
| (2.1) |
where the O/R (oxidized/reduced) and U/P (unprotonated/protonated) symbols are used to denote the state of the acceptor group. In concerted mechanisms, the electron and proton transfer simultaneously (i.e., (OU) → (RP)), along the diagonal in Fig. 2. In sequential mechanisms, the proton transfers prior to the electron (i.e., (OU) →(OP) → (RP)) or the electron transfers prior to the proton (i.e., (OU) → (RU) → (RP)), along the edges of the scheme in Fig. 2. This model is easily extended to proton-coupled electron transport or translocation processes involving multiple proton and electron transfers by including additional diabatic electronic states.47
Fig. 2.
Four-state model for coupled electron and proton transfer reactions. In the initial state (OU), the electron is on the donor site O (Oxidized acceptor), and the proton is on the U site (Unprotonated acceptor). In the final state (RP), the electron is on the acceptor site R (Reduced acceptor), and the proton is on the P site (Protonated acceptor). Intermediate states (OP) and (RU) correspond to activated states for sequential PT/ET and ET/PT reactions. The concerted reaction corresponds to an (OU) to (RP) transition. Figure reprinted with permission from Ref. 42. Copyright 2003 World Scientific.
In general, a concerted PCET mechanism is defined as a PCET reaction that does not involve a stable intermediate arising from single electron or proton transfer. Concerted PCET reactions are often described in terms of reactant and product states corresponding to the electron being localized on the donor or acceptor, respectively.48 In this case, the reactant state is dominated by (OU), and the product state is dominated by (RP). The proton vibrational states can be calculated for the reactant and product electronic states, leading to two sets of electron-proton vibronic states. Typically concerted PCET reactions can be described in terms of nonadiabatic transitions between the reactant and product electron-proton vibronic states.
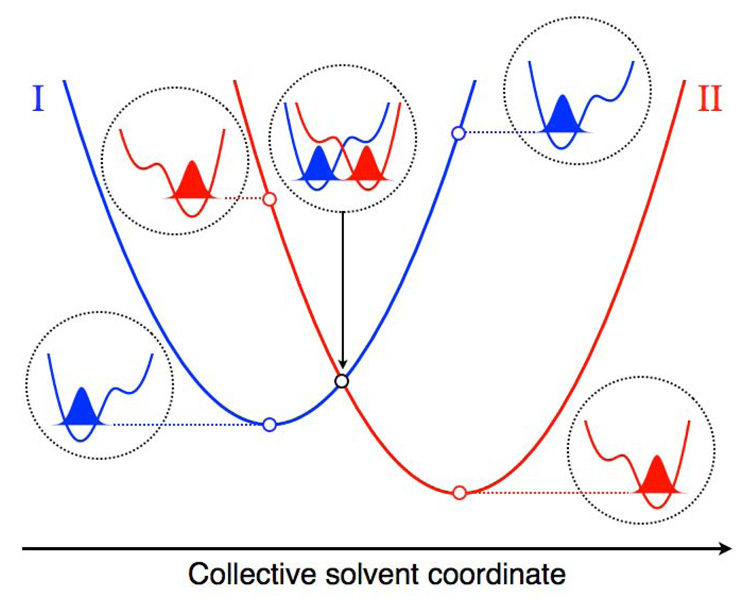
Analogous to Marcus theory for electron transfer, PCET reactions can be described in terms of reorganization of the solvent environment. Fig. 3 depicts a slice of the free energy surfaces along a collective solvent coordinate. Also shown are the proton potential energy curves and associated proton vibrational wavefunctions. Typically the proton donor well is lower in energy when the electron is localized on its donor, whereas the proton acceptor well is lower in energy when the electron is localized on its acceptor. Thus, the proton vibrational ground state wavefunction is localized near its donor in the reactant state and near its acceptor in the product state. Note that this general description encompasses the cases in which the electron and proton are transferred in the same or in different directions. The shapes of the proton potential energy curves are usually not significantly influenced by the solvent coordinate in the region of interest because the asymmetry is dominated by the electrostatic interaction between the proton and the solute electronic charge distribution. The relative energies of the proton potential energy curves, however, are strongly influenced by the solvent coordinate.
Fig. 3.
Slices of the free energy surfaces for the ground reactant (I) and product (II) vibronic states along a collective solvent coordinate. The proton potential energy curves along the proton coordinate and the corresponding ground state proton vibrational wavefunctions are depicted for the reactant minimum, the crossing point, and the product minimum of the free energy curves. The energies of these proton vibrational states correspond to the open circles on the free energy curves. The proton potential energy curves associated with the crossing point are shifted higher in energy for clarity. Figure and caption reprinted with permission from Ref. 31. Copyright 2008 American Chemical Society.
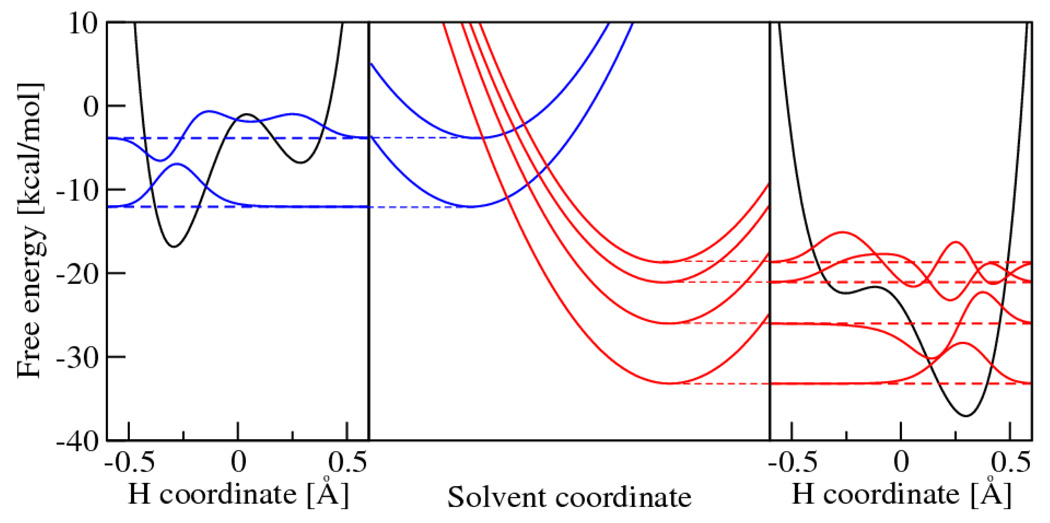
The basic mechanism for concerted PCET may be analyzed in the context of Fig. 3. Initially, the system is in thermal equilibrium in the reactant state, and both the electron and proton are localized near their donors. Fluctuations of the solvent environment cause the system to evolve to the intersection between the two curves, where a nonadiabatic transition from the reactant to the product vibronic state occurs with a probability proportional to the square of the vibronic coupling. After this nonadiabatic transition, the electron and proton are localized near their acceptors, and the system relaxes to thermal equilibrium in the product state. Often excited vibronic states and the proton donor-acceptor vibrational motion also play important roles in PCET reactions.31 Figure 4 depicts slices of the free energy surfaces and the corresponding proton vibrational wavefunctions for two reactant and four product vibronic states for a PCET reaction.
Fig. 4.
Calculated free energy curves for the PCET reaction in a rhenium-tyrosine complex. In the center frame are slices of the free energy surfaces along a collective solvent coordinate. In the left/right frames are the reactant/product proton potential energy curves and the corresponding proton vibrational wavefunctions along the proton coordinate. Figure reprinted with permission from Ref. 137. Copyright 2007 American Chemical Society.
2.2. Rate Constants
A series of rate constant expressions for vibronically nonadiabatic PCET have been derived49,50 in various well-defined limits using Fermi’s Golden rule formalism and linear response theory. For fixed proton donor-acceptor distance R, the rate constant is:49
| (2.2) |
where the summations are over reactant and product vibronic states, Pμ is the Boltzmann population for the reactant state μ, Vμν is the vibronic coupling between the reactant and product vibronic states μ and ν, λμν is the solvent reorganization energy for states μ and ν, and is the free energy of reaction for states μ and ν. All of these quantities depend on the fixed proton donor-acceptor distance R. As discussed in Sec. 2.3, the vibronic coupling is the product of the electronic coupling and the overlap between the reactant and product proton vibrational wavefunctions in the electronically nonadiabatic regime.
Rate constant expressions including the dynamical effects of the R coordinate and the solvent have also been derived.50 In these derivations, the vibronic coupling is assumed to depend exponentially on R:
| (2.3) |
where R̄μ is the equilibrium value of R for the reactant state μ, and is the vibronic coupling between states μ and ν at distance R̄μ. This form of the coupling is a reasonable approximation in the region of R near its equilibrium value, as illustrated by expanding in a Taylor series around R = R̄μ and retaining only the linear terms.51 Typically the Condon approximation, in which the electron-proton vibronic coupling is assumed to be independent of the nuclear configuration, is invoked for PCET reactions, with the important exception of the R-mode. In the dynamical formulation,50 the rate constant is represented by the time integral of a time-dependent probability flux correlation function, which is expressed in terms of the vibronic coupling and the time correlation functions of the R coordinate, the energy gap, and the derivative of the energy gap with respect to the R coordinate. These time correlation functions can be calculated from classical molecular dynamics simulations on the reactant surface. This formulation can be used with any potential energy surface and includes the dynamical effects of the solvent and R mode, but it has a complicated form and requires numerical integration over time.
Using the short-time, high-temperature approximation for the solvent modes and representing the R-mode time correlation function by that of a quantum mechanical harmonic oscillator, the rate constant can be expressed as:50
| (2.4) |
with the dimensionless parameters defined as
| (2.5) |
Here β = 1/kBT, is the coupling reorganization energy defined as , and λR is the R-mode reorganization energy defined as λR = MΩ2 δR2/2, where M and Ω are the R-mode effective mass and frequency, respectively, and δR = R̄ν − R̄μ. Here δR and the solvent reorganization energy λs are assumed to be the same for all pairs of states, although in general they could be allowed to vary for different pairs of states. The short-time, high-temperature approximation for the solvent is valid when the dynamics of the solvent fluctuations are fast on the time scale of the coherent nonadiabatic transitions. Note that this rate constant still requires integration over time. Further simplified expressions have been derived in limiting regimes pertaining to the R-mode frequency.
In the high-temperature (low-frequency) limit for the R mode (ℏΩ ≪ kBT), the rate constant simplifies to52
| (2.6) |
where the total reorganization energy is defined as . This rate constant can be further simplified by assuming that δR = 0 (i.e., the equilibrium R value is the same for the reactant and product vibronic states) and , which is equivalent to the replacement of the R-mode time correlation function with its value at zero time. The resulting rate constant expression is
| (2.7) |
Related expressions have been derived for vibrationally nonadiabatic proton transfer reactions and for electron transfer reactions.53–57
In the low-temperature (high-frequency) limit for the R mode (βℏΩ ≫ 1), the rate constant simplifies to:50
| (2.8) |
This analytical expression was derived using the stationary phase method and is valid only in the strong solvation regime (i.e., for all relevant pairs of states). In this limit, the R-mode remains predominantly in its ground state, and the vibronic coupling is averaged over the ground state vibrational wavefunction of the R-mode. In principle, other high-frequency solute modes could also be included in the rate constant expression.
The effects of intramolecular solute modes (i.e., inner-sphere reorganization) have been incorporated within this theoretical framework49 in various well-defined limits.58–60 In the high-temperature approximation for the uncoupled solute modes, the rate constant expressions given above are modified by adding the inner-sphere reorganization energy to the solvent reorganization energy.
In some cases, the assumption that the vibronic coupling decreases exponentially with the proton donor-acceptor distance R is not valid. Typically this assumption is valid only near the equilibrium R value and will break down for lower proton donor-acceptor vibrational frequencies that enable sampling of a wider range of R values.61 In addition, this assumption will not be valid when the proton vibrational wavefunctions change character in the relevant range of R values. Specifically, the shapes of the proton potentials may change with R (i.e., the barrier of an asymmetric double well potential energy curve could become lower, possibly becoming only a shoulder, as R decreases). In this case, a given proton vibrational state could shift from being localized on one side to the other, or possibly being delocalized, as R changes. The assumption in Eq. (2.3) will break down in these situations, and the rate constant expressions based on this assumption are no longer valid.
For the general form of the vibronic coupling, the effects of the R-mode can be included with the expression
| (2.9) |
where k(R) is the rate constant in Eq. (2.2) evaluated at a given R value and P(R) is the normalized probability distribution function for R at a specified temperature. In practice, P(R) is often chosen to be a classical or quantum mechanical harmonic oscillator probability distribution function.62 In general, it could be a more complicated probability distribution function reflecting the Boltzmann probabilities for the relevant R values. The R value corresponding to the maximum of the integrand in Eq. (2.9) is determined by a balance between the probability distribution function, which tends to be greatest at the equilibrium R value, and the vibronic coupling, which tends to favor shorter R values because of the larger overlap between the reactant and product proton vibrational wavefunctions.63 Thus, typically the dominant contribution to the rate constant arises from an R value that is shorter than the equilibrium value.
Recently PCET rate constant expressions that include the effects of solvent dynamics and interpolate between the golden rule and solvent-controlled limits were derived.64 The golden rule limit is defined in terms of weak vibronic coupling and fast solvent relaxation. As shown above, the rate constant is proportional to the square of the vibronic coupling and is independent of the solvent relaxation time in this limit. In contrast, the rate constant is independent of the vibronic coupling and increases as the solvent relaxation time decreases in the solvent-controlled limit. The interconversion between the solvent-controlled and golden rule limits can be induced by altering the proton donor-acceptor mode frequency, the vibronic coupling, or the solvent relaxation time. The kinetic isotope effect behaves differently in the solvent-controlled and golden rule limits and thus provides a unique probe for characterizing the nature of PCET processes.64
These theoretical formulations have been extended to electrochemical PCET at metal-solution interfaces.52,64,65 In addition, a theory has been developed for studying the ultrafast dynamics of both homogeneous and interfacial photoinduced PCET reactions.66,67 These directions are important for the development of solar cells and other energy conversion devices.
2.3. Vibronic Coupling: Electronically Adiabatic and Nonadiabatic Proton Transfer
All of the rate constant expressions given above depend on the vibronic coupling Vμν, which is defined as the Hamiltonian matrix element between the reactant and product electron-proton vibronic wavefunctions. PCET reactions are usually vibronically nonadiabatic, i.e., Vμν ≪ kBT and the quantum subsystem comprised of the electrons and transferring proton does not respond instantaneously to the solvent motions. Even for vibronically nonadiabatic reactions, however, the proton transfer can be electronically adiabatic, electronically nonadiabatic, or in the intermediate regime. These regimes are defined in terms of the relative timescales of the rearranging electrons and the transferring proton. In the electronically adiabatic limit, the electrons respond instantaneously to the proton motion, but in the electronically nonadiabatic limit, the electronic response is slower than the proton tunneling.
A semiclassical expression for the vibronic coupling that spans both of these limits has been derived.43 In this formulation, the general vibronic coupling is given by
| (2.10) |
where is the adiabatic vibronic coupling and the factor κ is defined as
| (2.11) |
Here Γ(x) is the gamma-function, and p is the proton adiabaticity parameter defined as
| (2.12) |
where Vel is the electronic coupling between the diabatic electronic states, νt is the tunneling velocity of the proton at the crossing point of the two proton potential energy curves, and |ΔF| is the difference between the slopes of the proton potential energy curves at the crossing point. The tunneling velocity νt can be expressed in terms of the energy Vc at which the potential energy curves cross, the tunneling energy E, and the mass m of the proton: .
This formulation provides simplified expressions in the electronically adiabatic and nonadiabatic limits. In the electronically adiabatic limit, p≫1, κ = 1, and the vibronic coupling becomes , which is defined as half of the tunneling splitting. In the electronically nonadiabatic limit, p≪1, , and the vibronic coupling becomes , where Sμν is the overlap between the reactant and product proton vibrational wavefunctions. These limits can be understood in terms of the relative timescales for the proton tunneling and the electronic transition. The adiabaticity parameter is the ratio of the proton tunneling time τp and the electronic transition time τe: p = τp/τe. The proton tunneling time is defined as the time spent by the tunneling proton in the crossing region, τp ~ Vel/|ΔF|νt, and the electronic transition time is defined as the time required to change the electronic state, τe ~ ℏ/Vel. When the proton tunneling time is much longer than the electronic transition time, the electronic states have enough time to mix completely, and the proton transfer occurs on the electronically adiabatic ground state surface (i.e., the proton transfer is electronically adiabatic). When the proton tunneling time is much less than the electronic transition time, the proton transfer is electronically nonadiabatic because the electronic states no longer have enough time to mix completely during the proton tunneling process.
2.4. Hydrogen Atom Transfer
Hydrogen atom transfer (HAT) may be viewed as a special case of PCET. In HAT, the electron and proton transfer between the same donor and acceptor (i.e., De ≡ Dp and Ae ≡ Ap). Such reactions do not involve substantial charge redistribution, and the solvent reorganization energy is small. Thus, these reactions may require an explicit dynamical treatment of intramolecular solute modes rather than the treatment described above in terms of collective solvent coordinates. In addition, the probability flux correlation function formalism may require special treatment such as inclusion of coupling between the proton donor-acceptor vibrational mode and the solvent modes to avoid divergent integrals.68
The criteria for distinguishing between HAT and PCET have been debated in the literature. The distinction based on the same proton and electron donors and acceptors is not rigorous because of the quantum mechanical behavior and associated delocalization of the electron and proton. The distinction based on molecular orbital analysis32 is also problematic due to the dependence on the level of theory and representation. The degree of electronic nonadiabaticity for the proton transfer reaction described in the previous subsection provides a quantitative diagnostic for differentiating between HAT and PCET.69 The HAT mechanism corresponds to the electronically nonadiabatic limit (i.e., p≪1), and the PCET mechanism corresponds to the electronically adiabatic limit (i.e., p≫1). This distinction between HAT and PCET has been illustrated by a comparison between the phenoxyl/phenol and benzyl/toluene self-exchange reactions.69 Based on this type of analysis, the phenoxyl/phenol reaction, which involves electronically nonadiabatic proton transfer, corresponds to PCET, while the benzyl/toluene reaction, which involves electronically adiabatic proton transfer, corresponds to HAT. This analysis is discussed in more detail below in Section 6.1. The relation between PCET and HAT has also been explored in the context of the photosystem II oxygen-evolving complex.36
2.5. Kinetic Isotope Effects
A hallmark of a concerted PCET reaction is the observation of a kinetic isotope effect (KIE), the ratio of the rate constant for hydrogen to the rate constant for deuterium. Typically the magnitude of the KIE is strongly influenced by the vibronic coupling. As discussed above, in the electronically nonadiabatic regime, the vibronic coupling is the product of the electronic coupling and the overlap between the reactant and product proton vibrational wavefunctions. Thus, for a given pair of vibronic states, the rate constant is proportional to , the square of the hydrogen vibrational overlap for that pair of states at the equilibrium proton donor-acceptor distance, and the KIE is proportional to the ratio . Due to the smaller mass of hydrogen, the hydrogen overlap is typically substantially larger than the deuterium overlap, leading to a significant KIE. Moreover, the deuterium overlap SD decreases faster than the hydrogen overlap SH as the proton donor-acceptor distance increases, so αD > αH. This parameter, which represents the distance dependence of the vibronic coupling defined in Eq. (2.3), influences the temperature dependence of the KIE in certain regimes.
The dependence of the KIE on system properties can be analyzed for each specific rate constant expression given above. Neglecting the isotopic dependence of all quantities except the vibronic coupling and including only the ground reactant and product vibronic states, Eq. (2.2) for fixed proton donor-acceptor distance predicts that the KIE will be , which is independent of temperature. This ratio will increase as the equilibrium proton donor-acceptor distance increases. In the low-frequency limit for the proton donor-acceptor mode (Eq. (2.7)), the same approximations lead to the following expression:
| (2.13) |
indicating that the KIE will decrease with increasing temperature. In this regime, the magnitude of the KIE is determined mainly by the ratio of the squares of the hydrogen and deuterium overlaps, the proton donor-acceptor mode frequency, and the distance dependence of the vibronic coupling. The temperature dependence of the KIE depends strongly on the proton donor-acceptor mode frequency in this regime.61
When excited vibronic states contribute significantly to the total reaction rate, these simple expressions for the KIE are not valid. The relative weightings of the contribution from each pair of reactant and product vibronic states are determined by several competing factors, including temperature, and are usually different for hydrogen and deuterium. Moreover, altering only a single parameter without influencing the other parameters is not always experimentally possible. For example, increasing the proton donor-acceptor equilibrium distance often decreases the associated frequency. Thus, the dependence of the KIE on system properties, such as proton donor-acceptor distance or temperature, is often not straightforward and may not be intuitive.61 In the high-frequency limit for the proton donor-acceptor mode, the KIE could even increase with increasing temperature, as observed for a quinol oxidation reaction.70
3. Sequential Electron and Proton Transfer. Four State Models
The reactions discussed in this section occur along the edges of the scheme shown in Fig. 2.
3.1. Rate of a Sequential Coupled Reaction
Sometimes in the literature the rate constant of a sequential ET/PT reaction is written in the following form:
| (3.1) |
where ke and kp are the individual electron and proton transfer reaction rate constants. This expression assumes that the reaction occurs in sequence: first electron (proton) transfer, then proton (electron) transfer. The reaction is complete when both an electron and a proton are in their final states. The overall average time to complete two transfers is the sum of those for each of the consecutive steps, as stated in the above formula. The overall rate is limited by the slowest step.
A tacit assumption made in Eq. (3.1) is that the first electron/proton step in the reaction is irreversible, i.e. if a proton jumps first to the final state, it stays there long enough for an electron to make its own transfer. (The coupling between an electron and a proton is such that electron transfer will most likely occur when the proton is in the final state.) This can be the case when, for example, the first step of the reaction is downhill in free energy, or if the second step is fast enough to beat the reverse reaction of the first step.
This is not the most common situation in enzymatic reactions.8,27,28 Typically, each of the separate ET and PT reactions is uphill in energy. As a result, the lifetime of the intermediate excited state after the first transfer may not be long enough for the second reaction to be complete. Such is the case, for example, in the Photosynthetic Reaction Center (PRC) for the quinone reduction reaction.8,26
The simplest type of such reactions can be described in terms of the scheme shown in Fig. 2. The states are denoted according to the state of the acceptor group: (Oxidized/Reduced) and (Unprotonated/Protonated). Thus, the initial state is OU and the final state is RP. There are two intermediate states, RU and OP. Electron transfer can occur before or after protonation, with corresponding rates . Likewise, the proton transfer can occur before or after reduction, with rates . The reverse reaction for each of these steps will be denoted as ke− and kp− with the appropriate superscript. The rate constant of such a reaction is:
| (3.2) |
where
| (3.3) |
| (3.4) |
The reaction can proceed along two channels: ET first, PT second, with rate constant kep, or PT first, ET second, with rate constant kpe, as shown in Fig. 5. The overall rate constant is the sum of the rate constants of the two channels. Each rate constant is a product of the rate constant for the formation of the activated complex (for ET without PT, the rate constant is ; for PT without ET, the rate constant is ), and the probability that the reaction will proceed from the intermediate activated state in the direction of the final state RP, instead of the initial state via back reaction.
Fig. 5.
Free energies of sequential ET/PT and PT/ET reactions shown in Fig. 2. Figure reprinted with permission from Ref. 42. Copyright 2003 World Scientific.
Consider the (EP) channel. If the proton is "fast", so that the proton transfer reaction can be completed while the electron is in the activated state, , the reaction rate constant is given by the rate constant for formation of the activated complex,
| (3.5) |
If the proton is “slow” , then the lifetime of the activated complex, , is shorter than the timescale of the PT reaction, , and several electron transfer "attempts" are needed to complete the PT reaction. The number of such attempts is τp/τe−; hence the overall time needed to complete the reaction is τep = τe(τp/τe−), where . Here we assume τe ≫ τe−. Then the rate constant is given by
| (3.6) |
where Ke is the equilibrium constant for electron transfer (without proton transfer):
| (3.7) |
where is the free energy of the electron transfer reaction without proton transfer. It will be assumed that ET is uphill, so is a negative driving force. The equilibrium constant Ke can be interpreted as the population of the activated (reduced) state, from which the proton transfer occurs with rate constant . The overall rate constant is given by Eq. (3.6).
Similarly, for the PE channel, if the electron is “fast,” the rate constant is
| (3.8) |
If the electron is “slow,” the rate constant is
| (3.9) |
where
| (3.10) |
and is the driving force of the proton transfer reaction without electron transfer. The equilibrium constant Kp can be interpreted as the population of the activated (protonated) state, from which electron transfer occurs with rate . The overall rate constant is given by Eq. (3.9).
In general, either the EP or PE channel can dominate, depending on the rate of the individual reactions. For example, when the electron is slow/proton fast
| (3.11) |
and in the opposite case of a slow proton/fast electron
| (3.12) |
When both the electron and the proton are fast
| (3.13) |
Consider the slow electron case, Eq. (3.11). Although it is expected that , for an uphill proton reaction, Kp ≪ 1, and hence the relative magnitude of the two terms will be determined by the energetics of the reaction (or how fast the proton is). If the first term dominates, one can say that an electron jumps first and "pulls out" a proton. If the second term dominates, a proton goes first and, by frequent but short visits of the acceptor site, it eventually pulls out an electron from its donor state. Similar interpretation can be given for the slow proton case described by Eq. (3.12). In the third case, Eq. (3.13), the dominant channel is defined by the relative rates of PT (first term) and ET (second term) uphill reactions. A more detailed classification of all possible cases is described in Ref.42.
The differences in the rate constants for ET to protonated and unprotonated acceptor, , and in the rate constants for PT to oxidized and reduced acceptor, , are related to the interaction energy between an electron and a proton in the final state. The positive driving force for the overall ETPT reaction is due to the favorable electrostatic interaction between an electron and a proton in the final state. Symbolically, this stabilizing energy will be described as
| (3.14) |
where R0 is the "effective distance" between an electron and a proton in the final state. The free energy of the ETPT reaction is then
| (3.15) |
The driving force for electron transfer with a protonated acceptor is
| (3.16) |
Similarly, the driving force for proton transfer with a reduced acceptor is
| (3.17) |
The variations in ΔGp (via pKa) and ΔGe can be used in experimental studies to probe the nature of the coupled reaction, as in Refs. 8,26,27. Note that the change in pKa value of the proton acceptor site, which alters the value of ΔGp, does not affect the driving force of electron transfer, unless the change in pKa is electrostatic in nature, in which case it directly affects the reduction potential of the electron acceptor site. (The independence of the electron transfer driving force with respect to the pKa value of the proton acceptor may also break down when both electron and proton acceptors are on the same molecule, as, e.g., in quinone. The magnitude of such variations, or even their sign, is difficult to predict without detailed ab initio calculations.)
3.2. pH and Isotope Effects
Above we assumed that a proton is available in the donor state. In fact, protonation of the donor site in a protein will depend on the pH of the medium. The coupled ET/PT reaction will take place only if the proton donor site is protonated. Hence all rate constants discussed above will be proportional to the protonation fraction:
| (3.18) |
where pKa refers to the proton donor site. For an effective electron/proton coupling, the pKa's of the protonation sites in the enzyme should depend on the redox state. In the rate constant expressions above we assumed that the pH in the system is such that the pKa's of the donor (don) and acceptor (acc) sites satisfy
| (3.19) |
In other words, initially (in the OU state, Fig. 2) a proton is available at the proton donor site and the proton acceptor site is empty. We do not consider here the exchange kinetics between the medium and the proton donor and acceptor sites, which may introduce additional complications into the kinetics of the coupled reaction. For a discussion of such cases see Ref. 71.
The pKa values of those protonation sites that depend on the redox state of the enzyme are said to be redox coupled. We assume, for example, that when an electron is placed on its acceptor site, the proton equilibrium is shifted toward its final state. In this case, the pKa value of the proton acceptor site in the reduced form is higher than that of the donor site:
| (3.20) |
After electron transfer, the pKa value of the proton donor site, , is different from that before electron transfer, . The relative magnitude of the former with respect to the pH of the medium determines whether an electron transfer reaction will induce an uptake of a proton from the medium or not. If , then one additional proton will be uptaken (i.e. after ET, both proton donor and proton acceptor sites are protonated). If , no extra protons will be taken from the medium upon electron transfer, and the proton transfer is intra-protein. In general, the pKa values of the protonation sites in a protein are not only redox dependent, but also depend on the protonation states of other sites due to their Coulomb interactions. Thus the kinetics of proton redistribution associated with a change in the redox state of the enzyme can be very complicated (see discussion of the pumping mechanisms in Section 6.3).
Generally, reactions involving protons have either large, or small but observable kinetic isotope effects.30,31,72–74 This is not always the case with PT/ET reactions. It should be noticed that in both the (EP) and (PE) channels, when the electron is slow and the proton is fast, the rate-limiting step is electron transfer. The reaction in this case does not have a significant KIE, as seen from Eqs. (3.5) and (3.9).
For the quinone reaction in PRC, for example, according to our classification, we have the case of a slow electron, in which a fast proton goes first and makes several transitions to the activated intermediate state, establishes quasi-equilibrium with this state, and gradually pulls out an electron. The rate constant is then . There should be no strong KIE, other than the relatively small equilibrium isotope effect, and the overall observed rate constant is orders of magnitude (by a factor of Kp) slower than that of pure electron transfer to a protonated acceptor, .
To measure , one can achieve the protonated state of the acceptor site by lowering the pH. However, one needs to remember that in a real protein at low pH several other sites may become protonated as well. The driving force for electron transfer in this case may not be the same as that assumed in . Alternatively, at fixed pH one can increase protonation of the acceptor site by increasing its pKa value. Again, one needs to make sure that the driving force for (i.e., reduction potential of the electron acceptor) will not be affected by the changes in pKa.
3.3. PT vs ET: Which is Faster?
Typically, electron transfer reactions in proteins are nonadiabatic. Therefore, for similar activation energies, the PT rate constant is expected to be much larger than the ET rate constant. In the simplest case, the rate constant of a proton transfer reaction would be given by
| (3.21) |
where Ea is the activation (free) energy and ν0 is a typical frequency of nuclear motions that result in attempts to overcome the activation barrier. This frequency is in the range 1012–1013 s−1. (Here PT is assumed to be adiabatic. For a discussion of nonadiabatic PT see Ref. 43 and Section 2.3.) For nonadiabatic electron transfer, the rate constant is roughly
| (3.22) |
where PLZ is the Landau-Zener (LZ) parameter for electron transfer, which for nonadiabatic reactions is less than unity. The LZ parameter for an ET reaction is
| (3.23) |
where λ is the reorganization energy, which is typically of the order 0.5eV, VDA is the electronic coupling, which is typically less than 1 cm−1 in proteins,10,11,75 and ε̇ is the rate of energy fluctuations. Hence, typically
| (3.24) |
On the basis of the above estimates, and assuming the same activation energies, one could conclude that the fast proton/slow electron case would be the most likely one. For example, such is the case for the quinone reduction reaction in PRC.8,26–28 However, proton transfer reactions in proteins are generally complex and are likely to include many intermediates. In this case, the free energy of activation for PT may be significantly higher than that of ET, and the opposite case of slow proton/fast electron will be realized. For example, in cytochrome oxidase, the ET reactions occur on the timescale of 10µs or faster (see Sec. 5.3), and PT is believed to be on the timescale of 100 µs or slower.76 In addition, the proton transfer is often electronically nonadiabatic, as discussed in Sec. 2.3.
3.4. Statistics of Transitions in a Single Molecule
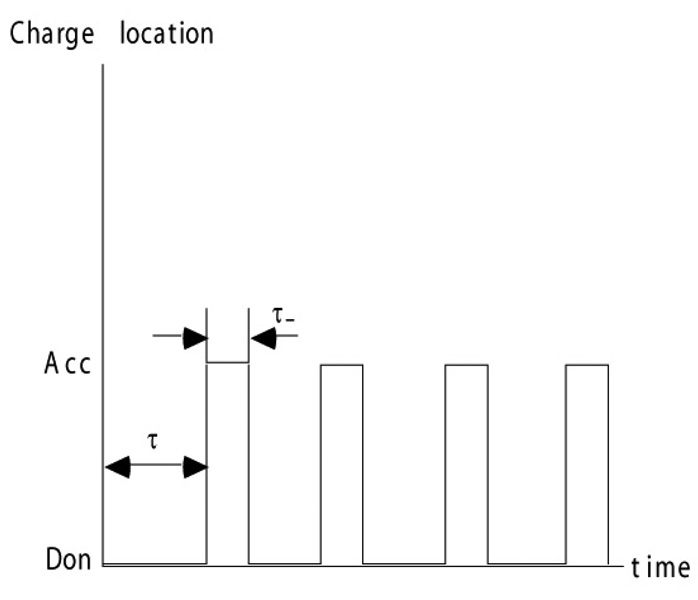
In a single protein molecule, the transition between the initial and the final state of each of the individual reactions is a random event (i.e., follows a Poisson process). For a typical two-state reaction, the system would jump between initial and final states at random, as shown in Fig. 6.
Fig. 6.
Random transitions of charge between donor and acceptor states in an ET or PT reaction of a single molecule assumed in the four-state model. Figure reprinted with permission from Ref. 42. Copyright 2003 World Scientific.
The average times that the system will spend in the initial and final states are related as
| (3.25) |
where ΔGx is the free energy of the electron or proton transfer reaction. For an uphill reaction the system stays some long time in the initial state, then at random makes a quick transition to the activated state, stays there a short period of time and goes back. Such random jumps repeat in time. The transition time itself between the initial and final states is considered here to be much smaller than both τx and τx−. In this case, the four state model described in Eq. 2.1 is applicable.
The probability (per unit time) that such a random transition will occur at time t is
| (3.26) |
The average lifetime, as seen from above, is τ = k−1.
In the EP channel, when an electron is in the activated state, and the proton is fast enough, the electrostatic attraction can pull out the proton from the donor. The proton transfer will occur as a random jump within time τp < τe−. Alternatively, when the proton is slow, several electron jump attempts are required to complete the reaction, i.e., time is required to find a coincidence that the proton will make its jump when the electron is already in the final state. The same picture is applicable to the PE channel.
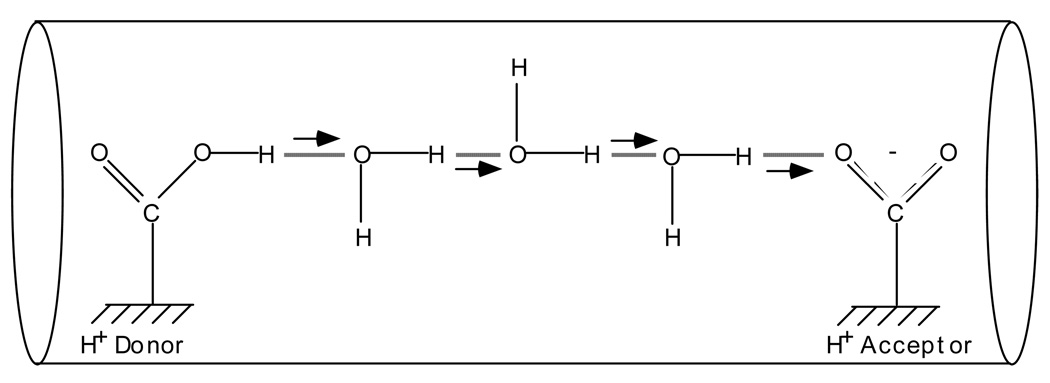
In proteins, both electrons and protons are typically transferred over long distances (tens of angstroms). The mechanisms of transfer, however, are completely different. Electrons are light and can tunnel over long distances in proteins. (In addition, hopping mechanisms of long-distance electron transport are also possible.) Protons are heavy and can tunnel only over short distances, less than one angstrom, and many steps are required for the net transport of a proton over a long distance. The carrier water molecules are also needed to pass protons along the chain via the Grotthuss mechanism, as depicted in Fig. 7. If water molecules are already assembled in a hydrogen bonded chain (proton wire), the transfer could be as fast as in liquid water, i.e., transfer between two water molecules in 1ps, or significantly slower, depending on the state of the proton conducting wire.77–83
Fig. 7.
Qualitative scheme of proton transfer via a chain of hydrogen bonds in a proton conducting channel. The proton transfer can occur either as a random walk of a localized charge along the chain, or as a single transition of a delocalized soliton-like object, in which several protons along the chain are transferred simultaneously. Figure reprinted with permission from Ref. 42. Copyright 2003 World Scientific.
While for an electron transfer the time of a single tunneling jump is in the sub-femtosecond range,43,84 and the picture of instantaneous transition between the two states is typically valid, for protons such an idealization may not always be correct. The protons are moving via many intermediate steps, and a more accurate picture should explicitly include a random walk along the proton conducting channel.71
3.5. ET Induced by PT
Here we consider one interesting possibility that occurs in the PE channel. Namely, when electrons are slow, , several proton transitions (order of ) to the activated state OP are required to pull out an electron from the donor state. As the proton moves along a proton-conducting channel, such as the one depicted in Fig. 7, the energy of the electron acceptor state continuously changes and at some point crosses that of the donor state. At this point the usual Landau-Zener electronic transition may occur. Thus, every time the proton moves back and forth along the channel the energy levels cross, and with some non-zero probability electron transfer induced by the proton may occur. (In a similar way motion of other charges of the protein medium may induce the usual electron transfer.) The question is whether this additional channel of coupled electron and proton transfer can be competitive with the sequential channel that we considered so far, for which the rate constant is .
In this case, the proton motion can be considered as part of the reorganization of the medium for electron transfer. The proton coordinate, however, is quite different from those of other fluctuating charges in the system. The latter are described as a set of harmonic oscillators in the usual model of electron transfer.85 This description is obviously not applicable to a proton moving along the proton conducting channel. The complete model for such a system will be discussed in Sec. 5; here we consider a simple case of nonadiabatic transitions.
As the two energy levels cross, the Landau-Zener probability of an electronic transition is given by Eq. (3.23). The velocity of the level crossing, ε̇, depends on the proton velocity at the moment when the LZ level crossing occurs. In this case, the overall rate constant of the reaction is given by the LZ probability times the number of instances, per second, that such a crossing will occur. Thus, the rate of PCET is
| (3.27) |
The factor of two accounts for the two level crossings as the proton moves up and down the channel during a single activation event. This rate is to be compared with
| (3.28) |
To estimate the ratio of the two rate constants,
| (3.29) |
we write the rate constant of the electron transfer reaction in the standard form:
| (3.30) |
where λ is the reorganization energy and . The rate constant of the proton back transfer reaction (from the oxidized acceptor) is written in the form:
| (3.31) |
where is the activation free energy for the reaction, and is a characteristic frequency with which the proton moves. (It is difficult to ascribe a precise value to the prefactor; roughly, τ0 is the characteristic time for a proton to transfer from one water molecule to another at the transition state, which is in the range of 10−12–10−13s.)
On the other hand, the velocity of the crossing of electronic levels is related to τ0 as follows:
| (3.32) |
where Δε is the shift of electronic energy levels as the proton jumps from one water molecule to another in the channel. The shift of energy has a purely electrostatic nature and can be estimated as
| (3.33) |
where R0 is the typical distance that characterizes the stabilizing electrostatic interaction between an electron and a proton, and ΔR is the distance that a proton travels in a single jump, i.e., on the order of one Angstrom. (Here we do not consider protein dielectric effects, assuming instead that they are accounted for in the effective distance.) Realistic numbers for the above order of magnitude estimate would be e2/R0 ~ 0.5 eV, ΔR/R0 ~ 0.1 and therefore Δε ~ 500 cm−1. This value should be compared with . Typically in proteins λ ~ 0.5 eV and therefore . We conclude that
| (3.34) |
i.e., the ratio depends on the relative magnitudes of the activation free energy barriers for the proton back reaction in the oxidized state (rate constant ) and for electron transfer in the protonated state (rate constant ). Both reactions are downhill, but here we are assuming that there are reaction barriers.
We conclude that the proton random motions along the proton conducting channel can induce electron transfer. When , this type of transition can be the primary mechanism for the coupled reaction. The opposite case of a usual sequential reaction occurs when .
3.6.Concerted vs. Sequential Proton Transport
Proton transport over long distances is a complicated process, which involves the dynamics of the water molecules, along which the protons move, and the protons themselves.77,78,81,86–93 Moreover, protein and membrane surfaces can significantly modify proton diffusion mechanisms in biological systems.94–97 In contrast to electrons, which in principle can tunnel in proteins in any direction over distances up to 20–30 Angstroms, proton transfer requires special "wiring" of donor and acceptor sites by chains of hydrogen bonds.98 This wiring occurs in proton conducting channels, which require special structural organization of the protein. A typical conducting channel consists of a chain of water molecules and possibly a few intermediate protonatable residues. The intermediate protonatable sites would be connected by a few (typically one to five) water molecules. Three to five water molecules can provide coupling over a distance of ten angstroms, as depicted in Fig. 7. If the state of hydrogen bonding in the channel were the same as in liquid water, protons would randomly jump between water molecules at a rate of one jump per picosecond, which could give diffusion coefficients as high as 10−4 cm2/s. In protein channels, the dynamics of water molecules is different from that in the liquid state, and the corresponding rates of proton transport can be much slower than in the bulk.
Depending on the strength of hydrogen bonds along the conducting wire, proton transport can either occur as a delocalized soliton, or as a localized (to a single hydrogen bond) charge.83 In the latter case, the transfer occurs as a random walk, or through diffusion of a localized charge (positive or negative) along the wire, a process which involves many activated steps. In the former case, the transition can be viewed as an activated single step process in which several protons shift coherently along the wire. Strictly speaking, the concerted PCET rate constant expressions presented in Section 2 are applicable only to the first type of proton transfer, although the general theoretical formulation is easily extended to the second type of proton transfer using additional diabatic states. The diffusion type process will be discussed in Sec. 5.
If the proton transport occurs via a delocalized soliton, then the wire should be formed first. The formation of the wire is itself an activated process.99 There is also a finite lifetime associated with the wire. (If the wire were a thermodynamically stable structure, there would be no reorientations of water molecules required for Grotthuss transfer. 77,86,88,89,92) Proton transfer along the channel is therefore a "gated" sequential reaction. The rate constant of proton transfer along a proton conducting channel can then be written as83
| (3.35) |
where is the rate constant for formation of the wire, τw is its life-time, and kPT is the rate constant of proton transfer along the assembled wire. The latter itself is a complex activated process. If the PT transition occurs via a delocalized soliton, then the transition itself is a fast process, on the order of one period of nuclear vibration (in which all protons along the wire shift in a concerted way), while most of the reaction time involves the system "waiting" until the necessary reorganization of the medium and the wire itself occurs. The classical (or adiabatic) rate constant of such a process is given by the generic expression
| (3.36) |
where τ0 ~ 10−12–10−13 s, and is the activation free energy for proton transfer.
On the other hand, if proton transport along the wire occurs as a random walk of a localized charge, then the above formula (3.35) for kp is not applicable when proton diffusion is too slow, and kPT < 1/τw. In this case, the proton will never reach the acceptor during the lifetime of a connected wire. Moreover, in the case of slow diffusion of a localized charge, the formation of a continuous wire along the whole channel is not necessary, thus the above formalism is not applicable. In this case, proton transport can be described simply as a random walk along the channel, with some effective diffusion coefficient, and an energy profile along the channel, specific for a given redox state of the enzyme.
On the basis of the structures of PRC, bc1 complex, and cytochrome oxidase, we cannot identify a unique organization of a proton conducting channel, and different scenarios of proton transport seem to be possible. It appears that the most likely type of long-distance proton transfer (or translocation), however, is a random walk along a chain of intermediate protonatable sites, with quick delocalized transitions between them. Each individual transition would be described by Eq. (3.35). The transitions between intermediate sites should be quick because it is energetically costly to have a charge on a water molecule (H3O+ or OH−) in a low dielectric protein medium.
4. Concerted vs. Sequential PCET
As discussed above, sequential and concerted PCET reactions, respectively, can be defined in terms of the presence or lack of a stable intermediate arising from single electron or proton transfer. From the experimental perspective, a stable intermediate would be defined in terms of a specified lifetime, but the ability to detect such an intermediate species may depend on the experimental apparatus. In the context of computing potential energy surfaces, a stable intermediate would be characterized by a minimum on the potential energy surface. In the context of Marcus theory and the four diabatic states defined in Eq. (2.1), a concerted mechanism corresponds to (OU) → (RP), along the diagonal of the scheme in Fig. 2, while sequential mechanisms correspond to (OU) →(OP) → (RP) or (OU) → (RU) → (RP), along the edges of the scheme in Fig. 2. In this framework, the mechanism is determined mainly by the relative energies of the four diabatic states and the couplings between them. A PCET reaction is typically concerted when the energies of the intermediates (OP) and (RU) are significantly higher than the energies of the PCET reactant and product (OU) and (RP).
While the detection of a stable intermediate provides proof of a sequential PCET mechanism, proving a concerted PCET mechanism is more challenging. The most convincing evidence can be obtained from the relative energetics of the charge transfer reactions. In some cases, the experimental measurement of redox potentials and pKa values indicates that the single electron and single proton transfer reactions are thermodynamically unfavorable, with reaction free energies greater than ~30 kcal/mol, whereas the combined electron-proton transfer is more thermodynamically favorable and even exoergic.34,63,70 The measurement of an unusually large KIE (i.e., greater than ~10) is consistent with a concerted PCET mechanism, but not all concerted PCET reactions exhibit such large KIEs. Thus, a moderate KIE does not distinguish between the sequential and concerted mechanisms.
In some situations, the distinction between concerted and sequential mechanisms is not well-defined. One particular example is the ultrafast dynamics in photoinduced PCET reactions. The experimental detection of intermediates on the femtosecond timescale is challenging. Typically such intermediates will not be thermally equilibrated since these photoinduced reactions are inherently nonequilibrium processes. From the perspective of propagating nonadiabatic molecular dynamics trajectories on the excited vibronic surfaces, many different pathways that encompass multiple mechanisms may be explored.100 Thus, the terminology of concerted and sequential mechanisms may not be applicable to these types of processes.
5. Kinetics of Electron Transfer Reactions Coupled to Proton Translocation
The four-state model discussed above does not consider intermediate proton states in a proton-conducting channel. This approximation can be justified based on the fact that the proton spends most of the time on either the donor or the acceptor site, and very little time in the channel itself. While for a tunneling electron the two-state representation is typically adequate, for a proton, the neglect of intermediate states is not always possible. Here we discuss a model that includes intermediate proton states in the channel explicitly.42
5.1. Coordinates and Energetics
Let X be a one-dimensional proton coordinate, representing the center of positive charge along the channel, that varies from 0 to L. Let R represent the rest of the nuclear coordinates of the protein medium relevant to electron transfer. (Note that this R is not to be confused with the proton donor-acceptor distance R in Sec. 2.) In the semiclassical description, the reaction coordinate for electron transfer is the difference between the free energies of the acceptor and donor electronic states, Δda, which depends on the coordinates of the medium. In our case,
| (5.1) |
The dynamics of both X and R results in variations in Δda. Whenever energy levels cross, Δda = 0, the system can undergo an electronic transition with some non-zero probability. To a good approximation, the coordinates X and R can be treated as independent; therefore our model is a two-dimensional generalization of the usual electron transfer theory. This two-dimensional model is reminiscent of that of Sumi and Marcus for solvent-controlled ET reactions.101,102 Various models for Ea(R,X) and Ed(R,X) can be developed.
Given Ea(R,X) and Ed(R,X), the free energies of the proton in the donor and acceptor electronic states are:
| (5.2) |
| (5.3) |
Here R represents a set of appropriately chosen dimensionless coordinates. (Note that the functional dependence of G(X) would not depend on units of R, except for an unimportant constant.) These free energies determine the equilibrium probability distributions of X in both electronic states,
| (5.4) |
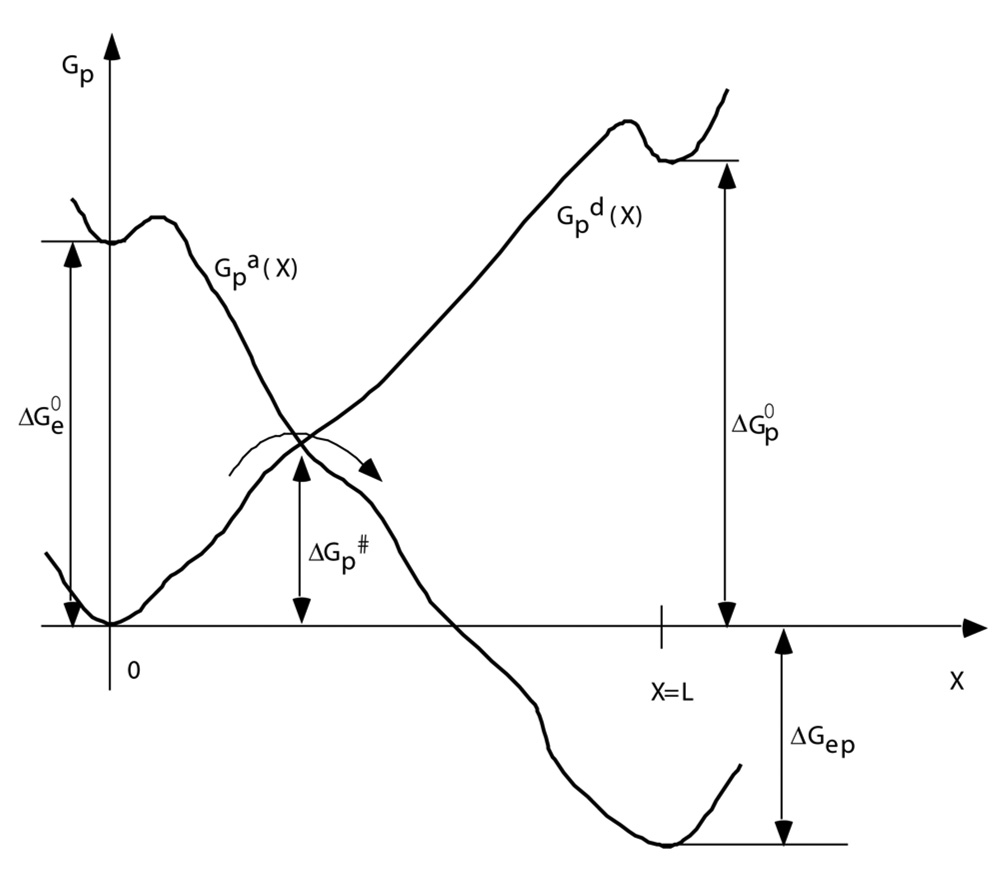
where is the partition function for the proton. Qualitatively, the proton free energy profiles along the channel in the two electronic states would typically resemble the schematic diagram in Fig. 8.
Fig. 8.
Qualitative free energy profiles along the proton conducting channel. The initial and final states of the proton (i.e., the centers of positive charge for these two states) are at X=0, and X=L, respectively. The two curves correspond to electron Oxidized (O) and Reduced (R) states, respectively. are the free energies of electron and proton (uphill) transfer, respectively, in the uncoupled reaction. For the slow proton diffusion case, the effective potential is the lower of the two curves for a given X. is the activation free energy for such a reaction. Figure reprinted with permission from Ref. 42. Copyright 2003 World Scientific.
5.2. Reaction Dynamics
In the course of thermal dynamics, the coordinates R and X and the corresponding energy difference Δda (R,X) undergo random variations. The randomness of R is due to its complex nature: R represents many nuclear coordinates, point charges, dipoles, and so forth, in the protein medium. The randomness of X is due to a diffusion-like, random walk motion of the protons. Whenever the variables X and R assume values such that Δda(R,X) = 0, the energy levels of the donor and acceptor electronic states cross, and a transition between these states can occur. The probability of the transition is given by the Landau-Zener formula.
For simplicity, we will assume that the energy mismatch between the two electonic states, Δda (R,X), is such that the contribution of the proton to the energy shift is additive:
| (5.5) |
Thus for a given position of the proton X, the R-coordinate’s fluctuations can cause the Landau-Zener transition, and hence induce electron transfer; the rate of such a reaction will depend on the position of the proton, X. Alternatively, for a given configuration of R, the proton motion in the channel can cause the electron transfer.
If one assumes that the electronic coupling TDA is sufficiently small (which is the case for long-distance ET), the reaction can be viewed as a usual electron transfer reaction whose driving force, , depends on the position of the proton in the proton conduction channel, X. The rate constant for such a reaction is:
| (5.6) |
Various simple models of can be developed,42 and the overall rate of such reactions will be determined by the distribution function of the proton position X in the proton conducting channel. This distribution should be considered as changing in a self-consistent manner together with the progress of the reaction, as in the Sumi-Marcus type models of electron transfer, see e.g. Refs.103,104. Below we consider a few simple limiting cases and show how the approach extends some known results for the rate constants.
5.3. Rate Constants in Limiting Cases
In the initial state of the system, the electron is on the donor (d), and the proton is in the lower end of the channel (X = 0). In this state the electron acceptor is Oxidized (O) and the proton acceptor site is Unprotonated (U), as illustrated by Figs. 1 and 2. In the final state, the electron is on the acceptor (a) and the proton is in the upper part of the channel (X = L). In this state, the electron acceptor is Reduced (R), and the proton acceptor site is Protonated (P). The population of the initial state is described by for X in the region close to X = 0, where the proton donor site is located; the population of the final state is described by with X in the region X = L, where the proton acceptor is located.
The kinetics of both is due to two contributions: diffusion along the channel and electronic transitions. These two contributions correspond to the two sequential processes PT and ET in the four-state model depicted in Fig. 2. Obviously, multiple transitions such as EP-PE-EP-… are now possible. We now consider the limiting cases that correspond to the cases in the four-state model.
5.3.1. Fast PT, Slow ET
Suppose in both electronic states, the proton transfer in the channel is very fast, so that the proton quasi-equilibrium distributions are quickly established and maintained during the reaction. Initially, . The rate constant is given by
| (5.7) |
There is a point along the proton coordinate X where the integrand in the above expression is maximum. This point gives the maximum contribution to the rate and can be considered a kind of transition state along the coordinate X (in the sense that one can consider the reaction occurring only at that position of the proton along X).
First, we will explicitly show that both sequential and concerted ET and PT are present in the above expression. For example, let the initial proton distribution in the channel be such that the corresponding distribution in energy mismatch between the two electronic states, Δp, see Eq. (5.5), is a generic Gaussian function written as
| (5.8) |
This form of distribution would be obtained if the proton dynamics in the channel were similar to those of other nuclear degrees of freedom. The proton in this case could be treated as one of the medium degrees of freedom R. In terms of P̃p, the rate constant is written as:
| (5.9) |
where we assume is evaluated at X=0, and the notation indicates that ke(X) is evaluated by replacing . Integration in the above formula results in a standard ET rate constant expression with λ = λe + λp and , c.f Sec. 3.1. Therefore, the proton motion in this case induces electron transfer in the same way as the other coordinates of the medium. The transfer of the electron occurs in a concerted manner with the motion of the proton.
Suppose now that the proton in the channel has two stable states: X = 0 (proton donor) and X = L (proton acceptor). The energies of these states are different by , as depicted in Fig. 8. In this case, the equilibrium distribution for the proton is approximately
| (5.10) |
where Kp is the proton equilibrium constant. Then Eq. (5.7) gives
| (5.11) |
The first term is the rate constant for ET to unprotonated acceptor, and the second term is proportional to the rate constant for ET to protonated acceptor. Depending on the energetics of the system, either the first or the second term can dominate. This is identical to what we had in Sec. 3 for the four-state model. The use of a distribution function is more realistic for the proton and can give more accurate results than those obtained within the four-state model.
5.3.2. Fast ET, Slow PT: Effective Proton Potential
We now consider the opposite case of fast ET and slow PT. In this case the rate-limiting process is proton diffusion along the channel. In the four-state model, the slow proton transfer can occur in two ways. The proton can jump uphill to its final state first, and while it stays there, the fast electron is quickly transferred downhill to its protonated acceptor. The overall rate for this process is . In the second mechanism, the electron makes several uphill jumps to its unprotonated acceptor, and via several attempts pulls out the proton. The overall rate here is . In the channel model, the transfer process is qualitatively similar, however, the details are different.
In the case of two electronic states, the free energy profiles along the channel are , as depicted in Fig. 8. Note that the free energy along X will be referred to as the proton potential since the change in entropy along X is negligible. In the course of the reaction, when the electron jumps back and forth between the donor and acceptor sites, the proton is moving in a time-dependent potential, which switches between . When electron transfer is fast, for every position of the proton in the channel, electronic equilibrium is quickly established. The average time that the electron remains on the donor, during which the proton potential is , is τd = 1/ke(X). The acceptor time, during which the potential is , is τa = τdKe(X), where Ke is the local equilibrium constant for electron transfer,
| (5.12) |
Since the donor and acceptor times are not equal, the effective proton potential is not simply the average of . The potential and dynamics in the channel can be described in terms of the effective potential Gp(X) for the proton in the channel:
| (5.13) |
Qualitatively,
| (5.14) |
as shown in Fig. 8.
The overall coupled reaction occurs as follows. If electron transfer is fast, or proton diffusion is slow, for every position of the proton in the channel electronic equilibrium is established. Initially, for small X, , the electron equilibrium is shifted toward the donor state, and the potential on which the diffusion occurs is . This diffusion is uphill. When the proton reaches the transition point, X†, at which roughly , the electron equilibrium shifts toward the acceptor state, and further diffusion for X > X† occurs on the potential. For X > X† the proton diffusion is downhill. Since the diffusion is much slower uphill than downhill, the overall proton diffusion time along the channel is equal to that of reaching the transition point X†. The latter is the rate-limiting step for the overall ET/PT reaction. The following calculation gives an estimate for the rate constant of such a reaction.
5.3.3. Fast ET, Slow PT: Reaction Rate Constant
The reaction occurs via one-dimensional diffusion over a barrier. In this case, the rate constant k is:
| (5.15) |
where D† is the proton diffusion coefficient at the transition state point X†, is the activation free energy, and L0 and L† are partition functions (defined as integrals of exp (−Gp(X)/kBT) over X and having units of length) of the proton donor site and the barrier site, respectively. The two lengths L0 and L† characterize the thermal widths at the donor site and at the barrier, respectively. The pre-exponential factor in the rate constant expression, therefore, is the inverse time for proton diffusion over a characteristic length .
The simplified picture considered above assumes classical diffusion of a proton along the proton-conducting channel. It is clear, however, that in a more detailed quantum description of proton diffusion, the form of the expression will remain the same. By dimensional analysis, each partition function - the characteristic lengths L0 and L† - will be reduced to a distance between the diffusion sites, which is roughly the distance a between water molecules in the channel. Since the diffusion constant D = a2/τp, with some characteristic time τp, the rate constant expression will have the expected form:
| (5.16) |
In the above expression, the pre-exponential factor should have a weak isotope dependence, characteristic of proton diffusion, and the activation barrier should depend on the driving force for electron transfer, , as depicted in Fig. 8. The proton conducting channels in proteins are very inhomogeneous, so D is expected to depend strongly on X. Then both the diffusion coefficient D(X) and the free energy profile Gp(X) will be important in defining the position of the transition point X† in the channel.42
The coupled PT/ET reaction occurs when the proton passes the critical point X†. To reach this point the proton first moves uphill in energy along the channel, while the electron remains mainly on the donor site. Once the critical point is passed, the electron is quickly transferred to its acceptor site, and the proton completes the reaction by moving downhill in energy to its acceptor site in the channel.
The described process resembles one in the four-state model, in which the proton jumps first onto the oxidized acceptor, and a quick downhill electron transfer follows. The overall rate constant for the reaction is . A similar expression is obtained above. However, in the channel model, the proton does not need to move all the way up to the acceptor site before the electron makes the transition.
As in the four-state model, the above rate constant for the PT/ET process should be compared to the rate constant for the ET/PT process. While the former rate constant corresponds to , the latter corresponds to in the four-state model. In the ET/PT process, proton transfer occurs in the reduced state. In the present model, will be given by
| (5.17) |
where is the activation free energy barrier for proton transfer along the channel in the electron acceptor state. Overall, it is a downhill reaction. Given that , the total activation free energy barrier for such a reaction is . This value should be compared with , the activation free energy barrier for proton transfer along the channel in the electron donor state, in order to determine which channel, PT/ET or ET/PT, is dominant in the coupled reaction.
5.3.4. Proton Induced Electron Transfer
Similarly, one can consider a reaction in which the proton motion along the channel induces electron transfer. The motion of the proton causes variations in the energy difference of the electron donor and acceptor states, Δda (X). There can be such a point Xc in the channel at which the electronic energy levels cross, where an electronic transition can occur. The condition for level crossing is Δda (R, X) = 0. So far, we assumed that the coordinate R was very fast, so that an equilibrium distribution in R was established for each X. We now assume the opposite, i.e., the coordinate R is slow, or, equivalently, that the change of Δda due to variations of R is small; in other words we assume that the main variation of Δda is due to the motion of the proton along the channel. We assume there is an Xc such that Δda (Xc) = 0.
The rate constant in this case is
| (5.18) |
where is the stationary distribution function of the proton along the proton conducting channel in the electron donor state. The unknown in the above equation can itself be expressed in terms of k in a self-consistent way. For simplicity, assume the diffusion coefficient D along the proton-conducting channel to be constant. Further analysis shows that the rate constant in this case can be written as 42
| (5.19) |
where is the proton partition function in the donor state.
The above equation gives the rate constant for both the slow and fast proton diffusion cases. For slow diffusion, we obtain a diffusion-controlled reaction, k ~ D, and for fast diffusion, the usual nonadiabatic reaction, k ~|TDA|2. In both cases, the activation free energy, depends on the free energy profile along the channel. The free energy curves here are not the usual Marcus parabolas, however; therefore the activation energy dependence on the driving force, for example, is different from the usual one. For linear dependence of free energies on X, we have (see Fig. 8)
| (5.20) |
| (5.21) |
Then the activation free energy of the coupled reaction is:
| (5.22) |
With the general formula Eq. (5.19), different cases of energy profiles along the channel can be investigated. Both the nonadiabatic and adiabatic diffusion controlled cases are included in one expression. These results are similar to those obtained by Zusman,105 Burshtein106 and other workers, e.g. 101,107–111, for solvent-controlled ET reactions.
6. Applications
6.1. HAT vs. PCET Mechanisms
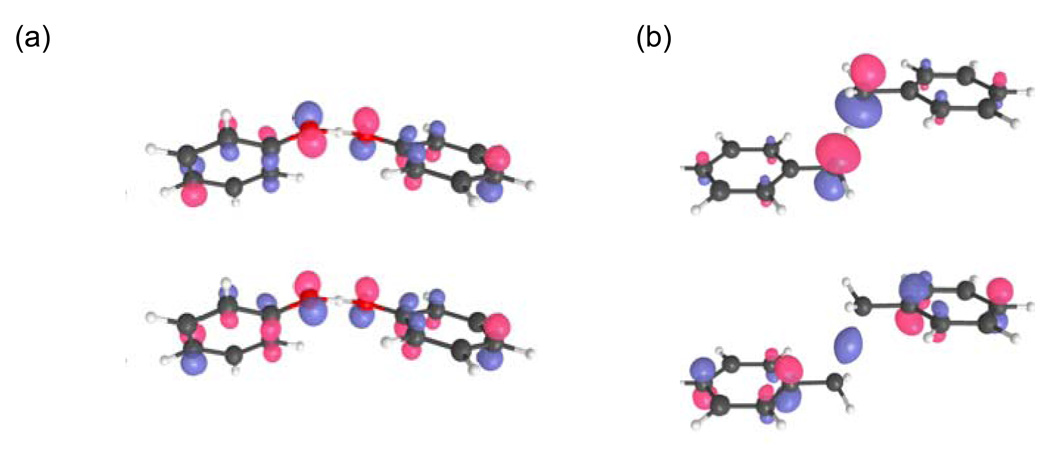
In general, HAT reactions can be viewed as a subset of the PCET reactions described in Section 2. Nevertheless, to aid in discussions of chemical reactions, it is often useful to distinguish between these two types of mechanisms. A textbook example of the fundamental differences between the HAT and PCET mechanisms is provided by the comparison between the phenoxyl/phenol and benzyl/toluene self-exchange reactions. These systems have been analyzed in terms of the singly occupied molecular orbitals (SOMOs) obtained from density functional theory calculations of the transition state structures (i.e., the first-order saddle points).32 As depicted in Fig. 9, the SOMO is dominated by 2p orbitals perpendicular to the proton donor-acceptor axis for the phenoxyl/phenol system, but the SOMO is dominated by atomic orbitals oriented along the proton donor-acceptor axis for the benzyl/toluene system. These results were interpreted to signify that the electron and proton are transferred between different sets of orbitals for the former system but between the same sets of orbitals for the latter system. This interpretation led to the identification of the phenoxyl/phenol reaction as PCET and the benzyl/toluene reaction as HAT.
Fig. 9.
The two highest-energy occupied molecular orbitals for (a) the phenoxyl/phenol and (b) the benzyl/toluene system for the transition state structures. Figure reprinted with permission from Ref. 69. Copyright 2006 American Chemical Society.
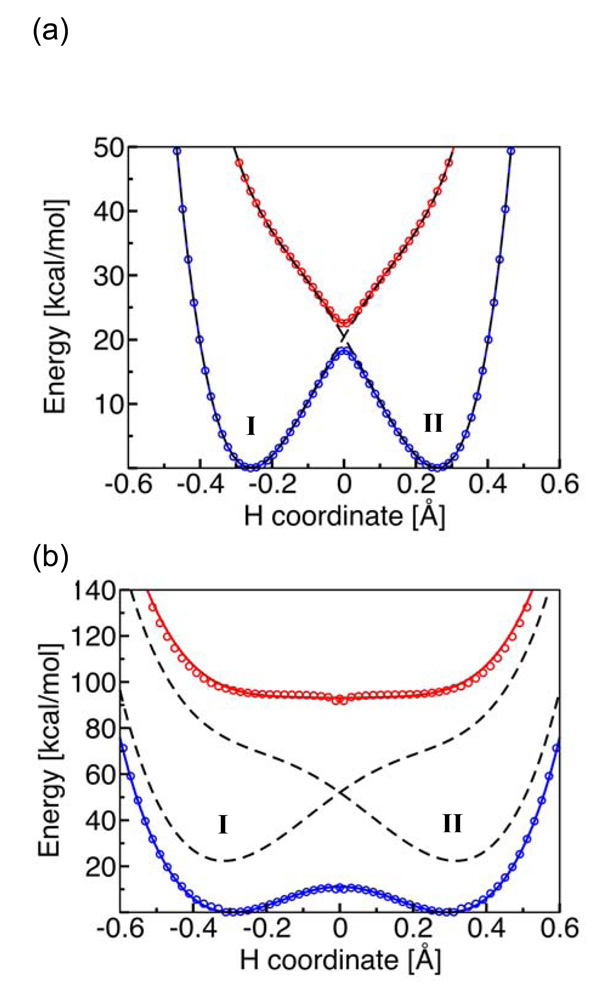
These systems have also been analyzed with the semiclassical formalism described in Section 2.3.69 The electronically diabatic potential energy curves corresponding to the reactant and product PCET states defined in Sec. 2.1 were obtained by fitting to the CASSCF (complete active space self-consistent-field) electronically adiabatic ground- and excited-state potential energy curves. Mixing the two diabatic states with the appropriate electronic coupling leads to the CASSCF electronically adiabatic curves, as depicted in Fig. 10. The parameters comprising the electronic transition time τe and the proton tunneling time τp defined in Section 2.3, as well as the proton adiabaticity parameter p = τp/τe (Eq. 2.12), were obtained from these diabatic potential energy curves. As discussed in Section 2.4, the degree of electronic nonadiabaticity for the proton transfer reaction provides a quantitative diagnostic for distinguishing between HAT and PCET. Specifically, the PCET mechanism corresponds to the electronically nonadiabatic limit (p ≪ 1), and the HAT mechanism corresponds to the electronically adiabatic limit (p ≫ 1).
Fig. 10.
State-averaged CASSCF ground and excited state electronically adiabatic potential energy curves along the transferring hydrogen coordinate for (a) the phenoxyl/phenol and (b) the benzyl/toluene system. The coordinates of all nuclei except the transferring hydrogen correspond to the transition state geometry. The CASSCF results are depicted as open circles that are blue for the ground state and red for the excited state. The black dashed lines represent the diabatic potential energy curves corresponding to the two localized diabatic states I and II. The mixing of these two diabatic states with the electronic coupling Vel leads to the CASSCF ground and excited state electronically adiabatic curves depicted with solid colored lines following the colored open circles. For the phenoxyl/phenol system, the solid colored lines and the black dashed lines are nearly indistinguishable because the adiabatic and diabatic potential energy curves are virtually identical except in the transition state region. Figure and caption reprinted with permission from Ref. 69. Copyright 2006 American Chemical Society.
These calculations revealed that the phenoxyl/phenol reaction involves electronically nonadiabatic proton transfer and corresponds to PCET, whereas the benzyl/toluene reaction involves electronically adiabatic proton transfer and corresponds to HAT.69 For the phenoxyl/phenol system, the adiabaticity parameter p = 0.013, which is in the electronically nonadiabatic limit with τe ≈ 80 τp. In this case, the electronic transition time is significantly greater than the proton tunneling time, so the electrons are not able to rearrange fast enough for the proton to remain on the electronically adiabatic ground state surface. For the benzyl/toluene system, the adiabaticity parameter p = 3.45, which is found to be in the electronically adiabatic limit with τe ≈ 0.29 τp. In this case, the electronic transition time is less than the proton tunneling time, so the electrons can respond instantaneously to the proton motion, allowing the proton to remain on the electronically adiabatic ground state surface. This characterization of the phenoxyl/phenol system as PCET and the benzyl/toluene system as HAT is consistent with the qualitative analysis based on the SOMOs.
Further analysis of the semiclassical calculations provides insight into the fundamental differences between these two systems. The electronic coupling Vel was estimated to be half the splitting between the two electronically adiabatic CASSCF potential energy curves at the midpoint between the proton donor and acceptor atoms. From Fig. 10, this electronic coupling was found to be 700 cm−1 for the phenoxyl/phenol system and 14,300 cm−1 for the benzyl/toluene system. Note also that the diabatic states exhibit greater slopes at the crossing point for the former system than for the latter system, resulting in a larger |ΔF| for the phenoxyl/phenol system. The smaller Vel and larger |ΔF| lead to a smaller value of the proton adiabaticity parameter (Eq. 2.12) for the phenoxyl/phenol system. As a result of these differences, the vibronic coupling has different forms for these two systems: it is the product of the electronic coupling and the overlap of the reactant and product proton vibrational wavefunctions for the phenoxyl/phenol system, but it is half the tunneling splitting on the electronically adiabatic ground state for the benzyl/toluene system.
We point out that the splittings between the ground and excited electronic states are significantly larger than the thermal energy kBT at room temperature for both systems. The significance of electron-proton nonadiabatic effects is not determined by comparing this splitting to the thermal energy, but rather by comparing the electronic transition time to the proton tunneling time. In contrast, the overall vibronic couplings for both systems were found to be smaller than the thermal energy, mainly due to contributions from the proton vibrational wavefunctions, indicating that both reactions are vibronically nonadiabatic with respect to a solvent or protein environment. Thus, the types of rate constant expressions given in Section 2 are applicable to these systems.
6.2. Concerted PCET in Solution and Enzymes
The parameters in the rate constant expressions given in Section 2 can be determined using various experimental and theoretical methods. The driving force can be estimated from experimentally measured redox potentials and pKa values.34,63,70 The solvent reorganization energy of a PCET reaction is often similar to that of the corresponding ET reaction because the solvent reorganization energy for PT is typically much smaller than that for ET (i.e., the proton transfers a much shorter distance than the electron). Thus, the solvent reorganization energy can be estimated from the experimental measurement of the solvent reorganization energy for the corresponding ET reaction. From the theoretical standpoint, the PCET solvent reorganization energy can be calculated with dielectric continuum models112–114 or molecular dynamics simulations,115 analogous to the methods used for ET. In principle, the equilibrium proton donor-acceptor distance could be obtained with experimental methods for structure determination, and the associated frequency could be determined spectroscopically, although the separation of this mode from other modes is challenging. In practice, the equilibrium proton donor-acceptor distance and frequency, as well as the proton potential energy curves, are usually obtained from electronic structure calculations. Alternatively, molecular dynamics simulations may be used to estimate this distance and frequency.115 The reactant and product proton vibrational wavefunctions and the associated overlaps can be calculated for the proton potential energy curves using Fourier grid methods.116,117 The electronic coupling can be calculated with the same electronic structure methods that are used for calculating this parameter in electron transfer theory.118–120 Note that the magnitude of the electronic coupling is usually similar for related PCET and ET reactions, but the PCET electron-proton vibronic coupling is substantially smaller due to inclusion of the overlap between the reactant and product proton vibrational wavefunctions. Currently methods for calculating the combined electron-proton vibronic coupling in terms of mixed nuclear-electronic wavefunctions are being developed.121–123
The formulation described in Section 2 has been used to predict the dependence of the PCET rate constants and KIEs on system properties, including temperature and driving force, as well as the equilibrium proton donor-acceptor distance and frequency.61 From the experimental standpoint, altering only a single parameter without influencing the other parameters is often not possible. For example, an increase in the equilibrium proton donor-acceptor distance is often associated with a decrease in the frequency. In addition, changing the driving force for proton transfer often impacts the equilibrium proton donor-acceptor distance.
The driving force dependence of the rate constant is particularly interesting in the context of the Marcus inverted region behavior, where the rate constant decreases as the driving force increases (i.e., as the reaction becomes more exoergic). Inverted region behavior has been observed experimentally for electron transfer reactions.124,125 Inverted region behavior is predicted to be experimentally inaccessible for PCET reactions because of the availability of excited electron-proton vibronic product states with greater vibronic coupling.61,126 As illustrated for model systems, however, apparent inverted region behavior could be observed if varying the driving force also impacts other properties of the system, such as the proton donor-acceptor distance.126
The theory described in Section 2 has been applied to a variety of experimentally studied PCET reactions in solution and enzymes.31,127,128 These applications include PCET in amidinium-carboxylate salt bridges,114,129,130 iron bi-imidazoline complexes,131,132 ruthenium-polypyridyl complexes,133–135 ruthenium-polypyridyl-tyrosine systems,33,136 rhenium-polypyridyl-tyrosine systems,137–139 thymine-acrylamide complexes,140,141 and ruthenium-polypyridyl-quinol systems.70,142 This theory has also been applied to PCET in the enzyme soybean lipoxygenase,63,115,143 as well as to a series of mutant forms of this enzyme.144,145 Furthermore, the extension of this theory to electrochemical systems41,52,65 has been applied to osmium complexes attached to a self-assembled monolayer on a gold electrode.146,147 Three of these systems are depicted in Fig. 11. All of these calculations have reproduced the experimentally observed trends in the rates and KIEs, as well as the temperature and pH dependences in some cases. In addition, these studies have elucidated the fundamental principles underlying PCET reactions, assisted in the interpretation of experimental data, and provided experimentally testable predictions.
Fig. 11.
PCET systems studied theoretically with the framework described in Section 2. Figures reprinted with permission from Refs. 70,137,146. Copyright 2009, 2007, and 2010 American Chemical Society.
6.3. Cytochrome c Oxidase
A marvelous illustration of many aspects of coupled electron and proton transfer reactions in biology is provided by Cytochrome c Oxidase. This enzyme is a redox-driven proton pump that utilizes the energy of oxygen reduction to pump protons across the membrane.148–151 The A-type oxidases have two proton-conducting input channels (D- and K-channels) to transfer protons required for oxygen reduction and for proton pumping, with the D-channel transporting all pumped protons. Electrons are transferred along a chain of metal cofactors: from cyt c to CuA, then to heme a, and finally to the Fea3-CuB binuclear catalytic center of the enzyme. The electron transport is coupled to proton translocation in such an intricate way that as electrons flow to the catalytic center of the enzyme to accomplish oxygen reduction (and produce water), the protons are pumped across the membrane against the electrochemical proton gradient.
6.3.1. Proton Pumping Mechanism
Since the discovery of the proton pumping by CcO in 1977 by Wikström,152 there were many proposals for the mechanism of the enzyme, see e.g. Refs. 153–157. Some computational studies158–161 point to a mechanism of pumping shown in Fig. 12. Recent experiments162 and their modeling163 support the mechanism in its general form; however, some details (i.e., the identity of the so-called Proton Loading Site, see below) remain experimentally untested and may in fact be different (see e.g. discussions in refs 162,163 164,165). Schematically, the proposed mechanism is as follows.
Fig. 12.
(A) The key structural elements of the proposed pumping mechanism of CcO and the sequence of transitions during one pumping cycle. Two protonation sites, the PLS and a site in the BNC, are shown as H-circles. PT and ET steps are shown by blue and red arrows, respectively. The residue notation is for bovine enzyme. (B) Schematic depiction of the model. The key assumption of the model is that upon ET between the hemes (step 2), the proton transfer to the Proton Loading Site (step 3) occurs before the proton transfer to the BNC (step 5). Figure reprinted with permission from Ref. 159. Copyright 2004 Elsevier.
During the cycle, the stable state of the catalytic center, before an additional electron is supplied to the system, is such that one of the metal centers is formally oxidized, e.g., Fe3+H2O, or Cu2+H2O. This state is established in a previous step of the cycle, when a “chemical” proton is accepted by one of the hydroxy ligands of the binuclear center. (Here and below for clarity we distinguish protons that participate in oxygen reduction, which we denote “chemical” protons, from the protons that are pumped through the membrane, which we denote “pumped” protons.) In this state, His291, the so-called proton loading site (PLS), is deprotonated, and Glu242 is protonated. The following steps are involved:
-
1) and 2)
An electron is supplied to the system via cyt c and CuA, which is transferred to heme a and then to the heme a3 – CuB binuclear center. One of the metal ions is reduced, and the overall charge of the binuclear center (BNC) becomes one charge unit more negative. The driving force of pure electron transfer is about 20 meV.158
-
3)
In response to the increased negative charge of the binuclear center, the proton from Glu242 now has a driving force to move closer to the binuclear center. There are two pathways leading from Glu242 to two possible sites:166 one is the BNC itself, and the other is His291 – the PLS. The assumption (gating) is made that the rate of proton transfer to His291 is much higher than that to the binuclear center. Therefore, the protonation of His291 occurs before that of the binuclear center. The fast proton transfer from Glu242 to His291 occurs by the Grotthuss mechanism via Arg438 and PRDa3. The driving force for this transfer is about 100 meV.158 With this transition, His291 becomes protonated.
-
4)
In this step Glu 242 is reprotonated.
-
5)
Now the second, chemical proton is transferred to the binuclear center, using the second path connecting Glu242 and the catalytic center of CcO. The driving force for this transition is about 250 meV.158 A significant driving force, despite the presence of the proton on a nearby His291, is due to formation of a water molecule in the BNC – this is the main source of energy in the process. This transition occurs after the first proton has moved to the His291 proton loading site.
-
6)
The previously formed state has two additional protons present in two closely located sites: the PLS (His291) and the BNC, but only one additional electron residing on one of the metal ions of the BNC. This state is meta-stable because of significant proton repulsion. The state is stabilized, therefore, by the expulsion of the proton from the His291 PLS site. The additional energy of stabilization gained is about 250 meV.158 The expulsion of the proton from His291 from a state in which one of the metal centers is formally oxidized is predicted by electrostatic calculations, which show that in this redox state, His291 has to be deprotonated.
-
7)
Glu 242 is reprotonated again, and one turnover of the cycle is complete. The formed state is stable until the next electron is passed through the system. This last step of reprotonation of Glu242 may be correlated with the expulsion from His291 and/or subsequent re-reduction of heme a in the next turnover in the cycle.
Each time a proton is pumped, in a single turnover of the pump, a stable state is formed until the next electron is injected into the system. Thus, for each electron passing through the chain, there is one pumped proton. For each oxygen molecule, four electrons are required to form two water molecules; therefore a maximum of four protons can be pumped.
The above model is based on the energetics of the system described originally in Ref. 158 (and subsequent studies 160,161), and a key kinetic assumption is that upon reduction of the BNC, the first (pumping) proton is transferred to the PLS of the pump, and later the second, chemical proton, arrives at the BNC. The first proton transfer is fast; however, it leads to a state (proton on the PLS) that is not most favorable energetically. The most energetically favorable state (proton on OH− in the BNC) is achieved by the second, slow proton transfer to the BNC. Since the PLS and BNC sites are closely located, due to electrostatic repulsion, the two protons cannot co-exist, and the first proton is expelled for the sake of achieving an energetically more stable state. Since both chemical and pumping protons are derived from the same source – protonated Glu242 (one or two chemical protons can possibly come via the K-channel 167,168), and due to the special arrangement of the two channels leading to the PLS and to the BNC, the transfer of the second chemical proton blocks the return (back transfer) of the first proton to Glu242.
The difference in rates of proton transfer along the “fast” pumping channel leading from Glu242 to His291 and the “slow” chemical channel leading from Glu242 to the BNC presumably is based on the structural arrangements of the key groups. The protonated Arg438 is located in the immediate vicinity of His291, so that when the proton is needed on His291, Arg438H+ quickly donates the proton to this residue. This proton transfer is achieved via a water molecule Wa3. Immediately after that, the chain of water molecules connecting the PRDa3 and Arg438 site with Glu242 provides a proton from Glu242 to reprotonate Arg438.159 The net result of these transitions is that a proton from Glu242 is quickly transferred to His291. The exact mechanism of gating, however, is still unknown. Recently, Wikström and co-workers proposed that that water dynamics in the catalytic cavity might in fact be responsible for proton gating.169
For proper function of the pump (i.e., to pump protons in the right direction, against the membrane electrochemical gradient), another key requirement should be fulfilled, namely, that the protonation of the PLS occurs by a proton from the negative side of the membrane with low chemical potential, and not from the opposite side with high chemical potential. Otherwise, the protons would flow in the wrong direction. Closely related to this requirement is the one that is usually assumed in the form of a mechanical gate that would prevent the leak of protons through the pump between the pumping events.169
The two-step pumping mechanism, in which the pumped proton is first loaded to the PLS from the N-side of the membrane and then expelled by the chemical proton arriving to the BNC on the P-side of the membrane, is part of many recently discussed models. The main difference between the models is the nature of the PLS site, whose identity is still not known; however, recent experimental and theoretical studies point to one of the residues in the group His291, propionate A or D of heme a3, or a group (including a water molecule) nearby.162,163,170,171
6.3.2. Coupled Electron and Proton Transfer Reactions
The individual steps of the mechanism illustrate various aspects of proton-coupled electron transfer discussed in this paper. We will now demonstrate how these analytical models can be utilized in the analysis of specific reactions in cytochrome c oxidase.
The step (1) of ET from CuA to CuB is rather fast, on the order of 10 µs, and does not show a KIE. Sometimes the absence of a KIE (and also pH dependence) is taken as an indication of the absence of the coupled proton, even internal to the enzyme. We have seen that this is not always the case; there are several examples of coupled reactions where a KIE is not present at all. In these cases, the actual rate constant for the coupled reaction is often a product of the pure electron transfer rate constant and the proton equilibrium constant Kp. Obviously when the proton transfer is uphill, the overall rate constant is a factor of Kp≪1 smaller than the pure electron transfer rate constant. In this specific case, however, the distance between redox cofactors is such that the 10 µs timescale is the maximum that one typically expects from ET in proteins. If indeed a proton were coupled, and (10 µs)−1 is the rate constant of the coupled reaction, that would mean that the rate of ET alone is much faster (by a factor 1/Kp), which is unlikely.
If there is no coupling, however, the role of heme a is not clear, except that in the next step the pure electron transfer is much faster (on the order of ns172). In fact, this may be the reason for heme a: the key electron transfer to the BNC should be fast, because only in this case does a coupled reaction have a chance to be in the physiological range of (order of magnitude) 0.1–1 ms.173 In addition, there is an interesting proposal for electrostatic regulation of water chains and proton gating in the region between heme a and heme a3 which would also explain the need for heme a.157
The most intriguing and most fundamental part of the mechanism of CcO is the second step shown in Fig. 12: the ET between heme a and heme a3. This electron transfer appears to be driving all proton translocations in the enzyme; this was clearly demonstrated in recent potentiometric experiments,162 where the injection of the electron into the system (10 µs phase) was observed to generate a sequence of much slower, and much higher in amplitude kinetic phases, which apparently refer to individual proton transfer reactions coupled to the injected electron.163 There are several interesting aspects of the coupling in this transition.
A) There is a proton loading reaction coupled to ET in step (2). The coupled proton is transferred from Glu242 along the chain of water molecules in the catalytic cavity; however, the dynamic character of the water chain connecting Glu242 and PropD is not entirely clear. Moreover, the exact number of water molecules in the catalytic cavity is not known, and most likely is even ill-defined, in the sense that water molecules constantly move in and out of the cavity; this process is likely to define the overall kinetics of the coupled reaction (2)+(3) (see discussion in Sec. 3.6.). There is a gating of the proton: upon step (2) ET, the proton from Glu242 does not go to the BNC, but instead makes a “mistake” and moves to the PLS.
The driving force of electron transfer (2) was estimated to be about 20 meV.158 This means that an electron is initially equilibrated between the two hemes, and the transfer is incomplete. However, this electron transfer is directly coupled with a proton transfer to the PLS located near the BNC. The proton transfer to the PLS significantly increases the redox potential of the BNC, thereby stabilizing the electron at the BNC, which in turn further increases the driving force for proton transfer to the PLS. Therefore, one can say that the electron and the proton drive each other at this step to the more stable (intermediate) state of the enzyme, where they occupy the BNC and the PLS, respectively. This type of reactions was discussed earlier in this review.
B) After the loading is complete, and Glu242 gets reprotonated, the second proton is transferred from Glu242, this time to the BNC. In this case the reaction is completely different, because the electron is already at the final state, but the electrostatic driving force for the chemical proton is diminished by the presence of the first proton at the PLS. Yet, obviously there is non-zero driving force, both as calculations showed,160,161 and as is evident from the kinetics of the potentiometry, which indicate that the second proton transfer (corresponding to the 800 µs kinetic phase in the experimental measurement of the membrane potential) 162 is well separated from the first loading phase (150 µs). In this case it can be considered as pure proton transfer; its rate is determined by both the driving force and the kinetics of water chain formation in the catalytic cavity connecting Glu242 and the BNC. It was predicted earlier 166 that there is a stable chain of water molecules; however, as mentioned earlier, the exact number of water molecules in the BNC cavity is not known.174
C) The expulsion of the proton from the PLS also appears to be a pure proton transfer reaction, which is governed by the proton-proton interactions, rather than electron-proton interactions. The proton transfer pathway between the PLS and the outside of the protein is not known with certainty, but theory and simulations provide some clues about this process.175,176
7. Conclusions
As is evident from this review, the main characteristic of proton-coupled electron transfer reactions is their great diversity. There is no one magic formula for the reaction rate constant as in the pure ET case. As has been shown, however, most cases involve a reaction bottleneck typically described by a rate constant that can be cast in the form of a product of a statistical (Arrhenius) exponential factor and a dynamic pre-factor, or as a sum of such terms. In addition, the quantum mechanical effects of the electrons and the transferring protons play an important role in these processes. As a result, PCET processes can exhibit large kinetic isotope effects and interesting dependence of the rate constants and kinetic isotope effects on temperature, pH, and driving force. Many cases of ET reactions coupled to proton translocation, where proton dynamics can be described as a random walk, bear close resemblance to common models of ET, where a distinction is made between “fast” vibrational modes and “slow” solvent or protein dynamics modes. Typically such reactions are described in terms of the Sumi-Marcus model101 or related models developed in the field.177,178,179,180 Although the physics and mechanics of these models are very similar, the actual realization is quite different.
The great variety of theoretical cases provides many possibilities in the way that electrons can be coupled to protons. The result of such coupling is that, in cases where electron or proton transfer is not possible separately (i.e., is energetically unfavorable), a coupled reaction of both electron and proton transfer is possible. The main reason for such reactions is the electrostatic stabilization; as a result, either electrons can be driven to species where they are needed, or protons can be delivered to a site where they are needed with the help of collateral proton/electron transfer. In most cases, the fundamental reason for this coupling is obvious: positive protons and negative electrons are attracted to each other, thereby electrons can “pull” protons, or vice versa, protons can pull the electrons to sites where they are needed. There are some non-trivial cases such as CCO, however, where negative electrons are somehow “pushing” positive protons against the external field gradient. Such cases underscore the wonderful richness of the field of electron and proton coupled transport.
The future prospects in the theoretical study of PCET are exciting and challenging. Based on the significance of designing solar cells, which often involve PCET at a fundamental level, the development of methods to study photoinduced PCET reactions is critical. These reactions are often inherently nonequilibrium processes, so the standard Marcus theory expressions may not be applicable. A promising approach for studying the ultrafast dynamics of such systems is the use of nonadiabatic molecular dynamics simulations on electron-proton vibronic surfaces.100 Another important direction is the further development of methods to study proton-coupled electron transport involving multiple electron and proton transfers.46,114 These extensions are vital for the investigation of the complex biological processes of respiration and photosynthesis, as well as the design of catalysts for various energy conversion processes.
Biological reactions involving electrons and protons are particularly challenging to describe theoretically. Despite a variety of models that are fundamentally possible, the real challenge is to achieve a quantitative level of description of specific biological systems, such as cytochrome oxidase. The principal difficulty of studying proton translocation driven by redox chemistry is that the proton motions in the protein are extremely difficult to monitor experimentally. In contrast to electrons, which can be detected using optical spectroscopy of redox centers, protons are not as easy to “see” in proteins. In this case, computer simulations become absolutely indispensable. Development of accurate methods for biological systems that reflect the richness of the field represents a major challenge for computational chemists.
Acknowledgements
This work was supported in part by NSF grant PHY 0646273 and NIH grant GM54052 (AAS) and NSF grant CHE-07-49646 and NIH grant GM56207 (SHS). We acknowledge helpful discussions with Marshall Newton, Jim Mayer, and Leif Hammarstrom.
Biographies

Sharon Hammes-Schiffer received her B.A. in 1988 from Princeton University and her Ph.D. in Chemistry at Stanford University in 1993. She was a postdoc at AT&T Bell Laboratories and was appointed the Clare Boothe Luce Assistant Professor of Chemistry and Biochemistry at the University of Notre Dame in 1995. She has been at Pennsylvania State University since 2000, when she was appointed the Shaffer Associate Professor of Chemistry and subsequently appointed the Eberly Professor of Biotechnology in 2006. She is a Senior Editor for The Journal of Physical Chemistry and The Journal of Physical Chemistry Letters. Dr. Hammes-Schiffer’s current research centers on the investigation of proton, electron, and proton-coupled electron transfer reactions in chemical, biological, and interfacial processes. Her work encompasses the development of analytical theories and computational methods, as well as applications to a wide range of experimentally relevant systems. She has been a recipient of the National Science Foundation CAREER Award (1996), Alfred P. Sloan Research Fellowship (1998), Camille Dreyfus Teacher-Scholar Award (1999), Iota Sigma Pi Agnes Fay Morgan Research Award (2005), International Academy of Quantum Molecular Science Medal (2005), and American Chemical Society Akron Section Award (2008).

Alexei Stuchebrukhov received a Ph.D. degree in theoretical physics from Moscow Physical and Technical Institute in 1985, in the theory group of Academician Vitaly L. Ginzburg, and was a research fellow in the Institute of Laser Spectroscopy and the Research Center for Laser Technology of Russian Academy of Sciences until 1990. During this time he worked in a Laboratory directed by V. S. Letokhov. In 1990 he joined the group of Rudy Marcus at California Institute of Technology, with whom he was a research fellow until 1994. Until this time his research interests were mainly in the area of vibrational dynamics and spectroscopy of polyatomic molecules. Since 1994 he has been at UC Davis, where he is currently a Professor of Chemistry and Biophysics. His current interests are in the general area of chemical kinetics, and biological electron and proton transfer reactions; his main current efforts are focused on understanding molecular aspects of electron transport chain of aerobic cells and biological energy transduction. He has been a recipient of Alfred P. Sloan Foundation Fellow (1996) and Arnold and Mabel Beckman Foundation Young Investigator Award (1997).
References
- 1.Nicholls DG, Ferguson S. Bioenergetics 2. San Diego: Academic Press; 1992. [Google Scholar]
- 2.Cramer WA, Knaff DB. Energy transduction in biological membranes. New York: Springer-Verlag; 1990. [Google Scholar]
- 3.Skulachev VP. Membrane bioenergetics. New York: Springer-Verlag; 1988. [Google Scholar]
- 4.Wikström M. Curr. Opin. Struct. Biol. 1998;8:480. doi: 10.1016/s0959-440x(98)80127-9. [DOI] [PubMed] [Google Scholar]
- 5.Michel H. Biochemistry. 1999;38:15129. doi: 10.1021/bi9910934. [DOI] [PubMed] [Google Scholar]
- 6.Berry EA, Guergova-Kuras M, Huang LS, Crofts AR. Annu. Rev. Biochem. 2000;69:1005. doi: 10.1146/annurev.biochem.69.1.1005. [DOI] [PubMed] [Google Scholar]
- 7.Crofts AR, Lheeb S, Croftsb SB, Chengb J, Rose S. Biochim Biophys Acta. 2006;1757:1019. doi: 10.1016/j.bbabio.2006.02.009. [DOI] [PubMed] [Google Scholar]
- 8.Okamura MY, Paddock ML, Graige MS, Feher G. Biochim. Biophys. Acta, Bioenerg. 2000;1458:148. doi: 10.1016/s0005-2728(00)00065-7. [DOI] [PubMed] [Google Scholar]
- 9.Saraste M. Science. 1999;283:1488. doi: 10.1126/science.283.5407.1488. [DOI] [PubMed] [Google Scholar]
- 10.Moser CC, Keske JM, Warncke K, Farid RS, Dutton PL. Nature. 1992;355:796. doi: 10.1038/355796a0. [DOI] [PubMed] [Google Scholar]
- 11.Gray HB, Winkler JR. Annu. Rev. Biochem. 1996;65:537. doi: 10.1146/annurev.bi.65.070196.002541. [DOI] [PubMed] [Google Scholar]
- 12.Page CC, Moser CC, Chen X, Dutton PL. Nature. 1999;402:47. doi: 10.1038/46972. [DOI] [PubMed] [Google Scholar]
- 13.Winkler JR. Curr. Opin. Chem. Biol. 2000;4:192. doi: 10.1016/s1367-5931(99)00074-5. [DOI] [PubMed] [Google Scholar]
- 14.Gray HB, Winkler JR. Proc Natl Acad Sci USA. 2005;102:3534. doi: 10.1073/pnas.0408029102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gray HB, Winkler JR. In: Biological Inorganic Chemistry, Structure and Reactivity. Bertini I, Gray HB, Stiefel EI, Valentine JS, editors. Sausalito: University Science Books; 2007. p. 261. [Google Scholar]
- 16.Wenger OS, Leigh BS, Villahermosa RM, Gray HB, Winkler JR. Science. 2005;307:99. doi: 10.1126/science.1103818. [DOI] [PubMed] [Google Scholar]
- 17.Moser CC, Page CC, Dutton PL. Phil Trans R Soc B. 2006;361:1295. doi: 10.1098/rstb.2006.1868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Beratan DN, Betts JN, Onuchic JN. Science. 1991;252:1285. doi: 10.1126/science.1656523. [DOI] [PubMed] [Google Scholar]
- 19.Skourtis SS, Beratan DN. Electron Transfer-from Isolated Molecules to Biomolecules, Pt 1. Vol. 106. New York: John Wiley & Sons, Inc.; 1999. [Google Scholar]
- 20.Regan JJ, Onuchic JN. In: Electron Transfer-from Isolated Molecules to Biomolecules, Pt 2. Prigogine I, Rice SA, editors. Vol. 107. New York: John Wiley & Sons, Inc.; 1999. [Google Scholar]
- 21.Newton MD. Int. J. Quantum Chem. 2000;77:255. [Google Scholar]
- 22.Stuchebrukhov AA. In: Advances in Chemical Physics, Vol 118. Prigogine I, Rice SA, editors. Vol. 118. Wiley, John & Sons; 2001. [Google Scholar]
- 23.Newton MD. Theor. Chem. Acc. 2003;110:307. [Google Scholar]
- 24.Stuchebrukhov AA. Theor. Chem. Acc. 2003;110:291. [Google Scholar]
- 25.Beratan DN, Balabin IA. Proc Natl Acad Sci USA. 2008;105:403. doi: 10.1073/pnas.0711343105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Graige MS, Paddock ML, Feher G, Okamura MY. Biochemistry. 1999;38:11465. doi: 10.1021/bi990708u. [DOI] [PubMed] [Google Scholar]
- 27.Paddock ML, Feher G, Okamura MY. Biochemistry. 1997;36:14238. doi: 10.1021/bi971192m. [DOI] [PubMed] [Google Scholar]
- 28.Graige MS, Paddock ML, Bruce JM, Feher G, Okamura MY. J. Am. Chem. Soc. 1996;118:9005. [Google Scholar]
- 29.Cukier RI, Nocera DG. Annu. Rev. Phys. Chem. 1998;49:337. doi: 10.1146/annurev.physchem.49.1.337. [DOI] [PubMed] [Google Scholar]
- 30.Hammes-Schiffer S. Acc. Chem. Res. 2001;34:273. doi: 10.1021/ar9901117. [DOI] [PubMed] [Google Scholar]
- 31.Hammes-Schiffer S, Soudackov AV. Journal of Physical Chemistry B. 2008;112:14108. doi: 10.1021/jp805876e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mayer JM, Hrovat DA, Thomas JL, Borden WT. Journal of the American Chemical Society. 2002;124:11142. doi: 10.1021/ja012732c. [DOI] [PubMed] [Google Scholar]
- 33.Sjodin M, Styring S, Akermark B, Sun L, Hammarstrom L. Journal of the American Chemical Society. 2000;122:3932. [Google Scholar]
- 34.Mayer JM. Annu. Rev. Phys. Chem. 2004;55:363. doi: 10.1146/annurev.physchem.55.091602.094446. [DOI] [PubMed] [Google Scholar]
- 35.Sjodin M, Ghanem R, Polivka T, Pan J, Styring S, Sun L, Sundstrom V, Hammarstrom L. Phys. Chem. Chem. Phys. 2004;6:4851. [Google Scholar]
- 36.Cukier RI. BBA-Bioenergetics. 2004;1655:37. doi: 10.1016/j.bbabio.2003.06.011. [DOI] [PubMed] [Google Scholar]
- 37.Li B, Zhao J, Onda K, Jordan KD, Yang J, Petek H. Science. 2006;311:1436. doi: 10.1126/science.1122190. [DOI] [PubMed] [Google Scholar]
- 38.Costentin C, Robert M, Saveant J-M. Journal of Electroanalytical Chemistry. 2006;588:197. [Google Scholar]
- 39.Rosenthal J, Nocera DG. Accounts of Chemical Research. 2007;40:543. doi: 10.1021/ar7000638. [DOI] [PubMed] [Google Scholar]
- 40.Huynh MH, Meyer TJ. Chemical Reviews. 2007;107:5004. doi: 10.1021/cr0500030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Costentin C. Chemical Reviews. 2009;108:2145. doi: 10.1021/cr068065t. [DOI] [PubMed] [Google Scholar]
- 42.Stuchebrukhov AA. J. Theor. Comp. Chem. 2003;2:91. [Google Scholar]
- 43.Georgievskii Y, Stuchebrukhov AA. J. Chem. Phys. 2000;113:10438. doi: 10.1063/1.1796751. [DOI] [PubMed] [Google Scholar]
- 44.Iordanova N, Hammes-Schiffer S. J. Am. Chem. Soc. 2002;124:4848. doi: 10.1021/ja017633d. [DOI] [PubMed] [Google Scholar]
- 45.Cukier RI. J. Phys. Chem. B. 2002;106:1746. [Google Scholar]
- 46.Costentin C, Robert M, Saveant J-M, Tard C. Angew. Chem. Int. Ed. 2010;49:1. doi: 10.1002/anie.200907192. [DOI] [PubMed] [Google Scholar]
- 47.Soudackov A, Hammes-Schiffer S. Journal of Chemical Physics. 1999;111:4672. [Google Scholar]
- 48.Hammes-Schiffer S. Accounts of Chemical Research. 2001;34:273. doi: 10.1021/ar9901117. [DOI] [PubMed] [Google Scholar]
- 49.Soudackov A, Hammes-Schiffer S. Journal of Chemical Physics. 2000;113:2385. [Google Scholar]
- 50.Soudackov A, Hatcher E, Hammes-Schiffer S. Journal of Chemical Physics. 2005;122:014505. doi: 10.1063/1.1814635. [DOI] [PubMed] [Google Scholar]
- 51.Hatcher E, Soudackov A, Hammes-Schiffer S. Chem. Phys. 2005;319:93. doi: 10.1063/1.1814635. [DOI] [PubMed] [Google Scholar]
- 52.Venkataraman C, Soudackov AV, Hammes-Schiffer S. Journal of Physical Chemistry C. 2008;112:12386. doi: 10.1021/jp805876e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Borgis D, Lee S, Hynes JT. Chem. Phys. Lett. 1989;162:19. [Google Scholar]
- 54.Borgis D, Hynes JT. J. Chem. Phys. 1991;94:3619. [Google Scholar]
- 55.Matyushov DV. Chem. Phys. 1992;164:31. [Google Scholar]
- 56.Daizadeh I, Medvedev ES, Stuchebrukhov AA. Proc. Natl. Acad. Sci. USA. 1997;94:3703. doi: 10.1073/pnas.94.8.3703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Medvedev ES, Stuchebrukhov AA. J. Chem. Phys. 1997;107:3821. [Google Scholar]
- 58.Kestner NR, Logan J, Jortner J. J. Phys. Chem. 1974;78:2148. [Google Scholar]
- 59.Bixon M, Jortner J. Adv. Chem. Phys. 1999;106:35. [Google Scholar]
- 60.Ulstrup J, Jortner J. J. Chem. Phys. 1975;63:4358. [Google Scholar]
- 61.Edwards SJ, Soudackov AV, Hammes-Schiffer S. J. Phys. Chem. A. 2009;113:2117. doi: 10.1021/jp809122y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hammes-Schiffer S, Hatcher E, Ishikita H, Skone JH, Soudackov AV. Coord. Chem. Rev. 2008;252:384. doi: 10.1016/j.ccr.2007.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hatcher E, Soudackov AV, Hammes-Schiffer S. Journal of the American Chemical Society. 2004;126:5763. doi: 10.1021/ja039606o. [DOI] [PubMed] [Google Scholar]
- 64.Navrotskaya I, Hammes-Schiffer S. Journal of Chemical Physics. 2009;131:024112. doi: 10.1063/1.3158828. [DOI] [PubMed] [Google Scholar]
- 65.Navrotskaya I, Soudackov AV, Hammes-Schiffer S. Journal of Chemical Physics. 2008;128:244712. doi: 10.1063/1.2940203. [DOI] [PubMed] [Google Scholar]
- 66.Venkataraman C, Soudackov AV, Hammes-Schiffer S. Journal of Chemical Physics. 2009;131:154502. doi: 10.1063/1.3249964. [DOI] [PubMed] [Google Scholar]
- 67.Venkataraman C, Soudackov AV, Hammes-Schiffer S. Journal of Physical Chemistry C. 2010;114:487. [Google Scholar]
- 68.Ohta Y, Soudackov A, Hammes-Schiffer S. J. Chem. Phys. 2006;125:144522. doi: 10.1063/1.2354500. [DOI] [PubMed] [Google Scholar]
- 69.Skone JH, Soudackov AV, Hammes-Schiffer S. Journal of the American Chemical Society. 2006;128:16655. doi: 10.1021/ja0656548. [DOI] [PubMed] [Google Scholar]
- 70.Ludlow MK, Soudackov AV, Hammes-Schiffer S. J. Am. Chem. Soc. 2009;131:7094. doi: 10.1021/ja9001184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Kotelnikov AI, Medvedev ES, Medvedev DM, Stuchebrukhov AA. J. Phys. Chem. B. 2001;105:5789. [Google Scholar]
- 72.Antoniou D, Schwartz SD. Proc. Natl. Acad. Sci. U. S. A. 1997;94:12360. doi: 10.1073/pnas.94.23.12360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Antoniou D, Schwartz SD. J. Phys. Chem. B. 2001;105:5553. [Google Scholar]
- 74.Kiefer PM, Hynes JT. Journal of Physical Chemistry A. 2004;108:11793. [Google Scholar]
- 75.Langen R, Chang IJ, Germanas JP, Richards JH, Winkler JR, Gray HB. Science. 1995;268:1733. doi: 10.1126/science.7792598. [DOI] [PubMed] [Google Scholar]
- 76.Karpefors M, Adelroth P, Namslauer A, Zhen YJ, Brzezinski P. Biochemistry. 2000;39:14664. doi: 10.1021/bi0013748. [DOI] [PubMed] [Google Scholar]
- 77.Cukierman S. Biochim. Biophys. Acta. 2006;1757:876. doi: 10.1016/j.bbabio.2005.12.001. [DOI] [PubMed] [Google Scholar]
- 78.Cukierman S. Front Biosci. 2003;8:1118. doi: 10.2741/1192. [DOI] [PubMed] [Google Scholar]
- 79.Vuilleumier R, Borgis D. J. Phys. Chem. 1998;102:4261. [Google Scholar]
- 80.Schmitt U, Voth GA. Isr. J. Chem. 1999;39:483. [Google Scholar]
- 81.Swanson JMJ, Maupin CM, Chen H, Petersen MK, Xu J, Wu Y, Voth GA. J. Phys. Chem. B. 2007;111:4300. doi: 10.1021/jp070104x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Kato M, Pisliakov AV, Warshel A. Proteins. 2006;64:829. doi: 10.1002/prot.21012. [DOI] [PubMed] [Google Scholar]
- 83.Stuchebrukhov AA. Phys. Rev. E. 2009;79:031927. doi: 10.1103/PhysRevE.79.031927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Stuchebrukhov AA. Laser Physics. 2009;19:1. doi: 10.1134/S1054660X09170186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Kuznetsov AM. Charge transfer in physics, chemistry, and biology. Amsterdam: Gordon and Breach Publishers; 1995. [Google Scholar]
- 86.Agmon M. Chem. Phys. Lett. 1995;244:456. [Google Scholar]
- 87.Agmon N. J. Chim. Phys. Phys.-Chim. Biol. 1996;93:1714. [Google Scholar]
- 88.Schmitt UW, Voth GA. Isr. J. Chem. 1999;39:483. [Google Scholar]
- 89.Pomes R. Isr. J. Chem. 1999;39:387. [Google Scholar]
- 90.Vuilleumier R, Borgis D. J. Phys. Chem. B. 1998;102:4261. [Google Scholar]
- 91.Decornez H, Hammes-Schiffer S. Isr. J. Chem. 1999;39:397. [Google Scholar]
- 92.Wraight CA. Biochim. Biophys. Acta. 2006;1757:886. doi: 10.1016/j.bbabio.2006.06.017. [DOI] [PubMed] [Google Scholar]
- 93.Warshel A. Annu. Rev. Biophys. Biomol. Struct. 2003;32:425. doi: 10.1146/annurev.biophys.32.110601.141807. [DOI] [PubMed] [Google Scholar]
- 94.Georgievskii Y, Medvedev ES, Stuchebrukhov AA. J. Chem. Phys. 2002;116:1692. [Google Scholar]
- 95.Georgievskii Y, Medvedev ES, Stuchebrukhov AA. Biophys. J. 2002;82:2833. doi: 10.1016/S0006-3495(02)75626-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Medvedev ES, Stuchebrukhov AA. J. Math. Biology. 2005;52:209. doi: 10.1007/s00285-005-0354-2. [DOI] [PubMed] [Google Scholar]
- 97.Agmon N. Chem. Phys. 2010;370:232. [Google Scholar]
- 98.Nagle JF, Morowitz HJ. Proc. Natl. Acad. Sci. USA. 1978;75:298. doi: 10.1073/pnas.75.1.298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Brewer ML, Schmitt UW, Voth GA. Biophys. J. 2001;80:1691. doi: 10.1016/S0006-3495(01)76140-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Hazra A, Soudackov AV, Hammes-Schiffer S. J. Phys. Chem. B. 2010 doi: 10.1021/jp1051547. (in press) [DOI] [PubMed] [Google Scholar]
- 101.Sumi H, Marcus RA. J. Chem. Phys. 1986;84:4894. [Google Scholar]
- 102.Nadler W, Marcus RA. J. Chem. Phys. 1987;86:3906. [Google Scholar]
- 103.Medvedev ES, Kotelnikov AI, Barinov AV, Psikha BL, Ortega JM, Popovic DM, Stuchebrukhov AA. J. Phys. Chem. B. 2008;112:3208. doi: 10.1021/jp709924w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Medvedev ES, Kotelnikov AI, Goryachev NS, Psikha BL, Ortega JM, Stuchebrukhov AA. Molecular Simulation (Electron Transfer Special Issue) 2006;32:735. [Google Scholar]
- 105.Zusman LD. Chem. Phys. 1980;49:295. [Google Scholar]
- 106.Yakobson BI, Burshtein AI. Chem. Phys. 1980;49:385. [Google Scholar]
- 107.Alexandrov IV. Chem. Phys. 1980;51:449. [Google Scholar]
- 108.Calef DF, Wolynes PG. J. Phys. Chem. 1983;87:3387. [Google Scholar]
- 109.Hynes JT. J. Phys. Chem. 1986;90:3701. [Google Scholar]
- 110.Maroncelli M, Macinnis J, Fleming GR. Science. 1989;243:1674. doi: 10.1126/science.243.4899.1674. [DOI] [PubMed] [Google Scholar]
- 111.Frantsuzov PA. J. Chem. Phys. 1999;111:2075. [Google Scholar]
- 112.Basilevsky MV, Rostov IV, Newton MD. Chem. Phys. 1998;232:189. [Google Scholar]
- 113.Newton MD, Basilevsky MV, Rostov IV. Chem. Phys. 1998;232:201. [Google Scholar]
- 114.Rostov I, Hammes-Schiffer S. Journal of Chemical Physics. 2001;115:285. [Google Scholar]
- 115.Hatcher E, Soudackov AV, Hammes-Schiffer S. J. Am. Chem. Soc. 2007;129:187. doi: 10.1021/ja0667211. [DOI] [PubMed] [Google Scholar]
- 116.Marston CC, Balint-Kurti GG. J. Chem. Phys. 1989;91:3571. [Google Scholar]
- 117.Webb SP, Hammes-Schiffer S. J. Chem. Phys. 2000;113:5214. [Google Scholar]
- 118.Cave RJ, Newton MD. Chem. Phys. Lett. 1996;249:15. [Google Scholar]
- 119.Cave RJ, Newton MD. J. Chem. Phys. 1997;106:9213. [Google Scholar]
- 120.van Voorhis T, Kowalczyk T, Kaduk B, Wang L-P, Cheng C-L, Wu Q. Annu. Rev. Phys. Chem. 2010;61:149. doi: 10.1146/annurev.physchem.012809.103324. [DOI] [PubMed] [Google Scholar]
- 121.Webb SP, Iordanov T, Hammes-Schiffer S. J. Chem. Phys. 2002;117:4106. [Google Scholar]
- 122.Chakraborty A, Pak MV, Hammes-Schiffer S. J. Chem. Phys. 2008;129:014101. doi: 10.1063/1.2943144. [DOI] [PubMed] [Google Scholar]
- 123.Chakraborty A, Pak MV, Hammes-Schiffer S. Phys. Rev. Lett. 2008;101:153001. doi: 10.1103/PhysRevLett.101.153001. [DOI] [PubMed] [Google Scholar]
- 124.Marcus RA, Sutin N. Biochim. Biophys. Acta. 1985;811:265. [Google Scholar]
- 125.Closs GL, Miller JR. Science. 1988;240:440. doi: 10.1126/science.240.4851.440. [DOI] [PubMed] [Google Scholar]
- 126.Edwards SJ, Soudackov AV, Hammes-Schiffer S. Journal of Physical Chemistry B. 2009;113:14545. doi: 10.1021/jp907808t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Hammes-Schiffer S, Iordanova N. Biochimica et Biophysica Acta-Bioenergetics. 2004;1655:29. doi: 10.1016/j.bbabio.2003.07.009. [DOI] [PubMed] [Google Scholar]
- 128.Hammes-Schiffer S. Acc. Chem. Res. 2009;42:1881. doi: 10.1021/ar9001284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Soudackov A, Hammes-Schiffer S. Journal of the American Chemical Society. 1999;121:10598. [Google Scholar]
- 130.Kirby JP, Roberts JA, Nocera DG. Journal of the American Chemical Society. 1997;119:9230. [Google Scholar]
- 131.Iordanova N, Decornez H, Hammes-Schiffer S. Journal of the American Chemical Society. 2001;123:3723. doi: 10.1021/ja0100524. [DOI] [PubMed] [Google Scholar]
- 132.Roth JP, Lovel S, Mayer JM. J. Am. Chem. Soc. 2000;122:5486. [Google Scholar]
- 133.Iordanova N, Hammes-Schiffer S. Journal of the American Chemical Society. 2002;124:4848. doi: 10.1021/ja017633d. [DOI] [PubMed] [Google Scholar]
- 134.Binstead RA, Meyer TJ. Journal of the American Chemical Society. 1987;109:3287. doi: 10.1021/ja000517a. [DOI] [PubMed] [Google Scholar]
- 135.Farrer BT, Thorp HH. Inorganic Chemistry. 1999;38:2497. doi: 10.1021/ic990833u. [DOI] [PubMed] [Google Scholar]
- 136.Carra C, Iordanova N, Hammes-Schiffer S. Journal of the American Chemical Society. 2003;125:10429. doi: 10.1021/ja035588z. [DOI] [PubMed] [Google Scholar]
- 137.Ishikita H, Soudackov AV, Hammes-Schiffer S. Journal of the American Chemical Society. 2007;129:11146. doi: 10.1021/ja072708k. [DOI] [PubMed] [Google Scholar]
- 138.Reece SY, Nocera DG. Journal of the American Chemical Society. 2005;127:9448. doi: 10.1021/ja0510360. [DOI] [PubMed] [Google Scholar]
- 139.Irebo T, Reece SY, Sjodin M, Nocera DG, Hammarstrom L. Journal of the American Chemical Society. 2007;129:15462. doi: 10.1021/ja073012u. [DOI] [PubMed] [Google Scholar]
- 140.Carra C, Iordanova N, Hammes-Schiffer S. Journal of Physical Chemistry B. 2002;106:8415. [Google Scholar]
- 141.Taylor J, Eliezer I, Sevilla MD. Journal of Physical Chemistry B. 2001;105:1614. [Google Scholar]
- 142.Cape JL, Bowman MK, Kramer DM. Journal of the American Chemical Society. 2005;127:4208. doi: 10.1021/ja043955g. [DOI] [PubMed] [Google Scholar]
- 143.Knapp MJ, Rickert KW, Klinman JP. Journal of the American Chemical Society. 2002;124:3865. doi: 10.1021/ja012205t. [DOI] [PubMed] [Google Scholar]
- 144.Meyer MP, Tomchick DR, Klinman JP. Proceedings of the National Academy of Sciences (USA) 2008;105:1146. doi: 10.1073/pnas.0710643105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Edwards SJ, Soudackov AV, Hammes-Schiffer S. Journal of Physical Chemistry B. 2010;114:6653. doi: 10.1021/jp100133p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Ludlow M, Soudackov AV, Hammes-Schiffer S. Journal of the American Chemical Society. 2010;132:1234. doi: 10.1021/ja910277p. [DOI] [PubMed] [Google Scholar]
- 147.Madhiri N, Finklea HO. Langmuir. 2006;22:10643. doi: 10.1021/la061103j. [DOI] [PubMed] [Google Scholar]
- 148.Gennis RB. Front. Biosci. 2004;9:581. doi: 10.2741/1237. [DOI] [PubMed] [Google Scholar]
- 149.Wikström M. Curr Opin Struct Biol. 1998;8:480. doi: 10.1016/s0959-440x(98)80127-9. [DOI] [PubMed] [Google Scholar]
- 150.Belevich I, Verkhovsky MI. Antioxidants & Redox Signaling. 2008;10:1. doi: 10.1089/ars.2007.1705. [DOI] [PubMed] [Google Scholar]
- 151.Brzezinski P, Gennis RB. Journal of Bioenergetics and Biomembranes. 2008;40:521. doi: 10.1007/s10863-008-9181-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Wikström M. Nature. 1977:266. doi: 10.1038/266271a0. [DOI] [PubMed] [Google Scholar]
- 153.Gennis RB. Proc. Natl. Acad. Sci. USA. 1998;95:12747. doi: 10.1073/pnas.95.22.12747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Brzezinski P, Ädelroth P. Curr. Opin. Struct. Biol. 2006;16:465. doi: 10.1016/j.sbi.2006.06.012. [DOI] [PubMed] [Google Scholar]
- 155.Michel H. Proc. Natl. Acad. Sci. U. S. A. 1998;95:12819. doi: 10.1073/pnas.95.22.12819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Michel H. Biochim Biophys Acta. 2004;1658:264. [Google Scholar]
- 157.Wikström M, Verkhovsky MI, Hummer G. Biochim. Biophys. Acta. 2003;1604:61. doi: 10.1016/s0005-2728(03)00041-0. [DOI] [PubMed] [Google Scholar]
- 158.Popovic DM, Stuchebrukhov AA. J. Am. Chem. Soc. 2004;126:1858. doi: 10.1021/ja038267w. [DOI] [PubMed] [Google Scholar]
- 159.Popovic DM, Stuchebrukhov AA. FEBS Lett. 2004;566:126. doi: 10.1016/j.febslet.2004.04.016. [DOI] [PubMed] [Google Scholar]
- 160.Quenneville J, Popovic DM, Stuchebrukhov AA. In: Computational Inorganic and Bioinorganic Chemistry. Solomon EI, King RB, Scott RA, editors. Wiley; 2009. [Google Scholar]
- 161.Quenneville J, Popovic DM, Stuchebrukhov AA. Biochim. Biophys. Acta. 2006;1757:1035. doi: 10.1016/j.bbabio.2005.12.003. [DOI] [PubMed] [Google Scholar]
- 162.Belevich I, Bloch DA, Belevich N, Wikström M, Verkhovsky MI. Proc. Natl. Acad. Sci. U. S. A. 2007;104:2685. doi: 10.1073/pnas.0608794104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Sugitani R, Medvedev ES, Stuchebrukhov AA. Biochimica Et Biophysica Acta-Bioenergetics. 2008;1777:1129. doi: 10.1016/j.bbabio.2008.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Pisliakov AV, Sharma PK, Chu ZT, Haranczyk M, Warshel A. Proc. Natl. Acad. Sci. U.S.A. 2008;105:7726. doi: 10.1073/pnas.0800580105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Olsson MHM, Warshel A. Proc. Natl. Acad. Sci. U.S.A. 2006;103:6500. doi: 10.1073/pnas.0510860103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Zheng XH, Medvedev DM, Swanson J, Stuchebrukhov AA. Biochim. Biophys. Acta. 2003;1557:99. doi: 10.1016/s0005-2728(03)00002-1. [DOI] [PubMed] [Google Scholar]
- 167.Wikström M, Jasaitis A, Backgren C, Puustinen A, Verkhovsky MI. Biochim. Biophys. Acta. 2000;1459:514. doi: 10.1016/s0005-2728(00)00191-2. [DOI] [PubMed] [Google Scholar]
- 168.Zaslavsky D, Gennis RB. Biochim. Biophys. Acta. 2000;1458:164. doi: 10.1016/s0005-2728(00)00066-9. [DOI] [PubMed] [Google Scholar]
- 169.Kaila VRI, Verkhovsky MI, Hummer G, Wikstrom M. Proc. Natl. Acad. Sci. USA. 2008;105:6255. doi: 10.1073/pnas.0800770105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Sharpe MA, Ferguson-Miller S. Journal of Bioenergetics and Biomembranes. 2008;40:541. doi: 10.1007/s10863-008-9182-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Pisliakov AV, Sharma PK, Chu ZT, Haranczyk M, Warshel A. Proc. Natl. Acad. Sci. U.S.A. 2008;105:7726. doi: 10.1073/pnas.0800580105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Pilet E, Jasaitis A, Liebl U, Vos MH. Proc. Natl. Acad. Sci. USA. 2004;101:16198. doi: 10.1073/pnas.0405032101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Page CC, Moser CC, Chen X, Dutton PL. Nature. 1999;402:47. doi: 10.1038/46972. [DOI] [PubMed] [Google Scholar]
- 174.Tashiro M, Stuchebrukhov AA. J. Phys. Chem. B. 2005;109:1015. doi: 10.1021/jp0462456. [DOI] [PubMed] [Google Scholar]
- 175.Popovic DM, Stuchebrukhov AA. J. Phys. Chem. B. 2005;109:1999. doi: 10.1021/jp0464371. [DOI] [PubMed] [Google Scholar]
- 176.Sugitani R, Stuchebrukhov AA. Biochim. Biophys. Acta. 2009;1787:1140. doi: 10.1016/j.bbabio.2009.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Tembe BL, Friedman HL, Newton MD. J Chem Phys. 1982;76:1490. [Google Scholar]
- 178.Agmon N, Hopfield JJ. J Chem Phys. 1983;79:2042. [Google Scholar]
- 179.Agmon N, Hopfield JJ. J Chem Phys. 1983;78:6947. [Google Scholar]
- 180.Newton MD, Friedman HL. J Chem Phys. 1988;88:4460. [Google Scholar]