Postsynaptic Signal Transduction Models for Long-Term Potentiation and Depression

Abstract

More than a hundred biochemical species, activated by neurotransmitters binding to transmembrane receptors, are important in long-term potentiation (LTP) and long-term depression (LTD). To investigate which species and interactions are critical for synaptic plasticity, many computational postsynaptic signal transduction models have been developed. The models range from simple models with a single reversible reaction to detailed models with several hundred kinetic reactions. In this study, more than a hundred models are reviewed, and their features are compared and contrasted so that similarities and differences are more readily apparent. The models are classified according to the type of synaptic plasticity that is modeled (LTP or LTD) and whether they include diffusion or electrophysiological phenomena. Other characteristics that discriminate the models include the phase of synaptic plasticity modeled (induction, expression, or maintenance) and the simulation method used (deterministic or stochastic). We find that models are becoming increasingly sophisticated, by including stochastic properties, integrating with electrophysiological properties of entire neurons, or incorporating diffusion of signaling molecules. Simpler models continue to be developed because they are computationally efficient and allow theoretical analysis. The more complex models permit investigation of mechanisms underlying specific properties and experimental verification of model predictions. Nonetheless, it is difficult to fully comprehend the evolution of these models because (1) several models are not described in detail in the publications, (2) only a few models are provided in existing model databases, and (3) comparison to previous models is lacking. We conclude that the value of these models for understanding molecular mechanisms of synaptic plasticity is increasing and will be enhanced further with more complete descriptions and sharing of the published models.

1. Introduction

Synaptic plasticity is an activity-dependent change in the strength or efficacy of the synaptic connection between a pre- and postsynaptic neuron. It is induced with brief periods of synaptic activity, for example, using tetanic, high-frequency neuronal activity. Changes in synapses, in general, can last from milliseconds into years. These long-lasting changes, which require protein synthesis and gene transcription, are suggested to lead to learning and formation of memories.

The long-term activity-dependent strengthening and weakening of synapses are known as long-term potentiation (LTP; Bliss and Gardner-Medwin, 1973; Bliss and Lømo, 1973) and long-term depression (LTD; Ito et al., 1982; Ito, 1989; Dudek and Bear, 1992), respectively. Frequency-dependent LTP and LTD in the cornu ammonis 1 (CA1) region of the hippocampus, triggered by activation of N-methyl-d-aspartate (NMDA) receptors (NMDARs), are the most studied forms of long-term plasticity (see, e.g., Malenka and Bear, 2004; Citri and Malenka, 2008). In addition to hippocampal NMDAR-dependent LTP and LTD, diverse forms of LTP and LTD have been discovered in different brain regions. One example of non-NMDAR-dependent plasticity is cerebellar LTD. Some forms of LTP require neither the NMDA nor the non-NMDA ionotropic glutamate receptors (non-NMDARs include kainate receptors and α-amino-3-hydroxy-5-methylisoxazole-4-propionic acid receptors, AMPARs), but do require activation of metabotropic glutamate receptors (mGluRs). This form is found, for example, in the CA1 region of the hippocampus (Lanté et al., 2006). Despite the variation in NMDAR dependence, all forms of synaptic plasticity are calcium ion (Ca²⁺)-dependent; only the mechanisms for Ca²⁺ elevation vary.

Two broad types of computational models, phenomenological and biophysical models, have been developed to understand the pre- and postsynaptic events in LTP and LTD. Phenomenological models use abstract equations to describe a relationship between neuronal activity and synaptic plasticity. Biophysical models include electrophysiological models, biochemical models, and models that include both electrophysiological properties and biochemical reactions (signaling pathways) underlying the relationship between neuronal activity and synaptic plasticity, though even these include simplifications because all the mechanisms cannot be modeled in detail. The focus of the present study is on biophysical models which concentrate on postsynaptic biochemical reactions.

This review presents an overview of 117 postsynaptic signal transduction models, categorizes them so that similarities and differences are more readily apparent, and explains how these models can be used to identify key molecules and address questions related to mechanisms underlying LTP and LTD. Section 2 presents the biological background of synaptic plasticity, Section 3 classifies the computational postsynaptic signal transduction models, and Section 4 summarizes the directions and trends of this field.

2. Synaptic Plasticity

Many different classification schemes for synaptic plasticity exist. Synaptic potentiation can be classified into three main types: short-term potentiation (STP), which lasts as long as 30–45 min; early phase LTP (E-LTP), which lasts for 1–2 h; and late phase LTP (L-LTP), which persists for considerably more than 2 h (Sweatt, 1999; Soderling and Derkach, 2000; Citri and Malenka, 2008). Synaptic depression, on the other hand, is typically classified into two types: short-term depression (STD) and LTD (Ito, 2001); though there appears to be an early and late phase LTD (E-LTD, L-LTD) also (Kauderer and Kandel, 2000). In addition, all types of plasticity involve three processes: induction, in which the mechanisms leading to plasticity are engaged; expression, which involves mechanisms allowing the plasticity to be exhibited and measured; and maintenance, which involves processes occurring after the induction phase is complete and allowing the plasticity to persist for long periods of time (Sweatt, 1999).

2.1. Mechanisms to trigger synaptic plasticity

Many different plasticity induction protocols have been developed. In general, potentiation is induced by a high-frequency stimulation and depression by a low-frequency stimulation of a chemical synapse, but there are variations in the experimental procedures depending on the cell type. Short-term plasticity is triggered typically by short trains of stimulation (Citri and Malenka, 2008). LTP is typically triggered with longer 1 s trains of high-frequency (100 Hz) stimulation (Citri and Malenka, 2008). One train triggers only E-LTP, whereas repetitive trains trigger L-LTP (Citri and Malenka, 2008). L-LTD is typically triggered with prolonged repetitive low-frequency (1 Hz) stimulation (Citri and Malenka, 2008). Theta stimulation consists of short bursts of trains repeated with 200 ms intervals and produces L-LTP, even though the number of pulses is more similar to that producing E-LTP. Spike-timing-dependent plasticity (STDP) is another protocol to trigger LTP as well as LTD. In STDP, pre- and postsynaptic neurons are stimulated independently and the timing between pre- and postsynaptic spikes determines whether potentiation or depression occurs (Markram et al., 1997; Bi and Poo, 1998; Bi and Rubin, 2005; Dan and Poo, 2006).

2.2. Molecular mechanisms of synaptic plasticity

There are various mechanisms, both pre- and postsynaptic, that lead to changes in synaptic strength, for example changes in neurotransmitter release, conductance of receptors, numbers of receptors, numbers of active synapses, and structure of synapses (Hayer and Bhalla, 2005). Several reviews about the molecular mechanisms underlying synaptic plasticity have been published (see, e.g., Bliss and Collingridge, 1993; Malenka and Nicoll, 1999; Sweatt, 1999; Soderling and Derkach, 2000; Ito, 2002; Lisman et al., 2002; Malenka and Bear, 2004; Blitzer et al., 2005; Cooke and Bliss, 2006; Wang et al., 2006; Bruel-Jungerman et al., 2007; Citri and Malenka, 2008; Santos et al., 2009). Cytosolic Ca²⁺ is inarguably the most critical factor: chemical buffering of Ca²⁺ or pharmacological blocking of Ca²⁺ influx prevents both potentiation and depression. There are several sources of Ca²⁺, depending on the brain region and the cell type. Influx through NMDARs is the most common source for LTP; influx through Ca²⁺-permeable AMPARs, voltage-gated Ca²⁺ channels, or release from intracellular stores (triggered by mGluRs which are G protein-coupled receptors) are important in many cell types. Ca²⁺ can activate, both directly and indirectly, protein kinases and phosphatases leading to phosphorylation–dephosphorylation cycles and, ultimately, to LTP and LTD. The next paragraphs focus on the molecular mechanisms behind NMDAR-dependent LTP and LTD, as well as cerebellar LTD, because these forms of plasticity have been studied the most both experimentally and computationally.

NMDAR-dependent potentiation is triggered by release of the neurotransmitter glutamate from the presynaptic neuron and subsequent binding to NMDARs on the postsynaptic neuron (Bliss and Collingridge, 1993; Malenka and Nicoll, 1999; Sweatt, 1999; Malenka and Bear, 2004; Citri and Malenka, 2008). After NMDARs are activated, Ca²⁺ can flow into the cell if the postsynaptic membrane is sufficiently depolarized to relieve the magnesium ion block from NMDAR. NMDAR-dependent LTP requires a large increase in postsynaptic Ca²⁺ concentration which triggers several events inside the cell. One of the most important events is Ca²⁺ binding to calmodulin, which then activates Ca²⁺/calmodulin-dependent protein kinase II (CaMKII), leading to phosphorylation of AMPARs, increase in single-channel conductance of AMPARs, and incorporation of additional AMPARs into the postsynaptic density (Citri and Malenka, 2008). Ca²⁺ also binds to protein kinase C (PKC) which is involved in E-LTP in some cell types (Malinow et al., 1989; Klann et al., 1993). In the hippocampus, the calmodulin-4Ca²⁺ complex (CaMCa₄) further activates adenylyl cyclase, leading to activation of cyclic adenosine monophosphate (cAMP)-dependent protein kinase (PKA) which is required for some forms of L-LTP (Woo et al., 2003).

Transcription and also somatic and dendritic protein synthesis are required for induction of L-LTP (Bradshaw et al., 2003b), but it is unclear whether protein synthesis is required for induction of E-LTP. These nuclear and somatic events involve Ca²⁺/calmodulin-dependent protein kinase IV (CaMKIV), mitogen-activated protein kinase (MAPK, ERK), and PKA. For maintenance of L-LTP, the atypical PKC isozyme (PKMζ), which is an autonomously active form of PKC, is required in addition to local dendritic protein synthesis (Serrano et al., 2005).

NMDAR-dependent LTD needs only a modest increase in Ca²⁺ concentration (instead of the large Ca²⁺ increase for LTP). This modest increase in Ca²⁺ concentration leads to preferential activation of protein phosphatase 2B also known as calcineurin, because it has a much higher affinity for CaMCa₄ than CaMKII has. Activation of protein phosphatases leads to dephosphorylation and endocytosis of AMPARs located on the plasma membrane (Citri and Malenka, 2008), and thereby the expression of LTD. Protein translation may be needed for expression and maintenance of L-LTD (Citri and Malenka, 2008), but otherwise mechanisms behind maintenance of NMDAR-dependent LTD have not been studied extensively. Some forms of LTD also require Ca²⁺-dependent production of endocannabinoids which travel retrogradely to produce changes in presynaptic release of neurotransmitters (Gerdeman and Lovinger, 2003).

Cerebellar LTD, the best studied form of non-NMDAR-dependent LTD, is observed at the parallel fiber to Purkinje cell synapse. Purkinje cells form synapses with several thousand parallel fibers and also receive many synaptic contacts from a single climbing fiber (Ito, 2002; Citri and Malenka, 2008). Cerebellar LTD is induced when parallel fibers and a climbing fiber are activated simultaneously. Glutamate released by parallel fibers activates mGluRs which in turn activate phospholipase C (Ito, 2002). Phospholipase C catalyzes the reaction producing diacylglycerol and inositol trisphosphate (IP₃). Diacylglycerol activates PKC, and IP₃ causes the release of Ca²⁺ from endoplasmic reticulum through IP₃ receptors (IP₃Rs). Phospholipase A₂, which is activated by an elevation in Ca²⁺ concentration, produces arachidonic acid which more persistently activates PKC that is transiently activated by diacylglycerol. PKC phosphorylates AMPARs and this leads to endocytosis of AMPARs from the plasma membrane. As in hippocampal LTP, protein synthesis is needed for L-LTD (Ito, 2001).

Given that Ca²⁺ activates multiple processes and enzymes, such as endocannabinoid production, calcineurin, and CaMKII, it is still not clear why some stimulation protocols produce depression and some produce potentiation. Non-linear interactions between multiple pathways make a quantitative understanding difficult solely from experiments. Computer modeling synthesizes information from myriad studies ranging from plasma membrane level phenomena to intracellular phenomena. Simulations therefore provide deeper insight into mechanisms underlying plasticity and this is why modeling studies have become more and more popular during the last 10 years.

3. Computational Models

Many computational models have been developed to understand pre- and postsynaptic events in LTP and LTD. Several focused reviews that include models of a specific neural system or type of plasticity have appeared during the last 20 years (Brown et al., 1990; Neher, 1998; Hudmon and Schulman, 2002a,b; Bi and Rubin, 2005; Holmes, 2005; Wörgötter and Porr, 2005; Ajay and Bhalla, 2006; Klipp and Liebermeister, 2006; Zou and Destexhe, 2007; Morrison et al., 2008; Ogasawara et al., 2008; Bhalla, 2009; Ogasawara and Kawato, 2009; Tanaka and Augustine, 2009; Urakubo et al., 2009; Castellani and Zironi, 2010; Gerkin et al., 2010; Graupner and Brunel, 2010; Hellgren Kotaleski and Blackwell, 2010; Shouval et al., 2010); however, a comprehensive review on postsynaptic signal transduction models for LTP and LTD is lacking.

In this study, an analysis of altogether 117 postsynaptic signal transduction models published through the year 2009 is presented (see Table 1). We limit the present analysis to models of postsynaptic signal transduction pathways that are defined using several characteristics. First, the output of the model needs to be a postsynaptic aspect of the neuron. Second, some part of intracellular signaling is explicitly modeled. Thus, models in this review are required to include at least mechanisms for postsynaptic Ca²⁺ dynamics, Ca²⁺ buffers, phosphorylation–dephosphorylation cycles, LTP and LTD related enzymes, retrograde signals, or synaptic strength that depends on Ca²⁺ concentration. Alternatively, models that explicitly include the kinases and phosphatases underlying changes in AMPAR phosphorylation or synthesis of plasticity-related proteins are included. Models which have intracellular signaling pathways in neurons but do not address plasticity are excluded. Models of AMPAR and NMDAR activation alone, or models including only anchoring and scaffolding proteins as intracellular molecules are excluded. Lastly, purely phenomenological models of plasticity are excluded. These strict criteria are needed because of the large number of models. In addition, a few models published during 2010 are excluded (see, e.g., Clopath et al., 2010; Kim et al., 2010; Kubota and Kitajima, 2010; Nakano et al., 2010; Pepke et al., 2010; Qi et al., 2010; Rackham et al., 2010; Santamaria et al., 2010; Tolle and Le Novère, 2010a).

Table 1.

List of postsynaptic signal transduction models published each year.

Year	Models	No.
1985	Lisman (1985)	1
1987	Gamble and Koch (1987)	1
1988	Lisman and Goldring (1988a,b)	2
1989	Lisman (1989)	1
1990	Holmes (1990), Holmes and Levy (1990), Kitajima and Hara (1990), Zador et al. (1990)	4
1993	De Schutter and Bower (1993), Migliore and Ayala (1993)	2
1994	Gold and Bear (1994), Kötter (1994), Michelson and Schulman (1994)	3
1995	Matsushita et al. (1995), Migliore et al. (1995), Schiegg et al. (1995)	3
1996	Dosemeci and Albers (1996), Fiala et al. (1996)	2
1997	Coomber (1997), Holmes and Levy (1997), Kitajima and Hara (1997), Migliore et al. (1997)	4
1998	Coomber (1998a,b), Markram et al. (1998), Murzina and Silkis (1998)	4
1999	Bhalla and Iyengar (1999), Kötter and Schirok (1999), Kubota and Bower (1999), Migliore and Lansky (1999a,b), Volfovsky et al. (1999)	6
2000	Holmes (2000), Kitajima and Hara (2000), Li and Holmes (2000), Okamoto and Ichikawa (2000a,b), Zhabotinsky (2000)	6
2001	Castellani et al. (2001), Franks et al. (2001), Kubota and Bower (2001), Kuroda et al. (2001), Yang et al. (2001)	5
2002	Abarbanel et al. (2002), Bhalla (2002a,b), Hellgren Kotaleski and Blackwell (2002), Hellgren Kotaleski et al. (2002), Holthoff et al. (2002), Karmarkar and Buonomano (2002), Karmarkar et al. (2002), Saftenku (2002), Shouval et al. (2002a,b)	11
2003	Abarbanel et al. (2003), Bradshaw et al. (2003a), d'Alcantara et al. (2003), Dupont et al. (2003), Kikuchi et al. (2003)	5
2004	Ajay and Bhalla (2004), Holcman et al. (2004), Ichikawa (2004), Murzina (2004), Steuber and Willshaw (2004), Yeung et al. (2004)	6
2005	Abarbanel et al. (2005), Castellani et al. (2005), Doi et al. (2005), Hayer and Bhalla (2005), Hernjak et al. (2005), Miller et al. (2005), Naoki et al. (2005), Rubin et al. (2005), Saudargiene et al. (2005), Shouval and Kalantzis (2005)	10
2006	Badoual et al. (2006), Lindskog et al. (2006), Miller and Wang (2006), Shah et al. (2006), Smolen et al. (2006), Zhabotinsky et al. (2006)	6
2007	Ajay and Bhalla (2007), Cai et al. (2007), Cornelisse et al. (2007), Delord et al. (2007), Gerkin et al. (2007), Graupner and Brunel (2007), Ichikawa et al. (2007), Kubota et al. (2007), Ogasawara et al. (2007), Schmidt et al. (2007), Smolen (2007), Tanaka et al. (2007)	12
2008	Achard and De Schutter (2008), Brown et al. (2008), Canepari and Vogt (2008), Clopath et al. (2008), Helias et al. (2008), Keller et al. (2008), Kubota and Kitajima (2008), Kubota et al. (2008), Pi and Lisman (2008), Santucci and Raghavachari (2008), Smolen et al. (2008), Stefan et al. (2008), Urakubo et al. (2008), Yu et al. (2008)	14
2009	Aslam et al. (2009), Byrne et al. (2009), Castellani et al. (2009), Jain and Bhalla (2009), Kalantzis and Shouval (2009), Kitagawa et al. (2009), Ogasawara and Kawato (2009), Schmidt and Eilers (2009), Smolen et al. (2009)	9
All		117

Altogether 117 models have been published between the years 1985 and 2009. For chosen criteria, see the beginning of Section 3.

3.1. Main characteristics of models

The lists of LTP models (Table 2), LTD models (Table 3), and dual LTP and LTD models (Table 4) order the models alphabetically by the first author and by the publication month and year. Dual LTP and LTD models are able to simulate both forms of plasticity. Characteristics listed under the methods include the computational techniques: either deterministic ordinary and partial differential equations (Det.) or stochastic techniques (Stoch.) which include, for example, reaction algorithms such as the Gillespie stochastic simulation algorithm (Gillespie, 1976, 1977) and diffusion algorithms such as Brownian dynamics. A few studies also use so-called hybrid methods where different techniques are combined. The models are further classified according to the biochemical phenomena that are modeled: some models only describe reactions between chemical species (Reac.) and some also take into account the diffusion of at least some chemical species (Diff.). In addition to biochemical models, there are models which not only describe intracellular events associated with synaptic plasticity, but also take into account the associated plasma membrane and ion channel level phenomena by modeling the membrane voltage; these models are referred to as electrophysiological (Elect.). Tables 2–4 indicate the simulation tool or programing language used when known, but this piece of information is not always given in the publications. Other characteristics included in Tables 2–4 are the cell type of the model, which process of synaptic plasticity is modeled [induction (Ind.), expression (Expr.), or maintenance (Maint.)] according to the publications, time required for the dynamics of the model to reach a steady state, the model outputs used to demonstrate the change in synaptic strength, and the size of the model [less than 20 different chemical species or other model variables is defined as small (S), between 20 and 50 is medium (M), and more than 50 is large (L)]. If several different types of models are used in one publication, the size of the largest model is given. The time required for the dynamics of the model to reach a steady state is suggestive and it is not possible to compare all the models according to the time because different models use, for example, different inputs.

Table 2.

List of LTP models.

Model	Methods	Cell type	Phases	Time	Outputs	Size
Ajay and Bhalla (2004)	Det. Reac./GENESIS/Kinetikita	Hippocampal CA1 N	Ind./Maint. LTP	60–80 min	ERKII	L
Ajay and Bhalla (2007)	Det. Reac. Diff. Elect./GENESIS/Kinetikita	Hippocampal CA1 PN	Ind./Maint. LTP	1–4 h	ERKII	L
Aslam et al. (2009)	Det. Reac./MATLAB®	Generic	Ind./Maint. L-LTP	100 min to 40 d	CaMKII	S
Bhalla and Iyengar (1999)	Det. Reac. Elect./GENESIS/Kinetikita	Hippocampal CA1 N	Ind. E-LTP	30 min	CaMKII	L
Bhalla (2002a)	Det. Reac. Diff. Elect./GENESIS/Kinetikita	Hippocampal CA1 N	Ind. E-LTP	50 min	CaMKII	L
Bhalla (2002b)	Det. Reac./GENESIS/Kinetikita	Hippocampal CA1 N	Ind. E-LTP	15–60 min	CaMKII	L
Bradshaw et al. (2003a)	Det. Reac.	Hippocampal CA1 N	Ind. LTP		CaMKII	M
Canepari and Vogt (2008)	Det. Reac.	Cerebellar PC	Ind. LTP	0.01–0.25 s	Ca2+	S
Cornelisse et al. (2007)	Det. Reac. Diff./CalCb	Visual cortical layer V PN	Ind. LTP	0.06–0.1 s	CaMCa1	S
De Schutter and Bower (1993)	Det. Reac. Diff. Elect./GENESISc	Hippocampal N	Ind. LTP	0.2 s	Ca2+	L
Dupont et al. (2003)	Det. Reac.	Generic	LTP	10–100 s	CaMKII	S
Franks et al. (2001)	Det. Stoch. Reac. Diff. Elect./MCelld, NEURONe	Neocortical PN	Ind. LTP	0.2–2 s	CaMCa4	L
Gamble and Koch (1987)	Det. Reac. Diff. Elect.	Hippocampal PN	Ind. LTP	0.3 s	CaMCa4	M
Gold and Bear (1994)	Det. Reac. Diff. Elect.	Hippocampal N	Ind. LTP	0.2–0.3 s	Ca2+	M
Holmes and Levy (1990)	Det. Reac. Diff. Elect.	Hippocampal DGC	Ind. LTP	0.05–0.3 s	Ca2+	L
Holmes (1990)	Det. Reac. Diff. Elect.	Hippocampal DGC	Ind. LTP	2 s	Ca2+	L
Holmes and Levy (1997)	Det. Reac. Diff. Elect.	Hippocampal DGC	Ind. LTP	0.2 s	Ca2+, CaMCa4	L
Holmes (2000)	Det. Stoch. Reac. Diff. Elect./MCelld	Hippocampal DGC	Ind. LTP	2 s to 2 h	CaMKII	L
Kikuchi et al. (2003)	Det. Reac./E-Cellf	Hippocampal N	Ind. E-LTP	10–100 min	AMPAR	L
Kitagawa et al. (2009)	Det. Reac./GENESIS/Kinetikita	Cerebellar PC	Ind./Expr./Maint. LTP	2–60 min	CaMKII	L
Kitajima and Hara (1990)	Det. Stoch. Reac. Elect.	Hippocampal PN	Ind./Maint. LTP	0.3 s	Ca2+	S
Kubota and Bower (1999)	Stoch. Reac.	Generic	Ind. LTP	0.02 s	CaMKII	M
Kubota and Bower (2001)	Det. Reac./XPPAUTg, MATLAB®	Generic	Ind. LTP		CaMKII	L
Kötter (1994)	Det. Reac.	Striatal MSN	LTP		DARPP, MAP2	S
Kötter and Schirok (1999)	Det. Reac./XPPg	Striatal MSN	LTP	1–2 s	cAMP	S
Li and Holmes (2000)	Det. Stoch. Reac. Diff. Elect./MCelld	Hippocampal DGC	Ind. LTP	1–35 s	CaMKII	L
Lindskog et al. (2006)	Det. Reac./XPPAUTg	Striatal MSN	Ind. E-LTP	3–30 min	DARPP32, PKA	L
Lisman (1985)	Det. Reac.	Generic	LTP		Kinase	S
Lisman and Goldring (1988b)	Det. Stoch. Reac.	Generic	LTP		CaMKII	M
Lisman and Goldring (1988a)	Det. Stoch. Reac.	Generic	LTP		CaMKII	M
Lisman (1989)	Det. Reac.	Hippocampal N	LTP		CaMKII	S
Markram et al. (1998)	Det. Reac. Diff.	Neocortical layer V PN	STP/LTP	0.002–2 s	Buffered Ca2+	L
Matsushita et al. (1995)	Det. Reac.	Generic	LTP	20 s to 60 min	CaMKII	M
Michelson and Schulman (1994)	Stoch. Reac.	Generic	LTP	10 s to 3 min	CaMK	L
Migliore and Ayala (1993)	Det. Reac.	Generic	Ind./Expr./Maint. STP/LTP		Postsyn. signal	S
Miller et al. (2005)	Det. Stoch. Reac.	Generic	Ind./Maint. LTP	2 s to 100 y	CaMKII	L
Miller and Wang (2006)	Stoch. Reac.	Generic	Ind./Maint. LTP	1–50 y	CaMKII	L
Okamoto and Ichikawa (2000b)	Det. Reac.	Generic	Ind. LTP		CaMKII	M
Okamoto and Ichikawa (2000a)	Det. Reac. Diff.	Hippocampal CA1 N	Ind. LTP	1–10 s	CaMKII	L
Santucci and Raghavachari (2008)	Det. Stoch. Reac. Diff. Elect.	Hippocampal CA1 PN	Ind. LTP	0.5–1 s	CaMKII	L
Schiegg et al. (1995)	Det. Reac. Diff. Elect.	Hippocampal CA1 PN	Ind. LTP	0.1–1.5 s	Ca2+	L
Smolen et al. (2006)	Det. Reac./Java	Hippocampal CA1 N	Ind./Expr. L-LTP	2–4 h	Synaptic strength	M
Smolen (2007)	Det. Reac.	Hippocampal CA1 N	Maint. L-LTP	10 h to 3 mo	Synaptic strength	M
Smolen et al. (2008)	Det. Stoch. Reac./Java	Hippocampal CA1 or neocortical PN	Ind./Maint. L-LTP	2 h to 8 d	MAPK	M
Smolen et al. (2009)	Det. Stoch. Reac./Java	Generic	Ind./Maint. LTP	1–6 h	CaMKII or MAPK	S
Volfovsky et al. (1999)	Det. Reac. Diff. Elect./FIDAPh	Hippocampal N	LTP	0.1–1.2 s	Ca2+	L
Zador et al. (1990)	Det. Reac. Diff. Elect.	Hippocampal CA1 N	Ind. LTP	0.2–0.3 s	CaMCa4	L
Zhabotinsky (2000)	Det. Reac.	Hippocampal N	Ind./Maint. LTP	2 s to 2 y	CaMKII	S

Models are in alphabetical order by the first author and according to the publication month and year. Tabulated characteristics are the method and model types (Det., Stoch., Reac., Diff., Elect., and simulation environment), cell type, phases of LTP, time required for the dynamics of the model to reach a steady state, model outputs, and size of the model based on the number of different chemical species or other model variables [less than 20 different chemical species or other model variables is defined as small (S), between 20 and 50 is medium (M), and more than 50 is large (L)]. All abbreviations are given in the list of abbreviations.

^aGENESIS/Kinetikit (http://www.genesis-sim.org/GENESIS/; http://www.ncbs.res.in/index.php?option=com_content&task=view&id=307; Bower and Beeman, 1998; Bhalla, 2002c).

^bCalC (http://web.njit.edu/~matveev/calc.html; Matveev et al., 2002).

^cGENESIS (http://www.genesis-sim.org/GENESIS/; Bower and Beeman, 1998).

^dMCell (http://www.mcell.cnl.salk.edu/; Stiles and Bartol, 2001).

^eNEURON (http://www.neuron.yale.edu/neuron/; Carnevale and Hines, 2006).

^fE-Cell (http://www.e-cell.org; Tomita et al., 1999).

^gXPP, XPPAUT (http://www.math.pitt.edu/~bard/xpp/xpp.html; Ermentrout, 2002).

^hFIDAP (Engelman, 1982, 1996).

Table 3.

List of LTD models.

Model	Methods	Cell type	Phases	Time	Outputs	Size
Achard and De Schutter (2008)	Det. Reac. Elect./GENESIS/Kinetikita	Cerebellar PC	Ind. LTD	1 s	Ca2+	L
Brown et al. (2008)	Det. Reac. Diff./Virtual Cellb	Cerebellar PC	LTD	0.4–2 s	IP3	M
Doi et al. (2005)	Det. Reac./GENESIS/Kinetikita	Cerebellar PC	Ind. LTD	0.2–1 s	Ca2+	L
Fiala et al. (1996)	Det. Reac. Elect.	Cerebellar PC	Ind. LTD		$g_{KCa}$	M
Hellgren Kotaleski and Blackwell (2002)	Det. Reac. Diff./XPPc	Cerebellar PC	LTD	1–5 s	Ca2+	S
Hellgren Kotaleski et al. (2002)	Det. Reac. Diff./XPPc	Cerebellar PC	Ind. LTD	5–30 s	PKC	M
Hernjak et al. (2005)	Det. Reac. Diff./Virtual Cellb	Cerebellar PC	Ind. LTD	0.1–4 s	Ca2+	M
Holthoff et al. (2002)	Det. Reac. Diff. Elect./MATLAB®	Neocortical layer V PN	Ind. LTD	0.5 s	Ca2+	S
Kuroda et al. (2001)	Det. Reac./GENESIS/Kinetikita	Cerebellar PC	Ind. STD/E-,L-LTD	15–100 min	AMPAR	L
Murzina (2004)	Det. Reac. Diff. Elect.	Cerebellar PC	Ind. LTD		Kinase, receptor	M
Ogasawara et al. (2007)	Det. Reac. Diff. Elect.	Cerebellar PC	Ind./Expr./Maint. LTD	20–60 min	AMPAR	L
Ogasawara and Kawato (2009)	Det. Stoch. Reac.	Cerebellar PC	Ind./Maint. LTD	10 s to 70 min	Kinase	S
Schmidt et al. (2007)	Det. Reac. Diff./Mathematica, FEMLAB	Cerebellar PC	Ind. LTD	0.2–4 s	Ca2+, CaM	L
Schmidt and Eilers (2009)	Det. Reac. Diff./Mathematica	Cerebellar PC	Ind. LTD	0.04–3 s	Ca2+, CaM	S
Steuber and Willshaw (2004)	Det. Reac. Elect.	Cerebellar PC	Ind. LTD		$g_{KCa}$	S
Tanaka et al. (2007)	Det. Reac.	Cerebellar PC	Ind. LTD		AMPAR	M
Yang et al. (2001)	Det. Reac. Elect./GENESIS/Chemesisd	Cerebellar PC	Ind. LTD	10–100 s	PKC	L

Models are in alphabetical order by the first author and according to the publication month and year. Tabulated characteristics are the method and model types (Det., Stoch., Reac., Diff., Elect., and simulation environment), cell type, phases of LTD, time required for the dynamics of the model to reach a steady state, model outputs, and size of the model based on the number of different chemical species or other model variables (S, M, L). All abbreviations are given in the list of abbreviations.

^aGENESIS/Kinetikit (http://www.genesis-sim.org/GENESIS/; http://www.ncbs.res.in/index.php?option=com_content&task=view&id=307; Bower and Beeman, 1998; Bhalla, 2002c).

^bVirtual Cell (http://vcell.org; Schaff et al., 1997; Slepchenko et al., 2003).

^cXPP (http://www.math.pitt.edu/~bard/xpp/xpp.html; Ermentrout, 2002).

^dGENESIS/Chemesis (http://www.genesis-sim.org/GENESIS/; http://krasnow.gmu.edu/CENlab/software.html; Bower and Beeman, 1998; Blackwell and Hellgren Kotaleski, 2002).

Table 4.

List of dual LTP and LTD models.

Model	Methods	Cell type	Phases	Time	Outputs	Size
Abarbanel et al. (2002)	Det. Reac. Elect.	Hippocampal GluN	Ind. LTP/LTD		Synaptic strength	S
Abarbanel et al. (2003)	Det. Reac. Elect.	Hippocampal CA1 PN	Ind. LTP/LTD		Synaptic strength	S
Abarbanel et al. (2005)	Det. Reac. Elect.	Hippocampal CA1 PN	Ind. LTP/LTD		Synaptic strength	M
Badoual et al. (2006)	Det. Reac. Diff. Elect./NEURONa	Cortical PN	Ind. LTP/LTD	0.05–0.25 s	Enzyme	S
Byrne et al. (2009)	Stoch. Reac. Diff./Java	Hippocampal CA1 PN	Ind. LTP/LTD	1–5 s	Ca2+, CaM	L
Cai et al. (2007)	Det. Stoch. Reac. Elect./Java	Hippocampal or visual cortical N	Ind. LTP/LTD	100 s	Synaptic strength	S
Castellani et al. (2001)	Det. Reac. Elect.	Generic	Ind. LTP/LTD		AMPAR	S
Castellani et al. (2005)	Det. Reac.	Cortical N	Ind. LTP/LTD		AMPAR	M
Castellani et al. (2009)	Det. Stoch. Reac.	Generic	Ind./Maint. LTP/LTD		AMPAR	S
Clopath et al. (2008)	Det. Stoch. Reac. Elect./Python	Hippocampal CA1 PN	Ind./Maint. E-, L-LTP/LTD	3–5 h	Synaptic strength	L
Coomber (1997)	Det. Reac. Diff. Elect./GENESISb	Neocortical PN	Ind./Maint. LTP/LTD	1 s	gAMPAR	L
Coomber (1998a)	Det. Reac./C	Generic	Ind. LTP/LTD	5 s to 15 min	CaMKII	L
Coomber (1998b)	Det. Reac.	Generic	Ind. LTP/LTD	2–60 min	CaMKII	L
d'Alcantara et al. (2003)	Det. Reac./MATLAB®	Cerebral cortical or hippocampal CA1 N	Ind. LTP/LTD	20 s to 10 min	AMPAR	S
Delord et al. (2007)	Det. Stoch. Reac.	Generic	Ind./Maint. LTP/LTD	4 s to 4 mo	Substrate	S
Dosemeci and Albers (1996)	Stoch. Reac./FutureBASIC	Generic	Ind. LTP/LTD	20 s to 6 min	CaMKII	L
Gerkin et al. (2007)	Det. Reac.	Hippocampal N	Ind. LTP/LTD	5 s	Synaptic strength	S
Graupner and Brunel (2007)	Det. Reac. Elect./C++, XPPAUTc	Hippocampal N	Ind./Maint. LTP/LTD	1–3.5 min	CaMKII	M
Hayer and Bhalla (2005)	Det. Stoch. Reac. Diff./GENESIS/Kinetikitd, GENESIS 3/MOOSEe	Generic	LTP/LTD	200 s to 30 h	AMPAR, CaMKII	L
Helias et al. (2008)	Det. Stoch. Reac. Elect./NESTf	Cortical N	Ind. LTP/LTD		CaMKII	L
Holcman et al. (2004)	Stoch. Reac. Diff.	Generic	Ind. LTP/LTD	0.4–0.6 s	Ca2+	L
Ichikawa (2004)	Det. Reac. Diff./A-Cellg	Generic	Ind. LTP/LTD		CaMKII	L
Ichikawa et al. (2007)	Det. Reac. Diff. Elect./A-Cellg	Hippocampal CA1 PN	Ind./Expr. LTP/LTD		CaMKII, CaN	M
Jain and Bhalla (2009)	Det. Reac./GENESIS/Kinetikitd, GENESIS 3/MOOSEe	Hippocampal N	Ind. LTP/LTD	3 h	Protein	L
Kalantzis and Shouval (2009)	Det. Stoch. Reac. Diff. Elect.	Hippocampal CA1 PN	Ind. LTP/LTD	0.15 s	Synaptic strength	L
Karmarkar and Buonomano (2002)	Det. Reac. Elect./NEURONa	Hippocampal N	Ind. LTP/LTD		Synaptic strength	S
Karmarkar et al. (2002)	Det. Reac. Elect./NEURONa	Auditory cortical layer II/III PN	Ind. LTP/LTD		Synaptic strength	S
Keller et al. (2008)	Det. Stoch. Reac. Diff. Elect./MCellh, NEURONa	Hippocampal CA1 PN	Ind. LTP/LTD	0.01–0.2 s	CaM	L
Kitajima and Hara (1997)	Det. Reac. Elect.	Generic	Ind./Expr. LTP/LTD	0.04–0.05 s	Vm	M
Kitajima and Hara (2000)	Det. Reac. Elect.	Generic	Ind. LTP/LTD		gAMPAR	M
Kubota and Kitajima (2008)	Det. Stoch. Reac. Elect./C	Cortical PN	Ind. LTP/LTD	100 s to 80 min	Synaptic strength	L
Kubota et al. (2007)	Det. Stoch. Reac. Diff.	Hippocampal CA1 PN	Ind. LTP/LTD	0.05 s	CaM	L
Kubota et al. (2008)	Det. Reac. Elect.	Hippocampal CA1 PN	Ind. LTP/LTD	0.05–1 s	Synaptic strength	M
Migliore et al. (1995)	Det. Reac.	Hippocampal N	Ind./Expr./Maint. LTP/LTD		Postsyn. signal	S
Migliore et al. (1997)	Det. Reac.	Hippocampal N	Ind./Maint. LTP/LTD		Postsyn. signal	S
Migliore and Lansky (1999b)	Det. Reac. Elect./FORTRAN	Neocortical PN	Ind./Maint. LTP/LTD	20 s	Postsyn. signal	S
Migliore and Lansky (1999a)	Det. Reac./FORTRAN	Hippocampal N	Ind./Maint. LTP/LTD		Postsyn. signal	S
Murzina and Silkis (1998)	Det. Reac. Elect.	Hippocampal CA3 PN	Ind. LTP/LTD	0.1 s	Vm	M
Naoki et al. (2005)	Det. Reac. Diff./MATLAB®	Generic	Ind./Expr. LTP/LTD	0.5–10 s	CaMCa4	L
Pi and Lisman (2008)	Det. Reac./MATLAB®	Generic	Ind./Maint. LTP/LTD, depotentiation, dedepression	3–8 s	AMPAR	S
Rubin et al. (2005)	Det. Reac. Diff. Elect./XPPAUTc	Hippocampal CA1 PN	Ind. LTP/LTD	10 s	Synaptic strength	M
Saftenku (2002)	Det. Reac. Elect./NEURONa	Cerebellar GrC	Ind. LTP/LTD	100 s	Postsyn. signal	L
Saudargiene et al. (2005)	Det. Reac. Elect.	Generic	Ind. LTP/LTD	0.06–0.1 s	Synaptic strength	S
Shah et al. (2006)	Det. Reac. Elect./Java, MATLAB®	Generic	Ind. LTP/STD/LTD		Synaptic strength	S
Shouval et al. (2002a)	Det. Reac. Elect.	Generic	Ind. LTP/LTD		Synaptic strength	S
Shouval et al. (2002b)	Det. Reac. Elect.	Generic	Ind. LTP/LTD		AMPAR	S
Shouval and Kalantzis (2005)	Det. Stoch. Reac. Elect.	Generic	Ind. LTP/LTD		Synaptic strength	S
Stefan et al. (2008)	Det. Reac./COPASIi	Generic	LTP/LTD		CaMKII, CaN	L
Urakubo et al. (2008)	Det. Reac. Diff. Elect./GENESIS/Kinetikitd	Visual cortical layer II/III PN	Ind. LTP/LTD	20 min	gsyn	L
Yeung et al. (2004)	Det. Reac. Elect.	Generic	Ind. LTP/LTD	2 h	Synaptic strength	L
Yu et al. (2008)	Det. Stoch. Reac. Elect.	Hippocampal place N	Ind. LTP/LTD		Synaptic strength	L
Zhabotinsky et al. (2006)	Det. Reac. Diff./XPPAUTc	Hippocampal CA1 N	Ind./Maint. E-, L-LTP/LTD	10 s to 60 min	AMPAR	L

Models are in alphabetical order by the first author and according to the publication month and year. Tabulated characteristics are the method and model types (Det., Stoch., Reac., Diff., Elect., and simulation environment), cell type, phases of LTP/LTD, time required for the dynamics of the model to reach a steady state, model outputs, and size of the model based on the number of different chemical species or other model variables (S, M, L). All abbreviations are given in the list of abbreviations.

^aNEURON (http://www.neuron.yale.edu/neuron/; Carnevale and Hines, 2006).

^bGENESIS (http://www.genesis-sim.org/GENESIS/; Bower and Beeman, 1998).

^cXPP, XPPAUT (http://www.math.pitt.edu/~bard/xpp/xpp.html; Ermentrout, 2002).

^dGENESIS/Kinetikit (http://www.genesis-sim.org/GENESIS/; http://www.ncbs.res.in/index.php?option=com_content&task=view&id=307; Bower and Beeman, 1998; Bhalla, 2002c).

^eGENESIS 3/MOOSE (http://www.genesis-sim.org/GENESIS/; http://moose.sourceforge.net/).

^fNEST (http://www.nest-initiative.org/; Gewaltig and Diesmann, 2007).

^gA-Cell (http://www.fujixerox.co.jp/crc/cng/A-Cell/; Ichikawa, 2001).

^hMCell (http://www.mcell.cnl.salk.edu/; Stiles and Bartol, 2001; Kerr et al., 2008).

ⁱCOPASI (http://www.copasi.org/; Hoops et al., 2006).

3.2. Categorization of models

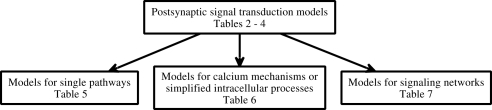
In this study, models are further categorized (Figure 1) into models for single pathways (Table 5), models for calcium mechanisms or simplified intracellular processes (Table 6), and models for signaling networks (Table 7). Models for single pathways involve at most one kinase as a model variable and do not include any receptors, ion channels, or pumps on the plasma membrane. Typically single pathways contain a pathway involving calmodulin and CaMKII and sometimes also phosphatases. Models for calcium mechanisms or simplified intracellular processes include postsynaptic Ca²⁺ buffers together with ion channels, receptors, or pumps, or simplified intracellular processes. The last group of models, consisting of signaling networks, takes into account interactions between at least two pathways and thus often have several protein kinases and phosphatases. These models can also include ion channels, receptors, and pumps. Several characteristics, such as model inputs, number and types of morphological compartments, molecules, ion channels, and receptors, are described for the models in the following sections. In some cases it is difficult to determine the model inputs based on the information given in the publications. For detailed biophysical models, the input is typically coupled with the plasma membrane level phenomena, such as membrane voltage. In these cases, we have indicated the change in membrane current (ΔI_m) or membrane voltage (ΔV_m) as the input. For more simplified models, a variety of mathematical equations are used to describe the model and the input. In these cases, we have indicated which physical property the input equation represents, such as synaptic stimulus (causing elevation in Ca²⁺ concentration). See also Section 4 for further comments on the presentation of input for models.

Figure 1.

Categorization of postsynaptic signal transduction models models.

Table 5.

Characteristics of models for single pathways.

Type	Model	Inputs	Subunits/States/Residues	Ions and molecules
LTP	Bradshaw et al. (2003a)	Ca2+	6/3a/Thr-286	Ca2+, CaM, CaMKII, PP1
LTP	Dupont et al. (2003)	Ca2+, CaM, CaMCa4	b/5c/Thr-286	Ca2+, CaM, CaMKII
LTP	Kubota and Bower (2001)	Ca2+	2–4/5d/Thr-286, Thr-305/306	Ca2+, CaM, CaMKII, PP1
LTP	Kötter and Schirok (1999)	Ca2+	No	AC, ATP, Ca2+, CaM, cAMP, PDE
LTP	Lisman (1985)	Kinase	1/2e	2 kinases, phosphatasef
LTP	Lisman and Goldring (1988b)	Ca2+	b/3g	Ca2+, CaMKII, phosphate ion
LTP	Lisman and Goldring (1988a)	Ca2+	b/3g	Ca2+, CaMKII, phosphate ion
LTP	Matsushita et al. (1995)	CaMCa4	10/5d/Thr-286, Thr-305, Ser-314	ATP, Ca2+, CaM, CaMKII, phosphatase, phosphate ion
LTP	Michelson and Schulman (1994)	Ca2+	10/5d/Thr-286, Thr-305/306	Ca2+, CaM, CaMK
LTP	Miller et al. (2005)	Ca2+	12/2e/Thr-286/287	Ca2+, CaM, CaMKII, CaN, I1, PKA, PP1
LTP	Miller and Wang (2006)	Ca2+	12/2e/Thr-286/287	Ca2+, CaM, CaMKII, PP1
LTP	Okamoto and Ichikawa (2000b)	Ca2+	b/4h/Thr-286/287	Ca2+, CaM, CaMKII
LTP	Okamoto and Ichikawa (2000a)	Ca2+	10/4h/Thr-286/287	Ca2+, CaMi, CaMCa4-binding protein, CaMKII
LTP	Smolen et al. (2009)	Ca2+	1/2e	Ca2+, CaMKII or MAPK
LTP	Zhabotinsky (2000)	Ca2+	10/3j/Thr-286	Ca2+, CaM, CaMKII, CaN, I1, PKA, PP1
Dual	Byrne et al. (2009)	Ca2+	12/6k	Ca2+, CaM, CaMKIIl
Dual	Coomber (1998a)	Ca2+	5/7m/Thr-286	ATP, Ca2+, CaM, CaMKII, phosphatase (CaN)
Dual	Coomber (1998b)	Ca2+	4/12/Thr-286, Thr-305/306	ATP, Ca2+, CaM, CaMKII, phosphatase (PP1)
Dual	Delord et al. (2007)	Ca2+	1/2e	Ca2+, kinase, phosphatase, substrate
Dual	Dosemeci and Albers (1996)	Ca2+	10/4n/Thr-286, Thr-305/306	Ca2+, CaM, CaMKII, phosphatase
Dual	Kubota et al. (2007)	Ca2+	No	Ca2+, CaMo, Ng
Dual	Stefan et al. (2008)	Ca2+	1/5p	Ca2+, CaM, CaMKII, CaN

Models are in alphabetical order by the first author and according to the publication month and year. First all LTP models are listed and then all dual LTP and LTD models. Tabulated characteristics are the model inputs, number of CaMKII or kinase subunits, number of states for each subunit, specified threonine (Thr) and serine (Ser) residues of CaMKII that are phosphorylated, as well as ions and molecules whose interactions are modeled. Note that it is not always clear if all the subunits and number of states mentioned in the publications are actually modeled and simulated. Molecules that are modeled as constants are also listed. All abbreviations are given in the list of abbreviations.

^aFirst three states of those mentioned under d below are modeled.

^bIt is not clearly stated in the publication how many CaMKII subunits are modeled.

^cInactive, bound with CaMCa₄, bound with CaMCa₄ and autophosphorylated, Ca²⁺ dissociated from CaM bound to the phosphorylated form (trapped), and CaM dissociated from the trapped form but remains phosphorylated (autonomous).

^dInactive, bound with CaMCa₄, bound with CaMCa₄ and autophosphorylated (trapped), CaMCa₄ dissociated from the trapped form but remains phosphorylated (autonomous), and autonomous state secondary autophosphorylated (capped).

^eInactive and phosphorylated.

^fCa²⁺ is not included in the model.

^gInactive, bound with Ca²⁺ and autophosphorylated, and Ca²⁺ dissociated but remains phosphorylated.

^hFirst four states of those mentioned under d above are modeled.

ⁱ1-D CaM diffusion is modeled to five spines connected by a dendrite.

^jInactive, bound with CaMCa₄, and bound with CaMCa₄ and phosphorylated or autophosphorylated.

^kInactive and bound with CaM, CaMCa₁, CaMCa₂, CaMCa₃, or CaMCa₄.

^l3-D CaM and CaMKII diffusion are modeled in a spine.

^mInactive, bound with CaMCa₄, bound with CaMCa₄ and autophosphorylated, and autophosphorylated on any 1–4 sites.

ⁿInactive, bound with CaMCa₄ and autophosphorylated, autophosphorylated, and secondary phosphorylated.

^o3-D CaM diffusion is modeled in a spine.

^pInactive and bound with CaMCa₁, CaMCa₂, CaMCa₃, or CaMCa₄.

Table 6.

Characteristics of models for calcium mechanisms or simplified intracellular processes.

Type	Model	Inputs	Compartments	VGICs	LGICs	Molecules and mechanisms
LTP	Canepari and Vogt (2008)	ICa	1 dendritic	No	No	CD28k, FF, and PV buffers, PMCA pump
LTP	Cornelisse et al. (2007)	JVGCC	Several dendritic and spine compartments	No	No	CaM, CD28k, OGB-1, and PV buffers, 1-D diffusion of Ca2+ and some of the buffers, PMCA pump
LTP, Elect.	De Schutter and Bower (1993)	ΔIm or ΔVm	Neuron with 1192 compartments	No	NMDAR, non-NMDAR	Buffer, 1-D Ca2+ diffusion, PMCA pump
LTP, Elect.	Franks et al. (2001)	ΔIm or ΔVm	1 spine	CaL, CaT	NMDAR	CaM and other buffers, 3-D Ca2+ diffusion, PMCA pump
LTP, Elect.	Gamble and Koch (1987)	Isyn	1 dendritic, 2 spine-head, 2 spine-neck	Ca2+, KM	No	CaM buffer, CaN, 1-D Ca2+ diffusion, PMCA pump
LTP, Elect.	Gold and Bear (1994)	ΔIm or ΔVm	1 dendritic, 4 spine-head, 3 spine-neck	No	NMDAR	Buffer, 1-D Ca2+ diffusion, PMCA pump
LTP, Elect.	Holmes and Levy (1990)	ΔIm or ΔVm	Neuron with several 4-compartment dendrites, 4304 spines with 4 spine-head and 3 spine-neck, 1–115 synapses	No	NMDAR, non-NMDAR	Buffer, 1-D Ca2+ diffusion, PMCA pump
LTP, Elect.	Holmes (1990)	ΔIm or ΔVm	Neuron with several 4-compartment dendrites, 3 spines with 5 spine-head and 3 spine-neck, 96 synapses	No	NMDAR, non-NMDAR	Buffer, 1-D Ca2+ diffusion, PMCA pump
LTP, Elect.	Holmes and Levy (1997)	ΔIm or ΔVm	Neuron with several 12-compartment dendrites, several spines with 4 spine-head and 4 spine-neck, several synapses, 1 axonal, 1 somatic	Ca2+, KA, KCa, Nafast	GABAAR, NMDAR, non-NMDAR	CaM and other buffers, 1-D Ca2+ diffusion, PMCA pump
LTP, Elect.	Holmes (2000)	ΔIm or ΔVm	Neuron with several 12-compartment dendrites, several spines with 4 spine-head and 4 spine-neck, several synapses, 1 axonal, 1 somatic	Ca2+, KA, KCa, Nafast	NMDAR, non-NMDAR	CaM buffer, CaMKIIa, CaN, 1-D Ca2+ diffusion, PMCA pump
LTP, Elect.	Kitajima and Hara (1990)	ΔIm or ΔVm	1 somatic, 1 spine-head, 1 spine-neck	No	NMDAR, non-NMDAR	CaM buffer, CaMKIIb
LTP, Elect.	Li and Holmes (2000)	ΔIm or ΔVm	Neuron with several 12-compartment dendrites, several spines with 4 spine-head and 4 spine-neck, several synapses, 1 axonal, 1 somatic	Ca2+, KA, KCa, Nafast	NMDAR, non-NMDAR	CaM buffer, CaMKIIa, CaN, 1-D–3-D Ca2+ and Glu diffusion, PMCA pump
LTP	Markram et al. (1998)	ICa	1 or 25 dendritic	No	No	Buffer, 1-D Ca2+ diffusion, PMCA pump
LTP	Migliore and Ayala (1993)	Presyn. stimulus	1 pre-, 1 postsynaptic	No	No	Simplified intracellular processesc
LTP, Elect.	Santucci and Raghavachari (2008)	ΔIm or ΔVm	1 pre-, 1 postsynaptic	No	AMPAR, NMDAR	CaM buffer, CaMKIId, CaN, 3-D Glu diffusion, I1, PKA, PP1, 2 vesicles
LTP, Elect.	Schiegg et al. (1995)	ΔIm or ΔVm	Neuron with 8 dendritic, 1 somatic, 3 spine-head, 3 spine-neck	No	AMPAR, NMDAR	CaM buffer, CaN, CICR, 1-D Ca2+ diffusion, Na+/Ca2+ exchanger, PMCA pump, Ca2+ store
LTP, Elect.	Volfovsky et al. (1999)	JCa, ΔIm or ΔVm	Several multi-compartment spines and dendrites	Ca2+	No	CaM and CG-1 buffers, CaN, CICR, 3-D Ca2+ and CG-1 diffusion, PMCA and SERCA pumps, Ca2+ store
LTP, Elect.	Zador et al. (1990)	ΔIm or ΔVm	Neuron with 28 compartments	No	NMDAR, non-NMDAR	CaM buffer, 1-D Ca2+ diffusion, 2 PMCA pumps
LTD	Hellgren Kotaleski and Blackwell (2002)	Ca2+	1 spine	No	IP3R	Buffer, 1-D Ca2+ diffusion, IP3, PMCA pump
LTD	Hernjak et al. (2005)	JCa	1–32 1-compartment spines, 2 dendritic	No	IP3R	CD28k, CG-1, and PV buffers, 1-D and 2-D diffusion of all molecules, IP3, PMCA and SERCA pumps, Ca2+ store
LTD, Elect.	Holthoff et al. (2002)	ΔIm or ΔVm	1 dendritic, 1 spine-head, 1 spine-neck	CaL	No	CG-1 and other buffers, 1-D Ca2+ diffusion, PMCA and SERCA pumps
LTD	Schmidt et al. (2007)	ICa	1 or 7 1-compartment spines, 1 or 7 dendritic	No	No	CaM, CD28k, OGB-1, and PV buffers, 1-D–3-D diffusion of all molecules, PMCA pump
LTD	Schmidt and Eilers (2009)	ICa	1 spine, 1 dendritic	No	No	CaM, CD28k, OGB-1, and PV buffers, 1-D diffusion of all molecules, PMCA pump
Dual, Elect., STDP	Abarbanel et al. (2002)	Synaptic stimulus	1 pre-, 1 postsynaptic	Noe	Simplified processes	Simplified intracellular processesc
Dual, Elect., STDP	Abarbanel et al. (2003)	ΔIm or ΔVm	Neuron with 1 compartment	CaT, K+, Na+	AMPAR, NMDAR	Phosphorylation, dephosphorylation
Dual, Elect., STDP	Abarbanel et al. (2005)	ΔIm or ΔVm	2 neurons with 1 presynaptic and 1 2-compartment postsynaptic	Ca2+, K+, KA, KM, Na+	AMPAR, NMDAR	Phosphorylation, dephosphorylation
Dual, Elect., STDP	Badoual et al. (2006)	ΔIm or ΔVm	Neuron with 1 spine, 1 axonal, 1 dendritic, 1 somatic	CaL, KCa, KDR, KM, Na+	AMPAR, NMDAR	1-D Ca2+ diffusion, PMCA pump, 3 enzymes
Dual, Elect., STDP	Cai et al. (2007)	Synaptic stimulus	1 pre-, 1 postsynaptic	No	NMDAR	Simplified intracellular processes, vesicle
Dual, Elect.	Castellani et al. (2001)	ΔIm or ΔVm	1 spine	No	AMPAR, NMDAR	2 kinases, 2 phosphatases
Dual	Castellani et al. (2009)	CaMKII	1 postsynaptic	No	AMPAR	CaMKII, PKA, PP1c
Dual, Elect.	Clopath et al. (2008)	ΔIm	Neuron with 1 compartment, 100 synapses	Nof	Simplified processes	Protein synthesisc
Dual, Elect.	Coomber (1997)	ΔIm or ΔVm	Neuron with 149 compartments	CaL, KA, KAHP, KCa, KDR, KM, Na+	AMPAR, NMDAR	Buffer, 1-D Ca2+ diffusion, PMCA pump
Dual, STDP	Gerkin et al. (2007)	Synaptic stimulus	1 pre-, 1 postsynaptic	No	No	Simplified intracellular processesc
Dual, Elect., STDP	Helias et al. (2008)	Synaptic stimulus	Neuron with 1 compartment, max 10000 synapses	Nog	NMDAR	CaMKII
Dual	Holcman et al. (2004)	JNMDAR	4-compartment spine	No	No	CaM buffer, CaN, 2-D Ca2+ diffusion, PMCA pump
Dual	Ichikawa (2004)	JNMDAR	3112-compartment spine	No	No	CaM buffer, CaMKII, CaN, 3-D diffusion of all molecules
Dual, Elect.	Ichikawa et al. (2007)	ΔIm or ΔVm	1 spine, 1 dendritic	No	AMPAR, NMDAR	CaM and other buffers, CaMKII, CaN, 1-D Ca2+ diffusion, PMCA pump
Dual, Elect., STDP	Kalantzis and Shouval (2009)	ΔVm	6 spine-head, 10 spine-neck	No	NMDAR	Buffer, 1-D Ca2+ diffusion, PMCA pump
Dual, Elect., STDP	Karmarkar and Buonomano (2002)	Synaptic stimulus	2 1-compartment neurons	Ca2++h	AMPAR, NMDAR	Simplified intracellular processes
Dual, Elect., STDP	Karmarkar et al. (2002)	Synaptic stimulus	2 1-compartment neurons	Noh	AMPAR, NMDAR	Simplified intracellular processes
Dual, Elect.	Keller et al. (2008)	ΔIm or ΔVm	1 dendritic, 1 extracellular, 1 presynaptic, 1 spine-head	Ca2+	AMPAR, NMDAR	CaM, CD28k, OGB-1, and other buffers, 3-D diffusion of all molecules, Na+/Ca2+ exchanger, PMCA pump
Dual, Elect.	Kitajima and Hara (1997)	Presyn. stimulus	Several spines with 1 spine-head and 1 spine-neck, 3 dendritic, 1 presynaptic	Ca2+	AMPAR, GABAR, NMDAR	Kinase, phosphatase, PMCA pump, vesicle
Dual, Elect.	Kitajima and Hara (2000)	ΔIm or ΔVm	Neuron with 2 1-8-compartment dendrites, 1 spine, 1 axonal, 1 somatic	CaL, CaN, CaT, KA, KDR, Na+	AMPAR, NMDAR	Phosphorylation, dephosphorylation
Dual, Elect., STDP	Kubota and Kitajima (2008)	ΔIm or ΔVm	Neuron with 2 4-7-compartment dendrites, 1 spine, 4800 synapses, 1 somatic	KA, KAHP, Nafast'	AMPAR, GABAR, NMDAR	Simplified intracellular processes
Dual, Elect.	Kubota et al. (2008)	ΔIm or ΔVm	1 spine	No	NMDAR	CaM buffer, Ng
Dual	Migliore et al. (1995)	Presyn. stimulus	1 pre-, 1 postsynaptic	No	No	Simplified intracellular processesc
Dual	Migliore et al. (1997)	Presyn. stimulus	Several synapses with 1 pre- and 1 postsynaptic	No	No	Simplified intracellular processesc
Dual, Elect.	Migliore and Lansky (1999b)	Presyn. stimulus	1 pre-, 1 postsynaptic	Noj	No	Simplified intracellular processesc
Dual	Migliore and Lansky (1999a)	Presyn. stimulus	1 pre-, 1 postsynaptic	No	No	Simplified intracellular processesc
Dual	Naoki et al. (2005)	INMDAR	15-compartment spine	No	No	CaM and other buffers, 1-D diffusion of all molecules, Na+/Ca2+ exchanger, PMCA and SERCA pumps
Dual	Pi and Lisman (2008)	JNMDAR	1 spine	No	AMPAR	Buffer, CaMKII, PP2A, AMPAR trafficking
Dual, Elect., STDP	Rubin et al. (2005)	ΔIm or ΔVm	Neuron with 1 spine (dendritic), 1 somatic	CaL, KA, KAHP, KDR, Na+	AMPAR, NMDAR	Buffer, Ca2+ detectors, 1-D Ca2+ diffusion
Dual, Elect.	Saftenku (2002)	ΔIm or ΔVm	Neuron with several compartments	BKCa, CaN, KA, KDR, KIR, Kslow, Nafast, Nar, Naslow	AMPAR, NMDAR	Simplified intracellular processes
Dual, Elect., STDP	Saudargiene et al. (2005)	ΔIm or ΔVm	1 dendritic	No	AMPAR, NMDAR	Simplified intracellular processes
Dual, Elect., STDP	Shah et al. (2006)	Synaptic stimulus	1 pre-, 1 postsynaptic	No	NMDAR	Simplified intracellular processes
Dual, Elect., STDP	Shouval et al. (2002a)	Synaptic stimulus	1 synaptic	No	NMDAR	Simplified intracellular processes
Dual, Elect., STDP	Shouval et al. (2002b)	Synaptic stimulus	1 pre-, 1 postsynaptic	No	AMPAR, NMDAR	2 kinases, 2 phosphatases
Dual, Elect., STDP	Shouval and Kalantzis (2005)	Synaptic stimulus	1 synaptic	No	NMDAR	Simplified intracellular processes
Dual, Elect., STDP	Yeung et al. (2004)	Synaptic stimulus	Neuron with 1 compartment, 120 synapses	Nog	NMDAR	Simplified intracellular processes
Dual, Elect., STDP	Yu et al. (2008)	Synaptic stimulus	Neuron with 1 compartment, 1000 synapses	Noi	NMDAR	Simplified intracellular processes

Models are in alphabetical order by the first author and according to the publication month and year. First all LTP models are listed, then all LTD models, and finally all dual LTP and LTD models. Furthermore, electrophysiological (Elect.) models taking into account membrane voltage and spike-timing-dependent plasticity (STDP) models are indicated in the first column. Tabulated characteristics are the model inputs, compartments, voltage-gated ion channels (VGICs), ligand-gated ion channels (LGICs), as well as molecules and Ca²⁺ mechanisms modeled. I_Ca denotes in this study the Ca²⁺ current but dependency in membrane voltage is not modeled. I_NMDAR denotes in this study the Ca²⁺ current via NMDARs but dependency in membrane voltage and NMDAR kinetics are not modeled. I_syn denotes the synaptic current. J_Ca denotes the Ca²⁺ influx, J_VGCC denotes the Ca²⁺ influx via VGCC, and J_NMDAR denotes the Ca²⁺ influx via NMDARs. For complex CaMKII models, number of CaMKII subunits, number of states for each subunit, and specified threonine (Thr) residues of CaMKII that are phosphorylated are given. Molecules that are modeled as constants are also listed. All abbreviations are given in the list of abbreviations.

^aTen CaMKII subunits/Thr-286, Thr-305/306 with five states: inactive, bound with CaMCa₄, bound with CaMCa₄ and autophosphorylated (trapped), CaMCa₄ dissociated from the trapped form but remains phosphorylated (autonomous), and autonomous state secondary phosphorylated (capped).

^bIt is not clearly stated in the publication how many CaMKII subunits are modeled but they have two states: inactive and phosphorylated.

^cCa²⁺ is not included in the model.

^dModel is by Miller et al. (2005), 12 CaMKII subunits/Thr-286/287 with two states: inactive and phosphorylated.

^ePre- and postsynaptic membrane voltage are modeled.

^fPostsynaptic neuron is described using adaptive exponential IF neuron model.

^gPostsynaptic neuron is described using IF neuron model.

^hPre- and postsynaptic neurons are described using IF neuron model.

ⁱPostsynaptic neuron is described using LIF neuron model.

^jPostsynaptic membrane voltage is modeled.

Table 7.

Characteristics of models for signaling networks.

Type	Model	Inputs	Compartments	VGICs	LGICs	Other	Mechanisms	Pathways
LTP	Ajay and Bhalla (2004)	Glu, JNMDAR	1 postsynaptic	No	No	EGFR, mGluR	CaM and other buffers	AC, CaM, CaMKIIa, CaN, Gq, MAPK, MKP, PKA, PKC, PKMζ, PLA2, PLC, PP1, Ras, SoS
LTP, Elect.	Ajay and Bhalla (2007)	Ca2+, ΔIm or ΔVm, JCa	Neuron with 1–324 compartments	Ca2+, KA, KAHP, KCa, KDR, Na+	AMPAR, NMDAR	No	CaM buffer, 1-D diffusion of all molecules, PMCA pump, transport of all molecules	CaM, MAPK, PKC, PKM, PLA2, Ras
LTP	Aslam et al. (2009)	CaMCa4	1 postsynaptic	No	No	No	CaM buffer	CaMKII, CPEB1
LTP, Elect.	Bhalla and Iyengar (1999)	ΔIm or ΔVm, EGF, Glu	Neuron with several compartments	Ca2+, KA, KAHP, KCa, KDR, Na2+	AMPAR, IP3R, NMDAR	EGFR, mGluR	CaM buffer, PMCA pump, Ca2+ store	AC, CaM, CaMKIIa, CaN, Gq, MAPK, PKA, PKC, PLA2, PLC, PP1, Ras, SoS
LTP, Elect.	Bhalla (2002a)	ΔIm or ΔVm, EGF, Glu, hormone	Neuron with 24 dendritic, 1 somatic, 4 spine-head, 3 spine-neck	Ca2+, KA, KAHP, KCa, KDR, Na+	AMPAR, IP3R, NMDAR	EGFR, mGluR	CaM and other buffers, 1-D Ca2+ diffusion, PMCA and SERCA pumps, Ca2+ store	AC, CaM, CaMKIIa, CaN, Gq, Gs, MAPK, PKA, PKC, PLA2, PLC, PP1, Ras, SoS
LTP	Bhalla (2002b)	EGF, Glu, hormone, JCa	1 extracellular, 1 intracellular, 1 store	No	IP3R	EGFR, mGluR	CaM buffer, PMCA and SERCA pumps, Ca2+ store	AC, CaM, CaMKIIa, CaN, Gq, Gs, MAPK, PKA, PKC, PLA2, PLC, PP1, Ras, SoS
LTP	Kikuchi et al. (2003)	Glu, JNMDAR	1 postsynaptic	No	AMPAR, IP3R	mGluR	CaM buffer, Ca2+ store	AC, CaM, CaMKII, CaN, Gq, I1, MAPK, MEK, MKP, PKA, PKC, PLA2, PLC, PP1, PP2A, Raf, Ras
LTP	Kitagawa et al. (2009)	Ca2+, GABABR	1 postsynaptic	No	GABAAR	GABABR	CaM buffer	AC, CaM, CaMKIIb, cAMP, CaN, DARPP32, PDE1, PDE4, PKA, PP1
LTP	Kubota and Bower (1999)	Ca2+	1 spine-head	No	AMPAR	No	CaM buffer, Ca2+ transport	AC, CaM, CaMKIIc, cAMP, CaN, I1, MAPK, PDE, PKA, PP1, Ras
LTP	Kötter (1994)	Ca2+, DA	1 postsynaptic	No	No	No	Buffer	AC, CaMKII, cAMP, CaN, DARPP, MAP2, PDE, PKA, PP1
LTP	Lindskog et al. (2006)	Ca2+, DA	1 spine	No	No	D1R	CaM buffer	AC, CaM, CaMKII, CaN, DARPP32, PDE1, PDE4, PKA, PP1, PP2A
LTP	Lisman (1989)	Ca2+	1 postsynaptic	No	No	No	CaM buffer	AC, CaM, CaMKII, cAMP, CaN, I1, PDE, PKA, PP1
LTP	Smolen et al. (2006)	Ca2+, cAMP, kf, Raf	1 nucleus, 1 somatic, 1 synaptic	No	No	No	Buffer	CaMKII, CaMKIV, MAPK, PKA, gene expression
LTP	Smolen (2007)	Ca2+	1–5 synapses	No	No	No	Buffer	CaMKII, CaMKIV, MAPK, PKA, gene expression
LTP	Smolen et al. (2008)	Raf	1 spine	No	No	No	No	ERK, MEK, MKKP, MKP, Rafd
LTD, Elect.	Achard and De Schutter (2008)	ΔIm or ΔVm	Neuron with 1600 compartments, 1 cytosolic, 1 ER, 1 PSD	BKCa, CaP, CaT, K2Ca, KA, KDR, KIR, KM, Nafast, Naslow	AMPAR, IP3R	mGluR	CD28k, MgGreen, PV, and other buffers, Na+/Ca2+ exchanger, PMCA and SERCA pumps, Ca2+ store	Gq, IP3 3-kinase, IP3 5-phosphatase, PLC
LTD	Brown et al. (2008)	PIP2, PLC	1 or several 1-compartment spines, 1 dendritic	No	No	No	Buffers, 1-D and 3-D diffusion of all molecules	PIP2, PLC
LTD	Doi et al. (2005)	Glu, JCa	1 cytosolic, 1 ER, 1 PSD	No	IP3R	mGluR	CD28k, MgGreen, PV, and other buffers, Na+/Ca2+ exchanger, PMCA and SERCA pumps, Ca2+ store	Gq, IP3 3-kinase, IP3 5-phosphatase, PLC
LTD, Elect.	Fiala et al. (1996)	cGMP, Glu	1 cytosolic, 1 ER, 1 extracellular	KCa	IP3R	mGluR	Na+/Ca2+ exchanger, SERCA pump, Ca2+ store	CaN, G, PKC, PLC
LTD	Hellgren Kotaleski et al. (2002)	Ca2+, Glu	1 spine-head, 2 spine-neck	No	IP3R	mGluR	2 buffers, 1-D Ca2+ diffusion, Ca2+ store	G, PKC, PLA2, PLC
LTD	Kuroda et al. (2001)	Ca2+, Glu, NO	1 postsynaptic	No	AMPAR	CRHR, mGluR	No	cGMP, Gq, Lyn, MAPK, MEK, PKC, PLA2, PLC, Raf
LTD, Elect.	Murzina (2004)	ΔVm, Glu	Neuron with 2 1-compartment spines, 5 dendritic, 1 somatic	Ca2+, K+, KCa, K Na+	AMPAR, GABAAR	GABABR, mGluR	CaM buffer, 1-D diffusion of NO	CaM, CaMKII, CaN, cGMP, G, GC, PKC, PKG, PP1
LTD, Elect.	Ogasawara et al. (2007)	ΔIm or ΔVm, Glu, NO	1350 1-compartment spines, 30 dendritic	BKCa, CaP	AMPAR, IP3R	mGluR	CD28k, MgGreen, PV, and other buffers, 3-D diffusion of NO, PMCA and SERCA pumps, Ca2+ store	cGMP, Gq, MAPK, MEK, PKC, PLA2, PLC, Raf
LTD	Ogasawara and Kawato (2009)	Generic	1 postsynaptic	No	No	No	No	4 kinasesd
LTD, Elect.	Steuber and Willshaw (2004)	cGMP, Glu	0 or 10 dendritic, 1 somatic	KCa	IP3R	mGluR	Buffer, Na+/Ca2+ exchanger, SERCA pump, Ca2+ store	CaN, G, PKC, PLC
LTD	Tanaka et al. (2007)	Ca2+	1 postsynaptic	No	AMPAR	No	No	MAPK, MEK, PKC, PLA2, Raf
LTD, Elect.	Yang et al. (2001)	Ca2+	Neuron with 1600 compartments	BKCa, CaP, CaT, K2Ca, KA, KDR, KIR, KM, Nafast, Naslow	AMPAR, IP3R	mGluR	Ca2+ store	Gq, PKC, PLA2, PLC
Dual	Castellani et al. (2005)	Ca2+	1 postsynaptic	No	AMPAR	No	CaM buffer	CaM, CaMKII, cAMP, CaN, I1, PKA, PP1
Dual	d'Alcantara et al. (2003)	Ca2+	1 postsynaptic	No	AMPAR	No	CaM buffer	CaM, CaMKII, CaN, I1, PP1
Dual, Elect., STDP	Graupner and Brunel (2007)	ΔIm	1 spine	CaL, KDR, Na+	AMPAR, NMDAR	No	Simplified, CaM and other buffers	CaM, CaMKIIe, I1, PP1
Dual	Hayer and Bhalla (2005)	Ca2+, cAMP, JNMDAR	1 dendritic, 1 PSD, 1 spine-head	No	AMPAR	No	CaM buffer, 1-D diffusion of some of the molecules	AC, CaM, CaMKIIa, CaN, PKA, PP1
Dual	Jain and Bhalla (2009)	BDNF, JNMDAR, MAPK	1 postsynaptic	No	No	TrkB	CaM buffer	40S, 4E-BP, AKT, CaM, CaMKIII, MAPK, mTOR, PKC, Ras, S6K, SoS
Dual, Elect.	Murzina and Silkis (1998)	ΔIm or ΔVm	Neuron with several compartments	Ca2+, K+, $K_{GAB{A}_{B}R}$, Na+	AMPAR, GABAAR, NMDAR	GABABR, mGluR	Buffer, Ca2+ store	AC, CaMKII, cAMP, PKA, PKC
Dual, Elect., STDP	Urakubo et al. (2008)	ΔIm or ΔVm	Neuron with 2-compartment spine, 20 dendritic, 1 somatic	CaL, KA, KDR, Na+, Naslow	AMPAR, NMDAR	No	CaM buffer, 1-D diffusion of most of the molecules, PMCA pump, AMPAR trafficking	CaM, CaMKIIf, CaN, cAMP, I1, PKA, PP1, PP2A
Dual	Zhabotinsky et al. (2006)	JNMDAR	1 spine, 1 dendritic, 1 cell body	No	AMPAR	No	CaM buffer, 1-D diffusion of some of the molecules, AMPAR trafficking	CaM, CaMKIIg, CaN, I1, Ng, PKA, PP1, PP2A

Models are in alphabetical order by the first author and according to the publication month and year. First all LTP models are listed, then all LTD models, and finally all dual LTP and LTD models. Furthermore, electrophysiological (Elect.) models taking into account membrane voltage and spike-timing-dependent plasticity (STDP) models are indicated in the first column. Tabulated characteristics are the model inputs, compartments, voltage-gated ion channels (VGICs), ligand-gated ion channels (LGICs), other receptors, Ca²⁺ mechanisms, and signaling pathways modeled. J_Ca denotes the Ca²⁺ influx and J_NMDAR denotes the Ca²⁺ influx via NMDARs. For complex CaMKII models, number of CaMKII subunits, number of states for each subunit, and specified threonine (Thr) residues of CaMKII that are phosphorylated are given. All abbreviations are given in the list of abbreviations.

^aOne CaMKII subunit/Thr-286, Thr-306 with six states: inactive, bound with CaMCa₄, bound with CaMCa₄ and autophosphorylated (trapped), CaMCa₄ dissociated from the trapped form but remains phosphorylated (autonomous), autonomous state secondary phosphorylated (capped), and capped state dephosphorylated.

^bIt is not clearly stated in the publication how many CaMKII subunits are modeled. CaMKII subunits/Thr-286/287, Thr-305/306 with six states: inactive, bound with CaMCa₃, bound with CaMCa₃ and autophosphorylated (trapped), CaMCa₃ dissociated from the trapped form but remains phosphorylated (autonomous), autonomous state secondary phosphorylated (capped), and capped state dephosphorylated.

^cIt is not clearly stated in the publication how many CaMKII subunits are modeled. CaMKII subunits/Thr-286, Thr-305/306 with five states: inactive, bound with CaMCa₄, bound with CaMCa₄ and autophosphorylated (trapped), CaMCa₄ dissociated from the trapped form but remains phosphorylated (autonomous), and autonomous state secondary phosphorylated (capped).

^dCa²⁺ is not included in the model.

^eTwo to eight CaMKII subunits/Thr-286 with four states: inactive, bound with CaMCa₄, bound with CaMCa₄ and autophosphorylated, and autophosphorylated only.

^fOne CaMKII subunit/Thr-286 with several states: inactive, bound with CaM, CaMCa₁, CaMCa₂, CaMCa₃, or CaMCa₄, bound and phosphorylated, and dissociated but remains phosphorylated.

^gTwo models. Model 1 is one CaMKII subunit/Thr-286 with seven states: inactive, bound with CaMCa4, bound with two CaMCa4, bound with two CaMCa4 and auto-phosphorylated, CaMCa4-dissociated but remains phosphorylated, two CaMCa4 dissociated but remains phosphorylated, and autophosphorylated. Model 2 is by Miller et al. (2005), 12 CaMKII subunits/Thr-286/287 with two states: inactive and phosphorylated.

3.2.1. Models for single pathways

The models for single pathways typically focus on CaMKII (e.g., Dosemeci and Albers, 1996; Okamoto and Ichikawa, 2000a; Smolen et al., 2009), though one model for cAMP production (Kötter and Schirok, 1999) exists and several models are focused on calmodulin activation (e.g., Kubota et al., 2007; Stefan et al., 2008). Most of these models use Ca²⁺ concentration as the input and include reaction kinetics of CaMCa₄ binding and unbinding to CaMKII subunits. Many of the models do not take into account the dodecameric structure of the CaMKII holoenzyme nor the spatial aspect of CaMCa₄-dependent autophosphorylation of CaMKII between adjacent subunits. Because of the importance of CaMKII in LTP, most of these single pathway models address the same issues of amplitude and frequency dependence of Ca²⁺-bound calmodulin or CaMKII activation; subsequent models usually build on previous models and then advance the simulation technique (e.g., stochastic instead of deterministic simulations), or incorporate new experimental details on the CaMKII molecule.

Lisman (1985) presents one of the first models for LTP, which shows that a simple switch model has two stable states, one in which the kinase is dephosphorylated and the other in which it is almost completely phosphorylated. Switch-like behavior, important for memory formation, can be created even when reactions occur stochastically (Smolen et al., 2009), using fast and slow feedback loops. Another stochastic model (Miller et al., 2005) shows that the highly phosphorylated state of CaMKII can remain stable for years, another property which could be important for memory storage.

Okamoto and Ichikawa (2000a) demonstrate the crucial role of competition for calmodulin between spines by modeling several morphological compartments. They model CaMKII in a set of five spines connected to a dendrite and show that after autophosphorylation of CaMKII in a spine, calmodulin in the dendrite can diffuse into that spine for CaMCa₄ trapping, which leads to competition since there is a limited concentration of calmodulin. Most of calmodulin is taken by those spines that experience relatively large increases in Ca²⁺ concentration.

A few of the models contribute to understanding of CaMKII activation though they do not explicitly model CaMKII. Delord et al. (2007) use simple models for Ca²⁺-controlled phosphorylation–dephosphorylation cycles with non-specific phosphoprotein substrates. Despite the simplicity of these models, the fraction of phosphorylated protein remains elevated for prolonged time periods after Ca²⁺ concentration returns to its basal level, representing a form of memory storage. Furthermore, the substrate phosphorylation persists in the presence of substrate turnover. Kubota et al. (2007) demonstrate that neurogranin regulates the spatiotemporal pattern of Ca²⁺-bound calmodulin, which has important implications for CaMKII activation and spatial specificity, by modeling diffusion of single molecules in a spine using 3-D Brownian dynamics.

Several studies show the importance of phosphatases for persistence of synaptic plasticity. Kubota and Bower (2001) show that asymptotic Ca²⁺ frequency sensitivity of CaMKII depends on both CaMKII and protein phosphatase 1 (PP1). Matsushita et al. (1995) show that phosphatase concentration not only controls whether CaMKII remains phosphorylated, but also controls the intensity of the input required to switch on the persistently phosphorylated state. Lisman and Zhabotinsky (2001) revisit this issue, and show that the CaMKII and PP1 bistable switch activated during the induction of LTP remains active despite the protein turnover. The bistable switch allows CaMKII autophosphorylation to be maintained at low Ca²⁺ concentrations, even after considering the effect of phosphatases and protein turnover. On the other hand, Bradshaw et al. (2003a) show that the presence of PP1 transforms the CaMKII bistable switch into a reversible (ultrasensitive) switch because PP1 dephosphorylates CaMKII when Ca²⁺ concentration is lowered to a basal level. Coomber (1998a) studies autophosphorylation and dephosphorylation of CaMKII and includes autophosphorylation of an inhibitory site caused by low-frequency stimulation. In this manner, either LTP or LTD can occur. Though using different mechanisms, both Dosemeci and Albers (1996) and Coomber (1998a,b) show that the phosphorylation of CaMKII can be sensitive to the temporal pattern of Ca²⁺ pulses, and this may allow CaMKII in the postsynaptic density to act as synaptic frequency detectors. The large allosteric model for calmodulin activation in the postsynaptic density by Stefan et al. (2008) explains how different Ca²⁺ concentrations can trigger the activation of either CaMKII or calcineurin.

3.2.2. Models for calcium mechanisms or simplified intracellular processes

Models for calcium mechanisms or simplified intracellular processes are a diverse group of models which typically address the role of Ca²⁺ in producing changes in synaptic strength. Most of these models focus on mechanisms controlling Ca²⁺ dynamics, such as Ca²⁺ buffers, pumps, glutamate receptors, or Ca²⁺-permeable ion channels. Another set of these models use more abstract equations representing intracellular processes and include an equation describing the Ca²⁺-dependent change in synaptic strength, in order to evaluate whether LTP or LTD occurs with repeated patterns of stimulation.

One of the most compelling questions in the field of LTP is whether high-frequency stimulation increases the spine Ca²⁺ concentration more than low-frequency stimulation. This has been addressed using models of Ca²⁺ dynamics in spines alone (see, e.g., Gamble and Koch, 1987; Kitajima and Hara, 1990; Gold and Bear, 1994; Volfovsky et al., 1999; Franks et al., 2001) or spines that include NMDAR activation by electrical activity in models of an entire neuron (see, e.g., Holmes and Levy, 1990; Zador et al., 1990; Koch and Zador, 1993). Zador et al. (1990) further demonstrate that spines compartmentalize Ca²⁺ (i.e., the Ca²⁺ signal is limited to those spines that are stimulated), thus providing a mechanism for spatial specificity. Holmes and Levy (1990) show that the frequency sensitivity of LTP requires Ca²⁺ buffers in addition to NMDAR properties.

A variation of this question is the effect of spine geometry on Ca²⁺ concentration and synaptic plasticity. Both Volfovsky et al. (1999) and Schmidt and Eilers (2009) test different spine-neck lengths and show that a long neck isolates Ca²⁺ signaling and calmodulin activation to the spine while stubby spines have a strong coupling between spines and the dendrite. Cornelisse et al. (2007) investigate the role of spine geometry compared to the dendrite. In particular, they demonstrate that the surface area to volume does not completely explain the difference in Ca²⁺ decay between a spine and dendrite. Instead, a lower buffer capacity of the spine is required to explain the experimental data.

Another important question is the role of various Ca²⁺ buffers in controlling Ca²⁺ dynamics. Many models of Ca²⁺ dynamics have only one or two Ca²⁺-binding proteins, instead of the many types found in real neurons. Markram et al. (1998) show that competition among Ca²⁺-binding proteins of various speeds and affinities influences the differential activation of intracellular targets. Models of Ca²⁺ dynamics permit tight coupling between experiments and models, but require the use of both intrinsic buffers, such as calbindin and parvalbumin, as well as Ca²⁺ indicators, such as Fura-FF, which themselves are fast, highly diffusible buffers. Other models have shown that buffer saturation is a crucial factor producing supralinear increases in Ca²⁺ concentration (Hellgren Kotaleski and Blackwell, 2002; Hernjak et al., 2005; Canepari and Vogt, 2008).

Improvements in Ca²⁺ imaging techniques have been accompanied by the development of sophisticated models that investigate mechanisms underlying Ca²⁺ microdomains. Naoki et al. (2005) take into account buffering by Ca²⁺-binding proteins and show that the diffusion coefficient of calmodulin has a strong effect on calmodulin activation in the microdomain near NMDARs. Kubota et al. (2008) investigate the Ca²⁺-binding protein neurogranin which increases Ca²⁺ dissociation from calmodulin. Their results show that with no Ca²⁺ extrusion mechanism, neurogranin increases the steady state concentration of Ca²⁺; however, in the presence of Ca²⁺ extrusion mechanisms, neurogranin instead enhances the decay rate of Ca²⁺. Keller et al. (2008) use MCell (Stiles and Bartol, 2001; Kerr et al., 2008) to develop one of the most advanced models of Ca²⁺ dynamics in a spine, including Ca²⁺ pumps, and both voltage-gated Ca²⁺ channels and NMDA-type of glutamate receptors. The voltage-dependent activation of the channels is coupled to a NEURON (Carnevale and Hines, 2006) simulation of membrane voltage. Keller et al. (2008) show that the Ca²⁺ gradient and calmodulin activation in the postsynaptic density depend on the order of glutamate release and action potential, and thus may explain the results of STDP experiments.

Just as recent models of Ca²⁺ dynamics include additional biophysical details, other models explore how biophysical processes related to, for example, glutamate receptors modulate LTP induction. Santucci and Raghavachari (2008) study the role of different types of NMDAR NR2 subunits on subsequent CaMKII activation. They show that though NR2B subunits have a more prolonged time course, the higher open probability of NR2A subunits leads to greater Ca²⁺ influx and CaMKII activation. The model of Li and Holmes (2000) shows that the variability in NMDAR opening, the spine-head Ca²⁺ concentration, and levels of CaMKII activation can play an important role in LTP induction. The spine model by Schiegg et al. (1995) includes calcineurin and Ca²⁺ release from stores, for example through IP₃Rs, in the spine head. This study shows that the inclusion of calcineurin alone, which is a Ca²⁺ sensitive protein phosphatase important for synaptic depression, eliminates LTP; further inclusion of Ca²⁺ release from stores is required to restore LTP induction. Pi and Lisman (2008) study the role of AMPAR trafficking, modeled by inserting and removing AMPARs in the postsynaptic membrane with a rate that depends on phosphorylated CaMKII and dephosphorylated protein phosphatase 2A (PP2A). Pi and Lisman (2008) show that CaMKII activity is high during LTP, PP2A activity remains high during LTD, and neither activity is high during a basal state; thus, LTD is not a reversal of previous LTP, rather a distinct phenomenon. Clopath et al. (2008) focus on synaptic tagging, an experimental concept important for synaptic specificity of protein synthesis-dependent LTP. The model includes production of plasticity-related proteins which can be captured by tagged synapses. Non-tagged synapses can be tagged stochastically in either a high or low state. They show that synapses share protein synthesis processes which have an effect on the stabilization of potentiated synapses during the transition from E-LTP to L-LTP.

As with all computational models, verification by direct comparison with experimental data strengthens the ability to make experimental predictions and resolve conflicting experimental evidence. The study by Santucci and Raghavachari (2008) is an excellent example on developing a computationally realistic model from good quality data, using the model to resolve conflicting experimental evidence, and then making further experimental predictions. Other examples of direct comparison with experiments include studies by Markram et al. (1998), Volfovsky et al. (1999), Cornelisse et al. (2007), and Schmidt and Eilers (2009). In addition, the prediction that PP2A is critical for LTD induction has been confirmed experimentally (Nicholls et al., 2008). Cai et al. (2007) demonstrate that including the stochastic properties of synaptic transmission significantly affects the form of STDP curves, and indeed is required to explain the experimental data.

3.2.3. Models for signaling networks

Many LTP models for signaling networks are extensions of the single pathway CaMKII models. The model by Lisman (1989) is a landmark because it is one of the first to show that synaptic strength stored by CaMKII could be bidirectionally modified by physiological activity according to the postsynaptic Ca²⁺ concentration. Kubota and Bower (1999) predict that the CaMKII activity can be sensitive to small changes in the timing of presynaptic signal to the spine head and that CaMKII can exhibit temporal sensitivity even in the presence of PP1. Kitagawa et al. (2009) evaluate the effect of inhibitory G protein-coupled gamma-aminobutyric acid (GABA) B receptor (GABA_BR) activation on LTP. They show that a transient increase in Ca²⁺ concentration induces long-term activation of CaMKII, which is attenuated by GABA_BR activation due to inhibition of PKA. They further show a role for a novel positive feedback loop – one involving CaMKII-mediated downregulation of phosphodiesterase type 1.

Bhalla and Iyengar (1999), Bhalla (2002a,b), Ajay and Bhalla (2004, 2007), and Hayer and Bhalla (2005) have modeled pathways for several protein kinases and phosphatases to investigate information processing. The first study (Bhalla and Iyengar, 1999) uses synaptic stimulation of a compartmental neuron model (Holmes and Levy, 1990; Traub et al., 1991; De Schutter and Bower, 1993) to determine the Ca²⁺ concentration that is the input to signaling network models. Simulations show that several properties not present in individual pathways, such as feedback loops, thresholds, and sensitivity to signal strength and duration, can emerge from the interaction of pathways. Feedback loops and thresholds can give rise to bistability, offering the possibility that information can be stored within biochemical reactions in the signaling network. The role of temporal sensitivity is further explored (Bhalla, 2002a). This study shows that different input patterns are processed differently by the signaling network, thus giving rise to different outputs (input pattern discrimination). The role of the feedback loop involving MAPK and PKC is further explored in additional studies that integrate experiments and modeling (Bhalla, 2002b). The signaling network models are further refined to include PKMζ (Ajay and Bhalla, 2004, 2007), diffusional processes (Ajay and Bhalla, 2007), and electrical activity (Ajay and Bhalla, 2007) to explore mechanisms underlying MAPK activation in LTP. Ajay and Bhalla (2007) show that extracellular signal-regulated kinase (ERK, MAPK) type II (ERKII) activation after an LTP-inducing stimuli is not explained with reaction–diffusion alone but requires a distributed synaptic input and activation of voltage-gated Ca²⁺ channels. The model by Hayer and Bhalla (2005) shows that CaMKII and AMPAR phosphorylation form distinct bistable switches, allowing for multiple stable states of the system.

The models of striatal medium spiny neurons (Kötter, 1994; Lindskog et al., 2006) focus on integration of dopamine and glutamate signals, and explore mechanisms which are important for striatal learning. The model by Kötter (1994) is the first to investigate signaling pathways underlying plasticity in the striatum, and shows that, with Ca²⁺-activated adenylyl cyclase, dopamine and Ca²⁺ synergistically activate PKA. The model by Lindskog et al. (2006) includes the striatal adenylyl cyclase type 5, which is inhibited by Ca²⁺, and shows that separate transient dopamine or Ca²⁺ elevations each may increase the phosphorylation of cAMP-regulated phosphoprotein (DARPP32), due to Ca²⁺ activation of PP2A. Through this mechanism, paired stimuli yield increased PKA activation and DARPP32 phosphorylation compared to dopamine alone, in contrast to the effect of prolonged stimuli in which Ca²⁺ decreases DARPP32 phosphorylation. Fernandez et al. (2006) study the functions of DARPP32 with a detailed signaling network model but they do not address plasticity, thus this study is not included in Table 7. However, their study may be used as a valuable model to build on for future modeling efforts studying plasticity.

More recently models have been constructed to investigate mechanisms underlying L-LTP, by incorporating molecules such as CaMKIV, transcription factors, or the translation factor cytoplasmic polyadenylation element binding protein (CPEB1). Smolen (2007) shows that long periods of decreased activity reset synaptic strength to a low value, whereas episodic activity with short inactive periods maintains strong synapses. Smolen et al. (2008) implement a stochastic model to show that the feedback loop from MAPK to MAPK kinase kinase (Raf) increases the robustness of both stable states of MAPK activity to stochastic fluctuations. Aslam et al. (2009) show that the positive feedback loop between CaMKII and CPEB1 forms a bistable switch accounting for the protein synthesis dependence of L-LTP. In addition, Jain and Bhalla (2009) are interested in protein synthesis dependence of L-LTP, and thus investigate how the synaptic input pattern affects dendritic protein synthesis. These types of models are likely to increase because behavioral memories require protein synthesis.

Long-term depression is predominant for synapses in the cerebellum; thus, most models of LTD describe signaling networks in cerebellar Purkinje cells. Kuroda et al. (2001) investigate the mechanism producing persistent phosphorylation of AMPARs, required for LTD. Simulations show that the initial phase of phosphorylation of AMPARs depends on the activation of PKC by arachidonic acid, Ca²⁺, and diacylglycerol, whereas a later phase depends on the activation of a positive feedback loop and especially phospholipase A₂ and arachidonic acid. Tanaka et al. (2007) further demonstrate that disrupting the positive feedback loop between several protein kinases can affect Ca²⁺ triggering of LTD. Brown et al. (2008) present an elaborate three-dimensional model of a Purkinje cell dendrite with spines to investigate the issue of whether sufficient phosphatidylinositol biphosphate (PIP2) is available in a single spine to achieve the experimentally estimated concentrations of IP₃ required for Ca²⁺ release and subsequent LTD. They elegantly show that a relatively novel mechanism, namely stimulated synthesis of PIP2, is required to account for experimental results. Three of the LTD models (Yang et al., 2001; Ogasawara et al., 2007; Achard and De Schutter, 2008) use the multi-compartment, multi-channel Purkinje cell model by De Schutter and Bower (1994a,b) to simulate electrical activity leading to Ca²⁺ influx through synaptic and voltage-gated ion channels. Ogasawara et al. (2007) show that the nitric oxide concentration is critical for induction of LTD and for its input specificity. Achard and De Schutter (2008) re-evaluate the importance of conjunctive parallel fiber and climbing fiber inputs. They show that both inputs are required to produce a sufficient Ca²⁺ elevation to trigger LTD.

Because of the role of the cerebellum in eyeblink classical conditioning, several signaling network models investigate whether temporal characteristics of classical conditioning can be explained by temporal characteristics of LTD in single Purkinje cells. Fiala et al. (1996) have developed the first model to explain adaptive timing of the eyeblink response in classical conditioning. They use a biochemical variant of spectral timing for their parallel fiber inputs, and also include the effect of Ca²⁺-gated potassium channel activation on membrane voltage. They show that the phosphorylation state of target proteins responsible for LTD depends on the timing between climbing fiber and parallel fiber stimulation. Hellgren Kotaleski et al. (2002) include production of PKC activators by parallel fiber and climbing fiber stimulation in order to evaluate the relationship between LTD and behavior. Both Hellgren Kotaleski et al. (2002) and Doi et al. (2005) show that IP₃-dependent Ca²⁺ dynamics are sensitive to temporal interval between parallel fiber and climbing fiber stimulation. Hellgren Kotaleski et al. (2002) further demonstrate that PKC activation is sensitive to temporal interval between parallel fiber and climbing fiber inputs (which is analogous to classical conditioning being sensitive to temporal interval). The importance of conjunctive parallel fiber and climbing fiber inputs for Ca²⁺ elevation is confirmed using a multi-compartment, multi-channel Purkinje cell model by Ogasawara et al. (2007) which more accurately simulates Ca²⁺ influx through synaptic and voltage-gated ion channels. Steuber and Willshaw (2004) show that replacing the spectral timing mechanism with Ca²⁺-dependent phosphorylation of mGluRs allows a single Purkinje cell to learn the adaptive timing of the eyeblink response.

More recent dual LTP and LTD models evaluate signaling network activation using spike-timing-dependent protocols (Graupner and Brunel, 2007; Urakubo et al., 2008). Urakubo et al. (2008) show that Ca²⁺ influx through NMDARs does not vary with spike timing (contrary to expectations) without suppression of NMDARs by Ca²⁺-bound calmodulin. Graupner and Brunel (2007) have constructed models for Ca²⁺/CaM-dependent autophosphorylation of CaMKII and PP1-dependent dephosphorylation of CaMKII. Graupner and Brunel (2007) show that CaMKII plays a central role in LTD because it is dephosphorylated during induction of LTD. More importantly, their bistable model can reproduce plasticity in response to STDP and high-frequency stimulation, without requiring abnormally low Ca²⁺ concentrations for dephosphorylation.

4. Analysis and Discussion

This study provides an extensive overview of 117 computational models for postsynaptic signal transduction pathways in synaptic plasticity developed over the past 25 years through 2009. Our purpose is to categorize the models so that similarities and differences are more readily apparent. Due to the large number of models, many models, though valuable, are excluded since they do not reach our criteria given in the beginning of Section 3. Some of the models included in this study are very simplified biochemical models meaning that a specific phenomenon is expressed using only a couple of reactions (see, e.g., Delord et al., 2007; Pi and Lisman, 2008). In the other extreme are the complex biophysical models that include detailed reaction–diffusion systems coupled to neuronal electrical activity (see, e.g., Bhalla, 2002a; Urakubo et al., 2008). Though model complexity has been increasing (Figures 2 and 3), the simpler biochemical models remain a valuable approach. They are relatively easy to construct, and the number of parameters to be fine-tuned is small. Not only are they computationally efficient, but they allow theoretical analysis and identification of which pathway, or combination of pathways, produces which property. On the other hand, models with detailed mechanisms are ideal for investigating which of several candidate molecules and mechanisms control or modulate a particular response. Furthermore, the direct correspondence between a detailed model and real neuron allows specific model predictions to be tested experimentally.

Figure 2.

Evolution of postsynaptic signal transduction models from 1985 to 2009. The starting point of an arrow represents the model which is used by the latter model indicated as the arrowhead. A dotted line in the arrow means that the two studies use exactly the same model (the latter study is not presented in Tables 1–9).

Figure 3.

Numbers of published postsynaptic signal transduction models per year from 1985 to 2009. (A) Numbers of LTP, LTD, and dual LTP and LTD models. (B) Numbers of reaction, reaction and diffusion, reaction and electrophysiological, as well as reaction, diffusion, and electrophysiological models. (C) Numbers of different size (S, M, and L) models. (D) Numbers of deterministic, stochastic, and deterministic and stochastic models.

In our study, the emphasis is more on evaluating the model components and on the significance of the models rather than on comparison of the actual model responses. The comparison of model responses is not trivial because all models would need to be implemented and simulated before a comparative analysis could be performed (see also Pettinen et al., 2005). Indeed, this is not only time consuming, but impossible since many of the models are neither described in sufficient detail nor provided in model databases or by other open-access means (see Table 8). Even qualitative comparison is difficult since only a few publications provide a graphical illustration of the model components and in many cases it is difficult to interpret the model input or stimulus. These observations serve also as guidelines for reviewers evaluating future publications and models: (1) all models should be described in sufficient detail including equations, inputs, outputs, compartments, variables, constants, parameters, and initial conditions; (2) graphical illustration of the model should include only those model components that actually participate in simulations; (3) the simulation tool or programing language should be specified; and (4) the model should be provided in a model database. Nordlie et al. (2009) propose a good model description practice for neuronal network models. A similar description practice is needed for signal transduction models and our study is one step toward this, as is the BioModels Database project (Le Novère et al., 2006).

Table 8.

Models provided in databases or by other open-access means.

Model	Simulation environment	Databases
Ajay and Bhalla (2004)	GENESIS/Kinetikita, MATLAB®, SBMLb	DOQCSc
	SBMLb	BioModels Databased
Ajay and Bhalla (2007)	GENESIS/Kinetikita, MATLAB®, SBMLb	DOQCSc
	SBMLb	BioModels Databased
Aslam et al. (2009)	MATLAB®	Supplementary material by Aslam et al. (2009)
Badoual et al. (2006)	NEURONe	ModelDBf
Bhalla and Iyengar (1999)	GENESIS/Kinetikita, MATLAB®, SBMLb	DOQCSc
	SBMLb	BioModels Databased
	SBMLb	CellMLg
Bhalla (2002b)	GENESIS/Kinetikita, MATLAB®, SBMLb	DOQCSc
Brown et al. (2008)	Virtual Cellh	Virtual Cellh
Clopath et al. (2008)	Python	ModelDBf
Cornelisse et al. (2007)	CalCi	ModelDBf
d'Alcantara et al. (2003)	SBMLb	BioModels Databased
Doi et al. (2005)	GENESIS/Kinetikita	ModelDBf
Gerkin et al. (2007)	IGOR Proj	ModelDBf
Graupner and Brunel (2007)	XPPAUTk	ModelDBf
Hayer and Bhalla (2005)	GENESIS/Kinetikita, GENESIS 3/MOOSEl, MATLAB®, SBMLb	DOQCSc
Hernjak et al. (2005)	MathSBMLm	Virtual Cellh
	MathSBMLm	BioModels Databased
Ichikawa (2004)	A-Celln	http://www.his.kanazawa-it.ac.jp/∼ichikawa/
	EnglishTop.html
Ichikawa et al. (2007)	A-Celln	http://www.his.kanazawa-it.ac.jp/∼ichikawa/
	EnglishTop.html
Jain and Bhalla (2009)	GENESIS/Kinetikita, GENESIS 3/MOOSEl	DOQCSc
	XML	Supplementary material by Jain and Bhalla (2009)
Kitagawa et al. (2009)	SBMLb	Supplementary material by Kitagawa et al. (2009)
Kuroda et al. (2001)	GENESIS/Kinetikita, MATLAB®, SBMLb	DOQCSc
	GENESIS/Kinetikita	http://www.cns.atr.jp/neuroinfo/kuroda/
	SBMLb	BioModels Databased
Lindskog et al. (2006)	XPPAUTk	ModelDBf
Migliore and Lansky (1999b)	QuickBASIC	ModelDBf
Saftenku (2002)	NEURONe	ModelDBf
Schmidt and Eilers (2009)	Mathematica	Supplementary material by Schmidt and Eilers (2009)
Stefan et al. (2008)	BioPAXo, CellMLg, SBMLb, Scilabp, Virtual Cellh, XPPk	BioModels Databased
Urakubo et al. (2008)	GENESIS/Kinetikita	ModelDBf
	GENESIS/Kinetikita	http://www.bi.s.u-tokyo.ac.jp/kuroda-lab/info/
		STDP/index.html

^aGENESIS/Kinetikit (http://www.genesis-sim.org/GENESIS/; http://www.ncbs.res.in/index.php?option=com_content&task=view&id=307; Bower and Beeman, 1998; Bhalla, 2002c).

^bSBML (http://sbml.org/).

^cDOQCS (http://doqcs.ncbs.res.in/; Sivakumaran et al., 2003).

^dBioModels Database (http://www.biomodels.net/; Le Novère et al., 2006).

^eNEURON (http://www.neuron.yale.edu/neuron/; Carnevale and Hines, 2006).

^fModelDB (http://senselab.med.yale.edu/modeldb/; Migliore et al., 2003; Hines et al., 2004).

^gCellML (http://www.cellml.org; Lloyd et al., 2008).

^hVirtual Cell (http://vcell.org; Schaff et al., 1997; Slepchenko et al., 2003).

ⁱCalC (http://web.njit.edu/~matveev/calc.html; Matveev et al., 2002).

^jIGOR Pro (http://www.wavemetrics.com/).

^kXPP, XPPAUT (http://www.math.pitt.edu/~bard/xpp/xpp.html; Ermentrout, 2002).

^lGENESIS 3/MOOSE (http://www.genesis-sim.org/GENESIS/; http://moose.sourceforge.net/).

^mMathSBML (http://sbml.org/Software/MathSBML).

ⁿA-Cell (http://www.fujixerox.co.jp/crc/cng/A-Cell/; Ichikawa, 2001, 2005).

^oBioPAX (http://www.biopax.org/; Luciano and Stevens, 2007).

^pScilab (http://www.scilab.org/; Gomez, 1999).

Every computational model needs to be stimulated to study evoked activity even though this aspect is not always clearly indicated in the publications. In other words, an input similar to the one given in experimental wet-lab studies or as in the physiological in vivo state is required. In many cases, however, it is a challenge to mimic the input used in experiments. The construction of input stimulus is quite straightforward in cases where biophysically detailed models and a high-frequency stimulation protocol are used. In the other extreme are the models which use some function mimicking synaptic stimulus. This input type is not adequately described in many of the publications analyzed in the present study. This makes the reproduction of simulation results and the comparison of the models impossible. Therefore, the description of input stimuli should be taken into account when developing specific description language solutions for computational neuroscience and neuroinformatics.

Testing sensitivity to changes in parameter values is very important because many of the model parameters are not sufficiently constrained by experimental data. Table 9 highlights the models that evaluate whether the simulation results are sensitive to changes in parameter values. In this study, small-scale testing means that values for 10 parameters or less (for example rate constants) are varied, and large-scale testing means that values for greater than 10 parameters are varied. Table 9 shows that only a few models employ the large-scale testing of sensitivity to changes in parameter values. Publications that only test sensitivity to changes in input parameter values or do parameter estimation to fit experimental data, without analyzing the different model responses, are not included in Table 9.

Table 9.

Models testing sensitivity to changes in parameter values.

Testing	Models
Small-scale	Holmes (1990, 2000), Holmes and Levy (1990), Gold and Bear (1994), Matsushita et al. (1995), Migliore et al. (1995), Schiegg et al. (1995), Dosemeci and Albers (1996), Fiala et al. (1996), Coomber (1998a,b), Volfovsky et al. (1999), Okamoto and Ichikawa (2000b), Zhabotinsky (2000), Kuroda et al. (2001), Hellgren Kotaleski et al. (2002), Karmarkar and Buonomano (2002), Shouval et al. (2002a,b), Abarbanel et al. (2003, 2005), d'Alcantara et al. (2003), Kikuchi et al. (2003), Hayer and Bhalla (2005), Hernjak et al. (2005), Miller et al. (2005), Naoki et al. (2005), Rubin et al. (2005), Lindskog et al. (2006), Smolen et al. (2006, 2008), Zhabotinsky et al. (2006), Cai et al. (2007), Cornelisse et al. (2007), Delord et al. (2007), Graupner and Brunel (2007), Ogasawara et al. (2007), Smolen (2007), Brown et al. (2008), Kubota and Kitajima (2008), Urakubo et al. (2008), Yu et al. (2008), Aslam et al. (2009), Castellani et al. (2009), Jain and Bhalla (2009), Kalantzis and Shouval (2009)
Large-scale	Bhalla and Iyengar (1999), Doi et al. (2005), Achard and De Schutter (2008), Kitagawa et al. (2009)

Small-scale testing means that values for 10 parameters or less (for example rate constants) are varied, and large-scale testing means that values for greater than 10 parameters are varied.

In order to predict the future direction of the field, trends regarding the development of models of postsynaptic signal transduction pathways underlying LTP and LTD are illustrated (Figures 2 and 3). Figure 2 shows how different models reviewed in this study have evolved from each other. Two models are connected in Figure 2 if the publication either states directly that other models are used or the publication uses a subset of the exact same equations appearing in the older publications by the same authors. Models are excluded from Figure 2 if there is no clear evidence that they have used some other model as the basis, or if they are only based on models not reviewed in this study. Figure 2 shows that the models by Holmes and Levy (1990), Bhalla and Iyengar (1999), and Shouval et al. (2002a) are most often used as a starting point when developing new models. Zhabotinsky et al. (2006) and Graupner and Brunel (2007) cite the largest number of models when developing their models, but, on the other hand, they do not clearly state which parts of their model are taken from which other models.

Though LTP models appeared first, most of the new models are dual LTP and LTD models (Figure 3A), suggesting that these are being developed to investigate which characteristics of synaptic input patterns lead to LTP versus LTD. Despite limiting the review to models of signaling pathways, the models are extremely diverse in scope, with less than half including only reactions. Other models combine reactions and diffusion, or reactions and electrophysiological phenomena; about one-fifth have all three (Figure 3B). About one-third of the models are size small, meaning that there are less than 20 different chemical species or other model variables, and about half of the models are size large meaning that there are more than 50 different chemical species or other model variables (Figure 3C). The trend is toward increasing numbers of large models, reflecting both the increase in computational power and increasing knowledge of the biochemical pathways. Nonetheless, the continued development of small models reflects their utility in theoretical analysis. Most of the models are still deterministic even though stochastic methods have been developed more and more recently (Figure 3D). The scarcity of stochastic models compared to large models may reflect the availability of software modeling tools and analytic tools. However, several stochastic reaction–diffusion simulation tools have appeared recently (see, e.g., Kerr et al., 2008; Wils and De Schutter, 2009; Andrews et al., 2010; Byrne et al., 2010; Oliveira et al., 2010; Tolle and Le Novère, 2010b). Stochastic methods are important because very small numbers of molecules can have a dramatic effect on either strengthening or weakening the synapses and these effects should be taken into account. Another possibility is to develop and use so-called hybrid simulation methods where specific events are modeled as stochastic and others as deterministic. Though not illustrated graphically, only about one-fourth of the reviewed publications specify the simulation tool or programing language used. Most often the simulation tool used is GENESIS/Kinetikit (Bower and Beeman, 1998; Bhalla, 2002c), XPPAUT (Ermentrout, 2002), and NEURON (Carnevale and Hines, 2006). Programing languages most often used are Java and MATLAB^®.

The trends in Figure 3 lead to several predictions about the future of signaling pathway modeling. The first prediction is that both the number of large models and the size of the largest model will continue to increase. Thus, existing models will be expanded to include additional signaling pathways, in parallel with the increase in experimental data of additional molecular mechanisms. Second, the trend in Figure 3D suggests that increasing number of models will be implemented stochastically or using hybrid deterministic–stochastic methods. The stochastic part of the models in particular may focus on events in the postsynaptic density and other multi-protein complexes. The third prediction is that the scope of the models will expand, with more models of dual LTP and LTD phenomena, in part because both phenomena have been measured in most cell types, and in part because the increase in size of the models is expanding to include signaling pathways for both phenomena. Related to the increase in scope of the models, more will blend reactions with diffusion or electrophysiological phenomena in order to study spatial aspects of signaling and also to better relate to experiments. In particular, modeling reactions alone is not sufficient for understanding synaptic plasticity but also electrophysiological phenomena needs to be taken into account by modeling neuronal networks (Hellgren Kotaleski and Blackwell, 2010). Further development of simulation tools (Pettinen et al., 2005; Alves et al., 2006) together with improvements in parallel computing should help in this endeavor.

Though the trend is toward larger and more complex models, this does not imply that all larger models are better than simpler models. As explained above, the quality of a model depends on many factors. Probably the most important criteria is whether the model can address a question of general scientific interest. For this reason, we have tried to organize our description of the models in order to highlight the questions addressed. Another related criteria is whether a model can make verifiable, i.e. falsifiable, predictions. Using these two criteria, models incorporating more biochemical details often appear superior, but only if the parameters can be adequately constrained. However, models which simplify the equations describing intracellular signaling pathways are more easily integrated with whole neuron electrophysiological models or able to simulate longer time frames. From this perspective they may excel for investigating whether different stimulation patterns change synaptic strength differently. It is important to note that earlier models may have been groundbreaking at the time of publication, yet their perceived quality decreases as more is learned about the interactions of intracellular molecules. Only a couple of studies reduce complex models to simpler ones and show comparative simulation results between the models (see, e.g., Hayer and Bhalla, 2005; Smolen, 2007). The reduction of model complexity will be an important research area in the future because simplified models that can capture relevant aspects of dynamics could be embedded, for example, into biologically-inspired neuronal network models when the activity of individual neurons is modeled in more detail.

To fully understand synaptic plasticity, many different characteristics of signaling pathways need to be considered. Temporal and spatial aspects of signaling are crucially important because they relate the cellular phenomenon of plasticity to the behavioral phenomenon of learning. Not only do theoreticians and modelers need to incorporate experimental findings, but also experimental progress can be enhanced by using model simulations to select the most promising experiments. Careful attention to these issues should improve the utility of modeling approaches for investigating molecular mechanisms of synaptic plasticity. The ultimate future goal of LTP and LTD modeling is to find such models for different brain regions and cells that can explain all the phases of synaptic plasticity, and then use these models to explain the differences in plasticity between brain regions or cell types. Many of the modeling studies have so far concentrated on only one type of synaptic plasticity. We believe that an analysis like the one provided by us will help in this endeavor to make more predictive models for synaptic plasticity in the future.

Abbreviations

4E-BP, 4E-binding protein; AC, adenylyl cyclase; AKT, serine/threonine kinase; AMPAR, α-amino-3-hydroxy-5-methylisoxazole-4-propionic acid receptor; ATP, adenosine triphosphate; BDNF, brain-derived neurotrophic factor; BK_Ca, high-threshold Ca²⁺- and voltage-gated K⁺ channel; CA1, cornu ammonis 1; Ca²⁺, calcium ion; CA3, cornu ammonis 3; Ca_L, high-threshold L-type Ca²⁺ channel; CaM, calmodulin; CaMCa₁, CaM–1Ca²⁺ complex; CaMCa₂, CaM–2Ca²⁺ complex; CaMCa₃, CaM–3Ca²⁺ complex; CaMCa₄, CaM–4Ca²⁺ complex; CaMK, Ca²⁺/CaM-dependent protein kinase; CaMKII, CaMK type II; CaMKIII, CaMK type III; CaMKIV, CaMK type IV; cAMP, cyclic adenosine monophosphate; Ca_N, high-threshold N-type Ca²⁺ channel; CaN, calcineurin; Ca_P, high-threshold P-type Ca²⁺ channel; Ca_T, low-threshold T-type Ca²⁺ channel; CD28k, calbindin; CG-1, Calcium-Green 1; cGMP, cyclic guanosine monophosphate; CICR, Ca²⁺-induced Ca²⁺ release; CPEB1, cytoplasmic polyadenylation element binding protein; CRHR, corticotropin-releasing hormone receptor; ΔI_m, change in membrane current; ΔV_m, change in V_m; D, dimensional; D₁R, dopamine receptor; DA, dopamine; DARPP, cAMP-regulated phosphoprotein; DARPP32, DARPP of 32 kDa; DGC, dentate granule cell; DOQCS, Database of Quantitative Cellular Signaling; EGF, epidermal growth factor; EGFR, EGF receptor; E-LTD, early phase LTD; E-LTP, early phase LTP; ER, endoplasmic reticulum; ERK, extracellular signal-regulated kinase; ERKII, ERK type II; FF, Fura-FF; G, G protein; GABA, gamma-aminobutyric acid; GABA_AR, GABA receptor A; GABA_BR, GABA receptor B; GABAR, GABA receptor; g_AMPAR, AMPAR conductance; GC, guanylate cyclase; $g_{K_{Ca}},$ K_Ca channel conductance; Glu, glutamate; GluN, glutamatergic neuron; Gq, G protein type q; GrC, granule cell; Gs, G protein type s; g_syn, synaptic conductance; I1, inhibitor 1; I_Ca, Ca²⁺ current; IF, integrate-and-fire; I_NMDAR, Ca²⁺ current via NMDAR; IP₃, inositol trisphosphate; IP₃R, IP₃ receptor; I_syn, synaptic current; J_Ca, Ca²⁺ influx; J_NMDAR, Ca²⁺ influx via NMDAR; J_VGCC, Ca²⁺ influx via VGCC; K⁺, potassium ion; K2_Ca, low-threshold K2-type Ca²⁺-gated K⁺ channel; K_A, transient A-type K⁺ channel; K_AHP, after-hyperpolarization K⁺ channel; K_Ca, Ca²⁺- and voltage-gated K⁺ channel; K_DR, delayed-rectifier K⁺ channel; k_{f, Raf}, activation rate for Raf; $K_{GAB{A}_{A}R},$ GABA_AR-activated K⁺ channel; $K_{GAB{A}_{B}R},$ GABA_BR-activated K⁺ channel; K_IR, inward-rectifier K⁺ channel; K_M, muscarine-sensitive K⁺ channel; K_slow, slow Ca²⁺-independent tetraethylammonium-insensitive K⁺ channel; L, large; LGIC, ligand-gated ion channel; LIF, leaky IF; L-LTD, late phase LTD; L-LTP, late phase LTP; LTD, long-term depression; LTP, long-term potentiation; Lyn, Lyn tyrosine kinase; M, medium; MAP2, microtubule-associated protein 2; MAPK, mitogen-activated protein kinase; MEK, MAPK kinase; MgGreen, Magnesium Green 1; mGluR, metabotropic glutamate receptor; MKKP, MEK phosphatase; MKP, MAPK phosphatase; MSN, medium spiny neuron; mTOR, mammalian target of rapamycin; N, neuron; Na⁺, sodium ion; Na_fast, fast Na⁺ channel; Na_r, recurrent Na⁺ channel; Na_slow, non- or slowly inactivating Na⁺ channel; Ng, neurogranin; NMDA, N-methyl-d-aspartate; NMDAR, NMDA receptor; NO, nitric oxide; OGB-1, Oregon Green BAPTA-1; PC, Purkinje cell; PDE, phosphodiesterase; PDE1, PDE type 1; PDE4, PDE type 4; PIP2, phosphatidylinositol biphosphate; PKA, cAMP-dependent protein kinase; PKC, protein kinase C; PKG, protein kinase G; PKM, atypical PKC isozyme; PKMζ, atypical PKC isozyme; PLA₂, phospholipase A₂; PLC, phospholipase C; PMCA, plasma membrane Ca²⁺-ATPase; PN, pyramidal neuron; PP1, protein phosphatase 1; PP2A, protein phosphatase 2A; PSD, postsynaptic density; PV, parvalbumin; Raf, MEK kinase; S, small; S6K, 40S ribosomal protein S6 kinase; SBML, Systems Biology Markup Language; Ser, serine; SERCA, sarco/ER Ca²⁺-ATPase; SoS, son of sevenless; STD, short-term depression; STDP, spike-timing-dependent plasticity; STP, short-term potentiation; Thr, threonine; TrkB, tropomyosin-receptor kinase B; VGCC, voltage-gated Ca²⁺ channel; VGIC, voltage-gated ion channel; V_m, membrane voltage.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.