Probabilistic learning and inference in schizophrenia

Abstract

Patients with schizophrenia make decisions on the basis of less evidence when required to collect information to make an inference, a behavior often called jumping to conclusions. The underlying basis for this behaviour remains controversial. We examined the cognitive processes underpinning this finding by testing subjects on the beads task, which has been used previously to elicit jumping to conclusions behaviour, and a stochastic sequence learning task, with a similar decision theoretic structure. During the sequence learning task, subjects had to learn a sequence of button presses, while receiving noisy feedback on their choices. We fit a Bayesian decision making model to the sequence task and compared model parameters to the choice behavior in the beads task in both patients and healthy subjects. We found that patients did show a jumping to conclusions style; and those who picked early in the beads task tended to learn less from positive feedback in the sequence task. This favours the likelihood of patients selecting early because they have a low threshold for making decisions, and that they make choices on the basis of relatively little evidence.

Introduction

A number of studies have shown that patients with schizophrenia respond faster than healthy subjects in tasks that require them to integrate information to make a response, an effect often called jumping to conclusions (Fine et al, 2007; Garety and Freeman, 1999; Garety et al, 1991; Huq et al, 1988; Moritz and Woodward, 2005; Moritz et al, 2007; Van Dael et al, 2006). In the original version of this task known as the beads or urn task (Huq et al, 1988), subjects were told that beads would be drawn from one of two urns. One urn had 85% red beads and 15% blue beads and the other had 85% blue beads and 15% red beads. The subjects were then shown beads one at a time, and asked to indicate when they thought they had enough information to decide from which urn the beads had been drawn. Patients were more likely than controls to stop the task and make their choice after 1 or 2 draws, and were also more likely to report a stronger belief about the origin of the bead after only a single bead had been drawn. This was taken as evidence for disorganized inference processes in patients with schizophrenia. Aspects of this finding have been replicated in first degree relatives of patients and subjects prone to delusions (LaRocco and Warman, 2009; Van Dael et al, 2006; Warman et al, 2007).

To further examine the cognitive underpinnings of this effect, we compared the performance of patients with schizophrenia with a group of control subjects on the beads task and a stochastic sequence learning task (SSLT). The SSLT was matched closely to the beads task in several respects. Specifically, subjects had to learn a sequence of four button presses using explicit feedback given after each button press. However, on 15% of the trials the feedback given was incorrect, such that if subjects had pressed the correct button they were told that it was incorrect and if they had pressed the incorrect button they were told that it was correct. Thus, if subjects were pressing the correct button, they would receive 85% green feedback and 15% red feedback and if they were pressing the incorrect button they would receive the opposite feedback ratio. Thus, depending upon whether they were receiving predominantly red or green feedback, the subjects could infer whether they were pressing the correct button. This is equivalent to inferring which urn is being drawn from in the beads task. Importantly, in both the beads and the urn task, there is ostensibly a correct answer, and therefore these tasks differ from reinforcement learning tasks in which subjects must associate rewards to visual images, as these tasks have optimal but not necessarily correct answers.

As the SSLT required subjects to learn multiple sequences over multiple blocks of trials, each subject generated sufficient data to allow us to fit accurately a formal learning model, which parameterized learning behavior. Furthermore, this learning model allowed us to separate how much subjects were learning from both positive and negative feedback. This is an important feature of our approach, as previous work has shown that dopamine levels can affect how much subjects learn from positive vs. negative feedback (Frank et al, 2007; Frank and O'Reilly R, 2006; Frank et al, 2004; Klein et al, 2007; Pessiglione et al, 2006; Seo et al, In Press) and therefore behavior on the sequence task might allow us to link performance more directly to changes in the underlying neurobiology, hypothesized to be an increase in striatal dopamine levels in patients with schizophrenia (Abi-Dargham et al, 1998; Laruelle et al, 1996; Waltz et al, 2007), and previously linked to the beads task (Speechley et al, 2010). Previous versions of the beads task have also elicited subjective probability estimates from subjects to address how much was learned from positive vs. negative (i.e. confirmatory vs. disconfirmatory) evidence (Garety et al, 1991; Huq et al, 1988; Langdon et al, 2010; Speechley et al, 2010; Warman, 2008; Warman et al, 2007; Young and Bentall, 1997). However, it is known that even healthy subjects misreport how well they know something (Gigerenzer and Todd, 1999). Therefore, eliciting simple motor responses via the sequence task gives us a more direct estimate of how much the participants had learned, without the intervening step of mapping learning into a subjective probability statement.

The goal of the present study was to extend the previous work in several ways. First, we tested whether the observed deficit was specific to the beads task or represented a more general deficit in decision making behavior evident in related tasks, complementary to other recent work (Ziegler et al, 2008). Second, we examined behavior in a task in which subjects were required to learn repeatedly over multiple blocks, thus generating sufficient data to accurately fit formal learning models. While models can be fit to the beads data, there is normally a limited amount of data available and therefore model fitting can be difficult. Third, we examined the behavior of patients on a task that would allow us to estimate the differential effects of positive and negative feedback on their choices. Finally, we compared performance on the beads task to learning from positive and negative feedback in a related task.

Methods

Subjects

We studied 33 dextral patients (27 male) with DSM-IV schizophrenia (APA, 1994) and 39 control (23 male) subjects (table 1). As there were a larger fraction of males in the control group (χ₁ ² = 4.24, p = 0.039), we included gender as a nuisance factor in all of the ANOVA analyses. One patient and two controls did not finish both the beads and the sequence task, so analysis of the beads task reflects the decreased number of subjects. The maximum number of subjects was used to analyse the data from each task, and when comparisons between tasks were made, the number of subjects that completed both are used. The degrees of freedom in the ANOVA analyses reflect this. Subjects were excluded if they had a history of neurological illness, head injury or illicit substance or alcohol dependence as defined by DSM-IV. Written informed consent was obtained and the study was approved by the Institute of Psychiatry Research Ethics Committee.

Table 1.

Descriptive statistics on patients and control subjects. Medication is expressed in chlorpromazine equivalent units. Medication data was not available for 5 subjects, due to a lack of conversion to chlorpromazine equivalent units for the particular medication.

	Patient group (N = 33, Male = 27)	Control group (N = 39, Male = 23)
	Mean (s.d.)	Mean (s.d.)
Age	38.2 (8.9)	34.9 (13.2)
NART IQ	104.2 (11.8)	110.4 (14.8)
PANSS score
Positive	13.6 (1.0)
Negative	14.7 (1.1)
General	24.8 (1.3)
Five factor PANSS*
Positive	12.7 (1.0)
Negative	13.2 (1.2)
Disorganization	14.8 (0.9)
Excitement	5.4 (6.9)
Emotional Distress	6.9 (0.5)
Medication	322 (50)

^*The five factor PANSS model was taken from (van der Gaag et al, 2006).

Sequence Task

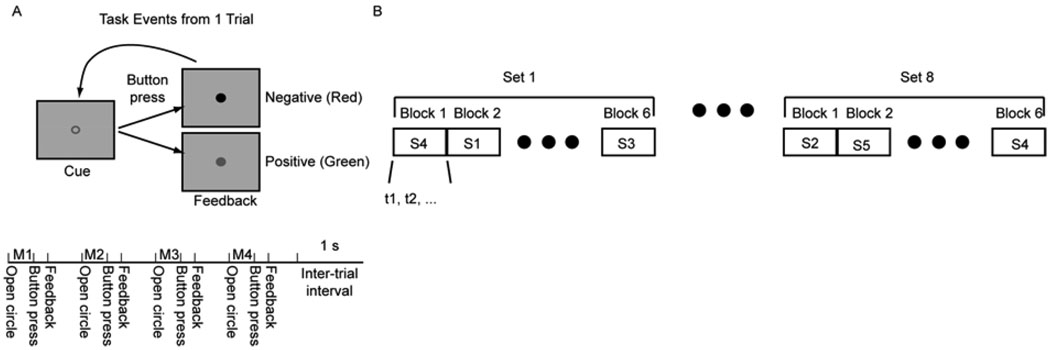
Subjects learned sequences of 4 button presses using two buttons, which were positioned under their left and right hands. Each trial began with the presentation of a green outline circle at the center of the screen which cued the subjects to execute a movement (Fig. 1A, top). They responded by executing a button press with either their left or right index finger. After each response, they were given feedback about whether or not they had pressed the correct button for that movement of the sequence. If they were correct, the outline circle usually filled green, if they were incorrect the outline circle usually filled red. After the feedback had been given they were again presented with a green outline circle which cued the next movement of the sequence. They again pressed one of two buttons and were given feedback. This was repeated 4 times, such that each trial was composed of 4 button presses, with each button press followed by feedback (Fig. 1A, bottom). In 15% of the cases the wrong feedback was given. In other words, if they had pressed the correct button, they were given red feedback, and if they had pressed the incorrect button, they were given green feedback. Subjects were informed of the fact that 15% of the feedback would be inaccurate. Thus, the feedback from any individual button press did not necessarily allow the subjects to correct their mistakes and execute the correct sequence in the subsequent trial. Integrated over trials, however, the subjects could infer the correct button press sequence.

Fig. 1.

Task. A. Top shows sequence of images presented in a single trial. Bottom shows sequence of trial events. Each cue, button press, feedback series is presented 4 times in a single trial. M1 – movement 1, M2 – movement 2, etc. B. Sequence of sets, blocks and trials. Each set is composed of 6 sequence blocks and each block is composed of a single sequence, executed until the learning criterion is met (t1, t2, … refers to trial 1, trial 2, etc.). Subjects progress through a single sequence block by learning and executing the sequence correctly 6 times.

We used 6 of the 16 possible sequences (i.e. 4 button presses with either the left or right thumb gives 16 possible sequences), which were balanced for first order button press probabilities and contained at least two left and two right button presses. The sequences used were LLRR, RRLL, LRLR, RLRL, LRRL and RLLR. Each subject executed 6 sets of 6 blocks, where each block was one sequence (Fig. 1B). A single set consisted of all 6 sequence blocks where the order of the blocks was chosen pseudo-randomly. For example, a block of sequence 4 followed by a block of sequence 1, etc. In each block, subjects had to determine the correct sequence using the stochastic feedback and execute it correctly 6 times before they advanced to the next block. Subjects were informed when the block switched, and thus they knew when they had to start learning a new sequence. If they failed to complete the sequence correctly 6 times by 20 trials they were advanced to the next sequence. In addition, subjects received at least one set of training on all 6 sequences before data collection began. This training familiarized them with the sequences, the stochastic feedback and other aspects of the task. Thus, within the experiment the subjects were familiar with the mechanics of the task and the sequences and their task was to use the stochastic feedback for each sequence to estimate which sequence was correct, and then execute that sequence.

Beads task

The beads task was similar to previous designs (Huq et al, 1988). The task was administered on a laptop computer and instructions were given to the subject as a series of screens on the computer. The experimenter then confirmed that the subject understood the task and answered any questions. Subjects were told that beads would be drawn from one of two urns. One of the urns had 85 blue beads and 15 red beads and the other urn had 15 blue beads and 85 red beads. Beads were shown to the subject one at a time at the center of the screen. Subjects were not informed of whether beads would be replaced or not after each draw. However, given the large number of beads and the limited number of draws, this should have had a minimal effect on decision processes. The subject requested an additional bead by pressing the space bar and guessed that the predominantly blue urn had been drawn from by pressing the ‘B’ key on the keyboard and the predominantly red urn by pressing the ‘R’ key. After each bead was shown it was removed from the screen and no memory aid was provided. Each subject was given five sequences of bead draws and the maximum number of draws was 6. Whether the red or blue urn was more likely correct was randomized within subjects.

Behavioral model

We fit Bayesian statistical models to the subjects’ behavior in the sequence task. The models allowed us to quantify trial-by-trial how much the subjects had learned about which button was correct in the current trial. The model began with a binomial likelihood function for each movement of the sequence, given by:

$$p(D_T|{\theta }_{i,j})={\theta }_{i,j}^{r_{i,j}}{(1-{\theta }_{i,j})}^{N_j-r_{i,j}}$$ (1)

Where θ_i,jis the probability that pressing button i (i ∈ {left, right}) on movement j (j ∈ {1,…,4}) would lead to green feedback. The variable r_i,j, defined below, is the number of times reward (green feedback) was given when button i was pressed on movement j (or red feedback was given when the other button was pressed), and N_j is the number of trials. The vector D_T represents all the data collected up to trial T for the current block, which in this case are the values of r and N. This was the only data relevant to inferring the correct sequence of button presses. Importantly, the model does not contain any information about previous sequences from the current set. Participants were not told that all sequences were given in each set, and therefore it was unlikely that they would be able to infer set boundaries and use this information to improve learning, by estimating which sequences they had not yet executed.

The probability that the left button should be pressed for movement j after T trials (i.e. that it is more likely to be the correct button) is given by:

$${\mathrm{\Delta }}_{j,T}\equiv p_T(p({\theta }_{\mathit{\text{left}},j}|D_T)>p({\theta }_{\mathit{\text{right}},j}|D_T))={\displaystyle {\int }_0^{1}p({\theta }_{\mathit{\text{left}},j}|D_T){\displaystyle \underset{0}{\overset{{\theta }_{\mathit{\text{left}},j}}{\int }}p({\theta }_{\mathit{\text{right}},j}|D_T)d{\theta }_{\mathit{\text{right}},j}d{\theta }_{\mathit{\text{left}},j}.}}$$ (2)

We have written the posterior here under the integral (i.e. p (θ_right,j | D_T)). Button probabilities were equally likely in the experiment so the prior was flat and the posterior is just the normalized likelihood for this estimate.

In order to better predict participant behaviour we added 2 parameters to the basic model that allowed for differential weighting of positive and negative feedback. The differential weighting was implemented by using the following equation for the feedback:

$$\begin{array}{c}\hfill {\mathit{\text{fb}}}_{\mathit{\text{positive}}}=0.5+\alpha \hfill \\ \hfill {\mathit{\text{fb}}}_{\mathit{\text{negative}}}=0.5-\beta \hfill \end{array}.$$ (3)

The subscripts positive and negative indicate whether the feedback was positive (green) or negative (red). The total reward (feedback), in equation 1 was then given by:

$$r_{i,j}(T)={\displaystyle \sum _{t=1}^T{\mathit{\text{fb}}}_{\mathit{\text{positive}},i,j}u(t)+{\mathit{\text{fb}}}_{\mathit{\text{negative}},i,j}(1-u(t)).}$$ (4)

The parameter u(t) is one if green feedback was given and zero if red feedback was given on trial t, and T indicates the current number of movements in the block. Thus, α and β scale the amount that is learned from positive and negative feedback. For an ideal observer both parameters would be 0.5. We also fit a discounted version of this equation to examine the effects of recent feedback on learning. Thus, in this form, the parameter values fit by the model reflect the effects of feedback on the next few choices, with the size of the effect weighted by an exponential decay in time. This allows us to look at how much evidence at the end of the block affects decisions, and whether or not subjects are more strongly revising their choices late in the block. In this case equation 4 becomes

$$r_{i,j}(T)={\displaystyle \sum _{t=1}^T\text{exp}(-\tau (T-t))({\mathit{\text{fb}}}_{\mathit{\text{positive}},i,j}u(t)+{\mathit{\text{fb}}}_{\mathit{\text{negative}},i,j}(1-u(t)))}$$ (5)

In this case τ is the decay parameter, which was set at 0.5. Thus, the feedback in the previous trial (T-1) is weighted with a value 0.6, the feedback in trial T-2 is weighted 0.37, etc. This is in comparison to equation 4 in which all feedback is given equal weight. The parameters, α and β were fit to individual participant decision data by maximizing the likelihood of the participant’s sequence of decisions, given the model parameters. Thus, we maximized:

$$p(D^{*}|\alpha ,\beta )={\displaystyle \prod _{t=1}^T({\mathrm{\Delta }}_t{C}_t+(1-{\mathrm{\Delta }}_t)(1-C_t)),}$$ (6)

where C_t is the choice that the participant made for each movement at time t (C_t=1 for left, C_t=0 for right) and D* indicates the vector of decision data with elements C_t. Here t iterates over the data without explicitly showing sequence boundaries, as this is how the data is analyzed and T is all the data for a single subject. This function was maximized using nonlinear function maximization techniques in Matlab. We also utilized multiple starting values for the parameters (−0.1, 0, 0.1) to minimize the effects of local minima.

Results

Our goal was to address several specific questions. First, do patients with schizophrenia show deficits in the stochastic sequence learning task relative to controls, suggesting a generalized deficit in decision processes? Second, if we examine learning in the SSLT can we see specific deficits in integrating either positive or negative feedback, supporting the dopamine hypothesis? Third, does performance in the SSLT, and specifically learning from either positive or negative feedback in the SSLT correlate with performance in the beads task, which might provide insight into the mechanism that underlies differential performance in patients?

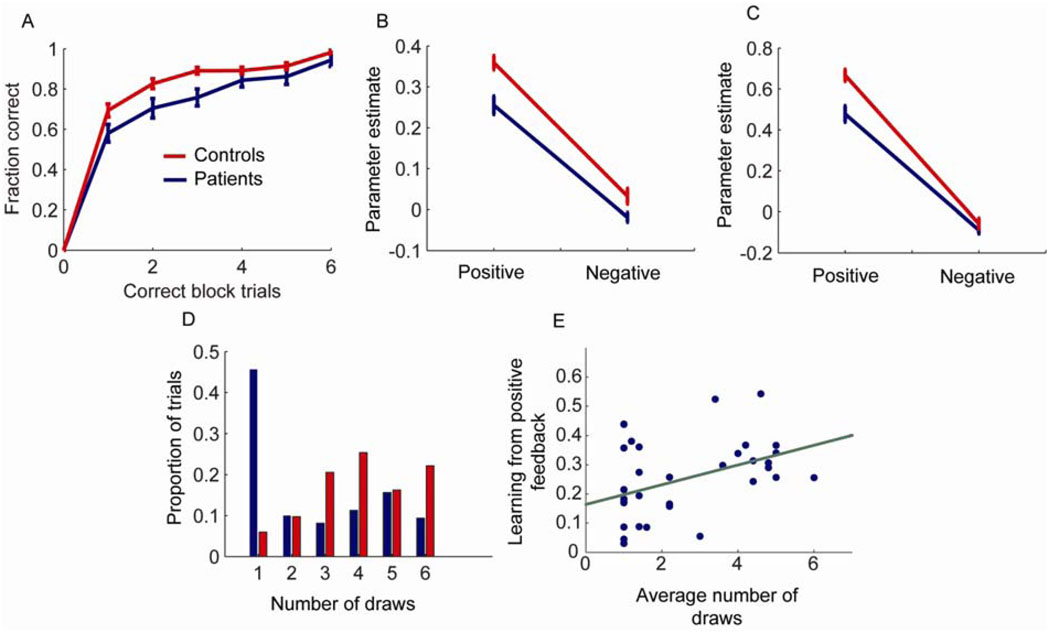
We collected data for analysis from 39 control subjects and 33 patients (Table 1). In the stochastic sequence learning task (SSLT), patients were able to learn the correct sequence but learned more slowly than control subjects (Fig. 2A). Specifically, they executed fewer trials correctly as the block progressed. Repeated measures analysis of the fraction correct data showed a main effect of group (F(1, 70) = 6.8, p = 0.011), a main effect of position in the block (i.e. correct block trials; F(6, 420) = 438.7, p < 0.001) and an interaction between group and position in the block (F(6, 420) = 2.56, p = 0.019). This suggests that patients have a deficit in the SSLT

Fig. 2.

Behavioral and modeling results. A. Fraction of correct trials as a function of the number of correct trials per block. Zero correct trials will always have zero correct by definition. B. Parameter estimates for data fit to entire block of trials for patients and controls showing how much was learned from positive and negative feedback. C. Parameter estimates for data fit to entire block of trials with discounting of old evidence. This analysis emphasizes response to feedback at the end of the block. Note, the overall increase in the parameter values reflects the discount parameter, so they cannot be directly compared to the results in (B). D. Number of draws to decision in the urn task for controls and patients. E. Correlation between average number of draws to decision in patients and learning from positive feedback. Green line shows least squares fit.

Next we fit the Bayesian behavioral model to separate the effects of learning from positive and negative feedback in the SSLT. We first fit the model to all the data from each block of trials, such that the parameters indicate how much each piece of positive or negative feedback affects all subsequent choices (methods equation 4). In this case we found, consistent with the learning data, that patients learned less from both positive and negative feedback, where learning less is shown by smaller parameter values for positive and negative feedback (Fig. 2B). Specifically, there was a main effect of group (F(1, 70) = 13.46, p < 0.001), and a main effect of type of feedback (F(1, 70) = 428.04, p < 0.001) but the group by type of feedback interaction only showed a trend (F(1,70) = 3.3, p = 0.074). Thus, patients generally learned less from both positive and negative feedback and did not differentially learn less from one or the other, relative to controls. Next, we fit the model such that it emphasized recent feedback (methods equation 5). In this case we estimated how much each piece of positive or negative feedback affected the next few decisions, instead of all subsequent decisions. These results were similar (Fig. 2C), in that there was a main effect of group (F(1, 70) = 13.26, p < 0.001), and a main effect of type of feedback (F(1, 70) = 517.88, p < 0.001). In this case, however, there was also a significant interaction between feedback and group (F(1,70) = 7.75, p = 0.007), such that both groups learned similarly from negative feedback, but patients learned relatively less from positive feedback. In effect, late in the block both groups were generally ignoring the negative feedback, which is what they should have been doing if they had inferred the sequence and were executing it correctly.

Examining the performance on the beads task, consistent with previous results, we found that patients guessed the urn earlier than controls (Fig. 2D), and the mean number of draws for each subject was significantly lower for patients (Wilcoxon Rank Sum = 842, p = 0.001). In patients, this inclination to make an early decision, indexed by the average number of draws in the beads task, was significantly associated with learning from positive feedback in the sequence task (Fig. 2E; r(30) = 0.43, p = 0.014, correlating with positive feedback parameter from Fig. 2B). However, patients did not demonstrate a similar correlation with learning from negative feedback (r(30) = 0.27, p = 0.129). Although there was a significant correlation with positive feedback but not negative feedback, these two correlation coefficients were not significantly different (z = 0.697, p > 0.05). In controls there was neither a significant correlation between learning from positive feedback and number of draws (r(35) = 0.13, p = 0.454) nor between learning from negative feedback and number of draws (r(35) = 0.31, p = 0.063).

In the final series of analyses we examined correlations between PANSS scores (positive, negative, general and total), medication (chlorpromazine equivalent units) and performance in the tasks. There were no correlations between learning from positive or negative feedback and any of the clinical variables (p > 0.147). There was a significant positive correlation between the number of draws in the beads task and the positive symptom score (r(30) = 0.372, p = 0.036), although this would not have survived correction for multiple comparisons. The correlation between medication and number of draws in the beads task was also not significant (r(23) = −0.109, p = 0.605).

Discussion

We found, similar to previous studies, that patients with schizophrenia chose an urn more often on the first draw of the beads task than control subjects (Corcoran et al, 2008; Garety and Freeman, 1999; Garety et al, 1991; Huq et al, 1988; Moritz and Woodward, 2005; Moritz et al, 2007; Van Dael et al, 2006). We further found that patients learned more slowly than controls on a stochastic sequence learning task (SSLT). We used a formal model to characterize how well patients and controls were learning from positive and negative feedback in the SSLT. Subsequent to this analysis, we found that the average draw on which patients picked in the beads task was positively correlated with how much they learned from positive feedback, such that patients that picked early also tended to learn relatively less from positive feedback.

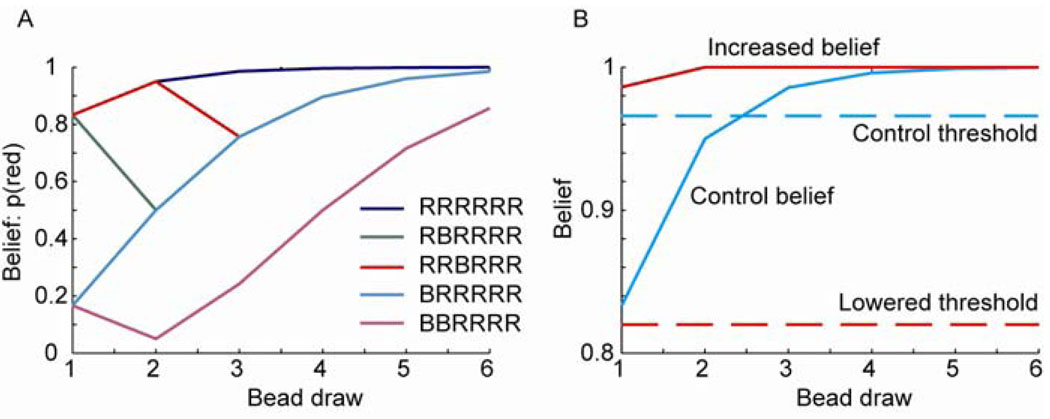
The fact that patients pick early or “jump to conclusions” has been posited as an important component in the development of psychotic symptoms, particularly in cognitive models of delusional beliefs (Garety and Freeman, 1999). It also has some face validity in the classic descriptions of patients attributing delusional interpretations to routine sensory stimuli. While there are several non-specific reasons why patients may select an urn on the basis of less evidence than healthy subjects, two specific formal hypotheses could account for this finding (Fig. 3). Firstly, the patients may over estimate the evidence provided by each bead, leading to an artificially increased confidence. In fact, this has been reported on the basis of subjective probability or certainty statements in the beads and related tasks (Garety et al, 1991; Glockner and Moritz, 2009; Huq et al, 1988; Speechley et al, 2010), although some studies have reported that this is not the case (Dudley et al, 1997; Langdon et al, 2010). Interestingly, work has shown that under some conditions patients can be closer to Bayes optimal than controls in their belief statements (Speechley et al, 2010). This suggests a mechanism by which normal sensory perception may be imbued with an abnormal degree of salience and importance leading to a fixed, false belief (Kapur et al, 2005). The second hypothesis is that there may be a lowered threshold for making decisions, with the decisions based on an accurate belief estimate, consistent with the liberal acceptance account (Moritz et al, 2007). It is also possible that a combination of these mechanisms might be involved.

Fig. 3.

Bayesian belief estimates for the beads task. A. Estimates based on an ideal observer for the indicated sequences. B. Belief estimates of an ideal observer, and two possible hypotheses for why patients jump to conclusions: either they make their decision based on a lowered threshold, or they believe more strongly than they should on the basis of limited feedback. Dashed lines indicate the threshold; solid lines indicate belief estimates for the RRRRRR sequence. Red lines indicate hypotheses for patient performance; blue lines indicate possible control values.

In support of the first hypothesis, positive symptoms, including delusions and hallucinations are often controlled by anti-psychotic medications, which act on dopamine D2 receptors (Seeman et al, 1976), patients with schizophrenia have increased dopamine release under amphetamine challenge compared to healthy control subjects (Abi-Dargham et al, 1998; Breier et al, 1997; Laruelle et al, 1996), and contemporary data suggests that dopamine is involved in learning from feedback (Schultz, 2002). Additionally, studies in patients with Parkinson’s disease on and off medication (Frank et al, 2004), healthy subjects given either dopamine agonists or antagonists (Frank and O'Reilly R, 2006; Pessiglione et al, 2006) and healthy subjects carrying genetic alleles that either up or down regulate dopamine (Frank et al, 2007; Klein et al, 2007), have shown that increasing dopamine availability can increase learning from positive feedback and decrease learning from negative feedback. These three facts suggest that if we assume that there is increased dopamine release in patients during evidence accumulation patients may show early responses or increased probability estimates because they release too much dopamine for each piece of evidence (compare “increased belief” to “control belief”, Fig. 3B). Our data in the sequence task, however, did not support this hypothesis as patients did not learn more from positive feedback than controls. Interestingly, however, in the SSLT increasing dopamine levels in PD leads to less learning from positive feedback (Seo et al, In Press), similar to what we found in patients with schizophrenia. Thus, our data does not support the hypothesis that patients infer the urn early because they are overweighting evidence, but it is consistent with patients having increased dopamine levels.

The alternative hypothesis suggests that patients may integrate belief appropriately, but they might make their choice based upon less evidence (compare “lowered threshold” to “control threshold”, Fig. 3B). Given that the data from the sequence task did not support increased learning from positive feedback, our data suggests that patients respond early because they have a lowered threshold for responding, as indicated in Fig. 3B. This is not likely due to impulsiveness, as patients with schizophrenia draw more beads when the task becomes more difficult, (i.e. using 60/40 beads ratios instead of 85/15 beads ratios leads to more draws) (Dudley et al, 1997; Garety et al, 2005; Lincoln et al, 2010; Moritz and Woodward, 2005). It is important to point out that relatively little is known, at this time, about when subjects choose to respond in belief estimation tasks, or other inference tasks. It is possible, however, that dopamine and/or the basal ganglia play a role in choosing when to respond as much data implicate the basal ganglia in action selection, and often action selection is posed as a go/no-go process.

The proposal that patients make decisions based on less evidence has been described previously as the liberal acceptance hypothesis (Moritz et al, 2009; Moritz et al, 2007). This hypothesis has been supported by experiments which show that patients with schizophrenia show confidence deficits with respect to control subjects in memory tasks (Moritz and Woodward, 2002; Moritz and Woodward, 2006; Moritz et al, 2006; Moritz et al, 2005). In these task subjects were given lists of words to learn under various conditions. After an interval of about 10 minutes the subjects were given words that were either new, or were shown to them during the earlier learning phase of the experiment and asked to indicate whether or not the word was new or learned, and how sure they were. It has been shown that patients with schizophrenia are less confident of their correct answers and over confident when they make errors, a deficit known as a confidence gap. In general, our results are consistent with this. However, it is not easy to directly relate the cognitive constructs in this task with the constructs we are using in our sequence task which makes comparison between the tasks indirect.

We found that patients who picked early also tended to learn less from positive feedback. Thus, the lowered threshold for making choices in patients was associated with decreased learning from positive feedback – compatible with underweighting of each piece of positive evidence. Consistent with this, some previous studies of the beads task have shown that patients actually have lower levels of belief for a given amount of evidence than control subjects (Young and Bentall, 1997). While this could be ascribed to medication effects secondary to dopamine blockade, this is unlikely for two main reasons; first, there was no significant association with dose of antipsychotic medication and second, the jumping to conclusions bias has been demonstrated in healthy subjects with paranoid beliefs and in relatives of patients with schizophrenia (Van Dael et al, 2006).

We also examined whether patients tended to weight recent evidence more heavily by fitting a model which specifically examined the effects of recent feedback on choices. We did not, however, find that patients weighted positive evidence more heavily than control subjects in this analysis, which is inconsistent with results which suggest that patients make larger updates to their belief estimates when given evidence, after the first few pieces of evidence (Garety et al, 1991; Huq et al, 1988; Langdon et al, 2010; Young and Bentall, 1997). However, it is important to point out that our patients were not giving verbal belief estimates, but rather making motor responses on the basis of some internal belief representation. Thus, the differences between our study and previous work may be due to task differences, but it does suggest that the increased belief updating is not a general feature of schizophrenia across inference tasks.

In summary, consistent with previous studies, we found that patients with schizophrenia make decisions early in the urn task. Additionally, the patient group showed robust decreased performance in a sequence learning task, in which they had to integrate feedback to determine the correct sequence of button presses. Furthermore, learning from positive feedback in the sequence task was positively correlated with the number of draws in the beads task. Thus, it seems that these two tasks engage related behavioral processes. Given this, our data suggest that patients with schizophrenia jump to conclusions on the basis of a lower threshold for evidence supporting their decision, rather than increased levels of belief.