Inverse perturbation for optimal intervention in gene regulatory networks

Abstract

Motivation: Analysis and intervention in the dynamics of gene regulatory networks is at the heart of emerging efforts in the development of modern treatment of numerous ailments including cancer. The ultimate goal is to develop methods to intervene in the function of living organisms in order to drive cells away from a malignant state into a benign form. A serious limitation of much of the previous work in cancer network analysis is the use of external control, which requires intervention at each time step, for an indefinite time interval. This is in sharp contrast to the proposed approach, which relies on the solution of an inverse perturbation problem to introduce a one-time intervention in the structure of regulatory networks. This isolated intervention transforms the steady-state distribution of the dynamic system to the desired steady-state distribution.

Results: We formulate the optimal intervention problem in gene regulatory networks as a minimal perturbation of the network in order to force it to converge to a desired steady-state distribution of gene regulation. We cast optimal intervention in gene regulation as a convex optimization problem, thus providing a globally optimal solution which can be efficiently computed using standard toolboxes for convex optimization. The criteria adopted for optimality is chosen to minimize potential adverse effects as a consequence of the intervention strategy. We consider a perturbation that minimizes (i) the overall energy of change between the original and controlled networks and (ii) the time needed to reach the desired steady-state distribution of gene regulation. Furthermore, we show that there is an inherent trade-off between minimizing the energy of the perturbation and the convergence rate to the desired distribution. We apply the proposed control to the human melanoma gene regulatory network.

Availability: The MATLAB code for optimal intervention in gene regulatory networks can be found online: http://syen.ualr.edu/nxbouaynaya/Bioinformatics2010.html.

Contact: nxbouaynaya@ualr.edu

Supplementary information:Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The cell maintains its function via an elaborate network of interconnecting positive and negative feedback loops of genes and proteins that send different signals to a large number of pathways and molecules. Understanding the dynamic behavior of gene regulatory networks is essential to advance our knowledge of disease, develop modern therapeutic methods and identify targets in the cell needed to reach a desired goal. In classical biological experiments, cell function is ascertained based on rough phenotypical and genetic behavior. On the other hand, the use of dynamical system models allows one to analytically explore biological hypotheses. Within this context, investigators have sought to discover preferable stationary states, the effect of distinct perturbations on gene dynamics and the ‘dynamical function’ of genes (Abhishek et al., 2008; Datta et al., 2007; Fathallah-Shaykh et al., 2009; Fathallah-Shaykh, 2005; Qian and Dougherty, 2009; Qian et al., 2009; Ribeiro and Kauffman, 2007; Shmulevich et al., 2002b).

The complexity of biological systems and the noisy nature of the sampled data suggest the use of probabilistic methods for system modeling, analysis and intervention. Markov chain models have been shown to accurately emulate the dynamics of gene regulatory networks (Kim et al., 2002). In particular, the dynamics of Probabilistic Boolean Networks (PBNs) (Shmulevich et al., 2002b) and Dynamic Bayesian Networks (Murphy, 2002) can be studied using Markov chains. The long-run behavior of a dynamic network is characterized by the steady-state distributions of the corresponding Markov chain. It has been argued that steady-state distributions determine the phenotype or the state of the cell development, such as cell proliferation and apoptosis (Ivanov and Dougherty, 2006; Kauffman, 1993). The long-run dynamic properties of PBNs and their sensitivity with respect to network perturbations were investigated in several manuscripts (Qian and Dougherty, 2008, 2009; Shmulevich et al., 2003).

The ultimate objective of gene regulatory network modeling and analysis is to use the network to design effective intervention strategies for affecting the network dynamics in such a way as to avoid undesirable cellular states. As futuristic gene therapeutic interventions, various control strategies have been proposed to alter gene regulatory network dynamics in a desirable way. Biologically, such alterations may be possible by the introduction of a factor or drug that alters the extant behavior of the cell. Current control strategies can be grouped into three main approaches (Datta et al., 2007): (i) reboot the network by resetting its initial condition (Shmulevich et al., 2002c), (ii) introduce external control variables to act upon some control genes, in such a way as to optimize a given cost function (Datta et al., 2003, 2007; Faryabi et al., 2008; Pal et al., 2006), (iii) alter the underlying rule-based structure of the network in order to shift the steady-state mass of the network from undesirable to desirable states. This last type of intervention is also referred to as structural intervention (Qian and Dougherty, 2008; Qian et al., 2009; Shmulevich et al., 2002a).

The first strategy requires knowledge of the basin of attraction of the desirable steady-state distribution. For large networks, finding the basin of attraction of a given steady state is a computationally expensive task (Kauffman, 1993; Wuensche, 1998). The second strategy minimizes a given cost function by controlling the expression level of target genes in the network. In particular, this strategy assumes prior knowledge of the genes to be used as control agents and the cost associated with each state of the network. More importantly, this strategy produces a recurrent control policy, over a possibly infinite time horizon interval (Datta et al., 2003, 2007; Faryabi et al., 2008; Pal et al., 2005b, 2006). Clinically, such an infinite-horizon intervention can be viewed as connecting the patient to an infinitely recurrent feedback control loop. If the control is applied over a finite time horizon and then stopped, the steady-state distribution of the network (and hence the cell fate) may not change.

The third strategy aims at altering the long-run behavior of the network or its steady-state distributions. A simulation-based study was first conducted in Shmulevich et al. (2002a), where a procedure to alter the steady-state probability of certain states was implemented using genetic algorithms. Xiao et al. (Xiao and Dougherty, 2007) considered an analytical study, where they explored the impact of function perturbations on the network attractor structure. However, their algorithms are rather cumbersome as they need to closely investigate the state changes before and after perturbations. Moreover, their practical usefulness is limited to singleton attractors, and they do not provide a steady-state characterization for Boolean networks (Qian and Dougherty, 2008). An analytical characterization of the effect on the steady-state distribution caused by perturbation of the regulatory network appears in Qian and Dougherty (2008). They relied on the general perturbation theory for finite Markov chains (Kemeny and Snell, 1960) to compute the perturbed steady-state distribution in a sequential manner. They subsequently proposed an intervention strategy for PBNs that affects the long-run dynamics of the network by altering its rule structure. However, they considered rank-one perturbations only. The extension of their method to higher rank perturbations is iterative and computationally very expensive. Finally, a performance comparison of the above strategies has been conducted in Qian et al. (2009).

In summary, the first two approaches do not guarantee convergence toward the desired steady-state distribution. The third approach, referred to as structural intervention, aims to shift the steady-state mass from undesirable to desirable states. The proposed solutions thus far have been limited to either simulation-based studies (Shmulevich et al., 2002a) or special cases (e.g. rank-one perturbations) (Qian and Dougherty, 2008; Xiao and Dougherty, 2007). In this article, we provide a general solution to the problem of shifting the steady-state mass of gene regulatory networks modeled as Markov chains. We formulate optimal intervention in gene regulation as a solution to an inverse perturbation problem and demonstrate that the solution is (i) unique, (ii) globally optimum, (iii) non-iterative and (iv) can be solved efficiently using standard convex optimization methods. The analytical solution to this inverse problem will provide a minimally perturbed Markov chain characterized by a unique steady-state distribution corresponding to a desired distribution. Such a strategy introduces an isolated, one-time intervention that will require a minimal change in the structure of the regulatory network and converges to a desired steady-state. Moreover, we cast optimal intervention as a convex optimization problem, thus providing a globally optimal solution that can be efficiently computed using standard toolboxes for convex optimization (Boyd and Vandenberghe, 2003). In particular, we no longer need simulation-based or computationally-expensive algorithms to determine the optimal intervention. The criteria adopted for optimality is designed to minimize potential adverse effects caused by the intervention strategy. Specifically, we will focus on minimization of the change in the structure of the network and maximization of the convergence rate toward the steady-state distribution. We will therefore investigate the following criteria for minimal-perturbation control in the solution of the inverse perturbation problem.

• Reduce the level of change in the expression level of specific genes that are introduced by control agents; that is , we will minimize the overall energy of change between the original and perturbed transition matrices as characterized by the Euclidean norm of the perturbation matrix.

• Increase the rate of convergence of the network to the desired steady-state distribution; thus, we will minimize the time needed to reach the desired steady-state distribution as evaluated by the second largest eigenvalue modulus of the perturbed matrix.

This work differs from previous research in optimal structural intervention in at least three ways: first, we do not evaluate the effect of network perturbation on the steady-state distribution (Qian and Dougherty, 2008, 2009; Qian et al., 2009). Although the subject of perturbation of Markov chains is a well-studied field, unlike the previous works reported in the literature, we do not tackle the subject of perturbation of Markov chains; instead we propose a new framework for the solution of the inverse perturbation problem. That is, the perturbation problem aims to characterize the variation in the stationary distribution in response to a perturbation of the transition matrix (Schweitzer, 1968). The inverse perturbation problem, on the other hand, investigates the perturbation required in order to reach a desired stationary distribution. The proposed approach to the inverse perturbation problem therefore has the potential to have a wide impact in many applications that rely on dynamic systems. Second, unlike the previous work, which is limited to rank-one perturbations, we consider any perturbation that preserves the irreducibility of the original network (Qian and Dougherty, 2008). Third, whereas previous efforts considered unconstrained optimal intervention strategies, we focus on optimal control strategies, which incorporate (energy and rate of convergence) constraints on the protocols employed in gene regulation designed to reduce adverse effects as a result of the intervention strategy.

The mathematical notation used in the article as well as the proofs of several new results are detailed in the Supplementary Material of this article.

2 METHODS

We consider a gene regulatory network with m genes g₁,…, g_m, where the expression level of each gene is quantized to l values. The expression levels of all genes in the network define the state vector of the network at each time step. Gene g_i evolves according to a time-invariant probabilistic law determined by the expression levels of the genes in the network; i.e. Pr(g_i = x_i|g₁ = x₁,…, g_m = x_m), for x_j ∈ {0, 1,…, l − 1} and j = 1,…, m. An approach to obtain the conditional probabilities of the genes from gene expression data has been presented in Kim et al. (2002), Shmulevich et al. (2002d) based on the coefficient of determination in Dougherty et al. (2000). The dynamics of this network can be represented as a finite-state homogeneous Markov chain described by a probability transition matrix P₀ of size n = l^m. The probability transition matrix encapsulates the one-step conditional probabilities of the genes thus indicating the likelihood that the network will evolve from one state vector to another.

The Markov probability transition matrix, describing the dynamics of the network at the state level, can be shown to be related to the actual gene network by observing that the probability law describing the genes' dynamics can be obtained as the marginal distribution of the state transition probabilities:

(1)

where 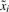denotes the set of all x_j's except x_i; i.e. 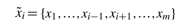. Consequently, if the probability transition matrix P₀ is perturbed linearly with a zero-row sum matrix E = {ϵ_i,j}_1≤i,j≤n, then conditional probability of each gene Pr(g_i = x_i|g₁,…, g_m) is perturbed linearly by ∑_j∈J ϵ_hj, where h is the index of the state vector [g₁,…, g_m] and J is an interval isomorphic to 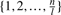. Thus, we observe that ‘small’ perturbations ϵ_ij ≪ 1 of the probability transition matrix that satisfy the zero−row sum condition ∑_j=1ⁿ ϵ_hj = 0, lead to ‘small’ perturbations of the genes' dynamics.

We assume that P₀ is ergodic, i.e. irreducible and aperiodic. Therefore, the existence and uniqueness of the steady-state distribution are guaranteed. In practice, there are several fast algorithms for checking irreducibility and aperiodicity in graphs (Sharir, 1981). If P₀ is ergodic, then the limiting matrix P₀^∞ = lim_n→∞ P₀ⁿ satisfies P₀^∞ = 1π₀^t (Seneta, 2006). In particular, the rows of the limiting matrix P^∞₀ are identical. This demonstrates that, in the ergodic case, the initial state of the network has no influence on the long-run behavior of the chain.

Definition 1. —

A row probability vector μ^t = (μ₁,…, μ_n) is called a stationary distribution or a steady-state distribution for P₀ if μ^tP₀ = μ^t.

Because P₀ is stochastic (i.e. its rows sum up to 1), the existence of stationary distributions is guaranteed (Kemeny and Snell, 1960).

Let π₀ denote the undesirable steady−state distribution of P₀. We wish to alter this distribution by linearly perturbing the probability transition matrix P₀. Specifically, we consider the perturbed stochastic matrix

(2)

where C is a zero row-sum perturbation matrix. The zero row-sum condition is necessary to ensure that the perturbed matrix P is stochastic. Let us denote by π_d the desired stationary distribution. We seek to design an optimal zero row-sum perturbation matrix C such that the perturbed matrix P is ergodic and converges to the desired steady-state distribution π_d.

2.1 The feasibility problem

Schweitzer (1968) showed that the ergodic perturbed matrix P = P₀ + C possesses a unique stationary distribution π_d, which satisfies

(3)

where Z₀ is the fundamental matrix of P₀ given by Z₀ = (I − P₀ + P₀^∞)⁻¹. Equation (3) requires the computation of π₀, the initial undesired steady−state distribution and the fundamental matrix Z₀, which involves the computation of the inverse of an n × n matrix. The following proposition shows that Equation (3) is equivalent to a simpler and computationally more efficient condition.

Proposition 1. —

Consider a stochastic n × n ergodic matrix P₀ with steady-state distribution π₀ and fundamental matrix Z₀. If C is any n × n matrix, and π_d any probability distribution vector, then we have

(4)

In the gene regulatory control problem, we are interested in the inverse perturbation problem. Namely, given the desired stationary distribution, π_d, we wish to determine a perturbation matrix C that satisfies Equation (4). Notice that there may be multiple solutions to Equation (4); i.e. different perturbation matrices C could lead to the same desired stationary distribution. The problem of finding the set of perturbation matrices satisfying Equation (4) can be formulated as the following feasibility problem.

The feasible set of the control problem: Given an ergodic network characterized by its probability transition matrix P₀, with stationary distribution π₀, and given a desired stationary distribution π_d, then the set of perturbation matrices C, which force the network to transition from π₀ to π_d satisfy the following constraints:

(5)

Constraints (ii) and (iii) ensure that the perturbed matrix P is a proper probability transition matrix: constraint (ii) imposes that the perturbation matrix C is zero-row sum, and hence the perturbed matrix P is stochastic and constraint (iii) requires the matrix P to be element-wise non-negative. Let 𝒟 denote the feasible set of perturbation matrices, i.e.

(6)

𝒟 is a polyhedra as the solution of a finite number of linear equalities and inequalities (Boyd and Vandenberghe, 2003). It is easily shown that polyhedra are convex sets (Boyd and Vandenberghe, 2003). Observe that 𝒟 is non-empty because it contains the perturbation matrix C = 1π_d^t − P₀.

Observe that there are numerous (possibly infinite) perturbation matrices C which can force the network to transition from an undesirable steady state to a desirable one. All such perturbations, in principle, constitute plausible control strategies and can therefore be used to drive the network from one steady state to another. We impose the minimum-energy and fastest convergence rate constraints in order to limit the structural changes in the network and reduce the transient dynamics after perturbation.

2.2 The minimal intervention problem

Because the feasible set defined in Equation (5) is non-empty, there exists at least one perturbation matrix C, which forces the network to converge to the desired distribution. A natural question arises then: ‘Which perturbation matrix should we choose?’. In practice, we are interested in perturbation matrices, which incorporate specific biological constraints; e.g. the potential side effects on the patient and the length of treatment. We translate these limitations into the following optimality criteria.

2.2.1 Minimal-perturbation energy control

The minimal perturbation energy control is defined by minimization of the Euclidean-norm of the perturbation matrix. It corresponds, biologically, to the control which minimizes the overall ‘energy’ of change between the perturbed and unperturbed gene regulatory networks. The Euclidean- or spectral-norm of C is defined as

(7)

(8)

where λ_max(C^tC) ≥ 0 is the highest eigenvalue of the positive-semi-definite matrix C^tC, and <, > denotes the inner product operator. The minimum perturbation energy control can be formulated as the following optimization problem:

Minimal-perturbation energy control:

(9)

where 𝒟 is the feasible set in Equation (6).

The optimization problem formulated in Equation (9) is a convex optimization problem. A convex optimization problem is defined as one that satisfies the following three requirements: (i) the objective function is convex; (ii) the inequality constraint functions are convex; and (iii) the equality constraint functions are affine (Boyd and Vandenberghe, 2003). A fundamental property of convex optimization problems is that any locally optimal point is also globally optimal.

Next, we express the convex optimization problem as a semi-definite programming (SDP) problem, which can be solved efficiently using standard SDP solvers, such as SDPSOL (Wu and Boyd, 1996), SDPpack (Alizadeh et al., 1997) and SeDuMi (Sturm, 1999). A list of 16 SDP solvers can be found at the SDP website maintained by Helmberg (2003). We can thus rely on SDP solvers to efficiently compute the optimal perturbation of Boolean gene networks consisting of 10–15 genes (i.e. 2¹⁰ = 1024 to 2¹⁵ = 32 768 states). Note, however, that the computational efficiency of SDP solvers for larger networks will be lower.

Semi-definite programming formulation: using the fact that

we can express the problem in Equation (9) in the following form

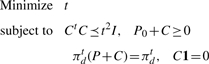(10)

with variables t ∈ ℝ and C ∈ ℝ^n×n. The problem (10) is readily transformed to a SDP standard form, in which a linear function is minimized, subject to a linear matrix inequality and linear equality constraints. We first observe that, from the Schur complement, we have

(11)

The inequalities in (10) can be expressed as a single linear matrix inequality by using the fact that a block diagonal matrix is positive-semi-definite if and only if its blocks are positive semi-definite.

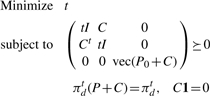(12)

At this stage, it is important to notice that we can similarly consider the L₁ norm to produce a sparse perturbation matrix (Boyd and Vandenberghe, 2003).

2.2.2 Fastest convergence rate control

A clinically viable optimality criterion is to select the perturbation that yields the fastest convergence rate to the desired steady-state distribution. We know that the convergence rate of ergodic Markov chains is geometric with parameter given by the second largest eigenvalue modulus (SLEM) of the probability transition matrix (Seneta, 2006). The smaller the SLEM, the faster the Markov chain converges to its equilibrium distribution. The fastest convergence rate control can be casted as the following optimization problem:

Fastest convergence rate control:

(13)

where 𝒟 is the feasible set in Equation (6). Observe that for a general (non-symmetric) matrix, about the only characterization of the eigenvalues is the fact that they are the roots of the characteristic polynomial. Therefore, the objective function in (13) is not necessarily convex, and thus the optimization problem is not convex.

The following obvious proposition determines the optimal fastest convergence rate perturbation matrix.

Proposition 2. —

The optimal solution of the optimization problem in (13) is given by

(14)

The optimal SLEM (P₀ + C*) = 0.

That is the perturbation C* reaches the desired state in a single jump.

The fastest convergent perturbation may, however, result in a large energy deviation between the original and perturbed networks. Next, we will investigate the trade-offs between minimal-energy and fastest convergence criteria.

2.2.3 Trade-offs between minimal-energy and fastest convergence rate control

We denote by P_E^* the minimal-energy perturbed matrix, i.e. P_E^* = C_E^* + P₀, where C_E^* is the solution of the SDP problem in (12). Let us consider the family of matrices parameterized by s, along the line between P_E^* and the fastest convergent matrix 1π_d^t,

(15)

Equation (15) can be thought of as a continuous transformation of P_E^* into 1π_d^t. The perturbation matrix C(s) = P(s) − P₀ is then given by

(16)

It is easy to check that C(s) ∈ 𝒟 for all 0 ≤ s ≤ 1. When s = 0, we obtain the minimal energy perturbation, and when s = 1, we obtain the perturbation that results in the fastest convergence rate toward the desired steady state. When 0 < s < 1, we will show that we have an inherent trade-off between minimizing the energy and maximizing the convergence rate.

We say that the vector f is a non-trivial eigenvector of a stochastic matrix P if f is not proportional to the vector 1. The following proposition provides an explicit expression of the SLEM of P(s).

Proposition 3. —

λ is an eigenvalue of P(s), 0 ≤ s ≤ 1, corresponding to a non-trivial eigenvector if and only if is an eigenvalue of P_E^* with a non-trivial eigenvector. In particular, we have

(17)

The following proposition shows that the spectral-norm of C(s) is an increasing function of s.

Proposition 4. —

‖C(s)‖₂, where C(s) is given by Equation (16), is an increasing function of s, for all 0 ≤ s ≤ 1.

From Proposition (3), it follows that when s increases, the SLEM of the perturbed matrix decreases, and hence the convergence (toward the desired state) is faster. On the other hand, from Proposition 4, the norm of the perturbation matrix, and hence the energy deviation between the original and perturbed networks, increases as a function of s. Therefore, we have an inherent trade-off between the energy of the perturbation matrix and the rate of convergence. The faster we converge toward the desired steady state, the higher the energy between the initial and perturbed networks.

We would, therefore, like to find the optimal trade-off perturbation matrix. Specifically, we determine the optimal perturbation matrix, which minimizes the SLEM while keeping the energy bounded. Such a constraint can be imposed, for instance, to minimize the side effects due to the rewiring of the original network. The optimal trade-off problem is readily written as the following optimization problem:

(18)

where ϵ ≥ ‖C_E^*‖ is a given threshold. We consider the solution to the optimization problem in (18) along the line defined in Equation (15). A local minimum of the optimization problem in (18) might not belong to the family {P(s)}_s∈[0,1]. However, the line search seems a reasonable choice, and presents several advantages: (i) it provides a closed-form expression of the SLEM of P(s) for all 0 ≤ s ≤ 1; (ii) Contrary to most eigenvalue problems, which are numerically unstable, the line search has an explicit formula, and hence is numerically stable; and (iii) it describes a linear behavior of the optimal solution.

It is straightforward to see that the optimal trade-off perturbation matrix on the line, defined by Equation (15), is given by C* = C(s*), where s* is the unique solution to ‖C(s*)‖₂ = ϵ. However, the optimal trade-off perturbation matrix requires a numerical computation of the minimal energy perturbed matrix ‖P_E^*‖. More importantly, if the bound on the energy ϵ < ‖C_E^*‖₂, then we have no solution for the problem (18). Indeed, in some cases, we might want to constrain the energy of the perturbation matrix C to be no larger than a ‘small’ specified threshold (i.e. ϵ < ‖C_E^*‖₂). We will show that, in this case, we might not be able to reach the desired steady-state distribution. Intuitively, if the energy of the perturbation matrix is constrained to be too small, then we might not be able to force the network to transition from one steady state to another. In this case, we will quantify how far we are from the desired steady state.

Mathematically, the general energy constrained optimization problem can be formulated as follows

Energy-constrained fastest convergence rate control:

(19)

where ϵ ≥ 0. Observe that the optimization problem in (19) is different from the problem in (18) in two points: first, the bound ϵ can be any non-negative number. Second, the perturbation matrix C does not necessarily belong to 𝒟. Observe that the optimization problem in (19) is not a convex optimization problem as the SLEM of a general (non-symmetric) matrix is not necessarily convex. We will look for a solution on the line between P₀ and 1π_d^t, i.e. we consider the family

(20)

The perturbation matrix, C_Q, is therefore given by

(21)

In particular, the norm ‖C_Q‖₂ = s‖1π_d^t − P₀‖₂ can be made arbitrarily small by choosing a small s. On the other hand, it is easy to see that

(22)

The proof of Equation (22) follows the same steps of the proof of Proposition 3. Therefore, it seems that the family {Q(s)}_0≤s≤1 provides a perturbation matrix with an arbitrarily small energy, and an explicit formula for the SLEM of the perturbed network as a function of the SLEM of the original network. The drawback, however, is that Q(s) does not necessarily converge to the desired steady-state distribution. The following proposition quantifies the difference between the steady state of Q(s) and the desired steady-state π_d.

Proposition 5. —

The family of matrices Q(s), given in Equation (20), is ergodic for all 0 ≤ s ≤ 1, and therefore converges toward a unique steady-state distribution π_d(s) given by

(23)

That is

(24)

Furthermore, we have

(25)

where A(P₀) = 1 + sup_k≥1 ‖P₀^k‖₂, which is finite because P₀^k has a limit as k → ∞. If P₀ is symmetric, then we have a simpler upper bound given by

(26)

From Proposition 5, it is clear that when s → 1, π_d(s) → π_d.

3 OPTIMAL INTERVENTION IN THE HUMAN MELANOMA GENE REGULATORY NETWORK

The inverse perturbation control is applicable in every gene regulatory network that can be modeled as a Markov chain. In particular, we note that two of the most popular gene regulatory network models, PBNs and Dynamic Bayesian Networks (DBNs) can be modeled as Markov chains (Lähdesmäkia et al., 2006). In this article, we consider the Human melanoma gene regulatory network, which is one of the most studied gene regulatory networks in the literature (Datta et al., 2007; Pal et al., 2006; Qian and Dougherty, 2008). The abundance of mRNA for the gene WNT5A was found to be highly discriminating between cells with properties typically associated with high versus low metastatic competence. Furthermore, it was found that an intervention that blocked the Wnt5a protein from activating its receptor, the use of an antibody that binds the Wnt5a protein, could substantially reduce Wnt5A's ability to induce a metastatic phenotype (Pal et al., 2006). This suggests a control strategy that reduces WNT5A's action in affecting biological regulation.

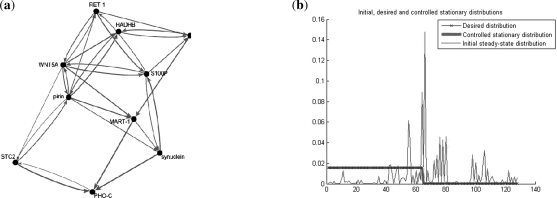
A seven-gene probabilistic Boolean network model of the melanoma network containing the genes WNT5A, pirin, S100P, RET1, MART1, HADHB and STC2 was derived in Pal et al. (2005a). Figure 1a illustrates the relationship between genes in the human melanoma regulatory network. This diagram is a conceptual abstraction and is not intended as an explicit mechanistic diagram of regulatory actions. The influences depicted may be the result of many intervening steps that are not shown. Some generalizations that emerge from this conceptual diagram, such as the wide influence of the state of WNT5A on the states of other genes, have been confirmed experimentally (Kim et al., 2002). Note that the Human melanoma Boolean network consists of 2⁷ = 128 states ranging from 00 … 0 to 11 … 1, where the states are ordered as WNT5A, pirin, S100P, RET1, MART1, HADHB and STC2, with WNT5A and STC2 denoted by the most significant bit (MSB) and least significant bit (LSB), respectively. The probability transition matrix of the human melanoma network, derived in Zhou et al. (2004) and used in this article, is courtesy of Dr Ranadip Pal.

Fig. 1.

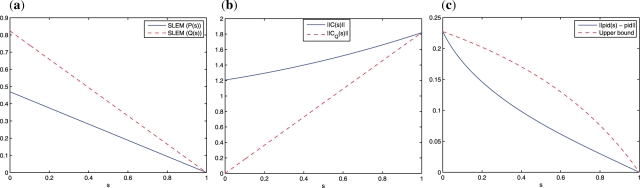
Optimal intervention in the human melanoma gene regulatory network. (a) An abstract diagram of the melanoma gene regulatory network (Kim et al., 2002). Thicker lines or closer genes are used to convey a stronger relationship between the genes. The notion of stronger relation between genes is used convey a higher probability of influence on their gene expression levels. For instance, WNT5A and pirin have a strong relationship to each other as illustrated by their proximity in the diagram and the thickness of the lines connecting between them; (b) The original (red line), desired (blue line) and minimal-perturbation energy controlled (green line) steady-state distributions of the human melanoma gene regulatory network. The x-axis represents the 128 states of the network ranging from 00…0 to 11 … 1, and the y-axis indicates the probability of each state. Note that the controlled and desired steady-state distributions are identical.

A naive control strategy, which would exclusively target the gene WNT5A by reducing its expression level while keeping the expression levels of the other genes in the network unchanged, will inevitably fail as it basically resets the initial state of the underlying process and does not alter the network structure. Biologically, the complex gene interactions in the network will almost certainly bypass this gene perturbation and return to their initial cancerous state. On the other hand, determining the optimal gene intervention by a brute-force approach is computationally intractable and experimentally infeasible: even within the context of Boolean regulation (two-level quantization), the number of experiments to perform increases exponentially in the number of genes in the network. For instance, in the seven-gene melanoma network, an extensive control search amounts to performing 2186 laboratory experiments; i.e. downregulate and upregulate the expression level of every gene, every pair of genes, every triple of genes, etc., thus requiring 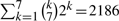laboratory experiments. The proposed inverse perturbation control provides the optimal one-time intervention that rewires the network in order to force it to converge to the desired steady state.

Using the breadth first search algorithm (Russell and Norvig, 2003), we found that the melanoma probabilistic Boolean network is irreducible. Therefore, it has a unique stationary distribution, and we can apply the inverse perturbation control developed in this article. Because the control objective is to downregulate the WNT5A gene, we consider the desired steady-state distribution where the probability of the states having WNT5A upregulated is 10⁻⁴ and the probability of the other states, which correspond to WNT5A downregulated is set equal to 0.015 525 (see Fig. 1b). Observe that the states from 0 to 63 have WNT5A downregulated (0) and hence are desirable states, as compared with states 64 to 127 that have WNT5A upregulated (1) and hence are undesirable. The probability transition matrices of the human melanoma networks corresponding to the original and perturbed networks are portrayed in Figure 2. Observe that the family of perturbed matrices {P(s)}_s∈[0,1], defined in Equation (15), converges toward the desired steady-state distribution π_d, in the sense that P(s)ⁿ → 1π_d^t as n → ∞. On the other hand, the family of matrices Q(s), defined in Equation (20), does not converge to the desired distribution π_d, for 0 ≤ s < 1. Figure 3c shows the norm difference between the steady-state distribution of Q(s), π_d(s), and π_d as a function of s. As the parameter s increases, π_d(s) → π_d. The advantage of considering the family {Q(s)} resides in the ability to design perturbation matrices C(s) with arbitrary small norms (energy) (see Fig. 3b). This is in contrast to the family {P(s)} where the norm of the perturbation matrices is lower bounded by the minimal-energy perturbation matrix norm ‖C_E^*‖. The trade-off between the minimal-energy and fastest convergence rate is depicted in Figure 3a and 3b. The steady-state distribution of the human melanoma network of the original and perturbed networks are shown in Figure 1. Observe that the after-control steady state is identical to the desired steady state. Therefore, the control has enabled us to shift the steady-state probability mass from the undesirable states to states with lower metastatic competence.

Fig. 2.

Initial and controlled probability transition matrices for the human melanoma gene regulatory network. The matrix plots are obtained using the function MatrixPlot in MATHEMATICA. They provide a visual representation of the values of elements in the matrix. The color of entries varies from white to red corresponding to the values of the entries in the range of 0 – 1. (a) The probability transition matrix of the original melanoma network P₀, which converges toward an undesirable steady-state distribution; (b) the minimal-energy perturbed probability transition matrix P_E^*; (c) P_E^*10; (d) the fastest convergence rate perturbed probability transition matrix 1π_d^t; (e) P(0.1) in Equation (15); (f) P(0.9) in Equation (15); (g) P(0.1)¹⁰; (h) P(0.9)¹⁰; (i) Q(0.1) in Equation (20); (j) Q(0.9) in Equation (20); (k) Q(0.1)¹⁰; (l) Q(0.9)¹⁰. Observe from (c) and (g) that P_E^* and P(s) ‘converge’ toward the desired steady-state distribution π_d, whereas Q(s) ‘converges’ toward π_d only for s = 1.

Fig. 3.

The human melanoma gene regulatory network: (a) Plot of SLEM(P(s)) in Equation (17) (blue continuous line) and SLEM(Q(s)) in Equation (22) (red dashed line) versus s; (b) Plot of ‖C(s)‖ in Equation (16) (blue continuous line) and ‖C_Q(s)‖ in Equation (21) (red dashed line) versus s; (c) Plot of ‖π_d(s) − π_d‖ (blue continuous line), and the upper bound 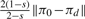(red dashed line) versus 0 ≤ s ≤ 1, in Proposition 5. The trade-off between minimal-energy and fastest convergence rate control is clear from (a) and (b). The parameterized family of perturbed matrices P(s) in Equation (15) results in a faster convergence toward the desired steady-state π_d at the expense of a higher norm (energy) of the perturbation matrix. On the other hand, the family of perturbed matrices Q(s) in Equation (20) leads to a perturbation matrix with norm (energy) as small as desired, but at the expense of not converging toward the desired steady state for small s. The distance between the steady state of Q(s) and the desired steady state as a function of s is shown in (c).

The minimal-energy perturbed matrix, which optimally solves the SDP problem in (12), is ‖C_E^*‖₂ = 1.20 667 and its SLEM = 0.4696. We have shown that the optimal SLEM of the fastest convergence rate control is equal to 0, and its energy is given by ‖C‖₂ = ‖1π_d^t − P₀‖₂ = 1.81 854. The SDP problem has been implemented in MATLAB and uses the CVX software for convex optimization (Grant and Boyd, 2010).

The mathematical findings derived were confirmed by computer simulation experiments by demonstrating that the optimal perturbation of a known melanoma gene regulatory network leads to a desired steady state. In order to reach the full impact of the proposed research on gene regulation in biological systems, we plan to investigate changes in the cell that induce the optimal perturbed transition matrix. In particular, our current and future work will focus on determining the optimal biological design rules needed to induce the optimal intervention strategy while limiting ourselves to biologically viable design rules that rely on modern methods for molecular control in cellular systems.

4 CONCLUSION

In this article, we introduced a novel method for optimal intervention in gene regulatory networks posed as an inverse perturbation problem. The optimal perturbation has been derived such that the regulatory network will transition to a desired stationary or steady-state, distribution. Biological evidence suggests that steady-state distributions of molecular networks reflect the phenotype of the cell. In other words, both malignant (e.g. cancer) and benign phenotypes correspond to steady-state distributions in dynamic system models of gene regulatory networks.

We developed a mathematical framework for the solution of the inverse perturbation problem for irreducible and ergodic Markov chains. Our aim was to derive a minimal-perturbation intervention policy designed to introduce an isolated, one-time intervention and induce few changes in the original network structure, thus minimizing potential adverse effects on the patient as a consequence of the intervention strategy. The mathematical analysis presented provides a general framework for the solution of the inverse perturbation problem for arbitrary discrete-event ergodic systems.