Biophysical information representation in temporally correlated spike trains

Abstract

Spike trains commonly exhibit interspike interval (ISI) correlations caused by spike-activated adaptation currents. Here we investigate how the dynamics of adaptation currents can represent spike pattern information generated from stimulus inputs. By analyzing dynamical models of stimulus-driven single neurons, we show that the activation states of the correlation-inducing adaptation current are themselves statistically independent from spike to spike. This paradoxical finding suggests a biophysically plausible means of information representation. We show that adaptation independence is elicited by input levels that produce regular, non-Poisson spiking. This adaptation-independent regime is advantageous for sensory processing because it does not require sensory inferences on the basis of multivariate conditional probabilities, reducing the computational cost of decoding. Furthermore, if the kinetics of postsynaptic activation are similar to the adaptation, the activation state information can be communicated postsynaptically with no information loss, leading to an experimental prediction that simple synaptic kinetics can decorrelate the correlated ISI sequence. The adaptation-independence regime may underly efficient weak signal detection by sensory afferents that are known to exhibit intrinsic correlated spiking, thus efficiently encoding stimulus information at the limit of physical resolution.

Negative-feedback processes are ubiquitous in biological systems. In neurons, spike-triggered adaptation processes inhibit subsequent spiking and can produce temporal correlations in the spike train, in which a longer than average interspike interval (ISI) makes a shorter subsequent ISI more likely and vice versa. Such correlations are common in neurons (1–7) and model neurons (8–14). The impact of temporal relationships in spike trains, including ISI correlations, on neural information processing has been under intense investigation (1, 2, 15–22). Temporally correlated spike trains pose a challenge for ISI-based sensory inferences because each ISI depends on both present and past stimulus activity, requiring complex strategies to make accurate inferences (23, 24). Some ISI correlations can be attributed to long-time-scale autocorrelations of the input (23, 25) or correlations related to long-time-scale adaptive responses (23, 26). However, if the ISI correlations arise from inputs or noise with fast autocorrelation time scales relative to both the mean ISI and the adaptation time scales of the cell, the resulting fine-grained time structure of spike trains can shape information processing of the underlying slower input fluctuations (2, 3, 11, 15, 18, 19, 27–29). Specifically, Jacobs et al. (29) have recently shown that fine-grained temporal coding of ISIs that takes into account adaptive responses (e.g., refractoriness) not only conveys significant information, but the information benefit accounts for behaviorally important levels of stimulus discrimination.

If fine-grained temporal encoding is utilized for neural spike patterns, how are the temporal codes computed and communicated to postsynaptic neurons? This question is commonly posed as a “decoding” problem, in which statistical models are used to infer likely inputs (15, 17, 22, 29, 30). Whereas these analyses can evaluate if an encoding of the spike train is viable, in this article we investigate the subjacent question of how internal cellular dynamics can represent a fine-grained spike train encoding and carry out decoding.

Commonly, spike-triggered adaptation currents (ACs) decay exponentially, reflecting state transitions of a large number of independent molecules governing the current’s conductance (31). Through analysis of mathematical models, we show that an AC can efficiently represent spike train information. Our main result is that the dynamics of correlated spike emission can create statistical independence in the adaptation process. That is, we have found an independent statistical decomposition of correlated spike trains. Decoding of correlated ISIs involves inferences on the basis of conditional probability distributions (11, 29, 30). Yet, we find the AC activation states are a probabilistically independent and biophysical representation of the ISI code that does not require decoding on the basis of more computationally costly conditional probabilities. This dynamical coding property is distinct from coarse-grained integrative coding by slow-time-scale, activity-dependent processes (32–35). We further show that the entropy of the AC states represents the maximal stimulus information when the AC system is sufficiently activated and displays weak signal detectability levels equivalent to noncorrelated Poisson ISI coding but at a much-reduced firing-rate gain. We conclude by showing how simple synaptic dynamics may communicate adaptation state information to postsynaptic targets, which provides a testable experimental prediction of our theory. The adaptation-independence property is relevant to information transmission in regular-firing sensory afferents (1, 3, 36), in which correlated spike sequences are used to discriminate weak underlying signals from noise (2, 3, 11).

Results

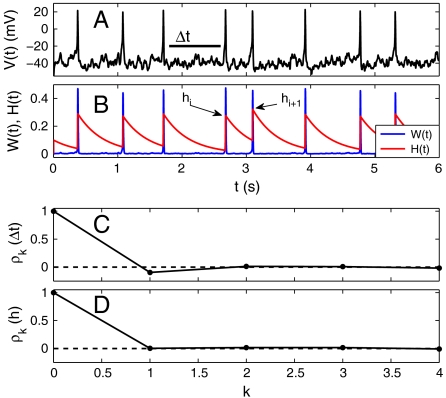
Noisy stimulus current injection x(t) to a Morris–Lecar (ML) model (37), with generic parameters (38), produced input fluctuation-driven spike patterns (Fig. 1A and SI Text, SI Methods). We set the constant injected current I_m = 38 nA/cm² to be just below the deterministic threshold for firing, so that fluctuations in the noisy input x(t) determine spike times {t_i}. The strength of the fluctuations was large enough to perturb V(t) past spiking threshold but small enough to not obscure the intrinsic spike kinetics. In addition to the fast-activating potassium current W(t) responsible for spike repolarization, the model possessed a slower-decaying spike-activated AC: H(t) (31, 35) (Fig. 1B). The AC kinetics were modeled as a voltage-gated potassium channel, similar to a KV3.1 channel (2, 31).

Fig. 1.

Morris–Lecar model exhibits fast-fluctuating input-driven spike trains (A). A spike at time t_i activates the AC, which can vary in peak amplitude h_i, depending on the previous ISI: Δt_i-1 = t_i - t_i-1 (B). Serial ISI correlations ρ_k between Δt_i and Δt_i+k exist only between subsequent ISI pairs (k = 1), whereas longer-range pairs (k > 1) are uncorrelated (C). Paradoxically, peak AC amplitudes (h_i) are uncorrelated (D).

Activation of the AC hyperpolarizes the membrane and discourages spiking. Spikes that occur in quick succession induce elevated AC activation, making the later ISIs longer on average, whereas low AC values make subsequent ISIs shorter on average; both cases result in temporal ISI correlations. Monte Carlo simulations reveal that ISI correlations ρ_k = Corr(Δt_i,Δt_i+k) (where Δt_i = t_i+1 - t_i) exist only between subsequent ISIs (Δt_i and Δt_i+1), but all later ISIs (k > 1) have effectively zero correlation in the parameter regime we have chosen (Fig. 1C). Note that without random fluctuations in x(t) there would be no ISI correlations and only rhythmic firing or silence, depending on the bias current I_m. Hence, the ISI correlations are induced by the fast-fluctuating input x(t), and so the correlations can be used to infer properties of x(t).

In addition to ISI correlations, we also investigated correlations in the AC conductance H(t). We measured the peak activation of H(t), defined as h_i, that occurs immediately after each spike (see Fig. 1B). The h_i value defines the activation level of the current, and so we refer interchangeably to h_i as the AC activation state associated with each spike. Paradoxically, the h_i activation states are uncorrelated (Fig. 1D). How this zero correlation property emerges through the dynamical coupling between the adaptation H(t) and the spike generation mechanism is investigated in the following.

Mathematical Analysis.

What conditions allow for ISI correlations to emerge together with uncorrelated AC activation states h_i? To answer this question, we derived a more analytically tractable model of AC-limited spike emission, starting with H(t). To simplify, note that the smooth H dynamics in Fig. 1B exhibit a long exponential decay phase between spikes followed by a fast activation phase during a spike. By approximating these phases of H(t) with piecewise exponentials (see SI Text, Approximation of H(t) and Derivation of Q(h|h^′)), we derived a map from h_i to h_i+1:

[1]

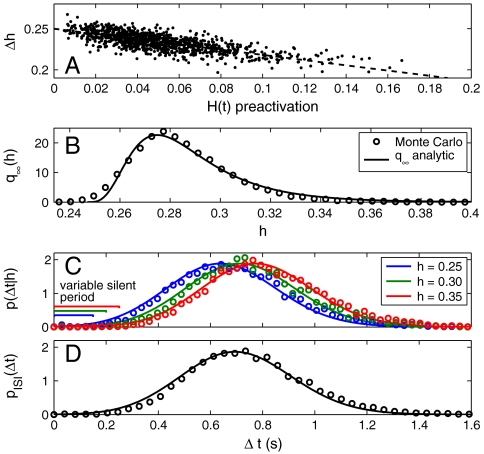
The parameter Λ∈(0,1) is the minimum activation level for H(t), and τ is the decay time scale. Setting Λ = 1 is an extreme case in which the current is always maximally activated for every spike, whereas the other extreme (Λ = 0) is a nonadapting process [H(t) = 0]. The linear map [1] approximates the activation states h_i of H(t) as evidenced in the plot of the activation change Δh ≡ h_i+1 - h_ie^-Δt_i/τ as a function of the AC level just prior to the activation phase H ≈ h_ie^-Δt_i/τ (Fig. 2A). This linear relationship has a y intercept Λ and slope -Λ.

Fig. 2.

Analytical model [6] captures the spike statistics of the biophysically realistic model with α = 16.7, β = 29, and τ = 400 ms. (A) The H(t) pre- minus postactivation change Δh = h_i+1 - h_ie^-Δt_i/τ exhibits a linear relationship with the preactivation level H(t) ≈ h_ie^-Δt_i/τ with slope -Λ ≈ -0.246. The Morris–Lecar system’s empirical limiting distributions (dots) of AC states h (B), and ISI distributions, conditioned on h, with h-dependent variable silent periods (C), and unconditioned (D), are fit by Eqs. 1–6 (solid lines).

Because Λ < 1, the map f, [1], can always be inverted to solve for Δt_i:

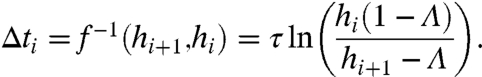[2]

Hence, the h_i sequence contains the same information as the ISI sequence. Note that the h_i values are contained in the interval (Λ,1), from which we infer from [2] that Δt_i≥0 implies h_i+1 ≤ Λ + h_i(1 - Λ).

The sequence from h_i to h_i+1 is determined by the intervening ISI, which is stochastically determined by the fluctuating input x(t). Here we derive the stochastic dynamics of the h_i sequence by approximating the stochastic spike process that generates Δt_i. Following Muller et al. (12), the likely times of the next ISI, conditioned on h_i, are decided by the probability density p(Δt_i|h_i) (defined below). Longer ISIs should be more likely for larger h values and vice versa (Fig. 2C). Assuming for now that p(Δt_i|h_i) is known, we define the Markov transition function Q from h^′ ≡ h_i to h ≡ h_i+1 by substituting Δt = f^-1(h,h^′):

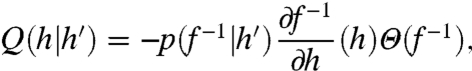[3]

where the negative sign ensures positivity of the operator, ∂f^-1/∂h is the Jacobian of f^-1 [we abbreviate f^-1 = f^-1(h,h^′)], and Θ(x) is the Heaviside step function (see SI Text, Approximation of H(t) and Derivation of Q(h|h^′)). The Heaviside factor in [3] disallows (h,h^′) combinations that lead to impossible negative ISIs. We define the stochastic dynamics of the h sequence in terms of the evolution of an h distribution q_i(h^′) at the ith spike, to the next q_i+1(h):

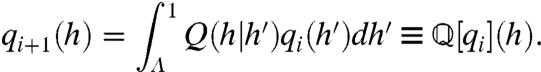[4]

Note that 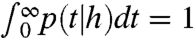and 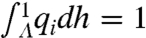imply 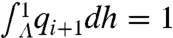. Thus, [4] maps densities to densities. Under mild conditions of irreducibility and ergodicity, Frobenius–Perron theory (39) predicts that there exists a unique limiting distribution q_∞(h) such that 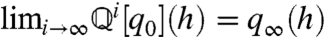, in which 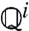is the ith operator composition, for any starting distribution q₀. Given q_∞ exists, the ISI density is calculated as

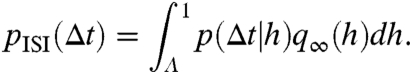[5]

Fig. 2 B–D shows analytical approximations to the ML Monte Carlo results for q_∞(h), p(Δt|h), and p_ISI(Δt), respectively, which are derived as follows.

We generated p(Δt|h) with a spike rate function λ(H)≥0, in which the probability of a spike in a small time interval δt is λ(H)δt (12, 30, 40). To correctly model the effect of the AC on spiking, λ(H) must elicit lower rates for large H and vice versa. The conditional ISI density is calculated as 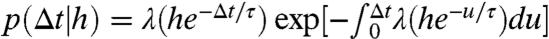. Without loss of generality, we used the specific model (12):

[6]

The parameter α > 0 sets the overall spike rate of the cell, and β≥0 sets the strength of AC. If β is large, then moderate activation levels of H induce a silent period until H(t) decays sufficiently (see Fig. 2C). Conversely, a small β reduces the effect that H has on spike probability. Choosing β = 0 or Λ = 0 yields homogeneous Poisson firing statistics from the model in [6] with rate α. Hence, there is a homotopy between adapting and Poisson trains through β or Λ.

The exponential dependence of firing rate on H in [6] arises commonly from spiking neural models on the basis of diffusion processes, where the effect of noisy input x(t) is represented as a probability of spiking per unit time (12, 14, 30, 40–42). Moreover, Eq. 6 approximates biophysically realistic models such as ML (Fig. 2) effectively over a realistic range of baseline input and fluctuation levels, provided that the autocorrelation time scale of input current is fast relative to the mean ISI (12, 40), which is consistent with the fast-fluctuating noisy input x(t) used in Fig. 1.

Adaptation Independence.

By analyzing the transition function Q in [3], we can show that the sequential h values can be not only uncorrelated (Fig. 1D) but also statistically independent. For a general rate function λ(H), Eq. 3 becomes

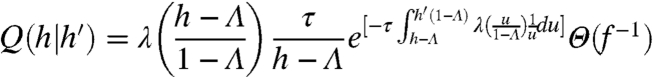[7]

(see SI Text, Approximation of H(t) and Derivation of Q(h|h^′)). Independence is established by proving that the Markov transition [7] does not depend on h^′: Q(h|h^′) = Q(h), which also implies q_∞(h) = Q(h). Independence is achieved if the rate function

[8]

The condition [8] requires the peak activation h≥Λ to inhibit spiking for a nonzero time period until the AC decays. For the specific λ in [6], independence occurs if β (the strength of the AC) is sufficiently large: βΛ - ln(ατ)≫1. The physiological meaning of the condition [8] is that each AC activation must induce a nonzero postspike silent period Δw ≡ τ ln(h^′/Λ), as is illustrated in Fig. 2C, in addition to the usual absolute and relative refractory periods. The silent period is nonstochastic for a given h^′ and ends when H(t) decays below the threshold value Λ so that λ[H(t)] > 0—the larger the h^′ value, the longer the silent period. The selection of h is determined by the remaining stochastic portion of the ISI Δt - Δw, which is a renewal process, and thus is independent of h^′. Note also that the independence condition [8] is generic for all AC time scales τ because λτ in the integral of [7] is nondimensional. Of course, an AC-mediated silent period is a common phenomenon, so the result is broadly applicable, including to the model in Figs. 1 and 2 and SI Text, Fitting the ML Model.

To prove that [8] implies independence, assume [8] holds. Then the upper integration limit of [7] can be replaced with the lower bound h^′ = Λ≥Λ(1 - Λ) or any value above it with no consequence because the integrand is effectively zero above the bound. Furthermore, [8] gives an upper bound for h, because Q(h|h^′) ∼ 0 for h≥Λ(1 - Λ) + Λ≥Λ, so h∈[Λ, min(2Λ - Λ²,1)]. Note that h∈[Λ, min(2Λ - Λ²,1)] implies f^-1 > 0, and so the Heaviside factor in [7] can be omitted. Finally, the Jacobian 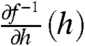in [3] depends only on h and not h^′. Taken together, the above deductions imply Q(h|h^′) = Q(h) = q_∞(h), which is independence (see SI Text, Fitting the ML Model). In the following, we analyze how changes in mean firing rate affects adaptation independence and spike statistics, including correlations.

Spike Train Statistics.

In the independence regime, realistic correlated spike trains can be generated from independent realizations of q_∞-distributed activation states {h_i} by f^-1(h_i+1,h_i) = Δt_i. Independence also explains why only adjacent ISIs are correlated in Fig. 1C: Δt_i and Δt_i+1 both depend on h_i+1 and so are correlated, whereas Δt_i and Δt_i+k for k≥2 are independent because they are determined by distinct and independent activation states. Conversely, in the nonindependent regime, nonadjacent ISIs exhibit correlations (see SI Text, Fitting the ML Model, and Fig. 3 below).

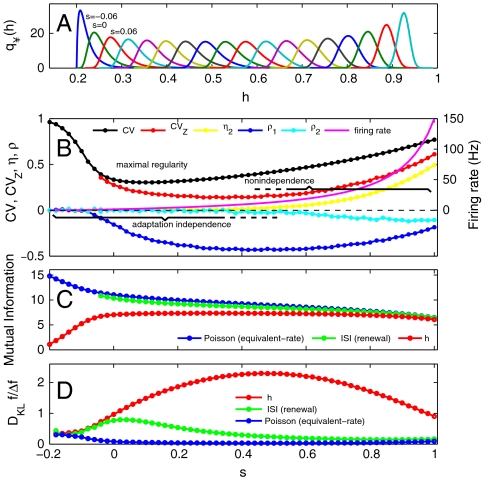
Fig. 3.

Input discrimination from AC states is efficient relative to similar uncorrelated spike trains. (A) over a range of inputs s from s = -0.06 to 1 for the model (Eq. 6, τ = 400 ms, Λ = 0.2, α = 14.63 s^-1, β = 30; see SI Text, Fitting the ML Model for an analysis of parameter variation). (B) CV versus input s has Poisson statistics (CV = 1) for low input levels (s < 0). Increased input leads to more regular spiking that overlaps the region of adaptation independence (s approximately less than 0.4) where the secondary eigenvalue of the h operator is essentially zero (η₂ ∼ 0). As input increases, it causes a loss of independence (η₂ > 0), corresponding to increased spike train irregularity measured by CV_Z. (C) Mutual information I_AC exhibits a plateau region of elevated information for sufficiently activated AC states but is uniformly lower than the mutual information of the renewal ISI process [p_ISI(Δt), Eq. 5, lower points omitted but are very near Poisson] and the bounding equivalent-rate Poisson mutual information. (D) The information gain D_KL divided by the proportional change in firing rate Δf_A/f_A for Δs = 0.02 shows the AC system has greater discriminability per firing-rate change compared to the equivalent renewal ISI process and the equivalent-rate Poisson process.

The variability in the h_i sequence is also the source of the negative ISI correlation structure in the adaptation-independence regime (Fig. 1C). By inserting f^-1(h_i+1,h_i) = Δt_i into the ISI covariance formula Cov(Δt_i,Δt_i+1) = 〈Δt_iΔt_i+1〉-〈Δt_i〉² and using Chebyshev’s algebraic inequality (see SI Text, ISI Correlations), we deduce from independence that

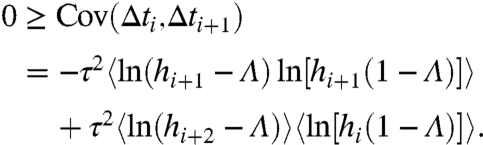[9]

Thus, sequential ISIs have nonpositive correlations in the adaptation-independent regime, consistent with Fig. 1C. Furthermore, ISI correlations are zero only if h does not vary. That is, Cov(Δt_i,Δt_i+1) → 0 only if q_∞(h) → δ(h - 〈h〉), where δ(·) is the Dirac functional, which occurs only in the limit of zero stochastic input [i.e., x(t) → 0].

Negative serial ISI correlations regularize the spike train over long time scales, as can be understood by analyzing the variability of the sum of n sequential ISIs: 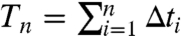(10). Recall that Δt_i/τ = ln[h_i(1 - Λ)] - ln(h_i+1 - Λ), so T_n is a telescoping sum of n + 1 summands: 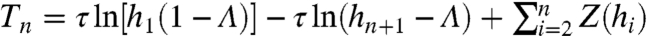, where

[10]

In the adaptation-independent regime, the Z(h_i) terms are independent time intervals making up T_n, with mean 〈Z〉 = 〈Δt〉. If there is independence, the variance of T_n is

[11]

[12]

Note that Var(Z) is the dominant term in [12] for large n and thus is a good measure of long-time-scale spike train variability. Note, however, with nonindependence [11] and [12] would contain higher-order covariance terms, and, in general, Var(Z) can be computed from moments of Z given q_∞ (as in Fig. 3). However, in the adaptation-independence regime we deduce from [11] that

[13]

The first term of [13] accounts for intrinsic variability of a single ISI, and the negative-valued second term (see [9]) lowers the resulting variance. Thus, spike pattern regularity is a direct result of ISI covariance. In the following, we study how the variability in the spike train and adaptation independence are modulated as a function of mean firing rate.

Suppose we introduce a nonfluctuating baseline input conductance s to the model: λ(H - s). Increasing (decreasing) the input s has the same effect as increasing (decreasing) injected current I_m in the ML model (see SI Text, Fitting the ML Model). The baseline s sets the overall firing rate of the cell by effectively scaling α. The input s modulates the ISI correlations, ISI variability, and adaptation independence, as we now show.

The baseline s defines a set of operators , [4], and operator spectra. For each operator 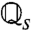there is a single unit eigenvalue η₁ = 1 and corresponding eigenfunction 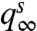(Fig. 3A). The secondary spectrum (η_j for j > 1) is effectively zero for low input values (s ≲ 0.4). Increasing s leads to an increase in the secondary spectrum from zero at s ∼ 0.4, corresponding to a loss of adaptation independence (η₂, Fig. 3B). The secondary spectrum η₂ measures the degree of independence because it is the fractional contraction due to 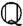[4] of the linear subspace orthogonal to q_∞ (see SI Text, Fitting the ML Model).

The loss of adaptation independence for increasing baseline levels s occurs concomitantly with changes in ISI regularity, which is measured by the coefficient of variation of the ISI [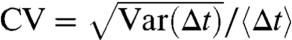]. There is a nonmonotonicity in the s-input-CV graph (Fig. 3B), first declining from unity, which is associated with a transition from subthreshold and very-low-firing-rate Poisson statistics, to more regular firing at a minimum CV value (s ∼ 0.1). This drop is associated with baseline input levels near the deterministic spike threshold (see SI Text, Fitting the ML Model). The CV then increases for higher baseline levels, which is a unique feature of adapting models (14, 40) and contrasts with the monotonic s-input-CV graph of nonadapting models (42). Very high baselines (s ≳ 0.8) result in exponential firing-rate gains that are considered nonphysiological and will not be considered further (see SI Text, Fitting the ML Model.

Long-time-scale spike train regularity, measured by the CV_Z [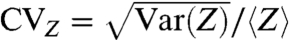], exhibits a local minimum similar to the CV, but it occurs at a higher baseline level that is near the upper boundary of adaptation independence (s ∼ 0.4). This minimum point occurs for input levels above the deterministic threshold for spiking (see SI Text, Fitting the ML Model. The minimum point of CV_Z depends on the variability of ISIs but is dominated by the minimum point of the first serial correlation coefficient ρ₁ (see Eq. 13). Previous studies have detailed how ISI correlations can increase spike train regularity and enhance coarse-grained firing-rate-coding precision (1, 2). Here we observe a broad range of baseline inputs exhibiting high spike train regularity associated with a sufficiently activated AC. However, our analysis also reveals that there is a subset of this range that exhibits adaptation independence, which we will show provides additional advantages for fine-grained sensory coding. In the next two sections, we investigate information-theoretical measures of the AC (Fig. 3C), and we show how independent adaptation states can be utilized to detect small changes in the baseline Δs (Fig. 3D).

Information-Theoretic Analysis of Activation States.

The ISI sequence encodes information about the fluctuating stimulus x(t) (17) that is accessible from the AC activation states h_i. We find that the AC states better encode the effect of stimulus fluctuations x(t) when the AC is activated sufficiently to produce discernible variations in the AC from spike to spike. To measure this property, we derived the mutual information (MI) per spike I_AC between the stimulus x(t) and the AC states and discovered that it was the entropy of the h-process

[14]

where 0 < δh ≪ 1 sets the resolution of the MI (43). A rigorous derivation of [14] and the representation of x(t) in the rate model [6] is given in SI Text, Mutual Information. Note that adaptation independence implies 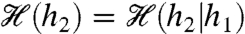, which is significant because the MI of any N-spike sequence length (i.e., “word” length; see ref. 20) scales linearly as 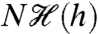. Fig. 3C shows a broad “plateau” region of elevated MI (red) for baseline levels -0.06 ≲ s ≲ 1 associated with higher-variance 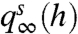distributions (Fig. 3A). This plateau decreases to zero MI for decreasing baseline levels because 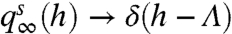, because this is a regime of very long ISIs (minimal h values) that can be distinguished only by small differences in AC states. Thus, AC-based encoding carries more information if the AC is sufficiently activated by the input s.

Fig. 3C also shows the MI of the renewal ISI process p_ISI(Δt) (see Eq. 5). The renewal ISI information is close to the MI of a maximal-entropy Poisson spike train that bounds all processes with the equivalent mean firing rate: I_Poisson = ln(〈Δt〉) + 1 - ln(δt) (see SI Text, Mutual Information) for λ = 〈Δt〉^-1. Thus, there is a significant loss of MI when using AC states for input coding relative to similar renewal processes, coding that is worse for low baselines where the AC is minimally activated. However, this information loss does not hinder detection of weak changes in the baseline input Δs, as we show in the next section.

Weak Signal Detection.

Changes in the AC states can be used to discriminate small changes in the baseline Δs. We consider Δs as an adiabatic change in the baseline, effectively constant over the time period of many spikes. Such signal detection is commonly performed by correlated fast-spiking sensory afferents that detect small changes in mean input level in the presence of noisy fluctuations (1, 3, 27). We wish to determine if a given h sequence 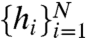more likely originated from baseline level s or baseline level s + Δs. The most statistically efficient discriminator for this task is the log likelihood ratio (LLR) (43)

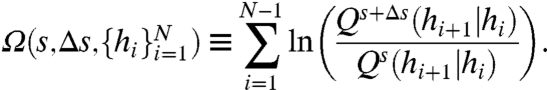[15]

If the h data originate from a perturbed-input distribution (Δs ≠ 0), the LLR will grow positive on average with increasing N; a threshold can then be set and utilized for hypothesis testing (43). The average rate of growth of the LLR, termed the information gain, is equal to the Kullback–Leibler divergence between distinct h distributions: 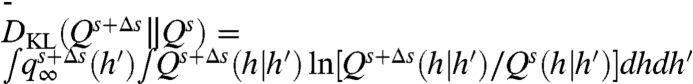, so that 〈Ω〉 = (N - 1)D_KL. For the exponential rate function λ(H - s) in [6], the information gain is

[16]

as detailed in SI Text, Information Gain. Thus, the information gain using the h data depends only on Δs and β but is independent of s, α, Λ, and τ. The uniformity over s is a unique property of the rate function in [6]. Because [16] is independent of all parameters but β and Δs, the result holds for a continuum of spike train behaviors, from those with strong AC currents (large Λ) that have ISI correlations and adaptation independence to the limiting case of a pure Poisson process with a nonexistent AC (Λ → 0): λ(-s) = αe^βs. This Poisson process with rate λ(-s), which has no ISI correlations and maximal entropy, provides a useful comparison to AC systems and highlights an important aspect of how AC states represent information: Knowledge of the h activation states yields the equivalent information gain to that obtained from Poisson ISIs undergoing the same baseline change Δs; however, to achieve this gain, the Poisson model λ(-s) undergoes a much larger (exponential) change in firing rate λ[-(s + Δs)] because there is no additional activation of the AC to counteract the baseline change Δs.

Alternatively, the above Poisson equivalence property ([16]) can be expressed by computing the proportional firing rate change Δf_A/f_A given Δs for the AC model and examining the difference in the information gain of a Poisson spike train with the equivalent firing-rate change. Fig. 3D plots D_KL [16] divided by the Δf_A/f_A (red) versus s, for Δs = 0.02. The ratio D_KLf_A/Δf_A reaches a maximum for baseline levels concomitant with the point of maximal regularity of the T_n interval (CV_Z), and the transition point to the non-adaptation-independence regime (Fig. 3B). This concomitance indicates that the maximal inhibitory effect of the AC on firing-rate change coincides with the baseline level where the AC can no longer produce a significant silent period. Conversely, for a Poisson model with the equivalent rate change, D_KLf_A/Δf_A is inversely related, to first order, to the AC system; so as one goes up, the other goes down (Fig. 3D; see SI Text, Poisson Information Gain for calculation). Therefore, signal detection of the fine-grained AC coding per change in firing rate is significantly enhanced for AC systems relative to both ISI coding of Poisson and similar renewal trains.

We also plotted D_KLf_A/Δf_A for uncorrelated (renewal) ISI sequences from the ISI distribution p_ISI(Δt) (Eq. 5; Fig. 3D, green). For low s values (s ≲ -0.04), the AC model has no ISI correlations (see Fig. 3B) and thus approximates a Poisson process; thus all three models in Fig. 3D are approximately equivalent. As the input increases, the D_KLf_A/Δf_A of both the adapting and renewal ISI models increase and stay approximately the same because there are no significant ISI correlations in the AC model. At s ∼ 0.04 the renewal ISI model peaks (Fig. 3D) at the minimum CV point, whereas the adapting model diverges further as significant negative ISI correlations allow for greater information gain and less firing-rate gain relative to the renewal models.

As stated in the previous section, AC states resolve the underlying ISIs better when the baseline level s is high enough to produce broad h distributions (Fig. 3A), thus eliciting the plateau MI region (Fig. 3C). In addition to resolvability, decoding is less computationally costly for independent AC states. In the nonindependent regime, the LLR [15] is computed by using the conditional distribution Q(h|h^′), which requires a decoder to represent and compute multivariate data (h^′ and h) in independent memory buffers. In contrast, in the independence regime, only univariate data must be represented for decoding because the AC dynamics “self-decorrelate” the ISI information. Therefore, sensory information is more economically decoded for baseline excitability levels below the transition to non-adaptation independence yet high enough for sufficient AC activation (-0.06 ≲ s ≲ 0.4).

Synaptic Decoding of AC States.

How then are the h data, a sequence of variables hidden from direct experimental observation, accessed by postsynaptic decoders? Spike-triggered exponential processes such as H(t) are ubiquitous in the nervous system. Namely, standard models of postsynaptic receptor binding dynamics are characterized as exponentially activating and decaying processes (31). Similar to h_i, we let r_i be the peak activation of postsynaptic receptors, the first stage of possibly many stages of postsynaptic processing, and we also define φ to be the minimum activation level, a parameter similar to Λ, and let τ_r be the decay time scale, which defines a map similar to that in [1]:

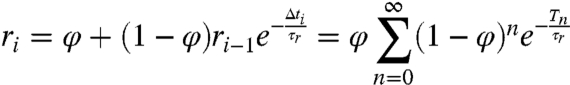[17]

[18]

The r sequence is a function of the n-interval 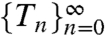sequence [17], so the statistical properties of T_n are transmitted postsynaptically. Moreover, if both φ and τ_r are near Λ and τ, respectively, then r_i will approximate h_i, and with identical parameters there is equality: r_i = h_i [18]. This finding suggests an original experimental prediction: If synaptic kinetics are matched to presynaptic adaptation kinetics, then postsynaptic responses can exhibit the independence property and effectively represent the h-code information postsynaptically.

Discussion

We have discovered a stochastic regime of input-driven spiking models associated with correlated spiking, in which the activation states of the AC are probabilistically independent from spike to spike. Adaptation independence is met by the mild physiological condition that the minimum activation state is strong enough to stop spiking for a brief period. Independence occurs in a regime associated with perithreshold regular firing, and so we speculate that it is a common property of neurons (see SI Text, Fitting the ML Model).

Sensory afferent cells are challenged with representing information at the limits of physical resolution, in which noise fluctuations must be quickly disambiguated from baseline signals over a wide range of intensities. The adaptation-independent regime is important in this context because it enhances signal detection with minimal firing-rate change, by using a fine-grained code that utilizes both the ISIs and ISI correlations (11, 29, 36). This fine-grained coding contrasts with the previously reported regularization effect of ISI correlations on coarse-grained rate coding (2, 3) or Poisson coding commonly reported in central neurons (44). We have shown that AC activation states represent the same information gain that can be achieved with Poisson spike statistics but at a reduced firing-rate change.

It has been proposed that decoding of stimulus information is achieved through inferences on the basis of conditional probabilities from sequential data (e.g., Δt_i+1, conditioned on Δt_i, and so on) (1, 11, 20, 29, 30). This scheme requires a postsynaptic decoder to represent multivariate data in independent memory buffers and compute conditional probability distributions. It has been proposed, yet is unproven (11), that synaptic processing could perform such a computation or be used for Bayesian inference (45). However, we have shown that correlated spike trains can be represented independently causa sui by the adaptation dynamics, providing a simple biophysical means of information representation that does not require more costly multivariate decoding.

We have also shown that simple postsynaptic dynamics can represent the AC states, which suggests a testable experimental prediction that synaptic activation kinetics can decorrelate the correlated ISI sequence and synaptic and dendritic nonlinearities (46) could decode the AC activation.

Methods

All numerical computations were performed on a Macintosh computer using MATLAB software. See SI Text, Notes to Numerical Computations for specific methods used in Figs. 1–3.