Coupling governs entrainment range of circadian clocks

Abstract

Circadian clocks are endogenous oscillators driving daily rhythms in physiology and behavior. Synchronization of these timers to environmental light–dark cycles (‘entrainment’) is crucial for an organism's fitness. Little is known about which oscillator qualities determine entrainment, i.e., entrainment range, phase and amplitude. In a systematic theoretical and experimental study, we uncovered these qualities for circadian oscillators in the suprachiasmatic nucleus (SCN—the master clock in mammals) and the lung (a peripheral clock): (i) the ratio between stimulus (zeitgeber) strength and oscillator amplitude and (ii) the rigidity of the oscillatory system (relaxation rate upon perturbation) determine entrainment properties. Coupling among oscillators affects both qualities resulting in increased amplitude and rigidity. These principles explain our experimental findings that lung clocks entrain to extreme zeitgeber cycles, whereas SCN clocks do not. We confirmed our theoretical predictions by showing that pharmacological inhibition of coupling in the SCN leads to larger ranges of entrainment. These differences between master and the peripheral clocks suggest that coupling-induced rigidity in the SCN filters environmental noise to create a robust circadian system.

Introduction

Daily rhythms in physiology, metabolism and behavior are controlled by an endogenous circadian timing system, which has evolved to synchronize an organism to periodically recurring environmental conditions, such as light–dark or temperature cycles. In mammals, the circadian system relies on cell-autonomous oscillators residing in almost every cell of the body. Essentially the same molecular components are arranged as interlocked transcriptional–translational feedback loops generating ∼24-h rhythms at the molecular level (for a review see Reppert and Weaver, 2002). Precise synchronization of rhythms is an essential part of circadian organization, which usually follows hierarchically organized steps: (i) Periodic light detected by the eyes entrains (i.e., synchronizes) ∼20 000 neurons in the bilateral suprachiasmatic nucleus (SCN) of the hypothalamus via neuronal signals traveling along the retinohypothalamic tract (for a review see Maywood et al, 2007). (ii) Within SCN tissue, individual neurons synchronize each other via neuropeptide coupling/synaptic signaling and/or gap junctions (Shirakawa et al, 2001; Aton and Herzog, 2005). This generates precise and self-sustained ∼24-h oscillations, e.g., of electrical activity in the SCN or of locomotor behavior, even in the absence of external signals (Pittendrigh and Daan, 1976; Reppert and Weaver, 2002; Herzog et al, 2004). Inhibition of this intra-SCN synchronization shows that the periods of the individual SCN neurons are quite variable ranging from 20 to 28 h (Welsh et al, 1995; Honma et al, 2004). (iii) Subsequently, the SCN synchronizes other peripheral tissues orchestrating the rhythmicity and phasing of their circadian clocks. Little is known about the mechanisms of this communication; however, hormonal signals, sympathetic enervation and/or indirect cues, such as body temperature, feeding time and activity rhythms, have been discussed (Levi and Schibler, 2007). In contrast to the SCN, cellular clocks within a peripheral tissue seem to be much less coupled, leading to rapid desynchronization of individual oscillator cells when a rhythmic environment is removed (Nagoshi et al, 2004; Liu et al, 2007).

Many theoretical studies underline that coupled rhythms of similar periods synchronize (Huygens, 1673; von Holst, 1939; Winfree, 1980; Kuramoto, 1984; Balanov et al, 2009). They discuss detailed bifurcation diagrams, including toroidal oscillations and deterministic chaos (Glass et al, 1987; Pikovsky et al, 2001; Anishchenko et al, 2007). Even though in circadian rhythms complex nonlinear phenomena are found under certain experimental circumstances (Helfrich-Förster, 2004; de la Iglesia et al, 2000, 2004), a stable entrainment is observed in most physiological situations. Nevertheless, the robust and relatively fast synchronization of circadian rhythms in mammals is nontrivial due to the quite limited synchronization strengths (i.e., entrainment signals, intra-SCN signals and signals from the SCN to the periphery). In general, immediate synchronization is not surprising when the stimuli are very strong (e.g., defibrillation of the heart). Yet a robust and fast synchronization in systems with weak synchronization signals probably requires a specific evolutionary design of oscillator properties and coupling schemes. Little is known about which oscillator properties govern synchronization characteristics of circadian oscillators, such as the range of entrainment (i.e., the range of zeitgeber periods to which a cell, a tissue or an organism is able to entrain (Pittendrigh and Daan, 1976; Chiesa et al, 2007)). In addition, the oscillator properties of SCN and peripheral tissues that govern entrainment behavior have not been systematically studied, although examples indicate that entrainment properties are substantially different: The circadian oscillator in mouse liver entrains to an inverted environmental temperature cycle, while the SCN does not (Brown et al, 2002). Moreover, SCN oscillations usually exhibit moderate phase shifts in response to a zeitgeber stimulus (Prosser and Gillette, 1989; Piggins et al, 1995; Wisor and Takahashi, 1997; Gribkoff et al, 1998; Best et al, 1999), while organotypic lung slices were recently shown to exhibit remarkably large phase responses (Gibbs et al, 2009).

Here, we report a systematic theoretical and experimental study of the entrainment range of the central circadian clock (SCN) on one hand and a peripheral clock (lung) on the other hand. We subjected lung and SCN tissue slices to identical temperature cycles to compare their entrainment properties. We show that—in contrast to lung tissue—the SCN constitutes a rigid oscillator that cannot easily entrain to temperature cycles with experimental periods of 20 or 28 h. We further set out to understand theoretically which properties of a tissue determine the entrainment range. This approach allowed us to infer features of the tissue, particularly about the involved biological oscillators and their coupling. Using generic oscillator models we show how the period, the relaxation rate, the coupling strength, as well as the ratio between zeitgeber strength and amplitude govern the entrainment range. In particular, simulations predict that reduced coupling strength leads to a weak oscillatory state and consequently a larger entrainment range. We tested and confirmed these predictions experimentally by studying the entrainment of SCN slices treated with drugs that attenuate coupling.

Results

Amplitude and zeitgeber strength determine the entrainment range

To set the stage for a systematic theoretical investigation of entrainment, we first summarize established concepts of entrainment and state our assumptions and definitions. Figure 1A schematically describes the concept of oscillator entrainment to external signals (zeitgebers, e.g., light, temperature or food). Zeitgeber cycles interact with the endogenous oscillator in such a way that the frequencies are locked in a 1:1 entrainment ratio, leading to a stable phase relation between the external entraining signal and the entrained oscillator. Critically, upon release into constant conditions, entrained oscillations persist with a phase predicted from the previous zeitgeber cycle. Note that we do not yet assume anything about the physical nature of the oscillator: it could be a single-cell biochemical oscillator (Leloup and Goldbeter, 2003; Forger and Peskin, 2003; Becker-Weimann et al, 2004) or a synchronized population of cells, such as the SCN. However, many details of the kinetic mechanisms are not known, and in particular, the chosen nonlinearities in detailed models, which shape the dynamics of the self-sustained oscillations, are not based on experimental data. Consequently, we follow in this section the tradition of Winfree (1980), Kronauer et al (1982) and Glass and Mackey (1988) and study generic amplitude-phase oscillators.

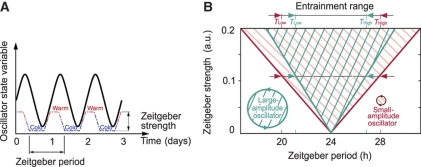
Figure 1.

Basic concepts of entrainment. (A) Schematic representation of a circadian rhythm entrained by 24-h temperature cycles. The quasi-square-wave temperature cycle represents the zeitgeber cycle used in the experiments of this study (see Figures 4 and 6). Note that upon complete entrainment the phase angle between rhythmic variable and zeitgeber cycle is constant. (B) Schematic representation of the entrainment region. The entrainment region is dependent on zeitgeber period (T) and zeitgeber strength and is also known as 1:1 Arnold tongue. Small-amplitude oscillators exhibit a broader range of entrainment than large-amplitude oscillators. For a constant zeitgeber strength, the entrainment region is confined between its lower (T_Low) and upper (T_High) limit.

Figure 1B illustrates that the range of entrainment depends on zeitgeber strength and oscillator amplitude. Entrainment is most easily achieved if the endogenous and zeitgeber periods are similar. For example, the circadian behavior in laboratory rodents can be entrained to zeitgeber cycles with deviations of up to 2 h from the endogenous ∼24-h period. The entrainment range can be enlarged if the zeitgeber strength is increased. Thus, the entrainment region typically shows a tongue-shaped form (Berge et al, 1984). Alternatively, small-amplitude oscillators can be entrained more easily as the effect of the zeitgeber is stronger (Pittendrigh et al, 1991; Vitaterna et al, 2006; Brown et al, 2008).

Proceeding in general terms, we assume the oscillator can be characterized by its amplitude, its intrinsic period and its stability with respect to amplitude perturbations (amplitude relaxation rate or Floquet exponent (Guckenheimer and Holmes, 1983)). These general oscillator properties are conveniently parametrized by the Poincaré oscillator (Glass and Mackey, 1988), which is given by the following equations in polar coordinates with the radial coordinate r and phase ϕ:

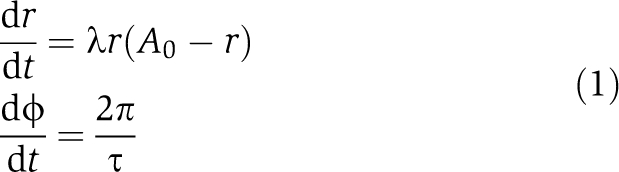A₀ and τ denote amplitude and intrinsic period of the oscillator. The parameter λ quantifies the relaxation of amplitudes to the stable oscillation (limit cycle) characterized by r=A₀. We term oscillators with small radial relaxation rates as λ weak oscillators. Conversely, we term oscillators with large relaxation rates as rigid oscillators. In terms of timescales, we define an oscillator as rigid if the radial relaxation time 1/λ is faster than the intrinsic period, i.e., 1/λ <τ. From dynamical systems theory, it is known that a set of synchronized coupled oscillators can be dynamically described as a one-oscillator model, such as the Poincaré oscillator, where the parameters and variables represent the whole synchronized population. Thus, we demonstrate (see below and Supplementary Information) that the results obtained by studying this generic oscillator are general enough to apply to either single cells, or a synchronized rhythm generated by coupled oscillators.

Relaxation rate affects range of entrainment, entrained amplitude and phase shifting properties

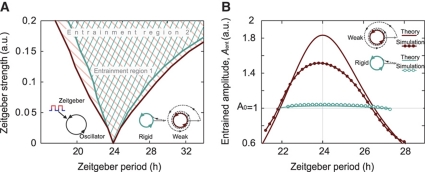
Which properties of an oscillator are crucial for determining its range of entrainment? To test how the amplitude relaxation rate affects the response to zeitgeber cycles, i.e., the entrainment range, we calculated the entrainment range for different relaxation rates λ for the Poincaré oscillator (Figure 2A). Such an illustration of the entrainment region is also termed 1:1 ‘Arnold tongue’ (Berge et al, 1984). Even for a relative small zeitgeber strength, entrainment to cycles with deviations of up to 2 h from the endogenous ∼24-h period can be achieved (with A₀=1 and a zeitgeber strength of 0.05 h⁻¹ in these simulations). The Arnold tongue is somewhat skewed, i.e., an external signal with long periods can entrain the oscillator more easily. The comparison of the inner curves (fast amplitude relaxation λ=1 h⁻¹) and the outer curves (slower relaxation λ=0.03 h⁻¹) reveals that weak oscillators are more easily entrained. These particular values of the amplitude relaxation rates λ are comparable with experimental measurements (Brown et al, 2008; Westermark et al, 2009). Our results for the generic Poincaré oscillator also hold for other oscillator models, such as the standard Hopf oscillator (Guckenheimer and Holmes, 1983) or the more realistic biophysical circadian clock Becker-Weimann–Bernard model (Becker-Weimann et al, 2004; Bernard et al, 2007) (see Supplementary Information and Supplementary Figures S1 and S2).

Figure 2.

Entrainment range and amplitude depend on the oscillator relaxation rate. (A) Numerically calculated entrainment region for a Poincaré oscillator with radius 1 plotted as a function of zeitgeber period and zeitgeber strength. The entrainment range is broader for weak oscillators with low relaxation rates λ. (B) Entrained amplitude of weak and rigid oscillators within the entrainment range. Weak oscillators exhibit a strong amplitude expansion for zeitgeber periods close to the oscillator's intrinsic period (24 h), and an amplitude reduction for zeitgeber periods close to both upper and lower limit of entrainment. Rigid oscillators remain almost unperturbed along the entrainment range. Numerical simulations results (dots) and analytically derived curves (lines) are in good agreement.

Interestingly, also the oscillator amplitude during entrainment depends on the amplitude relaxation rate λ (Figure 2B). Weak oscillators exhibit a considerable amplitude expansion (A_ent>A₀) for zeitgeber periods close to the oscillator's intrinsic period, and an amplitude reduction (A_ent<A₀) for zeitgeber periods close to both upper and lower limit of entrainment (LLE). Rigid oscillators exhibit almost no amplitude variations (A_ent≈A₀) within the range of entrainment. Some of these effects were described earlier in experimental and theoretical studies (Wever, 1972; Aschoff and Pohl, 1978; Roenneberg et al, 2005; Kurosawa and Goldbeter, 2006). Here, we also find amplitude expansion upon entrainment of lung tissue (Figure 4A and C, for details see below).

The effect of the amplitude relaxation rate λ on entrainment is also reflected in its effect on the shape of the phase–response curves (describing the response of the oscillator to single zeitgeber pulses) of weak and rigid oscillators. Already Pittendrigh (1965) and later Honma et al (1985) argued that entrainment range and phase–response curve amplitude are closely related. We also find in our simulations that weak oscillators—while having a larger range of entrainment—also react with overall larger phase shifts to a zeitgeber stimulus than rigid oscillators (Supplementary Figure S3A). Experimentally, several studies have shown that the SCN reacts with small-to-moderate phase shifts upon zeitgeber stimuli (Wisor and Takahashi, 1997), whereas peripheral clocks such as the lung elicit large phase shifts upon zeitgeber stimuli (Gibbs et al, 2009), suggesting that SCN might constitute a rigid and lung a weak oscillator. We confirmed these findings with forskolin as a zeitgeber—forskolin activates cAMP-mediated signaling to the clock (Yagita and Okamura, 2000; Obrietan et al, 1999; Brown et al, 2008)—in direct comparison of these two tissues (Supplementary Figure S3B).

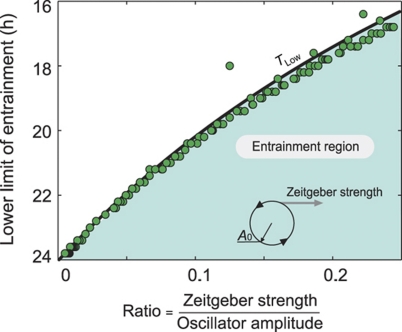
The ratio of zeitgeber strength to oscillator amplitude determines the range of entrainment

It has been discussed earlier (Pittendrigh et al, 1991; Vitaterna et al, 2006; Brown et al, 2008; van der Leest et al, 2009) that zeitgeber stimuli can have a strong effect on small-amplitude oscillators. We hypothesized that a single quantity, the ratio between zeitgeber strength and oscillator amplitude, can predict the entrainment range if the amplitude relaxation and the oscillator period are known. To test this theoretically, we numerically calculated the LLE T_low as a function of the zeitgeber strength to oscillator–amplitude ratio (Figure 3 and Supplementary Figure S4). The dots represent values for the Poincaré oscillator for a large number of combinations of zeitgeber strengths and amplitudes. In addition to these numerical results for the Poincaré oscillator, we derived analytically the LLE under very general assumptions. The analytically derived relationship (solid curve) is in good agreement with the numerical results. We conclude that the ratio between the zeitgeber strength and oscillator amplitude indeed determines the entrainment range for a given oscillator period and relaxation rate λ. In the Supplementary Information section, we apply an analytical theory of entrainment from which the phase of entrainment Ψ_ent and entrained amplitude A_ent are obtained. In Equation 2 these analytical results are given as functions of the oscillator period τ, amplitude A₀, zeitgeber strength B, zeitgeber period T, and amplitude relaxation rate λ and detuning defined as Δ=2π/τ−2π/T.

Figure 3.

The ratio of zeitgeber strength to oscillator amplitude determines entrainment range. The lower limit of entrainment is plotted as a function of the ratio of zeitgeber strength to oscillator amplitude. The area under the analytically derived curve represents the entrainment region. The dots are numerically simulated lower limits of entrainment for a Poincaré oscillator with λ=1 h⁻¹. Computational details are given in Material and methods, and theoretical details are provided in Supplementary Information.

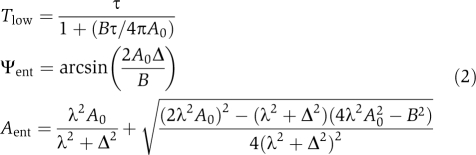Together, the results shown above (Figures 2 and 3) reflect very general entrainment properties of simple, generic oscillator models: the entrainment behavior of an oscillator is essentially determined by its intrinsic period, its amplitude relaxation rate and by the ratio between zeitgeber strength and amplitude. We justify these claims by analytical calculations, as well as by numerical simulations of a generic Hopf oscillator and the more realistic biophysical circadian clock Becker-Weimann–Bernard model (see Supplementary Information and Supplementary Figures S1, S2 and S3A).

Lung tissue behaves as a weak oscillator and SCN as a rigid oscillator

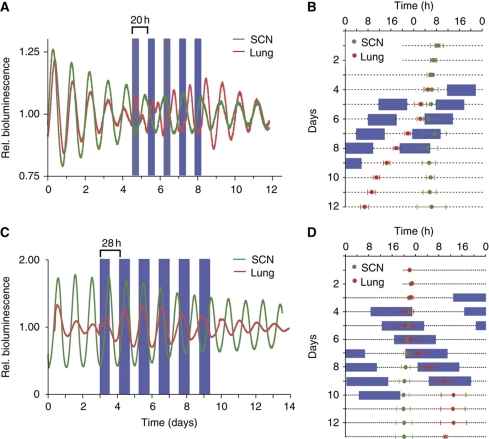
Based on our theoretical considerations elaborated above, we predict that weak, small-amplitude oscillators exhibit a larger range of entrainment compared with more rigid, high-amplitude oscillators. To test these predictions experimentally, we investigated the entrainment of circadian oscillators using temperature as a zeitgeber. Temperature is a key environmental factor for the regulation of circadian rhythms of many species (Sweeney and Hastings, 1960; Rensing and Ruoff, 2002). In addition to being an environmental input, temperature cycles have also been shown to act as a synchronizing factor in vivo (Brown et al, 2002). Mice usually experience daily temperature variations of up to 2°C (Kapás and Krueger, 1996), which are considered to contribute to tissue clock synchronization in vivo. Thus, we used a quasi-square-wave temperature profile ranging from 35.5°C (cold) to 37°C (warm) with gradual transitions between these two conditions (see Materials and methods). We tested two different temperature cycles consisting of either 10 h of cold and 10 h of warm, or 14 h of cold and 14 h of warm. Hence, these cycles represent zeitgeber periods T of 20 or 28 h, which both are presumably close to the borderline of the entrainment range for circadian oscillators. As readout for clock dynamics, we used a bioluminescence-based mouse model, where the rhythmic clock protein PER2 (a state variable for the circadian clock) is fused to luciferase as a reporter (Yoo et al, 2004).

Tissue explants from PER2::LUC mice were subjected to temperature cycles and simultaneously monitored for bioluminescence rhythms. To test for predicted differences in the entrainment behavior of rigid and weak oscillators, we used SCN tissue as an example of a putatively rigid oscillator (Wisor and Takahashi, 1997) and lung tissue as an example of a putatively weak, peripheral oscillator (Gibbs et al, 2009; see also Supplementary Figure S3). Whereas explanted lung tissue entrained to both the 20-h and the 28-h temperature cycles, SCN tissue did not entrain to either (Figure 4). It took the lung tissue about three so-called ‘transient cycles’ (days 4–6, Figure 4B and D) to adopt a stable phase relationship to the zeitgeber cycles. This can be, for example, nicely seen in Figure 4A, as initially two daily peaks of PER2 abundance: one decreasing peak during the cold phase corresponding to the phase before entrainment, and a second, increasing peak during the warm phase representing the new, entrained phase (Figure 4A). This increased amplitude of the second peak corresponds nicely to our theoretical prediction, concerning amplitude expansion upon entrainment (Figure 2B). The phase of the entrained PER2 abundance persisted upon release into constant temperature, strongly suggesting true entrainment of the lung clock to the temperature cycle rather than direct temperature effects (so-called ‘masking’). In contrast to lung, SCN oscillation appeared unperturbed by temperature (e.g., we did not observe any transient effects on SCN oscillation, such as an increasing secondary peak of PER2 abundance). This becomes even clearer in Figure 4B and D, where peak expression times in the lung moved along with the daily progression of cold phases, while SCN tissue peaked unaltered at similar times each day, i.e., is presumably free-running. The successful entrainment of lung tissue, but not SCN tissue, to such extreme zeitgeber periods with relatively small temperature differences confirms the predictions of our model. It further indicates that lung tissue is probably indeed a weak oscillator, whereas the SCN is a rigid oscillator.

Figure 4.

Lung tissue behaves like a weak and the SCN like a rigid circadian oscillator. (A, C) Temperature entrainment experiment with SCN and lung slices from PER2::LUC knockin mice. Tissues were cultured in luciferin-containing medium at 37°C, and bioluminescence derived from rhythmic PER2-LUC abundance was continuously monitored. Between days 4 and 8 or 9, tissues were subjected to 20 or 28-h temperature cycles with 10 or 14 h 35.5°C (blue boxes) and 10 h or 14 h 37°C before releasing them in constant 37°C conditions. Periods before, during and after entrainment are given in Supplementary Table S1. (B, D) Double plots of the peak times (±s.d.; n=4) of PER2-LUC bioluminescence. The circadian clock of lung tissue entrains to the ΔT=1.5°C temperature cycles (blue: low temperature), while the SCN clock does not: The bioluminescence peaks of the lung slices adopt a stable phase relation to the temperature cycle, while the SCN-derived peaks ‘run through’. After release in constant 37°C (from day 9 on), lung-derived bioluminescence rhythms continue with a phase that is predicted from the previous temperature cycles, thus excluding temperature-driven, so-called, masking effects. Source data is available for this figure at www.nature.com/msb.

Source data for figure 4B ^{(650KB, xls)}

Source data for figure 4D ^{(622.5KB, xls)}

Our theoretical considerations also predict that increasing the zeitgeber strength enlarges the range of entrainment (Figure 2A), and at the same time affects the phase of entrainment (Supplementary Figure S5A) as already noted by others (Roenneberg et al, 2003). Thus, we speculated that—although having a smaller range of entrainment than lung clocks—SCN clocks might entrain to extreme zeitgeber cycles, if we would use a stronger zeitgeber. Therefore, we again applied an extreme temperature cycle (T=20 h) to lung and SCN explant cultures, but this time with increasing zeitgeber strength (0.75, 1.5, 3 and 6°C temperature variation). We found that (i) the SCN clock still did not entrain to these stronger zeitgebers and (ii) the lung clocks entrained in every case, but with a zeitgeber dose dependence of the phase of entrainment, as predicted by theory (Supplementary Figure S5). Thus, the entrainment range of SCN clocks seems to be even smaller than anticipated. To verify that SCN clocks are able to entrain to temperature cycles at all (as shown by others, e.g., Herzog and Huckfeldt, 2003), we then applied a less extreme zeitgeber cycle (T=22 h) again with increasing zeitgeber strength (4, 6 and 8°C temperature variation). Now, we observe entrainment for the two stronger zeitgebers (with, again, different phases of entrainment), but not for the weaker zeitgeber (Supplementary Figure S6). Together, these experiments nicely recapitulate the theoretical entrainment concepts illustrated by the so-called Arnold tongue: whether an oscillator entrains depends on how close the zeitgeber cycle is to the intrinsic period of the oscillator and how strong the zeitgeber is. In addition, zeitgeber strength also determines the phase of entrainment.

Coupling makes oscillators more rigid

What is the fundamental difference between lung and SCN tissue that so profoundly affects entrainment behavior? As suggested earlier (Bernard et al, 2007; van der Leest et al, 2009), coupling of circadian rhythms can have a huge effect on the properties of oscillators. So far, we have considered oscillators in a general sense: they could be individual cells or a synchronized, orchestrated population of a large number of coupled cells. To investigate the influence of coupling strength on the entrainment behavior, we focus on coupled oscillators (e.g., SCN cells coupled via neuropeptides, Aton and Herzog, 2005) and analyze period, amplitudes and relaxation rate of the synchronized system. As an elucidating example, we study two coupled Poincaré oscillators described by the following equations:

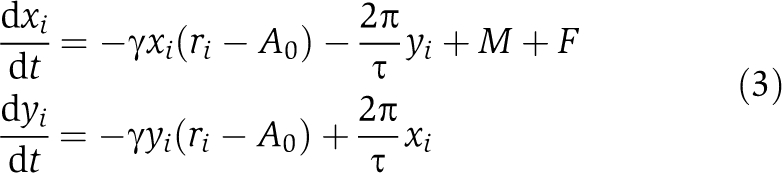The single-uncoupled oscillator i has an intrinsic period of τ=24 h. Here, we consider two oscillators: i=1 or 2 with r_i=(x_i+y_i)^1/2 being equivalent to the radial coordinate in the polar representation of the oscillator (Equation 1). A₀ is the amplitude of the stable limit cycle oscillation, and γ is the amplitude relaxation rate of the single-non-coupled oscillator (note, in Equation 1 we use λ for the relaxation rate to emphasize that it characterizes either a single oscillator or an oscillatory system). Coupling is modeled as an average of the states of the two oscillators (a mean field M, Kuramoto, 1984):

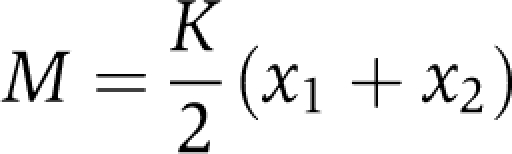This type of coupling has been previously suggested for coupled SCN neurons assuming fast (relative to the 24-h oscillation period) diffusion of coupling neuropeptides (Gonze et al, 2005; Locke et al, 2008). Finally, we allow the system to be entrained by a square-wave forcing term F that represents, for example, light or temperature entrainment. Our conclusions derived from this simple system of two coupled oscillators (see below) are also valid for more realistic biochemical circadian clock models (see Supplementary Information and Supplementary Figure S2).

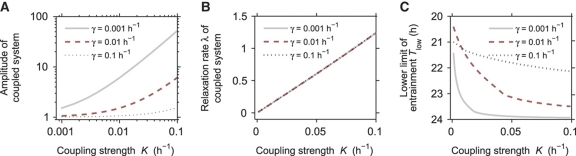
To understand how coupling governs the dynamical properties of a system of coupled oscillators, we first analyzed the model (Equation 3) without entrainment (i.e., F=0). In this case, the resulting limit cycle of the coupled system can be again characterized by its period, amplitude and relaxation rate. We find that increasing coupling strength leads to a drastic increase of the amplitude most pronounced for small values of γ, the relaxation rate of the individual oscillators (Figure 5A)—a well-known resonance phenomenon (Guckenheimer and Holmes, 1983). It implies that coupling of resonating clock cells, i.e., weak oscillators, may lead to increased amplitudes of the oscillating system and, as a consequence (Figure 3), to a smaller range of entrainment. Interestingly, the amplitude relaxation rate of the coupled system λ is primarily dominated by the coupling strength, and, surprisingly, this rate is independent of the radial relaxation rates γ of the individual oscillators (Figure 5B). The coupling rather than the single-cell oscillators determines the amplitude relaxation rate of the synchronized system—with the described implications for entrainment (Figure 2). This intriguing finding reflects the fact that deviations from the synchronized state are damped via the coupling term (Pikovsky, 1984). In other words, in a network of oscillators almost all perturbations affect synchrony. This implies that the relaxation to the equilibrium is strongly influenced by the coupling that brings the network back to synchrony. For sufficiently small coupling, the dominant amplitude relaxation rate of the coupled system is proportional to the coupling strength as shown in Figure 5B, and determines the relaxation to synchrony rather than the individual oscillator properties. In summary, coupling makes the synchronized oscillatory state more rigid in two aspects: (i) resonance increases the amplitude and (ii) coupling leads to faster relaxation.

Figure 5.

Coupling constrains the entrainment range of oscillators. (A) Coupling increases the amplitude of the synchronized, coupled system. Given are numerically calculated results of two coupled Poincaré oscillators (see Equation 3). Coupling is quantified by the coupling strength parameter K. The amplitude increase upon coupling is more pronounced, if the individual oscillators are weak, i.e., for small relaxation rates γ. (B) Coupling makes oscillators more rigid by increasing the relaxation rate λ of the coupled system. Shown are numerically calculated results of two coupled Poincaré oscillators. Note that the effect of the coupling strength on the rigidity of the coupled system is not dependent on the amplitude relaxation rates γ of the individual oscillators. As coupling slightly affects the period of the coupled system, the relaxation rate λ was normalized by multiplying with the coupling-dependent period. (C) Coupling makes an oscillatory system harder to entrain. Two coupled Poincaré oscillators were entrained by adding a periodic square-wave forcing of period T, alternating with equal duration and a forcing between 0 and 0.1 (term F in Equation 3). The lower limit of entrainment T_Low of the coupled system was calculated for different coupling strengths K and different amplitude relaxation rates γ of individual oscillators. As the coupling affects the intrinsic (non-forced) period itself, the lower limit of entrainment was normalized with respect to a constant intrinsic period of 24 h to visualize the effects on the entrainment range that are entirely due to the effects on the rigidity and amplitude of the coupled system.

These theoretical considerations now predict that decreasing the coupling should enlarge the range of entrainment, as (i) amplitude should decrease, and (ii) the coupled oscillatory state should become weaker (i.e., the relaxation rate should decrease). This is indeed the case for coupled Poincaré oscillators (Equation 3): When we calculate the LLE as a function of coupling strength (for different single-oscillator relaxation rates), we see that the LLE increases as the coupling strength increases (Figure 5C), i.e., coupling makes the system harder to entrain. Furthermore, the LLE also generally decreases with increasing relaxation rates of the single oscillators. In other words, the weaker the individual oscillators within a coupled system are, the harder is it to entrain this system. This at first glance seems counterintuitive (because for individual oscillators the opposite is true, Figure 2A), but is due to the amplitude expansion that occurs when the single-oscillator relaxation rates are low (Figure 5A). This increase in amplitude of the coupled system leads to smaller ranges of entrainment (Figure 3).

Reducing coupling facilitates entrainment of SCN tissue

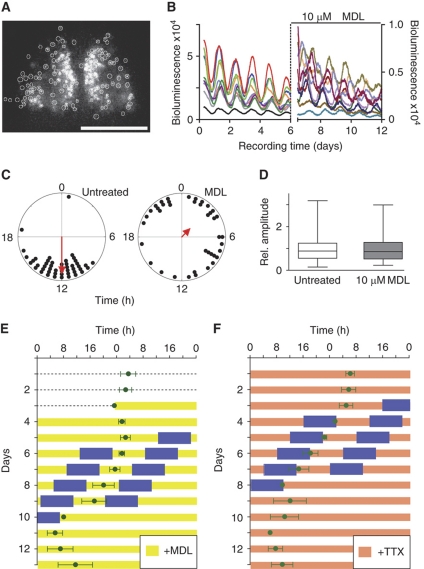
To test our theoretical prediction—attenuating coupling makes the coupled oscillatory system weaker and thereby enlarges the entrainment range—experimentally, we pharmacologically reduced coupling in cultured SCN slices taken from PER2::LUC mice. To this end, we subjected SCN slices to N-(Cis-2-phenyl-cyclopentyl)azacyclotridecan-2-imine-hydrochloride (MDL)—a known inhibitor of adenylate cyclase (Hagen et al, 2006) that interferes with VIP-mediated coupling (O’Neill et al, 2008). PER2-LUC bioluminescence rhythms of individual SCN neurons were recorded using a high-resolution camera system (Figure 6A). SCN neurons of untreated slices exhibit well-synchronized cellular rhythms, while treatment with MDL leads to their immediate desynchronization due to the relatively wide distribution of individual cellular periods (Figure 6B and C; Supplementary Figure S7 and Supplementary Movies). While the magnitude of PER2-LUC bioluminescence is substantially reduced (and—as a consequence—also the absolute amplitude values, as also described by O’Neill et al, 2008), we did not find a significant effect of MDL on the relative amplitude of the circadian rhythms of single SCN neurons (Figure 6D). We determine relative amplitudes because the effect of a zeitgeber (e.g., the induction of transcription) is more likely to be relative than absolute and define it as the ratio of the maximal/minimal values of an oscillating variable to its mean (see also Materials and methods). Thus, we conclude that in this experimental setting, MDL reduces primarily cellular coupling with no detectable effect on relative amplitude.

Figure 6.

Decoupling of SCN cells broadens the entrainment range of SCN tissue. (A) Circadian rhythms of individual SCN cells can be monitored. The digital image shows a 10-min exposure of bioluminescence emitted from a medial section through the SCN of a PER2::LUC mouse. Bioluminescence reporting abundance of the clock protein PER2 was quantified from 130 single cells (marked by white circles) over the course of several days. Scale bar, 500 μm. (B) Representative bioluminescence traces from 10 different single cells. Typical for SCN slices, individual cells oscillate with a circadian period, and the majority of cells have their bioluminescence peaks at similar times. After addition of the adenylyl cyclase inhibitor MDL on day 6, bioluminescence recording was resumed as shown for 10 representative cells (note that representative cells before and after MDL treatment were not identical). While MDL addition reduced the magnitude of PER2 abundance and lead to random phasing of peak bioluminescence, relative amplitudes of untreated and MDL-treated cells were similar. (C) Polar plots showing the peak times of PER2 expression of individual SCN cells from the experiment shown in (B) during the third day of slice recording. Each dot represents the phase of a single cell. Single-cell phases in an untreated SCN slice (left) clustered significantly at 12 h (Rayleigh test, r=0.8, P<0.0001, n=49), but were randomly distributed upon MDL treatment (right, Rayleigh test, r=0.26, P=0.07, n=40). Arrows in polar plots represent the mean vectors, the direction denotes the mean phase, and length measures the tendency of the data to cluster based upon a Rayleigh test, in which r-values range from 0 (randomly phased) to 1 (all cells peak at the same time). (D) The relative amplitudes of single-cell oscillations do not vary with treatment (Mann–Whitney test, one-tailed, P=0.47, n=169 for untreated cells; n=94 for MDL-treated cells). Displayed are normalized median amplitudes±quartiles±minima/maxima from three independent imaging experiments. For each experiment, individual amplitude values were normalized to the mean amplitudes of untreated cells. (E, F) SCN cultured in the presence of MDL (10 μM final concentration) or TTX (2-4 μM final concentration), respectively, entrain to a 20-h temperature cycle consisting of 10 h cold (35.5°C, blue boxes) and 10 h warm (37°C). Given are double plots of the peak times (±s.d.; n=8 for MDL, and n=6 for TTX) of PER2-LUC bioluminescence. Periods before, during and after entrainment are given in Supplementary Table S1. Thus, the range of entrainment for SCN slices is increased (compare with Figure 4) when SCN oscillators are decoupled (see B and C). Source data is available for this figure at www.nature.com/msb.

Source data for figure 6C and Supplementary figure S7 ^{(2.9MB, xls)}

Source data for figure 6E ^{(638.5KB, xls)}

Source data for figure 6F ^{(517.5KB, xls)}

If reducing the coupling strength indeed makes an oscillatory system weaker, MDL-treated SCN slices should have a wider range of entrainment than untreated SCN slices. To test this, we entrained MDL-treated SCN slices to a 10-h 35.5°C (cold)/10-h 37°C (warm) temperature cycle. In contrast to untreated SCN slices that do not entrain to this 20-h temperature cycle (Figure 4), SCN slices treated with different MDL concentrations entrained in a MDL dose-dependent manner (Figure 6E and Supplementary Figure S8A). This clearly indicated an expanded range of entrainment, as predicted by our theoretical arguments. In addition, when we used an alternative way to reduce the coupling between SCN neurons, i.e., application of tetrodotoxin (TTX), the SCN also entrained to the 20-h temperature cycle. TTX is an inhibitor of voltage-gated sodium channels that prevents the generation of action potentials. TTX-treated SCN neurons have been described to lose the synchrony of their circadian oscillations, while also decreasing their amplitude significantly (Yamaguchi et al, 2003). Indeed, when analyzing original single-cell time series data from the study reported by Yamaguchi et al (2003), we also find a substantial (about threefold) and highly significant reduction of relative amplitude upon TTX treatment (P<0.00001; Mann–Whitney test, one-tailed; n=78 for untreated cells; n=185 for TTX-treated cells; not shown)—very different from the effects of MDL on relative amplitude. Interestingly, the differential effect of these drugs on SCN single-cell amplitudes might also result in different phases of entrainment of MDL- and TTX-treated SCN slices (Brown et al, 2008), which we indeed see a trend for (Figure 6E and F). In addition, it is conceivable that MDL and TTX might also have a differential effect on coupling and thereby on the amplitude relaxation rate of the oscillatory system, which also can influence phase of entrainment (Supplementary Figure S8B).

In summary, subjecting cultured SCN slices to decoupling agents (MDL and TTX) leads to an expanded entrainment range. In the case of MDL, this is an amplitude-independent effect and probably due to a weakening of the oscillator system (i.e., reducing the amplitude relaxation rate λ). In the case of TTX, also the amplitude of cellular rhythms is affected, which leads to an expansion of the range of entrainment. Thus, as predicted by our theoretical considerations, coupling governs the entrainment range of SCN tissue because it can affect both amplitude and rigidity of circadian oscillators.

Discussion

Entrainment is one of the cornerstones of circadian biology. In evolution, the phase of a rhythmic variable is selective rather than its endogenous period. Thus, the synchronization of endogenous rhythms to zeitgeber cycles of the environment (resulting in a specific phase of entrainment) is fundamental for the adaptive value of circadian clocks. In this study, we systematically investigated the properties of circadian oscillators that are essential for entrainment behavior and describe coupling as a primary determinant.

As an experimental starting point of this study, we found that the circadian oscillators of lung tissue have a larger range of entrainment than SCN tissue—they readily entrained to an experimental temperature cycle, whereas SCN tissue did not (Figure 4). In theoretical analyses, we show that both the ratio of amplitude and zeitgeber strength (Figure 3) and, importantly, inter-oscillator coupling are major determinants for entrainment (Figure 5). The reason for coupling being critical is twofold: (i) Coupling makes an oscillatory system more rigid, i.e., it relaxes faster in response to a perturbation, and (ii) coupling increases the amplitude of the oscillatory system. Both of these consequences of coupling lead to a smaller entrainment range, because zeitgeber stimuli affect the oscillatory system less if the relaxation is fast (Figure 2) and the amplitude is high (Figure 1). From these theoretical considerations, we conclude that the lung clock probably constitutes a weak oscillatory system, likely because a lack in coupling leads to a slow amplitude relaxation. (Circadian amplitude is not particularly low in lung (Figure 4)). In contrast, the SCN constitutes a rigid oscillator, whereby coupling and its described consequences probably are the primary causes for this rigidity. We then tested these theoretical predictions by experimentally perturbing coupling in the SCN, and find that, indeed, reducing the coupling weakens the circadian oscillatory system in the SCN, which results in an enlargement of the entrainment range (Figure 6).

Why is the SCN designed to be a stronger circadian oscillator than peripheral organs? We speculate that the position of the SCN—as the tissue that conveys environmental timing information (i.e., light) to the rest of the body—makes it necessary to create a circadian clock that is robust against noisy environmental stimuli. The SCN oscillator needs to be robust enough to be protected from environmental noise, but flexible enough to fulfill its function as an entrainable clock even in extreme photoperiods (i.e., seasons). By the same token, peripheral clocks are more protected from the environmental zeitgebers due to intrinsic homeostatic mechanisms (e.g., temperature control in homeotherms). Thus, they do not necessarily need to develop a strong oscillatory system (e.g., by strengthening the coupling) rather they need to stay flexible enough to respond to direct or indirect signals from the SCN, such as hormonal, neural, temperature or metabolic signals. Such a design ensures that only robust and persistent environmental signals trigger an SCN resetting response, while SCN signals can relatively easily be conveyed to the rest of the body. Thus, the robustness in the SCN clock likely serves as a filter for environmental noise.

These speculations are supported by observations suggesting that circadian clocks in primary sensory organs—such as the eyes or the olfactory system—are more robust than other peripheral clocks (Tosini and Menaker, 1996; Granados-Fuentes et al, 2004). These clocks are directly exposed to environmental zeitgebers, such as light and odor (Amir et al, 1999). For example, the retinal clock seems to be special among extra-SCN oscillators in that one of its rhythmic functional outputs (melatonin secretion) persists for at least 5 days in culture without substantial dampening (Tosini and Menaker, 1996). In addition, while SCN lesion abolishes most overt circadian rhythms, some rhythms in cornea and retina persist (Scheving et al, 1983, Terman et al, 1993, Sakamoto et al, 2000), indicating a robust clock in the eye. In addition, the clock in the olfactory bulbs seems to be self-sustained and SCN independent, i.e., in vivo oscillation persists even in the absence of the SCN (Abraham et al, 2005)—a property that has not been shown for other oscillators. In fact, clocks in other brain regions that are not directly exposed to environmental signals that may act as zeitgebers are usually much weaker, low-amplitude oscillators (for a review, see Guilding and Piggins, 2007). Although, to our knowledge, it has not yet been tested whether clocks in the eyes or olfactory bulbs are less responsive to zeitgeber stimuli than other brain clocks (as it would be predicted for a robust clock), the fact that their cells do not quickly desynchronize suggests that some kind of coupling is in place in these tissues.

Coupling seems to have an important role for robust synchronization, yet the effects of coupling and zeitgeber-to-amplitude ratio are probably well balanced. If the coupling between SCN neurons would be very strong (e.g., as strong as the effect of constant light that substantially lengthens behavioral periods in rodents, Daan and Pittendrigh, 1976), the period of synchronized SCN neurons might be different from the mean period of the dispersed neurons, which is clearly not the case (Honma et al, 1998). By the same token, the zeitgeber-to-amplitude ratio together with the intra-SCN coupling allow environmental stimuli, such as experimental 1-h light pulses (Comas et al, 2006), to phase shift the SCN clock only moderately by maximally 3 h. This restricts the entrainment range of circadian rhythms to typically 24±2 h (Pittendrigh and Daan, 1976). Thus, a necessary robustness against variable and noisy inputs is balanced with a moderate responsiveness to zeitgeber stimuli to allow daily entrainment, but probably also stable entrainment in different seasons.

As an additional means, daily or seasonal plasticity in the coupling properties may contribute to the flexibility of the circadian system. In fact, in recent years it became obvious that the phase distribution of the SCN neurons is strongly dependent on the photoperiod. In long photoperiods, the phases of SCN neurons are more broadened (Schaap et al, 2003) implying an altered, but not necessarily weaker coupling. Interestingly, this SCN-intrinsic encoding of the photoperiod results in different responses toward zeitgeber stimuli (van der Leest et al, 2009), suggesting that the type of coupling indeed may affect entrainment properties. How the coupling in long photoperiods is altered within the SCN is unclear at present. Further experiments are necessary, e.g., by directly measuring amplitude relaxation rates, to determine the rigidity of SCN (and peripheral oscillators) in different zeitgeber periods.

In summary, using a combination of simulation studies, analytical calculations and experiments, we uncovered critical features for entrainment, such as zeitgeber-to-amplitude ratio and amplitude relaxation rate. Coupling is a primary factor that governs these features explaining important differences in the design of SCN and peripheral oscillators that ensure a robust, but also flexible circadian system.

Materials and methods

Numerical calculations

The simulations were designed to explore how the entrainment range depends on a few generic parameters that are representative for a large class of oscillators. Results presented in Figures 2 and 3 and Supplementary Figure S3 were numerically calculated using a forced Poincaré oscillator in Cartesian coordinates:

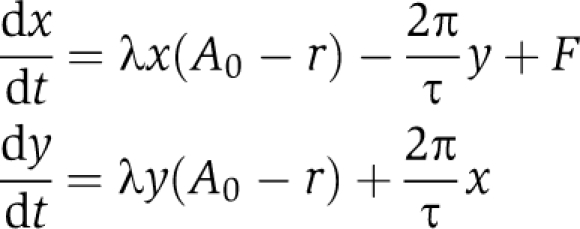The parameters represent the oscillator period τ, amplitude A₀ and amplitude relaxation rate λ. Introducing the radius r=(x+y)^1/2 and ϕ=arctan(y/x) leads to our model in Equation 1. The oscillator is entrained by a forcing term F that represents light or temperature entrainment. Without forcing, the oscillator has a 24-h period, i.e., τ=24 h. In Figure 2A, a Poincaré oscillator is entrained to square-wave zeitgeber cycles in analogy to the temperature cycles used in the experiments. In Figure 2 and Supplementary Figure S3, the weak oscillator has an amplitude relaxation rate λ=0.03 h⁻¹, the rigid oscillator has an amplitude relaxation rate λ=1 h⁻¹ and both oscillators have an amplitude A₀=1. In Figure 2B, the theoretical curves are plotted using our expression for the entrainment amplitude A_ent (see Equation 2). In Figures 2B and 3, and Supplementary Figure S3, the Poincaré oscillator is entrained to sinusoidal cycles, i.e., F=Bsin(2πt/T) with zeitgeber strength B, zeitgeber period T and time t. Figure 3 shows 112 different ratios of B/A₀ smaller than 0.25 with λ=1 h⁻¹. Supplementary Figure S4 shows the LLE for a linear, a Poincaré and a Hopf oscillator with an amplitude relaxation rate λ=0.01 h⁻¹ for each model. Computational and mathematical details regarding square-wave entrainment and the linear oscillator are given in the study by Granada and Herzel (2009).

The entrainment regions and lower limits of entrainment in Figures 2 and 3, Supplementary Figures S1 and S3 were calculated following the same numerical protocol: (i) Choose an oscillator amplitude A₀, relaxation rate λ, zeitgeber strength B and zeitgeber period T. (ii) Define a set of 24 initial conditions equally distributed around the limit cycle. (iii) Start the simulation and integrate 105 days. (iv) For each initial condition, the system is considered to reach entrainment if the mean phase difference of eight consecutive cycles is smaller than 1 min. (v) If more than 70% of the 24 initial conditions reach entrainment, consider the oscillator to be entrained for the given zeitgeber period T_i. (vi) For the LLE calculation take a shorter zeitgeber period T_j < T_i and repeat steps (iii–v) n times until a zeitgeber period T_n is reached, under which no entrainment is achieved. (vii) The limit of entrainment is the last zeitgeber period under which the oscillator entrains, i.e., T_low = T_n−1. For the upper limit of entrainment take a longer zeitgeber period T_j>T_i for each loop. For Figure 2 and Supplementary Figure S1, the whole protocol is repeated for an increasing zeitgeber strength B. In addition, for Figures 3 and Supplementary Figure S2, we repeated the protocol for 112 different ratios of B/A₀ <0.25.

Numerical integrations were implemented in Matlab (The MathWorks, Inc.) and XPPAUT (Ermentrout, 2003) with the use of Rob Clewley's XPP-Matlab interface. We used the CVODE integrator implemented in XPPAUT with stepsize setting of 0.2 h⁻¹, and error tolerance settings tol=1e–5 and atol=1e–5. To test our algorithm, we repeated the most sensitive numerically integrated results with the continuation software Cl_MatCont (Dhooge et al, 2008), which allows computation of bifurcations, limit cycles and Floquet exponents, and observed a fairly good agreement. Results shown in Figures 5A–C were entirely calculated with Cl_MatCont. The LLE is composed of a torus and a fold bifurcation (this is a general situation, see Balanov et al, 2009, chapter 3), both were accurately computed with Cl_MatCont. As the intrinsic (unforced) period τ of the coupled system (Equation 3) varies with the coupling strength K, this change (<1 h) slightly affects the LLE: the intrinsic period increases with increasing coupling strength, making the effect shown in Figure 5C even more pronounced. To exclude this drift, and hence, to show that the coupling strength and the amplitude relaxation rate of the single oscillators indeed exert a strong bona fide effect on the LLE, the LLE was normalized such that

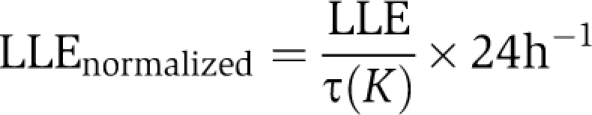where τ(K) is period of the unforced but coupled system at coupling strength K. Note that the unforced, uncoupled single-oscillator period is 24 h. Continuation results were compared with standard numerical integrations to assert accuracy and correctness.

Animals

Heterozygous male PER2::LUC knockin mice (Yoo et al, 2004;gift of Dr Joseph Takahashi, Northwestern University, IL, USA) expressing a PERIOD2::LUCIFERASE fusion protein were bred and raised in our animal facility (FEM, Berlin, Germany), and maintained in a 12 h light/12 h dark cycle. All procedures were authorized by and performed in accordance with guidelines and regulations of the German animal protection law (Deutsches Tierschutzgesetz).

Bioluminescence recording and temperature entrainment

Animals were killed by cervical dislocation and their brains and lungs transferred to chilled Hank's buffered saline solution, pH 7.2. For tissue culture, 300 μm coronal sections of the brain and lung were obtained with a tissue chopper. Brain slices containing the SCN were identified, and the bilateral, medial SCN dissected out using a pair of scalpels. All tissues were cultured individually on a Millicell membrane (Millipore) in a Petri dish with 1 ml of supplemented Dulbecco's Modified Eagle's Medium (DMEM, for details see Supplementary methods), containing 0.1 mM beetle luciferin (BioThema, Sweden). Petri dishes were covered with glass slides, sealed with grease and placed in temperature-adjustable light-tight boxes (Technische Werkstätten Charité, Berlin, Germany), equipped with photomultiplier tubes (HC135-11MOD, Hamamatsu, Japan) at 5% CO₂ for bioluminescence recording. During bioluminescence recording, a daily temperature cycle with a period of 20 h (10 h of 35.5°C and 10 h of 37°C) was applied to each SCN and lung slice. In order to simulate gradual temperature changes at dusk and dawn, each temperature step comprised a gradual temperature increase or decrease, respectively, over a course of 2 or 3 h. The first phase of the temperature entrainment cycle was always the cold phase (10 h of 35.5°C) and started at the minimum of PER2::LUC expression, as determined by online registration. Temperature entrainment comprised five or six temperature cycles. To inhibit cAMP-dependent signaling, which has been described to be crucial for intra-SCN coupling (O’Neill et al, 2008), we supplemented the culture medium with 10 μM (final concentration) of the adenylyl cyclase inhibitor MDL (Sigma). In an additional experiment, TTX (Sigma) were added to the culture medium (2–4 μM final concentration) to block voltage-gated sodium channels, i.e., to inhibit neuronal communication via action potentials. As both drugs are solved in aqueous solution, solvent control experiments are those shown in Figure 4. Bioluminescence from all slices was recorded in 5-min bins for at least 13 days. For pharmacological treatments, cultures were briefly removed from the recording incubator, and a complete medium change was performed. Recording was resumed immediately.

Single-cell recordings and image analysis

SCN tissues were cultured individually on pieces of Millicell membrane, inverted and cultured in 100 μl DMEM at 37°C and 5% CO₂ on the bottom of poly-D-lysine- and 5% laminine-coated 35-mm microscopic tissue culture dishes with grid (IBIDI, Germany). On day 3–5, the culture medium was replaced by 500 μl DMEM supplemented with 0.18 mg ml⁻¹ NaHCO₃ and 0.1 mM beetle luciferin. The Petri dish was sealed with grease and placed in a light-tight imaging chamber. Bioluminescence imaging was carried out in complete darkness and constant temperature with a 10 × objective and an inverse setup, including an intensified digital camera (XR/Mega-10Z, Stanford Photonics, USA). Images were stored in 10-min bins over the course of several days. For MDL treatment, culture medium was exchanged by DMEM supplemented with NaHCO₃, 0.1 mM beetle luciferin, and 10 μM MDL, and imaging was resumed immediately. Control treatment (DMEM supplemented with NaHCO₃, luciferin, and the corresponding amount of MDL solvent (H₂O)) did not have an effect on circadian oscillations (data not shown).

Ten-min exposures were stacked and resulting movies were smoothed using a 15-image running average (Piper 1.3. software, Stanford Photonics, USA). Alternatively, 10-min exposures were subjected twice to a Kalman filter (ImageJ software, NIH, USA). Single bioluminescent cells in random parts of the SCN were manually traced over several days and their gray values quantified using ImageJ software. Raw time series data were visually inspected and only cells that fulfilled certain criteria (Supplementary Information) were included in further analysis. Note that due to technical limitations cells tracked before and after MDL treatment were not identical.

Analysis of time series data

Bioluminescence time series data from single cells and tissue slices were first trend eliminated, and then analyzed for their period, phase and relative amplitude using ChronoStar 1.6 (Stephan Lorenzen, Institute for Theoretical Biology, Humboldt-University, Germany). Time series were trend eliminated by dividing values by a 24-h running average, thereby normalizing the magnitude to 1 to be independent of any measurement specifics, such as sensitivity/background of the photomultiplier or efficacy of the luciferase. Resulting time series oscillate around 1 with amplitudes that are relative to its mean. Periods, phases and amplitudes were estimated by fitting the cosine wave function y=a × exp(bt) × cos(2πt × 24/c+d), which includes an exponential term for damping (a=amplitude, b=damping, c=period, d=phase). Statistical analyses were performed using GraphPad Prism 4 software (GraphPad software, USA) and Rayleigh statistics after Batschelet (1981).

Supplementary Material

Supplementary Information

Supplementary Materials and Methods, Supplementary Figures S1–8, Legends to Supplementary Movies, Supplementary Table S1