Abstract
Enhancer-promoter interactions in eukaryotic genomes are often controlled by sequence elements that block the actions of enhancers. Although the experimental evidence suggests that those sequence elements contribute to forming loops of chromatin, the molecular mechanism of how such looping affects the enhancer-blocking activity is still largely unknown. In this article, the roles of DNA looping in enhancer blocking are investigated by numerically simulating the DNA conformation of a prototypical model system of gene regulation. The simulated results show that the enhancer function is indeed blocked when the enhancer is looped out so that it is separated from the promoter, which explains experimental observations of gene expression in the model system. The local structural distortion of DNA caused by looping is important for blocking, so the ability of looping to block enhancers can be lost when the loop length is much larger than the persistence length of the chain.
Introduction
Gene expression in eukaryotic cells is often regulated by enhancers that act on promoters in chromatin. The distance between enhancers and promoters is frequently larger than thousands of basepairs (bp) along the sequence and they sometimes are separated in different chromosomes. Questions should then arise about how the range of enhancer-promoter interactions is controlled to prevent promiscuity in their function. An important mechanism employed in cells for specific enhancer-promoter interactions is the action of insulators (1–5). Insulators are sequence elements of DNA that prevent inappropriate interactions between adjacent chromatin domains. At least two types of insulator activity, not necessarily exclusive of each other, have been pointed out (4,5); insulators that protect against spreading of heterochromatin regions are barrier insulators, whereas those that protect from activation by enhancers are enhancer-blocking insulators. In this article, the physical mechanism of enhancer-blocking activity is examined by numerically simulating a prototypical system of gene regulation.
Although the molecular mechanism of the enhancer-blocking activity has not yet been clarified, several models of activity have been proposed. The promoter decoy model assumes that interactions between insulators and enhancers prevent enhancer-promoter interactions (6). The structure model assumes that insulator-mediated formation of looped chromatin structures controls the transcription process (7–9). The tracking model is based on the assumption that RNA polymerase bound to an enhancer site can slide along the chromatin but is trapped by an insulator before it reaches the promoter (10). Though these models are not mutually exclusive, the significance of how the looped structure is formed is evident in the observation that the loop-forming interactions between a pair of tandemly arranged insulators (11–13) or insulatorlike elements (14) (Fig. 1, a and b) neutralize the insulator activity, making it possible for the unblocked enhancer to promote transcription.
Figure 1.
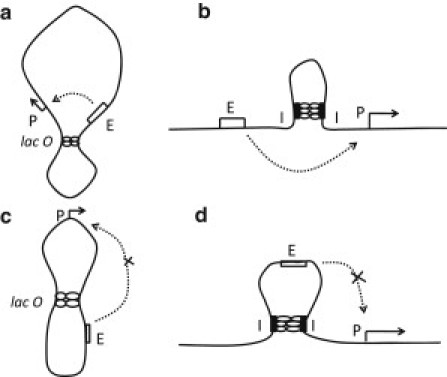
Schemes of DNA looping. (a) Looping in a plasmid ring through the interaction between tandemly arranged insulatorlike elements, lacO, which confines enhancer E and promoter P in the same loop. (b) Looping in a linear DNA chain through the interaction between tandemly arranged insulatorlike elements, I, which does not confine either enhancer or promoter. (c) Looping in a plasmid ring. (d) Looping in a linear DNA chain. In a and b, the enhancer action is not blocked by looping (11–14), but in c and d, the enhancer is looped out and its activity can be blocked (14–17).
The effects of DNA looping on enhancer-blocking activity were further analyzed by using the designed plasmid sequences, which encoded enhancers and promoters. Designed plasmids have been examined in vitro (14) and in vivo in transfected HeLa cells (15) and Drosophila cells (16,17). Bondarenko et al. (14) used a plasmid of several kilobasepairs (kbp) into which a bacterial enhancer-promoter pair was embedded. Also embedded was a pair of lac operators (lacO) that mimicked eukaryotic insulators. It was shown that the enhancer action of this system in vitro is blocked when interactions between the lacO pair form two closed loops with enhancer and promoter in separate loops (Fig. 1 c). Although the level of gene expression may become high in a supercoiled ring of DNA when the slithering motion of DNA brings enhancer and promoter spatially close to each other (18), Bondarenko et al. suggest that this slithering motion is pinned in a looped structure by the interaction between insulators, so that the expression level is lowered by the looping (14). Although insulator actions in eukaryotic genomes should be associated with histone modification or chromatin remodeling (4), the observations of Bondarenko et al. show that DNA looping alone is sufficient to suppress the enhancer activity in this model system and hence should also play an important role in eukaryotic cells.
Similar results were obtained by Ameres et al. by using HeLa cells transfected with designed DNA sequences (15). They showed that insulatorlike elements in an open fragment of DNA chain exhibit the same enhancer-blocking ability as observed in a closed ring of plasmid: The gene expression is much suppressed when interaction between insulatorlike elements confines the enhancer in a closed DNA loop separated from the promoter (Fig. 1 d). Because the slithering motion is less important in open fragments of DNA, this result showed that a mechanism other than pinning of slithering motion is important for insulatorlike elements to suppress enhancers. Thus, in this model system, the structure of looped DNA itself should be responsible for enhancer blocking, but this mechanism still remains unclear. Here, we analyze enhancer blocking in this prototypical system, the open short-DNA chain, to shed light on problems in gene regulation:
Open or closed plasmid chains in transfected mammalian cells can interact with histones to form minichromosomes (19), and this raises intriguing problems regarding the structure and dynamics of plasmid chains in vivo. To express the reporter gene, however, the chain should at least have a relaxed euchromatin structure, and for the enhancer to act efficiently in the small system (Fig. 2), there is no room for a nucleosome inserted around the enhancer. Therefore, interactions of this small system with histones should prevent enhancer activity, so the chromatinized model does not provide an adequate focus on the enhancer-blocking activity of loop formation. We therefore use an unchromatinized naked DNA as the model system in the next part of this article. We discuss the physical mechanism of this model system to take a step toward understanding insulator mechanisms.
Figure 2.
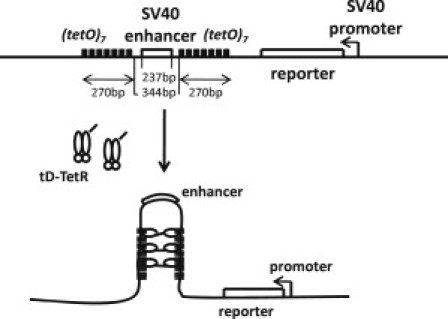
The designed sequence used in the experiment of Ameres et al. (15). SV40 enhancer is flanked by two boxes, each of which consists of seven repeats of tetR elements. When tD-TetR (TetR protein fused with the dimerization domain tD) binds to tetR elements, the dimerized tD-TetR connects two boxes and loops out SV40 enhancer, which can block the enhancer action on SV40 promoter, leading to the decrease of the level of the reporter protein, luciferase.
Model
We consider a linearized plasmid ∼6 kbp in length used in the experiment of Ameres et al. (15) as a model system of gene regulation. This open short DNA chain encoded SV40 enhancer, and its promoter was placed at 2.0 kbp distance from the enhancer. As shown in Fig. 2, the SV40 enhancer was flanked by two boxes of a repeat of seven tet operators (tetO). For further details about this model DNA chain, see Fig. 2. Introduced into HeLa cells together with this DNA chain was a plasmid that encoded a dimerization domain (tD) fused to the C-terminal end of the Tet repressor (TetR). When the tD-TetR produced from this plasmid binds to the tetO of the DNA chain examined, dimerized tD-TetRs connect two elements of tetO boxes to loop out the enhancer (Fig. 2).
Since this model chain is short enough, it may remain a naked DNA when the gene is actively expressed. We use this assumption to highlight the effects of DNA structure by treating them separately from those of histones. Thus, we use a combined wormlike chain and bead model (20–23) of DNA to simulate the system. The chain consists of i = 1−N beads and the segment length is assumed to be 30 bp. We use N = 200, so that the total length of the chain is 5970 bp. In this model chain, the enhancer is represented by a sequence of nine beads, i = 29−37, which in turn represent the SV40 enhancer of length 237 bp (15); the corresponding promoter is represented by beads i = 108−116. A box of repeats of tetO is simulated by n − m + 1 beads from i = m to i = n, which are assumed to interact with another box consisting of beads at j = j0 − i. Shown in Fig. 3 are five arrangements of sequences tested in this study: arrangement A, with no insulatorlike elements (Fig. 3 A); arrangement B-1, with (m,n) = (18,27) and j0 = 66; Arrangement B-2, with (m,n) = (3,12) and j0 = 66; arrangement B-3, with (m,n) = (24,27) and j0 = 66; and arrangement C, with (m,n) = (50,59) and j0 = 129.
Figure 3.
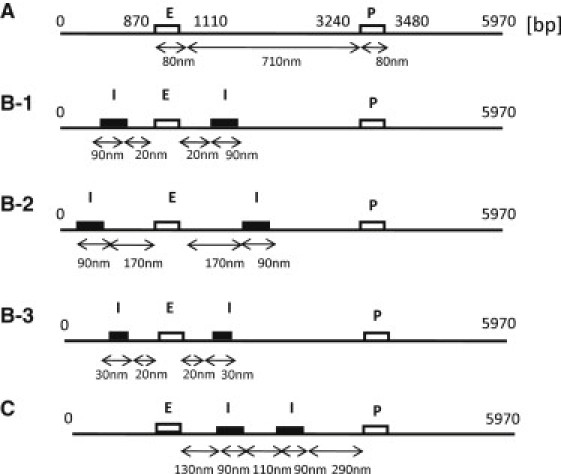
DNA chains with the different arrangements of sequence elements examined in this article: Arrangement A, no insulatorlike elements; Arrangement B-1, insulatorlike elements at almost the same positions as in the Ameres et al. experiment (15); Arrangement B-2, insulatorlike elements more widely separated than in the Ameres et al. experiment (15); Arrangement B-3, shorter insulatorlike elements; and Arrangement C, tandemly arranged insulatorlike elements.
The energy of the system consists of several terms,
| (1) |
Here, the first four terms of Eq. 1 are potential energies for a wormlike chain, and standard values are used for parameters in those four terms (18,23). Es is the energy of stretching the chain,
| (2) |
where h is the stretching force constant, li is the length of the ith segment, and l0 is the equilibrium segment length. We chose based on the works of Allison et al. (20) and Jian and Vologodskii (23), where is the Boltzmann constant. We consider the physiological conditions of T = 298 K and 0.2 M monovalent ions in solution, so that the length of the 30-bp segment should be around 10 nm, and hence we use nm (18). Eb is the energy of bending the chain,
| (3) |
where g is the bending rigidity constant, and θi is the angular displacement of segment i relative to segment i + 1. Based on the studies of other groups (18,24,25), we use . Erep is the repulsion of the excluded volume:
| (4) |
where is the distance between the ith and jth beads, and is the summation over all pairs of beads farther away than the nearest neighbor, , and nm (26). The electrostatic interaction is approximated as
| (5) |
where ν is the effective linear charge density of DNA, D is the dielectric constant of water, and κ is the inverse of the Debye length. We use e/nm for 0.2 M ion concentration (27), and . The Debye length is nm, and hence, nm–1.
Eloop represents interactions between a pair of insulatorlike elements, i.e., interactions necessary for closing the loop. Though we can expect that binding of tD-TetR to tetO brings about torsion or bending of the DNA chain to some extent, we neglect these effects and use a simplified assumption that two elements of tetO form an antiparallel sheet without torsion. Effects of torsion in looped DNA have been extensively studied on small loops of prokaryotic DNA (28–30), but here, torsion would give minor effects on the loop larger than the persistence length of nm (see Appendix for lp in the model presented here). Because structure and flexibility of the dimerized tD-TetR complex that mediates the interaction between two tetO elements are not known, we assume that the dimerized tD-TetR complex is flexible enough, so that the potential energy of interaction between bead i in one element and bead j in another element is assumed to be a flat function of if is smaller than a certain threshold b. For , we consider that the protein complex is stretched to increase Eloop. We do not consider the dynamical opening and closing processes of the loop but compare how the enhancer-promoter interactions are affected depending on whether the loop is set to be opened or closed. The purpose of introducing this energy term is to focus only on the condition of the loop being closed. For this purpose, it is sufficient that the energy function of Eloop is designed so that insulatorlike elements would be constrained to form a loop configuration. As one of the simplest choices for such a function, we choose as the functional form of Eloop
| (6) |
where we use nm as the typical size of protein homodimers. For simplicity, we use the same constant for the stretching rigidity of the DNA chain, , for arrangements other than Arrangement A (for Arrangement A, a is set to be zero). By estimating the thermal fluctuation of stretching energy as , we can see that the distance should be stretched from b due to the thermal fluctuation as nm for this choice of a, exhibiting the reasonable amplitude of fluctuation for a dimerized protein complex. By using a smaller rigidity value, such as , for comparison, we have nm, but the simulated results of the enhancer-promoter interactions in the latter case were almost the same as those shown in this article; the results are robust against the choice of the parameter value a.
Eep is the energy to form a transcription complex that involves transcription factors, enhancer, and promoter (8,31,32). Structure and dynamics of the transcription complex are not known, but there are many examples of how the intrinsically disordered proteins constitute core parts of transcription complexes (33), and hence, we assume that the distance between enhancer and promoter in the transcription complex can flexibly change without a large energy loss. Here, the formation of the transcription complex is simulated by juxtaposition of the enhancer element and the promoter element. Corresponding to the assumed structural flexibility of the transcription complex, we define Eep to be insensitive to the structural change of the juxtaposed enhancer-promoter pair by using the same form of a linear function of distance as in Huang et al. (18);
| (7) |
where is the distance between a bead in the enhancer element and a bead in the promoter element, and the enhancer element extends from to i = l with (, and the promoter element is the corresponding region of . As an alternative to the linear functional form of Eq. 7, we also examined with a square-well potential, but the simulated results were qualitatively the same, so that the results are insensitive to the detailed functional form of Eep. Formation of the transcription complex results in formation of a loop of the DNA chain in addition to the preexisting loop formed through interactions between insulatorlike elements. Unlike the constrained interactions between insulatorlike elements in this model, we consider the dynamical association and dissociation of the enhancer-promoter pair and measure the equilibrium probability, Pprox, of forming the proximity pair of enhancer and promoter. Torsion of the DNA chain may play a role in evaluating the free energy of loops in general, but we neglect such effects here, since there should be a minor statistical effect to calculate Pprox in a loop much longer than the persistence length.
Here, we define the average enhancer-promoter distance, ;
| (8) |
where implies the thermal average. Then, Pprox is defined by the probability that < 10 nm. In Eq. 7, μ is calibrated to be to make in the simulated results for Arrangement A. This value of μ corresponds to when the transcription complex is fully formed with for all ij pairs, which is of the same order as the typical energy of binding of transcription factors to DNA, 10–15 kcal/mol (34), so that this choice of μ should be consistent with its physical meaning as a coefficient to decide the energy of binding of transcription factors to enhancer and promoter regions. The effects of variation of the value of μ will be argued in the Discussion section.
By using thus defined energy function, we perform Metropolis Monte Carlo (MC) calculations to simulate the equilibrium distribution of structures of the DNA chain. See Appendix for details of the MC calculation.
Results
In the experiment of Ameres et al. (15), expression level of the reporter gene was monitored and compared among different experimental conditions for looped and unlooped DNA chains. When the probability that the transcription complex is formed is denoted by Pon, the expression level of the reporter gene, that is, the amount of synthesized reporter protein, is estimated by , where g is the rate of protein synthesis and kd is the rate constant of protein degradation (35). Pon, on the other hand, should be proportional to Pprox as , where is the probability that the transcription factors are properly arranged to function on the juxtaposing enhancer and promoter. In this simulation, various looped and unlooped chains with different arrangements of sequence are compared (Fig. 3). When we write Np, q, and Pprox in the sequence of Arrangement X as , , and , the relative expression level with different arrangements of and X is expressed by the ratio
| (9) |
Because DNA looping can bring about local structural distortion at the enhancer site, the looping may distort the transcription complex and lower q. Hence, for X of the unlooped chain and of the looped chain, we can expect the inequality , so that gives the upper bound of the relative level of gene expression in the looped chain. Hereafter, we estimate Pprox from MC calculation of DNA conformation and examine whether the calculated Pprox is consistent with the experimentally observed enhancer-blocking effects of DNA looping (15).
Shown in Fig. 4 are the simulated results of Pprox for Arrangements A, B-1, and B-2. Arrangement A has no insulatorlike element. Arrangement B-1, on the other hand, has insulatorlike elements at almost the same positions as in the experiment (15). Arrangement B-2 also has two boxes of insulatorlike elements, but they are separated farther from each other than in Arrangement B-1 to form a larger loop than observed in the experiment. We can see that the DNA looping in Arrangement B-1 much suppresses Pprox as , which is consistent with the experimentally observed apparent blocking of enhancer through looping (see Fig. 4 of Ameres et al. (15)). In Arrangement B-2, on the other hand, and blocking is not much evident. Thus, the blocking activity of looping is sensitive to the size of the loop, and the simulated results suggest that the loop size has to be small enough to assure blocking.
Figure 4.
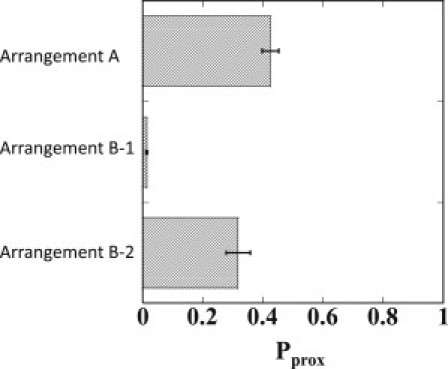
The simulated proximity probability, Pprox, to form juxtaposed pair of enhancer and promoter for Arrangement A, B-1, and B-2.
In Fig. 5, simulated Pprox results for Arrangements B-3 and C are compared with the result for Arrangement A. In the experiment, seven repeats of tetO were used for the assured binding of tD-TetR to the DNA chain (15), but in the case of stronger binding affinity of proteins to DNA, the smaller number of repeats of binding sites should be enough for looping. Arrangement B-3 corresponds to such a case of a smaller number of binding sites with shorter insulatorlike elements. Pprox in B-3 is similar to that in B-1 (Figs. 4 and 5), implying that Pprox is insensitive to the length of insulatorlike elements when there is strong enough binding affinity of proteins to mediate the looping. When the binding affinity is not strong, the shorter insulatorlike elements should bring about a smaller probability of looping to decrease the enhancer-blocking activity. It would be interesting to experimentally assess these predictions by using engineered TetRs whose binding affinities to DNA are altered (36). In Arrangement C, Pprox is slightly larger than that in Arrangement A, which is consistent with the observations that the enhancer blocking ability in vivo (11,12) or in vitro (14) is lost when a tandem pair of insulators or insulatorlike elements is inserted between enhancer and promoter, as in Arrangement C.
Figure 5.
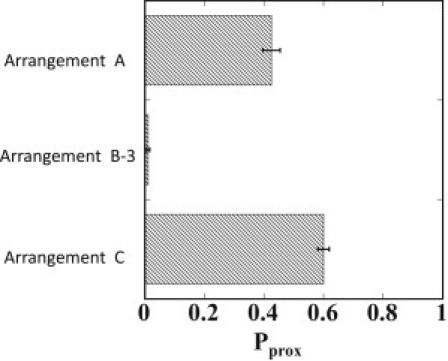
The simulated proximity probability, Pprox, of forming a juxtaposed enhancer-promoter pair for Arrangements A, B-3, and C.
The corresponding free energy of the chain, F, is shown in Fig. 6 as a function of . shows a minimum at the juxtaposing position of nm in all sequence arrangements as well as at the distance for the separated enhancer-promoter pair at nm in Arrangements A, B-1, and B-2 and nm in Arrangement C. We write . The free energy to stabilize the juxtaposed state, , is in Arrangement A, in Arrangement B-1, and in Arrangement C, demonstrating the insufficient stabilization of the juxtaposed state in Arrangement B-1.
Figure 6.
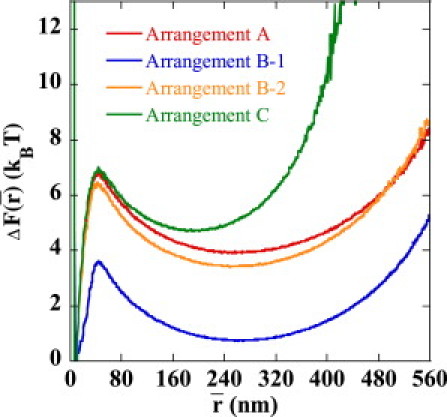
Free energy to stabilize the juxtaposed state, , i.e., the relative free energy of the state at the average enhancer-promoter distance, , to the state at nm is plotted as a function of , for Arrangements A (red), B-1 (blue), B-2 (orange), and C (green).
The reason for the small in Arrangement B-1 is clarified when is decomposed into the averaged energy, , and entropy, . Plotted in Figs. 7 and 8 are and , respectively. We can see that is smaller in Arrangement B-1 than in Arrangements A, B-2, or C, so that the juxtaposed state in Arrangement B-1 is energetically destabilized. On the other hand, of Arrangement B-1 is almost the same as that of A and B-2, so the strong suppression of enhancer activity in Arrangement B-1 is due not to the entropic effect but to the energetic effect of the DNA chain configuration. of Arrangement C is smaller than those of other arrangements, showing that the juxtaposed state in Arrangement C is entropically stabilized compared with other arrangements.
Figure 7.
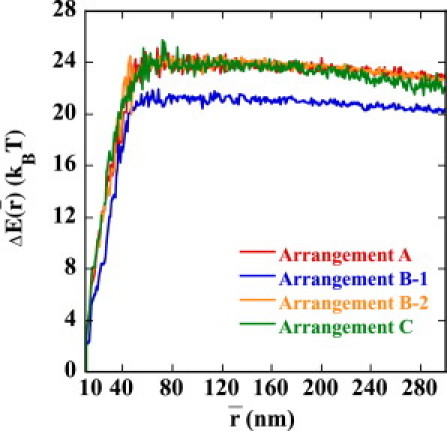
The average energy to stabilize the juxtaposed state, , i.e., the relative energy at the average enhancer-promoter distance, , to the state at nm is plotted as a function of for Arrangements A (red), B-1 (blue), B-2 (orange), and C (green).
Figure 8.
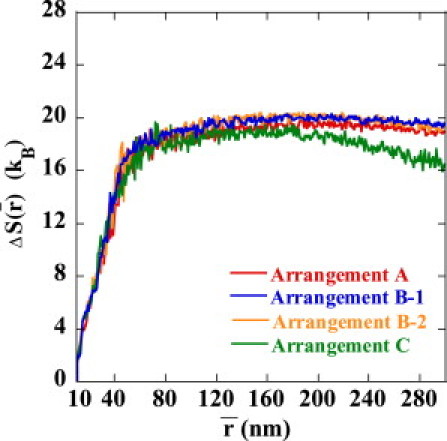
Entropy cost to form the juxtaposed state, , i.e., the relative entropy at the average enhancer-promoter distance, , to the state at nm is plotted as a function of for Arrangements A (red), B-1 (blue), B-2 (orange), and C (green).
Shown in Fig. 9 are snapshots of configurations of the simulated DNA chain. In Arrangements A and C, both the enhancer and promoter elements tend to have linear extended configurations. In Arrangement B-1, on the other hand, it is shown that the enhancer element confined in a small loop is bent and the enhancer-promoter complex has a distorted configuration, which should necessarily raise the energy of the complex and destabilize the juxtaposed state. This distortion should be a natural consequence that the loop size, Lloop, of Arrangement B-1 is nm , whereas the condition to make the enhancer element undistorted should be .
Figure 9.
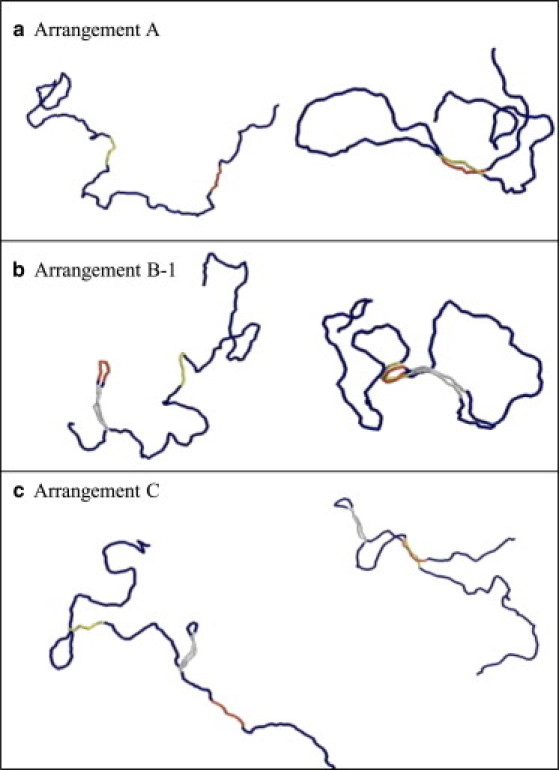
Snapshots of Monte Carlo simulations of a linear chain of ∼ 6 kbp DNA. In each column, the left image is the state where the enhancer and promoter are separated and the right is the state where they are juxtaposed. The enhancer element (240 bp) is red, the promoter element (240 bp) is yellow, and the insulatorlike regions (270 bp) are gray.
This effect can be quantitatively analyzed by plotting bond angle as a function of segment number i. Shown in Fig. 10 are distributions of in the state that enhancer and promoter are juxtaposing to form a proximity pair. In Arrangements A, B-2, and C, angles at the enhancer and promoter elements show values smaller than the average, implying that the juxtaposed enhancer-promoter pair has a more straightened structure than that in the free DNA chain. The same effect can be seen in the pair of insulatorlike elements. In Arrangements B-1 and C, on the other hand, bond angles in the loop region exhibit large values corresponding to the structural distortion (Fig. 9). In Arrangement C, this structural distortion is separated from the enhancer and promoter regions and gives no significant effect on . In Arrangement B-1, however, this distorted region overlaps with the enhancer region, and hence, the juxtaposing promoter is also distorted to have large angles. The distorted conformation increases Eb of Eq. 3 to bring about the small stabilization of the juxtaposed state and the corresponding small , which leads to the small Pprox in Arrangement B-1. Thus, the small size of the loop that confines the enhancer is the origin of enhancer blocking in this model system: the simulated local structural features of the DNA chain explain the observed data of gene expression.
Figure 10.
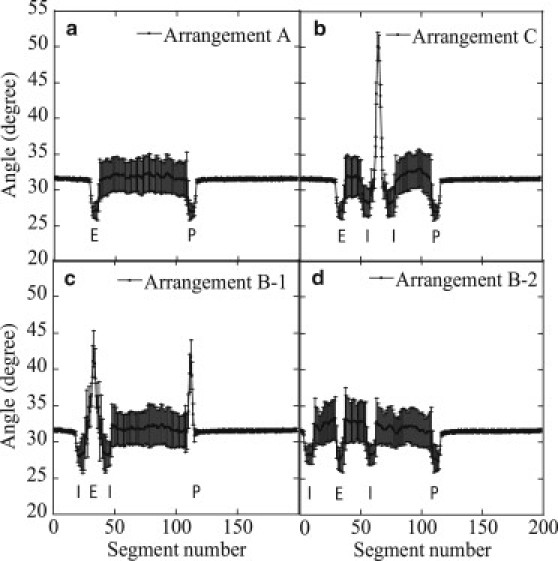
The average bond angle, , of the DNA chain in which enhancer and promoter are juxtaposed to form a proximity pair is plotted as a function of the segment number, i. The average was taken over 100 samples, and error bars are standard deviations.
Discussion
In this article, a prototypical system of gene regulation was investigated with MC simulation, and the enhancer activity in this system was shown to be blocked when the enhancer is confined in a small loop, which inevitably induces local structural distortion at the enhancer site to destabilize the juxtaposition of enhancer and promoter. This effect is energetic, which is in sharp contrast to the mechanism of the reduction of entropy due to the pinning of slithering motion expected in a small ring of DNA. The simulation results showed that the blocking effect can be less evident as the loop size gets larger, with the pair of insulatorlike elements further separated. Since we did not explicitly examine the factor q in Eq. 9 in this simulation, we cannot exclude the possibility that small q leads to the low expression level, even in the case where Pprox is not much reduced. The bond-angle distributions in Fig. 10, however, show that the structure of the DNA chain in Arrangement B-2 is similar to those in Arrangements A and C, and hence, we can maybe expect that the transcription complex in Arrangement B-2 is not much distorted and exhibits a relatively large q value . It is possible to test this prediction by experimentally examining a series of arrangements with different distances between insulatorlike elements.
In this model, the electrostatic interactions were treated with the Debye-Hückel approximation, but ion-specific modeling is required for a more realistic description of electrostatics at short distances (37). Even with the Debye-Hückel treatment described here, however, the model suggests an interesting effect that can be tested with experiments: when charges on DNA are further screened due to the larger strength of counterions, the stiffness of the DNA chain is decreased and the persistence length, lp, hence becomes smaller, which increases both and , but with a more prominent increase in . As a result, the enhancer-blocking activity in B-1 is reduced, as demonstrated by the larger value of compared with the results presented here. In this model, with the limit of , for example, the simulated results show that and .
DNA chains in the cell are in a crowded environment, which affects interactions in biopolymers and promotes their compaction (38). In the model presented here, this effect should enhance the probability of enhancer-promoter juxtaposition, which could be implicitly represented by the increase in value of μ in Eq. 7. It is obvious that in the limit of large μ, Eep dominates E in Eq. 1 and , and in the limit of small μ, we should have . The insulator action is evident at intermediate μ. The simulated results showed that for , so the results shown in this article are valid over a wide range (30% difference in μ) around the assumed physiological condition. It is interesting to examine the effects of crowding on in vitro by changing the crowding condition in solution.
Ameres et al. (15) have discussed three scenarios to describe the mechanism of insulator action: 1), the internal contact scenario, in which the tandemly arranged insulatorlike elements form loops but the enhancer is not included in these loops; 2), the bead-string scenario, in which a loop is not formed due to the insulatorlike elements; and 3), the loop scenario, in which the enhancer is looped out due to the interactions between insulatorlike elements, as simulated in Arrangement B in this article. Ameres et al. have shown experimentally that the internal contact scenario cannot explain the experimental results, but the loop scenario is consistent with the observed data (15). In this simulation, the small explains the validity of the loop scenario, and the large shows the implausibility of the internal contact scenario. Ameres et al. have also shown that binding of TetR to tetO alone slightly affects the expression level, but this effect is insignificant when the loop is not formed, and hence, the bead-string scenario is inappropriate (15). Such a small change in the observed expression level in the case where the loop is not formed may be due to the distortion at the tetO region to which TetR binds, but this delicate effect could not be examined using the simplified model in this study.
Results of this study showed that the topological effect of looping, which has been discussed only qualitatively, should be reexamined in light of local structural deformation in the DNA-protein complex. It is reminiscent of prokaryotic cases that the local structure deformation plays a key role in the topological effect of the DNA chain (39). In the eukaryotic genome, of course, the structures of the looped chromatin should be much more complex than in this model system by interacting with histones or with the nuclear surface structures. Comparison between structural simulations of DNA and experimental observation of simplified prototypical systems, however, provides bases for a deeper understanding of the local DNA structure change in gene regulation and forms a guide for further simulation studies using coarse-grained models of chromatin with larger persistence length and with additional necessary energy terms (40) or using models that explicitly consider nucleosome structures (41). The results presented here show the importance of the local structure of chromatin and suggest that the local structure of more sophisticated chromatin models should play key roles in our understanding of enhancer-blocking activity in the eukaryotic genome.
Appendix
We adopt two types of trial MC moves: 1), the local move, with which one bead i is randomly selected and its coordinate is randomly displaced from to , with ; and 2), the global move, the same move adopted in Jian and Vologodskii (23), where one bead i is randomly selected and the chain of is rotated with a randomly chosen set of Euler angles. In each MC step, the local move is selected with the probability 0.4, and the global move is selected with the probability 0.6. Either of these types of motion is applied as a trial and accepted or rejected with the Metropolis criterion. The initial conformation of the chain is a zigzag structure; for even i and for odd i. Starting from this conformation, 4 × 107 steps of moves are tried and the data are sampled every 103 steps by disregarding the initial 2 × 107 steps for equilibration.
When we put , i.e., when we use the ordinary wormlike chain model and nm (5970 bp), the simulated mean-square end-to-end distance of the chain, , can be fitted by the expression with a persistence length of nm (42), confirming that the model presented here is consistent with the generally accepted notion that the persistence length of DNA in the physiological condition is ∼50 nm.
References
- 1.Valenzuela L., Kamakaka R.T. Chromatin insulators. Annu. Rev. Genet. 2006;40:107–138. doi: 10.1146/annurev.genet.39.073003.113546. [DOI] [PubMed] [Google Scholar]
- 2.Bushey A.M., Dorman E.R., Corces V.G. Chromatin insulators: regulatory mechanisms and epigenetic inheritance. Mol. Cell. 2008;32:1–9. doi: 10.1016/j.molcel.2008.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Geyer P.K., Clark I. Protecting against promiscuity: the regulatory role of insulators. Cell. Mol. Life Sci. 2002;59:2112–2127. doi: 10.1007/s000180200011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gaszner M., Felsenfeld G. Insulators: exploiting transcriptional and epigenetic mechanisms. Nat. Rev. Genet. 2006;7:703–713. doi: 10.1038/nrg1925. [DOI] [PubMed] [Google Scholar]
- 5.Raab J.R., Kamakaka R.T. Insulators and promoters: closer than we think. Nat. Rev. Genet. 2010;11:439–446. doi: 10.1038/nrg2765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Geyer P.K. The role of insulator elements in defining domains of gene expression. Curr. Opin. Genet. Dev. 1997;7:242–248. doi: 10.1016/s0959-437x(97)80134-7. [DOI] [PubMed] [Google Scholar]
- 7.Hou C., Zhao H., Dean A. CTCF-dependent enhancer-blocking by alternative chromatin loop formation. Proc. Natl. Acad. Sci. USA. 2008;105:20398–20403. doi: 10.1073/pnas.0808506106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tolhuis B., Palstra R.J., de Laat W. Looping and interaction between hypersensitive sites in the active β-globin locus. Mol. Cell. 2002;10:1453–1465. doi: 10.1016/s1097-2765(02)00781-5. [DOI] [PubMed] [Google Scholar]
- 9.Majumder P., Cai H.N. The functional analysis of insulator interactions in the Drosophila embryo. Proc. Natl. Acad. Sci. USA. 2003;100:5223–5228. doi: 10.1073/pnas.0830190100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhao H., Dean A. An insulator blocks spreading of histone acetylation and interferes with RNA polymerase II transfer between an enhancer and gene. Nucleic Acids Res. 2004;32:4903–4919. doi: 10.1093/nar/gkh832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cai H.N., Shen P. Effects of cis arrangement of chromatin insulators on enhancer-blocking activity. Science. 2001;291:493–495. doi: 10.1126/science.291.5503.493. [DOI] [PubMed] [Google Scholar]
- 12.Muravyova E., Golovnin A., Georgiev P. Loss of insulator activity by paired Su(Hw) chromatin insulators. Science. 2001;291:495–498. doi: 10.1126/science.291.5503.495. [DOI] [PubMed] [Google Scholar]
- 13.Mongelard F., Corces V.G. Two insulators are not better than one. Nat. Struct. Biol. 2001;8:192–194. doi: 10.1038/84905. [DOI] [PubMed] [Google Scholar]
- 14.Bondarenko V.A., Jiang Y.I., Studitsky V.M. Rationally designed insulator-like elements can block enhancer action in vitro. EMBO J. 2003;22:4728–4737. doi: 10.1093/emboj/cdg468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ameres S.L., Drueppel L., Berens C. Inducible DNA-loop formation blocks transcriptional activation by an SV40 enhancer. EMBO J. 2005;24:358–367. doi: 10.1038/sj.emboj.7600531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Savitskaya E., Melnikova L., Georgiev P. Study of long-distance functional interactions between Su(Hw) insulators that can regulate enhancer-promoter communication in Drosophila melanogaster. Mol. Cell. Biol. 2006;26:754–761. doi: 10.1128/MCB.26.3.754-761.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Maksimenko O., Golovnin A., Georgiev P. Enhancer-promoter communication is regulated by insulator pairing in a Drosophila model bigenic locus. Mol. Cell. Biol. 2008;28:5469–5477. doi: 10.1128/MCB.00461-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huang J., Schlick T., Vologodskii A. Dynamics of site juxtaposition in supercoiled DNA. Proc. Natl. Acad. Sci. USA. 2001;98:968–973. doi: 10.1073/pnas.98.3.968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Reeves R., Gorman C.M., Howard B. Minichromosome assembly of non-integrated plasmid DNA transfected into mammalian cells. Nucleic Acids Res. 1985;13:3599–3615. doi: 10.1093/nar/13.10.3599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Allison S.A. Brownian dynamics simulation of wormlike chains. Fluorescence depolarization and depolarized light scattering. Macromolecules. 1986;19:118–124. [Google Scholar]
- 21.Allison S., Austin R., Hogan M. Bending and twisting dynamics of short linear DNAs. Analysis of the triplet anisotropy decay of a 209 base pair fragment by Brownian simulation. J. Chem. Phys. 1989;90:3843–3854. [Google Scholar]
- 22.Chirico G., Langowski J. Brownian dynamics simulations of supercoiled DNA with bent sequences. Biophys. J. 1996;71:955–971. doi: 10.1016/S0006-3495(96)79299-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jian H., Vologodskii A.V. A combined wormlike-chain and bead model for dynamic simulations of long linear DNA. J. Comput. Phys. 1997;136:168–179. [Google Scholar]
- 24.Hagerman P.J. Flexibility of DNA. Annu. Rev. Biophys. Biophys. Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- 25.Frank-Kamenetskii M.D., Lukashin A.V., Vologodskii A.V. Torsional and bending rigidity of the double helix from data on small DNA rings. J. Biomol. Struct. Dyn. 1985;2:1005–1012. doi: 10.1080/07391102.1985.10507616. [DOI] [PubMed] [Google Scholar]
- 26.Liu Z., Chan H.S. Efficient chain moves for Monte Carlo simulations of a wormlike DNA model: excluded volume, supercoils, site juxtapositions, knots, and comparisons with random-flight and lattice models. J. Chem. Phys. 2008;128:145104–145131. doi: 10.1063/1.2899022. [DOI] [PubMed] [Google Scholar]
- 27.Vologodskii A., Cozzarelli N. Modeling of long-range electrostatic interactions in DNA. Biopolymers. 1995;35:289–296. doi: 10.1002/bip.360350304. [DOI] [PubMed] [Google Scholar]
- 28.Cloutier T.E., Widom J. DNA twisting flexibility and the formation of sharply looped protein-DNA complexes. Proc. Natl. Acad. Sci. USA. 2005;102:3645–3650. doi: 10.1073/pnas.0409059102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Goyal S., Lillian T., Perkins N.C. Intrinsic curvature of DNA influences LacR-mediated looping. Biophys. J. 2007;93:4342–4359. doi: 10.1529/biophysj.107.112268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shimada J., Yamakawa H. Ring-closure probabilities for twisted wormlike chain. Application to DNA. Macromolecules. 1984;17:689–698. [Google Scholar]
- 31.Su W., Porter S., Echols H. DNA-looping and enhancer activity: association between DNA-bound NtrC activator and RNA polymerase at the bacterial glnA promoter. Proc. Natl. Acad. Sci. USA. 1990;87:5504–5508. doi: 10.1073/pnas.87.14.5504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dekker J., Rippe K., Kleckner N. Capturing chromosome conformation. Science. 2002;295:1306–1311. doi: 10.1126/science.1067799. [DOI] [PubMed] [Google Scholar]
- 33.Liu J., Perumal N.B., Dunker A.K. Intrinsic disorder in transcription factors. Biochemistry. 2006;45:6873–6888. doi: 10.1021/bi0602718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jen-Jacobson L. Protein-DNA recognition complexes: conservation of structure and binding energy in the transition state. Biopolymers. 1997;44:153–180. doi: 10.1002/(SICI)1097-0282(1997)44:2<153::AID-BIP4>3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
- 35.Sasai M., Wolynes P.G. Stochastic gene expression as a many-body problem. Proc. Natl. Acad. Sci. USA. 2003;100:2374–2379. doi: 10.1073/pnas.2627987100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhou X., Symons J., Das A.T. Improved single-chain transactivators of the Tet-On gene expression system. BMC Biotechnol. 2007;7:6. doi: 10.1186/1472-6750-7-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Savelyev A., Papoian G.A. Inter-DNA electrostatics from explicit solvent molecular dynamics simulations. J. Am. Chem. Soc. 2007;129:6060–6061. doi: 10.1021/ja070207t. [DOI] [PubMed] [Google Scholar]
- 38.Minton A.P. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J. Biol. Chem. 2001;276:10577–10580. doi: 10.1074/jbc.R100005200. [DOI] [PubMed] [Google Scholar]
- 39.Liu Z., Deibler R.W., Zechiedrich L. The why and how of DNA unlinking. Nucleic Acids Res. 2009;37:661–671. doi: 10.1093/nar/gkp041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rosa A., Becker N.B., Everaers R. Looping probabilities in model interphase chromosomes. Biophys. J. 2010;98:2410–2419. doi: 10.1016/j.bpj.2010.01.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Schiessel H. The physics of chromatin. J. Phys. Condens. Matter. 2003;15:R699–R774. doi: 10.1088/0953-8984/27/6/060301. [DOI] [PubMed] [Google Scholar]
- 42.Rubinstein M., Colby R.H. Oxford University Press; 2003. Polymer Physics. [Google Scholar]


