Abstract
The cyanobacterium Synechococcus elongatus uses both a protein phosphorylation cycle and a transcription–translation cycle to generate circadian rhythms that are highly robust against biochemical noise. We use stochastic simulations to analyze how these cycles interact to generate stable rhythms in growing, dividing cells. We find that a protein phosphorylation cycle by itself is robust when protein turnover is low. For high decay or dilution rates (and compensating synthesis rates), however, the phosphorylation-based oscillator loses its integrity. Circadian rhythms thus cannot be generated with a phosphorylation cycle alone when the growth rate, and consequently the rate of protein dilution, is high enough; in practice, a purely posttranslational clock ceases to function well when the cell doubling time drops below the 24-h clock period. At higher growth rates, a transcription–translation cycle becomes essential for generating robust circadian rhythms. Interestingly, although a transcription–translation cycle is necessary to sustain a phosphorylation cycle at high growth rates, a phosphorylation cycle can dramatically enhance the robustness of a transcription–translation cycle at lower protein decay or dilution rates. In fact, the full oscillator built from these two tightly intertwined cycles far outperforms not just each of its two components individually, but also a hypothetical system in which the two parts are coupled as in textbook models of coupled phase oscillators. Our analysis thus predicts that both cycles are required to generate robust circadian rhythms over the full range of growth conditions.
Keywords: Kai, oscillations
Many organisms use circadian clocks to anticipate changes between day and night (1). It had long been believed that these clocks are driven primarily by transcription–translation cycles built on negative feedback. However, although some circadian clocks can maintain robust rhythms for years in the absence of any daily cue (1), recent experiments have vividly demonstrated that gene expression is often highly stochastic (2). This raises the question of how these clocks can be so robust against biochemical noise. In multicellular organisms, the robustness might be explained by intercellular interactions (3, 4), but it is now known that even unicellular organisms can have very stable circadian rhythms. The clock of the cyanobacterium Synechococcus elongatus, for example, has a correlation time of several months (5), even though the clocks of the different cells in a population hardly interact with one another (5, 6). How circadian clocks can be so stable even at the single cell level is not understood.
Interestingly, it has recently been discovered that the S. elongatus clock combines a transcription–translation cycle (TTC) with a protein phosphorylation cycle (PPC). The central components of the clock are the three genes kaiA, kaiB, and kaiC (7). Under continuous light conditions, the levels of mRNA from the kaiBC operon and of the protein KaiC oscillate in a circadian fashion (8); moreover, overexpression of KaiC abolishes kaiBC expression (9, 10). These observations led to the proposal that the Kai system is a transcription–translation oscillator, with KaiC negatively regulating its own transcription. In 2005, however, Kondo and coworkers showed that KaiC, which is a hexamer with two phosphorylation sites per monomer (11), is phosphorylated in a cyclical manner with a period of 24 h, even when kaiBC transcription is inhibited (12). Still more remarkably, the rhythmic phosphorylation of KaiC could be reconstituted in the test tube in the presence of only KaiA, KaiB, and ATP (13). This raised the possibility that the principal pacemaker of the clock is not a TTC, but a PPC (13). Yet, in 2008, the same group showed that circadian oscillations of gene expression persist even when KaiC is always held in a highly phosphorylated state (14). They thus concluded that the clock is driven by both a TTC and a PPC and suggested that the interactions between the two oscillators may enhance the robustness of the clock (14).
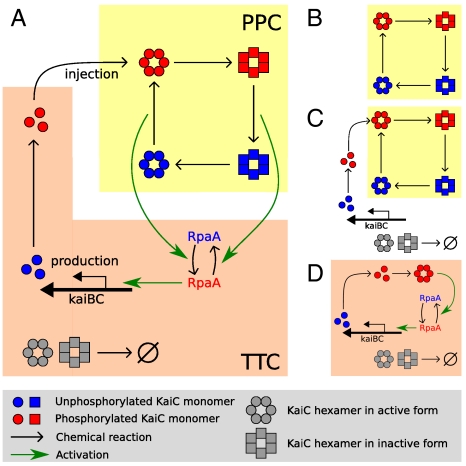
Here, we use mathematical modeling to study how a protein-modification oscillator and a transcription–translation oscillator interact in growing, dividing cells. To this end, we study four models, schematically shown in Fig. 1: (i) PPC-in vitro model (Fig. 1B); (ii) PPC-in vivo model (Fig. 1C); (iii) PPC-TTC model (Fig. 1A); (iv) TTC-only model (Fig. 1D). We first study the PPC-in vitro model, which describes the PPC that has been reconstituted in the test tube (13) (Fig. 1B). In this system, the total number of each Kai protein is constant—they are neither produced nor destroyed—and only the PPC is operative. We show that in this case the PPC is highly robust against noise arising from the intrinsic stochasticity of chemical reactions. Even for reaction volumes smaller than the typical volume of a cyanobacterium, the correlation time is longer than that observed experimentally (5). Living cells, however, constantly grow and divide, and proteins must thus be synthesized to balance dilution. In fact, dilution can be thought of as introducing an effective protein degradation rate set by the cell doubling time. We therefore next study the PPC-in vivo model (Fig. 1C), which describes a PPC in which the Kai proteins are produced and degraded with rates that are constant in time. The simulations reveal that protein synthesis and decay dramatically reduce the viability of the PPC; we predict that for a cell doubling time of 24 h and a bacterial volume of 1 μm3, the PPC dephases in roughly 10 days, much faster than real S. elongatus (5). This is because the constant synthesis of proteins, which we assume are all initially created in the same phosphorylation state, necessarily injects KaiC with the “wrong” phosphorylation level at certain phases of the cycle (1, 15, 16); if these appear fast enough, they can destroy the oscillation. One role of the TTC is thus to introduce proteins only when the phosphorylation state of the freshly made KaiC matches that of the PPC. Our simulations of the PPC-TTC model (Fig. 1A), which combines a PPC and a TTC, reveal that a TTC can indeed greatly enhance the robustness of the PPC, yielding correlation times consistent with those measured experimentally (5). Finally, we consider whether the PPC is needed at all, or whether one could build an equally good circadian clock using only a TTC; to this end, we study the TTC-only model (Fig. 1D). We find that it is possible to construct a TTC with a period of 24 h and the observed correlation time of a few months (5). However, this comes at the expense of very high protein synthesis and decay rates, which impose an extra energetic burden on the cell. Our results thus suggest that a PPC allows for a more robust oscillator at a lower cost. Although our models are simplified, we argue in Principal Pacemaker and Discussion that our qualitative results are unavoidable consequences of the interaction between a circadian clock and cell growth and so should hold far more generally.
Fig. 1.
Overview of the models studied in this manuscript. (A) PPC-TTC model: A TTC of kaiBC expression (orange background) interacts with a KaiC PPC (yellow background) (40). KaiC is a hexamer that, in our model, switches between an active conformational state (circles) in which its phosphorylation level tends to rise and an inactive state (squares) in which it tends to fall. Active KaiC activates RpaA, whereas inactive KaiC inactivates RpaA; active RpaA (red) activates kaiBC expression, leading (after a delay) to the injection of fully phosphorylated KaiC into the PPC. (B) PPC-in vitro model: Only the PPC is present, and the concentration of each Kai protein is constant. (C) PPC-in vivo model: Only the PPC is present, but all Kai proteins are now continually synthesized and degraded, with rates that are constant in time. (D) TTC-only model: Only the TTC is present, and KaiC is always in a highly phosphorylated state. RpaA and kaiA are expressed constitutively; roles of KaiA and KaiB are discussed in the text.
Results
A. PPC-in Vitro: A Protein Phosphorylation Cycle with Constant Protein Concentrations Is Highly Robust.
The PPC has been characterized in detail (Fig. 1B). KaiC forms a hexamer (11) with two phosphorylation sites per protein monomer, which are phosphorylated and dephosphorylated in a definite sequence as a result of KaiC’s autokinase and autophosphatase activity (17, 18). KaiA stimulates KaiC phosphorylation (19, 20), whereas KaiB negates the effect of KaiA (19–22). Thanks to the wealth of available experimental data, the PPC has proven a fruitful system for mathematical modeling (18, 23–31) (for a review, see ref. 32).
In this manuscript, we adopt the mathematical model developed by us (26). In this model, each KaiC hexamer has an intrinsic ability to cyclically phosphorylate and dephosphorylate itself, while the phosphorylation cycles of the individual hexamers are synchronized via a mechanism that we called “differential affinity” (18, 23, 26, 27): KaiA stimulates KaiC phosphorylation, but the limited supply of KaiA dimers binds preferentially to those KaiC molecules that are falling behind in the cycle, allowing them to catch up. Specifically, in our model each KaiC hexamer can switch between an active conformational state Ci, where the number i of phosphorylated monomers tends to increase, and an inactive state 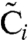 , where i tends to decrease (Fig. 1B); KaiA stimulates phosphorylation of active KaiC, but is sequestered by complexes containing KaiB and inactive KaiC. KaiC in the inactive state can thus delay the progress of fully dephosphorylated hexamers that have already switched back to the active state and are ready to be phosphorylated again. With A and B denoting, respectively, a KaiA dimer and a KaiB dimer, the model becomes
, where i tends to decrease (Fig. 1B); KaiA stimulates phosphorylation of active KaiC, but is sequestered by complexes containing KaiB and inactive KaiC. KaiC in the inactive state can thus delay the progress of fully dephosphorylated hexamers that have already switched back to the active state and are ready to be phosphorylated again. With A and B denoting, respectively, a KaiA dimer and a KaiB dimer, the model becomes
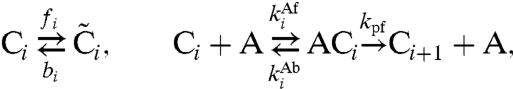 |
[1] |
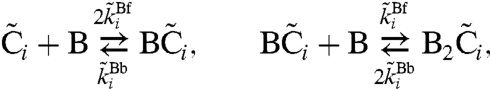 |
[2] |
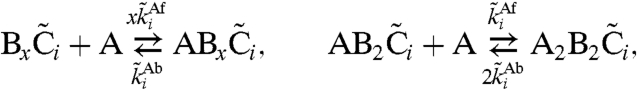 |
[3] |
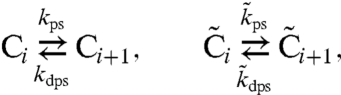 |
[4] |
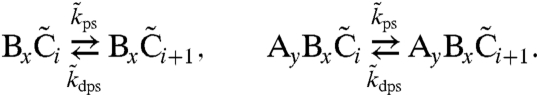 |
[5] |
This model reproduces the phosphorylation behavior of KaiC in vitro not only when all Kai proteins are present, but also when KaiA and/or KaiB are absent (26). It moreover correctly predicted the experimentally observed disappearance of oscillations when the KaiA concentration is raised (18, 33), a success that strongly supports the idea that KaiA sequestration is the primary driver of synchronization. Our model does not feature monomer exchange between KaiC hexamers, an alternative means of synchronization (24) that has been observed in experiments (28, 34); we and others find that monomer exchange is not critical for stable oscillations (18, 26, 27). In SI Text, we show that similar results are obtained with a model that focuses on the phosphorylation cycle of individual KaiC monomers (17, 18) rather than of KaiC hexamers.
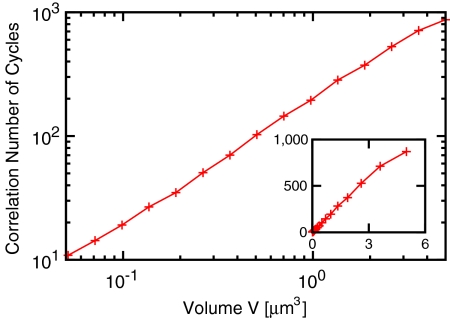
We quantify our model’s robustness to chemical noise by performing Monte Carlo simulations of the chemical master equation (35) describing the mass-action kinetics associated with reactions 1–5 in a well-mixed container. In our simulations, we vary the reaction volume V but adjust the protein copy numbers so that the concentrations of the Kai proteins remain constant, at levels comparable to those used in vitro (33, 34). Fig. 2 shows as a function of volume the correlation number of cycles n1/2, defined as the number of cycles after which the standard deviation in the phase of the oscillation is half a day (31). One issue that arises in comparing our results to the measured in vivo clock robustness is that the Kai proteins appear to be present in living cells in a ratio at which the in vitro system would not oscillate (21, 33, 34). It has been suggested that this discrepancy may indicate that the clock reactions are confined to a subdomain of the cell from which some KaiB and KaiC molecules are excluded (21), allowing the reactions to proceed at roughly the in vitro ratio (see SI Text). If we take the volume of this domain to be V ∼ 1 μm3, comparable to the size of the entire cell, then Fig. 2 shows that n1/2 ≈ 200, consistent with the measured 166 ± 100 (5). Even for V ∼ 0.5 μm3, we find that n1/2 ≈ 102, still within the experimental bounds (in contrast to predictions of some alternative models (18, 31); see SI Text). Our model thus predicts that the PPC is resistant to noise arising from the stochastic nature of chemical reactions.
Fig. 2.
PPC-in vitro model (Fig. 1B). Correlation number of cycles, n1/2, as a function of the reaction volume V. For V ≈ 1 μm3, comparable to the size of a cyanobacterium, n1/2 ≈ 200, in agreement with experiment (5). (Inset) The same data on a linear scale. The protein concentrations are those used in the in vitro experiments (33, 34): 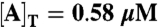 ; [B]T = 1.75 μM; [C]T = 0.58 μM. For other parameters, see Table S1. For a time trace of the phosphorylation level p(t), see Fig. S1.
; [B]T = 1.75 μM; [C]T = 0.58 μM. For other parameters, see Table S1. For a time trace of the phosphorylation level p(t), see Fig. S1.
B. PPC-in Vivo: A Phosphorylation Cycle with Constant Protein Synthesis and Degradation Rates Is not Stable.
Fig. 2 shows that the PPC is highly robust when the total concentrations of the Kai proteins are strictly constant. But, in vivo, proteins are continually being synthesized and degraded. To study how this affects the PPC, we consider the PPC-in vivo model (Fig. 1C). In this model, the Kai proteins are produced and degraded in a stochastic (memoryless) fashion with rates that are constant in time, with the effects of active degradation (36) and of passive dilution lumped into a single first-order decay rate μ (see SI Text).
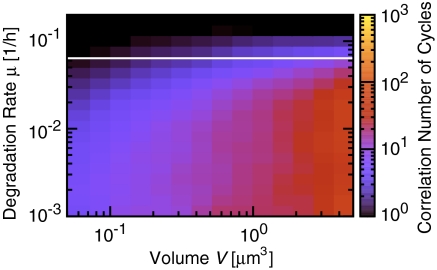
Fig. 3 shows the performance of the PPC as a function of degradation rate and cell volume; here, and in the models below, the synthesis rates are adjusted so that the mean concentrations are constant and equal to those used in the previous section. The PPC’s robustness clearly decreases dramatically with increasing protein synthesis and decay rate. For a volume comparable to that of a cyanobacterium and a degradation rate of 0.03 h-1, the correlation time is less than 20 days, much lower than that observed in vivo (5). This degradation rate is precisely the effective rate arising from protein dilution with a cell doubling time of 24 h. It is known, however, that KaiC is also degraded actively at a rate as high as 0.1 h-1 (36), leading to still worse stability.
Fig. 3.
PPC-in vivo model (Fig. 1C). Correlation number of cycles, n1/2, as a function of reaction volume V and degradation rate μ. n1/2 decreases as μ increases. Thus, a system in which the Kai proteins are produced and degraded with constant rates cannot sustain a stable phosphorylation cycle when the growth rate is high. The bifurcation line μ = 0.0621 h-1, where the system undergoes a supercritical Hopf bifurcation in the deterministic limit, is shown in white. KaiA, KaiB, and KaiC are produced with rates such that the average total concentrations equal those used in the in vitro experiments (see Fig. 2). For a time trace of p(t), see Fig. S1.
The disappearance of the oscillations for higher protein synthesis and decay rates can be understood by noting that fresh KaiC hexamers are made in a fixed phosphorylation state, which then has to catch up with that of the proteins already in the cycle (1, 15). When the degradation rate is high, the new proteins are likely to be degraded before the PPC can synchronize their phosphorylation levels; indeed, in the limit that the protein synthesis and decay rates go to infinity, the phosphorylation level p(t) (defined as the fraction of phosphorylated monomers) becomes constant in time and equal to the phosphorylation level of freshly made KaiC proteins. This is not a purely stochastic effect; the white bifurcation line of Fig. 3 shows that even in a deterministic model the oscillations disappear when the synthesis and decay rates become too big (see SI Text).
C. PPC-TTC: A Protein Phosphorylation Cycle with a Transcription–Translation Cycle Is very Stable.
To sustain a phosphorylation cycle, KaiC has to be made in an oscillatory fashion: Newly synthesized KaiC proteins should be injected into the phosphorylation cycle only when their phosphorylation state matches that of the PPC as a whole (1). This is the principal role of the transcription–translation cycle. Here, we present a mathematical model, the PPC-TTC model, for how such a cycle might interact with the PPC (Fig. 1A).
Although the TTC is much less well understood than the PPC, recently much progress has been made (37–39). In particular, several proteins important for transcriptional regulation of the kaiBC operon have now been identified. Our model is inspired by that of Taniguchi et al. (40) and contains the following key ingredients:
1. RpaA activates kaiBC expression.
Deletion of rpaA, which encodes a putative response regulator, reduces kaiBC expression (40–42). Because neither promoters nor transcription or chromosome-compaction factors have been identified that interact with RpaA (42), we make the phenomenological assumption that RpaA directly activates kaiBC expression (40).
2. RpaA is activated by KaiC when KaiC is in the active state.
RpaA is activated via phosphorylation by the histidine kinase SasA, whose activity is in turn stimulated by KaiC (38, 42); inactivation of SasA reduces kaiBC expression (40–42). Moreover, RpaA phosphorylation occurs 4–8 h before the peak of KaiC phosphorylation (42). This suggests that partially phosphorylated KaiC that is on the PPC’s active branch activates RpaA through SasA (40). Because SasA phosphorylation, occurring on time scales of minutes (38), is much faster than KaiC phosphorylation, occurring on time scales of hours, we assume that the SasA dynamics can be integrated out.
3. RpaA is inactivated by KaiC when KaiC is in the inactive state.
Inactivation of LabA (41) or CikA (40) increases kaiBC expression, with inactivation of both having a still stronger effect (40). SasA inactivation can compensate for both LabA (41) and CikA inactivation (40), but RpaA inactivation cannot compensate for LabA inactivation (41). Taken together, these results suggest that SasA, LabA, and CikA control kaiBC expression through different pathways, with at least the SasA and LabA pathways converging on RpaA (40). Because phosphorylation of KaiC is critical for negative feedback on kaiBC expression (10), LabA and CikA appear to act downstream of phosphorylated KaiC (40). Because the mechanisms by which LabA and/or CikA repress RpaA activation are unknown, we make the phenomenological assumption that inactive KaiC deactivates RpaA.
4. KaiC is injected into the system as fully phosphorylated hexamers.
Imai et al. reported that newly synthesized KaiC is phosphorylated in vivo within 30 min (36), much faster than phosphorylation of KaiC hexamers in vitro, which takes about 6 h (12); we thus assume that newly synthesized KaiC is injected into the system as fully phosphorylated KaiC hexamers.
5. KaiA and RpaA are synthesized at constant rates.
The mRNA levels of kaiA and rpaA exhibit much weaker oscillations than those of kaiB and kaiC (43). We therefore assume that kaiA and rpaA are expressed at constant rates.
6. The phosphorylation cycle in vivo is similar to that in vitro.
Fig. 1A shows a cartoon of this model, which is described by the reactions of formulas 1–5 for the PPC together with the following reactions for the TTC and the coupling between them:
| [6] |
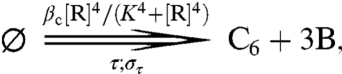 |
[7] |
| [8] |
| [9] |
Formula 6 models activation of inactive RpaA, 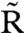 , by X∈{AC2,…AC5} and inactivation of active RpaA, R, by
, by X∈{AC2,…AC5} and inactivation of active RpaA, R, by 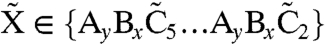 (see SI Text). Formula 7 models activation of kaiBC by RpaA, using a Hill function with coefficient 4. We assume a normally distributed delay, denoted by the double arrow, with mean τ = 5 h and standard deviation στ = 0.5 h, between the activation of kaiBC transcription and the appearance of KaiB and KaiC protein. The length of the delay is dictated by the requirement that fresh KaiC be produced when its phosphorylation state matches that of the PPC. Formula 8 models constitutive expression of kaiA and rpaA. Formula 9 describes degradation of all species with the same rate constant μ; we ignore rhythmic KaiC degradation (36), which is not essential to produce a robust clock. In SI Text we show that, because of the stabilizing effect of the PPC, the clock’s basic behavior is robust to variations in parameters such as the size of gene expression bursts, the width of the delay distribution, and the Hill coefficient of gene repression; there, we also discuss a more detailed model that includes cell growth and binomial partitioning upon cell division, which appreciably increases noise without changing qualitative trends. Although one can think of our model in loose terms as consisting of coupled transcriptional and posttranslational oscillators, it cannot be mathematically decomposed into two separate oscillatory systems, each with its own variables, nor can the strength of the coupling between the two cycles be independently tuned. It is thus formally quite different from textbook models of coupled oscillators (44).
(see SI Text). Formula 7 models activation of kaiBC by RpaA, using a Hill function with coefficient 4. We assume a normally distributed delay, denoted by the double arrow, with mean τ = 5 h and standard deviation στ = 0.5 h, between the activation of kaiBC transcription and the appearance of KaiB and KaiC protein. The length of the delay is dictated by the requirement that fresh KaiC be produced when its phosphorylation state matches that of the PPC. Formula 8 models constitutive expression of kaiA and rpaA. Formula 9 describes degradation of all species with the same rate constant μ; we ignore rhythmic KaiC degradation (36), which is not essential to produce a robust clock. In SI Text we show that, because of the stabilizing effect of the PPC, the clock’s basic behavior is robust to variations in parameters such as the size of gene expression bursts, the width of the delay distribution, and the Hill coefficient of gene repression; there, we also discuss a more detailed model that includes cell growth and binomial partitioning upon cell division, which appreciably increases noise without changing qualitative trends. Although one can think of our model in loose terms as consisting of coupled transcriptional and posttranslational oscillators, it cannot be mathematically decomposed into two separate oscillatory systems, each with its own variables, nor can the strength of the coupling between the two cycles be independently tuned. It is thus formally quite different from textbook models of coupled oscillators (44).
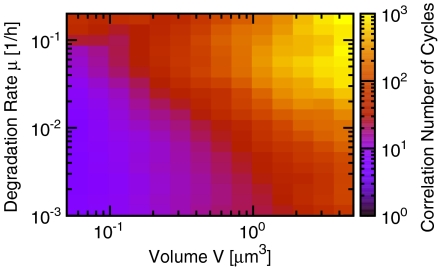
Fig. 4 shows the robustness of this PPC-TTC model as a function of cell volume and protein degradation rate μ. As expected, n1/2 decreases with decreasing cell volume. Its dependence on the degradation rate, however, is markedly different from that seen with constant KaiC synthesis (Fig. 3): A PPC sustained by a TTC becomes more robust with increasing decay rate. If we assume that proteins are lost only through dilution, then for a bacterial volume of 1 μm3 and a cell doubling time of 24 h (corresponding to a decay rate μ = 0.03 h-1), the correlation time is about 200 days, consistent with the value measured experimentally (5). If proteins are also degraded actively, increasing μ, this excellent behavior improves still further; even for V = 0.5 μm3, n1/2 ≈ 120 for μ = 0.1 h-1. This is in stark contrast to the stability of a PPC without a TTC (Fig. 3).
Fig. 4.
PPC-TTC model (Fig. 1A). Correlation number of cycles, n1/2, as a function of the volume V and degradation rate μ. The combination of a TTC and a PPC can generate stable circadian rhythms for a bacterial volume of V ∼ 1 μm3, even when the degradation rate is high (compare Fig. 3). The protein synthesis rates are varied with the degradation rates such that the average protein concentrations equal those used in vitro (see Fig. 2). For time traces of p(t) and [C](t), see Fig. S1.
D. TTC-only: A Protein Phosphorylation Cycle Dramatically Enhances the Robustness of a Transcription–Translation Cycle.
Figs. 3 and 4 show that a TTC can greatly improve the robustness of a PPC. One might thus ask whether the PPC is needed at all, or whether an adequate clock can be built with only a TTC. To address this question, we modify the PPC-TTC model (formulas 6–9) so that it consists only of a TTC, leading to the TTC-only model (Fig. 1D):
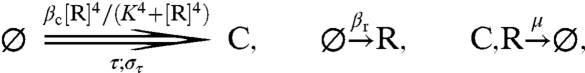 |
[10] |
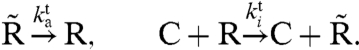 |
[11] |
In the simulations, we adjust not only the synthesis rate βc but also the delay τ so that both the average concentrations and the clock period remain constant when we vary μ (see SI Text).
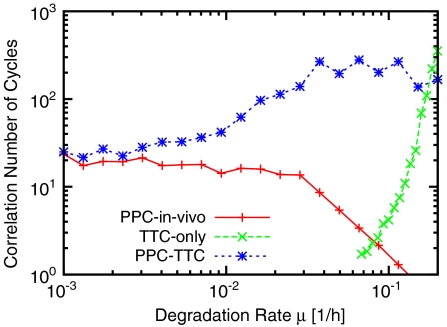
Fig. 5 shows, for a bacterial volume of 1 μm3, the robustness of this TTC-only model as a function of the degradation rate, together with the results for the PPC-TTC model (Fig. 4) and the PPC-in vivo model (Fig. 3). The TTC-only model’s behavior is the opposite of that of the PPC-in vivo model; the TTC-only model is most stable for high degradation rates, and its robustness falls dramatically when μ drops below 0.2 h-1. The combined PPC-TTC model, however, is robust for all degradation rates—its correlation time interpolates between those of the TTC-only model for large μ and of the PPC-in vivo model for small μ. Importantly, the relative advantage of the combined model is greatest when 1/μ is of order the oscillator period, and this is precisely the regime where physiological degradation and dilution rates for S. elongatus fall (36). Further, the combined oscillator does much better than either oscillator alone; in contrast, when two conventional phase oscillators with comparable noise levels are coupled, one expects only about a factor of two gain in n1/2 (44).
Fig. 5.
Correlation number of cycles n1/2 as a function of degradation rate μ for the PPC-in vivo (Fig. 1C), TTC-only (Fig. 1D), and PPC-TTC (Fig. 1A) models. V = 1 μm3 in all models; for the TTC, n1/2 was computed for [C](t) rather than for p(t) (see SI Text). Clearly, a PPC in combination with a TTC generates robust rhythms over a wide range of degradation rates. The protein synthesis rates are varied with the degradation rates such that the average concentrations equal those used in the in vitro experiments (see Fig. 2).
Dilution puts a lower bound on the degradation rate, which means that a stable oscillator cannot be based on a PPC only, especially when the growth rate of the bacterium is large. The degradation rate can, on the other hand, be increased by active degradation. For high degradation rates, i.e., μ > 0.2 h-1, an oscillator based only on a TTC can be sufficiently robust (Fig. 5). However, to balance these high decay rates, the protein synthesis rates have to be correspondingly large, which can be energetically costly (45). Combining a PPC with a TTC makes it possible to dramatically improve the robustness while keeping the synthesis rates the same. Although a phosphorylation cycle does not come entirely for free (46), this suggests that a PPC combined with a TTC gives the best performance-to-cost ratio.
E. The Principal Pacemaker.
What drives the circadian clock, the PPC or the TTC (1)? As our analysis shows, the answer depends on the growth rate. When protein turnover is slower than the oscillation period, the clock is primarily driven by the PPC, and adding a TTC does not enhance its robustness (Fig. 5). Indeed, a TTC can generate large-amplitude oscillations in KaiC concentration only if proteins are synthesized and degraded on time scales faster than the oscillation period. At high growth rates, on the other hand, adding a PPC to a TTC does not improve stability, and the TTC is the principal driver. In this regime, the time scale for protein turnover is much faster than that for protein (de)phosphorylation; KaiC hexamers are thus typically degraded before they can complete a single phosphorylation cycle, rendering the PPC irrelevant.
To gain a deeper understanding of the transition between these two limiting cases—and in particular of the crossover regime where 1/μ is of order 24 h and the gain in robustness from combining TTC and PPC is most dramatic—we introduce in SI Text section S2 minimal versions of the models discussed above together with two additional models designed to isolate specific modes of interaction between the two cycles (see also Fig. S2). The first of these, the PMS-TTC model, combines a TTC with a protein-modification sequence (PMS): the KaiC hexamers undergo a sequence of dephosphorylation steps on the PPC’s inactive branch, but not a full phosphorylation cycle. The second additional model, the UPPC-TTC model, combines a TTC with an unsynchronized protein phosphorylation cycle (UPPC); here, each KaiC can undergo a full cycle of protein-modification steps as in the original PPC, but no KaiA is present, and synchronization through differential affinity thus cannot occur. These two models reveal two distinct mechanisms by which coupling a TTC with a PPC enhances robustness in the crossover regime (Fig. S3). The PMS-TTC model shows that the sequence of Poissonian protein-modification steps, an inherent property of the PPC, narrows the distribution of the delay between gene repression and gene expression, which enhances the robustness of the TTC. The UPPC-TTC model shows that the TTC is not only necessary to sustain a PPC at higher growth rates, as discussed above, but in fact enhances it, because the periodic synthesis of KaiC in a given phosphorylation state has a synchronizing effect on the phosphorylation cycles of the individual KaiC hexamers.
The picture that emerges from the analysis of these models is thus the following: At small μ, the PPC functions as it does in vitro, with protein synthesis and degradation playing only a minor role. As μ increases, the burden of synchronization is gradually passed from the differential affinity mechanism to periodic protein synthesis; we can still usefully think of the oscillation as driven by the PPC, but with the TTC now lending an essential helping hand. Finally, at still larger μ, 1/μ becomes much larger than the oscillation period, and most hexamers do not survive long enough to complete a full phosphorylation cycle. At this point, the clock has become essentially a standard delayed negative feedback oscillator, with the twist that, unless μ is very large, the PPC helps to narrow the distribution of delay times and thus to reduce noise. Consistent with recent experiments (16), our simulations suggest that S. elongatus usually finds itself in the second of these regimes, in which the TTC plays an important part in synchronizing the PPC.
Discussion
The evidence is accumulating that circadian rhythms are driven by both transcription–translation and protein-modification cycles not just in cyanobacteria, but even in higher organisms (1, 47). Our analysis suggests that both cycles are required to generate stable circadian rhythms in growing, dividing cells over a wide range of conditions: Although a PPC alone must inevitably fail at high and a TTC without active degradation at low growth rates, the combined clock is robust for all growth rates. Although our PPC-TTC model is simplified, it does capture the essence of a coupled TTC and PPC. That is, it is built around a protein that not only undergoes a protein-modification cycle, but also regulates its own synthesis in a manner that depends on its modification state. Moreover, its qualitative behavior can be explained by the generic arguments of the preceding section, which are based on a simple comparison of the clock period with the time scales of protein modification and protein degradation. Our results should thus apply to any system that exploits both a PPC and a TTC to generate circadian rhythms.
Our combined PPC-TTC model is consistent with a number of experimental observations. It not only matches the average oscillations of the phosphorylation level and the total KaiC concentration in wild-type cells (Fig. S1), but also reproduces the observation that even in the presence of an excess of KaiA, the total KaiC concentration still undergoes at least a damped oscillation with a circadian period (14, 16) (see Fig. S4). Yet, because quite a few elements of the TTC have not been characterized experimentally, our model of the TTC is necessarily rather simplified and phenomenological; not surprisingly, some observations thus cannot be reproduced. For example, our model predicts that the phase of the oscillation in KaiC abundance lags behind that of the phosphorylation level by a few hours, whereas experiments seem to show that these oscillations are more in phase (12, 14). This may be due to our simplifying assumption that KaiC is produced as fully phosphorylated hexamers. Although phosphorylation of fresh KaiC has been reported to occur within 30 min (36), fragmentary evidence suggests that hexamerization is slow (48); one would then expect to detect KaiC monomers in experiments several hours before our simulations report the presence of fully functional hexamers.
In S. elongatus, the period of the circadian rhythm is insensitive to changes in the growth rate (49, 50). Because protein synthesis and decay rates, on the other hand, tend to vary with the growth rate (51), the question arises whether the period of the oscillator as predicted by our model is robust to such variations. In SI Text we show that a tenfold increase in the synthesis and degradation rates of all proteins decreases the period only by 10–20%. The reason is that the clock period is mostly determined by the intrinsic period of the PPC. The latter does not depend on the absolute protein synthesis and decay rates, although it does depend on the ratio of the concentrations of the Kai proteins (26, 33, 34). Clearly, it would be of interest to investigate how this ratio varies with the growth rate.
Finally, how could our predictions be tested experimentally? The most important testable prediction of our analysis is that the PPC requires a TTC when the growth rate is high. Kondo and coworkers have demonstrated that a PPC can function in the absence of a TTC (12). These experiments were performed under constant dark conditions, which means that the growth rate was (vanishingly) small, protein synthesis was halted, and even protein decay was probably negligible, because the KaiC level was rather constant (12). These experiments are consistent with our predictions, but the critical test would be to increase the growth rate while avoiding any circadian regulation of kaiBC expression. This means that the cyanobacteria must be grown under constant light conditions. Moreover, one would need to bring kaiBC expression under the control of a promoter that is constitutively active. However, most promoters of S. elongatus (37, 43), and even many heterologous promoters from Escherichia coli (52), are influenced by the circadian clock. Nevertheless, a number of promoters have been reported that exhibit arrhythmic activity (43), and these might be possible candidates. A still more challenging experiment would be to express the phosphorylation cycle in the bacterium E. coli (53). Our analysis predicts that in growth-arrested cells, the phosphorylation cycle should be functional, whereas in normal growing E. coli cells, with cell doubling times of roughly 1 h, the oscillations should cease to exist.
Methods
The simulations were performed using the algorithm of ref. 35, and n1/2 was computed from the decay of the correlation function of p(t), except for the TTC-only model, for which we used [C](t); our estimates for n1/2 are typically accurate to within 15–20% (see SI Text).
Supplementary Material
Acknowledgments.
We thank Tom Shimizu for critically reading the manuscript. This work was supported in part by FOM, which is financially supported by the “Nederlandse Organisatie voor Wetenschappelijk Onderzoek” (D.Z. and P.R.t.W.) and by NSF Grant PHY05-51164 to the Kavli Institute for Theoretical Physics (to D.K.L.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1007613107/-/DCSupplemental.
References
- 1.Johnson CH, Egli M, Stewart PL. Structural insights into a circadian oscillator. Science. 2008;322:697–701. doi: 10.1126/science.1150451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 3.Liu C, Weaver DR, Strogatz SH, Reppert SM. Cellular construction of a circadian clock: Period determination in the suprachiasmatic nuclei. Cell. 1997;91:855–860. doi: 10.1016/s0092-8674(00)80473-0. [DOI] [PubMed] [Google Scholar]
- 4.Yamaguchi S, et al. Synchronization of cellular clocks in the suprachiasmatic nucleus. Science. 2003;302:1408–1412. doi: 10.1126/science.1089287. [DOI] [PubMed] [Google Scholar]
- 5.Mihalcescu I, Hsing W, Leibler S. Resilient circadian oscillator revealed in individual cyanobacteria. Nature. 2004;430:81–85. doi: 10.1038/nature02533. [DOI] [PubMed] [Google Scholar]
- 6.Amdaoud M, Vallade M, Weiss-Schaber C, Mihalcescu I. Cyanobacterial clock, a stable phase oscillator with negligible intercellular coupling. Proc Natl Acad Sci USA. 2007;104:7051–7056. doi: 10.1073/pnas.0609315104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ishiura M, et al. Expression of a gene cluster kaiABC as a circadian feedback process in cyanobacteria. Science. 1998;281:1519–1523. doi: 10.1126/science.281.5382.1519. [DOI] [PubMed] [Google Scholar]
- 8.Xu Y, Mori T, Johnson CH. Circadian clock-protein expression in cyanobacteria: Rhythms and phase setting. EMBO J. 2000;19:3349–3357. doi: 10.1093/emboj/19.13.3349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nakahira Y, et al. Global gene repression by KaiC as a master process of prokaryotic circadian system. Proc Natl Acad Sci USA. 2004;101:881–885. doi: 10.1073/pnas.0307411100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nishiwaki T, et al. Role of KaiC phosphorylation in the circadian clock system of synechococcus elongatus pcc 7942. Proc Natl Acad Sci USA. 2004;101:13927–13932. doi: 10.1073/pnas.0403906101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kageyama H, Kondo T, Iwasaki H. Circadian formation of clock protein complexes by KaiA, KaiB, KaiC, and SasA in cyanobacteria. J Biol Chem. 2003;278:2388–2395. doi: 10.1074/jbc.M208899200. [DOI] [PubMed] [Google Scholar]
- 12.Tomita J, Nakajima M, Kondo T, Iwasaki H. No transcription-translation feedback in circadian rhythm of KaiC phosphorylation. Science. 2005;307:251–254. doi: 10.1126/science.1102540. [DOI] [PubMed] [Google Scholar]
- 13.Nakajima M, et al. Reconstitution of circadian oscillation of cyanobacterial KaiC phosphorylation in vitro. Science. 2005;308:414–415. doi: 10.1126/science.1108451. [DOI] [PubMed] [Google Scholar]
- 14.Kitayama Y, Nishiwaki T, Terauchi K, Kondo T. Dual KaiC-based oscillations constitute the circadian system of cyanobacteria. Genes Dev. 2008;22:1513–1521. doi: 10.1101/gad.1661808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ito H, et al. Autonomous synchronization of the circadian KaiC phosphorylation rhythm. Nat Struct Mol Biol. 2007;14:1084–1088. doi: 10.1038/nsmb1312. [DOI] [PubMed] [Google Scholar]
- 16.Qin X, Byrne M, Xu Y, Mori T, Johnson CH. Coupling of a core post-translational pacemaker to a slave transcription/translation feedback loop in a circadian system. PLoS Biol. 2010;8:e1000394. doi: 10.1371/journal.pbio.1000394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nishiwaki T, et al. A sequential program of dual phosphorylation of KaiC as a basis for circadian rhythm in cyanobacteria. EMBO J. 2007;26:4029–4037. doi: 10.1038/sj.emboj.7601832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rust MJ, Markson JS, Lane WS, Fisher DS, O’Shea EK. Ordered phosphorylation governs oscillation of a three-protein circadian clock. Science. 2007;318:809–812. doi: 10.1126/science.1148596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Iwasaki H, Nishiwaki T, Kitayama Y, Nakajima M, Kondo T. KaiA-stimulated KaiC phosphorylation in circadian timing loops in cyanobacteria. Proc Natl Acad Sci USA. 2002;99:15788–15793. doi: 10.1073/pnas.222467299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Xu Y, Mori T, Johnson CH. Cyanobacterial circadian clockwork: Roles of KaiA, KaiB and the kaiBC promoter in regulating KaiC. EMBO J. 2003;22:2117–2126. doi: 10.1093/emboj/cdg168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kitayama Y, Iwasaki H, Nishiwaki T, Kondo T. KaiB functions as an attenuator of KaiC phosphorylation in the cyanobacterial circadian clock system. EMBO J. 2003;22:2127–2134. doi: 10.1093/emboj/cdg212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Williams SB, Vakonakis I, Golden SS, LiWang AC. Structure and function from the circadian clock protein KaiA of Synechococcus elongatus: A potential clock input mechanism. Proc Natl Acad Sci USA. 2002;99:15357–15362. doi: 10.1073/pnas.232517099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Takigawa-Imamura H, Mochizuki A. Predicting regulation of the phosphorylation cycle of KaiC clock protein using mathematical analysis. J Biol Rhythm. 2006;21:405–416. doi: 10.1177/0748730406291329. [DOI] [PubMed] [Google Scholar]
- 24.Emberly E, Wingreen NS. Hourglass model for a protein-based circadian oscillator. Phys Rev Lett. 2006;96:038303. doi: 10.1103/PhysRevLett.96.038303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mehra A, et al. Circadian rhythmicity by autocatalysis. PLoS Comput Biol. 2006;2:e96. doi: 10.1371/journal.pcbi.0020096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.van Zon JS, Lubensky DK, Altena PRH, ten Wolde PR. An allosteric model of circadian KaiC phosphorylation. Proc Natl Acad Sci USA. 2007;104:7420–7425. doi: 10.1073/pnas.0608665104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Clodong S, et al. Functioning and robustness of a bacterial circadian clock. Mol Syst Biol. 2007;3:90. doi: 10.1038/msb4100128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mori T, et al. Elucidating the ticking of an in vitro circadian clockwork. PLoS Biol. 2007;5:e93. doi: 10.1371/journal.pbio.0050093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Miyoshi F, Nakayama Y, Kaizu K, Iwasaki H, Tomita M. A mathematical model for the Kai-protein-based chemical oscillator and clock gene expression rhythms in cyanobacteria. J Biol Rhythm. 2007;22:69–80. doi: 10.1177/0748730406295749. [DOI] [PubMed] [Google Scholar]
- 30.Yoda M, Eguchi K, Terada TP, Sasai M. Monomer-shuffling and allosteric transition in KaiC circadian oscillation. PLoS One. 2007;2:e408. doi: 10.1371/journal.pone.0000408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Eguchi K, Yoda M, Terada TP, Sasai M. Mechanism of robust circadian oscillation of KaiC phosphorylation in vitro. Biophys J. 2008;95:1773–1784. doi: 10.1529/biophysj.107.127555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Markson JS, O’Shea EK. The molecular clockwork of a protein-based circadian oscillator. FEBS Lett. 2009;583:3938–3947. doi: 10.1016/j.febslet.2009.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nakajima M, Ito H, Kondo T. In vitro regulation of circadian phosphorylation rhythm of cyanobacterial clock protein KaiC by KaiA and KaiB. FEBS Lett. 2010;584(5):898–902. doi: 10.1016/j.febslet.2010.01.016. [DOI] [PubMed] [Google Scholar]
- 34.Kageyama H, et al. Cyanobacterial circadian pacemaker: Kai protein complex dynamics in the KaiC phosphorylation cycle in vitro. Mol Cell. 2006;23:161–171. doi: 10.1016/j.molcel.2006.05.039. [DOI] [PubMed] [Google Scholar]
- 35.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- 36.Imai K, Nishiwaki T, Kondo T, Iwasaki H. Circadian rhythms in the synthesis and degradation of a master clock protein KaiC in cyanobacteria. J Biol Chem. 2004;279:36534–36539. doi: 10.1074/jbc.M405861200. [DOI] [PubMed] [Google Scholar]
- 37.Vijayan V, Zuzow R, O’Shea EK. Oscillations in supercoiling drive circadian gene expression in cyanobacteria. Proc Natl Acad Sci USA. 2009;106:22564–22568. doi: 10.1073/pnas.0912673106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Smith RM, Williams SB. Circadian rhythms in gene transcription imparted by chromosome compaction in the cyanobacterium Synechococcus elongatus. Proc Natl Acad Sci USA. 2006;103:8564–8569. doi: 10.1073/pnas.0508696103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Woelfle MA, Xu Y, Qin X, Johnson CH. Circadian rhythms of superhelical status of DNA in cyanobacteria. Proc Natl Acad Sci USA. 2007;104:18819–18824. doi: 10.1073/pnas.0706069104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Taniguchi Y, Takai N, Katayama M, Kondo T, Oyama T. Three major output pathways from the KaiABC-based oscillator cooperate to generate robust circadian kaiBC expression in cyanobacteria. Proc Natl Acad Sci USA. 2010;107:3263–3268. doi: 10.1073/pnas.0909924107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Taniguchi Y, et al. labA: A novel gene required for negative feedback regulation of the cyanobacterial circadian clock protein KaiC. Genes Dev. 2007;21:60–70. doi: 10.1101/gad.1488107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Takai N, et al. A KaiC-associating SasA-RpaA two-component regulatory system as a major circadian timing mediator in cyanobacteria. Proc Natl Acad Sci USA. 2006;103:12109–12114. doi: 10.1073/pnas.0602955103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ito H, et al. Cyanobacterial daily life with Kai-based circadian and diurnal genome-wide transcriptional control in Synechococcus elongatus. Proc Natl Acad Sci USA. 2009;106:14168–14173. doi: 10.1073/pnas.0902587106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pikovsky A, Rosenblum M, Kurths J. Synchronization, A Universal Concept in Nonlinear Sciences. Cambridge, UK: Cambridge Univ Press; 2001. [Google Scholar]
- 45.Dekel E, Alon U. Optimality and evolutionary tuning of the expression level of a protein. Nature. 2005;436:588–592. doi: 10.1038/nature03842. [DOI] [PubMed] [Google Scholar]
- 46.Terauchi K, et al. ATPase activity of KaiC determines the basic timing for circadian clock of cyanobacteria. Proc Natl Acad Sci USA. 2007;104:16377–16381. doi: 10.1073/pnas.0706292104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Merrow M, Roenneberg T. Circadian clock: Time for a phase shift of ideas? Curr Biol. 2007;17:R636–638. doi: 10.1016/j.cub.2007.06.041. [DOI] [PubMed] [Google Scholar]
- 48.Mori T, et al. Circadian clock protein KaiC forms ATP-dependent hexameric rings and binds DNA. Proc Natl Acad Sci USA. 2002;99:17203–17208. doi: 10.1073/pnas.262578499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mori T, Binder B, Johnson CH. Circadian gating of cell division in cyanobacteria growing with average doubling times of less than 24 hours. Proc Natl Acad Sci USA. 1996;93:10183–10188. doi: 10.1073/pnas.93.19.10183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kondo T, et al. Circadian rhythms in rapidly dividing cyanobacteria. Science. 1997;275:224–227. doi: 10.1126/science.275.5297.224. [DOI] [PubMed] [Google Scholar]
- 51.Klumpp S, Zhang Z, Hwa T. Growth rate-dependent global effects on gene expression in bacteria. Cell. 2009;139:1366–1375. doi: 10.1016/j.cell.2009.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ditty JL, Williams SB, Golden SS. A cyanobacterial circadian timing mechanism. Annu Rev Genet. 2003;37:513–543. doi: 10.1146/annurev.genet.37.110801.142716. [DOI] [PubMed] [Google Scholar]
- 53.Tozaki H, Kobe T, Aihara K, Iwasaki H. An attempt to reveal a role of a transcription/translation feedback loop in the cyanobacterial kaic protein-based circadian system by using a semi-synthetic method. Int J Bioinform Res Appl. 2008;4:435–444. doi: 10.1504/IJBRA.2008.021178. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.