Analysis of observer performance in unknown-location tasks for tomographic image reconstruction

Abstract

Our goal is to optimize regularized image reconstruction for emission tomography with respect to lesion detectability in the reconstructed images. We consider model observers whose decision variable is the maximum value of a local test statistic within a search area. Previous approaches have used simulations to evaluate the performance of such observers. We propose an alternative approach, where approximations of tail probabilities for the maximum of correlated Gaussian random fields facilitate analytical evaluation of detection performance. We illustrate how these approximations, which are reasonably accurate at low probability of false alarm operating points, can be used to optimize regularization with respect to lesion detectability.

1. INTRODUCTION

Several applications of emission tomography involve the detection of a spatially localized target signal in an image reconstructed from noisy data. When choosing among different reconstruction methods or tuning the parameters of individual methods, a reasonable approach is to seek the choice that leads to optimal performance in such detection tasks. In this work we focus on penalized-likelihood reconstruction methods for emission tomography. These methods involve one or more regularization parameters that control the noise-resolution trade-off in the reconstructed images. Instead of choosing the regularization parameters by numerical criteria, such as cross validation or L-curves [1,2], we would like to optimize these parameters analytically with respect to signal detectability.

In clinical practice, detection tasks are usually performed by human observers. The performance of humans can be evaluated empirically by tracing their receiver operating characteristic (ROC) in simple detection tasks [3–5], or their localization ROC (LROC) in tasks that involve both detection and localization [6]. However, the experiments required for such an evaluation are too time-consuming to perform for many values of a reconstruction parameter or to repeat every time that some aspect of the imaging process changes. Thus we turn to the mathematical observers that have been proposed in the literature to model human performance [7] and that allow analytical treatment.

Detection tasks where the observer knows the possible location of the target signal a priori have been analyzed with respect to optimal regularization methods [8–12]. Known-location tasks are also the ones for which model and human observer correlation has been investigated most extensively. In these tasks human observers appear to be effective in compensating for second-order image statistics. As a result, they are modeled well by mathematical observers that perform prewhitening, such as the channelized Hotelling observer (CHO) [13–18]. However, optimizing regularization parameters has less of an effect on the detection performance of such observer models, as has been concluded both experimentally [17] and analytically [19]. Thus it is of interest to optimize such parameters with respect to detection performance in tasks where the prewhitening capabilities of humans degrade. Such a degradation seems to occur in tasks where the location of the target signal is not known a priori [20,21].

Location uncertainty complicates the analysis of detectability. Observer models that have been compared to humans in unknown-location tasks usually base their decisions on the maximum value of a local test statistic over all possible signal locations. The exact distribution of the maximum of a correlated random field has the form of a multiple integral that is intensive to compute. A “brute-force” approach to evaluating the performance of such an observer model would be to perform a large number of time-consuming tomographic reconstructions of Monte Carlo–simulated projection data and produce realizations of the maximum test statistic from the reconstructed images. When optimizing some reconstruction parameter with respect to detection performance, this simulation would have to be repeated for every value of the parameter of interest.

To avoid performing multiple reconstructions, investigators have proposed analytical approximations of the moments of the local test statistics and used them to produce Monte Carlo–simulated realizations of the maximum test statistic directly [22,23]. This approach results in very significant time savings when compared to the brute-force method, but it still requires performing multiple simulations when the evaluation of detection performance needs to be repeated for various values of one or more parameters of interest.

We propose an alternative approach that does not require simulations. Although the exact expression for the distribution of the maximum is complicated, simple approximations of this distribution at high thresholds for correlated Gaussian random fields have been proposed by Adler [24]. These approximations assume (local) stationarity, so they are more accurate under the signal-absent than the signal-present hypothesis. The latter requires a different treatment, and we adopt the approach of Siegmund and Worsley to analyze it [25]. We illustrate how these analytical results, which are accurate at low probability of false alarm operating points, can be combined to approximate the performance of the observer models of interest as a function of regularization parameters.

This paper is structured as follows: Section 2 establishes the models that we will consider for the object, imaging system, reconstruction method, and observer. Section 3 reviews the tail probability approximations that we apply in Section 4 to analyze the detection performance of the observer models of interest in unknown-location tasks. Section 5 illustrates how these analyses can be used to optimize regularized reconstruction methods with respect to detection performance, and Section 6 discusses these results.

2. DETECTION TASK

A. Object Model

Let f denote the true object being imaged (or its approximation in 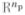, where n_p is the number of coefficients in a discrete representation of f). The object f consists of a background f_b and it may or may not also contain a spatially localized signal of interest f_s. We assume that, when the target signal is present within the object, it is centered at one of a finite set of locations ℓ = 1, …, n_L. We denote the target signal centered at location ℓ by f_s,ℓ.

In emission tomography, where the object f is a radioactivity distribution, the background could represent the distribution of radioactivity in the absence of disease and the signal could represent the additional radioactivity absorbed in the area of a lesion. Thus an additive model for the background and signal is reasonable. The detection/localization task at hand is then a decision among the following n_L +1 hypotheses:

$$\begin{array}{l}{H}_0:\mathit{f}={\mathit{f}}_b(\text{signal}\text{absent})\\ H_{\ell }:\mathit{f}={\mathit{f}}_b+{\mathit{f}}_{s,\ell }(\text{signal}\text{present}\text{at}\text{location}\ell ,\ell =1,\dots ,n_{\text{L}}).\end{array}$$ (1)

The background f_b and the signal f_s,ℓ are random due to patient variability. We assume that they are statistically independent under any of the signal-present hypotheses H_ℓ, ℓ = 1, …, n_L. We denote the expectations of f_b and f_s,ℓ by f̄_b ≜ E[f_b] and f̄_s,ℓ ≜ E[f_s,ℓ] = E[f_s|H_ℓ], respectively. We denote their covariances by 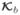= Cov{f_b} and 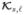≜ Cov{f_s,ℓ} = Cov{f_s|H_ℓ}, respectively. The covariances 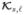, ℓ = 1, …, n_L express variability in the shape of the target signal and not in its location.

B. Image Reconstruction

To reflect medical practice, we assume that the decision is made by an observer applied on a reconstructed image f̂. The image f̂ is reconstructed from a measurement y that is acquired by a tomographic imaging system. For a given object f, y is random due to imaging noise. Specifically, the entries in y are statistically independent and Poisson-distributed conditionally on f with moments

$$\text{E}[\mathit{y}\mid \mathit{f}]=\mathcal{A}\mathit{f}+\mathit{r},$$ (2)

$$\text{Cov}\{\mathit{y}\mid \mathit{f}\}=\text{diag}\{\mathcal{A}\mathit{f}+\mathit{r}\},$$ (3)

where the linear operator 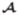models the tomographic imaging system and the vector r models scatter and/or random coincidences. We assume that the reconstructed image is given by

$$\widehat{\mathit{f}}(\mathit{y})=\mathcal{Z}\mathit{y}$$ (4)

for some linear reconstructor 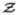. The linearity assumption holds either exactly or approximately for several common tomographic reconstruction techniques.

Here we are interested in regularized image reconstructors. A simple example that satisfies the linearity assumption is the quadratically penalized weighted least squares (QPWLS) family of reconstructors:

$$\mathcal{Z}={(\mathcal{F}+\mathcal{R})}^{-1}{\mathcal{A}}^{\prime }{\mathbf{\Pi }}^{-1},$$ (5)

where “′” denotes the adjoint of an operator (or the transpose of a matrix), 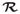is a (linear) regularization operator, 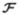≜ 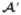Π⁻¹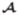, and Π ≜ diag{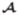E[f]+r} ≈ diag{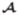f̄_b+r}. (Since we are interested in detecting small perturbations on the object background, we can assume that the signal intensity is weak with respect to the background intensity.) The QPWLS reconstruction strategy [Eq. (5)] yields an estimated image that satisfies f̂(y) =arg max_f[− (y − 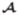f)′Π⁻¹(y−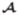f) −f′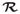f]. Note that, when the measurement likelihood is Poisson, QPWLS does not correspond to maximum a posteriori (penalized-likelihood) reconstruction. Although in the following we consider the QP-WLS reconstructor for simplicity, it is straightforward to extend our analysis to more general penalized-likelihood reconstructors using linearization approximations [12].

A commonly used form for the regularizer 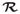is that of a quadratic roughness penalty, such that

$${\mathit{f}}^{\prime }\mathcal{R}\mathit{f}=\beta \sum _{j=1}^{n_{\text{p}}}\sum _{k\in {\mathcal{N}}_j}{(f_j-f_k)}^2,$$ (6)

where f_j is the intensity of the object f at the jth pixel, 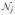is a neighborhood of pixels around the jth pixel, and β ≥ 0 is a regularization parameter. Regularizers of the form of Eq. (6) penalize differences between neighboring image pixels, thus favoring smoother images. For simplicity, we consider a first-order neighborhood 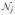, consisting of the four closest (top, bottom, left, and right) neighboring pixels. Then β is the only free parameter in .

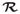C. Observer Model

Following the literature, we consider observers whose decision rule relies on computing some scalar local test statistic t_ℓ =t_ℓ(f̂(y)) for each of the candidate locations and then comparing the maximum test statistic,

$$t_{max}\triangleq \underset{\ell =1,\dots ,n_{\text{L}}}{max}{t}_{\ell },$$ (7)

to a data-independent threshold τ. If t_max > τ, it is decided that the signal is present; otherwise, it is decided that the signal is absent.

Local test statistics that have been used to model the suboptimality of human observers are linear, and they involve a set of M bandpass filters, attempting to mimic the visual system [13]. These test statistics sample the output of the M bandpass filters at a location of interest ℓ, to obtain a local feature vector ĉ_ℓ ∈ 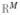, to which a local template w_ℓ ∈ 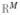is then applied:

$$t_{\ell }={\mathit{w}}_{\ell }^{\prime }{\widehat{\mathit{c}}}_{\ell },{\widehat{\mathit{c}}}_{\ell }={\mathcal{C}}_{\ell }^{\prime }(\widehat{\mathit{f}}-\text{E}[{\widehat{\mathit{f}}}_b])+{\epsilon }_{\ell },$$ (8)

where 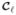= [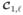, …, 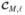] consists of M operators. The mth of these operators applies the impulse response of the mth bandpass filter and samples the output at location ℓ. The internal noise vector ε_ℓ ∈ 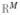models inherent uncertainty in the observer’s decisions and is typically assumed to contain independent, zero-mean, Gaussian-distributed entries. The mean of the reconstructed background, f̂_b ≜ 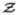(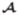f_b+r), is subtracted from the reconstructed image in Eq. (8) to signify that the observer determines the most suspicious location by comparing intensities relative to the background, rather than absolute intensities [22,23].

Two such models have been proposed in the literature to model the performance of human observers in detecting unknown-location lesions in tomographic images: The maximum channelized Hotelling observer (MaCHO), which includes both the first- and second-order statistics of the channel outputs in its template, and the maximum channelized nonprewhitening observer (MaCNPW) observer, which includes the first-order statistics only. In particular, the MaCNPW observer has been found to be well correlated with humans in simple unknown-location tasks [20,21]. This indicates that humans may not be effective at compensating for correlations in the images when they have to search for a lesion in more than one location.

Here we consider a generalization of these models that allows for an intermediate degree of prewhitening accuracy. For lack of a better term, we call this generalized model a maximum channelized partially prewhitening (MaCPPW) observer and define its local template at some location ℓ as

$${\mathit{w}}_{\ell }\triangleq {\left[(1-\gamma )\mathit{I}+\gamma \left(\frac{1}{2}\text{Cov}\{\widehat{\mathit{c}}\mid H_{\ell }\}+\frac{1}{2}\text{Cov}\{\widehat{\mathit{c}}\mid H_0\}\right)\right]}^{†}·(\text{E}[\widehat{\mathit{c}}\mid H_{\ell }]-\text{E}[\widehat{\mathit{c}}\mid H_0]),$$ (9)

where “^†” denotes the pseudoinverse and γ ∈ [0,1]. For γ = 0 and γ = 1, the above becomes equal to the well-known MaCNPW and MaCHO models respectively. An intermediate value of γ yields an observer with intermediate prewhitening accuracy. The expression in Eq. (9) is only one of several ways in which a prewhitening deficiency could be introduced in the channelized observer’s template. We use Eq. (9) here simply to evaluate our performance approximations, without making any claims about correlation with human observers.

D. Detection Performance

Our goal is to optimize the reconstructor 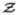in general, or β in the particular case of QPWLS, with respect to the detection performance a specific observer. Since we are ultimately interested in optimizing reconstruction parameters locally, we focus on an ROC curve as a metric of the observer’s signal detection performance within a search area around a given location ℓ ∈ {1, …, n_L}. Specifically, we consider the ROC curve that is obtained by plotting the probability of detection (deciding that the signal is present when it is actually present at ℓ),

$$P_{\text{D},\ell }(\tau )\triangleq \text{P}\{t_{max}\ge \tau \mid H_{\ell }\},\text{for}\text{some}\ell \in \{1,\dots ,n_{\text{L}}\},$$ (10)

versus the probability of false alarm (deciding that the signal is present when it is actually absent),

$$P_{\text{FA}}(\tau )\triangleq \text{P}\{t_{max}\ge \tau \mid H_0\}.$$ (11)

The curve is traced by varying the threshold τ. To trace an ROC or LROC curve for the test statistic t_max in Eq. (7), we need the cummulative distribution function (CDF) of t_max, from which we can compute the threshold-exceeding probabilities (10) and (11).

We are interested in an observer model that searches for the signal within an area consisting of n_L voxels around some voxel of interest ℓ. As seen in Eq. (10), we use the probability of detection at the voxel ℓ to quantify detection performance. Our motivation for this analysis is optimizing the regularization parameter for some voxel ℓ to maximize detectability at that voxel, an optimization that is to be repeated for each voxel in the image. An alternative approach would be to consider the overall probability of detection within the search area, which would require defining a priori probabilities of the signal presence at each location in the search area, but this is not the approach that we follow here.

If the local test statistics t_ℓ, ℓ = 1, …, n_L, were statistically independent, then the CDF of their maximum would be simply equal to the product of their individual CDFs. Thus, under the assumption of independent, Gaussian-distributed local test statistics, it is possible to derive the area under the LROC curve for observer models of the form of Eqs. (7) and (8) [26]. Furthermore, even with a somewhat weaker statistical independence assumption, one can show that maximizing the area under the ROC curve (AUC) of t_max would be equivalent to maximizing the area under its LROC curve [6].

Typical image reconstruction methods, and regularized ones in particular, produce images where the intensities at neighboring locations are correlated. Thus local test statistics at neighboring locations are also correlated, with more regularization leading to wider autocorrelation functions. Analyses that use independence assumptions can be applied to tasks where the candidate locations are at a distance from each other that is greater than the autocorrelation width. For tasks where all the pixels within some search area are candidate locations, correlations between the local test statistics must be taken into account.

Threshold-exceeding probabilities such as (10) and (11) are difficult to obtain in closed form when the t_ℓ’s are correlated, even if their joint distribution is available, since the exact distribution of the maximum of correlated random variables has the form of a multiple integral. As a result, investigators have proposed to trace the LROC of t_max for images reconstructed from tomographic data using regularized methods via simulations [22,23]. We propose an alternative approach to evaluating the performance of the t_max observer in the presence of correlations. Although closed-form expressions for the threshold-exceeding probabilities of t_max are generally not available for correlated Gaussian random fields, approximations of these probabilities for high values of the threshold τ have been developed. We use them here to trace a portion of the ROC curve.

3. THRESHOLD-EXCEEDING PROBABILITIES OF THE MAXIMUM TEST STATISTIC

By analyzing the Euler characteristic of excursion sets, Adler has derived approximations for the distribution tails of the maximum of a correlated random field [24,27]. In particular, if t_max = max_x∈ST(x) is the maximum value of a 2-D stationary random field T(x) = T(x₁, x₂) over a set S, then the probability of t_max exceeding a high threshold τ is approximately

$$\text{P}\{t_{max}\ge \tau \}\approx \sum _{d=0}^2{R}_d(S){\rho }_d(\tau ),$$ (12)

where the factors R_d(S), d=0,1,2, depend on the geometry of the search area S and the functions ρ_d(τ), d =0,1,2, depend on the distribution of T(x).

Approximation (12) is most accurate for search areas that are convex with sufficiently smooth boundaries [24]. If the search area S is a disk of radius r, then R₀(S) = 1, R₁(S) = πr, R₂(S) = πr². If the stationary field T(x) is Gaussian-distributed with zero mean, variance ${\sigma }_T^2$, and autocovariance function R_T(x) = R_T(x₁, x₂), then we can denote the dependence of ρ_d(·) on the moments of the field by writing ρ_d(τ) = ρ_d(τ; σ_T, Λ_T), where Λ_T is the 2 × 2 matrix with the ijth element equal to {Λ_T}_ij = −∂²R_T(0, 0)/∂x_i∂x_j, i,j = 1, 2. In particular, we have [28]

$${\rho }_0(\tau ;{\sigma }_T,{\mathrm{\Lambda }}_T)\triangleq 1-\mathrm{\Phi }(\tau /{\sigma }_T),$$ (13)

$${\rho }_1(\tau ;{\sigma }_T,{\mathrm{\Lambda }}_T)\triangleq \frac{{\mid det{\mathrm{\Lambda }}_T\mid }^{1/4}}{2\pi {\sigma }_T}{e}^{-{\tau }^2/2{\sigma }_T^2},$$ (14)

$${\rho }_2(\tau ;{\sigma }_T,{\mathrm{\Lambda }}_T)\triangleq \frac{{\mid det{\mathrm{\Lambda }}_T\mid }^{1/2}}{{(2\pi )}^{3/2}{\sigma }_T^3}\tau e^{-{\tau }^2/2{\sigma }_T^2},$$ (15)

where Φ(·) is the standard normal CDF. Approximations of the form of (12) have been applied to the problem of detecting activation in functional neuroimaging [28,29]. According to Worsley et al., they lead to satisfactory accuracy for tail probabilities as high as 0.2 [28].

The analysis leading to approximation (12) assumes a continuous random field. When the field is defined on a lattice, the results hold asymptotically as the lattice becomes finer [24]. Thus, expression (12) can be applied to approximate the tail distribution of the maximum test statistic in Eq. (7) when the discrete local test statistics t_ℓ, ℓ = 1, …, n_L can be considered stationary and their mean and autocovariance is known.

Under the signal-absent hypothesis, the t_ℓ’s may be considered stationary to within the accuracy of some local shift-invariance approximations discussed in the following section. The same can be said in terms of the second-order statistics of the t_ℓ’s under the signal-present hypothesis, assuming that the contribution of the signal profile variability to the covariance of the t_ℓ’s is insignificant. However, the mean of the t_ℓ’s cannot be considered constant throughout the search area in the presence of a spatially localized target signal such as the ones that we are interested in. Thus, expression (12) is not appropriate for the signal-present hypothesis.

An alternative approach for approximating threshold-exceeding probabilities in the signal-present case follows an argument by Siegmund and Worsley [25]. This approach decomposes the probability of detection at some location x_ℓ as

$$\text{P}\{t_{max}\ge \tau \mid H_{\ell }\}=\text{P}\{T({\mathit{x}}_{\ell })\ge \tau \mid H_{\ell }\}+\text{P}\{t_{max}\ge \tau ,T({\mathit{x}}_{\ell })<\tau \mid H_{\ell }\}=1-\mathrm{\Phi }\left(\frac{\tau -{\mu }_T({\mathit{x}}_{\ell })}{{\sigma }_T}\right)+{\int }_0^{\infty }\text{P}\{t_{max}\ge \tau \mid T({\mathit{x}}_{\ell })=\tau -s,H_{\ell }\}\times \phi \left(\frac{\tau -s-{\mu }_T({\mathit{x}}_{\ell })}{{\sigma }_T}\right)\text{d}s,$$ (16)

where Φ(·) and φ(·) are the standard normal CDF and probability distribution function (PDF), respectively, and μ_T(x) ≜ E[T(x)|H_ℓ]. Assuming that the maximum is most likely to occur near x_ℓ, i.e., near the center of the target signal, the integrand in Eq. (16) will be nonnegligible only for small values of s.

To derive an expression for the conditional probability inside the integral, Siegmund and Worsley also assume that the field T(x), in the signal-present case and in the immediate neighborhood of the target signal, can be approximated as quadratic in x. Under these assumptions, they show that the conditional probability in the integrand of Eq. (16) is approximately

$$\text{P}\{t_{max}\ge \tau \mid T({\mathit{x}}_{\ell })=\tau -s,H_{\ell }\}\approx \text{P}\{-\stackrel{.}{T}{({\mathit{x}}_{\ell })}^{\prime }\text{E}{[\ddot{T}({\mathit{x}}_{\ell })\mid T({\mathit{x}}_{\ell })=\tau -s]}^{-1}\stackrel{.}{T}({\mathit{x}}_{\ell })\ge 2s\},$$ (17)

where Ṫ(·) and T̈(·) denote the gradient and Hessian with respect to x, respectively, evaluated at x_ℓ. For Gaussian random fields, the conditional expectation in Eq. (17) can be obtained using

$$\text{E}[\ddot{T}(\mathit{x})\mid T(\mathit{x})]=\text{E}[\ddot{T}(\mathit{x})]+\text{Cov}\{\ddot{T}(\mathit{x}),T(\mathit{x})\}\frac{T(\mathit{x})-\text{E}[T(\mathit{x})]}{\text{Var}\{T(\mathit{x})\}}$$ (18)

and the linearity of derivatives. Approximating the field around the center of the target signal as quadratic and circularly symmetric yields a conditional expectation in Eq. (18) that is proportional to the identity matrix, and thus Eq. (17) corresponds to a χ² CDF. Substituting this CDF in Eq. (16) results in the following approximation for the probability of detection:

$$\text{P}\{t_{max}>\tau \mid H_{\ell }\}\approx 1-\mathrm{\Phi }\left(\frac{\tau -{\mu }_T({\mathit{x}}_{\ell })}{{\sigma }_T}\right)+\phi \left(\frac{\tau -{\mu }_T({\mathit{x}}_{\ell })}{{\sigma }_T}\right)\frac{1}{{\sigma }_T}\left[\frac{{\partial }^2{R}_T(\mathbf{0})}{{\partial }^2{x}_i}\right]/\left[\frac{{\partial }^2{\mu }_T({\mathit{x}}_{\ell })}{{\partial }^2{x}_i}\right].$$ (19)

In the following, we will combine expressions (12) and (19) with locally shift-invariant approximations to compute, respectively, the probabilities of false alarm and detection for observers of the form of Eq. (8).

4. APPROXIMATIONS OF DETECTION PERFORMANCE

A. Moments of the Local Test Statistics

Let t ∈ 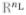be a vector whose components are the local test statistics t_ℓ, ℓ = 1, …, n_L. Let 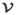= [v₁, …, v_nL] be a matrix whose columns consist of the image-domain templates v_ℓ ≜ 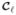w_ℓ. The latter are vectors in the same space as the reconstructed object f̂ and are formed by linear combinations of the channel responses.

To derive the moments of the test statistic vector t under each of the hypotheses in Eq. (1), we combine Eq. (8) with the moments of the tomographic data y from Eqs. (2) and (3), the linear reconstructor of Eq. (4), and the assumption that f_b and f_s,ℓ are independent. This yields the following expressions for the mean μ_t and covariance Π_t of the test statistic vector under each of the signal-absent and signal-present hypotheses:

$${\mathit{\mu }}_{t\mid H_0}=\mathbf{0},$$ (20)

$${\mathit{\mu }}_{t\mid H_{\ell }}=\mathcal{V}\text{'}\mathcal{Z}\mathcal{A}{\overline{\mathit{f}}}_{s,\ell },\ell =1,\dots ,n_{\text{L}},$$ (21)

$${\mathbf{\Pi }}_{t\mid H_{\ell }}={\mathcal{V}}^{\prime }\mathcal{Z}{\mathbf{\Pi }}_{\ell }{\mathcal{Z}}^{\prime }\mathcal{V}+\text{diag}\{{\mathit{w}}_{\ell }^{\prime }{\mathbf{\Pi }}_{{\epsilon }_{\ell }}{\mathit{w}}_{\ell },\ell =1,\dots ,n_{\text{L}}\},\ell =0,\dots ,n_{\text{L}},$$ (22)

where Π_εℓ is the M × M covariance matrix of the internal noise vector ε_ℓ and Π_ℓ ≜ Cov{y|H_ℓ}, i.e.,

$${\mathbf{\Pi }}_0=\text{diag}\{\mathcal{A}{\overline{\mathit{f}}}_b+r\}+\mathcal{A}{\mathcal{K}}_b{\mathcal{A}}^{\prime },$$ (23)

$${\mathbf{\Pi }}_{\ell }={\mathbf{\Pi }}_0+\text{diag}\{\mathcal{A}{\overline{\mathit{f}}}_{s,\ell }\}+\mathcal{A}{\mathcal{K}}_{s,\ell }{\mathcal{A}}^{\prime },\ell =1,\dots ,n_{\text{L}}.$$ (24)

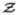
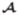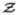For typical problem sizes, applying the operators and Π_ℓ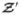 explicitly to compute the moments of t in Eqs. (21) and (22) is time-consuming for common statistical image reconstruction methods. Therefore, this approach would be impractical when one needs these moments to compute measures of detectability for many values of some reconstruction parameter that is to be optimized.

We use locally shift-invariant analysis to derive Fourier-domain approximations to the moments in Eqs. (21) and (22). A similar approach to computing the moments of the local test statistics has been followed and evaluated by others [22,23]. In this work we will combine such moment approximations with expressions (12) and (19) to speed up the computation of the ROC-related probabilities (11) and (10), respectively.

B. Locally Shift-Invariant Moment Approximations

For the Fourier analysis that follows, we will assume that we have a discrete representation of the object f ∈ 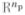. Let 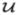be a discrete Fourier operator, mapping an object in 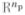to some vector in 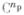known as the spectrum of the object. The Fourier operator 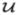is linear and, due to the shift property of the Fourier transform, it can be defined through its action on an object e₀ that consists of an impulse centered at the origin:

$$\mathcal{U}{\mathit{e}}_0=\frac{1}{\sqrt{n_{\text{p}}}}\mathbf{1},$$ (25)

where 1 is the vector of n_p ones. Without loss of generality, we choose the origin of the Fourier transform to coincide with the location where the signal f̄_s is centered. (The $1/\sqrt{n_{\text{p}}}$ factor ensures orthonormality.)

We consider tasks where the mean target signal f̄_s,ℓ has the same shape at all candidate locations ℓ = 1, …, n_L. Then f̄_s,ℓ is a copy of a common mean signal profile f̄_s shifted to location ℓ. We also assume that the observer’s channel responses at different image locations are shifted copies of each other. Thus we write

$${\overline{\mathit{f}}}_{s,\ell }={\mathcal{U}}^{-1}{\mathit{E}}_{\ell }{\mathit{X}}_0,$$ (26)

$${\mathcal{C}}_{\ell }={\mathcal{U}}^{-1}{\mathit{E}}_{\ell }{\mathit{T}}_0,$$ (27)

where ${\mathit{E}}_{\ell }\triangleq \sqrt{n_{\text{p}}}\text{diag}\{\mathcal{U}{\mathit{e}}_{\ell }\}$ consists of the complex exponential that corresponds to a circular shift from the origin (0,0) to location ℓ, and e_ℓ is an impulse centered at location ℓ. Finally, X₀ is the spectrum of f̄_s, when the latter is assumed centered at (0,0), and the M columns of T₀ contain the frequency responses of the observer’s M channels, when their impulse responses are assumed centered at (0,0).

We now assume that the mean target signal profile f̄_s is localized in space. In general, the operator 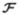is shift-variant for typical tomographic systems. However, if 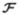is applied to an object that is contained within a small spatial extent around the origin, we can approximate 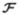as shift-invariant within the spatial extent of this object. The closer the object comes to resembling an impulse, the greater the accuracy of this approximation. Thus we approximate the operator 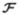(and similarly 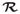) within a small spatial extent as

$$\mathcal{F}\approx {\mathcal{U}}^{-1}\mathbf{\Lambda }\mathcal{U},$$ (28)

$$\mathcal{R}\approx {\mathcal{U}}^{-1}\mathbf{\Omega }\mathcal{U},$$ (29)

where Λ ≜ diag{λ_k, k = 1, …, n_p} and Ω ≜ diag{ω_k, k = 1, …, n_p}. The λ_k’s and ω_k’s contain the local frequency response of 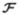and 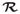, respectively, computed at the location of the signal. Such local diagonalization approximations have been used by other investigators to analyze observer performance with penalized-likelihood reconstruction [9,10,22,23].

Similarly, we assume that under any single hypothesis the object can be approximated as locally stationary around each of the locations ℓ = 1, …, n_L. This is more likely to be accurate when the signal profile is deterministic under all signal present hypotheses (i.e., 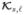= 0, ℓ = 1, …, n_L) or when the signal profile variability is negligible when compared to the background variability. Thus we approximate the object covariance within some small spatial extent by

$${\mathcal{K}}_b\approx {\mathcal{U}}^{-1}{\mathit{N}}_0\mathcal{U},$$ (30)

$${\mathcal{K}}_b+{\mathcal{K}}_{s,\ell }\approx {\mathcal{U}}^{-1}{\mathit{N}}_{\ell }\mathcal{U},\ell =1,\dots ,n_{\text{L}},$$ (31)

where ${\mathit{N}}_{\ell }\triangleq \text{diag}\{v_k^{\ell },k=1,\dots ,n_{\text{p}}\}$. The $v_k^{\ell }$’s contain the local power spectrum of f for hypothesis H_ℓ.

We take Λ, Ω, and N_ℓ to contain the local frequency responses of the respective operators at location ℓ_c, where ℓ_c ∈ {1, …, n_L} corresponds to the center of the observer’s search area. Thus we assume that these frequency responses capture the approximate behavior of the respective operators throughout the search area, if the latter is not too big.

We present here only the final expressions and refer the reader elsewhere for step-by-step derivations [19, Section 4.C]. Substituting the Fourier representations (26)–(31) into the MaCPPW local template in Eq. (9) yields

$${\mathit{w}}_{\ell }\approx {[(1-\gamma )\mathit{I}+\gamma ({\mathit{T}}_0^{\prime }{[\mathbf{\Lambda }+\mathbf{\Omega }]}^{-2}[\mathbf{\Lambda }+{\mathbf{\Lambda }}^2{\check{\mathit{N}}}_{\ell }]{\mathit{T}}_0+{\mathbf{\Pi }}_{{\epsilon }_{\ell }})]}^{†}·{\mathit{T}}_0^{\prime }{(\mathbf{\Lambda }+\mathbf{\Omega })}^{-1}\mathbf{\Lambda }{\mathit{X}}_0,$$ (32)

where ${\check{\mathit{N}}}_{\ell }\triangleq \frac{1}{2}{\mathit{N}}_{\ell }+\frac{1}{2}{\mathit{N}}_0$. By using the same Λ, Ω, and N_ℓ (i.e., the ones computed at the center ℓ_c) for every w_ℓ, ℓ = 1, …, n_L, we are approximating the templates as locally shift-invariant within the search area, i.e., w_ℓ ≈ w_ℓc, ℓ = 1, …, n_L. Then we can write

$$\mathcal{V}\approx \sqrt{n_{\text{p}}}{\mathcal{U}}^{-1}\text{diag}\{{\mathit{V}}_0\}\mathcal{U}{\mathcal{I}}_{\text{SA}},$$ (33)

where V₀ ≜ T₀w_ℓ is a linear combination of the channel responses and 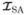≜ [e₁|…|e_nL] has as its columns the impulses e_ℓ, ℓ= 1, …, n_L, corresponding to the n_L locations in the search area.

Finally, substituting the frequency-domain representations (26)–(33) into the moments of the test statistic vector from Eqs. (21) and (22) yields the following locally shift-invariant approximations of these moments:

$${\mu }_{t\mid H_{\ell }}\approx n_{\text{p}}{\mathcal{I}}_{\text{SA}}^{\prime }{\mathcal{U}}^{-1}\mathbf{\Phi }\mathcal{U}{\mathit{e}}_{\ell },\ell =1,\dots ,n_{\text{L}},$$ (34)

$$\begin{array}{c}{\mathbf{\Pi }}_{t\mid H_{\ell }}\approx n_{\text{p}}{\mathcal{I}}_{\text{SA}}^{\prime }{\mathcal{U}}^{-1}\mathbf{\Psi }\mathcal{U}{\mathcal{I}}_{\text{SA}}+({\mathit{w}}_{{\ell }_c}^{\prime }{\mathbf{\Pi }}_{{\epsilon }_{{\ell }_c}}{\mathit{w}}_{{\ell }_c})\mathcal{I},\\ \ell =0,\dots ,n_{\text{L}},\end{array}$$ (35)

where

$$\begin{array}{c}\mathbf{\Phi }\triangleq \text{diag}\left\{\frac{V_k^{\ast }{X}_k{\lambda }_k}{{\lambda }_k+{\omega }_k},k=1,\dots ,n_{\text{p}}\right\},\\ \mathbf{\Psi }\triangleq \text{diag}\left\{\frac{{\mid V_k\mid }^2{\lambda }_k(1+{\lambda }_k{v}_k^{\ell })}{{({\lambda }_k+{\omega }_k)}^2},k=1,\dots ,n_{\text{p}}\right\},\end{array}$$

and V_k, X_k are the kth elements of V₀, X₀, respectively.

C. Approximations of P_FA and P_D

Regardless of the exact distribution of the data y, the term of t_ℓ in Eq. (8) that is linear in f̂ can be considered approximately Gaussian due to the central limit theorem. Thus the local test statistics can be considered approximately Gaussian. Assuming that the t_ℓ’s form a correlated Gaussian random field, we will use the approximations in (12) and (19) to evaluate the probabilities of false alarm and detection in Eqs. (11) and (10).

Approximation (12) assumes stationarity. For a typical shift-variant tomographic system, the t_ℓ’s are not globally stationary. However, as discussed above, we will consider the system to be locally shift-invariant and the object to be locally stationary over a small area around each of the candidate locations ℓ = 1, …, n_L. This implies that the t_ℓ’s are approximately stationary locally around each candidate location.

We use approximation (12) to calculate the probability of false alarm in Eq. (11) for channelized linear local test statistics and high detection thresholds τ. In particular, we write

$$P_{\text{FA}}(\tau )\approx \sum _{d=0}^2{R}_d(S){\rho }_d(\tau ;{\sigma }_{T\mid 0},{\mathrm{\Lambda }}_{T\mid 0})$$ (36)

where we use the notation σ_T|ℓ, Λ_T|ℓ to refer to moments under hypothesis H_ℓ. These moments can be computed fast from the Fourier approximation (35). In particular,

$${\sigma }_{T\mid 0}^2\approx \sum _{k=1}^{n_{\text{p}}}{\mid V_k\mid }^2{\lambda }_k(1+{\lambda }_k{v}_k^0)/{({\lambda }_k+{\omega }_k)}^2+{\mathit{w}}_{{\ell }_c}^{\prime }{\mathbf{\Pi }}_{{\epsilon }_{{\ell }_c}}{\mathit{w}}_{{\ell }_c}.$$ (37)

It would be possible to use an approximation like (36) for the probability of detection (10) as well, simply replacing ρ_d(τ; σ_T|0, Λ_T|0) with ρ_d(τ−μ_T|ℓc; σ_T|ℓc, Λ_T|ℓc) [30]. This would be satisfactory if the mean of the test statistic field, μ_T(x) ≜ E[T(x)|H_ℓ], were constant throughout the search area under each of the signal-present hypotheses. However, the mean cannot be considered constant throughout the search area in the presence of a spatially localized target signal. In this case, using a constant μ_T(x) =μ_T(x_ℓc) would lead to an overestimation of the probability of detection. Instead, we will use the signal-present approximation (19) for the probability of detection, combining it with Fourier approximations of the local test statistic moments:

$$P_{\text{D},{\ell }_c}(\tau )\approx 1-\mathrm{\Phi }\left(\frac{\tau -{\mu }_{T\mid {\ell }_c}}{{\sigma }_{T\mid {\ell }_c}}\right)+\phi \left(\frac{\tau -{\mu }_{T\mid {\ell }_c}}{{\sigma }_{T\mid {\ell }_c}}\right)·\frac{1}{{\sigma }_{T\mid {\ell }_c}}\left[\frac{{\partial }^2{R}_{T\mid {\ell }_c}(\mathbf{0})}{{\partial }^2{x}_i}\right]/\left[\frac{{\partial }^2{\mu }_{T\mid {\ell }_c}({\mathit{x}}_{{\ell }_c})}{{\partial }^2{x}_i}\right].$$ (38)

We compute μ_T|ℓc and σ_T|ℓc from the locally shift-invariant approximations (34) and (35), respectively:

$${\mu }_{T\mid {\ell }_c}\approx \sum _{k=1}^{n_{\text{p}}}{V}_k^{\ast }{X}_k{\lambda }_k/({\lambda }_k+{\omega }_k),$$ (39)

$${\sigma }_{T\mid {\ell }_c}^2\approx \sum _{k=1}^{n_{\text{p}}}{\mid V_k\mid }^2{\lambda }_k(1+{\lambda }_k{\nu }_k^{{\ell }_c})/{({\lambda }_k+{\omega }_k)}^2+{\mathit{w}}_{{\ell }_c}^{\prime }{\mathbf{\Pi }}_{{\epsilon }_{{\ell }_c}}{\mathit{w}}_{{\ell }_c}.$$ (40)

In the special case where the target signal is variable in its location only and not in its shape, i.e., 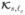=0, we have ${\nu }_k^{{\ell }_c}={\nu }_k^0$, which implies σ_T|ℓc = σ_T|0 and Λ_T|ℓc = Λ_T|0. Finally, we obtain the two derivatives in approximation (38) by applying finite differences to approximations (34) and (35).

In the following, we will use the approximations of the probability of false alarm and detection given in (36) and (38), respectively, to compute high-threshold points of the ROC curves corresponding to various observer models of interest.

5. SIMULATION RESULTS

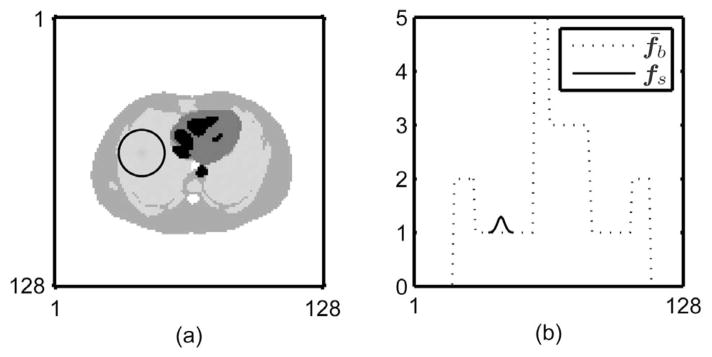
We present an example of using the above approximations to evaluate the effect of regularization on the detection performance of channelized observers applied to QPWLS-reconstructed images. In this example, corresponds to a 2-D PET system model with the characteristics of a CTI ECAT 931 scanner (matrix size 128 × 128, pixel size 4.7 mm, 192 radial samples with 3.1 mm spacing, 160 projection angles over 180°), as implemented in the ASPIRE software package [31]. We scale to produce measurements with a total of 10⁶ counts. We simulate the background events r by adding 10% of the total counts uniformly distributed over all measurement bins. The object background f_b has a Gaussian autocorrelation function with a full width at half-maximum (FWHM) of 12 pixels and a standard deviation of 0.075. The mean background f̄_b is the anthropomorphic phantom shown in Fig. 1, which corresponds to a slice of the Zubal phantom [32]. The target signal f_s,ℓ has a known Gaussian profile with a FWHM of 4 pixels and an amplitude of 0.3, but unknown location ℓ. The search area is assumed to be a disk. Any pixel inside the disk is a candidate location for the target signal. Figure 1 shows the mean background, the signal profile, and the largest of the concentric disk search areas that we consider in this example.

Fig. 1.

PSfrag replacements. Mean background f̄_b with the target signal f_s superimposed (a) and a profile through them (b). The largest of the search areas considered (diameter of 23 pixels) is indicated as a black circle in (a).

We assume a channelized observer model that involves four circularly symmetric, square-profile channels, as defined by Abbey et al. [17]. We consider local templates of the form of Eq. (9), where the CHO or CNPW templates are limiting cases. We evaluate detection performance for QPWLS reconstruction with the uniform quadratic regularizer in Eq. (6) and various values of the regularization parameter β. We compare results obtained from the proposed analytical approximations to results obtained from simulations.

(i) Proposed analytical approach

Using the analytical approximations (38) and (36), respectively, we calculate the probabilities of detection and false alarm for different values of the threshold τ. We repeat this for each value of β. Then we apply interpolation to these results to find the probability of detection at a fixed value of the probability of false alarm (0.02 in this example) for every β.

(ii) Empirical approach

We obtain the moments of the local test statistics for a range of different β’s from the local shift-invariant approximations (34) and (35). We then produce 5 × 10⁵ realizations of the local test statistics, t_ℓ, ℓ = 1, …, n_L, under each of the signal-present and signal-absent hypotheses, drawing from a Gaussian distribution with the respective moments. This yields multiple realizations of t_max under each hypothesis. For each β, we compare the realizations of t_max to a range of different thresholds τ to estimate the probabilities of detection and false alarm at every threshold. We then compute, as with the analytical approach, the probability of detection at a fixed value of the probability of false alarm for every β. We also compute the AUC for each β by numerical integration of the empirical probability of detection versus the empirical probability of false alarm.

Both the analytical and empirical methods perform a fast computation of the moments of the local test statistics based on local shift-invariance approximations. Khurd and Gindi followed a similar approach to compute the area under the LROC curve, using local shift-invariant moment approximations for CHO and CNPW local templates [22]. They compared the results to those produced by applying the observer templates to reconstructions of multiple noisy data sets. They reported very good agreement (for a range of signal contrasts) and a 10³-fold reduction in computation time when using local shift-invariant analysis. Thus, we do not repeat such an evaluation of local shift-invariance approximations. The comparison herein focuses on the approximation introduced by (38) and (36), rather than the approximation introduced by assuming a shift-variant system to be locally shift-invariant.

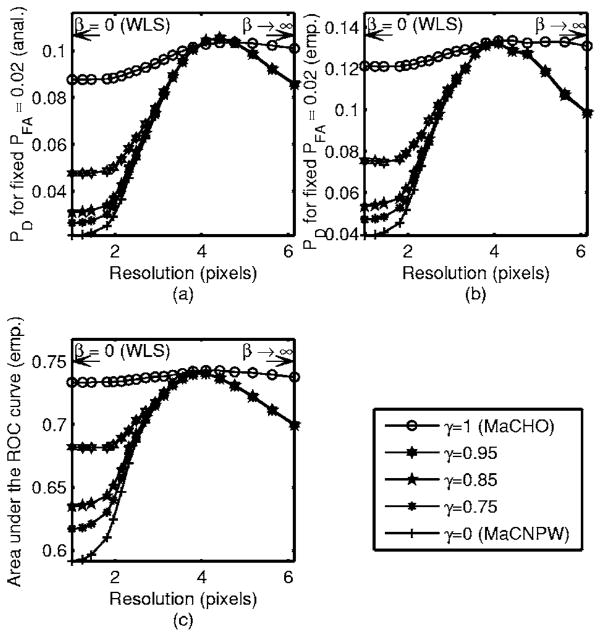
We compute the above analytical and empirical metrics for MaCPPW observers, including the MaCHO (γ = 1), MaCNPW (γ = 0), and three intermediate values of γ. Figure 2 shows results for these observers with a search area diameter of 9 pixels and QPWLS reconstruction with the roughness penalty in Eq. (6) and various values of β. The abscissa of the plots shows the resolution of the QPWLS reconstruction at the center of the search area, defined as the FWHM (in pixels) of the local impulse response [33] at that location. This local FWHM is a measure of the amount of smoothing imposed by QPWLS. It equals 1 pixel for β = 0, which corresponds to unregularized WLS, and it increases as β increases.

Fig. 2.

Detection performance of MaCPPW observers versus QPWLS reconstruction resolution: P_D obtained analytically (a), P_D obtained empirically (b), and AUC obtained empirically (c). Results are shown for five different degrees of prewhitening accuracy. The search area is a disk with a diameter of 9 pixels.

Figure 3(a) shows how the optimal QPWLS resolution varies with the size of the search area. Figure 3(b) shows the maximum increase in the AUC of the MaCNPW observer versus the diameter of the search area. The increase is defined as the ratio (AUC^*−AUC⁰)/AUC⁰, where AUC^* and AUC⁰ denote the AUC achieved by the observer when regularized QPWLS with optimal β and unregularized WLS is used, respectively.

Fig. 3.

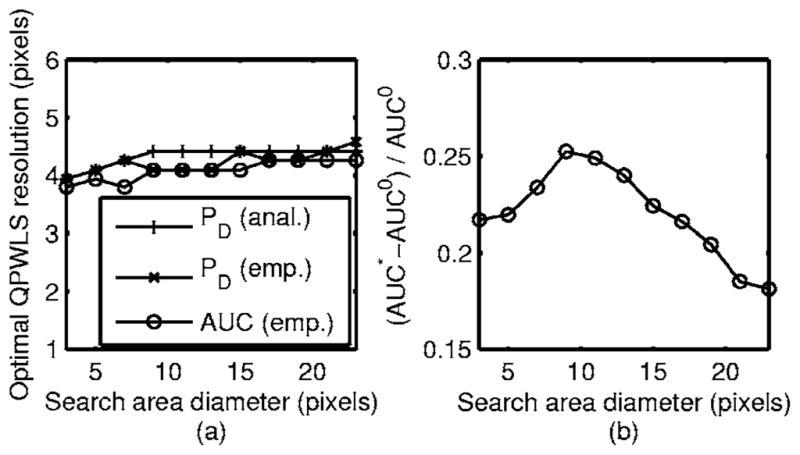
QPWLS resolution that maximizes the P_D (obtained analytically and empirically) or AUC (obtained empirically) versus search area diameter (a). AUC improvement with optimally regularized QPWLS over unregularized WLS versus search area diameter (b). Results are shown for the MaCNPW observer.

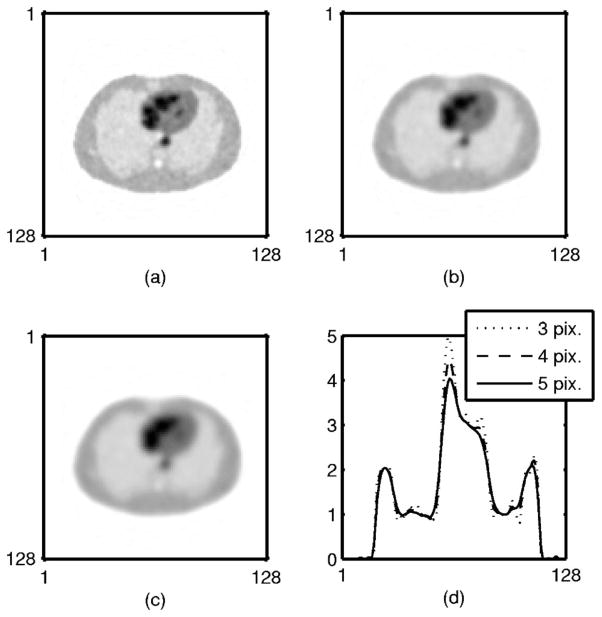
As seen in Fig. 3(a), the optimal QPWLS resolutions for different search area sizes are around 4 pixels in this example. For reference, Fig. 4 shows QPWLS-reconstructed images with resolutions of 3, 4, and 5 pixels, all from the same data set with Poisson noise and the signal present in the center of the search area.

Fig. 4.

QPWLS reconstructions of a noisy Poisson data set with a resolution of 3 pixels (a), 4 pixels (b), or 5 pixels (c), and profiles through the three images (d). The signal is present in the center of the search area.

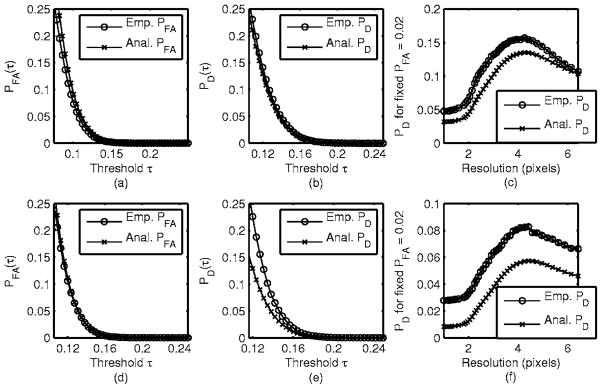
Figure 5 compares the analytical and empirical probabilities of detection and false alarm for the MaCNPW observer with two different search area sizes. Figures 5(a) and 5(b) show the probabilities of false alarm and detection, respectively, for a search diameter of 7 pixels and a fixed QPWLS resolution of 3 pixels. Figures 5(d) and 5(e) show the same probabilities for a search diameter of 15 pixels and a fixed QPWLS resolution of 3 pixels. The interpolated probability of detection at a fixed probability of false alarm (P_FA=0.02), with varying QPWLS resolution, is shown in Figs. 5(c) and 5(f) for a search diameter of 7 and 15 pixels, respectively.

Fig. 5.

Empirical and analytical probabilities of false alarm and detection for the MaCNPW observer with a search area diameter of 7 pixels [(a)–(c)] and 15 pixels [(d)–(f)]. The plots show the P_FA versus detection threshold [(a),(d)], the P_D versus detection threshold [(b),(e)], and the P_D (with error bars) versus QPWLS resolution for a fixed P_FA=0.02 [(c),(f)]. (The error bars are small enough to fit in the plot markers.)

6. DISCUSSION

The plots of Fig. 2 show that for the MaCHO observer, the peak detection performance achieved with regularized QPWLS is very close to the performance achieved with unregularized WLS. However, as the prewhitening capabilities of the observer deteriorate, the improvement achieved at the optimal amount of regularization becomes more and more significant. The MaCNPW observer is the most affected by the amount of regularization. The same trend is captured by all metrics, i.e., the analytical and empirical probability of detection at a fixed low probability of false alarm, as well as the empirical AUC. The optimal resolution was slightly lower for the AUC.

As indicated by these results, the observer’s prewhitening capabilities are important in determining whether optimized regularization can improve detectability significantly over unregularized reconstruction. This is in agreement with some prior results from the analysis of known-location tasks. In particular, we have shown that the gains in known-location detectability between optimized regularization and no regularization increase as the prewhitening deficiency of the observer increases [19, Section 3.4]. This occurs because, for an intermediate amount of regularization, the observer’s channel outputs are closest to white; hence prewhitening is less crucial for achieving good detection performance. Results by Qi also show that optimizing regularization parameters with respect to known-location detection performance has a more dramatic effect for a nonprewhitening (“maximum-constrast”) observer than the CHO [10]. Thus it seems that the effect of regularization depends less on whether the signal location is known or unknown to the observer and more on whether the observer can perform prewhitening. However, these two aspects of the observer model are not entirely unrelated in practice, since experimental results indicate that the prewhitening capabilities of human observers may deteriorate in unknown-location tasks [20,21]. In the simulations presented here, the size of the search area also played a role, with regularization being somewhat less beneficial for observers with very small or very large search areas. Although we show plots only for observers with square-profile channels, we obtain similar results with the difference-of-Gaussians channel sets from Abbey et al. [17]

Considering the range of QPWLS resolutions that achieve near-peak AUC for the MaCNPW observer, as seen in Fig. 2, the variation in optimal QPWLS resolution versus search diameter, as seen in Fig. 3(a), is small. Thus, a moderate uncertainty about the observer’s search area would not result in a significantly different conclusion about the optimal amount of regularization.

As seen in Fig. 3(b), the improvement in the AUC of the MaCNPW observer afforded by optimal regularization varies somewhat with the size of the search area. The maximum improvement is achieved for an intermediate search diameter (in this case, 9 pixels).

Approximation (38) for the probability of detection assumes that the test statistic field is quadratic around the target signal location. This quadratic approximation is more accurate for a search diameter of 7 pixels, as shown in Fig. 5(b), since this search area size is comparable to the support of the target signal. For a larger search area, however, this approximation breaks down, as shown in Fig. 5(e).

Even if the analytical approximations are not always accurate at predicting the value of the probability of detection, they follow the trends of the empirical curves and are maximized at the same or nearly the same QPWLS resolution. Thus, analytically computed plots like the ones in Figs. 2(a), 5(b), and 5(e) can be useful for choosing the regularization parameter β to optimize the probability of detection for a given low probability of false alarm within a small search area around some pixel.

For the small search diameter of 7 pixels, the analytical approach offers a tenfold reduction in computation, when compared to the empirical approach of simulating the local test statistics from the Fourier approximations of their moments. The computational savings increase with the size of the search area. They also increase with the number of realizations produced for the empirical approach. This tenfold reduction in computation augments the 10³-fold reduction, which is afforded by the use of locally shift-invariant approximations instead of image reconstructions and which was reported by Khurd and Ghindi [22]. The additional savings can be important when detectability needs to be evaluated at every voxel in the image to optimize regularization parameters locally.

The limitation of the proposed method is that analytical approximations (36) and (38) apply only to high thresholds τ. Thus these approximations are useful when a partial area under the curve or a single point on the curve (at low false-positive rates) is the desired figure of merit for observer performance. However, they cannot be used to trace the entire ROC and find the AUC. In the example of Section 5, the probability of detection at a low probability of false alarm behaved similarly to the AUC with respect to the regularization parameter (see Fig. 2). In general, however, the ranking of ROC curves at low probabilities of false alarm may not predict their ranking at high probabilities of false alarm, as ROC curves for different regularization parameters may cross. If one is interested in optimizing regularization with respect to performance at high probabilities of false alarm, one should check for crossing ROC curves by applying the simulation method for at least one voxel in the image before applying the analytical method to optimize regularization for the rest of the image. The analytical approach could also complement the empirical approach by providing an initial estimate of the optimal resolution, around which simulations can then be performed if more accuracy is needed.

We have considered observers that search for the target signal within a local search area, rather than within the entire image. We have made this choice for two reasons. First, locally shift-invariant approximations to the moments of the local test statistics are accurate within a local region. If the system is shift-variant and/or the object background is not stationary, these approximations are not accurate within the entire image. Second, our ultimate goal is to use the analyses above to optimize the amount of regularization locally at each pixel in the image. It seems reasonable for the optimal amount of regularization at some pixel to be determined by the image statistics within a local area around that pixel.

For the example presented above, we did not include internal noise in the observer model. The reason is that internal noise would manifest itself as an impulse at the center R_T(0) of the autocovariance function. In this case, the analytical approximations would break down, because they require the autocovariance function to be smooth so that its second derivative can be computed. In particular, the analytical approximations would deteriorate for large β, where the internal noise dominates. This issue arises because the observer models with internal noise that have been proposed in the literature assume that this noise is uncorrelated between different candidate locations. Whether this assumption is crucial, however, must ultimately be validated by human observer studies. In general, internal noise is intended to model the phenomenon that a human observer may make different decisions when presented with the same image on different occasions. An alternative way to express this uncertainty that would make the model more amenable to analysis would be to add noise to the maximum test statistic itself instead of adding noise to the local test statistics individually. Once again, the usefulness of such a model would have to be tested by studies with human observers.

The analytical approximations can also be applied to optimize anisotropic regularization, which has been reported to yield greater performance improvement than isotropic regularization in known-location tasks [12]. In addition to lesion detectability, the proposed method can be applied to the optimization of regularization with respect to the detectability of activations in functional neuroimaging. Improving the accuracy of the approximations for a wider range of search area sizes and for nonzero internal noise, as well as relaxing the assumption of a circularly symmetric signal shape, are topics for future investigation. Furthermore, since the threshold-exceeding probability approximations used here have been derived for continuous random fields, the analysis can be applied naturally to tomographic reconstruction methods that yield continuous-space images f̂.

Finally, it would be of interest to extend the analysis of the probability of detection to the probability of correct localization, thus considering a LROC instead of a ROC curve. Under certain assumptions of statistical independence on the local test statistics, it has been shown that maximizing the AUC is equivalent to maximizing the area under its LROC curve [6]. However, further investigation is needed to analyze the probability of correct localization for the correlated local test statistics considered here.