Recent improvements in prediction of protein structure by global optimization of a potential energy function

Abstract

Recent improvements of a hierarchical ab initio or de novo approach for predicting both α and β structures of proteins are described. The united-residue energy function used in this procedure includes multibody interactions from a cumulant expansion of the free energy of polypeptide chains, with their relative weights determined by Z-score optimization. The critical initial stage of the hierarchical procedure involves a search of conformational space by the conformational space annealing (CSA) method, followed by optimization of an all-atom model. The procedure was assessed in a recent blind test of protein structure prediction (CASP4). The resulting lowest-energy structures of the target proteins (ranging in size from 70 to 244 residues) agreed with the experimental structures in many respects. The entire experimental structure of a cyclic α-helical protein of 70 residues was predicted to within 4.3 Å α-carbon (C^α) rms deviation (rmsd) whereas, for other α-helical proteins, fragments of roughly 60 residues were predicted to within 6.0 Å C^α rmsd. Whereas β structures can now be predicted with the new procedure, the success rate for α/β- and β-proteins is lower than that for α-proteins at present. For the β portions of α/β structures, the C^α rmsd's are less than 6.0 Å for contiguous fragments of 30–40 residues; for one target, three fragments (of length 10, 23, and 28 residues, respectively) formed a compact part of the tertiary structure with a C^α rmsd less than 6.0 Å. Overall, these results constitute an important step toward the ab initio prediction of protein structure solely from the amino acid sequence.

Important progress has been made in recent years toward the physics-based computation of protein structure based solely on knowledge of the amino acid sequence. This approach, commonly referred to as an ab initio or de novo method (1–3), is based on the thermodynamic hypothesis formulated by Anfinsen (4), according to which the native structure of a protein corresponds to the global minimum of its free energy under given conditions. Protein structure prediction by using ab initio methods is accomplished by a search for a conformation corresponding to the global-minimum of an appropriate potential energy function without use of secondary structure prediction, homology modeling, threading, etc.

Until recently, ab initio protein structure prediction based solely on the thermodynamic hypothesis was considered unfeasible (5–7) mainly because of the inaccuracy of the potential functions used to describe protein conformational energy and the lack of powerful global optimization methods for exploring the energy landscapes represented by those functions. Other types of knowledge-based methodologies, such as homology modeling (8–13) or threading methods (9, 12, 14) have been considered to be the most successful approaches. However, the success of these methods depends on the presence of sequentially or structurally homologous proteins in the databases. Furthermore, they do not provide a general understanding of the role of particular interactions in the formation of protein structure and the mechanisms of protein folding. This understanding can be achieved only through the development of force fields based completely on the physics of interactions for which the native structure is the lowest-energy minimum.

United-residue models of polypeptide chains (14–21) have been the subject of special attention for many years. In particular, because a global minimum search of single-domain proteins of typical size (30–250 residues) is practically unfeasible at the all-atom level, a united-residue representation of the protein reduces the number of variables, making this optimization problem tractable with current computers. During the last few years, we have developed a physics-based united-residue force field (UNRES) (19–21) for off-lattice simulations (22). Initial predictive applications of the UNRES force field were carried out on helical proteins, as assessed during the CASP3 experiment (23, ‖); however, this initial version was unable to model β-structures (19). During the past 2 years, we continued to develop the force field and, with the aid of a cumulant expansion of the free energy, and a Z-score optimization, we determined the terms in the restricted free energy (RFE) function that are responsible for formation of β-structure (21). Thus, the current version of UNRES can treat proteins with both α and β structures.

General Form of the UNRES Force Field.

In the UNRES model (19–21), a polypeptide chain is represented by a sequence of α-carbon (C^α) atoms linked by virtual bonds with attached united side chains (SC) and united peptide groups (p). Each united peptide group is located in the middle between two consecutive α-carbons. Only these united peptide groups and the united side chains serve as interaction sites, the α-carbons serving only to define the chain geometry (see figure 1 of ref. 24). All virtual bond lengths (i.e., C^α—C^α and C^α—SC) are fixed; the distance between neighboring C^αs is 3.8 Å, corresponding to trans peptide groups, whereas the side-chain angles (α_SC and β_SC), and virtual-bond angles (θ and γ) can vary. The energy of the virtual-bond chain is expressed by Eq. 1.

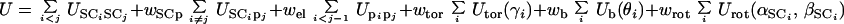1

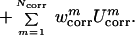The term U_SCiSCj represents the mean free energy of the hydrophobic (hydrophilic) interactions between the side chains as an orientation-dependent Gay-Berne potential (25); it implicitly contains the contributions from the interactions of the side chains with the solvent. The term U_SCipj denotes the excluded-volume potential of the side-chain–peptide-group interactions. The interaction potential (U_pipj) accounts mainly for the electrostatic interactions (i.e., the tendency to form backbone hydrogen bonds) between peptide groups p_i and p_j. U_tor, U_b, and U_rot represent the energies of virtual-dihedral angle torsions, virtual-bond angle bending, and side-chain rotamers, respectively; these terms account for the local propensities of the polypeptide chain. Details of the parameterization of all of these terms are provided in earlier publications (19). Finally, the terms U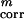, m = 1,2,… N_corr are the correlation or multibody contributions from the cumulant expansion of the RFE and w's are the weights of the energy terms.

The UNRES force field was derived as an RFE function, by averaging the all-atom energy over the degrees of freedom that are neglected in the united-residue model (19–21); these include solvent degrees of freedom, side-chain rotation angles, and the dihedral angles λ for rotation of the peptide groups about the C^α⋅⋅⋅C^α virtual bonds (26). The RFE function can be expressed as a sum of single-body, pairwise, and, generally, multibody contributions of various order in the framework of the so-called “cumulant” expansion (27). These cumulant terms are parameterized by fitting them to the free-energy surfaces of model systems such as tetra- and hexapeptides, as calculated from our all-atom potential, empirical conformational energy program for peptides (ECEPP/3; ref. 28).

Finally, the weights of the different terms in the UNRES energy function (Eq. 1) were determined by maximizing both the energy gap between the native-like and non-native conformations (ΔE) and the Z-score value (Z), both quantities being treated as functions of weights, as expressed by Eqs. 2 and 3.

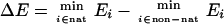2

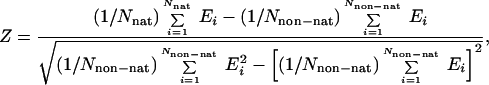3

where nat and non-nat indicate the sets of native-like and non-native conformations, respectively [the criterion being the rms deviation (rmsd) from the experimental structure], and N_nat and N_non−nat denote the number of native-like and non-native structures, respectively.

To obtain a force field that can be applied to α-helical-, β-, and α/β-structures, the weights were optimized by using two proteins simultaneously: the 10–55 fragment of the 60-residue B domain of staphylococcal protein A (hereafter referred to as protein A) (29), which has a three-helix bundle structure, and the 20-residue betanova (30), whose native structure is a three-stranded antiparallel β-sheet. The optimization procedure involves iterative cycles in each of which the conformational space annealing (CSA) method (22, 31, 32) is used to carry out a global search with the current set of weights. Details of the procedure to optimize the UNRES model will be presented elsewhere.

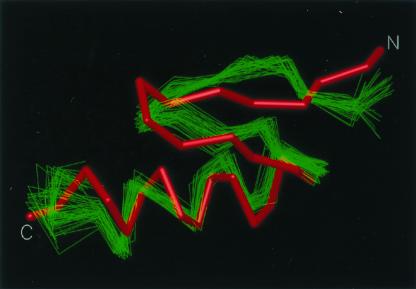
The resulting UNRES energy function was tested with a designed 28-residue peptide that contains the minimal α/β fold (33), identified in the Protein Data Bank (PDB) as 1fsd. It should be stressed that 1fsd was not used in the force-field optimization. In a series of global optimization runs with the CSA method, a structure with an rmsd for the C^α atoms of 3.4 Å from the average NMR structure (33) was obtained as the one with the lowest energy (see Fig. 1).

Figure 1.

Superposition of the predicted (red) structure of 1fsd on a family of experimental NMR structures (green) (33). The C^α atoms agree to within an rmsd of 3.4 Å.

Increased accuracy and speed of convergence is obtained by treating α, β and α/β proteins separately, with separate weights determined for each category by Eqs. 2 and 3. Further, by using only the lowest order of cumulants, an additional force field (α₀) to treat α-type proteins was developed. The latter force field is less accurate than the one that includes higher-order cumulants (α), but, despite the small loss in accuracy, we are able to treat α proteins of up to 250 residues with a 3-fold speed-up in the computations.

The CASP4 Exercise in Protein Structure Prediction.

The newly developed force field has recently been used in blind predictions of some of the target proteins provided for the Fourth Critical Assessment of Techniques for Protein Structure Prediction (CASP4). The three-dimensional structures of these targets were being determined by NMR spectroscopy or x-ray crystallography at the same time that the predictions were made. Our laboratory submitted predictions for 16 of the 43 targets that were volunteered by experimental structural biologists. The length of the target-sequences that we considered varied from 70 to 244 amino acids. In all cases, five predictions per target were submitted. The models correspond to the lowest-energy UNRES conformations of the five lowest-energy families obtained from a clustering analysis. Each model was then converted to an all-atom structure by using the dipole-path method (34) and later refined by using the electrostatically driven Monte Carlo (EDMC) method (35, 36) and ECEPP/3 (28).

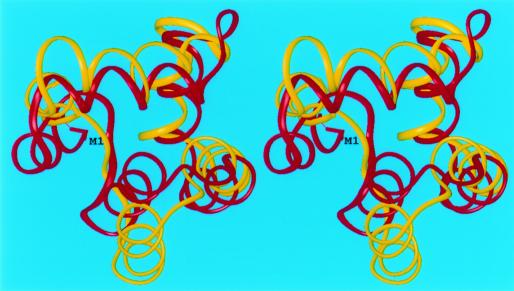
The analysis of our results for the α-helical targets shows reasonably accurate predictions. Our best α-helical prediction corresponds to target T0102 (bacteriocin AS-48), which is a 70-residue cyclic polypeptide from Enterococcus faecalis (PDB code: 1e68). The structure (37) consists of five α-helices arranged in a structural motif analogous to that of NK-lysin, but this information about a homologous structure was not used in the prediction. Our simulations were carried out by assuming an open chain (i.e., no loop-closing term was used in the energy function to force the N- and C-termini to come together). A version of our force field (viz., α) parameterized for α-helical structures that uses higher order correlation terms was used. Secondary structure information for this protein was available but was not used in our simulations. This information was used only to generate four additional sequences by cyclic permutations of the termini in such a manner that sequence cuts fell outside of the α-helical regions. Five CSA runs were carried out, one for each different sequence. Low-energy conformations, in which the N- and C-termini were in close proximity, were selected, and loop closure was imposed during the refinement at the all-atom level representation. Fig. 2 shows the superposition of model 1 for T0102 onto the experimental structure with an rmsd of 4.3 Å for the C^α atoms.

Figure 2.

Superposition of the crystal (red) and predicted (yellow) structures of the 70-residue protein bacteriocin AS-48 (target T0102). The C^α atoms were superposed with an rmsd of 4.3 Å.

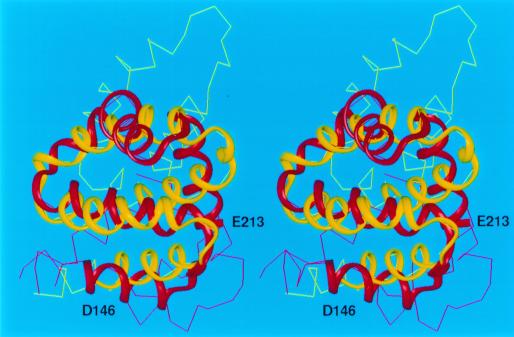
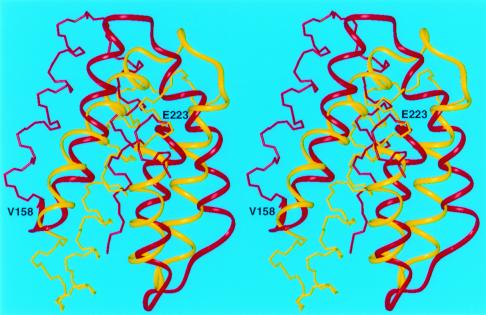
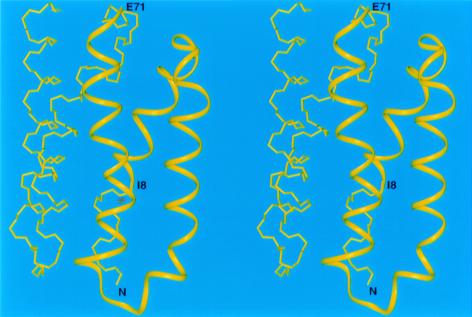
For other all-α target proteins, our predicted structures reproduced several features of the experimental structure. For example, the predicted structures of targets T0096 (PDB code: 1e2x), T0097 (PDB code: 1g7d), T0098(PDB code: 1fc3), T0106, and T0124 match the experimental structures to within 6.0 Å C^α rmsd for fragments varying in length from 52 to 68 residues (Figs. 3, 4, and 5). It should be noted that simulation studies (38) have demonstrated that it is extremely unlikely to obtain a predicted structure with a 6-Å rmsd by a random search for a chain of at least 60 residues and, hence, that a prediction with a 6-Å rmsd should be considered as a successful one. For the 121-residue target T0098, which represents a novel protein fold, our protocol reproduced a 68-residue fragment (model 3) with a 5.9-Å C^α rmsd (residues 146–213) (Fig. 3). For the 105-residue target T0097, a 66-residue fragment (residues V158-E223) superposed with a C^α rmsd of 5.9 Å (Fig. 4), whereas for the 128-residue target T0106, the 64-residue fragment between I8 and E71 superimposed with a C^α rmsd of 6.0 Å (Fig. 5).

Figure 3.

Superposition of the crystal (red) and predicted (yellow) structures of T0098. The C^α atoms of the 68-residue fragment included between residues D146 to E213 superimposed with an rmsd of 5.9 Å. This fragment is shown as colored ribbons.

Figure 4.

Superposition of the crystal (red) and predicted (yellow) structures of T0097. The C^α atoms of the 66-residue fragment included between residues V158 to E223 superimposed with an rmsd less than 6.0 Å. This fragment is shown as colored ribbons.

Figure 5.

The predicted structure of T0106. The C^α atoms of the illustrated 64-residue fragment included between residues I8 to E71 agree with the experimental structure with an rmsd of 6.0 Å. This fragment is shown as a yellow ribbon.

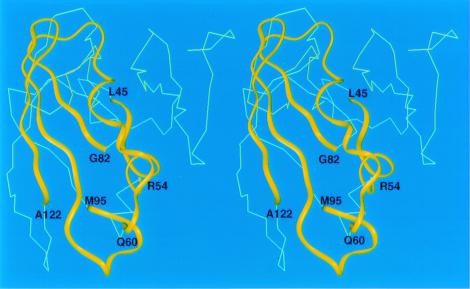
Predictions of α/β- and β-targets were in general less successful than those for α-helical targets. Nonetheless, some of them are quite encouraging, especially because our new procedure is now capable of predicting β structure whereas our older one was not. For the 163-residue target T0126, fragments involving residues 66–82 and 88–122 (52 residues) of model 1 (not shown) match the experimental structure within 6.8 Å C^α rmsd. Similarly, the fragments including residues 45–54, 60–82, and 95–122 of model 3 (61 residues) match the experimental structure within 6.0 Å C^α rmsd (Fig. 6) and correctly predicted the contact between noncontiguous strands involving residues 77–82 and 104–111.

Figure 6.

The predicted structure of T0126. The C^α atoms of three fragments defined by residues L45 to R54, Q60 to G82, and M95 to A122 agree with the experimental structure with an rmsd of 6.0 Å. These fragments are shown as yellow ribbons. The remaining residues are shown as a C^α trace.

Concluding Remarks.

We have shown that a reasonably accurate united-residue potential function for proteins can be developed by including multibody terms derived from a cumulant expansion of the restricted free energy. Even though further improvement of our approach is necessary, the results presented here demonstrate that prediction of the three-dimensional structures of proteins solely from the amino acid sequence (without the aid of knowledge-based information from secondary-structure prediction, multiple-sequence alignment, or fold recognition) is feasible.

Abbreviations

CSA

conformational space annealing

ECEPP

empirical conformational energy program for peptides

PDB

protein data bank

rmsd

rms deviation

UNRES

united-residue

RFE

restricted free energy

SC

side chain