Skip to main content
NCBI home page
Biophysical Reviews logoLink to Biophysical Reviews
. 2009 Jan 17;1(1):13. doi: 10.1007/s12551-008-0003-2

Properties of the nucleic-acid bases in free and Watson-Crick hydrogen-bonded states: computational insights into the sequence-dependent features of double-helical DNA

A R Srinivasan 1, Ronald R Sauers 1, Marcia O Fenley 3, Alexander H Boschitsch 4, Atsushi Matsumoto 1,5, Andrew V Colasanti 1,6, Wilma K Olson 2,✉
PMCID: PMC3016052  NIHMSID: NIHMS250600  PMID: 21218180

Abstract

The nucleic-acid bases carry structural and energetic signatures that contribute to the unique features of genetic sequences. Here, we review the connection between the chemical structure of the constituent nucleotides and the polymeric properties of DNA. The sequence-dependent accumulation of charge on the major- and minor-groove edges of the Watson–Crick base pairs, obtained from ab initio calculations, presents unique motifs for direct sequence recognition. The optimization of base interactions generates a propellering of base-pair planes of the same handedness as that found in high-resolution double-helical structures. The optimized base pairs also deform along conformational pathways, i.e., normal modes, of the same type induced by the binding of proteins. Empirical energy computations that incorporate the properties of the base pairs account satisfactorily for general features of the next level of double-helical structure, but miss key sequence-dependent differences in dimeric structure and deformability. The latter discrepancies appear to reflect factors other than intrinsic base-pair structure.

Electronic supplementary material

The online version of this article (doi:10.1007/s12551-008-0003-2) contains supplementary material, which is available to authorized users.

Keywords: Ab initio calculations, DNA base pairs, Conformation, Electronic structures, Electrostatic potential surfaces, Normal modes

Introduction

The energetic and structural information encoded in the DNA base-pair sequence has direct bearing on the overall shape and stability of the double-helical molecule. The basis of this code lies in the electronic characteristics of the heterocyclic bases—adenine (A), thymine (T), guanine (G), and cytosine (C)—and their hydrogen-bonded Watson–Crick complexes (Fig. 1). Although much of the net negative charge per nucleotide is concentrated on the phosphate group, there is a build-up of appreciable fractional charge on certain atoms of the heterocyclic bases. This article highlights a number of factors—partial atomic charges, intrinsic structures, binding energies, dipole moments, electrostatic potential surfaces, and rigid-body motions—that distinguish the two Watson–Crick base pairs and draws connections between these local chemical features and the higher-order structural information that is used to recognize and process the genetic information stored in long base-pair sequences. The capability to link basic chemical information with the polymeric properties of DNA rests upon technical advances that make it possible (a) to determine, with high accuracy, the electronic structures of hydrogen-bonded base complexes (Frisch et al. 2001; Frisch et al. 2003), (b) to represent the electrostatic potential of the base pairs at high resolution (Boschitsch et al. 2002; Boschitsch and Fenley 2004), and (c) to compare these chemical features with relevant spatial information (Lu and Olson 2003; Lu and Olson 2008) in the growing database of high-resolution nucleic-acid structures (Berman et al. 1992) and with classic physical measurements.

Fig. 1.

Fig. 1

Open in a new tab

Comparative hydrogen-bonding interactions, chemical structures (including double bonds), and displacement of bases comprising normal A·T and G·C Watson–Crick pairs. Hydrogen bonds are designated by dashed lines and the “weak” CH···O bond of the A·T base-pair by a thin wavy line. Conventional proton donor and acceptor atoms are colored red and blue, respectively. The donor and acceptor atoms involved in “weak” CH···O interactions are similarly highlighted in magenta and cyan. The line joining C1′ atoms on associated bases illustrates the isomorphous geometry of the Watson–Crick pairs, with roughly equivalent angles λ B (B = A, T, G, C) formed between the long, finely dotted C1′···C1′ virtual bond and each of the C1′–N9 and C1′–N1 glycosidic bonds. Atoms with partial charge differences of ±0.05 esu or more in the base-paired vs. base-separated state are highlighted by gray shading

Atomic charge distribution

Importantly, the distributions of electronic charge on the Watson–Crick base pairs differ from those on the free bases (see the Supplementary materials for a complete list of the atomic charges of base and base-pair atoms obtained within the Gaussian 98 and Gaussian 03 suites of programs (Frisch et al. 2001; Frisch et al. 2003)). The characteristic accumulation of electronic charge on the exposed major- and minor-groove edges of the base pairs presents unique motifs for direct sequence recognition (Seeman et al. 1976). For example, the much larger negative charge on the C5 atom of cytosine compared to the corresponding atom of thymine, e.g., −0.69 vs. −0.22 esu in the Watson–Crick pairs, influences the interactions of charged ligands with the major-groove edges of the two pyrimidines (see below).

These and other subtleties in local electronic structure surface at the base-pair level in terms of distinctly different A·T and G·C dipoles, with the computed magnitude of the G·C dipole more than double that of the A·T pair (6.6. vs. 2.4 Debye). Confidence in these predictions is strengthened by the agreement between the computed dipole moment of free adenine (3.0 Debye) and the measured dipole moment (3.0 ± 0.2 Debye) of 9-n-butyl-adenine in CCl4 (DeVoe and Tinoco Jr. 1962). On the other hand, the predicted dipole moment of guanine (7.2 Debye) exceeds the reported value (5.5 Debye; Párkányi et al. 2002). The latter measurement, performed in dioxane, is not directly relevant to the computations in that the polar solvent may form hydrogen bonds with the base and thereby perturb its electronic structure. No such interactions occur in the nonpolar CCl4 solvent. The orientations and directions of the computed dipole moments, depicted in Figs. 2 and 3 by black arrows, point to the unique electronic character of the free bases as well as the base pairs.

Fig. 2.

Fig. 2

Open in a new tab

Electrostatic potential surfaces of the methylated (purine N9 and pyrimidine N1) form of an optimized A·T base pair and its adenine (left) and thymine (right) components in a simulated aqueous environment. Views looking down the major- and minor-groove edges (top and bottom rows of images, respectively) and perpendicular to the base and base-pair planes (middle row). White wireframe models of the respective molecules are superimposed on the electrostatic potential surfaces. Dipole-moment vectors, noted by black arrows, are drawn in accordance with the computed structure and charges. The surfaces of bases and base pairs are color-coded such that the areas of greatest negative potential (−1 kcal mol-1/e-1) are yellow, those of greatest positive potential (+1 kcal mol-1/e-1) are green, and the intermediate regions of negative, neutral, and positive potential vary, respectively, from red to white and blue. See Supplementary materials for further details

Fig. 3.

Fig. 3

Open in a new tab

Electrostatic potential surfaces of the methylated (purine N9 and pyrimidine N1) form of an optimized G·C base pair and its guanine (left) and cytosine (right) components. See legend of Fig. 2

Base-pair nonplanarity

Conventional wisdom attributes the (negative) propeller twisting of the Watson–Crick base pairs seen in high-resolution DNA structures to a base-stacking effect, i.e., the out-of-plane rotation of complementary bases about the long base-pair axis seemingly enhances stacking overlaps with bases in adjacent residues (Levitt 1978); see illustrative image of propeller-twisted base-pair planes in Fig. 4. Calculations, however, show that negative propeller twist is intrinsic to isolated, unstacked A·T and G·C pairs and is a direct consequence of the pyramidal geometry of the proton-donating, exocyclic amino groups—an idea anticipated in earlier research (Komarov and Polozov 1990).

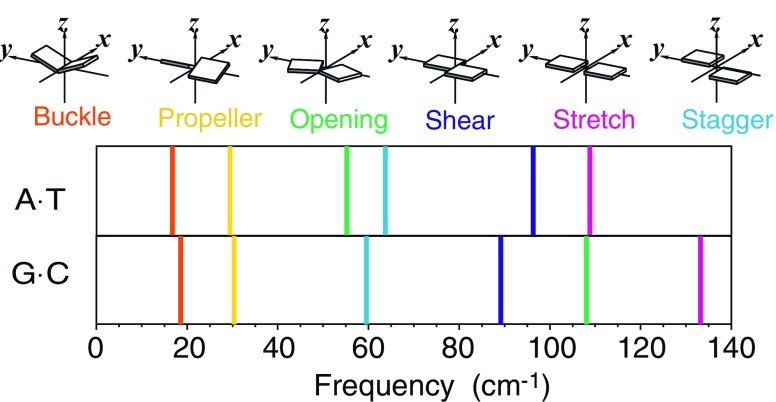
Fig. 4.

Fig. 4

Open in a new tab

Color-coded spectrum of the lowest frequency normal modes of A·T and G·C hydrogen-bonded Watson–Crick base pairs. The color coding denotes the base-pair fluctuations that dominate the respective modes: buckle (orange), propeller (yellow), opening (green), shear (deep blue), stretch (magenta), stagger (light blue). The normal modes, expressed in the Gaussian package (Frisch et al. 2001; Frisch et al. 2003) in terms of individual atomic displacements, are translated to fluctuations of base-pair parameters with the 3DNA software (Lu and Olson 2003). Structural distortions are modeled by moving the atoms along the predicted displacement vectors for each normal mode, such that the energies of the distorted structures are increased by k B T/2 over that of the minimum-energy structure, where k B is the Boltzmann constant and T is the absolute temperature. The differences between the base-pair parameters of the distorted structures and the minimum-energy structure provide the basis for the described motions. A pictorial definition of each base-pair parameter (illustrating positive values) is shown at the top

The displacement of the amino hydrogens out of the starting plane introduces nonzero values of propeller twist while concomitantly lowering the binding energy. For example, the A·T pair takes on negative propeller values, and the energy drops by −1.2 kcal/mol if the hydrogens attached to N6 of adenine fall below the starting base-pair plane. The hydrogens attached to a negatively propellered G·C pair, by contrast, lie above the starting plane owing to the different placement of the amino group on the G·C pair. The energy decrease in the propeller-twisted G·C pair, −1.0 kcal/mol, is not quite as pronounced as that of the similarly deformed A·T pair.

The degree of nonplanarity in the derived base pairs, reported in Table 1 in terms of the exocyclic torsion angles described by relevant heavy atoms, agrees fairly well with the mean values found in ultra-high-resolution structures of double-helical B-DNA, although the signs of rotation in the lowest-energy base-paired structures differ from the X-ray observations. The computed out-of-plane displacement of the exocyclic nitrogens in free, unpaired bases typically exceeds that in the paired bases, but there are no crystal data to test this prediction. The predicted displacement of nitrogen, however, is intermediate between that detected in neutron-diffraction studies of related compounds (McMullan et al. 1980; Weber et al. 1980; Klooster et al. 1991) and that deduced from measurements of the direction of the infrared transition moments of adenine and cytosine (Dong and Miller 2002; Choi et al. 2005; see Supplementary materials for numerical values).

Table 1.

Comparative geometric features of complementary Watson–Crick base pairs in energy-optimized and high-resolution B-DNA crystal structures

  A·T G·C
Computation X-ray Computation X-ray
Base-pair parametersa
 Buckle −5.7 +1.5 (±5.6) +7.0 +4.6 (±6.6)
 Propeller −3.6 −13.8 (±5.4) −7.3 − 8.7 (±5.9)
 Opening +0.3 +2.3 (±4.2) −1.7 −0.1 (±3.0)
 Shear +0.03 +0.06 (±0.31) −0.20 −0.18 (±0.20)
 Stretch −0.08 −0.12 (±0.14) −0.08 −0.14 (±0.14)
 Stagger +0.10 +0.06 (±0.21) +0.04 +0.15 (±0.25)
Virtual inter-base parametersb
 d C1′··· C1′ 10.54 10.47 (±0.22) 10.72 10.62 (±0.17)
 λ Y 56.1 55.5 (±3.4) 55.2 55.2 (±2.2)
 λ R 55.7 55.9 (±2.7) 54.0 54.8 (±2.7)
Hydrogen-bond lengths
 C2–H···O2 3.60 3.54 (±0.21) – –
 N1···H–N3 2.87 2.83 (±0.13) – –
 N6–H···O4 2.99 3.04 (±0.17) – –
 N2–H···O2 – – 2.96 2.81 (±0.14)
 N1–H···N3 – – 2.97 2.90 (±0.11)
 O6···H–N4 – – 2.85 2.92 (±0.16)
Exocyclic torsionsc
 Adenine
  C4–C5–C6–N6 −178.1 (+178.0) 177.3 (±2.2) – –
  C2–N1–C6–N6 +178.1 (−178.1) −178.1 (±1.3) – –
 Guanine
  C6–N1–C2–N2 – – +176.2 (−176.3) −179.9 (±1.6)
  C4–N3–C2–N2 – – −175.9 (+176.0) 178.6 (±2.2)
 Cytosine
  C2–N3–C4–N4 – – −179.8 (+179.8) −178.9 (±2.5)
  C6–C5–C4–N4 – – −179.7 (+179.7) 178.9 (±2.3)
Open in a new tab

Predicted structures obtained from calculations based on second-order Møller–Plesset perturbation theory within the Gaussian 98 and Gaussian 03 suites of programs (Frisch et al. 2001; Frisch et al. 2003). Except where noted, X-ray data are based on the analysis, within 3DNA (Lu and Olson 2003), of (181 A·T and 168 G·C) Watson–Crick base pairs in 78 B-DNA crystal structures of 2.0 Å or better resolution without chemical modification, mismatches, drugs, or proteins from the Nucleic Acid Database (Berman et al. 1992). “Weak” C–H···O distances taken from 181 A·T pairs in 58 structures. Mean values and standard deviations (subscripted values in parentheses) exclude chemically modified bases, terminal and penultimate base pairs, side groups attached to nicked backbone strands, and base pairs that stacked against modified or mispaired 3′- and 5′-nucleotides. All angles expressed in degrees and distances in Ångstrom units

aSee schematic illustrations in Fig. 4 for parameter definitions. Values given here for purine·pyrimidine (A·T and G·C) pairs are identical to those of the corresponding pyrimidine·purine (T·A and C·G) pairs, except that buckle and shear are of the opposite sign

bVirtual angles λ Y = ∠N1(Y)–C1′(Y)···C1′(R) and λ R = ∠N9(R)–C1′(R)···C1′(Y) describe the pivoting of complementary bases in the base-pair plane (Fig. 1). Virtual distance d C1′··· C1′ measures base-pair width

cPredicted torsions in parentheses correspond to base pairs in a secondary, higher energy minimum with positive propeller twist. Observations come from analyses of the specified paired base in ultra-high-resolution (0.99 Å or better resolution) B-DNA crystal structures: 27 A·T pairs from 16 structures and 36 G·C pairs from 15 structures

The predicted propeller twisting of the Watson–Crick base pairs, however, is less pronounced than that found in well-resolved X-ray structures, particularly for A·T pairs (Table 1). In addition to the standard rationalization of DNA melting properties in terms of the number of hydrogen bonds in A·T vs. G·C base pairs, the calculations suggest that there may be a built-in, sequence-dependent pressure for AT-rich DNA to disassemble more easily than GC-rich DNA. That is, the intrinsic structure of the free A·T base pair appears to be more significantly compromised than that of the free G·C pair in duplex DNA. On the other hand, the conformational stiffness of so-called DNA A-tracts, i.e., short stretches of four to six consecutive A·T base pairs, is often attributed to the bifurcated hydrogen bonding made possible by stacks of highly propeller-twisted A·T pairs (Nelson et al. 1987; Chan et al. 1993). Such hydrogen-bond stabilization occurs as well in overtwisted CA·TG dimer steps (Timsit 1999), which are known to be highly deformable (Olson et al. 1998).

Sequence-dependent structure and deformation

The energy-optimized Watson–Crick base pairs show many of the same subtle, sequence-dependent conformational features found in high-resolution DNA structures (Table 1). For example, the G·C pair opens in the opposite sense from the A·T pair, concomitantly shortening, straightening, and presumably strengthening the G(O6)···C(H41)–C(N4) interaction compared to the A(N6)–A(H61)···T(O4) hydrogen bond formed at the corresponding major-groove location on A·T. The former interaction also appears to be stronger, in terms of its more nearly ideal geometry, than the G(N2)–G(H21)···C(O2) hydrogen bond located on the minor-groove side of the G·C pair. The stronger hydrogen bond contributes, in turn, to the strong G·C dipole noted above.

The predicted base-pair structures account as well for gas-phase measurements. For example, the angle between the planes of paired adenine and thymine, which can be extracted from the buckle and propeller angles, is remarkably similar to the dihedral angle estimated from the measured moments of inertia of 2-aminopyridine·2-pyridone, an analog of the A·T base pair, in the gas phase, i.e., 6.7° predicted vs. 6.1° found experimentally (Roscioli and Pratt 2003). The predicted length of the A(N1)···T(H3)–T(N3) hydrogen bond also closely matches the value found in the same experiment, i.e., 2.87 Å computed vs. 2.898 Å observed. The measured value of the A(N6)–A(H6)···T(O4) interaction, however, is less than that determined here, i.e., 2.81 Å observed vs. 2.99 Å computed (Roscioli and Pratt 2003).

The global motions of the base pairs, deduced from the low-frequency normal modes of the energy-minimized structures, also mimic the pattern of rigid-body variation observed in well-resolved structures (see Supplementary materials). That is, the buckling and propeller-twisting motions, seen to dominate the deformations of Watson–Crick base pairs in high-resolution protein-DNA structures, are of lower frequency (energy) than all other normal modes. The predicted movements of base pairs are described in Fig. 4 by a color-coded spectrum of normal modes dominated by fluctuations of one of the six complementary base-pair parameters. The least costly (lowest frequency) modes are softer than the torsional modes of the C1′ methyl groups (with frequencies of ∼50 cm−1). The stiffest rigid-body modes are comparable in frequency to the out-of-plane bending modes of individual bases (data not shown).

The buckling and propeller-twisting motions do not appreciably distort the hydrogen bonding of complementary bases and are relatively insensitive to base-pair composition. By contrast, the rigid-body deformations via more costly modes (opening, shear, or stretch), which have a greater effect on hydrogen-bond geometry, differ in A·T vs. G·C pairs. The A·T pair deforms via stretch or opening much more easily than the G·C pair in both solid-state examples and the computed model, presumably reflecting the cost of distorting three G·C vs. two A·T hydrogen bonds. Changes in shear are easier, however, for G·C than A·T, possibly taking advantage of shared/bifurcated hydrogen bonding that is possible in G·C but not A·T.

Electrostatic potential and base recognition

Images generated by color-coding biomolecular surfaces according to the electrostatic potential have become extremely valuable in obtaining qualitative information about preferred ligand (metal, drug, protein) binding sites and the degree of electrostatic complementarity between molecules involved in recognition and association processes (Honig and Nicholls 1995). Such is the case here for the isolated DNA bases and the Watson–Crick base pairs, which, although electronically neutral, have distinct, sequence-dependent electrostatic fingerprints (Figs. 2 and 3). The distribution of hydrogen-bonding donor and acceptor atoms on the edges of the heterocyclic species gives rise to well-defined patterns of positive and negative electrostatic potential and confirm many of the general trends suggested by the very first calculations of the electrostatic potential from approximate atomic charges (Pullman et al. 1979; Lavery and Pullman 1981; Weiner et al. 1982).

The absolute potentials of selected donor and acceptor atoms on the isolated bases and base pairs immersed in a simulated aqueous medium (see Supplementary materials) are fairly small because of the null net charges on these chemical species. Literature values of the electrostatic potentials (Pullman and Pullman 1981; Weiner et al. 1982; Fogolari et al. 2002; Hud and Plavec 2003), based on various distributions of molecular charge, are typically computed with a single low dielectric constant and thus of much greater magnitude. Published potential surfaces, based on two-dielectric Poisson–Boltzmann modeling of the DNA duplex and surrounding aqueous solvent, are of greater magnitude but of lower resolution than the current images. The earlier, more approximate surfaces, however, do not lend themselves to the quantitative descriptions of atomic surface potentials reported here.

The images and numerical data clearly show that (a) the minor-groove edge of the A·T pair is more electronegative than the major-groove edge, (b) the major-groove side of guanine is more electronegative than the minor-groove side, and (c) the major-groove edge of cytosine is highly electropositive. The negative electrostatic potential of the A·T minor groove presumably underlies the preferential binding of ions (Hud and Polak 2001) and small cationic molecules, such as netropsin and distamycin (Kopka et al. 1985), and the specificity of cationic amino-acid side groups, such as those in the bacteriophage 434 repressor protein (Mauro and Koudelka 2004), for such sites. The deeper major-groove potential of the G·C pair seemingly accounts for the well-known binding of small cations with the N7 and O6 atoms on the major-groove edge of guanine (McFail-Isom et al. 1999; Auffinger and Westhof 2000; Hud and Polak 2001; Egli 2002; Subirana and Soler-López 2003). The positive potential on cytosine forms the basis for the many close contacts of small inorganic anions with the C(N4) atom in nucleic-acid structures (Auffinger et al. 2004) and the frequent participation of the C(C5) atom in “weak” C–H···O hydrogen bonds with bound proteins (Mandel-Gutfreund et al. 1998). The anionic amino acids, aspartic acid and glutamic acid, have long been expected to bind to the amino groups on A and C (Suzuki 1994).

The conventional assignment of the same sets of partial charges to free and paired nucleic-acid bases ignores the neutralization of the electrostatic potential surface upon base-pair formation. The strength of the potentials on the Watson–Crick edges of the free bases ostensibly contributes to both base-pair formation and ligand-binding specificity. For example, the highly electronegative N3 of the unpaired, catalytically essential cytosine 75 of the hepatitis delta virus ribozyme acts as a general base, accepting a proton from the substrate 2′-OH during phosphate cleavage (Ke et al. 2004), and the exposed electropositive N1 (NH) and N2 (NH2) atoms of unpaired guanines often donate hydrogens to the anionic side-chain carboxyl of glutamic acid in protein-RNA structures (Kim et al. 2003), including the trp RNA-binding attenuation protein (Antson et al. 1999) and various tRNA synthetases (Yaremchuk et al. 2001) and in the structures of proteins complexed with small guanine-containing ligands (Nobeli et al. 2001).

Binding energies

In addition to reproducing high-resolution structural data, the calculations reviewed here account satisfactorily for many of the traditional physical benchmarks used to assess computational reliability. For example, the Watson–Crick binding energies match gas-phase observations, −13.0 kcal/mol for A·T and −21.0 kcal/mol for G·C (Yanson et al. 1979). The calculated values, −14.3 kcal/mol for A·T and −25.0 kcal/mol for G·C, however, exceed the recent findings of Jurecka and Hobza (−15.4 and −28.3 kcal/mol, respectively; Jurecka and Hobza 2003), who assert that their results represent the lower boundaries of the true stabilization energies.

Electronic structure and large-scale computation

The future promise of atomic-level simulations in deciphering the sequence-dependent properties of DNA rests on continuing improvements of the force fields that underlie the calculations. The configurations and charges of the Watson–Crick base pairs presented here account for general features in the next level of double-helical structure, i.e., the preferred arrangements of neighboring base pairs, but miss key sequence-dependent differences in intrinsic structure and deformability. Correct predictions include (a) the anisotropy of DNA bending, i.e., preferable deformation via roll as opposed to tilt, (b) the relative ease of bending compared to twisting, and (c) the preferential displacement of base pairs via shift and slide. The predicted sense of AA·TT vs. GG·CC deformation, however, is incorrect (see Supplementary materials).

The A·T base pair adopts a different, more highly propellered arrangement within double-helical structures that appears to contribute to the observed stiffness of AA·TT compared to GG·CC dimers. High-resolution DNA structures also reveal a sequence-dependent build-up of water molecules and amino-acid residues around the nucleic-acid bases (unpublished data). Approximation of these features through reduction of the base-pair charges contributes to the “A-philicity” of GG·CC compared to AA·TT steps (Ivanov and Minchenkova 1995), i.e., the tendency of the GG·CC dimer to assume positive roll angles that close the major groove and negative values of slide that displace the G·C pairs with respect to the double-helical axis and concomitantly deepen the major groove. Interestingly, previous calculations that successfully mimicked the tendencies of GG·CC dimers to adopt A-like conformational states treated the partial charges of base atoms with a less polar, albeit highly approximate Poltev charge set (Zhurkin et al. 1980) and approximated the intervening solvent with a sigmoidal, distance-dependent dielectric constant (Mazur et al. 1989). The appropriate balance of charge on the DNA bases, backbone, and surrounding chemical environment is the key to the correct prediction of DNA fine structure and interactions.

Electronic supplementary material

Below is the link to the electronic supplementary material.

ESM (416KB, doc)

(DOC 416 KB)

Acknowledgment

The U.S. Public Health Service (research grant GM20861 to WKO) and the National Science Foundation (Advance Fellows Award 0137961 to MOF) have generously supported this work. We thank Dr. Suse Broyde for helpful discussions and Mr. Mauricio Esguerra for the scripts used to extract files from structural databases.

References

  1. Antson AA, Dodson EJ, Dodson G, et al. Structure of the trp RNA-binding attenuation protein, TRAP, bound to RNA. Nature. 1999;401:235–242. doi: 10.1038/45730. [DOI] [PubMed] [Google Scholar]
  2. Auffinger P, Westhof E. Water and ion binding around RNA and DNA (C,G) oligomers. J Mol Biol. 2000;300:1113–1131. doi: 10.1006/jmbi.2000.3894. [DOI] [PubMed] [Google Scholar]
  3. Auffinger P, Bielecki L, Westhof E. Anion binding to nucleic acids. Structure. 2004;12:379–388. doi: 10.1016/j.str.2004.02.015. [DOI] [PubMed] [Google Scholar]
  4. Berman HM, Olson WK, Beveridge DL, et al. The nucleic acid database: a comprehensive relational database of three-dimensional structures of nucleic acids. Biophys J. 1992;63:751–759. doi: 10.1016/S0006-3495(92)81649-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Boschitsch AH, Fenley MO. Hybrid boundary element and finite difference method for solving the nonlinear Poisson–Boltzmann equation. J Comput Chem. 2004;25:935–955. doi: 10.1002/jcc.20000. [DOI] [PubMed] [Google Scholar]
  6. Boschitsch AH, Fenley MO, Zhou H-X. Fast boundary element method for the linear Poisson–Boltzmann equation. J Phys Chem B. 2002;106:2741–2754. doi: 10.1021/jp013607q. [DOI] [Google Scholar]
  7. Chan SS, Breslauer KJ, Austin RH, et al. The thermodynamics and pre-melting conformational changes of phased d(A)5 tracts. Biochemistry. 1993;32:11776–11784. doi: 10.1021/bi00095a005. [DOI] [PubMed] [Google Scholar]
  8. Choi MY, Dong F, Miller RE. Multiple tautomers of cytosine identified and characterized by infrared laser spectroscopy in helium nanodroplets: probing structure using vibrational transition moment angles. Philos Transact A Math Phys. Eng Sci. 2005;363:393–412. doi: 10.1098/rsta.2004.1499. [DOI] [PubMed] [Google Scholar]
  9. DeVoe H, Tinoco I., Jr The stability of helical polynucleotides: base contributions. J Mol Biol. 1962;4:500–517. doi: 10.1016/s0022-2836(62)80105-3. [DOI] [PubMed] [Google Scholar]
  10. Dong F, Miller RE. Vibrational transition moment angles in isolated biomolecules: a structural tool. Science. 2002;298:1227–1230. doi: 10.1126/science.1076947. [DOI] [PubMed] [Google Scholar]
  11. Egli M. DNA-cation interactions: quo vadis? Chem Biol. 2002;9:277–286. doi: 10.1016/S1074-5521(02)00116-3. [DOI] [PubMed] [Google Scholar]
  12. Fogolari F, Brigo A, Molinari H. The Poisson–Boltzmann equation for biomolecular electrostatics: a tool for structural biology. J Mol Recognit. 2002;15:377–392. doi: 10.1002/jmr.577. [DOI] [PubMed] [Google Scholar]
  13. Frisch MJ, Trucks GW, Schlegel HB, et al. Gaussian 98. Pittsburgh: Gaussian; 2001. [Google Scholar]
  14. Frisch MJ, Trucks GW, Schlegel HB, et al. Gaussian 03. Pittsburgh: Gaussian; 2003. [Google Scholar]
  15. Honig B, Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
  16. Hud NV, Polak M. DNA–cation interactions: the major and minor grooves are flexible ionophores. Curr Opin Struct Biol. 2001;11:293–301. doi: 10.1016/S0959-440X(00)00205-0. [DOI] [PubMed] [Google Scholar]
  17. Hud NV, Plavec J. A unified model for the origin of DNA sequence-directed curvature. Biopolymers. 2003;69:144–159. doi: 10.1002/bip.10364. [DOI] [PubMed] [Google Scholar]
  18. Ivanov VI, Minchenkova LE. The A-form of DNA: in search of biological role (a review) Mol Biol. 1995;28:780–788. [PubMed] [Google Scholar]
  19. Jurecka P, Hobza P. True stabilization energies for the optimal planar hydrogen-bonded and stacked structures of guanine···cytosine, adenine···thymine, and their 9- and 1-methyl derivatives: complete basis set calculations at the MP2 and CCSD(T) levels and comparison with experiment. J Am Chem Soc. 2003;125:15608–15613. doi: 10.1021/ja036611j. [DOI] [PubMed] [Google Scholar]
  20. Ke A, Zhou K, Ding F, et al. A conformational switch controls hepatitis delta virus ribozyme catalysis. Nature. 2004;429:201–205. doi: 10.1038/nature02522. [DOI] [PubMed] [Google Scholar]
  21. Kim H, Jeong E, Lee SW, et al. Computational analysis of hydrogen bonds in protein-RNA complexes for interaction patterns. FEBS Lett. 2003;552:231–239. doi: 10.1016/S0014-5793(03)00930-X. [DOI] [PubMed] [Google Scholar]
  22. Klooster WT, Ruble JR, Craven BM, et al. Structure and thermal vibrations of adenosine from neutron diffraction data at 123 K. Acta Crystallogr B. 1991;47:376–383. doi: 10.1107/S0108768190012903. [DOI] [PubMed] [Google Scholar]
  23. Komarov VM, Polozov RV. On the propeller structure of isolated Watson–Crick base pairs. Z Naturforsch. 1990;45c:1080. doi: 10.1515/znc-1990-9-1025. [DOI] [PubMed] [Google Scholar]
  24. Kopka ML, Yoon C, Goodsell D, et al. The molecular origin of DNA-drug specificity in netropsin and distamycin. Proc Natl Acad Sci U S A. 1985;82:1376–1380. doi: 10.1073/pnas.82.5.1376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lavery R, Pullman B. Molecular electrostatic potential on the surface envelopes of macromolecules: B-DNA. Int J Quantum Chem. 1981;20:259–272. doi: 10.1002/qua.560200123. [DOI] [Google Scholar]
  26. Levitt M. How many base-pairs per turn does DNA have in solution and in chromatin? Some theoretical calculations. Proc Natl Acad Sci U S A. 1978;75:640–644. doi: 10.1073/pnas.75.2.640. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lu X-J, Olson WK. 3DNA: a software package for the analysis, rebuilding, and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003;31:5108–5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lu X-J, Olson WK. 3DNA: a versatile, integrated software system for the analysis, rebuilding, and visualization of three-dimensional nucleic-acid structures. Nat Protocols. 2008;3:1213–1227. doi: 10.1038/nprot.2008.104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Mandel-Gutfreund Y, Margalit H, Jernigan RL, et al. A role for CH···O interactions in protein-DNA recognition. J Mol Biol. 1998;277:1129–1140. doi: 10.1006/jmbi.1998.1660. [DOI] [PubMed] [Google Scholar]
  30. Mauro SA, Koudelka GB. Monovalent cations regulate DNA sequence recognition by 434 repressor. J Mol Biol. 2004;340:445–457. doi: 10.1016/j.jmb.2004.04.065. [DOI] [PubMed] [Google Scholar]
  31. Mazur J, Sarai A, Jernigan RL. Sequence dependence of the B-A conformational transition of DNA. Biopolymers. 1989;28:1223–1233. doi: 10.1002/bip.360280704. [DOI] [PubMed] [Google Scholar]
  32. McFail-Isom L, Sines CC, Williams LD. DNA structure: cations in charge. Curr Opin Struct Biol. 1999;9:298–304. doi: 10.1016/S0959-440X(99)80040-2. [DOI] [PubMed] [Google Scholar]
  33. McMullan RK, Benci P, Craven BM. The neutron crystal structure of 9-methyladenine at 126 K. Acta Crystallogr B. 1980;36:1424–1430. doi: 10.1107/S0567740880006206. [DOI] [Google Scholar]
  34. Nelson HCM, Finch JT, Luisi BF, et al. The structure of an oligo(dA)-oligo(dT) tract and its biological implications. Nature. 1987;330:221–226. doi: 10.1038/330221a0. [DOI] [PubMed] [Google Scholar]
  35. Nobeli I, Laskowski RA, Valdar WSJ, et al. On the molecular discrimination between adenine and guanine by proteins. Nucleic Acids Res. 2001;29:4294–4309. doi: 10.1093/nar/29.21.4294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Olson WK, Gorin AA, Lu X-J, et al. DNA sequence-dependent deformability deduced from protein–DNA crystal complexes. Proc Natl Acad Sci U S A. 1998;95:11163–11168. doi: 10.1073/pnas.95.19.11163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Párkányi C, Boniface C, Aaron J-J, et al. Theoretical and experimental dipole moments of purines. Collect Czech Chem Commun. 2002;67:1109–1124. doi: 10.1135/cccc20021109. [DOI] [Google Scholar]
  38. Pullman A, Pullman B. Molecular electrostatic potential of the nucleic acids. Q Rev Biophys. 1981;14:289–380. doi: 10.1017/S0033583500002341. [DOI] [PubMed] [Google Scholar]
  39. Pullman B, Perahia D, Cauchy D. The molecular electrostatic potential of the B-DNA helix. VI. The regions of the base pairs in poly (dG·dC) and poly (dA·dT) Nucleic Acids Res. 1979;6:3821–3829. doi: 10.1093/nar/6.12.3821. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Roscioli JR, Pratt DW. Base pair analogs in the gas phase. Proc Natl Acad Sci U S A. 2003;100:13752–13754. doi: 10.1073/pnas.2333806100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Seeman NC, Rosenberg JM, Rich A. Sequence-specific recognition of double helical nucleic acids by proteins. Proc Natl Acad Sci U S A. 1976;73:804–808. doi: 10.1073/pnas.73.3.804. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Subirana JA, Soler-López M. Cations as hydrogen bond donors: a view of electrostatic interactions in DNA. Annu Rev Biophys Biomol Struct. 2003;32:27–45. doi: 10.1146/annurev.biophys.32.110601.141726. [DOI] [PubMed] [Google Scholar]
  43. Suzuki M. A framework for the DNA-protein recognition code of the probe helix in transcription factors: the chemical and stereochemical rules. Structure. 1994;2:317–326. doi: 10.1016/S0969-2126(00)00033-2. [DOI] [PubMed] [Google Scholar]
  44. Timsit Y. DNA structure and polymerase fidelity. J Mol Biol. 1999;293:835–853. doi: 10.1006/jmbi.1999.3199. [DOI] [PubMed] [Google Scholar]
  45. Weber HP, Craven BM, McMullan RK. The structure of deuterated cytosine monohydrate at 82 K by neutron diffraction. Acta Crystallogr B. 1980;36:645–649. doi: 10.1107/S0567740880003986. [DOI] [Google Scholar]
  46. Weiner PK, Langridge RL, Blaney JM, et al. Electrostatic potential molecular surfaces. Proc Natl Acad Sci U S A. 1982;79:3754–3758. doi: 10.1073/pnas.79.12.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yanson IK, Teplitsky AB, Sukhodub LF. Experimental studies of molecular interactions between nitrogen bases of nucleic acids. Biopolymers. 1979;18:1149–1170. doi: 10.1002/bip.1979.360180510. [DOI] [PubMed] [Google Scholar]
  48. Yaremchuk A, Tukalo M, Grotli M, et al. A succession of substrate induced conformational changes ensures the amino acid specificity of Thermus thermophilus prolyl-tRNA synthetase: comparison with histidyl-tRNA synthetase. J Mol Biol. 2001;309:989–1002. doi: 10.1006/jmbi.2001.4712. [DOI] [PubMed] [Google Scholar]
  49. Zhurkin VB, Poltev VI, Florent’ev VL. Atom–atom potential functions for conformational calculations of nucleic acids. Mol Biol USSR. 1980;14:1116–1130. [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ESM (416KB, doc)

(DOC 416 KB)

Articles from Biophysical Reviews are provided here courtesy of Springer

RESOURCES