Derivation of Ca²⁺ signals from puff properties reveals that pathway function is robust against cell variability but sensitive for control

Abstract

Ca²⁺ is a universal second messenger in eukaryotic cells transmitting information through sequences of concentration spikes. A prominent mechanism to generate these spikes involves Ca²⁺ release from the endoplasmic reticulum Ca²⁺ store via inositol 1,4,5-trisphosphate (IP₃)-sensitive channels. Puffs are elemental events of IP₃-induced Ca²⁺ release through single clusters of channels. Intracellular Ca²⁺ dynamics are a stochastic system, but a complete stochastic theory has not been developed yet. We formulate the theory in terms of interpuff interval and puff duration distributions because, unlike the properties of individual channels, they can be measured in vivo. Our theory reproduces the typical spectrum of Ca²⁺ signals like puffs, spiking, and bursting in analytically treatable test cases as well as in more realistic simulations. We find conditions for spiking and calculate interspike interval (ISI) distributions. Signal form, average ISI and ISI distributions depend sensitively on the details of cluster properties and their spatial arrangement. In contrast to that, the relation between the average and the standard deviation of ISIs does not depend on cluster properties and cluster arrangement and is robust with respect to cell variability. It is controlled by the global feedback processes in the Ca²⁺ signaling pathway (e.g., via IP₃-3-kinase or endoplasmic reticulum depletion). That relation is essential for pathway function because it ensures frequency encoding despite the randomness of ISIs and determines the maximal spike train information content. Hence, we find a division of tasks between global feedbacks and local cluster properties that guarantees robustness of function while maintaining sensitivity of control of the average ISI.

The calcium ion Ca²⁺ is an important second messenger that transmits information from the plasma membrane to cytosolic targets in eukaryotic cells. Most Ca²⁺ signals appear as repeated short-lived increases in the cytosolic Ca²⁺ concentration, [Ca²⁺], referred to as Ca²⁺ spikes. An important class of Ca²⁺ signals requires binding of inositol 1,4,5-trisphosphate (IP₃) to its receptor (IP₃R), which acts as a channel that releases Ca²⁺ from the endoplasmic reticulum into the cytosol. The open probability of the IP₃R increases with a moderate rise of the cytosolic [Ca²⁺] [Ca²⁺-induced Ca²⁺ release (CICR)] (1–4). IP₃Rs involved in Ca²⁺ signaling exist in clusters. Recent experiments indicate that IP₃ can induce clustering of IP₃Rs and that in most cases a cluster consists of 4 to 10 IP₃Rs (5, 6). Fluorescence imaging studies and model simulations reveal a cascade of events leading to a Ca²⁺ spike: Openings of single Ca²⁺ channels (blips) are followed by collective openings of channels in a cluster (puffs). Ca²⁺ from a puff diffusing to neighboring clusters can activate them by CICR, eventually leading to a global Ca²⁺ spike (7–10). Channels within a cluster are strongly coupled by Ca²⁺ diffusion, whereas coupling between clusters is weak because of steep concentration gradients (11, 12). In many cell types, the number of pacemaker clusters that induce cellular Ca²⁺ spikes is limited to fewer than 10 (13, 14).

Detailed analysis of interspike intervals (ISIs) in different cell types has shown that Ca²⁺ signals are stochastic spike sequences (15, 16). The stochasticity arises from fluctuations in the state of individual channels and does not average out, because channel clusters are only weakly coupled. It is generally assumed that the transmitted signal is frequency encoded (17–19). However, stochastic signals do not exhibit a well-defined frequency, so that information is rather encoded in the statistical properties of ISIs determined by their distribution (15, 20).

The elemental events of cellular Ca²⁺ signals are Ca²⁺ puffs. Consequently, we formulate the model directly in terms of the puff properties (see Fig. 1). That is the basic idea of the modeling concept that we are presenting here. The puff properties are given as distribution functions of puff duration and interpuff intervals (IPIs), which can be directly measured. The description in terms of distributions requires the formulation of the master equations as integro-differential equations. This approach circumvents state space explosion, in contrast to master equation formulations based on transition rates between individual channel states. We use the model to investigate conditions for spiking, robustness of pathway function, and the possible biological advantages of a stochastic mechanism over a deterministic one.

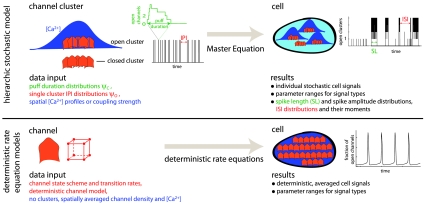
Fig. 1.

Summary of the modeling concept and comparison with traditional concepts. The stochastic hierarchic model takes advantage of the structural and functional hierarchy formed by channels, channel clusters, and the cell. It subsumes the dynamics of the lower structural level into waiting time distributions on the next higher one. Channels cause the IPI distribution ψ_o and puff duration distributions ψ_c of clusters, and clusters generate the ISI and spike length (SL) distributions on cell level. The waiting time distributions on cluster level can be measured in vivo. That circumvents the problems arising from using parameter values from in vitro experiments for cell simulations, as deterministic rate equation models usually do. The involvement of many channels is required for the validity of rate equation models, such that average deterministic dynamics apply. Therefore, they are based on the assumption of continuous channel densities neglecting channel clustering. The additional assumption of fast Ca²⁺ diffusion entails neglecting spatial gradients and a mathematical description of cell behavior by ordinary differential equations. But this is in contradiction to the steep concentration gradients occurring during Ca²⁺ release. See SI Text for details.

Results

Ca²⁺ spikes have been extensively investigated, but the relation between puff characteristics and cellular signals has not been established yet. What are the conditions for spiking in terms of puff characteristics and spatial cluster arrangement? Are typical spiking patterns, average ISI and the cell-type specific signaling determined by channel and cluster properties, or are they the result of emergent behavior of the complete pathway? We investigate what modeling can contribute to answering these questions in this section.

ISI Distributions Depend on the Details of Cluster Dynamics, Cluster Arrangement, and Concentration Dynamics.

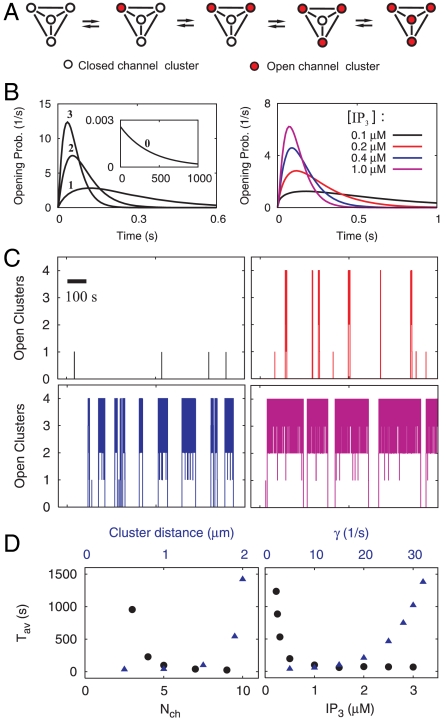
There is no clear separation between a cellular spike and local events. Nonetheless, in order to obtain a criterion for the occurrence of a global spike, we have chosen to call a release event a spike of cellular signaling if more than three-fourths of all clusters are open at the same time. Opening of fewer clusters defines a local event. Each spike starts with a puff. It can cause a global spike, if the probability that more clusters open before it closes is sufficiently large. The Ca²⁺ released by open clusters increases the propensity of other clusters to open. Fig. 2A shows a schematic representation of this spike generation mechanism for the example of a tetrahedral cluster geometry (compare Materials and Methods). The probability to open early increases with the number of open clusters N_o (Fig. 2B). This characterizes the properties of CICR.

Fig. 2.

Various patterns of Ca²⁺ signals can be inferred from properties of single clusters. (A) Configurations of open clusters (red) in the tetrahedral geometry. (B) Left: Waiting time distribution for the opening of a cluster in the rest state (0) and with N_o = 1, 2, or 3 clusters open. The probability to open early increases with N_o (number at lines). Because N_o determines [Ca²⁺], this corresponds to CICR. Right: Probability to open the second cluster at [IP₃] as indicated. It is very unlikely that the second cluster opens before the first one closes with small [IP₃]. (C) Stochastic simulations reveal different types of Ca²⁺ signals at various [IP₃]: only puffs (Upper Left), spiking (Upper Right), bursting (Lower Left), and overstimulation (Lower Right). The colors indicate [IP₃] as in B, p = 3.85 s^-1. (D) The average ISI T_av depends on many different parameters. Here, we show (Left) its dependence on the number of channels per cluster N_ch (black dots) and the cluster distance a (blue triangles), and (Right) its dependence on [IP₃] (black dots) and the channel closing rate γ (blue triangles). Parameter values not mentioned in this legend are given in Table 1.

The probability to open early increases also with [IP₃] (Fig. 2B). The signal types puffs, spikes, bursting, and overstimulation shown in Fig. 2C were obtained by varying [IP₃] (other parameters are given in Table 1). At low [IP₃], only puffs occur. Spikes can be found with slightly higher [IP₃]. Increasing [IP₃] further causes longer more frequent spikes and finally steady release at overstimulation. This spectrum of signal types and their sequence with increasing [IP₃] is in good agreement with experimental observations (4). Our model only considers puff properties characterized by duration and IPI distributions and spatial coupling mediated by Ca²⁺ diffusion. This means that the properties of these distribution functions are sufficient to generate a wide range of Ca²⁺ signals.

Table 1.

Standard parameter values

Parameter	Symbol	Value	Unit
Cluster distance	a	0.5–5	μm
Channels per cluster	Nch	5	—
IP3 concentration	[IP3]	1.0	μm
Base-level [Ca2+]	c0	0.03	μm
Puff rate	λ0	0.00755	s-1
Channel closing rate	γ	5–100	s-1
Ca2+ diffusion constant	D	220	μm2 s-1
Release current of the IP3R	ρ	0.2	pA
SERCA pumping rate	p	80	s-1

We are interested, in particular, in spike trains because of their function in signaling. Their average ISI T_av depends on the parameters of channel state dynamics and spatial coupling. Fig. 2D shows four dependencies. T_av decreases with increasing number of channels per cluster N_ch and [IP₃], because the cluster open probability is proportional to N_ch, and it also increases with [IP₃]. Another important parameter for the cluster dynamics is the channel closing rate γ. The larger γ, the sooner a cluster closes, and the less likely a second cluster opens before closing of the first cluster. Therefore, T_av increases with γ. T_av depends also on the buffer concentration, the channel current, and the sarco/endoplasmic reticulum Ca²⁺ATPase (SERCA) density (10). The IP₃-dependency and buffer dependency are experimentally verified (4, 15). The other parameters are difficult to measure, but the T_av dependencies comply with current ideas on IP₃R regulation by Ca²⁺ and IP₃ (3). T_av and the standard deviation of ISIs σ can also be modulated by changing the spatial arrangement of clusters (21).

With these sensitive dependencies of T_av on so many details and the usually observed cell variability even within one cell type, how can cells actually maintain the ability of spiking and frequency encoding at all? Many control processes converge on Ca²⁺ signaling (1–3). Why does their combined action not destroy the ability to spike rather than controlling it? These parameter dependencies also pose questions for typical properties: With T_av and signal forms depending so sensitively on parameters that vary greatly among cells of a single cell type, which features of Ca²⁺ spiking could actually characterize a pathway or cell type? We will see below that a property of the system, which we call functional robustness, suggests answers to these questions and that the relation between T_av and σ is pathway specific.

Conditions for Spiking and Bursting.

Global spikes are initiated by puffs. With the De Young–Keizer model at resting [Ca²⁺] c₀, puffs are generated by a process well described by a single puff rate λ₀ = λ₀([IP₃],N_ch,c₀). The average IPI of the cell is then T₀ = (N_clλ₀)^-1. The average ISI is proportional to T₀; i.e., , and does not depend on λ₀.

The transition between spiking and bursting is continuous, and we cannot define a sharp criterion separating spiking from bursting. Therefore, we consider a boundary for spiking toward large T_av and a boundary of bursting toward vanishing T_av; i.e., toward overstimulation. Because we are dealing with a stochastic system, short sojourns in the rest state happen even with overstimulation, and we define that regime by the condition T_av < 0.01T_sl, with T_sl being the average spike length. We limit spiking toward long T_av by a maximal average number of local events in-between two spikes, which should be a few tens. We choose .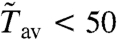

Ca²⁺ spikes result from a cascade of single cluster opening events, where, by Ca²⁺ diffusion, each open cluster enhances the opening probability of those still closed. This suggests spatial coupling to be a good indicator for spiking. In order to quantify spatial coupling, we define its strength as the probability C₁₂ that the first open cluster opens another one (see also Eq. 3). To obtain a value relating to coupling, we have to subtract the probability 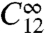that two uncoupled clusters very far apart open incidentally at the same time: . The channel closing rate γ is the most important parameter determining T_sl, rendering it also a good spike regime indicator.

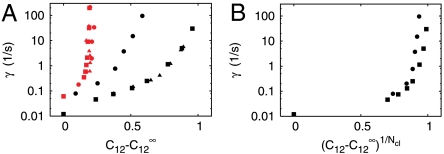
The ranges of γ and for which spiking occurs are shown in Fig. 3. We investigated spiking conditions with four clusters on a tetrahedron and eight clusters on a cube. The red symbols in Fig. 3 show the critical values for the long-T_av criterion C_l, and the black symbols show the values for the short-T_av criterion C_s. The C_l values with four and eight clusters are all quite close to each other. Spiking disappears for four clusters, eight clusters, and a large range of γ-values within a narrow range of coupling. It is so narrow because T_av increases steeply there with decreasing .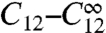

Fig. 3.

Conditions for spiking. (A) Spiking occurs for values of the coupling and the channel closing rate γ between the red and black symbols. They show the long-T_av criterion for spiking C_l (red) and the short-T_av criterion C_s (black), respectively (see Conditions for Spiking and Bursting). Coupling values smaller than C_l entail essentially only local puffs, and coupling values larger than C_s cause the regime of overstimulation. The spike range increases with γ. We investigated both the four-cluster model (squares) and the eight-cluster model (circles). C_l values are similar for both models, whereas C_s values depend on the number of clusters N_cl. The spike range becomes smaller for a larger number of clusters involved in spike nucleation. Each pair of squares and circles indicates the critical () at the standard parameters (Table 1), whereas coupling was changed by varying cluster distance (values range from 0.5 μm to ∞). The triangles show the critical values for the four-cluster model obtained when we varied 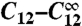by changing [IP₃]. That leads to very similar results. (B) The N_clth root of the short-T_av criterion C_s is shown. It suggests that C_s depends essentially exponentially on N_cl, because the N_clth root of C_s is similar for the four-cluster model (squares) and the eight-cluster model (circles).

The short-T_av criterion entails different C_s values for the four- and eight-cluster systems. C_s is smaller for eight clusters than for four clusters. The essential dependence on the number of clusters N_cl is exponential because the N_clth root of the critical values 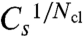is very similar for four and eight clusters (Fig. 3B). The experimentally relevant γ-values are about 60 s^-1 (6). Hence, about 0.8 is the short-T_av critical value for 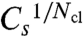, and about 0.18 is the long-T_av critical value C_l. Note that these values do not depend on how we change coupling. They are very similar whether we change the value of via [IP₃] or cluster distance. For γ > 1 s^-1, which includes the range of realistic values around 60 s^-1, we obtain very similar critical values even for different numbers of channels per cluster N_ch (SI Text). In this sense, 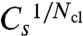and C_l are universal for the systems investigated here. We assume that this universality applies beyond these systems; how far has to be elucidated by future research.

Cell Type and Pathway-Related Properties: Relation Between Moments of ISI Distributions.

Because we are dealing with a stochastic system, it is not sufficient to consider average values only. We need to include higher moments of the ISI distribution in the description. The average ISI decreases upon stimulation. But the standard deviation also needs to decrease in order for a typical frequency to exist. That is warranted for Ca²⁺ spiking by the existence of a relation between the average ISI T_av and the standard deviation σ and its course from large σ and T_av to small σ and T_av. That relation is a property of the Ca²⁺ spiking mechanism. It does not exist for all spike-generating systems (see also SI Text).

Because the Ca²⁺ spike sequences are random, we also need to consider the conditions for their ability to transmit information. The maximal information content of a given spike sequence is a measure for how statistically different it is from the “most random sequence”; i.e., a pure Poisson process. If the maximal information content is larger than 0, downstream parts of the Ca²⁺ pathway have, in principle, the possibility to distinguish the given sequence from a Poisson process. That information content depends essentially only on the slope of the σ–T_av relation (20). The information content is larger than 0 for slopes smaller than 1 (20). Cells exhibiting stimulated spike trains have a smaller slope and larger maximal information content than spontaneously spiking cells (15, 20).

Hence, the existence of a σ–T_av relation, its course, and its slope are all essential for the function of Ca²⁺ spiking, and we will investigate them in detail below.

The σ–T_av relation has more useful properties. It also indicates the existence of feedbacks. As we will see below, a slope smaller than 1 results from negative feedback. Hence, simple spike train measurements with a group of cells can provide information on the pathway properties. Last but not least, the σ–T_av relation is a useful representation of experimental results with groups of cells of the same cell type. Typically, the spread of T_av values obtained from one sample of cells in a single experiment is large (15) because T_av depends on the details of cluster size, dynamics, and arrangement (Fig. 2D). The same applies to the relation between stimulation strength and spiking frequency. Both characteristics are strongly affected by cell variability, and therefore they are sample-specific to some degree. The σ–T_av relation does not have that drawback.

Clusters Determine T_av and σ but Do Not Shape the σ–T_av Relation.

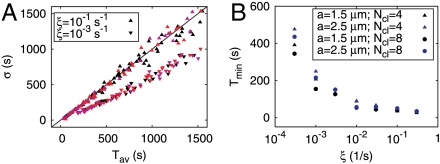
We calculated the σ–T_av relation analytically and by stochastic simulations, as described in SI Text. The σ–T_av relation is almost linear (Fig. 4A), as expected because of experimental observations (15). The minimal ISI T_min was determined as the smallest T_av observed in a set of simulations, which is a method close to the way T_min is obtained from experimental records. It is in the range of the average IPI of about 10 s for strong coupling at cluster distance a = 1.5 μm and about 80 s for weak coupling at a = 5 μm (Fig. 4B). This range is similar to values measured in astrocytes, microglia, processed lipoaspirate cells and HEK cells (15), SH-SY5Y cells (14), pancreatic acinar cells, and airway smooth muscle cells (22). Remarkably, we observe a T_min larger than 0 despite the fact that the theoretical ISI distributions do not exhibit absolute refractoriness.

Fig. 4.

Characteristics of the relation between average (T_av) and standard deviation (σ) of ISIs. The slope of the σ–T_av relation with constant rate for the first puff λ₀ is always 1. (A) Modification of the σ–T_av relation by the delayed puff rate given by Eq. 1. For moderate values of T_av, the slope of the σ–T_av relation decreases with ξ (upper triangles, ξ = 0.1 s^-1; lower triangles, ξ = 10^-3 s^-1). The relations are identical for the four-cluster model (black), the eight-cluster model (red), and the eight-cluster model with randomly shifted vertex positions (pink). (B) The minimal ISI T_min increases with decreasing ξ. T_min sets the deterministic part of the ISI, which accounts for the regular oscillations often observed in experiments with high stimulation (4, 15). Here, we show that T_min naturally occurs in a stochastic model. The four-cluster model has longer T_mins than the eight-cluster model. T_min has been identified with the smallest observed T_av in simulations.

Apart from a small range at small T_av, the slope of the σ–T_av relation is always 1 in the calculations presented until now. The model describes the properties of individual clusters and their coupling in its current state. It generates a slope equal to 1 for all parameter values in the spiking regime; i.e., the slope is robust with respect to changes of the values of the parameters. However, it was shown experimentally that the slope can be smaller than 1 even for large values of T_av (15).

Measured ISI distributions have been successfully described by the ansatz of a delayed exponential distribution (15, 20). It introduces a process of recovery from a global negative feedback upon a spike. The feedback is imposed on all clusters in contrast to coupling between clusters by Ca²⁺ diffusion, the spatial range of which is much shorter than the cell size. The global feedback might be depletion of the endoplasmic reticulum, a negative feedback from Ca²⁺ to [IP₃] via the Ca²⁺-dependence of IP₃-3-kinase (2, 23), or other feedbacks (24, 25) decreasing puff probability or amplitude. In order to be consistent with these experimental studies, we use the same description of recovery from global negative feedbacks here. We introduce it in our model as a slow rise of the opening probability for the first cluster opening from 0 just after a global spike to an asymptotic value λ₀ (see also SI Text):

[1]

with t_sp denoting the time of the last spike and ξ denoting the recovery rate. Fig. 4A shows that the slope of the σ–T_av relation decreases for decreasing values of ξ and that the nonlinear behavior at small T_av is more pronounced. We conclude that global negative feedback can change the slope of the σ–T_av relation, whereas properties of individual clusters and their coupling cannot. Slopes smaller than 1 are a result of emergent behavior; in other words, a property of the whole pathway but not a consequence of properties of individual clusters.

The σ–T_av relation is robust against a wide range of changes of the values of parameters describing the properties of clusters, their spatial arrangement, and the coupling strength, like γ, λ₀, cluster distance, position of clusters, number of clusters, number of channels per cluster, and buffer concentration (see Fig. 4 and ref. 21). These parameters do not determine the relation. Varying their values does not change the curve describing the dependence of σ on T_av. But they determine T_av, as we have seen above. Hence, they determine the position of a cell on the σ–T_av relation and can be used to control the average spiking frequency.

If the position on the σ–T_av relation of the cell without stimulation is at large or infinitely large T_av, it can move to smaller T_av by stimulation or by other means like rearranging channels and clusters. Indeed, clustering in cells is a dynamic process (5, 26–28). During this control of spiking, the positive slope of the σ–T_av relation and the existence of the minimal ISI guarantee that faster spiking is also more regular despite the stochastic character of spike generation.

The minimal ISI T_min is another property of the σ–T_av relation affected by the global recovery process (Fig. 4B). It increases with decreasing recovery rate ξ.

Discussion

We have developed a theory that is able to calculate the characteristics of cellular Ca²⁺ signals from puff property distribution functions, cluster arrangement, and—if it applies—an additional description of a global feedback process. We find that the pathway function of frequency encoding and information transmission is robust with respect to cell variability despite the sensitivity of ISIs to all cellular details. That robustness of function arises from the robustness of the relation between moments of ISI distributions; i.e., is specific to stochastic systems. This strongly suggests that one of the biological functions of stochasticity is to render Ca²⁺ signaling functionally robust. The functional robustness is closely related to the convergence of control by many biological parameters onto a few distribution parameters, and both can be imagined as arising from the time scale separation between IPIs and ISIs (see below).

The robustness of function is compatible with control of signaling, because T_av and the signal type depend sensitively on channel properties, cluster arrangement, buffering conditions, and other details. Control is possible because it is not specific values of the average ISI but pathway function that is robust against cell variability. Control of T_av shifts the cell’s position on the σ–T_av relation. Because it obeys that relation, stimulated spike trains will be as regular as possible and will exhibit a typical frequency. And as long as a slope smaller than 1 is maintained, spike trains can transmit information by frequency encoding (20). Therefore, robustness of the σ–T_av relation biologically means robustness of these two functionally important properties. Thus, the pathway meets the requirement of robustness against cell variability and component tolerances necessary for biological networks (29). This functional robustness is not the result of feedback and control, but it is a property of the stochastic spike generation mechanism.

In mathematical terms, functional robustness is independence of the σ–T_av relation from parameters, which vary between individual cells of the same cell type. Which mathematical structure causes this independence? By the calculations presented here and in experiments (15), we found that ISI distributions can be described by two or three parameters; e.g., P_ISI(T_av,ξ). The few distribution parameters are controlled by many biological parameters like [IP₃], cluster distance, channel state transition rates, etc. That is an enormous reduction of complexity, because all biological feedbacks and control circuits converge on only two distribution parameters.

Our findings imply that the cluster parameters do not control the recovery rate ξ. Consequently, the relation σ(T_av,ξ) does not depend on the cluster parameters, because the recovery rate ξ does not depend on them. It is robust against changes of these parameters. We established robustness with respect to buffer concentration and stimulation also experimentally (15, 20). Our calculations here and simulations (21) suggest that σ(T_av,ξ) is also robust with respect to changes of the number of channels per cluster, the channel closing rate, the spatial arrangement of clusters, and the pump rate. They change T_av and σ, but they do not change the relation between them. These theoretical results are strongly supported by a comparison of the experimentally determined individual relation with the population relation. The individual relation is obtained by analyzing two different experiments with the same cell, and the population relation from data from many cells. The slope of the individual σ–T_av relation is essentially the same as the slope of the population relation within one cell type (20), whereas the same group of cells exhibits a wide range of average ISIs. The differences between individual cells of the same cell type affect T_av but not the relation σ(T_av,ξ) (see also SI Text).

The slope of the relation, and therefore the maximal information content of spike sequences, is determined by the global recovery rate ξ. There is a variety of Ca²⁺ signaling pathways. They differ in the feedback upon a Ca²⁺ spike (i.e., with respect to the value of ξ), which agrees with the experimental finding that the recovery rate ξ is cell-type specific (15). The feedback could be store depletion, degradation of IP₃, phosphorylation of the IP₃R, etc. (see refs. 24 and 25 for reviews). Because the pathways determine the feedback and the recovery process, they also determine how much information can be transmitted by the ISI sequence. Hence, cells can tune spiking to the intracellular target of the Ca²⁺ signal by adjusting negative feedback. Pathways including it can control targets requiring more regular spiking; pathways without negative feedback are more eligible for targets with weak frequency dependency. In this study, we describe recovery from negative feedback in its most simple form only. We expect nonlinear recovery dynamics to lead to qualitatively similar σ–T_av relations (30).

We gain a mechanistic understanding of functional robustness by considering time scales. The ISI distribution is determined by the probability for a puff to set off a wave. Because not every puff starts a wave, IPIs are shorter than ISIs. Cluster properties and the whole complexity of channel state dynamics determine the IPI and the time course of a puff, but only the statistics of the occurrence of many puffs on longer time scales shape the ISI distribution and the σ–T_av relation. Distributions generated that way are often simple; i.e., are described by a few parameters only (31). That is also illustrated by examples from other signaling systems, cell mechanics, or gradient and quorum sensing (32–37). Because ISIs are the sum of several IPIs, the simplicity of the ISI distribution may arise from the central limit theorem. If one of the distribution parameters does not depend on some biological parameters, relations between moments of the distribution are functionally robust with respect to this group of biological parameters.

Our theory is formulated in terms of measurable quantities. The cluster closing time distribution has been measured in vivo (6). The dependence of the IPI distributions on [Ca²⁺] and [IP₃] has not been measured yet, but when this has been done, modeling will no longer need to rely on channel state models derived from patch clamp records for cellular models. That paves the road to realistic models of Ca²⁺ signaling pathways, which rely on in vivo data.

In addition to the experiments in refs. 15 and 20, the robustness of the σ–T_av relation can be tested pharmacologically by modifying elements of the local cluster dynamics like the activity of SERCA pumps or the phosphorylation state of the IP₃R. Our conclusion that the σ–T_av relation is sensitive to global feedbacks is supported by the experimental finding that the slope is cell-type specific (15). That could be further substantiated by experiments manipulating one of the many reported feedbacks from Ca²⁺ to IP₃R activity; e.g., via protein kinase C (25). Our findings also suggest investigating in detail how the Ca²⁺ signal is read by downstream parts of the pathway. Fluctuations of ISIs might be substantial in the range of frequencies relevant for Ca²⁺-controlled gene expression (15, 17, 38, 39). Because studies on frequency decoding used artificial regular signals (17, 38, 39), it is not known how frequency-sensitive processes respond to random sequences. In that context, it would be particularly interesting to investigate how the σ–T_av relation, the frequency sensitivity of the downstream parts of the pathway, and the decoding mode relate to each other.

What could be the reasons for a cell to prefer a stochastic mechanism for Ca²⁺ spiking over a deterministic one? A deterministic mechanism requires sufficient synchronization and large molecule numbers. The minimal error of such a mechanism decreases only with the quartic root of signaling events for arbitrarily complex feedback regulation (40). Is it worth the effort? The linear and robust σ–T_av relation of the stochastic mechanism (Fig. 4) implies a signal-to-noise ratio that is equal to or larger than the inverse of its slope, independent of the input signal (the IP₃ concentration). The signal-to-noise ratio can be controlled by a simple negative feedback. Such a well-defined and adaptive signal-to-noise ratio could be as effective as a more regular “deterministic” mechanism, but at much lower costs in terms of copy numbers of proteins; and the mechanism is robust with respect to cell variability. It seems that it suffices to be random.

Materials and Methods

The probability distribution densities for IPI ψ_o and puff duration ψ_c of individual clusters and a description of coupling of clusters by Ca²⁺ diffusion are the data input specifying the Ca²⁺ handling system of a cell. Changes in ψ_o by a [Ca²⁺] rise due to open clusters describe coupling. We call this modeling concept hierarchic stochastic model, because the random state transitions on one structural level specify the probability distributions for transitions on the next higher level (see Fig. 1) (41). We explain here only the basic assumptions entering the modeling concept. The complete theory can be found in SI Text.

Transition Probabilities.

Ca²⁺ channels form internally strongly coupled clusters. Each cluster has many states even if it comprises only a few channels. However, it is only relevant for the Ca²⁺ concentration dynamics whether a cluster releases Ca²⁺ or not. Therefore, we consider lumped cluster states. We lump all cluster states with at least one open channel into the state O and all the other states into C. The lumped state O corresponds to a puff. While the cluster is in O, it switches between individual open states including changes of the number of open channels. Similarly, it explores all its individual closed states while in C. The dynamics of the lumped states O and C can be described by the probability densities for the first transition to the other state; i.e., ψ_o(c,t - τ) for opening and ψ_c(t - τ) for closing. They depend on the time t - τ elapsed since the transition into the actual state at time τ. ψ_o also depends on [Ca²⁺] c at the cluster site; i.e., also on Ca²⁺ diffusing from open clusters toward other clusters. That provides for the spatial coupling. We compute the opening probability distribution ψ_o(c,t - τ) from the De Young–Keizer model, which is one of the standard models in the field (42, 43) (see SI Text for details). The closing time distribution can be derived from experimental results by Smith and Parker (6): They indicate that the individual channels in a cluster close independently with closing rate γ, which does not depend on [Ca²⁺]. Therefore, the cluster closing time distribution ψ_c(t - τ) is (31):

[2]

Ca²⁺ Diffusion.

The dynamics of the Ca²⁺ concentration can be described by a diffusion equation with point sources at the locations of open clusters, because clusters are small compared to the cell volume. Ca²⁺ pumps transport Ca²⁺ ions out of the cytosol into the endoplasmic reticulum with rate p (Table 1). Their spatial density is continuous. An open cluster causes a concentration rise in its vicinity and concentrations between 20 and 200 μM at the cluster itself. They decrease with gradients of two to three orders of magnitude per micrometer distance from the cluster (11, 12). The large local concentrations at the open cluster feed back to the channel state dynamics. They fluctuate with the number of open channels in the cluster. These fluctuations are large at the open cluster itself. But they are much smaller in a typical distance to a neighboring cluster, because they are smoothed by diffusion (SI Text). They do not follow the fluctuations of the number of open channels in detail. Therefore, the concentration rise caused by open clusters at neighboring clusters can be well approximated by a constant rise lasting as long as the cluster is open. We describe it by the stationary spatial concentration profile corresponding to the average current ρ (Table 1) through an open cluster. An analytic expression for the diffusion profile is given in SI Text.

Spatial Coupling and Cluster Arrangement.

We defined the strength of spatial coupling by the probability for a transition from one to two open clusters in Results (this definition is further discussed in SI Text). That transition is governed by the probability C₁₂ that upon opening of the first cluster, a second cluster opens before the first cluster closes:

[3]

where the c_m, m > 1 are computed with only the first cluster open. The factors after the product sign assure that none of the other clusters opens before cluster m when calculating the opening probability of the mth cluster. C₁₂ can be measured directly by the pairwise correlation of puffs. However, although there are plenty of published examples of puff sequences (7, 14, 44), the systematic measurements of puff correlations are still missing. The spatial coupling depends on the geometrical arrangement of clusters and the diffusion characteristics of the cytosol. We use spatial arrangements of clusters on the vertices of a tetrahedron or cube. Our major reason for the choice of regular arrangements are their symmetries (see Fig. 2A), which allow for the analytic calculations shown in SI Text. We also simulated some irregular arrangements of eight clusters. The small numbers of clusters we are using here are justified in small cells like SH-SY5Y neuroblastoma cells, where on average four clusters participate in a Ca²⁺ signal (14). They may also apply to pacemaker sites in other cells from which global signals nucleate and spread through the cell. As shown in Fig. 4, crucial results do not depend on the spatial arrangement of clusters because of the robustness properties of the σ–T_av relation, and simulations with more clusters and irregular arrangements produce very similar results (21).

We show in SI Text how a non-Markovian master equation for the probability of a configuration of open channels describing the cell state can be derived from these mathematical formulations of cluster properties. We obtain the ISI distribution of cellular signals, its moments, and parameter regions for signal types from these probabilities. We describe a fast stochastic simulation algorithm, and we derive the results analytically for regular cluster configurations.