Arginine Kinase. Joint Crystallographic & NMR RDC Analyses link Substrate-Associated Motions to Intrinsic Flexibility

Abstract

The phosphagen kinase family, including creatine and arginine kinases, catalyze the reversible transfer of a “high energy” phosphate between ATP and a phospho-guanidino substrate. They have become a model for the study of both substrate-induced conformational change and intrinsic protein dynamics. Prior crystallographic studies indicated large substrate-induced domain rotations, but differences among a recent set of arginine kinase structures was interpreted as a plastic deformation. Here, the structure of Limulus substrate-free arginine kinase is refined against high resolution crystallographic data and compared quantitatively with NMR chemical shifts and residual dipolar couplings (RDCs). This demonstrates the feasibility of this type of RDC analysis of proteins that are large by NMR standards (42 kDa), and illuminates the solution structure, free from crystal-packing constraints. Detailed comparison of the 1.7 Å resolution substrate-free crystal structure against the 1.2 Å transition state analog complex shows large substrate-induced domain motions which can be broken down into movements of smaller quasi-rigid bodies. The solution state structure of substrate-free arginine kinase is most consistent with an equilibrium of substrate-free and –bound structures, with the substrate-free form dominating, but with varying displacements of the quasi-rigid groups. Rigid-group rotations evident from the crystal structures are about axes previously associated with intrinsic millisecond dynamics using NMR relaxation dispersion. Thus, “substrate-induced” motions are along modes that are intrinsically flexible in the substrate-free enzyme, and likely involve some degree of conformational selection.

Introduction

Protein motions are intrinsically more difficult to study than their time-averaged structures, but as their potential relevance to function has come into light, the characterization of dynamics has become one of the central challenges in structural biochemistry ^{1; 2; 3; 4; 5; 6}. The notion of induced fit, introduced by Koshland ^{7; 8}, helped a generation understand how conformational changes, required for catalysis or needed in regulation, could be driven by specific substrate or ligand interactions. Implicit was the premise that such conformational changes were driven by the free energy of new substrate/ligand interactions. This premise has been questioned with increasing indications that, at least in some systems, the ligand might be more accurately represented as capturing or stabilizing one of the conformational variants sampled with intrinsic motions, even in the absence of ligand ^{9; 10; 11; 12}. In the emerging paradigm of conformational selection, binding of substrate/ligand is proposed to shift a pre-existing equilibrium in favor or a bound configuration. It is proposed to be at work in the substrate-associated conformational changes of a number of enzymes ^{9; 11; 13; 14; 15; 16}. For other enzymes, a more classical induced-fit mechanism is still considered to be more appropriate ¹⁷. Induced-fit and conformational selection represent the extremes on a continuum, where a mixture might be common ¹⁷. Selection of a particular conformation implies stabilization, presumably with energy coming from substrate/ligand association. It is also possible that selection of a conformation closer to the bound form is followed by an induced change that is driven by the energy of ligand-binding. There is very little understanding of how much of the substrate-associated conformational change exists intrinsically within an enzyme's ensemble of conformational variants.

Phosphagen kinases, such as creatine kinase, catalyze the reversible transfer of a phosphate between a phosphoguanidino substrate (such as phosphocreatine) and ADP to generate ATP ¹⁸. Phosphagen kinases function in cellular energy homeostasis, maintaining near constant levels of ATP in spite of transient fluctuations in demand. They have long been a model system for classical enzymology. Arginine kinase is usually a 42 kDa monomer in contrast to the dimeric or octameric forms of creatine kinase, and is chosen for its amenability to both x-ray crystallography and NMR spectroscopy. Structures first became available for creatine kinase in its “open” form, either substrate-free or with ADP bound ^{19; 20}, and then for the “closed” transition state analog form of arginine kinase ²¹ containing substrates arginine, ADP and a nitrate mimicking the trigonal-planar phosphate being transferred. Subsequently, transition state structures of creatine kinase ²² have become available, as have substrate-free structures of Limulus arginine kinase ^{23; 24}. These structures have revealed substantial conformational changes upon substrate binding that appear to be fundamentally similar throughout the enzyme family, and consistent with previously measured solution scattering ^{25; 26; 27; 28}. The conformational changes were characterized crystallographically as rotations inward by up to 18° of three quasi-rigid dynamic domains ²³. Dynamic domains are defined as groups of residues that are contiguous in 3D space (but not necessarily in linear sequence) whose displacement is predominantly rigid-group ^{29; 30}. It was proposed that the rigid group movements, together with the reordering of two flexible active site loops, not only moved amino acids into their catalytic configuration, but also excluded solvent from the active site (as proposed for other kinases), minimizing a wasteful hydrolytic side reaction ^{31; 32}.

Recently, structures of the distantly related Stichopus dimeric arginine kinase have been used to re-characterize the motion as an inward bending with the conformational changes occurring everywhere ²⁴. The structures were determined in substrate-free form and as a Michaelis-like complex with substrate arginine and analog AMPPNP at 1.75 and 2.45 Å resolutions respectively. The authors found little evidence of a rigid group rotation between Nand C-terminal domains, but did not report any attempt to sub-divide the C-terminal region as in the prior work ²³ (see also related comments ³³). Support for segmented rotation between quasi rigid groups in AK has come from NMR relaxation dispersion analysis. The sites of chemical exchange correlated approximately with the rigid group boundaries, indicating intrinsic flexibility (in the absence of substrates) roughly where the hinge points would be expected ³⁴. These experiments also revealed that the exchange rate for conformational changes in a flexible loop, and at the interface between the N- and C-terminal domains, was commensurate with enzyme turnover (~135 s⁻¹) ^{35; 36; 37}. This emphasizes the potential functional significance in that the protein conformational changes may be rate limiting on the enzyme.

In the work reported here, a crystallographic structure of substrate-free Limulus AK is extended to 1.7 Å resolution, so that comparison with the 1.2 Å resolution transition state analog structure can be used for a robust and detailed appraisal of the rigid-group approximation. Due to the size of AK (42 kDa), determination of the 3D structure of AK in solution by standard NMR methods is hard, so residual dipolar couplings (RDC), measured from weakly aligned protein and interpreted with the crystal structures (without the NOE information), is used to understand the solution structure ^{38; 39}.

Results & Discussion

Detailed analysis of the NMR results is based on the crystallographic structures, which are presented first. However, the NMR and crystallographic refinements proceeded in parallel, facilitating each other. In fact, it was greater consistency of the NMR chemical shifts for the substrate-free enzyme with the transition state analog crystal structure that motivated higher resolution refinement of the substrate-free crystal structure.

Crystallographic Structure Refinement

The current analysis extends the resolution of the substrate-free structure to 1.7 Å. Refinement statistics are presented in Table 1. Overall, the structure is similar to that refined at 2.4 Å resolution ²³; PDB id 1M80. A good indicator of model improvement is the decrease in the unrestrained C_α RMSD between A and B chains from 0.57 Å in the 2.4 Å structure to 0.36 Å here, a number consistent with the estimated overall coordinate error of ±0.23 Å.

Table 1.

Summary of diffraction data and refinement statistics

Space group	P21
Unit cell dimensions	a = 60.2 Å, b = 90.4 Å, c = 70.6 Å, β = 111°
Subunits per asymmetric unit	2
Resolution range (Å)a	27-1.73 (1.77-1.73)
Rmerge b	0.069 (0.517)
Completeness (%)	95 (98)
cRcryst	0.19 (0.26)
cRfree	0.24 (0.29)
RMSD bond lengths (Å) / RMSD bond angles (°)	0.005/0.856
No. protein atoms	5562
Wilson / Mean protein B-factor (Å2) (isotropic equivalent)	17.6 / 26.7
Estimated error (Max. likelihood, Å)	0.23

^aNumbers in parentheses are values in highest resolution shell

^bR_merge = Σ_hkl Σ_i | I_i(hkl) - <I(hkl)>|/Σ_hkl Σ_i I_i(hkl), where I_i(hkl) is the ith observation of a symmetry equivalent of reflection hkl.

Local improvements to the structure include the re-designation of residues 136-140, 192-197 and 289-292 as short α-helices, and of the extension of several secondary structural elements as hydrogen-bonding became clearer. Most noteworthy is the extension of a helix (previously residues 298-304) to now include 293-304. The prior tracing through weak density was incorrect, involving a local single-residue frame-shift error, and the higher resolution density showed the correct path clearly. All the changes improve the local agreement with the 1.2 Å transition state analog structure ⁴⁰. Thus, it is now apparent that there is not a partial unfolding of the 293-304 helix upon substrate-binding ²³. It is emphasized that even though the changes improve the local agreement of substrate-free and –bound structures, the overall difference between the two structures remains substantial at 2.9 Å (C_α RMSD), due to domain-sized rotations. However, improvement in the local consistency of the two structures, has allowed more precise analysis of the conformational changes (below).

Solution Structure by NMR Residual Dipolar Coupling

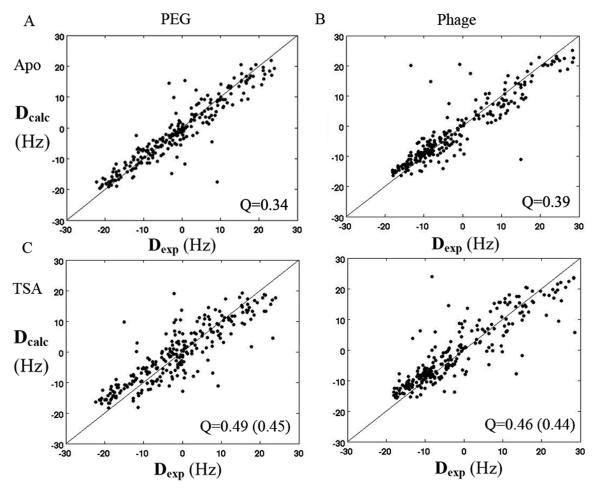
Two independent sets of RDCs of apo-AK were measured in polyethylene glycol-alkylether (PEG) and Pf1 Phage alignment media in solution by ¹⁵N-¹H TROSY & HSQC spectra (Figure 1). RDCs allow direct validation of a 3D-structural model of a protein. The two sets of RDCs were fit to the crystal structures of substrate-free AK (3M10) and the transition state (TSA) (1M15). Figure 2 shows the correlations between RDCs calculated from the substrate-free crystal structure (open form) and the experimental RDCs measured in PEG (A) and Pf1 phage (B). For comparison, Figure 2C and D show the RDCs calculated from TSA (closed form) ⁴⁰ vs. the experimental RDCs measured in PEG (C) and Pf1 phage (D).

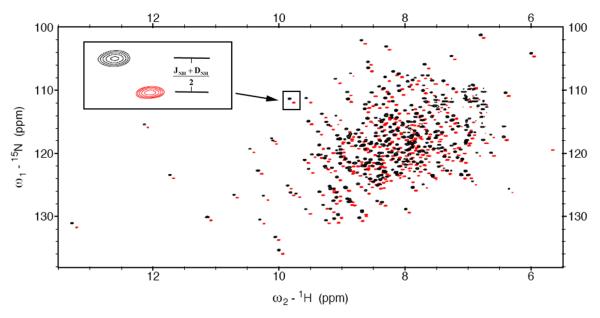
Figure 1.

Superposition of ¹⁵N-¹H TROSY (red) and HSQC (black) spectrum of substrate-free Arginine Kinase in 10 mg/ml Pf1 phage recoded at 800 MHz. The inset shows half of the one-bond ¹⁵N-¹H splittings (J_NH+D_NH)/2 were measured from the difference between ¹⁵N frequency in the TROSY and HSQC spectra.

Figure 2.

Correlation plot between the back-calculated ¹⁵N-¹H RDCs and the experimental RDCs of substrate-free AK from PEG (A, C) and Pf1 phage (B, D). For Panels A & B, the experimental RDCs were fit to the substrate-free crystal structure of AK (open form). For Panels C & D, the experimental RDCs were fit to the transition state crystal structure of AK (closed form). Parenthetical Q-values were calculated without loop 310-320, which is not visible in the substrate-free crystal structure.

The level of agreement between the experimental RDCs and the calculated RDCs is expressed in terms of a Q-value ³⁸. The substrate-free crystal structure yields significantly lower Q values (0.34 and 0.39), i.e. better agreement, than the transition state crystal structure (0.49 and 0.46) both for RDCs from PEG and Pf1 phage, which indicates that, following high resolution refinement, the substrate-free crystal structure is a better model for solution state substrate-free AK.

Crystallographic Analysis of Conformational Changes upon Substrate-Binding

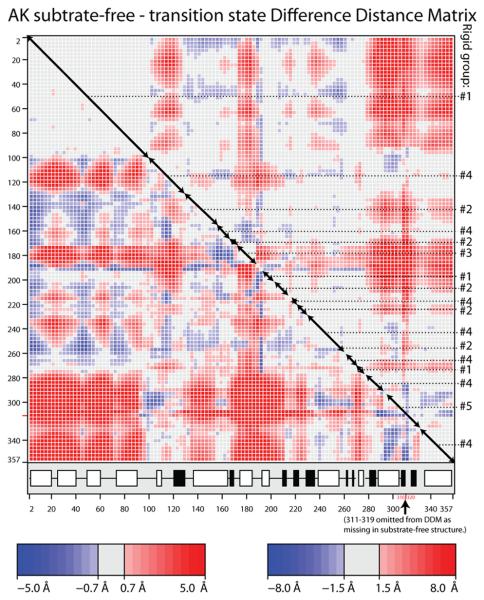
Regions with pseudo-rigid conformational transitions between substrate-free and transition state analog (TSA) crystal structures of arginine kinase were identified by analysis of the difference distance matrices (DDM) using the program ESCET ⁴¹. Quasi-rigid segments of the backbone can be recognized as blocks along the diagonal with consistently low values (grey in Figure 3). Qualitatively, there is good correspondence between our DDM for the Limulus TSA and one for the Stichopus AMPPNP·Arg·AK complex determined recently ²⁴. However, the higher precision Limulus structures give a cleaner DDM, from which it is clear that the conformational change is not an even plastic deformation as described for the Stichopus complex ²⁴. When the DDM is viewed with a high threshold (1.5 Å or 8 σ), it is apparent that the N-terminal domain of ~100 residues is the largest and most rigid of the blocks. It closes upon substrate-binding by ~12 Å relative to the C-terminal ~85 residues, as indicated by the intensely shaded regions in the bottom-left and top-right of the DDM (Figure 3). Within the middle ~200 residues, a series of blocks on the diagonal indicates segmented motions that the off-diagonal terms show are intermediate between the N- and C-terminal regions. One has to look at a lower threshold (0.7 Å or 3 σ) to see, in detail, how the C-terminal 260 residues are segmented into at least 12 diagonal blocks. These make sense only when one searches for combinations of non-contiguous segments of the sequence that behave like rigid groups (see below).

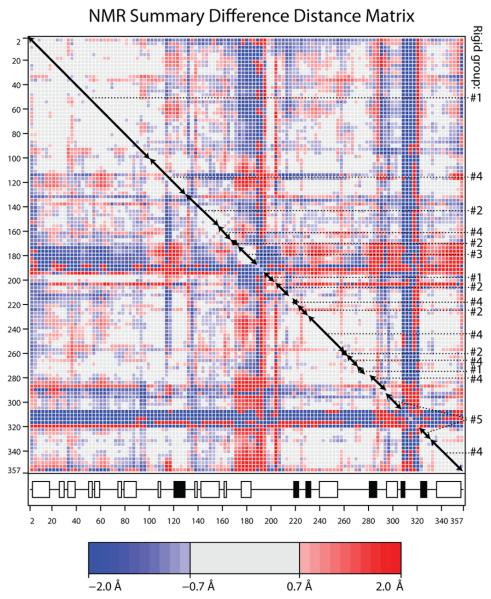
Figure 3.

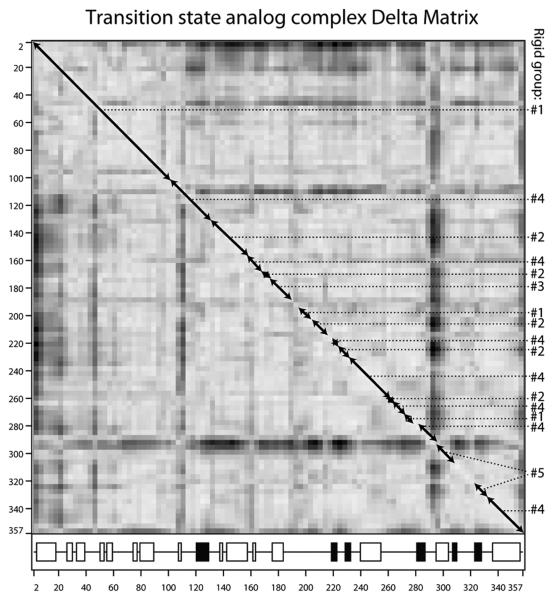
(A & B) Difference distance matrices for arginine kinase calculated with the program ESCET ⁴¹. The intensity of the color is proportional to the change in distance. Error weighting makes little difference, so Å-units are used rather than σ. Residue numbers are shown along the axes. The secondary structure is designated underneath with open boxes for α-helices and filled boxes for β-strands. Red pixels indicate residues that are closer in the transition state form than in the substrate-free form. There are more red regions than blue, because, overall, the enzyme closes upon substrate-binding. Segments of backbone that are moving as quasi-rigid groups will appear as mostly gray boxes along the diagonal. If disparate regions of the sequence have the same rigid transformation, the off-diagonal cross-terms will be close to zero (gray). Assignments to the consensus rigid groups (Error! Reference source not found.) are shown to the right of each panel. (A) Substrate-free minus the transition state analog complex structures (PDB ids 3M10 & 1M15 respectively). The top right half uses a high (1.5 Å) threshold to highlight features that are rigid in crude approximation. The bottom-left half reveals the intra-domain segment structure at lower threshold (0.7 Å). (B) Differences among the ensemble fit to the NMR data for the substrate-free enzyme. Unlike panel A that examined systematic differences between open and closed states, the NMR structures are distributed about an average, so there should be near equal positive (red) and negative (blue) terms. The amplitude of the intrinsic variation (B) is smaller than the amplitude of the substrate-induced change (A), so the DDM is less clear, but the distribution of rigid and flexible regions is similar to that in panel A. (C) Delta matrix calculated from the anisotropic individual B-factors of the 1.2 Å resolution structure of the transition state analog complex ⁴⁰; ⁴⁹. Darkness signifies deviation from Hirshfeld's rigid body postulate ⁴⁸ for the paired groups of atoms. Light regions indicate groups whose displacements are substantially rigid in the cryo-frozen structure: approximately residues 2-107; 112-286 & 300-353. This is in approximate agreement with the high-threshold difference distance matrix (panel A).

Both ESCET ⁴¹ and DynDom ⁴² were used to determine sets of residues that behaved as quasi-rigid bodies. The methods employ different algorithms. ESCET looks for near-zero off-diagonal regions in the DDM that indicate correlated displacement, while DynDom looks for regions in 3D space in which the residues from one structure map to the second with similar rotational transformations. Both methods favor five rigid bodies between which most of the residues of the structure are allocated. In spite of each method's sensitivity to input parameters, the two method have 79% agreement in the allocation of residues to each rigid group. About half of the remaining discrepancies involve choice in the exact boundary between rigid and flexible parts. The other discrepancies result from different sorting of backbone fragments into four rigid groups within the 257-residue C-terminal part. The challenge is apparent when the DDM is viewed at 3 σ or ± 0.7 Å. Near-zero cross-terms allow some of the fragments to be combined unambiguously, but for others the choice between two of the groups seems equally plausible, and the programs have not always made the same choice. In constructing a consensus designation (Table S1 & Table 2), locally, one or other solution, or a compromise, was chosen to minimize the fragmentation in sequence and 3D space.

Table 2.

Large rotations and small translations between the quasi-rigid groups in going from the substrate-free to transition state of arginine kinase. Residues are assigned according to the consensus designation. Transformations were calculated using the DomSelect program ⁴² and malign.py.

Rigid group (# residues)	Residues	1	2	3	4	5
1 (118)	2-102, 193-201, 269-276	Rotation:	10.9°	45.6°	21.1°	36.6°
		Translation:	0.32 Å	3.35 Å	0.20 Å	0.71 Å
		Movement (RMS):	2.7 Å	6.5 Å	7.5 Å	10.4 Å
		Closure:	96%	88%	91%	71%
2 (57)	129-155, 167-173, 202-213, 221-229, 258-259			36.4°	13.7°	31.1°
				1.29 Å	0.19 Å	0.42 Å
				3.4 Å	4.2 Å	8.4 Å
				100%	100%	99%
3 (14)	174-187				34.4°	44.4°
					4.1 Å	1.74 Å
					10.1 Å	13.8 Å
					48%	86%
4 (121)	103-128, 156-166, 216-220, 230-257, 260-268, 277-290, 330-357					18.0°
						0.47 Å
						2.9 Å
						100%
5 (28)	293-310, 320-329

The substrate-free and –bound structures differ by 2.9 Å (C_α RMSD) when superimposed as single rigid groups. When superimposed as the 5 rigid groups, the C_α RMSD drops to 0.7 Å. This is about twice the deviation between the chemically identical A & B chains of the substrate-free structure, so the rigid group approximation leaves some local changes unaccounted for. However, the decrease in RMSD from 2.9 to 0.7 Å corresponds to 94% of the mean-square deviation (variance), indicating that the rigid group designation is an excellent first order approximation for the actual conformational changes, especially considering that crystal packing interactions likely have some effect. The remaining 0.7 Å residual may also reflect uncertainties in the exact boundaries of the quasi-rigid groups. It also reflects the extent to which the actual structure bends gradually through hinge points, as opposed to the sharp transition implied in a rigid group approximation.

Rigid group rotations between the substrate-free and transition state structures are robustly determined and not sensitive to residual coordinate errors. When superimpositions of the transition state rigid groups to the A and B chains of the substrate-free form are compared, the directions of rotation axes have a maximum discrepancy of 13° (between groups 1 & 2) and a mean discrepancy of 5°. The average discrepancy in the magnitude of the rotations is only 2°.

The rotational component of the rigid-group transformations accounts for over 80% of the total movement between substrate-free and –bound forms. For group 3, up to half of the motion is translation, but for all other groups, rotation dominates (Table 2). The rotations are predominantly closure, except for group 3 which is more balanced in closure and twist components. Not only are the axes oriented consistently with closure (or opening), but the off-diagonal elements of the DDM show predominantly reductions of inter-group distances on substrate binding (Figure 3, below), consistent with physical closure.

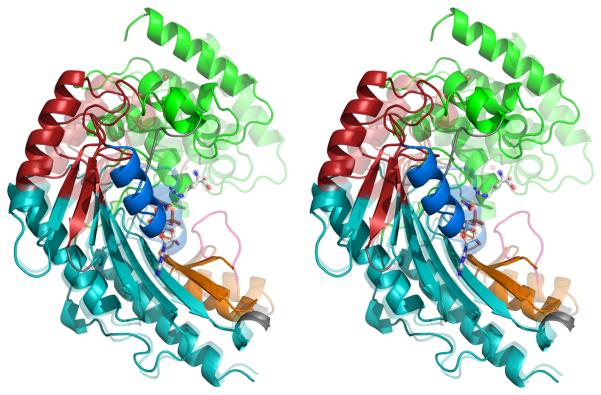
Several points are noteworthy about the quasi-rigid group interpretation of substrate-associated conformational changes: (1) When mapped to the 3-D structure (Figure 4), disparate regions of the sequence, grouped together by ESCET or DynDom, are brought into close proximity. One example is the grouping of loops 193-201 and 269-276 with the N-terminal domain (1-102) (green in Figure 4). (2) In the middle of the sequence, short stretches are alternately assigned to groups 2 and 4 (red & teal). The alternating segments correspond to opposite ends of the strands of the β-sheet which is divided by a hinge running diagonally across the strands (Figure 4A & B). Flexibility in a β-sheet might seem counter-intuitive, but supporting evidence will be provided below. (3) With the exception of group 3 (blue), the combined effect of the hinges (Figure 4B) is a segmented bending that brings rigid groups 1 and 5 (green & orange) towards each other. The inter-group rotation axes are not fully parallel, but constitute a spiral. (4) Relative to the transition state form, rotation of group 5 (orange) in the substrate-free form points the ends of flexible loop 311-319 away from the active site and towards exterior solvent (or crystal contacts). In the substrate-free form, the loop would form fewer intra-molecular interactions, explaining its apparent flexibility in both crystal and NMR structures (see below). In our substrate-free crystals, this puts the loop in contact with a neighboring molecule that is not related by lattice symmetry such that the two chains would have different configurations. Interactions with neighbors may account for the conformational diversity of this loop in the homologues where the structures can be resolved.

Figure 4.

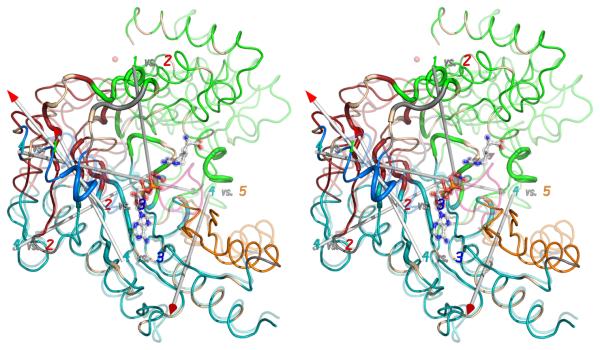
(A) The crystallographic structures of the open (substrate-free) form (opaque) and closed (transition state) form (transparent) have been superimposed within the largest rigid group (#4). Regions are colored according to the consensus rigid group designation: 1 – green; 2 – red; 3 – blue; 4 – teal; 5 – orange. Flexible regions are colored grey, except for the active site loop (311-319; pink) which is seen only when substrates (ball-&-stick) are bound. (B) Correlation of rigid-group hinge axes with sites of intrinsic dynamics. On top of the substrate-free (opaque) and transition state analog (translucent) structures are overlaid the axes of rotation between the different rigid groups. (With the exception of group 3, all of the transformations are predominantly rotations with small translational components.) Residues exhibiting NMR relaxation exchange, often indicative of local dynamics, were identified earlier ³⁴, and are highlighted here with a wider ribbon. Residues for which no determination was possible (missing or degenerate resonances) are colored light brown.

The largest displacement between substrate-free and substrate-bound forms is of group 5 (6.9 Å; orange) as it rotates 30° with respect to the rest of the protein. Relative to its immediate neighbor (group 4, teal), the rotation is 18° (Table 2), so the total rotation has contributions from the other inter-group hinges. Group 5 brackets the 311-319 flexible loop that is unseen in the substrate-free form, and therefore not part of any of the assigned groups. However, it likely plays a critical role in the transition state configuration of group 5, with interactions to both of the substrates: Thr₃₁₁ hydrogen-bonded to the ribose; Arg₃₀₉ salt-bridged to the α- and γ-phosphates; and Glu₃₁₄ having both a backbone hydrogen bond to the α-phosphate and side chain interactions with the substrate guanidinium.

It is when this is combined with the 17° rotation of the mostly N-terminal group 1, that the enzyme closure is achieved. The motions of groups 1 and 5 (green & orange) are mostly in opposite directions so that the 5.5 and 6.9 Å movements bring the groups 10.4 Å closer. The rotations of group 1 relative to 3-D neighbors, groups 2 and 4 (red & teal), and to group 3 (blue) are 11°, 21° and 37° respectively, so the effects of segmented rotation are once again apparent. There are several interactions that could stabilize the closed state. Residues 65 through 68, part of the substrate-specificity loop ^{43; 44}, hydrogen bond with the guanidinium substrate. The immediate neighbor of the specificity loop, and moving as part of group 1 (green), is the loop containing the active site Cys₂₇₁ that interacts with the substrate guanidinium ²¹.

The next most obvious change (Figure 4) is in group 3 (blue), containing the helix 174-185. One component of the motion is along the helix axis towards the active site, bringing His₁₈₅ into hydrogen-bonding distance with the substrate ribose. This motion helps to close the active site, but does not appear linked to other changes. There is also a swinging out of the N-terminal end of the helix that can be seen in Figure 4A and which seems to be coupled with the bending of the β-sheet (below).

It is groups 2 and 4 (red & teal) that form the core of the C-terminal domain. It is here that the newly refined structure has helped most in understanding the perhaps surprising flexing of the β-sheet spanning both groups. The rotation between groups 2 & 4 is 14° (a 4 Å movement, Table 2), and it is visible in Figure 4A where groups 4 (teal) have been superimposed, and groups 2 (red) are clearly rotated. From Figure 4A, it is difficult to distinguish a hinged motion between rigid groups from a gradual deformation through the sheet. The reality is likely to be neither one or other exclusively, but some combination. However, there is evidence that a hinged motion is a good first approximation. Firstly, the fitting of two rigid groups accounts for 4.2 of the 4.3 Å RMS deviation in the superimposed coordinates. The remaining residual of only 0.8 Å includes experimental error as well as the deviations from rigid behavior, which are therefore quite small. Later, evidence will be presented of intrinsic conformational variation at the residues at the interface of these rigid groups.

Comparison of the NMR solution structure to the crystal structures

Optimizations of atomic models against the NMR RDC and chemical shift observations were stable only with restraints to the crystallographic structures. The number of NMR observables is insufficient for independent analysis at amino acid level. However, insights are possible without explicit optimization of an atomic model (later), or through the fitting of an ensemble of explicit atomic models followed by analysis of the ensemble variance in ways that are not sensitive to the exact restraints employed. Distance-dependent matrices offer such an opportunity. While the overall magnitude of the terms depends on the strength of structural restraints to a crystallographic target, the spatial distribution of small and large terms shows where the NMR data indicate flexibility and deviation from the restraint target.

The DDM calculated from the NMR ensemble shows features that are strikingly similar to those calculated between the open (substrate-free) and closed (transition state) crystal structures (Figure 3). The magnitudes of the terms differ, due to differences between intrinsic (NMR) and induced (crystallographic) conformational changes, and due to the structural restraints used in NMR refinement. The signs (red/blue coloring) may also be inverted, because the DDM of an (NMR) ensemble is the average of all possible pair-wise comparisons where the reference structures of each pair are chosen consistently, but the program makes an implicit arbitrary choice whether the reference state of each pair is the more open or closed form. The NMR DDM clearly indicates that loops 170-196 and 307-320 are weakly restrained by the NMR data and/or the most flexible of the structure. This is fully consistent with atomic displacement parameters and disorder in the crystal structures, and prior NMR relaxation characterization of dynamics ³⁴. Even more noteworthy is the similarity of the NMR and crystallographic DDMs in their distribution of low-value (gray) blocks along the diagonal (Figure 3) which indicate that similar groups of residues are moving as quasi-rigid bodies.

NMR RDC analysis of rigid-group re-orientation

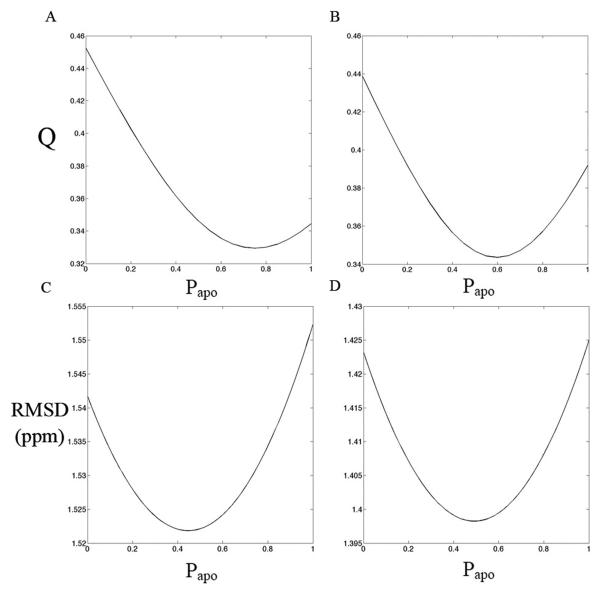
Figure 5 A and B show the variation of RDC Q-value with respect to populations of substrate-free (P_apo) and transition-state forms (1-P_apo) in a mixed model. (The mixed model is comprised of the crystallographic atomic structures that have not been optimized against the NMR data.) The lowest Q-values lie between those of the two crystal structures, indicating that the solution structure is intermediate between the substrate-free and transition state analog crystal structures. The optimum is closer to the substrate-free crystal structure. However, the variation in Q is very small, the optimal value being only 0.01 lower than that of the substrate-free crystal structure for the PEG RDCs, and 0.05 lower for the Pf1 phage RDCs.

Figure 5.

Q-values between the experimental RDCs from PEG (A) and phage (B) and RDCs calculated by assuming that the open (substrate-free) and closed (TSA) structures are rapidly inter-converting. Q-value vary with the populations of the substrate-free form, P_apo, and the transition state, 1-P_apo, used to build the model. The lowest Q values are found between the two crystal states. Panels C & D: the RMSD of experimental Cα and Cβ chemical shifts and the chemical shifts predicted from the two state model using Shiftx (C) and Sparta (D).

For the above mixed-model Q-value calculations, a two-state dynamic equilibrium was assumed. Previously reported NMR relaxation dispersion experiments had suggested intrinsic conformational exchange in substrate-free AK ³⁴. Thus, the calculations tested whether the deviation between solution-state NMR data and crystal structures resulted from conformational exchange between rapidly interconverting open and closed form structures. An alternative to a dynamic equilibrium would be an average static structure model. This was tested by calculating RDCs from the population-weighted average orientations of N-H vector orientations taken from the 2 crystal structures (see Methods). The static and dynamic equilibrium models yield very similar Q-values, which makes it impossible to differentiate, based on RDCs alone, between the two possibilities. To further explore the static vs. dynamic models, Cα and Cβ chemical shifts were predicted from the substrate-free and TSA crystal structures and compared with the experimental chemical shifts reported previously. Based on a two-state dynamic equilibrium model, the RMSDs between experimental and predicted Cα & Cβ chemical shifts were plotted against the population of the substrate-free crystal structure (P_apo) used in the model (Figure 5C & D). The optimal fit to the solution-state NMR data comes from a near-equal mixture of solution-state and TSA crystal structures, SHIFTX (Figure 5C) and SPARTA (Figure 5D) giving consistent results. The RMSD variations of the Cα and Cβ chemical shifts are remarkably small throughout the structure. The optimum in the chemical shift analysis (P_apo = 0.4 - 0.5) is somewhat lower than for the RDC analysis (P_apo = 0.6 - 0.8). Cα and Cβ chemical shifts are sensitive primarily to local secondary structure and less dependent on the orientations that are important in RDC analysis. The lower P_apo for chemical shift analysis may therefore reflect better consistency of the NMR data with the higher resolution secondary structure of the transition state crystal structure. Although there can be several reasons for differences between observed and modeled chemical shifts, they are mostly (5 of 8) at the same flexible sites in both TSA and substrate-free forms, either at sites undergoing NMR relaxation exchange ³⁴ or immediate neighbors. Although the changes in RDC Q-value vs. P_apo are modest, they are statistically significant. The excess of RDC observations (N ≈ 250) over model degrees of freedom (5 alignment tensor parameters plus a population parameter for the population-weighted model) makes even a small reduction in χ²-value (and hence Q-value) highly significant. The magnitudes of χ² indicates that differences between predicted and experimental RDCs cannot be explained by an estimated RDC error of ~ 1-2 Hz, and that the combination of residual coordinate error in the crystal structures, and systematic differences between the solution and crystalline structures translate into RDC changes that exceed the experimental error in RDC measurement.

At this point, it is fair to conclude that the solution structure is perturbed slightly from the substrate-free crystal structure, but there is no constraint that movement towards the transition state form need be uniform in all parts of the protein. Using the crystallographically-determined rigid-group assignments, Q-values were determined separately for each of the 5 rigid groups by individually fitting an alignment tensor to the RDC data. The level of agreement was expressed as Q^sub_,j for sub-domain j. For comparison, Q^part values for the 5 groups were also determined using single alignment tensors fit to the crystal structures of substrate-free or transition state forms as single rigid bodies (Table 3). All the Q^sub values turn out to be smaller than the corresponding Q^part values, supporting the applicability of this rigid group approximation to the solution state. Improved fitting of individual rigid groups indicates that the global conformation for the solution structure of AK deviates somewhat from both crystal structures. It is interesting that the Q^sub values of the TSA crystal structure are smaller than that of the substrate-free crystal structure except for rigid group 2 (57 residues) and rigid group 3 (14 residues). This indicates that in solution, even though overall the substrate-free crystal structure is a better match, the internal structures of the individual rigid groups are better matched by the TSA crystal structure, perhaps because the 1.2 Å TSA crystal structure is of higher precision. It is also interesting to note that the amount of improvement differs between the rigid groups, an indication that the rigid groups are re-oriented non-uniformly in the solution state, and that the solution state should be regarded as more than just a linear combination of the two crystal structures.

Table 3.

Q^sub_j values showing the agreement between experimental and calculated NMR RDCs for each rigid group (as shown in Table 3) using the substrate-free and transition state crystal structures. Each quasi-rigid group was assumed to have an independent alignment tensor during the RDC fitting. The parenthetical values (Q^part_j ) were calculated using a single alignment tensor for the whole structure.

Substrate-free			Transition state analog
Rigid group	PEG	Phage	PEG	Phage
1	0.38 (0.38)	0.35 (0.36)	0.35 (0.44)	0.33 (0.36)
2	0.16 (0.20)	0.20 (0.23)	0.21 (0.29)	0.21 (0.32)
3	0.37 (0.78)	0.19 (0.72)	0.22 (1.3)	0.37 (1.2)
4	0.33 (0.35)	0.47 (0.49)	0.29 (0.37)	0.26 (0.30)
5	0.35 (0.43)	0.31 (0.34)	0.28 (0.75)	0.31 (0.55)

Indications of Rigid-Group Displacements through Anisotropic Thermal Parameters

With a crystallographic structure of sufficiently high resolution (better than 1.2 Å), like the AK transition state structure ⁴⁰, anisotropic atomic displacement parameters can be refined providing a description for the direction of preferred displacements. For the lower resolution 1.7 Å substrate-free form, it is possible to refine parameters for the rigid translation, libration and screw-translation correlation (TLS) motions of assumed rigid groups ^{45; 46; 47}, which here are taken to be the quasi-rigid groups inferred from the substrate-associated conformational changes (Table 2). With the higher resolution ADP refinement of the transition state form, rigid groups do not need to be pre-defined, but can be inferred from the Delta Matrix (Figure 3C) ^{46; 48; 49}. Conceptually, interpretation is similar to the DDM (Figure 3A), regions approximating rigid bodies should have low values. However, close agreement should not be expected between the DDM and Delta matrix, because the former represents substrate-associated changes and the latter intrinsic disorder as constrained by the crystal lattice. Even though less detail is apparent (Figure 3), it is remarkable that the principal features of the DDM can be discerned in the Delta matrix with three quasi-rigid blocks. The first (residues 2-107) corresponds closely to rigid group 1. The last (residues ~300-353) includes most of rigid group 5 and some of 4. A middle block (residues ~112-286) combines most of rigid groups 2 – 4. Thus, the Delta matrix of the TSAC crystal structure provides a hint of intrinsic motions that are consistent with the substrate-associated domain closure.

Both high resolution ADP analysis for the transition state form, and TLS refinement for the substrate-free crystals provide descriptions of the directionality of rigid group displacements ^{46; 47}. Generally, the correlation is unimpressive between the principal axes of thermal displacement librations and either librations between NMR ensemble members, or crystallographically-observed substrate-associated group rotations. This is expected – coherent intra-molecular motions of functional interest are just one small component of crystallographic disorder ^{50; 51; 52}; crystal packing and experimental temperatures have disparate impacts; and the experiments probe motions in very different time-scales. The most impressive agreement is in the principal axes of librations for group 3, where variation between NMR ensemble members is aligned 9° and 36° from librations in the substrate-free and transition state crystal structures respectively. Group 3 undergoes a large (37°, blue in Figure 4) rotation upon substrate binding. It is also the most prominent region in the intrinsic millisecond dynamics probed by relaxation dispersion analysis ³⁴. Here we add that crystallographic and NMR RDC analyses provide consistent evidence of intrinsic dynamics in both the presence and absence of substrates.

Correlations with NMR Relaxation Dispersion Analysis

There is intriguingly good agreement when comparing the axes of rotation between rigid groups and the distribution of amino acids exhibiting NMR relaxation dispersion, indicative of millisecond-to-microsecond motions. The prior relaxation dispersion experiments had indicated that 35 residues, or roughly 10% of the enzyme, undergo microsecond-to-millisecond timescale dynamics in the absence of substrates³⁴. These residues cluster into four, distinct regions of the enzyme: (1) the interface and (2) the hinge between the N- and C-terminal domains; (3) a segment running through the middle of the C-terminal domain β-sheet; and (4) the loop spanning residues I182-G209. Assuming two-state exchange, summed forward and reverse exchange rates (k_ex) and minor state populations (p_B) had been determined collectively for all residues in any given cluster. For the interface, k_ex = 800 ± 100 s⁻¹ and p_B =1.1 ± 0.1%; for the inter-domain hinge, k_ex = 1930 ± 350 s⁻¹ and p_B = 0.4 ± 0.1%; for the β-sheet k_ex = 790 ± 70 s⁻¹ and p_B = 0.4 ± 0.1% for the β-sheet; and for the I182-G209 loop, k_ex = 790 ± 60 s⁻¹ and p_B = 2.6 ± 0.6%. The applicability of unified parameters for all residues in each cluster suggests, but does not prove, a concerted motion. Similar rate constants suggests that there may be some coupling between the clusters, but it was not possible to fit a single set of parameters to all clusters, suggesting that it is not a rigidly coupled, fully concerted global motion. (In passing, it is noted that the relaxation dispersion data indicate that in the absence of substrates, the low energy form, presumably an open comformation, dominates at > 97%.)

Returning to the current comparison of the substrate-free and transition state analog crystal structures, axes of rotation were calculated by C_α superposition for all possible pairs of the consensus rigid groups. With the exception of rigid group 3, which has a significant translational component (up to 4 Å), all of the motions are primarily rotational, predominantly (70-100%) closure rather than twist (Table 2), as evaluated by DomSelect ⁴². The rotation axes that relate neighboring rigid groups are overlaid upon the open and closed form structures in Figure 4B. Two nearly parallel axes near the group-3 helix (dark blue) can be thought of as the same - relating group 3 to its two neighboring groups. The other axes nearly intersect, forming a spiral through which the enzyme undergoes a segmented bending upon substrate-binding. Particularly unexpected is the axis between groups 1 & 4 that passes nearly in the plane of the β-sheet, orthogonal to its strands. This suggests that a hinge runs across the middle of the sheet, an observation that is unexpected, but supported by the NMR relaxation dispersion data (above).

First, some caveats should be noted. Firstly, the determination of hinge points is at best approximate ⁴², and is only as good as the underlying rigid-group assumption. Secondly, one would expect the group 1/4 rotation axis to be most reliable where the two groups come into contact (green & teal) than where they are separated by group 2 (red). Thirdly, the group 1/4 axis bisects the intersecting and nearly orthogonal 2/4 and 1/2 axes, meaning that apparent rotations in the 1/4 axis could approximate coordinated compound rotations of the 2/4 and 1/2 axes.

Notwithstanding these caveats, two observations lend credence to the hypothesis that the axes approximate real hinges. Firstly, all of the axes determined this way pass very close to the interfaces between rigid groups (colored differently in Figure 4B). Secondly, there is very strong spatial correlation between the rotation axes (hypothetical hinges) and residues that are observed by NMR relaxation dispersion as undergoing exchange in the milli- to micro-second regime (shown as thickened ribbon in Figure 4B) ³⁴. It is usually assumed that the underlying changes in NMR chemical shift are the result of local changes in conformation or in tertiary contacts. We now see that the vast majority of the residues exhibiting relaxation exchange are in close proximity to one of the rotation axes and/or are at an interface between rigid groups where contacts would be changing. Thus, the NMR relaxation dispersion provides independent experimental evidence that the residues close to the rotation axes are flexible and actually exhibit intrinsic dynamics.

In passing, it is noted that the only proposed hinge point where relaxation dynamics is not observed is between groups 5 and 4. It was within group 4, and the flexible loop (311-319) only crystallographically resolved in the transition state from, that fast (nano-/pico-second) internal dynamics were identified through NMR R₁/R₂/NOE measurements and Lipari-Szabo analysis³⁴. Thus, this region is also dynamic, but on a faster time-scale than accessible to the relaxation dispersion analysis.

Returning to the juxtaposition of rigid-group hinges and residues exhibiting relaxation exchange, four important conclusions can be drawn. Firstly, it is emphasized that the rigid-group analysis is based on crystallographic structures of substrate-free and –bound structures and thus pertains to substrate-associated changes. In contrast, the NMR data, obtained in the absence of substrates, pertains to intrinsic dynamics. This includes the prior NMR relaxation dispersion analysis implicating dynamic hinge points ³⁴, and the current NMR RDC analysis showing structural perturbation towards the substrate-bound form. The consistency of these different data supports the hypothesis that on binding substrates, at least some of the conformational change is achieved by selecting conformations that are part of an intrinsic dynamic equilibrium in the absence of substrates.

Secondly, nearly all of the residues exhibiting relaxation dynamics are close to inter-group rotation axes. This suggests that much of the total intrinsic (substrate-free) backbone dynamics at millisecond timescales might result from motions between quasi-rigid groups. In the earlier paper ³⁴, this was apparent for motions of the N-terminal domain. Now, particularly with the refined designations of groups 3 and 2, it appears more generally true.

Thirdly, there are multiple data pointing to the flexibility of the β-sheet. Both the 1/4 and 2/4 rotation axes run across the β-sheet nearly orthogonal to the strands, so rigid group motions apparently require flexibility the β-sheet. It is unexpected that a β-sheet, which one might anticipate to be relatively rigid, exhibits flexing central to the enzyme's conformational changes. In Figure 4A, it certainly appears as if the sheet bends substantially on substrate-binding. Furthermore, from Figure 4B we see that where both the 1/4 and 2/4 axes pass through the β-strands, local NMR relaxation dispersion provides evidence of intrinsic conformational dynamics. Much of the β-sheet falls between or near these two putative hinge axes, and much of it exhibits the relaxation dynamics. The extent to which the axes should be regarded literally as discrete hinges between segments of β-sheet, or as the best rigid-group approximation to a more evenly distributed flexing of the whole sheet, is not clear.

Fourthly, the relaxation dynamics established that the motions of at least some of the residues were commensurate with the enzyme turnover rate (even in the absence of substrates) and could potentially be rate-limiting ³⁴. Given the high correlation between the relaxation dynamics and the rigid-group analysis here, it is likely that the long-range conformational dynamics analyzed here is critically relevant to the enzyme's function.

Conclusion

High resolution refinement has improved the local consistency of the substrate-free crystal structure of AK with the 1.2 Å transition state analog form, enabling more precise determination of which parts of the molecule remain congruent in the two states. The application of two different algorithms gives an improved designation of five quasi-rigid groups whose transformation, predominantly closure rotations, can account for most of the differences between the substrate-free and -bound crystal structures. Thus, a rigid-group description offers an excellent first order approximation in the characterization of conformational changes.

Overall closure is achieved by segmented 11 - 18° rotations between groups 1 & 2, 2 & 4 and 4 & 5, where the groups are numbered from N- to C-termini. The groups contain non-contiguous and sometimes alternating regions of the linear sequence that come together in the 3-D structure. Newly apparent is the 14° rotation between groups 2 & 4 (red & teal in Figure 4) around one of two axes that (perhaps surprisingly) run across the β-sheet. Group 3 (blue), containing the helix 174-185 plus subsequent loop is newly recognized as a group rotating 40° about an independent axis. The loop is prominent in the NMR relaxation dispersion analysis of the substrate-free enzyme, indicating that it undergoes intrinsic motion as well as substrate-associated changes.

Comparison of the observed NMR RDCs with the two crystallographic models indicates that the solution state overall is most faithfully represented by a mixed population of the substrate-free and –bound crystal structures. The molar fractions of each remain an open question with the population of substrate-free form estimated as ~0.5 using chemical shifts, ~0.7 using RDCs (this paper) and > 0.97 by relaxation dispersion ³⁴. Each focuses on different characteristics of the structure, and its dynamics, and is subject to its own biases. RDCs and chemical shifts reflect conformational averaging in the pico-/milli-second time scales and give a consistent population (P_apo = 0.5 – 0.7). By contrast, relaxation dispersion reports on small populations of excited states in the low millisecond regime that might be different sub-states from those probed by RDC / chemical shift. Nevertheless, all three approaches support the qualitative conclusion that the solution structure contains elements of the substrate-bound form.

The solution state NMR RDCs provide evidence that the adoption of substrate-associated structural characteristics in the substrate-free solution state is not uniform throughout the structure: the use of independent alignment tensors for each rigid group markedly improves the fit of calculated and observed RDCs, but by different degrees.

The NMR RDC data do not indicate the degree to which the intermediate nature of the solution state represents a perturbation of a single structure, and/or a dynamic equilibrium between multiple states. However, the prior NMR relaxation dispersion data indicate that there is at least some intrinsic dynamic exchange ³⁴. Furthermore, spatial correlation between the sites of relaxation dispersion and the hinge axes inferred from the two crystal structures make a strong circumstantial case that the solution state represents, at least in part, a dynamic exchange between open and partially or substantially closed enzyme configurations.

Finally, it has been argued that for lid-closing enzymes that exclude solvent from the active site, conformational selection is insufficient, and that the energy of substrate-binding is needed to change the energy landscape and drive the conformational change ¹⁷. The phosphagen kinases are such lid-closing enzymes. The results here by no means rule out traditional induced fit in final loop closure, but emphasize that intrinsic dynamics, and possibly conformational selection, could also have important roles in the lid-closing paradigms of induced-fit.

Materials and Methods

Crystal Structure Determination for substrate-free AK

Protein expression, crystallization, diffraction data collection and molecular replacement structure determination are as described for the prior 2.4 Å resolution structure ²³; PDB id 1M80. In the prior work, serial transfer to a number of commonly used cryo-protectants had proved problematic, yielding only 3 Å diffraction. The 2.4 Å data had been obtained by using 26% PEG5000 MME as a joint crystallizing agent and cryo-protectant, avoiding changes upon serial transfer. When larger crystals were grown by macro-seeding, the PEG5000 MME was no longer sufficient to completely inhibit ice formation. The highest resolution data set (1.73 Å) was compromised by the presence of diffraction from cubic ice. The current analysis takes advantage of recently developed methods to integrate diffraction data in the presence of ice rings ⁵³.

Refinement was performed using Phenix ⁵⁴, alternated with interactive re-building using Coot ⁵⁵. Atomic displacement parameters (ADPs; B-factors) were modeled with anisotropic components coming from the translation, libration and screw (TLS) tensors ⁴⁵ initially fit to four rigid bodies per subunit, and with additional restrained individual isotropic atomic ADPs. The rigid groups were taken initially from Yousef et al. ²³. The test-set for the 1.7 Å refinement was selected as a super-set of that used for the 2.4 Å to avoid bias in cross-validation. The diffraction data and an atomic model were deposited with PDB id 3M15. Following analysis of the conformational differences between the newly refined substrate-free structure and the transition state analog form, the TLS rigid groups were adjusted and expanded to 5 per subunit, and the model was subject to an additional round of refinement. While this provided TLS parameters consistent with the rigid groupings described below, there was no further improvement in the refinement statistics.

Residual Dipolar Coupling & NMR Chemical Shift Analysis

Uniformly ¹⁵N and ²H enriched Limulus polyphemus arginine kinase was prepared as described previously ⁵⁶. The final NMR sample was concentrated to about 1 mM in a buffer containing 10 mM sodium citrate, 50 μM sodium azide, 90% H₂O, and 10% D₂O (pH 6.5). For Residual dipolar coupling (RDC) measurements, AK was aligned in two different alignment media: polyethylene glycol-alkylether (PEG) liquid crystalline medium (3% C12E5/hexanol at a molar ration r=0.85) ⁵⁷ and 10 mg/mL Pf1 phage ⁵⁸. Due to the large size of AK (42 kDa), the RDCs cannot be measured by the standard IPAP technique ⁵⁹, because of significant line broadening of the anti-TROSY component. Thus, RDCs were determined from the differences in peak positions of the ¹⁵N resonances measured in the anisotropic and isotropic samples using HSQC and TROSY spectra ⁶⁰. For the isotropic sample, the peak displacement is J_NH/2 whereas for the aligned sample it is (J_NH + D_NH)/2. Hence, their difference multiplied by 2 yields the desired dipolar couplings D_NH (Figure 1). Experiments were performed at 298K on a Bruker 800 MHz spectrometer equipped with a TCI cryoprobe. Chemical shift assignments for the apo state AK have been reported ⁵⁶.Spectra were processed by NMRPipe ⁶¹ and analyzed with SPARKY ⁶².

RDCs were fit to the substrate-free (open) & TSA (closed) crystal structures (PDB code: 3M10 & 1M15) via singular value decomposition ⁶³ using the MATLAB software. The calculation of the alignment tensor was initially performed with all the available residues, then the calculation was repeated for individual sub-domains.

The experimental RDCs were also fit to a two-state dynamic equilibrium model in which the open (substrate-free) and closed (TSA) structures are assumed to be rapidly inter-converting. The two X-ray structures (substrate-free and TSA) were aligned with respect to each other using the backbone Cα atoms and the backbone N-H bond unit vectors v=(x,y,z) were extracted from the two structures. The 6 bilinear terms <x²>, <y²>, <z²>, <xy>, <xz>, and <yz> are population averages ⁶⁴:

$$\begin{array}{cc}\hfill & \langle x^2\rangle =p_1\langle {x_1}^2\rangle +p_2\langle {x_2}^2\rangle ,\hfill \\ \hfill & \langle y^2\rangle =p_1\langle {y_1}^2\rangle +p_2\langle {y_2}^2\rangle ,\hfill \\ \hfill & \langle z^2\rangle =p_1\langle {z_1}^2\rangle +p_2\langle {z_2}^2\rangle ,\hfill \\ \hfill & \langle \mathit{xy}\rangle =p_1\langle x_1{y}_1\rangle +p_2\langle x_2{y}_2\rangle ,\hfill \\ \hfill & \langle \mathit{xz}\rangle =p_1\langle x_1{z}_1\rangle +p_2\langle x_2{z}_2\rangle ,\hfill \\ \hfill & \langle \mathit{yz}\rangle =p_1\langle y_1{z}_1\rangle +p_2\langle y_2{z}_2\rangle ,\hfill \end{array}$$ (Equation 1)

where p₁ = P_apo and p₂ = 1-P_apo.

A static average structure was also tested. In this model, a new set of N-H bond vectors <v> is built by population averaging the vectors extracted from the substrate-free and TSA crystal structures:

$$\begin{array}{cc}\hfill & \stackrel{-}{x}=p_1{x}_1+p_2{x}_2,\hfill \\ \hfill & \stackrel{-}{y}=p_1{y}_1+p_2{y}_2,\hfill \\ \hfill & \stackrel{-}{z}=p_1{z}_1+p_2{z}_2,\hfill \end{array}$$ (Equation 2)

where p₁ = P_apo and p₂ = 1-P_apo .

After normalization of the average vector orientations (x̄, ȳ, z̄) to unity, RDCs were fitted by systematically varying P_apo between 0 and 1 and the level of agreement between the experimental and calculated RDCs is expressed in terms of a Q value.

Experimental Cα and Cβ chemical shifts (δ_exp) were compared with the chemical shifts predicted from individual structures and the two-state model (δ_calc). Chemical shifts were predicted from substrate-free (${\delta }_{\mathit{calc}}^{\mathit{apo}}$) and transition state (${\delta }_{\mathit{calc}}^{\mathit{TSA}}$) crystal structure using SHIFTX 4.3 ⁶⁵ and SPARTA ⁶⁶. The two-state model was also used for back-calculation of an average chemical shift (assuming that the states exchange rapidly on the chemical shift time scale):

$${\delta }_{\mathit{calc}}=P_{\mathit{apo}}\times {\delta }_{\mathit{calc}}^{\mathit{apo}}+(1-P_{\mathit{apo}})\times {\delta }_{\mathit{calc}}^{\mathit{TSA}},$$ (Equation 3)

NMR Solution Structure Determination

The solution structure of substrate-free AK was determined by combining NMR RDC and chemical shift observations with restraints from the crystallographic structures. Due to the sparseness of the NMR observations, restraints from the crystallographic structures are necessary, but the resulting structures show bias in their detailed features. Therefore, the NMR ensemble (Figure S1) was analyzed only with regard to the distributions of flexible and rigid parts, which are independent of restraints to a particular structure. Restraints were of several forms. Local Cα-Cα distances (< 10 Å) were restrained within the range spanned by the substrate-free and transition state crystals and the Φ, ψ backbone torsion angles were weakly restrained toward the TSA structure. The effect of the dihedral angle constraints is primarily the conservation of secondary structure with minimal impact on the relative orientations of the subdomains. O-N hydrogen bond distance restraints were also used for conserved secondary structural elements. For the NMR restraints, two independent sets of backbone N-H RDCs from PEG and Pf1 phage were used in addition to the Cα, Cβ chemical shift restraints.

Structures were optimized using torsion angle dynamics, followed by Cartesian coordinate refinement, starting with either the transition state or substrate-free crystal structures. Simulated annealing and optimization were carried out using the IVM internal variable module within the molecular structure determination package of XPLOR-NIH ^{67; 68}. From an ensemble size of 50, the 25 best structures were used for further analysis.

Analysis of Conformational Changes

Conformational changes between the substrate-free and transition analog complex forms were analyzed first using difference distance matrices (DDM) calculated with the ESCET program ⁴¹. With high precision structures (estimated coordinate errors of 0.03 & 0.14 Å for 1M15 & 3M10 respectively ⁶⁹), and large conformational changes (up to ~15 Å), initial analysis was at the 8 σ level, corresponding to differences of 1.25 Å. Quasi-rigid groups were identified two ways. One was through clustering of near-zero terms in the DDM (< 8 σ or < 1.25 Å) using ESCET ⁴¹. DynDom ⁴² was also used to find clusters of residues that mapped from one structure to another with similar rotations (window ≥ 11 residues; interdomain fluctuation / intradomain fluctuation ≥ 1.0). The designation was somewhat sensitive to the choice of parameters, but good consistency was obtained between DynDom, ESCET and the sub-8σ regions of the DDM. Both programs found 5 quasi-rigid groups, and there was 79% agreement in the residues allocated to each. Discrepancies were of two types. About half were differences in the exact boundaries between rigid and flexible regions and are unlikely to be of great consequence (Table S1). The other half were due to slightly different groupings of ~15 quasi-rigid backbone segments into rigid groups 2 & 4. A consensus designation was obtained manually, choosing a compromise that minimized fragmentation of the sequence, consolidated regions within the 3D structure, and was visually consistent with the 3σ-DDM (Table S1 & Table 2).

Relationships between the rigid groups were analyzed using DomSelect (http://fizz.cmp.uea.ac.uk/dyndom/domainSelect.do) ⁴², LsqKab ⁷⁰ and malign.py. The latter was written to extend the functionality of phenix.superpose_pdbs (Zwart et al., http://www.phenix-online.org/documentation/superpose_pdbs.htm). In all cases the consensus rigid group assignments were explicitly input rather than relying on automatically generated assignments. Malign.py determines domain re-orientations using the same approach as DomSelect. It first performs least-squares rigid-body super-position of two structures based on a reference selection of atoms, then a subsequent alignment of a second selection of “moving atoms” to their corresponding targets. Any inter-group change is then given by the transformation between the reference and second super-positions. Malign.py extended the functionality of prior programs by supporting statistical analysis of multi-chain and ensemble (NMR) models and comparison with TLS librations. The similarity of rotational (and librational) operators was assessed from the magnitude of rotation (square root of mean square libration), as well as the magnitudes of the dot products between unit vectors along the rotational (principal librational) axes. For these comparisons, the TLS tensors were first decomposed using the CCP4 program TLSANL ⁷¹. Graphical analysis was performed with PyMol ⁷².

The Delta Matrix (Figure 4) was used for identification of quasi-rigid groups from the individually refined ADPs of the transition state structure ⁴⁰. It was calculated using the CCP4 program Anisoanl ^{49; 73}. Residues were binned into the maximum 100 bins. The output matrix was inverted horizontally for consistency with ESCET.

Abbreviations and symbols

ADP

adenosine diphosphate

ADPs

atomic displacement parameters

AK

arginine kinase

DDM

difference distance matrix

RDC

residual dipolar coupling

TSAC

transition state analog complex