Single-gene tuning of Caulobacter cell cycle period and noise, swarming motility, and surface adhesion

Abstract

Sensor histidine kinases underlie the regulation of a range of physiological processes in bacterial cells, from chemotaxis to cell division. In the gram-negative bacterium Caulobacter crescentus, the membrane-bound histidine kinase, DivJ, is a polar-localized regulator of cell cycle progression and development. We show that DivJ localizes to the cell pole through a dynamic diffusion and capture mechanism rather than by active localization. Analysis of single C. crescentus cells in microfluidic culture demonstrates that controlled expression of divJ permits facile tuning of both the mean and noise of the cell division period. Simulations of the cell cycle that use a simplified protein interaction network capture previously measured oscillatory protein profiles, and recapitulate the experimental observation that deletion of divJ increases the cell cycle period and noise. We further demonstrate that surface adhesion and swarming motility of C. crescentus in semi-solid media can also be tuned by divJ expression. We propose a model in which pleiotropic control of polar cell development by the DivJ–DivK–PleC signaling pathway underlies divJ-dependent tuning of cell swarming and adhesion behaviors.

Introduction

Simple estimates of diffusion in bacterial cells suggest that cytoplasmic and membrane protein concentrations would become uniform in seconds to minutes (Mignot and Shaevitz, 2008). However, a spatially uniform concentration of protein across a cell precludes a nonequilibrium driving force that can lead to proper differentiation and development in many bacterial species. Indeed, it is known that surface structures such as pili and flagella are asymmetrically distributed on a bacterial cell, and that subcellular structures such as chemoreceptor complexes are selectively localized at the cell pole (Alley et al, 1992; Nelson, 1992; Maddock and Shapiro, 1993). Recent developments in live cell imaging have shown that cytoskeletal and signaling/regulatory proteins also exhibit complex subcellular localization that varies temporally across the cell cycle (Gitai et al, 2005; Bardy and Maddock, 2007; Shapiro et al, 2009). Thus, deciphering mechanisms of bacterial cell cycle regulation and development requires in-depth characterization of the organization and activity of proteins in both time and space (McAdams and Shapiro, 2003).

In Caulobacter crescentus, a model system for the study of asymmetric cell division and cell cycle regulation, specific regulatory proteins that exhibit temporal polar localization underlie the control of cell cycle progression, cell development, and cell adhesion (Shapiro et al, 2002; Ebersbach and Jacobs-Wagner, 2007). C. crescentus begins its life as a non-replicative and motile ‘swarmer’ cell containing a single polar flagellum and polar type-IV pili. The cell occupies this motile developmental phase for a period ranging from as little as 15% (Keiler and Shapiro, 2003; Siegal-Gaskins et al, 2009) to more than 50% (Poindexter and Staley, 1996) of its cell cycle depending on the physical and chemical composition of the culture environment. After proceeding through the swarmer phase, C. crescentus differentiates into a replicative and sessile ‘stalked’ cell (Figure 1A), which differs both morphologically (Poindexter, 1964) and metabolically (Felzenberg et al, 1996) from its swarmer precursor. This dimorphic developmental cycle is controlled by a suite of signaling/regulatory proteins that exhibit dynamic spatial localization during the cell cycle (Brown et al, 2009).

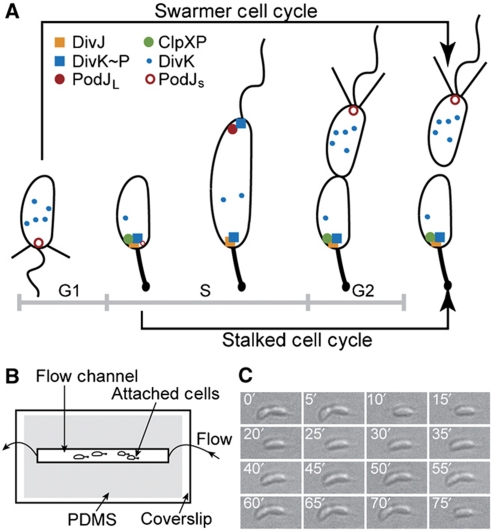
Figure 1.

Caulobacter crescentus cell cycle and experimental schematic. (A) C. crescentus swarmer (SW) and stalked (ST) division cycles and dynamic protein localization. The life cycle of C. crescentus begins at the SW stage (G1 phase), transitions into the stalked stage (S phase), and then progresses through early predivisional and late predivisional stages. Two morphologically and functionally distinct progeny are generated. Subcellular localization of DivK, DivJ, ClpXP, and PodJ are illustrated. (B) Top view of our microfluidic device (not drawn to scale). The microfluidic flow chamber is defined by a microscope coverslip and a PDMS channel, allowing for time-lapse single-cell analysis by bright-field and fluorescence microscopy. (C) A dividing wild-type C. crescentus cell (CB15) on the coverslip surface. Successive DIC images (time is indicated in white) of a dividing C. crescentus cell are shown. Images are arranged from left to right and from top to bottom. The direction of flow is from right to left.

Included among these dynamically localized regulatory proteins is the sensor histidine kinase, DivJ (Wheeler and Shapiro, 1999; Figure 1A). Co-localized with DivJ in the early stalked phase is the phosphorylated response regulator DivK∼P (Jacobs et al, 2001), and the protease ClpXP (McGrath et al, 2006) (Figure 1A), which degrades the master cell cycle regulator, CtrA (Jenal and Fuchs, 1998). CtrA is synthesized and accumulates as the stalked cell develops into a pre-divisional cell. The increased concentration of CtrA drives various processes required for cell replication, development, and division, but also induces the expression of the response regulator DivK. DivK, in turn, controls the stability and activity of CtrA through two essential phosphorelays (Biondi et al, 2006). All of these regulatory proteins are localized to the stalked pole (the former flagellar pole), whereas the nascent pili and flagellum are assembled at the pole opposite the stalk, where the polar development factor PodJ co-localizes (Viollier et al, 2002; Figure 1A). Thus, constriction of the membrane in the longitudinal middle of the cell body during the late-predivisional stage results in an asymmetric distribution of subcellular structures and proteins between the stalked and swarmer compartments, creating two progeny with distinct morphologies, protein compositions, and developmental programs (Shapiro et al, 2002; Figure 1A).

Recent optical microscopy measurements of single C. crescentus cells have revealed an intriguing role for DivJ in the control of noise in cell division period (Siegal-Gaskins and Crosson, 2008). The variance in interdivision timing of single cells increases abruptly upon disruption of the divJ gene, and is accompanied by a relatively small increase in the mean generation time. Whereas abundant genetic and biochemical data on regulatory/signaling proteins have facilitated modeling the complex transcriptional network underlying the C. crescentus cell cycle (Li et al, 2008, 2009; Shen et al, 2008), the existing cell cycle models do not explain experimental data that demonstrate an increase in cell cycle period and noise in a divJ null strain (Siegal-Gaskins and Crosson, 2008). Moreover, mechanistic descriptions of how DivJ and its signaling partners become localized and how these proteins underlie the control of polar cell development and cell adhesion in C. crescentus remain incomplete.

In this study, we study single cells in a microfluidic flow chamber to probe the effects of perturbation of divJ expression on multiple aspects of cell physiology, including the (mean) period of division and noise in the period, swarm behavior in semi-solid medium, and surface adhesion. Moreover, we characterize the mechanism of subcellular localization of DivJ–EGFP, which provides further insight into the regulation of C. crescentus physiology by DivJ. The measured single-cell division periods and the distributions thereof as presented herein reveal a striking tunability in both the mean and variance of the C. crescentus cell cycle, which depends solely on the level of divJ expression. Stochastic simulations with a simplified cell cycle model establish that DivJ-dependent phosphorylation of DivK is critical in maintaining low noise in the C. crescentus cell division period. In addition to its role in regulating the cell cycle period, high divJ expression also affects the frequency of swarmer cell adhesion to a glass surface and the swarm rate of C. crescentus cells in semi-solid growth medium. Control of swarming in semi-solid medium cannot be explained by an altered rate or frequency of swimming motility of individual cells. We propose that divJ-mediated regulation of swarming and adhesion stems from the pleiotropic control of the DivJ–DivK–PleC signaling pathway on multiple aspects of polar cell development and morphology. Finally, we provide direct evidence from experiments and simulations that the DivJ histidine kinase becomes localized to the cell pole through a dynamic diffusion-and-capture mechanism during the C. crescentus cell cycle.

Results

DivJ-mediated tuning of C. crescentus cell cycle dynamics at the single-cell level

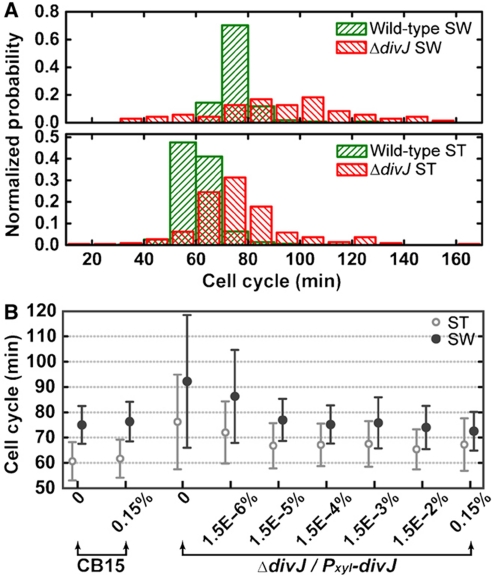
C. crescentus has two different cell cycles, the swarmer (SW) cell cycle (i.e. full cell cycle) and the stalked (ST) cell cycle (Figure 1A). Our microfluidic culture/imaging assay (Figure 1B) permits single-cell resolution (Figure 1C). We analyzed each (i.e. ST and SW) cell cycle separately (see Materials and methods section for details) and obtained the distribution of cell cycle times as shown in Figure 2A. This distribution yields information about fluctuations in the period of cell cycle oscillations (i.e. noise). The data in Figure 2B allow quantifying the amplitude of the noise as the coefficient of variation (COV=s.d./mean; Siegal-Gaskins and Crosson, 2008; Kar et al, 2009).

Figure 2.

Single-cell analysis of the dependence of cell cycle timing on xylose-inducible divJ expression. (A) Distributions of SW and ST cell cycle times. The SW and ST cell cycle time (in minutes) distributions (normalized frequency) for wild-type and ΔdivJ mutant cells (ΔdivJ/P_xyl-divJ) at 0% xylose (i.e., no divJ induction) are shown (n=118, 519, 71, and 224 for wild-type SW and ST, mutant SW and ST, respectively). (B) The mean and s.d. value of the SW and ST cell cycle time distributions measured for increasing divJ induction levels in the ΔdivJ/P_xyl-divJ mutant strain. Cell cycle time statistics (mean and s.d.) are plotted for wild-type at 0 and 0.15% (w/v) xylose and for the divJ mutant from 0 to 0.15% xylose (n=41 to 689).

The upper panel in Figure 2A corresponds to the swarmer cell cycle time distributions for wild-type and a chromosomal divJ null mutant carrying a xylose-inducible copy of divJ on a low-copy plasmid (see Materials and methods section for strain information; 75.0±7.5 and 92.2±26.2 min, respectively), whereas the lower panel shows the stalked cell cycle time distributions for the same two strains (60.6±7.6 and 76.2±18.7 min, respectively). Single-cell interdivision time (i.e. division period) data for wild-type C. crescentus and the divJ mutant measured with a range of xylose concentrations (0–0.15% w/v) are summarized in Figure 2B. The results for wild-type and the divJ mutant agree well with previously reported data (Siegal-Gaskins and Crosson, 2008) although there are slight differences in the mean and variance that are likely the result of different experimental conditions. We restrict our discussion to the stalked cell cycle time as the trends for both swarmer and stalked distribution statistics are similar across various conditions.

It is clear from Figure 2B that the mean stalked cell cycle of the divJ mutant in the absence of xylose induction of divJ expression is ∼20% longer than wild type. As the concentration of xylose is increased above 1.5 × 10⁻⁵%, the mean stalked cell cycle time remains almost unchanged (between 65.4 and 67.5 min). Calculating the COV in interdivision timing for increasing xylose concentration (Supplementary Table I) shows that the noise in the cell cycle time is highest in the absence of divJ expression, and diminishes to the wild-type level in an abrupt manner as DivJ is restored. The threshold for this transition is between 1.5 × 10⁻⁶ and 1.5 × 10⁻⁵% xylose (Supplementary Table I). This threshold is revealed to be in the same range as the transition of cell morphology from elongated/filamentous to normal (Supplementary Figure 1). However, even at high divJ induction levels, we observe that a small fraction of the cells exhibit abnormal filamentous morphology (Supplementary Figure 1). We do not have a mechanism to explain such morphological defects in the inducible divJ expression strain, but note that we are monitoring mutant cells (C. crescentus divJ∷Tn5/Pxyl-divJ) under atypical culture conditions.

Deterministic and stochastic simulations of cell cycle oscillations with a simplified protein interaction network

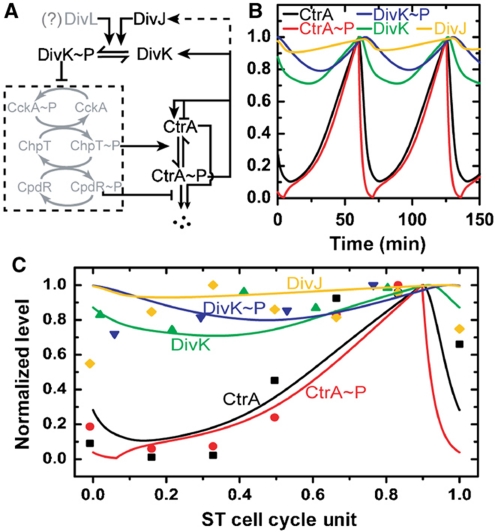
A simplified cell cycle network was constructed to provide mechanistic insight into our experimental data (Figure 3A; see Materials and methods section for details). Our simulation uses five coupled differential equations that describe the simplified network (Supplementary Table II with parameters in Supplementary Table III); the results are shown in Figure 3B. In Figure 3C, we compare the temporal protein (concentration) profiles obtained from our simulations with experimental cell cycle protein levels obtained by immunoblot analysis (from literature). The simulated CtrA and CtrA∼P concentration during the ST cell cycle are in good agreement with the experimental data. The DivK, DivK∼P, and DivJ simulated time traces are also in good agreement with experiment, except for some early time points. However, it should be noted that this comparison is not definitive largely due to the absence of true synchrony in the population-based immunoblot data (Siegal-Gaskins et al, 2009). Nevertheless, our simulation captures the ST cell cycle oscillatory behaviors of CtrA and CtrA∼P and the relatively stable profiles for DivK, DivK∼P, and DivJ measured in experiments. Moreover, the simulation shows that deleting divJ does not ablate cell division (Supplementary Figure 2D), as has been previously observed experimentally (Wheeler and Shapiro, 1999).

Figure 3.

Deterministic simulation of C. crescentus ST cell cycle oscillatory period. (A) Simplified regulatory network for ST cell cycle. Regulation of CtrA oscillation is modeled by a five-component protein interaction network (see Materials and methods section for details). The model only includes the components shown in black (i.e. the gray-shaded part of the network is simplified). The dash box indicates a phosphorelay system that is approximated as a binary switch controlled by the DivK∼P level. (B) Protein concentrations (normalized) trajectories over about two cell cycle periods. The model is described by coupled differential equations and is solved to obtain trajectories as shown. (C) Comparison of simulation with experimental data. Experimental protein levels (solid symbols) are extracted from published immunoblot data for the five components included in the model (CtrA (Holtzendorff et al, 2004), CtrA∼P (Jacobs et al, 2003), DivK (Jacobs et al, 2001), DivK∼P (Jacobs et al, 2001), and DivJ (Wheeler and Shapiro, 1999)). The cell cycle periods are normalized to 1. ST cell data are then taken from 15 to 100% of the SW cell data (∼15% of time for SW-ST transition (Keiler and Shapiro, 2003)) and the time is rescaled by 0.85 to yield ST cell cycle unit (0–1).

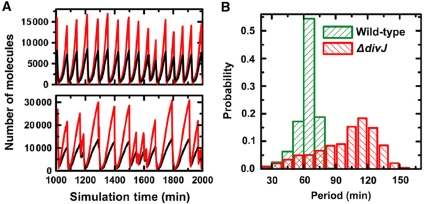
Agreement between in silico simulations and experiments with other cell cycle mutants is shown in Supplementary Figure 2 and Supplementary Table IV, which further demonstrate that our reduced model accurately represents the essential regulatory circuitry of the C. crescentus cell cycle. We approximate the period of CtrA oscillation as the ST cell cycle time: our simulation yields 64.5 min for wild-type cells (versus 60.6 min obtained in experiment) and 103.0 min for the ΔdivJ mutant (versus 76.2 min experimentally). Deletion of divJ results in a longer CtrA oscillatory period compared to wild type, in agreement with the trend observed in experiments. However, the magnitude of the increase in the simulation result is larger than what is observed in experiment. To computationally assess the role of DivJ in the statistical variation observed in the measured ST cell cycle period, we performed stochastic simulations (Gillespie, 1977) of our reduced protein interaction network (Supplementary Table V; see Materials and methods section for details). Representative time traces of the network components obtained from stochastic simulations are shown for wild-type and the ΔdivJ mutant (Figure 4A; Supplementary Figure 3). The simulated oscillation periods of the network components are noisier in the ΔdivJ mutant (Figure 4A), with the distribution of CtrA∼P oscillatory periods exhibiting an increase in COV (from 0.144 to 0.273) when the DivJ component is deleted from the model (Figure 4B). This is in good agreement with the experimentally determined division period COVs for wild-type and ΔdivJ cells, which change from 0.125 to 0.246, respectively (Supplementary Table I). Thus, the reduced (simplified) regulatory network presented here produces oscillatory behavior of the master regulatory protein CtrA during the ST cell cycle, and provides an adequate explanation of our new experimental measurements that describe the divJ-dependent regulation of noise in the cell cycle period.

Figure 4.

Stochastic simulation of C. crescentus cell cycle oscillations in the presence and absence of divJ. (A) Representative traces from stochastic model simulation. Sample CtrA (black) and CtrA∼P (red) trajectories are shown for wild-type (upper) and ΔdivJ (lower) cells. (B) CtrA oscillation period distributions for wild-type and ΔdivJ cells. Stochastic trajectories of CtrA∼P are used to calculate inter-peak distances (times) and normalized histograms of the inter-peak distances are plotted for wild-type (62.9±9.0 min, n=1419 versus 64.5 min from deterministic model) and ΔdivJ (100.0±27.4 min, n=889 versus 103.0 min from deterministic model) cells.

DivJ regulation of Caulobacter monolayer formation under laminar flow

The role of divJ in regulation of the cell cycle and development was first described 20 years ago (Sommer and Newton, 1991) and, since that time, has been well characterized both genetically and biochemically (for review, see Bowers et al, 2008; Curtis and Brun, 2010). Using our single-cell culture method, we sought to characterize and quantify additional aspects of C. crescentus cell physiology that are regulated by the DivJ sensor histidine kinase.

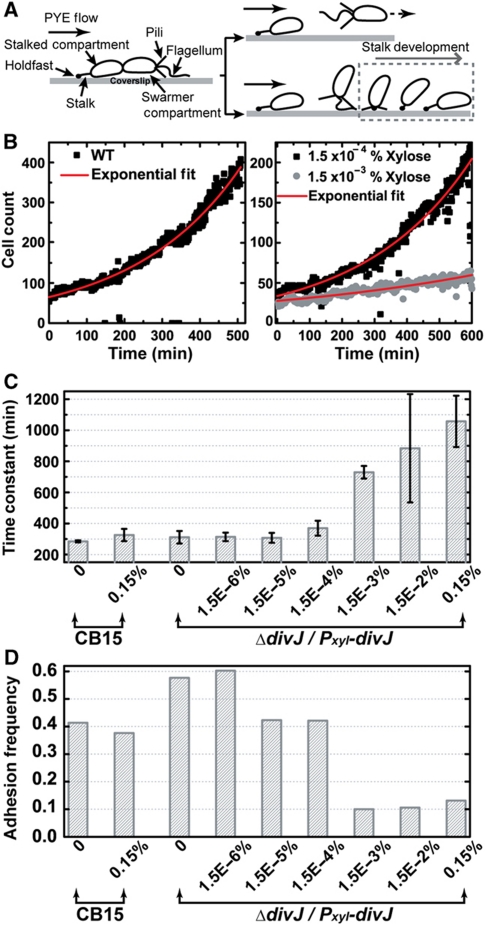
Whereas the formation of C. crescentus biofilms on an abiotic surface exposed to flow was first characterized in 1993 (Nivens et al, 1993), an accurate description of cell adhesion dynamics is lacking. The temporal progression of C. crescentus biofilms that form under hydrodynamic flow has been described as biphasic, consisting of an early-forming monolayer and late-forming mushroom structures (Entcheva-Dimitrov and Spormann, 2004). In our experiment, the surface adhesion capacity of early swarmer progeny, a modest hydrodynamic drag force (<10 pN; Siegal-Gaskins and Crosson, 2008), and the flow gradient in the microfluidic channel allow detailed study of monolayer formation at the early stages of biofilm development. Moreover, cell culture in a microfluidic flow environment enables acute control of gene expression from an inducible promoter, permitting us to assess the effects of divJ expression on surface adhesion. Our microfluidic culture assay allows continuous imaging of C. crescentus monolayer development with single-cell spatial resolution; in the present case we image the process at 1-min intervals.

For single C. crescentus cells attached to the surface of our microfluidic culture chamber, the swarmer-to-stalked transition occurs on the glass surface in the presence of constant (laminar) fluid flow (Figure 5A). A large fraction of the swarmer cells are carried away by flow after division (upper right, Figure 5A) and a smaller fraction adheres to the surface approximately one cell-length in distance downstream from the mother cell (lower right, Figure 5A). The development of swarmer cell surface adhesion is summarized and shown schematically in Figure 5A (lower right; Brown et al, 2009).

Figure 5.

The dependence of C. crescentus surface adhesion and monolayer biofilm formation on divJ expression. (A) Initial surface attachment of SW cells in the microfluidic channel. In the cartoon, a late pre-divisional cell exposed to hydrodynamic flow is drawn (left) with labels indicating its cellular structures. When the SW progeny detaches, it may either be carried away by the fluid flow (upper right) or adhere to the surface near its mother cell (lower right). (B) Monolayer biofilm formation dynamics. The time trajectory of the number of cells on the surface is plotted (solid symbols) and the data is fitted with an exponential growth model (red solid curve). Sample trajectories for wild-type C. crescentus strain CB15 without xylose (left) and the ΔdivJ/P_xyl-divJ mutant cells exposed to two xylose concentrations (right) are presented. The fitted time constants are 284 min for wild-type (left), 332 min for 1.5 × 10⁻⁴% xylose (right, upper), and 779 min for 1.5 × 10⁻³% (right, lower). (C) The rate of biofilm monolayer formation for increasing levels of divJ induction in ΔdivJ/P_xyl-divJ. The horizontal axis indicates the bacterial strain and xylose concentration. The time constants are obtained by exponential fitting of trajectories as shown in (B). Error bars represent s.d. (n=4). (D) SW cell adhesion frequency for increasing levels of divJ induction. The adhesion frequency is calculated as the ratio: (number of new born SW cells that adhere to the surface)/(total number of new born SW cells).

The dynamics of C. crescentus monolayer development are represented in Figure 5B and reveal exponential-growth behavior. We developed a mathematical description of C. crescentus monolayer formation to explain the observed growth behavior (see Materials and methods section). The time constant, T₀/α, characterizes the rate of the biofilm formation that depends on the adhesion probability (α) and cell cycle time (T₀). Such exponential growth is analogous to the standard turbidity-based measurement of growth; the former measures the growth at a surface and the latter measures the growth in a volume.

To assess the effect of divJ expression on surface adhesion dynamics, we used the same divJ mutant as above (see Materials and methods section). As summarized in Figure 5C, this divJ mutant has a similar biofilm formation rate constant (∼300 min) as wild-type C. crescentus in the absence of xylose-induced expression of divJ. Thus, loss of divJ neither blocks cell growth nor impairs swarmer adhesion. However, a sharp transition in cell adhesion dynamics occurs as the xylose concentration increases (Figure 5C), that is, as the amount of divJ being expressed increases. To demonstrate this threshold transition, two biofilm formation curves, one above and one below the threshold xylose concentration, are plotted in Figure 5B (right). The dynamics of monolayer formation differ substantially between these induction conditions, with the higher xylose condition (1.5 × 10⁻³%) exhibiting an approximately two-fold slower formation rate than that with 1.5 × 10⁻⁴% xylose (729 versus 370 min).

As the change in mean cell cycle time over the range of induction is only ∼20%, which is the maximum change of T₀ (Figure 2B), the rate of cell division cannot be the cause of the sharp change in the dynamics of biofilm monolayer formation. By contrast, the swarmer adhesion frequency, measured by analyzing single cells for various conditions (Figure 5D), reveals a sharp decrease in α, from 0.42 to 0.10, when the xylose level increases from 1.5 × 10⁻⁴ to 1.5 × 10⁻³%. Thus, a change in the adhesive capacity of the cell is the major cause of the decrease in rate of biofilm monolayer formation as a function of increasing divJ expression.

The effect of divJ expression on cell adhesion, swarming motility, and swimming motility

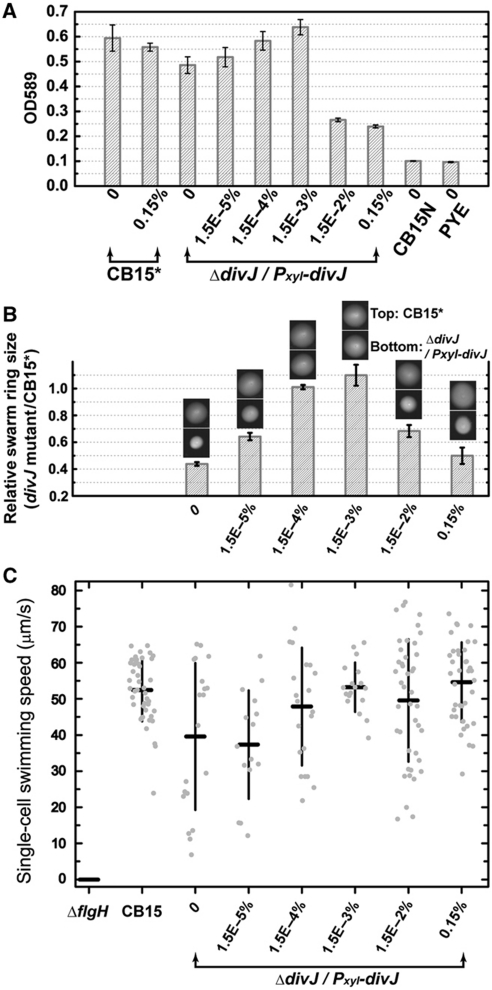
To further test the model that high divJ expression inhibits surface adhesion, we conducted an ensemble polystyrene-binding assay and quantified the number of attached cells by standard crystal violet staining. Considering that swarmer cells account for most of the attachment in such an assay (Bodenmiller et al, 2004), this result (Figure 6A) is directly comparable with the single-cell quantification of swarmer cell adhesion frequency (Figure 5D). The polystyrene binding assay validates our single-cell results, demonstrating that high divJ expression diminishes cell adhesion capacity (Figure 6A), with the threshold occurring between 1.5 × 10⁻³ and 1.5 × 10⁻²% xylose. We note that the threshold level observed in this population-based assay is higher than that observed in the single-cell-based microfluidic assay (Figure 5D; between 1.5 × 10⁻⁴ and 1.5 × 10⁻³% xylose). We attribute this to the difference between the two culture conditions: induction is more efficient in the case of constant xylose dosage experienced in microfluidic culture (i.e. the decreased gene expression in time due to xylose catabolism by the cells is mitigated in a flowing microfluidic culture).

Figure 6.

Characterization of ensemble surface adhesion, swarming motility, and swimming motility for different divJ expression levels. (A) Quantification of attachment of the ΔdivJ/P_xyl-divJ mutant strain to polystyrene surfaces for different (xylose induced) divJ expression levels. CB15^* is the CB15 strain carrying an empty Tet^R vector (FC 652). CB15N is the non-adhesive strain used as a negative control. Background is quantified by blank PYE. Error bars represent s.d. (n=4). (B) Quantification of the swarming motility of the ΔdivJ/P_xyl-divJ mutant for different divJ expression levels. The sizes (i.e. areas) of the swarm rings for the xylose-inducible divJ mutant strain were normalized to the mean sizes of the CB15^* swarm rings on the same plate. Sample photographs of swarm rings are shown for each xylose condition (top: CB15^*; bottom: divJ mutant). Error bars represent s.d. (n=5). (C) Quantification of the swimming motility of the ΔdivJ/P_xyl-divJ mutant for different divJ expression levels. A non-motile ΔflgH strain (FC1266) was used as negative control. The speeds for individual motile cells (gray dots, the spread on the horizontal axis is artificially added to allow the points to be visualized) and the mean±s.d. of the population were plotted for each culture (n=15–44), except for ΔflgH strain in which no motile cells were observed. The average speed for CB15 is consistent with the previously reported value (Li and Tang, 2006).

The polar flagellum, pili, and holdfast are critical for the development of cell adhesion (Bodenmiller et al, 2004; Entcheva-Dimitrov and Spormann, 2004; Levi and Jenal, 2006). To investigate the cause of greater than three-fold reduction in surface adhesion at high divJ expression levels, we conducted assays to ascertain the effect of DivJ on cell motility at the population level and single-cell level. Measurements of C. crescentus populations in semi-solid agar show that swarming of the divJ mutant in the absence of induced divJ expression is lower than wild-type cells (Figure 6B), consistent with previous reports (Sommer and Newton, 1991; Burton et al, 1997; Pierce et al, 2006). This phenotype is primarily caused by morphological defects, such as filamentation rather than a defect in swimming (Pierce et al, 2006). Induction of divJ expression with xylose gradually restores the swarm ring size to that of wild-type (Figure 6B; from 1.5 × 10⁻⁵ to 1.5 × 10⁻³% xylose). However, as the xylose level increases to ⩾1.5 × 10⁻²% (Figure 6B), the swarm size decreases sharply. The thresholds in Figure 6A and B are in the same range (between 1.5 × 10⁻³ and 1.5 × 10⁻²% xylose). A single-cell swimming motility assay of Figure 6C (see Materials and methods section for details) shows that the swimming velocity of individual cells in liquid culture at the highest levels of divJ induction is comparable to wild type. This result indicates that flagellar function is not impaired at high DivJ concentrations, providing evidence that the swarm defect at high divJ induction is not due to a defect in swimming. The inability of a population of motile cells to swarm in semi-solid agar (in the absence of defects in cell morphology) is a known phenotype of cells that are defective in chemotaxis (Johnson and Ely, 1979; Wang et al, 1993).

Experimental characterization and simulation of fluorescence dynamics upon induced expression of divJ–egfp

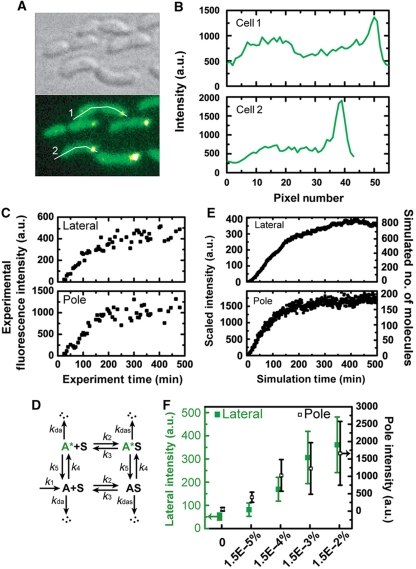
To characterize the subcellular distribution of DivJ molecules expressed from a xylose-inducible promoter, we devised a time-lapse single-cell fluorescence assay to visualize the temporal evolution and spatial localization of DivJ–EGFP in a divJ null background (see Materials and methods section for details). A Y-shaped microfluidic channel (instead of a single inlet channel in Figure 1B) connected to two media types (PYE complex medium with and without xylose) was used to precisely control the timing and level of divJ-egfp induction. After the addition of xylose, all cells in the field of view showed localized green fluorescence at the stalked pole for xylose concentrations ranging from 1.5 × 10⁻⁵ to 0.15%. Thus DivJ–EGFP proteins, being continuously expressed by the xylose promoter, localize to the proper pole in a divJ null background (Figure 7). The appearance of localized fluorescence spots, however, is not instantaneous at the time of induction (time zero in Figure 7C). Both the lateral membrane and the stalked pole of single cells show a gradual increase in fluorescence intensity (Figure 7C) and reach an apparent plateau at t=100–200 min. Moreover, the same steady-state behavior is observed over a wide range of xylose levels (Supplementary Figure 5 and Figure 7C). These observations provide evidence that complex kinetics probably involving transcription and translation, membrane insertion/diffusive motion, and chromophore folding/oxidation govern this process.

Figure 7.

Single-cell fluorescence localization, kinetics of DivJ–EGFP and model simulation. (A) C. crescentus cells in microfluidic culture expressing DivJ–EGFP. Bright-field DIC image (upper left) and a false-color fluorescence image from the same area (lower left) for divJ∷Tn5 (ΔdivJ) cells expressing divJ-egfp from the xylX chromosomal locus for 0.015% xylose induction. (B) Spatial profile of EGFP fluorescence. The plots are the fluorescence intensity profiles along the white lines indicated in (A) for cell #1 (upper) and cell #2 (lower). The horizontal coordinate represents the distance from the leftmost of each line in pixels. (C) Sample single-cell temporal fluorescence intensity traces obtained for 0.015% xylose for the same mutant construct. (D) Kinetic model where the species corresponding to experimental observables are A^* (lateral membrane-bound) and A^*S (pole localized). (E) Time traces for A^* and A^*S from simulation. The numbers of molecules are simulated with k₁=0.37 (Supplementary Table VII). The simulated molecule numbers are scaled as intensities for comparison with experimental trajectories (see Supplementary information for details). (F) Steady-state fluorescence intensities obtained for different inducer concentrations. Cells in the microfluidic channel were induced with different levels of xylose for 6 h and their intensities were characterized, except for the zero xylose condition in which the intensities were characterized before induction. Lateral membrane intensities (green solid squares) and stalked pole intensities (black open squares) are associated with the left and right y-axis, respectively. Error bars represent s.d. (n=23–29).

To explain the observed sub-cellular dynamics of fluorescence localization, we constructed a simple phenomenological model that is shown schematically in Figure 7D and Supplementary Figure 6A (see Materials and methods section for details). The numerical simulation results of this model demonstrate that A^* and A^*S (which correspond to experimentally detected fluorescent protein on the lateral membrane and at the stalked pole, respectively) both approach a steady-state after some simulation time regardless of the production rates of A (example traces are shown in Figure 7E; Supplementary Figure 6). The time scales for approaching steady-state are similar for a large range of DivJ–EGFP production rates (k₁) and these time scales are comparable to our experimental results (Supplementary Figures 5 and 6). In Supplementary Figure 6, we were able to show good correspondence of the simulated trajectories with experimental ones via the ratio between the number of molecules (or the integrated fluorescence intensity) in the lateral membrane and that in the stalked pole (Supplementary information and Supplementary Figure 7A and B). Each experimental induction condition (i.e. xylose concentration) corresponds to a DivJ–EGFP production rate (k₁) in simulation. An adsorption/desorption isotherm relation between reservoir molecules (A+A^*) and localized molecules (AS+A^*S) is also demonstrated (Supplementary Figure 7D).

Discussion

Cell cycle model predicts that robust phosphorylation of DivK by DivJ underlies the tight regulation of the cell cycle period

The elucidation of the molecular machinery that governs eukaryotic cell growth and division has lead to several successful mathematical models describing the cell cycle(s) in eukaryotic systems, including yeast (Chen et al, 2004) and Xenopus oocytes (Sha et al, 2003). Recent advances in our understanding of bacterial cell regulation (McAdams and Shapiro, 2003; Biondi et al, 2006) have prompted cell cycle modeling in prokaryotes, especially in C. crescentus (Brazhnik and Tyson, 2006; Li et al, 2008, 2009; Shen et al, 2008).

Our single cell division data on wild-type and ΔdivJ mutant cells (Figure 2B) called for construction of a network for cell cycle regulation that explained the observed differences in the division time statistics between wild-type and ΔdivJ. The agreement between the simulated trajectories resulting from in our (simplified) cell cycle model and ensemble experimental data (Figure 3C; Supplementary Figure 2; Supplementary Table IV), suggest the sufficiency of this simplified protein regulatory network. Specifically, deterministic (ODE) model simulation yields a longer ST cell cycle time for the ΔdivJ mutant than wild type, a finding that is consistent with our experiments. Stochastic simulations with this model offer further information on the noise as reflected in the measured COV of the cell cycle distributions. The finding of a larger simulated COV for CtrA∼P oscillation periods in a ΔdivJ mutant than in wild type recapitulates our experimental data and suggests the importance of robust DivJ-mediated phosphorylation of its cognate receiver protein, DivK, in regulating the variance of cell cycle oscillations. In our simulation, increased noise in the period of division in a ΔdivJ genetic background arises from increased cell-to-cell variability in the concentration of phosphorylated DivK∼P as driven by an indirect and minor (slow) DivL-dependent phosphorylation pathway (Reisinger et al, 2007) (Supplementary Figure 4A). Increased variability in the concentration of DivK∼P at the single-cell level subsequently leads to increased noise in the regulation of CtrA phosphorylation and degradation. Inducing divJ expression from the xylX promoter in a chromosomal ΔdivJ null mutant restores the fast pathway for phosphorylation of DivK and thus reduces the noise of cell cycle period (Supplementary Figure 4B).

It is well established that DivJ-mediated phosphorylation of DivK provides a negative control on the stability of CtrA and thus functions as a negative feedback signal in the C. crescentus cell cycle network. Our experiments and simulations demonstrate that the steady state level of DivK∼P at the single-cell level (as maintained by DivJ) is essential in regulating the timing and coherence of the cell division period in C. crescentus. However, we cannot exclude the existence of a positive feedback loop that also contributes to coherence in cell cycle timing, as has been demonstrated in budding yeast (Holt et al, 2008; Skotheim et al, 2008).

DivJ signaling and the pleiotropic control of swarming motility and surface adhesion

divJ exerts pleiotropic control over multiple aspects of cellular development (Wheeler and Shapiro, 1999; Jacobs et al, 2001). As such, the result that high divJ expression decreases swarming in a semi-solid medium (and in the absence of a defect in swimming) may be explained by multiple mechanisms including defects in the assembly of the chemoreceptor machinery or perturbation of the development of surface structures, such as type-IV pili, the stalk, or the adhesive holdfast. Given that decreased swarm rate at high divJ induction is correlated with decreased surface adhesion, it is likely that the adhesion and swarming phenotypes at high levels of divJ expression have a common cause (Bodenmiller et al, 2004; Entcheva-Dimitrov and Spormann, 2004; Levi and Jenal, 2006).

Specifically, the observed swarming and surface adhesion defects caused by overexpression of divJ may be explained by the regulation of PodJ through the DivJ–PleC–DivK signaling pathway. PodJ, a polar development factor, is important for pilus biogenesis, holdfast formation, and chemotaxis (Wang et al, 1993; Viollier et al, 2002; Hinz et al, 2003; Chen et al, 2006). There are two isoforms of PodJ: full-length PodJ (PodJ_L) and cleaved PodJ (PodJ_S). PodJ_L peaks at the early predivisional stage and is necessary for pilus biogenesis; its proteolytic product, PodJ_S, peaks at late predivisional and early swarmer stage and is required for holdfast formation and chemotaxis (Viollier et al, 2002; Chen et al, 2006). Proteolytic conversion from PodJ_L into PodJ_S requires compartmentalization of DivJ and its partner proteins DivK and PleC upon cytokinesis (Chen et al, 2006). However, the differential compartmentalization of DivJ can be perturbed by overexpression of the divJ gene in both cell compartments, as carried out in our experiments. Therefore, we suggest a model in which increased DivJ concentration in the swarmer compartment due to constitutive overexpression (Figure 7) results in premature localization of DivJ to the flagellar pole and elevated levels of DivK∼P (Supplementary Figure 8). This situation would be predicted to suppress the triggering signal for proteolytic conversion of PodJ_L to PodJ_S. Phenotypically, decreased PodJ_S levels are correlated with deficiencies in holdfast formation and chemotaxis without interfering with swimming motility (Viollier et al, 2002; Hinz et al, 2003). A deficiency in holdfast development results in cell-surface-adhesion defects (Bodenmiller et al, 2004; Entcheva-Dimitrov and Spormann, 2004; Levi and Jenal, 2006), whereas a deficiency in chemotaxis is reflected in reduced swarming motility in semi-solid agar (Wang et al, 1993). Both of these phenotypes are observed in our assays at high divJ expression levels (Figures 5 and 6).

Integrated time-lapse in vivo fluorescence measurements and kinetic modeling reveal a diffusion-and-capture pathway for DivJ localization

Our time-lapse single-cell fluorescence measurements establish the subcellular distribution of constitutively expressed DivJ–EGFP (Figure 7) and complex dynamics in the appearance of fluorescence (Figure 7C). A phenomenological model (Figure 7D) is sufficient to explain the time evolution of the single-cell fluorescence time traces. Viewing the membrane-bound molecules as the reservoir and the polar capture matrix as the adsorber (Supplementary Figure 6A), the adsorption of the reservoir molecules onto the adsorber is made in analogy to the Langmuir adsorption process of gas molecules onto a solid surface (Langmuir, 1916). The continuous expression of the protein increases the number of molecules in the reservoir which then partition between the reservoir and the adsorber by an adsorption/desorption relationship. The number of molecules adsorbed increases in accordance with the increasing number of reservoir molecules (Supplementary Figure 6B grey curves) before reaching a steady state. The steady state for the number of reservoir molecule occurs when the rate of reservoir molecule reduction (i.e. by adsorption, cell volume doubling, and degradation) equals its rate of production (i.e. by synthesis and desorption). Similar arguments with the addition of maturation kinetics can account for the plateau behavior of experimental observables (i.e. the bright molecules A^* and A^*S). The linear dependence of the ratio between the measured steady-state levels of integrated fluorescence intensities for lateral membrane and stalked pole on divJ induction level is also captured by our model (Supplementary Figure 7). This allows us to make a direct comparison between the experiment and simulation (compare Figure 7C versus Figure 7E and Supplementary Figure S5 versus Figure S6).

This localization mechanism is consistent with a diffusion-and-capture model. Given its simplicity, diffusion-and-capture is probably a widely used mechanism for protein localization in bacteria (Thanbichler and Shapiro, 2008). This model posits that proteins are randomly distributed and are freely diffusing until they are captured at the site in which they ultimately reside (Rudner et al, 2002; Shapiro et al, 2002; Bardy and Maddock, 2007). With a diffusion-and-capture pathway, it has been argued that proteins can be adsorbed either dynamically or statically (Shapiro et al, 2009). Our analysis of DivJ–EGFP in single cells supports a dynamic diffuse-and-capture mechanism for DivJ localization. The recent discovery and characterization of the pole-organizing protein, PopZ, at the poles of C. crescentus (Bowman et al, 2008; Ebersbach et al, 2008; Shapiro et al, 2009) supports the hypothesis that there is a multi-component polar docking station that dynamically sequesters signaling proteins (Shapiro et al, 2002). Our experiments and simulations are supportive evidence for this model of bacterial subcellular organization for the DivJ sensor histidine kinase.

Concluding remarks

In synthetic biology, actuators are engineered genetic circuits used to interface with natural networks and control cellular processes (Voigt, 2006). We have demonstrated a simple multiplex actuator in C. crescentus—a single gene (divJ) controlled by an inducible xylose promoter—that tunes cell cycle timing and its variance, swarming motility, and cell surface adhesion. Our measurements of single cells with controlled induction of divJ expression allow a systematic analysis of single-cell dynamics of cell cycle regulation and cell surface adhesion. By integrating a variety of experimental observables with the development of models and simulations, we have developed an improved mechanistic understanding of dynamical cellular processes regulated by the DivJ histidine kinase. Recent advances in controlling the rhythmicity of eukaryotic cell cycle oscillators by forcing (Battogtokh et al, 2006; Charvin et al, 2009) demonstrate the feasibility of precise manipulation and synchronization of naturally designed oscillators. Our simplified cell cycle model also suggests the possibility to entrain cell cycle oscillations in a population of prokaryotic cells through periodic genetic perturbations, which has been verified by experiments (Y Lin, Y Li, A Dinner, S Crosson and N Scherer, unpublished).

Investigating the connectivity between spatial localization of regulatory components and the function of regulatory networks is clearly a challenging frontier in the study of bacterial cell biology (McAdams and Shapiro, 2003). The microfluidic perturbation and imaging approach presented here allows spatial and temporal resolution of functional connectivities between localized protein components and overall network output (as assessed by monitoring various aspects of cellular growth and physiology at the single-cell level). The combination of acute experimental control and emerging theoretical understanding in this model system offers the possibility of a comprehensive mapping of connectivities in a cellular control network without prior assumptions (Ross, 2008).

Materials and methods

Bacterial strain construction

CB15 divJ∷Tn5/pMR20-P_xyl-divJ (tet^R) (ΔdivJ) was constructed by transformation of mutant strain CB15 divJ∷Tn5 (FC183) with plasmid pMR20-P_xyl-divJ (provided by M Laub). This strain was used for the study of the division cycle, surface adhesion, biofilm formation, and motility for inducible expression of divJ at different xylose concentrations.

To examine the polar localization of DivJ for constitutive divJ expression, a plasmid carrying P_xyl-divJ-egfp was integrated into the xylX locus of CB15 divJ∷Tn5 to generate a xylose-inducible expression of divJ-egfp for fluorescent characterization. The divJ (CC1063) coding sequence was PCR-amplified with primers divJNdeIfw (5′-CATATGGAAGCTGTGATCCTCCCCACCG-3′) and divJKpnIrev (5′-GGTACCGCGCGGCGCAAAGGC-3′), cloned into NdeI and KpnI sites of pMT603 (Thanbichler et al, 2007), transformed, and integrated into the xylX locus of CB15 divJ∷Tn5. However, the quantum yield and stability of DivJ–EGFP expressed in this strain was not acceptable for extended single-cell fluorescence measurements. With the suspicion that the polypeptide linker between DivJ and EGFP (20 aa) may affect the stability of EGFP folding, we substituted this 20-aa linker with a flexible peptapeptide linker (Gly-Gly-Ser-Gly-Gly) by site-directed mutagenesis (using primer 5′-TCGCCTTTGCGCCGCGCGGAGGATCTGGAGGAATGGTGAGCAAGGGCGAGGAG-3′ and its complementary strand). The DivJ–EGFP from this new construct has significantly improved brightness and stability and permits long time-lapse fluorescence measurements.

Microfluidic device for single-cell experiments

Microfluidic devices with rectangular cross-section (150 × 50 μm for straight channel (for non-fluorescent construct) or 300 × 50 μm for Y-shape channel (for fluorescent construct); W × H) were fabricated by rapid phototyping in poly(dimethylsiloxane) (PDMS, Sylgard Brand 184 Silicone Elastomer Kit, Dow Corning, Midland, MI; Duffy et al, 1998). The PDMS and microscope coverslip (Corning, Lowell, MA) were plasma-cleaned and sealed together to form channels with inlet and outlet ports punched in the PDMS. Teflon tubing (i.d.=0.012′ and o.d.=0.030′, Weico Wire & Cable, Edgewood, NY) connected to the ports was used for solution exchange. Before loading bacterial cells, the device was sequentially flow-rinsed with NaOH (2 M), ethanol, and autoclaved H₂O, clamped to the microscope sample holder, and heated to 30°C with a heater coupled to the sample holder under the control of a temperature controller (TC-344B, Warner Instrument, Hamden, CT).

Culture and preparation of bacteria for microfluidic experiments

Individual colonies were picked from a PYE-agar plate and cultured in PYE solution (with 1 μg/ml oxytetracycline and/or 5 μg/ml kanamycin; except for CB15) at 30°C in a rolled incubator overnight (to OD₆₆₀≈0.3). The culture was diluted back to OD₆₆₀≈0.1 with fresh PYE and cultured for an additional 2–3 h before loading into the pre-heated microfluidic device (30°C) with a syringe. Generally, less than 30-min incubation time is needed for enough C. crescentus cells to attach to the glass surface. Modest cell coverage on the coverslip is desired to prevent overgrowth and allow for long-time duration measurements. A syringe pump (PHD2000, Harvard Apparatus, Holliston, MA) was used to pump a xylose-containing PYE solution (with antibiotics) through the channel at a constant flow rate (10 μl/min for straight channel and 20 μl/min for Y-shape channel). The solution was warmed to 30°C by a home-built tubing heater (Teflon tubing wrapped by bare nickel–chromium wire (32BNC, Consolidated Electronic Wire & Cable, Franklin Park, IL); the heater operates in constant power mode with less than 0.5 W consumption and was allowed at least 1 h to stabilize before connecting to the microfluidic device. The temperature was measured with a home-built K-type thermocouple connected to a thermometer (HH802W, Omega Engineering, Stamford, CT) and the stability of the solution temperature after the heater was measured to be about ±0.5°C over a 10-h period. To minimize the heat loss, the tubing heater was mounted directly on top of the device inlet port (i.e. no bare tubing is exposed to the air between the heater and microfluidic device).

Microscopy measurements on single Caulobacter cells

All time-lapse measurements were done on a Nikon TE2000-E inverted microscope (Nikon Instrument, Melville, NY) equipped with a motorized stage, which was controlled by an automation controller (BioPrecision stage and MAC5000 controller, Ludl Electronics, Hawthorne, NY). A computer was used to communicate with both the microscope and stage controller through serial ports and controlled by a Labview program (Version 7.0, National Instruments, Austin, TX). The light source for all bright-field measurements was a collimated white light-emitting diode (LED) operated in pulse mode (LEDC19 LED and LEDD1 driver, Thorlabs, Newton, NJ) and was mounted onto the lamp port of the condenser arm. The analog voltage pulse used to modulate the LED was generated from a PCI-DAQ card (PCI-6052E, National Instrument, Austin, TX) through a BNC adaptor interface (BNC-2090, National Instrument, Austin, TX). For the fluorescence experiments, the sample was excited with a total-internal-reflected (TIR) blue 488 nm laser generated by frequency doubling the 100 fs pulses at 976-nm obtained from an infrared laser (MaiTai, Spectra-Physics, Mountain View, CA). A mechanical shutter (LS6Z2 shutter and VMM-T1 controller, Uniblitz, Rochester, NY) was placed in the laser line to control the laser illumination. A home-built Labview virtual instrument routine was used to automate the experiment by controlling and coordinating the sample stage (to move around different areas), the microscope objective step motor (to autofocus the image), the syringe pump (to flow PYE), the LED (to switch on/off the white light illumination and synchronize with the CCD), the laser shutter (to switch on/off the laser illumination that synchronizes with CCD readout), and the EM-CCD camera (to acquire images). Each experiment could run as long as 16 h depending on the cell coverage on the surface. For more details about microscope setup, refer to the More Details on Microscope Configurations section of the Supplementary information.

Data analysis for single-cell assays

The analysis of the bright-field and fluorescent images was done with ImageJ (NIH, Bethesda, MD). The detailed methodology is included in the Image Processing and Data Analysis section of the Supplementary information. The definitions/calculations for ST/SW cell cycle, adhesion frequency and filament fraction are also included.

Polystyrene-binding assay

The polystyrene-binding assay was performed as described previously (Bodenmiller et al, 2004) with minor modifications. CB15^* is the CB15 strain carrying an empty Tet^R vector (FC 652). Overnight bacterial cultures were diluted to OD₆₆₀=0.1 with fresh PYE supplemented with appropriate antibiotics. Diluted cultures supplied with various xylose concentrations (from 0 to 0.15%) were allowed to grow for 5 h until the OD₆₆₀ in every culture was >0.3. Cultures were then diluted back to OD₆₆₀=0.3. The diluted culture (and the blank PYE control) was incubated in the 48-well polystyrene plate (353078 TC-treated polystyrene, BD, Franklin Lakes, NJ) with shaking (400 r.p.m.) at 30°C for 20 min (240 μl each well; four wells each culture). Each well was rinsed with distilled water, stained with 240 μl 0.1% crystal violet by incubating with shaking (400 r.p.m.) at 30°C for 10 min followed by rinsing with distilled water. To solubilize the bound crystal violet, 500 μl of ethanol/acetone (80/20) mixture was added to each well and the plate was incubated with shaking (300 r.p.m.) at 30°C for 10 min. The final crystal violet solution was diluted 2 × and the optical absorbance was characterized at 589 nm.

Swarm plate assay

Bacterial cultures were grown overnight and diluted back to OD₆₆₀=0.1. A volume of 1 μl of diluted culture was injected ∼2 mm into the semi-liquid PYE-agar plate (0.15% agar) that was supplemented with xylose at various concentrations (from 0 to 0.15%) and antibiotics. Each plate, with a specific xylose concentration, contains five injections of the ΔdivJ mutant and CB15^*, separately. The plates were incubated in a 30°C oven for 60 h before photographing. The sizes (i.e. areas) of the swarm rings were quantified by thresholding and particle analysis tools in ImageJ, and normalized to the sizes of the mean CB15^* swarm sizes on the same plate, that is, relative size=divJ mutant swarm size/mean CB15^* swarm size on the same plate.

Single-cell motility assay

Overnight bacterial cultures were diluted to OD₆₆₀=0.1 with fresh PYE supplemented with appropriate antibiotics. Diluted cultures supplied with various xylose concentrations (from 0 to 0.15%) were allowed to grow for >6 h. Cultures were then diluted back to OD₆₆₀=0.3 with fresh PYE and mixed with silica microspheres (1.5 μm diameter, Duke Scientific, Palo Alto, CA) at 100:1 ratio. A volume of 2 μl of the mixture was used to form a liquid layer between a coverslip and microscope slide, and the device is sealed with VALAB (a 1:1:1 mixture of Vaseline, lanolin, and bee's wax). The sample was immediately imaged with an upright microscope Leica M5000 equipped with a × 63 phase contrast objective and an air-cooled CCD (ORCA-ER, Hamamastu Photonics, Japan). The movie was taken with minimal frame interval mode at about 10–17 frames per s for 1000 frames. Swimming cells were identified and tracked manually with the MTrackJ plugin in ImageJ. The tracks and the movie stack were then imported into Matlab (Mathworks, Natick, MA) for final processing.

Model simulation for C. crescentus cell cycle

We constructed a protein interaction network (Figure 3A) to describe the time evolving concentrations of proteins in C. crescentus during the cell cycle. This network also needed to account for the experimental observations that disruption of divJ results in an increased division time and its noise. Recently, several models have been reported to explain the cell cycle of C. crescentus, including the original Brazhnik–Tyson model (Brazhnik and Tyson, 2006) and its more developed versions (Li et al, 2008, 2009), and a hybrid model by McAdams, Horowitz, and colleagues (Shen et al, 2008). Although we incorporate their descriptions of some protein interactions, we take a different view of the system. The oscillatory behavior of CtrA, which directly or indirectly regulates 25% of Caulobacter cell cycle-regulated genes (Laub et al, 2002), and transcriptional and posttranscriptional mechanisms leading to such oscillation (Biondi et al, 2006; Bowers et al, 2008), is central to cell cycle progression. We have decreased the number of components and cellular processes included in previous models (Li et al, 2008, 2009; Shen et al, 2008), and present a reduced protein interaction network, with only five interacting components (CtrA, CtrA∼P, DivK, DivK∼P, and DivJ; Figure 3A). The following assumptions are made in this model: (i) the oscillation of CtrA directly and indirectly drives the progress of the cell cycle and hence various cellular processes. For example, low CtrA allows DNA replication while high CtrA promotes cell constriction/division through regulatory control of FtsAQ/FtsZ—both processes presumably occur as CtrA varies; (ii) most of the feedback from cellular processes (such as DNA replication and methylation) are ignored, whereas certain types of feedback, such as dilution by cell volume doubling, are implicitly included; (iii) by assuming a constitutive ctrA P1 promoter activity, regulatory signals from the other three components of the core cycle engine (i.e. DnaA, GcrA, and CcrM), as previously described (Laub et al, 2007), are ignored; (iv) by presuming that DivL functions as an indirect regulator of a slower pathway of DivK phosphorylation (Reisinger et al, 2007). We note that recent studies have shown that DivL-dependent regulation of DivK∼P is probably complex and involves localization of other regulators of CtrA (Iniesta et al, 2010). The details of the model are included in the Deterministic Simulation of the Simplified Caulobacter Network section of the Supplementary information. The description of the stochastic model simulation and in silico mutant simulations are included in the Stochastic Simulation of the Simplified Caulobacter Network and Mutant Simulations sections, respectively.

Mathematical description of monolayer biofilm development

The rate equation governing the total cell number, N(t), at time t is:

where N₀ is the initial number of cells on the surface, α is the probability for each swarmer daughter cell to adhere to the surface (lower right, Figure 5A), and T₀ is the average cell cycle period. In this model, the newly attached cells are produced from the stalked cells that are already in the defined area (i.e. the field of view of the camera). In doing so, we ignore the detachment process because we rarely observe stalked Caulobacter cells detaching from the surface under the modest hydrodynamic flow environment. This assumption may not be valid at later stages of film growth; that is after monolayer saturation.

Integration of Equation (1) gives:

which is used to fit the experimental curves.

Kinetic modeling of DivJ–EGFP fluorescence dynamics

In this kinetic model (Figure 7D), we assume a constant rate of production of DivJ–EGFP (k₁). When produced, it is assumed to be in the lateral membrane-bound dark state (A). This fusion protein is assumed to partition between a lateral membrane-bound state (A) and a polar localized state (AS) according to adsorption and desorption kinetics similar to the Langmuir isotherm (Langmuir, 1916). The lateral membrane-bound proteins (A) can be adsorbed onto the available sites (S) at the stalked pole and turn into pole localized state (AS) with a rate constant k₂. The EGFP tag of DivJ–EGFP in either state (A or AS) can fold into a bright state (A^* or A^*S, i.e. EGFP maturation) with a maturation rate constant k₄. The reverse processes, that is, desorption and unfolding processes, have rate constants k₃ and k₅, respectively. The degradation of all species are defined accordingly by first-order rate constants (k_da or k_das). The experimental observables are A^* and A^*S.

The molecules that diffuse in the lateral membrane act as a reservoir (A and A^*) whereas the anchors at the stalked pole act as an adsorber, in which the total number of anchoring sites (S₀) is assumed constant. We assume a constant cell volume and implicitly account for division by a rate of degradation. For example, to account for the dilution effect by cell volume doubling every division cycle, a degradation process with half-life time (i.e. 60 min) similar to the cell cycle time is assumed for the lateral membrane-bound DivJ–EGFP molecules (A and A^*). To evaluate the time-evolved dynamical behaviors of the experimental observed species (A^* and A^*S), the model was simulated with the Gillespie stochastic method, which allows for the assessment of the intrinsic molecular noise (Gillespie, 1976; see Supplementary Tables VI and VII for details).