Distinguishing Positive Selection From Neutral Evolution: Boosting the Performance of Summary Statistics

Abstract

Summary statistics are widely used in population genetics, but they suffer from the drawback that no simple sufficient summary statistic exists, which captures all information required to distinguish different evolutionary hypotheses. Here, we apply boosting, a recent statistical method that combines simple classification rules to maximize their joint predictive performance. We show that our implementation of boosting has a high power to detect selective sweeps. Demographic events, such as bottlenecks, do not result in a large excess of false positives. A comparison to other neutrality tests shows that our boosting implementation performs well compared to other neutrality tests. Furthermore, we evaluated the relative contribution of different summary statistics to the identification of selection and found that for recent sweeps integrated haplotype homozygosity is very informative whereas older sweeps are better detected by Tajima's π. Overall, Watterson's θ was found to contribute the most information for distinguishing between bottlenecks and selection.

A popular approach to statistical inference concerning competing population genetic scenarios is to use summary statistics (Tajima 1989b; Fu and Li 1993; Fay and Wu 2000; Sabeti et al. 2002; Voight et al. 2006). Since the complexity of the underlying models usually does not permit for a single sufficient statistic, this led to the development of a considerable number of summary statistics and consequently to the issue of which summary statistic should be used for a particular purpose. Methods that try to approximate the joint likelihood of several summary statistics via simulations suffer from the curse of dimensionality and are usually computationally intractable. Therefore proposals to combine summary statistics to a single number in a plausible way can be found in the literature (Zeng et al. 2006, 2007). In recent work, Grossman et al. (2010) use a Bayesian approach that is capable of combining the information of stochastically independent summary statistics.

Boosting (Freund and Schapire 1996; Bühlmann and Hothorn 2007) is a fairly recent statistical method that permits one to estimate combinations of summary statistics such that the sensitivity and specificity of the resulting classification rule is optimized. In contrast to the Bayesian approach of Grossman et al. (2010), boosting does not require independent summary statistics and is therefore more widely applicable. Here we explore boosting as a method to distinguish between competing population genetic scenarios. Although boosting could also be used in other settings, we chose positive selection, neutral evolution, and bottlenecks as our competing scenarios. The choice of such fairly well studied scenarios permits us to compare boosting with other summary statistics-based approaches available in the literature (Tajima 1983, 1989b; Fay and Wu 2000; Voight et al. 2006). Here the expectation is that boosting might gain something by deriving novel combinations of site frequency and linkage disequilibrium-based statistics. Since they measure different aspects of selection, their combination is not obvious. A comparison with a recently proposed method (Pavlidis et al. 2010) that uses support vector machines to combine site frequency and linkage disequilibrium (LD) information is also provided.

It may be also of interest to understand how boosting combines the summary statistics used in the light of what we know about the traces of selection. By now, the footprints of positive selection are quite well understood. They include a reduced number of segregating sites, as well as changes in the mutation frequency spectrum and the linkage disequilibrium structure (Biswas and Akey 2006; Sabeti et al. 2006). Besides selection, however, there may be other explanations for the observed deviation from neutrality, such as the demographic history of the population. Bottlenecks, for instance, lead to footprints that can be similar to those caused by selection (Tajima 1989a). In contrast to the demographic history, however, the effect of positive selection is usually thought to be local, changing the DNA pattern only in a limited spatial range. Typically, summary statistics show their extreme values right at the selected site and return to their normal values gradually when moving away from the selected site. This leads to a characteristic “valley” pattern that can be exploited for discriminating between selection and demography (Kim and Stephan 2002).

In methods, we first explain how boosting works and point out some relevant literature. We then explain how we implemented boosting for the purpose of detecting selection.

In results, we present simulations, illustrating the power of boosting for the detection of selective sweeps. In comparison with other methods, boosting seems to perform very well. We then explore the sensitivity of the method against demographic effects and consider also bottlenecks with and without a simultaneously occurring selective sweep. An application to real data from maize is also provided. We discuss furthermore what can be learned from boosting about the relative importance of various summary statistics. This may be helpful also in combination with other methods such as Approximate Bayesian Computation (ABC) (Beaumont et al. 2002), where boosting might be used in a first step, helping to choose a summary information measure to use in a further statistical analysis. In ABC, the choice of summary statistics is an important ingredient to ensure a good approximation to the posterior. Recently Joyce and Marjoram (2008) proposed to use approximate sufficiency as a guideline for choosing summary statistics, but further research is needed on this topic.

METHODS

Boosting:

Boosting is a popular machine-learning method that has recently attracted a lot of attention in the statistical community. (See Bühlmann and Hothorn 2007 for a recent review.) We use boosting as a classification method between competing population genetic scenarios, but boosting can also be used for regression purposes.

A boosting classifier is an iterative method that uses two sets of training samples simulated under two competing scenarios to obtain an optimized combination of simple classification rules. In each step, a base procedure leads to a simple (weak) classifier that is usually not very accurate. This classifier is combined with those obtained in previous steps and applied to the training samples. The training samples are then reweighed, giving more importance to those items that have not been correctly classified. This is done by using a loss function that measures the accuracy of the individual predictions. When the iterations are stopped, the final decision is made by a combination of weak classifiers in a way that might be viewed as a voting scheme. The better a weak classifier does, the more it contributes to the final vote. As a consequence of the aggregation step, boosting is called an ensemble method, with the ensemble of simple rules being usually much more powerful than the base classifiers themselves. An alternative way to understand boosting is as a steepest descent algorithm in function space [functional gradient descent, FGD (Breiman 1998, 1999)].

Several versions of boosting can be obtained by choosing among possible base procedures, loss functions, and some further implementation details. We use simple logistic regression with only one predictor a time as our base procedure, since this choice leads to results for which the relative importance of the input variables is particularly easy to interpret. However, several other versions of boosting have been proposed (Hothorn and Bühlmann 2002) and could in principle also be applied to our setting.

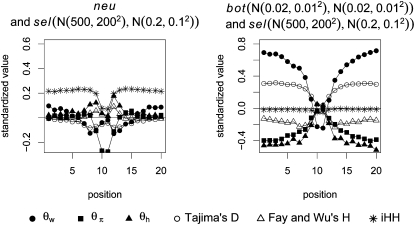
To obtain our boosting classifier, we simulated 500 training samples under each of two competing population genetic scenarios such as selection vs. neutrality in the simplest case. In total, our training data set thus contained n = 500 + 500 samples. For the ith training sample, we computed a predictor vector X_i that consists of all potentially useful summary statistics. The response variable Y_i indicates under which scenario the samples have been generated. (For instance, Y_i = 1 under selection and Y_i = 0 under neutrality.) Values for Y_i are known for the simulated training data but unknown for real and testing data. The whole data set can be then represented as

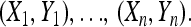We denote our classifier by f and use f(X) to predict Y. More specifically, we predict that Y = 1, if f(X) > γ for some threshold γ. We may choose γ = 0.5 if type I and type II errors are to be treated symmetrically. Otherwise one may want to calibrate γ to achieve a desired type I error probability.

A loss function ρ has to be chosen to measure the difference between the truth Y and the prediction f(X). The objective is then to find a function f that minimizes the empirical risk:

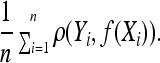The classifier f is obtained iteratively. Its initial value f^[0] is chosen as the mean of all the response variables in the training data set, and then f changes stepwise toward the direction of ρ's negative gradient, to approach the f that minimizes the empirical risk. Our focus has been on the squared error loss function ρ(Y_i, f) = 1/2(Y_i − f)². An alternative possible loss measure would be given by the negative binomial log-likelihood ρ(Y_i, p) = −Y_ilog(p) − (1 − Y_i)log(1 − p) with p(X) = P(Y = 1|X) = exp(f(X))/[exp(f(X)) + exp(−f(X))] (Bühlmann and Hothorn 2007).

Algorithm 1: An FGD procedure (Bühlmann and Hothorn 2007):

Algorithm 1 summarizes how a boosting classifier is obtained. The algorithm is available in the R package mboost (Hothorn and Bühlmann 2002), and a simple illustrative example is presented in supporting information, File S1.

1. Give f an offset value

   

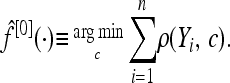
   Set m = 0.

2. Increase m by 1. Compute the negative gradient vector (U₁, …, U_n) and evaluate at 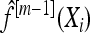; i.e.,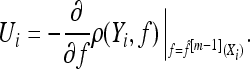

   
3. Fit the negative gradient vector (U₁, …, U_n) to X₁, …, X_n by a real-valued base procedure

   

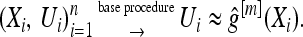
4. Update 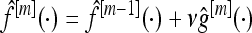, where 0 < ν ≤ 1 is a step-length factor.

5. Repeat steps 2–4 until m = m_stop.

For the step-length ν in the fourth step of Algorithm 1, we chose the default value ν = 0.1 of the R package mboost (Hothorn and Bühlmann 2002). A small value of ν increases the number of required iterations but prevents overshooting. According to Bühlmann and Hothorn (2007), however, the results should not be very sensitive with respect to ν.

A further tuning parameter is the number of iterations of the base procedure. The larger the number of iterations is, the better the classifier will predict the training data. A better performance on the training data, however, does not necessarily carry over to the real data to which boosting should eventually be applied. Indeed, a classifier may eventually perform worse when applied to real sequences, if too many iterations are carried out with the training data. This phenomenon is known as overfitting. According to the literature (Bühlmann and Hothorn 2007), however, boosting is believed to be quite resistant to overfitting and therefore not very sensitive to the number of iterations. Nevertheless, a criterion for stopping the iteration process is useful in practice. As stopping criteria, resampling methods such as cross-validation and bootstrap (Han and Kamber 2005) have been proposed to estimate the out-of-sample error for different numbers of iterations. Another computationally less demanding alternative is to use Akaike's information criterion (AIC) (Akaike 1974; Bühlmann 2006) or the Bayesian information criterion (BIC) (Schwarz 1978).

In our computations, we stop the iterations when

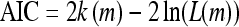attains a minimum. Here k(m) is the number of predictors used by the classifier f^[m] at step m, and L is the (negative binomial) likelihood of the data given f^[m].

Input to the boosting classifier:

We consider a sample consisting of several DNA sequences covering the same region and partition the region into several smaller subsegments. Our predictor variables are different summary statistics calculated separately for each subsegment. Computing the summary statistics separately for each subsegment permits us to identify valley patterns that are known to be a trace of positive selection. Considering j summary statistics on k subsegments leads to a total of k × j values that are combined to an input vector. Recall that the input vector is denoted by X_i for the ith training sample.

As our basic summary statistics, we choose Watterson's estimator (Watterson 1975),

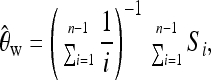and Tajima's 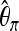(Tajima 1983),

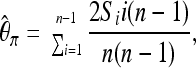as well as 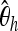(Fay and Wu 2000),

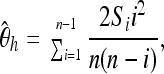where S_i is the number of derived variants found i times in a sample of n chromosomes.

We furthermore consider Tajima's D (Tajima 1989b) and Fay and Wu's H (Fay and Wu 2000; Zeng et al. 2006) that both combine the information of two of the above-mentioned summary statistics. Therefore they both are somewhat redundant. As a measure of linkage disequilibrium, we add the integrated extended haplotype homozygosity, iHH (Sabeti et al. 2002; Voight et al. 2006).

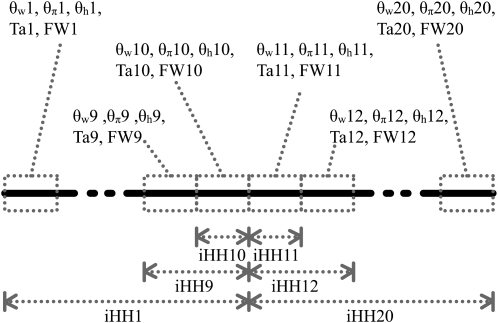
Figure 1 summarizes how a predictor vector X of length 120 is obtained for a 40-kb DNA sequence using these k = 6 statistics on 20 subsegments, each of length 2 kb. Whereas 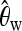, , 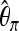, 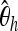Tajima's D, and Fay and Wu's H are calculated separately for each subsegment, iHH is computed from the center up to a distance of 2, 4, …, 20 kb separately on each side. As shown in Figure 1, iHH is first computed by integrating from the starting point of the sequence up to 20 kb. The result is denoted by iHH1. Next iHH2 uses the window from 2 kb up to 20 kb. The final iHH statistic for the left-hand part is iHH10, going from 18 kb up to 20 kb. For the right-hand part of the sequence extending from 20 kb up to 40 kb, 10 values of iHH are obtained analogously.

Figure 1.—

Predictor variables used as input X to boosting. Ta, Tajima's D; FW, Fay and Wu's H. We cut up the whole region (40 kb) into 20 subsegments, each of length 2 kb. For each subsegment, we compute 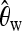, , 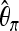, 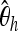Tajima's D, and Fay and Wu's H. Overlapping subsegments are used with iHH. In total, this leads to 6 × 20 = 120 predictor variables that are used as input vector X to boosting.

Simulation:

Both for training and for testing, we simulated scenarios involving n = 10 sequences each of length l = 40 kb with a recombination rate of ρ = 0.02. We chose several different values for α and the time τ since the beneficial mutation became fixed (in units of 2N generations) when simulating selection samples and assumed that the beneficial site is located in the middle of the sequence (Bsite = 20 kb). For each set of parameters, 500 neutral samples and 500 selection samples were simulated as a training data set. The same sample size was also used for the test data.

We considered two different mutation schemes: (1) a fixed mutation rate θ = 4Nμ = 0.005 and (2) a fixed number of segregating sites (K = 566, which is the expected number of segregating sites under neutrality when θ = 0.005; see Watterson 1975). In practical applications, the second mutation scheme corresponds to a strategy where, under both scenarios, one generates training samples with the number of segregating sites being equal to that observed for the actual data.

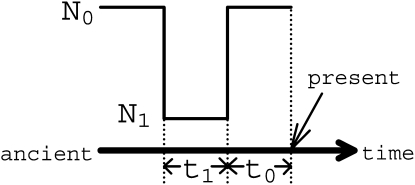
To simulate neutral samples and samples under selection, we used the SelSim (Spencer and Coop 2004) software. Bottleneck samples were simulated via the ms program of Hudson (2002). The mbs program by Teshima and Innan (2009) was adapted to simulate selective sweeps that occurred with bottlenecks. The simulation parameters and some notation are summarized in Table 1 and Figure 2.

TABLE 1.

Parameters and terminology

General parameters
n	The number of sequences in the sample
l	The length of the investigated region
θ	θ = 4Nμ, the population mutation rate per nucleotide, where N is the effective population size for a diploid population, and μ is the mutation rate per nucleotide per generation
K	Number of segregating sites in a sample
ρ	ρ = 4Nr, the population recombination rate per nucleotide, where r is the recombination rate per nucleotide per generation
Selection parameters
α	α = 2Ns, the selective strength, where s is the selective advantage of the beneficial allele over the ancient allele
τ	Time since the beneficial mutation became fixed, in units of 2N generations
Bsite	Distance between the beneficial site and the left end of the sequenced region
Bottleneck parameters (see Figure 2)
t0	Time since end of bottleneck, in units of 2N generations
t1	Duration of bottleneck, in units of 2N generations
D	D = N1/N0, depth of bottleneck
N0	Effective population size before and after bottleneck
N1	Effective population size during bottleneck
Notation
neu	500 simulated neutral samples
sel(α, τ)	500 simulated selection samples with given α and τ
bot(t0, t1)	500 simulated bottleneck samples with given t0 and t1
N(a, b2)	Gaussian distribution, where a = mean and b2 = variance
Fθ or FK	Simulation with fixed value for θ or K

Figure 2.—

Terminology for bottleneck scenarios. A bottleneck scenario that ended at time t₀ and lasted for t₁ is shown. Both the present and ancient effective population sizes are N₀. During the bottleneck the effective population size decreases to N₁ chosen such that N₀/N₁ = 100.

Controlling the type I error:

By default, boosting treats type I and type II errors symmetrically and predicts that Y = 1, if f(X) > γ = 0.5. If one desires to control the type I error probability under a null model such as neutrality, this can be achieved by adjusting the threshold γ. For this purpose, we first obtain a boosting classifier on the basis of training samples as usual. Then we generate 500 independent training samples under the null model and choose γ such that 95% of these samples are classified correctly. To investigate the efficiency of the resulting classifier under the alternative model, we generated 500 further independent test samples.

RESULTS

Discriminatory power:

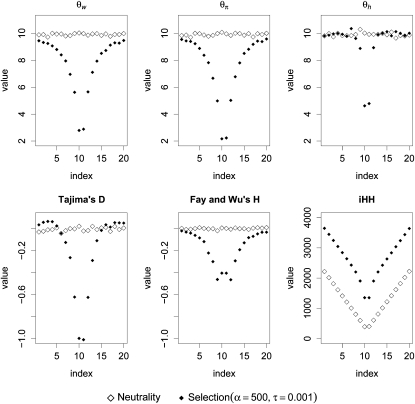
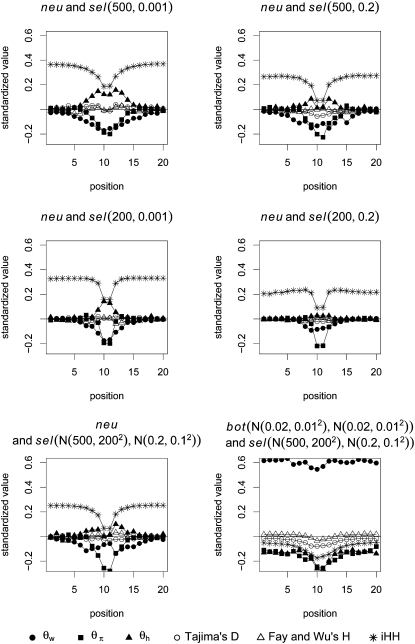
According to Figure 3, all our summary statistics, except for iHH, show a valley pattern under the selection scenario only. For iHH, the integration causes a valley both for the neutral and for the selection case. However, there are still differences in level and shape under the two competing scenarios.

Figure 3.—

Spatial patterns of summary statistics. The spatial effect of selection (vs. neutrality) on different summary statistics is shown. Each point corresponds to an average over 1000 independent samples with fixed θ. The x-axis gives the position within the sequence, whereas the y-axis displays the value of the summary statistic calculated at a subsegment centered at this position. For the selection scenario, the beneficial site is again assumed to be at 20 kb.

We first investigate samples generated under the same values for α and τ both for training and for testing. The results in Table 2 show that our method is quite efficient in distinguishing neutrality from selection. Even when the selective sweep is weak and old (α = 200 and τ = 0.2), we get an accuracy of 88.0% under a fixed value of θ. See Li and Stephan (2006) for a categorization of strong and weak selection in Drosophila.

TABLE 2.

Performance of boosting under different training strategies

Training data	Testing data	Acc (Fθ) (%)	Acc (FK) (%)
neu + sel(500, 0.001)	sel(500, 0.001)	100.0	100.0
neu + sel(500, 0.2)	sel(500, 0.2)	99.4	96.4
neu + sel(200, 0.001)	sel(200, 0.001)	98.6	97.8
neu + sel(200, 0.2)	sel(200, 0.2)	88.0	82.2
neu + sel(N(500, 2002), N(0.2, 0.12))	sel(500, 0.001)	99.8	98.4
	sel(500, 0.2)	98.4	96.6
	sel(200, 0.001)	93.8	86.2
	sel(200, 0.2)	87.6	75.8
neu + sel(500, 0.001)	sel(200, 0.8)	86.6	77.2
neu + sel(200, 0.8)	sel(500, 0.001)	100.0	99.6

The type I error probability (probability of incorrect classification of neutral samples) was adjusted to 5% according to 500 independent neutral samples. The predictive accuracy (Acc) is in terms of the percentage of correct classification. We consider two mutation schemes: Fθ and FK. The training and testing samples were independently generated under identical parameters. See Table 1 for the notation.

In practice this approach is too optimistic, since the parameters of the selection scenario are usually unknown. One more practical strategy is to do the training over a whole range of parameter values, representing the prior belief concerning possible parameter values. For this purpose we use samples generated under parameters chosen from a normal prior distribution with support restricted to the range of possible parameter values. We also generated parameters from a uniform distribution with very similar results (see Table S1). To facilitate interpretation, testing is usually done with samples generated under fixed parameter values. Not unexpectedly, training our classifier with samples generated under randomly chosen parameter values leads to some decrease in accuracy. According to Table 2, however, the power is still 87.6% in the most difficult test case (α = 200, τ = 0.2, with fixed θ).

If the alternative scenario is misspecified, our method seems to be quite robust at least in the situations we considered. When we trained the classifier with strong (α = 500) and recent (τ = 0.001) selection but tested on a weak (α = 200) and old (τ = 0.2) sweep, or vice versa, the power of the boosting classifier remains quite high (see the last two rows in Table 2).

Since θ is often unknown in practice and may also vary for reasons other than selection, an option is to simulate training data for the two competing scenarios under a fixed number of segregating sites K that equals the one seen in the actual test data. With this strategy, boosting is still able to learn the valley pattern. Obviously the exclusion of information concerning differences in the overall value of θ will lead to some decrease in power. Table 2 illustrates the amount of power lost. Among our considered scenarios, the predictive power turned out to be >75% in all cases.

The results are for boosting with the L2fm loss function (Bühlmann and Hothorn 2007). Using a different loss function does not affect the results much. (See Table S2 and Table S3.)

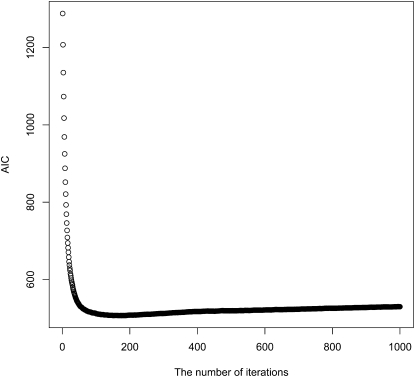
We also studied the use of AIC as a stopping rule for our boosting iterations. A typical example is provided in Figure 4. As the number of iterations increases, AIC decreases very rapidly at first, and then slows down, maintaining a steady level for a long period. In the example, the lowest AIC value is obtained at the 175th iteration. Stopping at the 1000th or 10,000th iteration led to almost the same predictive accuracy (results not shown), providing empirical support for the slow overfitting of boosting.

Figure 4.—

AIC. A typical AIC curve from a boosting run (500 neutral samples and 500 selection samples with α = 200, τ = 0.2, and fixed θ) is shown. The x-axis indicates the number of iterations and the y-axis the value of AIC. At the 175th iteration AIC reached its minimum. We can see that AIC decreases very fast at first, but changes only very slowly later on, which is in accordance with the slow overfitting feature of boosting.

Another quantity influencing the predictive accuracy is the sequence length. In Table 3, we investigate the decrease in power when the available sequences have a length <40 kb, the length considered so far. The results suggest that the decrease in power is not dramatic even when going down until sequences of length 1 kb.

TABLE 3.

Detection power in dependence of the sequence length

Testing samples	l = 20 kb (%)	l = 8 kb (%)	l = 4 kb (%)	l = 2 kb (%)	l = 1 kb (%)
sel(500, 0.001)	99.8	98.8	99.2	95.2	93.4
sel(500, 0.2)	99.0	97.8	96.8	96.2	89.0
sel(200, 0.001)	95.4	94.8	89.8	86.0	87.8
sel(200, 0.2)	88.4	84.0	78.8	80.8	79.6

We consider samples of sequences of length l and fixed θ to the same value in training and testing. Training was done with neu + sel(N(500, 200²), N(0.2, 0.1²)). The type I error probability (probability of incorrect classification of neutral samples) was adjusted to 5%. When l = 20, 8, or 4 kb, the length of the subsegments was chosen as 2 kb; when l = 2 or 1 kb, each subsegment was 0.5 kb. The summary statistics were computed independently for each subsegment. The predictive power remains quite high even for short regions.

Boosting-based genome scans:

It turns out that the boosting classifier is quite specific with respect to the position of the selected site. When training the classifier with the selected site at 20 kb, the power decreases quickly, if the position of the selected site is moved away from this position in the testing samples (Table 4). This can be exploited in the context of genome scans for selection. Indeed, if sufficiently large sequence chunks are available, it is possible to slide a window consisting of our 20 subsegments along the sequence. A natural estimate of the position of the selected location is then the center of the window with the strongest evidence for selection.

TABLE 4.

Accuracy depending on the position of the selected site

Bsite (kb)	Acc (Fθ) (%)
20	100.0
15	80.6
10	44.2

Training was done with neu + sel(500, 0.001) and Bsite = 20 kb, and the type I error probability was adjusted to 5%. Testing was done on sel(500, 0.001) with different positions Bsite of the beneficial mutation. It can be seen that the sweep detection power decreases quickly with increasing distance of the positions of the selected site between training and testing samples. Acc: percentage of cases where a sweep is detected. See Table 1 for details of the notation.

To learn which summary statistics are most specific with respect to the selected position, we investigate them separately by applying the boosting classifier on the basis of just one of the summary statistics at a time. It turns out that the effect of smaller deviations from the hypothetical selected site is particularly strong for 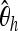, Tajima's D, and iHH (Table 5). One might therefore want to increase the specificity to position by using only 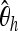, Tajima's D, and iHH. See Figure 5 for an example of a genome scan based on these three summary statistics.

TABLE 5.

Accuracy depending on the position of the selected site for different summary statistics

	Acc (Fθ) (%)
Bsite (kb)		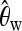		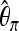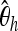Ta	FW	iHH
20	100.0	100.0	67.6	82.6	90.6	98.0
15	84.8	80.8	10.0	45.2	89.6	42.8
10	51.6	44.6	6.4	15.4	75.0	17.6

We show the power of detecting a selective sweep depending on the position Bsite of the selected site. To investigate the sensitivity of the individual statistics with respect to position, we used only one of the mentioned statistics at a time both in training and in testing. We trained with neu + sel(500, 0.001), Fθ, and Bsite = 20 kb and adjusted the type I error probability to 5%. 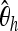, Tajima's D, and iHH are particularly sensitive to the selected position. Ta, Tajima's D; FW, Fay and Wu's H.

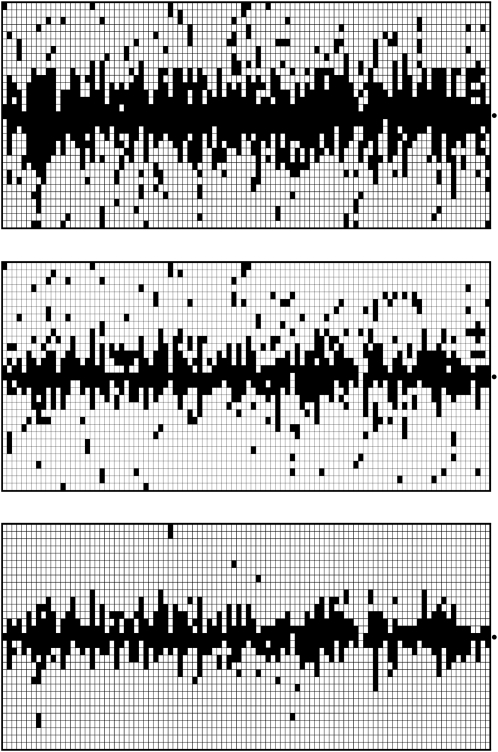
Figure 5.—

Boosting-based genome scans. In each of the three diagrams, each column represents an independently simulated 100-kb chromosome region where a beneficial mutation (α = 500, τ = 0.001) occurred. The rows indicate the position within the sequence. The dot to the right of each graph marks the position 50 kb where the beneficial mutation occurred. Within a column, each pixel indicates the classification result based on a 40-kb window sliding along the chromosome region (step length 2 kb). Training was done with neu + sel(500, 0.001). A solid pixel indicates that boosting predicted the considered position to have experienced a selection event. As desired, the solid pixels are concentrated at the selected position. In the top diagram, six different summary statistics were used, whereas in the middle diagram, only 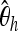, Tajima's D, and iHH were used. The type I error probability was adjusted to 5% in both cases. In the bottom diagram, the same six summary statistics were used as in the top diagram, but the type I error probability was reduced to 0.2%, corresponding to a threshold of γ = 0.5 for the boosting classifier. Both using position-specific summary statistics and decreasing the type I error probability lead to decreased false positive rates in a genome scan.

If a longer chromosome region is not available, or if a high specificity with respect to location is not desired, the specificity of the method can be reduced by cutting the sequences into fewer subsegments of larger size (Table 6), which intuitively smoothes the valley pattern.

TABLE 6.

Accuracy with respect to the number of subsegments

	Subsegments
Bsite (kb)	20 (%)	10 (%)	8 (%)	4 (%)	2 (%)	1 (%)
10	51.6	65.8	71.0	86.4	97.2	97.2
11	52.8	72.0	76.8	91.6	97.2	96.0
12	63.8	81.6	86.4	96.6	97.6	96.8
13	69.8	85.2	87.6	97.6	97.0	96.0
14	73.2	87.4	92.2	98.4	96.8	96.4
15	86.4	96.0	98.8	99.6	98.6	98.4
16	89.4	98.2	99.6	99.2	98.4	97.6
17	95.4	98.8	99.4	99.0	98.4	98.0
18	98.8	100.0	100.0	100.0	98.8	98.6
19	99.8	100.0	100.0	99.8	96.8	96.8
20	100.0	100.0	99.6	99.0	97.8	98.0

The percentages of correctly identified sweeps when the sequence is sliced into different numbers of subsegments are shown. We trained with neu + sel(500, 0.001), Fθ, and Bsite = 20 kb. The type I error probability was adjusted to 5%. Testing was performed on sel(500, 0.001) with different positions Bsite of the beneficial mutation. Each sequence was cut into subsegment(s) of equal size. We do not use iHH here. As iHH is very sensitive with respect to the sweep position Bsite, the decrease in power is now smaller than in Table 4 when the actual value of Bsite does not match the one simulated in the training samples. The percentage of times a sweep is called increases in most cases when the number of subsegments decreases.

Since the range of influence of a selective sweep depends on the strength of selection (α), the sensitivity of the classifier with respect to spatial position depends also on α. The smaller α is, the narrower the affected nearby region and the higher the sensitivity with respect to the assumed position of the sweep.

Sensitivity toward bottlenecks:

Demography leaves traces in genomic data similar to those caused by selective events (Tajima 1989a,b), making it difficult to distinguish between these competing scenarios (Schlötterer 2002; Schmid et al. 2005; Hamblin et al. 2006; Thornton and Andolfatto 2006). To investigate how often selective sweeps and bottlenecks are confounded, we applied the boosting classifier, previously trained on neutral and selective sweep samples, and tested it on bottleneck samples. When simulating bottleneck samples, we fixed D = 0.01, and tried different values of t₀ and t₁.

When training under neutrality and selection with fixed identical values for θ, bottlenecks and sweeps cannot be distinguished reliably [see the “First step (Fθ)” column in Table 7]. The reason is that a reduced number of segregating sites is observed both under bottlenecks and under sweeps but not under neutrality. One way to avoid this is to train the boosting classifier conditional on the observed number of segregating sites. With this strategy, the number of misclassifications (i.e., classifying a bottleneck as a sweep) goes down considerably [see the “First step (FK)” column in Table 7].

TABLE 7.

Rate of predicting selection with bottlenecks as an alternative scenario

Testing data	First step (Fθ) (%)	Second step (Fθ) (%)	First step (FK) (%)	Second step (FK) (%)
sel(500, 0.001)	99.8	99.8	98.4	76.0
sel(500, 0.2)	98.4	98.4	96.6	72.0
sel(200, 0.001)	93.8	93.8	86.2	62.2
sel(200, 0.2)	87.6	87.6	75.8	48.6
bot(0.002, 0.002)	46.0	43.2	7.8	1.6
bot(0.002, 0.02)	99.8	0.0	56.0	2.2
bot(0.002, 0.2)	100.0	0.0	30.2	0.4
bot(0.02, 0.002)	44.4	43.2	7.8	2.8
bot(0.02, 0.02)	99.8	0.6	61.6	1.8
bot(0.02, 0.2)	100.0	0.0	64.6	0.0
bot(0.2, 0.002)	32.6	32.6	8.0	1.4
bot(0.2, 0.02)	98.6	91.0	49.4	0.0
bot(0.2, 0.2)	100.0	97.2	27.4	0.0
bot no.	48.6	41.2	4.0	1.4

We investigate how often selection is predicted by the two-step boosting classifier discussed in Sensitivity toward bottlenecks. For selection scenarios, these cases contribute true positives; for bottleneck scenarios, they are false positives. First step, the percentage of testing samples classified as selection by classifier (C)1; second step, the percentage of testing samples classified as selection by both C1 and C2. C1 was trained with neu + sel(N(500, 200²), N(0.2, 0.1²)) and the type I error probability was adjusted according to 500 independent neutral samples. C2 was trained under bot(N(0.02, 0.01²), N(0.02, 0.01²)) + sel(N(500, 200²), N(0.2, 0.1²)) and the type I error probability was adjusted according to 500 independent bot(N(0.02, 0.01²), N(0.02, 0.01²)). Bot no. indicates that the bottleneck samples have the same average 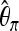-value (computed once across the whole region) as sel(500, 0.001). For Fθ, bot no. was bot(0.002, 0.002), and D = 0.0085; for FK, bot no. was bot(0.002, 0.002), and D = 0.07. See Table 1 for further notation.

To make our method even more specific, we propose a two-step method, which is in the spirit of Thornton and Jensen (2007). For this purpose, we use two classifiers (C), denoted by C1 and C2. C1 is trained under neutrality vs. selection, whereas C2 is under bottleneck vs. selection. For a test sample, we first apply C1. If selection is predicted, then we use C2, to classify between selection and bottleneck. The results [see in particular the “Second step (FK)” column in Table 7] indicate that this approach is quite efficient in the sense that misclassifications of bottleneck samples were very rare. On the other hand, the price for this is a somewhat decreased power of sweep detection when K is chosen equal in training and testing.

If a bottleneck sample and a selection sample are similar such that they produce similar overall values of a certain summary statistic, our method still works. In fact, the fixation of K implies that 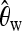is identical both for selection and for bottleneck samples when computed over the whole sequence. Ignoring subsegments, we also generated selection and bottleneck samples with an identical average value of the overall 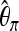. This was done by first generating sel(500, 0.001) samples and then choosing the bottleneck parameter D to get the same value of 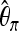under both scenarios. It turned out that even in this situation the false positive still remained low (see the “Bot no.” line in Table 7).

Comparison with other methods:

Currently there are several methods available to identify genomic regions affected by selection. Our main focus has been on comparing boosting with other approaches that also combine different pieces of information. More specifically, we considered both summary statistic-based approaches and the support vector machine approach of Pavlidis et al. (2010) that combines site frequency information [SweepFinder (Nielsen et al. 2005)] with linkage disequilibrium information [ω-statistic (Kim and Nielsen 2004)]. Further approaches, which we did not consider here, include the composite-likelihood method of Kim and Stephan (2002) and selection scans based on hidden Markov models (Boitard et al. 2009).

As tests that use summary statistics, we considered Tajima's D (Tajima 1989b) and Fay and Wu's H (Fay and Wu 2000), as well as their combined form, the DH test (Zeng et al. 2006). We calibrated all methods to give a type I error probability of 5% and then applied them to the same test data sets. In Table 8, we provide a comparison of the predictive accuracy between boosting and the above-mentioned methods that use summary statistics. We consider different selection scenarios, as well as bottleneck scenarios with randomly chosen parameters. Boosting always distinguished better between neutrality and selection than the other three methods. While one-step boosting often interpreted bottlenecked samples as evidence for selection, even when the DH test did not, the two-step boosting algorithm has a much better specificity than the DH test.

TABLE 8.

Comparison of boosting with other summary statistic-based methods

Testing data	One-step (%)	Two-step (%)	Ta (%)	FW (%)	DH (%)	Ta c (%)	FW c (%)	DH c (%)
Fθ
sel(500, 0.001)	99.8	99.8	26.6	79.0	41.6	73.8	71.8	67.8
sel(500, 0.2)	98.4	98.4	26.8	23.2	28.0	66.4	12.2	20.4
sel(200, 0.001)	93.8	93.8	11.0	25.8	21.4	51.0	52.0	50.0
sel(200, 0.2)	87.6	87.6	11.6	8.4	12.0	42.6	11.2	17.0
bot random	97.0	3.8	51.2	62.8	26.2	52.4	23.2	12.6
FK
sel(500, 0.001)	98.4	76.0	26.2	79.8	41.6	72.6	72.0	69.8
sel(500, 0.2)	96.6	72.0	29.8	26.4	37.0	69.4	9.4	19.0
sel(200, 0.001)	86.2	62.2	9.8	27.2	19.8	51.4	54.0	48.8
sel(200, 0.2)	75.8	48.6	13.2	8.2	13.2	42.6	7.8	15.2
bot random	55.8	3	52.8	62.4	26.4	62.4	24.0	12.0

The percentage of times selection was predicted for testing samples that were simulated under different selective and bottleneck scenarios is shown. We compared the following approaches that use summary statistics: Ta, Tajima's D; FW, Fay and Wu's H; DH, DH test; c, center. First, these statistics were computed only once across the whole 40-kb region, which may lead to a weakened selective signal according to an averaging effect. Since the signal in the center of the region will usually be the strongest, we then tried to use only the 4-kb center section of the region to compute the statistics. The results can be found under Ta c, FW c, and DH c. “One-step” and “two-step” indicate one-step boosting and two-step boosting, respectively. These results are the same as in Table 7. bot random = bot(N(0.02, 0.01²), N(0.02, 0.01²)). The type I error probability of boosting (both for one-step and for two-step) was adjusted to 5%, and we chose cutoff points for the other tests also according to the 5% quantile estimated from 50,000 simulated neutral samples. The samples were generated under both fixed θ (Fθ) and fixed K (FK). We can see that boosting always performed much better for distinguishing neutrality from selection, although the difference between the methods was reduced slightly when Tajima's D, Fay and Wu's H, and the DH test were calculated only from the center section of the region. Under the more difficult situations the advantage of boosting is particularly visible. Note that one-step boosting predicted most of the bottleneck samples as selection whereas the DH test did not. The application of two-step boosting, however, solved this problem.

Since the above-mentioned test statistics were computed only once across the whole 40-kb region, one might wonder whether the selective signal was weakened due to an averaging effect. We therefore recomputed the test statistics using only the center section of the region. This improved the performance of the test statistics, but boosting still performed better (Table 8). While the DH test that uses only the central window did better than the version using the whole sequence information, two-step boosting still provided the highest specificity toward bottlenecks. While two-step boosting can easily distinguish almost all the bottleneck events from selection, it can still recognize at least 87.6% of true selection events when θ is fixed and 75.8% when K is fixed (Table 8).

Additionally, we compared our method with another recently published method developed by Pavlidis et al. (2010). The method uses support vector machines, another machine learning method, to combine a site frequency-based statistic obtained from SweepFinder with the ω-statistic that measures linkage disequilibrium.

We first investigated the behavior when distinguishing neutrality from selection and also bottlenecks from selection. For our simulations, we used the same program ssw (Kim and Stephan 2002) as Pavlidis et al. (2010) and chose identical parameters (n = 12, l = 50 kb, Bsite = 25 kb, ρ = 0.05). The bottleneck samples were simulated with ms (Hudson 2002). For further parameters please refer to Table 9. To permit for a fair comparison, we followed Pavlidis et al. (2010) and used the same parameters for both training and testing. The results (Table 9) show that our method performs better under all considered scenarios.

TABLE 9.

Comparison of boosting with the method proposed by Pavlidis et al. (2010) under neutrality and bottlenecks vs. selective sweeps

Training data	Testing data	FP (%)	Acc (%)	Pavlidis's FP (%)	Pavlidis's Acc (%)
neu1 + sel1	sel1	0	98	3	90
neu2 + sel2	sel2	0	100	0	98
bot1 + sel1	sel1	1	100	26	75
bot2 + sel2	sel2	0	99	18	84

sel1, sel(500, 0.0001); sel2, sel(2500, 0.0001). To make the setup equal to that in Pavlidis et al. (2010), we generated 2000 training samples for each parameter set. (The results were almost identical when we followed our standard training procedure and used only 500 training samples.) Both sel1 and sel2 were generated under θ = 0.005. For each sample taken according to sel1, we computed Watterson's estimate 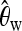(Watterson 1975) and generated a neutral sample with 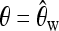. The training data neu1 consisted of 2000 neutral samples obtained in this way. We obtained neu2 analogously by matching θ to sel2. bot1 and bot2 were bottleneck samples with the parameters as in Li and Stephan (2006). This is a 4-epoch bottleneck model: Backward in time, a bottleneck happens from 0.0734 time units to 0.075 time units (in 2N₀ generations, where N₀ is the current effective population size), and the population size reduces to 0.002N₀, then instantly the population size changes to 7.5N₀, and finally it becomes 1.5N₀ at 0.279 time units. For each realization of sel1, θ was again estimated, and a corresponding bottleneck sample was obtained using 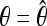. See Pavlidis et al. (2010) and Zivkovic and Wiehe (2008) for details. Again bot1 consists of samples obtained in this way and bot2 was obtained analogously. FP, false positive rate; Acc, accuracy (power of detecting a selective event). The FPs of the four rows were computed according to neu1, neu2, bot1, and bot2, respectively. The samples of the same parameter set for training, testing, and FP computing were independently generated. The Pavlidis's FP and Pavlidis's Acc columns show the accuracy of the support vector machine-based method of Pavlidis et al. (2010). Rows 1 and 2 of these columns are taken from Table 1 in Pavlidis et al. (2010), whereas rows 3 and row 4 are from Table 2.

Our next comparison with Pavlidis et al. (2010) involves a class of scenarios where a selective sweep happened within a bottleneck. We again simulated under identical parameters (n = 12, l = 50 kb, Bsite = 25 kb, ρ = 0.01) and used the same software mbs (Teshima and Innan 2009) to generate data. The results as well as further implementation details are shown in Table 10. Our method always provided better results in terms of both false positives (FP) and accuracy (Table 10).

TABLE 10.

Comparison of boosting with the method proposed by Pavlidis et al. (2010): detecting a sweep within a bottleneck

Training data	Testing data	FP (%)	Acc (%)	Acc* (%)	Pavlidis's FP (%)	Pavlidis's Acc (%)
bot1 + b_s1	b_s1	8	98	96	51	71
bot1 + b_s2	b_s2	11	95	85	20	73
bot1 + b_s3	b_s3	0	98	99	8	97
bot1 + b_s4	b_s4	19	84	60	56	63
bot1 + b_s5	b_s5	6	97	95	27	50
bot1 + b_s6	b_s6	8	97	94	22	60
bot1 + b_s7	b_s7	2	99	100	35	67
bot1 + b_s8	b_s8	15	88	69	25	46

As in Pavlidis et al. (2010), we used a broad uniform prior for θ and accepted only those realizations with K = 50 both for training and for testing. We considered the following scenarios: bot1, bot(0.02, 0.0015), D = 0.002; bot2, bot(0.02, 0.0375), D = 0.05; b_s1, …, b_s8, selective sweep within a bottleneck with Bsite = 25,000 bp; b_s1, t₀ = 0.002, t₁ = 0.0015, D = 0.002, s = 0.002, t_mut = 0.02. Here s is the selective coefficient, and t_mut is the time when the beneficial allele occurred in the population. Note that all the time indicators in Pavlidis's article are in the units of 4N generations, but 2N generations in this article. b_s2, t₀ = 0.02, t₁ = 0.0015, D = 0.002, s = 0.002, t_mut = 0.0214; b_s3, t₀ = 0.02, t₁ = 0.0015, D = 0.002, s = 0.8, t_mut = 0.0214; b_s4, t₀ = 0.02, t₁ = 0.0015, D = 0.002, s = 0.002, t_mut = 0.23; b_s5, t₀ = 0.02, t₁ = 0.0375, D = 0.05, s = 0.002, t_mut = 0.02; b_s6, t₀ = 0.02, t₁ = 0.0375, D = 0.05, s = 0.002, t_mut = 0.0214; b_s7, t₀ = 0.02, t₁ = 0.0375, D = 0.05, s = 0.1, t_mut = 0.0214; b_s8, t₀ = 0.02, t₁ = 0.0375, D = 0.05, s = 0.002, t_mut = 0.23. The other parameters n = 12, l = 50,000 bp, and ρ = 0.01 are also chosen to match those in Pavlidis et al. (2010). For each parameter set, 2000 replications were simulated. FP, false positive rate; Acc, accuracy (power of detecting a selective event). The false positive rate FP in rows 1–4 is under the bottleneck scenario bot1, whereas bot2 is used in rows 5–8. The results in Acc* provide the power when the false positive rate FP is adjusted to 0.05. The Pavlidis's FP and Pavlidis's Acc columns show the accuracy of the support vector machine-based method of Pavlidis et al. (2010). Rows 1–4 of these columns are taken from Table 3 in Pavlidis et al. (2010), whereas rows 5–8 are from Table 4.

To avoid a too optimistic picture of the performance in practice, we also present cross-testing results where training and testing parameters differ. The FP rates have been adjusted to 0.05 (Table 11). When testing for old sweeps (older than the bottleneck) (b_s4 and b_s8) while training with other scenarios, or vice versa, the power tends to be low. Classification tends to be particularly difficult in cases where the selective sweep happened much earlier than the bottleneck (see b_s4 and b_s8), and an explanation might be that the signal of the sweep gets diluted by the bottleneck event.

TABLE 12.

Training with selection vs. bottleneck and testing with selection within a bottleneck

Training data	Testing data	FP (%)	Acc (%)
bot1 + sel1	b_s1	11	96
bot1 + sel2	b_s2	11	93
bot1 + sel3	b_s3	6	99
bot1 + sel4	b_s4	1	36
bot2 + sel5	b_s5	5	94
bot2 + sel6	b_s6	5	93
bot2 + sel7	b_s7	2	99
bot2 + sel8	b_s8	2	44

Please refer to Table 10 for the definition of bot1, bot2, and b_s1, …, b_s8. sel1 and sel5, s = 0.002, t_mut = 0.02; sel2 and sel6, s = 0.002, t_mut = 0.0214; sel3, s = 0.8, t_mut = 0.0214; sel4 and sel8, s = 0.002, t_mut = 0.23; sel7, s = 0.1, t_mut = 0.0214. Here s is the selective coefficient, and t_mut is the time when the beneficial allele occurred in the population. In the simulations, we used a broad uniform prior for θ and accepted only those realizations with K = 50. For each parameter set, 2000 replications were simulated. The FP rates were computed according to bot1 in rows 1–4 and according to bot2 in rows 5–8.

TABLE 11.

Cross-testing: the power of detecting a sweep within a bottleneck if training and testing parameters do not coincide

	Testing data (%)
Training data	b_s1	b_s2	b_s3	b_s4	b_s5	b_s6	b_s7	b_s8	bot1	bot2
bot1 + b_s1	96	85	99	15	77	74	98	16	5	2
bot1 + b_s2	94	85	99	13	81	77	97	10	5	2
bot1 + b_s3	84	70	99	49	62	60	98	68	5	6
bot1 + b_s4	73	59	99	60	53	53	96	81	5	10
bot1 + b_s5	99	95	99	23	95	94	99	14	17	5
bot1 + b_s6	99	95	99	22	95	94	99	14	16	5
bot1 + b_s7	99	94	100	33	93	91	100	41	14	5
bot1 + b_s8	71	54	99	46	45	45	95	69	3	5

Please refer to Table 10 for the definition of the scenarios bot1, bot2, and b_s1, …, b_s8. The FP rates have been adjusted to 0.05 under the training null scenario. The percentages should therefore be compared with the Acc* column in Table 10.

In many situations, however, the power remains at an acceptable level, indicating to some extent the robustness of our method.

We also checked the robustness of the false positive rate with respect to the null scenario. For this purpose we again adjusted the boosting classifier to get a false positive rate of 5% under the null training scenario. When training is done under short and deep bottlenecks (bot1), long and shallow bottlenecks (bot2) without a simultaneous selective sweep are rarely misclassified and the false positive rate remains small except for bot1 + b_s4, where the sweep happened much earlier than the bottleneck (Table 11). The results in the opposite direction are less robust: Under training with long and shallow bottlenecks (bot2), short and deep bottlenecks (bot1) lead more frequently to false signals of selection. Depending on the specific alternative scenario used for training, we get false positive rates between 3 and 17% (Table 11).

As a further check for robustness, we trained under bottleneck vs. selection but tested on selection within a bottleneck without adjusting the false positive rate. Compared to the results shown in Table 10, the power decreases in b_s4 and b_s8, but remains higher than the one obtained by Pavlidis et al. (2010) in most cases. Detailed results can be found in Figure 12.

Application to real data:

We applied boosting to a small region of the maize genome. We follow an analysis by Tian et al. (2009), where they investigate 22 loci spanning ∼4 Mb on chromosome 10 and identify a selective sweep that affected this region. We implemented the two-step method and used the real sequence data as our testing data. For training, we simulated samples under the parameters estimated in Tian et al. (2009). We used in particular the estimated mutation rate θ = 0.0064 and the estimated recombination rate ρ = 0.0414.

We chose to investigate 12 of their 22 loci located at 85.65 Mb on chromosome 10, each of length 1 kb. Since the number of individuals varied slightly from 25 to 28 between the loci (Tian et al. 2009), we simply set n = 25. Training data under selection were generated with parameters chosen randomly according to sel(N(500, 200²), N(0.2, 0.1²)).

According to previous studies, maize experienced a bottleneck event and the bottleneck parameter k (population size during bottleneck/duration of bottleneck in units of generations) was 2.45 (Wright et al. 2005; Tian et al. 2009). We set t₀ = 0.02 and t₁ = 0.02 (in units of 2N generations, where N is the effective population size). We then chose D = 0.098 such that D × N/(t₁ × 2N) = 2.45.

In Tian's article, 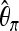, , 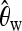and Tajima's D were computed for each locus (values at certain loci were unavailable). We used these three statistics and ignored missing values. Then we applied the two-step method using the L2fm loss. The threshold between neutrality (Y = 0) and selection (Y = 1) was 0.462, and the first-step result was f = 1.382; since f ≫ 0.462, this provides strong evidence for selection. The threshold between bottleneck (Y = 0) and selection (Y = 1) was 0.407, and the second-step result was 4.700, indicating that the signal at the considered locus cannot be explained by a bottleneck only. The result supports the findings in Tian et al. (2009), where a selective sweep was also identified. There α was estimated to be 22187.8, which is much larger than the value we used in our training data generated from (N(500, 200²)).

Learning about the relative importance of summary statistics:

One advantage of the version of boosting we used is that the approach leads to coefficients for each of the considered summary statistics. The coefficients can be used to measure the relative importance of each summary statistic. It is important to standardize the coefficients, since otherwise the estimated coefficients will depend on the scale of variation of the respective summary statistics. For the jth component of the predictor variable, X^(j), the coefficient is 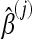, and the standardized coefficient is 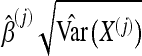. The importance of a statistic is indicated by the absolute value of its standardized coefficient. The closer a coefficient is to zero, the smaller the contribution of the statistic to the classifier. To make the results fairly independent of the randomness of an individual data set, we report the average coefficients over 10 trials, with each trial involving boosting with 500 neutral (or bottleneck) samples and 500 selection samples.

When considering the statistics at all positions simultaneously, the relative importance will depend on two components: the relative importance of different positions and the relative importance of different statistics. To get a clearer picture, we consider the different subsegments separately and use the boosting classifier on the information of only one subsegment at a time. The results can be found in Figure 6. Because iHH uses not only local information (see Figure 1), the information content for a given subsegment is higher than that for other summary statistics, especially at the border subsegments.

Figure 6.—

The relative importance of different summary statistics for the detection of selection under a fixed value of θ. Under different selective scenarios, we investigate the relative importance of our summary statistics. One way of measuring their importance is in terms of the absolute value of the coefficients given to the summary statistics by the boosting classifier. A large coefficient means that a certain statistic is very influential at the considered position for our classifier. Each graph is based on an average of 10 trials, with each trial containing 500 neutral (or bottleneck) samples and 500 selection samples. All the samples were generated with fixed θ. The relative importance of the six summary statistics was considered separately for each subsegment; that is, each time a boosting process was applied to only six statistics at a specific position.

Figure 6 provides the standardized coefficients for several scenarios. Here, we note some observations concerning the patterns shown in Figure 6:

1. For classifying between neutrality and selection, 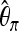plays an important role, consistently over all scenarios. On the other hand, 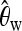plays a role only when selection happened recently, but not for old sweeps. A reason might be that the occurrence of new mutations after selection makes the relative amount of low-frequency mutations increase. But as age increases, some low-frequency mutations drift to intermediate-frequency mutations, and thus the proportion of low-frequency mutations decreases. Since 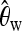should be more affected by such low-frequency mutations than 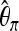(Fay and Wu 2000), 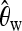becomes less important when selection gets older.

2. When discriminating against a neutral scenario, the iHH statistic seems particularly important for recent selective sweeps. If the fixation of the beneficial allele happened a longer time ago, the iHH statistic is much less important. A possible explanation is that the LD is then broken up by recombination or by the recurrent neutral mutations that occur after the fixation of the beneficial mutation.

3. When discriminating between bottlenecks and selection, 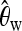seems most important, and its importance increases toward the border of the observation region. This indicates a larger difference in the number of low-frequency mutations between bottlenecks and selection farther away from the beneficial mutation. Linkage disequilibrium tends to contribute less in such a setup.

4. We also investigated the situation for samples where the number of mutations K is fixed (Figure 7). Compared with the previous samples where θ was fixed (Figure 6), there is not much difference when distinguishing between neutrality and selection. When classifying between bottleneck and selection, however, we observe differences. Since the overall number of segregating sites is now the same for the two scenarios, the classifier uses the spatial pattern of variation, leading to the spatial pattern of the coefficients shown in Figure 7.

Figure 7.—

The relative importance of different summary statistics for the detection of selection under a fixed value of K. As in Figure 6 we investigate the relative importance of different summary statistics, but here the samples were generated under a fixed number K of mutations instead of a fixed θ. Each graph is based on an average of 10 trials. Each trial contains either 500 neutral and 500 selection or 500 selection and 500 bottleneck samples.

DISCUSSION AND CONCLUSION

Boosting is a fairly recent statistical methodology for binary classification. It permits one to efficiently combine different pieces of evidence to optimize the performance of the resulting classifier. In population genetics, a natural choice for such pieces of evidence is individual summary statistics. By choosing an appropriate boosting method, one can actually learn about the relative importance of different summary statistics by looking at the resulting optimized classifier. For summary statistics that are otherwise difficult to combine (such as site frequency spectrum and LD measures), this seems to be particularly interesting.

It is well known that single population genetic summary statistics are usually not sufficient. For methods such as ABC that rely on inference from summary statistics, an important issue is the choice and/or combination of summary statistics to obtain precise estimates. A promising approach seems to be to use boosting as a first step: The situation remains challenging, though, since different summary statistics could in principle be important in different parameter ranges.

Although boosting could be applied for any set of competing population genetic scenarios, we focused on the detection of selective sweeps both within a bottleneck and within a neutral background. Such scenarios have been fairly well studied and several methods have already been proposed. It is therefore possible to judge the performance of boosting, given what is known about the performance of other methods. Our simulation results indicate that boosting performs better than other summary statistic-based methods. This indicates that boosting is able to come up with efficient combinations of summary statistics. We also applied boosting to the scenarios in Pavlidis et al. (2010), where the authors used support vector machines (SVMs) to combine the composite likelihood-ratio statistic obtained from a modified version of the SweepFinder software (Nielsen et al. 2005) with a measure of linkage disequilibrium. For sweeps both within and without bottlenecks, boosting usually provided a higher power of detection while the false positive rate was equal or lower.

Using a sliding-window approach, boosting may also provide a way to carry out genome scans for selection.

So far, our focus has been on an ideal situation where both the mutation rate and the recombination rate were constant; we considered only completed selective sweeps and no alternative types of selection; the population size was taken as either constant or affected by a bottleneck. However, in reality, a much more complex population history may have left its traces in our summary statistics, influencing the accuracy of our method. On the basis of knowledge from the current literature, we discuss how to carry out boosting-based scans for selection in the presence of such additional factors. Further simulations are needed to confirm our suggestions:

• Mutation heterogeneity: We considered regions of length 40 kb. If the mutation rates are heterogeneous within such a segment, this can lead to reduced values of θ_π and K and a positive Tajima's D, depending on how severe the heterogeneity is (Aris-Brosou and Excoffier 1996). If the extent of heterogeneity is large, this may lead to false detections of selection, since a reduced θ_π and a reduced K are also encountered under positive selection. If one suspects mutation rate heterogeneity as a possible alternative explanation for a positive classification result, one may try to resolve the issue by training the boosting classifier with mutation rates that vary from site to site according to a gamma distribution (Uzzell and Corbin 1971; Aris-Brosou and Excoffier 1996) to mimic mutation heterogeneity. On a genomic scale, the mutation rate may also vary. Scanning the whole genome with a classifier that has been trained under one single mutation rate may then give misleading results. Think, for instance, of a classifier that has been trained under a high mutation rate but is subsequently applied to DNA segments where the mutation rate has been much lower. A low level of polymorphism may then be viewed as a signal of selection. One possible solution is to divide the whole genome into segments and to scan each segment independently with a classifier that is trained under an appropriate mutation rate. Another approach that we investigated in this article is to carry out training under the same number K of mutation events that is observed at the currently scanned genome segment.

• Recombination heterogeneity: In the human genome, for instance, there is a recombination hotspot of length 1 kb approximately every 100 kb of sequence (Kauppi et al. 2004; Calabrese 2007). If the investigated region contains recombination hotspots, this will reduce the LD and may consequently reduce the power of sweep detection. Nevertheless, since the other summary statistics that use polymorphism and site frequency spectrum information are not affected, the decrease in power may be limited. An obvious option would again be to take potential recombination hotspots into account when training the boosting classifier.

• Ongoing selection (incomplete sweeps): In our simulations, the beneficial mutation was fixed when the samples were taken. If selection is ongoing, the mutation frequency spectrum will be notably different from the one under neutrality when the frequency of the beneficial allele reaches 0.6 (Zeng et al. 2006). Thus there should be a chance to detect selection when the frequency of the beneficial allele is >0.6.

• Recurrent selection: According to Pavlidis et al. (2010) recurrent selective sweeps will lead to a loss of the characteristic local pattern of selection events. On average, the sweep events will also often be quite old (Jensen et al. 2007; Pavlidis et al. 2010). Both effects suggest that the power of detecting recurrent sweeps in a region will be somewhat lower than with a single selective event.

• Background selection: Like positive selection, background selection will also reduce the polymorphism level but it will not generate high-frequency mutations (Fu 1997; Zeng et al. 2006). If we train under neutrality vs. selection and the excess of low-frequency mutations is recognized by the classifier, it is possible that background selection will be wrongly identified as positive selection. To avoid this, a two-step method should be helpful. If a sample is classified as under selection, one may want to train the classifier using both positive selection and background selection samples in a second step. When using summary statistics that measure the abundance of high-frequency mutations, we expect that the resulting classifier is able to distinguish between background and positive selection.

• Balancing selection: If the equilibrium frequency of the selected allele is not very high, it is difficult to discover balancing selection. If on the other hand the equilibrium frequency is fairly high (e.g., 75%) (Zeng et al. 2006), the signature of balancing selection resembles that of positive selection. After the selected allele reaches its equilibrium frequency, some hitchhiking neutral alleles will also have high frequencies and will stay segregating for a longer period than under a selective sweep. This is because their frequency will be lower when reaching equilibrium, requiring more time for fixing them by drift (Zeng et al. 2006). Thus our method should also detect balancing selection at high equilibrium frequency, and its age will affect the efficiency less than under positive selection.

• Population growth: Population growth will cause an excess of low-frequency variants, but will not affect high-frequency mutations (Fu 1997; Zeng et al. 2006). So like bottlenecks and background selection, a two-step method may be helpful to rule out population growth as an alternative explanation.

• Population shrinkage: Population shrinkage will cause the number of low-frequency variants to be smaller than those of intermediate and high frequency (Fu 1996; Zeng et al. 2006). Since this is quite different from the signature caused by a selective sweep, we do not expect large problems for shrinking populations.

• Population structure: When a population is structured, there may be an excess of low- or high-frequency derived alleles especially if the sampling scheme is unbalanced among the subpopulations (Zeng et al. 2006). In addition, population structure may increase LD (Slatkin 2008). This might obviously affect the results obtained from our boosting classifier and further research is needed to use boosting classifiers in the context of structured populations. Adding F_st as a summary statistic may obviously help in this context.