Landscape of finite-temperature equilibrium behaviour of curvature-inducing proteins on a bilayer membrane explored using a linearized elastic free energy model

Abstract

Using a recently developed multiscale simulation methodology, we describe the equilibrium behaviour of bilayer membranes under the influence of curvature-inducing proteins using a linearized elastic free energy model. In particular, we describe how the cooperativity associated with a multitude of protein–membrane interactions and protein diffusion on a membrane-mediated energy landscape elicits emergent behaviour in the membrane phase. Based on our model simulations, we predict that, depending on the density of membrane-bound proteins and the degree to which a single protein molecule can induce intrinsic mean curvature in the membrane, a range of membrane phase behaviour can be observed including two different modes of vesicle-bud nucleation and repressed membrane undulations. A state diagram as a function of experimentally tunable parameters to classify the underlying states is proposed.

1. Introduction

Understanding and quantifying the coupling between external signals and intracellular signal transduction is crucial in many biological applications such as receptor trafficking, internalization of targeted pharmacological nanocarriers, cell–cell communication, etc. There is growing appreciation that such processes are regulated and transduced by the interaction of proteins and membranes [1].

In the modeling of lipid-bilayer membranes, previous studies have followed either a particle-based simulation approach [2] or a field theoretic approach [3-5]. In the latter approach, the energetics of deformations in planar membranes as well as membranes with intrinsic curvature has been extensively described in previous works by using the Helfrich Hamiltonian. Based on the Helfrich description and through theoretical formalisms and simulation algorithms, the dynamics of elastic membrane sheets in the overdamped limit including hydrodynamic coupling to surrounding solvent and arbitrary external forces have been introduced in previous studies [6-10]. The infinitely thin elastic sheet assumption has also been relaxed and the inter-layer friction and slippage between the lipid monolayers have been incorporated [10-12]. Mechanistic models for cell membrane deformation and vesicle budding in the cellular context based on the elastic free energy formulations have also been proposed [13,14].

On the experimental front, direct measurements of bending-mediated force transduction and molecular organization in lipid membranes based on interferometry and fluorescence measurements have been reviewed [15]. Different modes by which proteins modulate the curvature of membranes have also been discussed by McMahon and Gallop [16]: membrane curvature can be modulated by changes in lipid composition, the oligomerization of curvature scaffolding proteins and the reversible insertion of protein regions that act like wedges or amphipathic sub-domains in membranes. The molecular dynamics and mosaic organization of the plasma membrane and their implications in cellular physiology primarily focused on studies involving fluorescent labeling and imaging have recently been reviewed [17]. These timely reviews of the experimental progress have motivated the development of models for protein diffusion in ruffled surfaces [18] and the simultaneous diffusion of protein and membrane dynamics [19-22]. In such models, there is one-way coupling between the membrane dynamics, i.e. the protein dynamics as the membrane topology impacts the diffusion of the proteins.

Recently, we extended these simultaneous protein diffusion and membrane motion models to treat the case of curvature-inducing proteins diffusing on the membrane [23]. The new aspect introduced in our continuum membrane model is the two-way coupling between the protein and membrane motion. In this case, the membrane topology not only influences the protein diffusion by presenting a curvilinear manifold, but also presents an energy landscape for protein diffusion. The protein diffusion in turn impacts membrane dynamics because the spatial location of the proteins determines the intrinsic curvature functions and hence the elastic energy of the membrane [23]. In this article, we apply this methodology and explore the equilibrium behaviour of bilayer membranes under the influence of cooperative effects induced by the diffusion of curvature-inducing proteins.

2. Methods

The models employed in this study were introduced and described in detail in our previous work [23]. Here we summarize the salient features of our model in relationship with existing models in related published studies.

2.1. Model for sampling membrane deformations in the canonical ensemble

We describe the relaxation of the membrane via a time-dependent Ginzburg–Landau (TDGL) model [3,24]. The membrane is represented in the Monge gauge, i.e. as a function z = z(x, y, t), where z is the height of the deformed membrane patch. The membrane energy is represented by the Helfrich Hamiltonian E, which treats the membrane as a single thin sheet with the assumption of unrestricted internal fluidity [25]. A model treating the membrane as a pair of slightly compressible monolayers bound together with non-instantaneous lipid density relaxation has also been proposed [11]. A full sophisticated model for cytoskeleton fortified membranes has also been developed [26] and applied to erythrocyte deformation [27]. This model includes the shear elasticity of the cytoskeleton in combination with the Helfrich Hamiltonian. However, we have followed the work of Liu et al. [14] and Lee et al. [28], who modeled the cytoskeleton fortified membrane using the Helfrich Hamiltonian with an effective bending rigidity five to 10 times larger than that of the bare membrane and neglected the contribution of shear elasticity of the cell membrane arising due to the cytoskeleton.

The Helfrich Hamiltonian is a sum of three contributions: the membrane bending energy due to deviation of the membrane mean curvature from the spontaneous curvature, the membrane energy due to its Gaussian curvature, and the frame energy due to the frame tension at the boundary of the membrane patch

$$E=\mathit{\int }\mathit{\int }(\frac{\kappa }{2}{(H-H_0)}^2+\overline{\kappa }K)\mathrm{d}A+\gamma (|A-A_{\mathrm{flat}}|),$$ (1a)

where A is the total area of the membrane, dA is the differential area element and A_flat is the projected area of the membrane patch on a plane. The membrane Hamiltonian depends on the frame tension γ, the bending rigidity κ, the splay modulus κ̄, and the inhomogeneous intrinsic curvature field H₀(x, y). We consider only those membrane shapes for which the membrane topology does not change and hence the contribution of Gaussian curvature to the Helfrich Hamiltonian is a constant and is neglected.

The linearized Helfrich Hamiltonian E in Monge or Cartesian gauge, obtained by linearizing the expression for mean curvature and the expression for the differential area element in Equation (1a), associated with membrane elasticity [3] is then given by [4]

$$E=\mathit{\int }\mathit{\int }\left[\right(\frac{\gamma }{2}+\frac{\kappa }{4}{H}_0^2){(\nabla z)}^2+\frac{\kappa }{2}{({\nabla }^{2}z-H_0)}^2]\mathrm{d}x\mathrm{d}y.$$ (1b)

The values of κ, γ for a cytoskeleton fortified phospholipid bilayer cell membrane are obtained from prior studies [28]: γ = 3 μN m⁻¹, κ = 400 k_BT. The value of intrinsic curvature H₀ is taken to be zero unless curvature-inducing proteins are membrane-bound, see below. The fictitious dynamics of the membrane is described in terms of a scalar mobility factor M, thermal noise ζ, and the linearized membrane Hamiltonian E functional associated with membrane elasticity in Equation (1b), given by the time-dependent Ginzburg–Landau (TDGL) model [24]:

$$\frac{\partial z}{\partial t}=-M\frac{\delta E}{\delta z}+\zeta .$$ (2)

Equation (2), described in terms of the scalar mobility factor (M = 10⁻⁵ μm⁴ s⁻¹ (k_BT)⁻¹ [29] in our simulations), represents fictitious dynamics because it ignores the important contribution from the hydrodynamic interaction with the surrounding fluid as well as the viscous dissipation within the membrane. However, for the linearized elastic energy functional E, and by making the choice that the noise term in Equation (2) is generated by drawing a random number from a Gaussian distribution with zero mean and with variance depending on the temperature T and mobility factor, i.e. 〈ζ〉 = 0, 〈ζ(0)ζ(t)〉 = 2k_BTMδ(t), the membrane configurations generated by Equation (2) are consistent with the canonical ensemble with probability ∝exp(−E/k_BT). Moreover, we have ensured that changing the value of M by one order of magnitude does not change the equilibrium properties (such as radial distribution functions) we calculate. We stress that, in the present study, we are only interested in the equilibrium sampling of the deformations in the linearized elastic free energy model; however, in the future, an extension to describe the model dynamics of the membrane by including the hydrodynamic interactions can be made by closely following the formalisms briefly discussed in the introduction [6-12].

We note that while reducing the variational problem to a partial-differential form, we assumed that |∇_z|² < 1, which states that the solution of linearized TDGL (in Monge gauge) is valid only when the difference in height of adjacent grid points on the membrane is less than the spatial grid size. Moreover, the Monge gauge (i.e. representing z as a function x, y) does not support multi-valued topologies of z that are necessary to describe large membrane deformations such as membrane overhangs. Thus the model we are exploring is inherently limited in only being able to describe early nucleation events such as the formation of a vesicle-bud rather than tracking the evolution of the entire vesicle. Still, we consider it worthwhile to implement this linearized membrane elastic model and combine it with diffusing curvature-inducing functions (see Sections 2.2 and 2.3), with the outlook that it will enable us to widely explore the tunable parameter space and to classify the emergent membrane response in this approximate, but tractable, benchmark model.

2.2. Model for protein–protein interaction and protein–membrane interaction

Protein molecules are approximated as structureless hard spheres and non-specific protein–protein interactions are considered only as size exclusions (i.e. repulsive interactions on the scale of the size of the solvated protein). The three-dimensional space is discretized into a lattice using a rectilinear grid with grid size corresponding to the size exclusion parameter, a₀ = 20 nm. Consistent with the evidence in the literature [30], specific interactions between the proteins (i.e. protein–protein binding) are not considered and the parameter for size exclusion is obtained from crystallographic data [30]. The lattice points are categorized as either belonging to the extracellular domain, intracellular domain, or the membrane. This division is time-dependent because the membrane can undulate, deform, and stretch as a function of time, in response to thermal fluctuations and protein-mediated interactions. The density of proteins bound to the membrane is given by the dimensionless number ρ* = N^bounda₀²/A. Here, A is the total projected area of the membrane, a₀ is the lattice spacing, ρ* is the reduced surface density, and $N_i^{\mathrm{bound}}$ is the number of membrane-bound proteins.

Proteins such as epsin and Ap180 interact with the membrane by inducing curvature in the membrane [30,31]. To capture this protein-mediated membrane deformation, in the vicinity of a membrane-bound protein, the membrane is assumed to have an intrinsic curvature H₀(x, y). The form of this localized function is assumed to be Gaussian, with a range R and a magnitude C₀; i.e. for a protein located at (x₀, y₀) on the membrane, H₀(x, y) = C₀ exp[−2{(x − x₀)²+(y − y₀)²}/R²]. We note that the range R = 2*σ, where σ is the standard deviation (characteristic length) of the decay of the curvature-inducing Gaussian function. A multitude of R and C₀ values are explored in our simulations. R is the range of the curvature induction (reported in units of nm or in scaled form R* = R/a₀, where a₀ is the lattice length). C₀ is the maximum curvature (1/radius) reported in units of μm⁻¹.

At first glance, the hardsphere nature of protein–protein interactions considered in our model appears too simplistic. However, there are several factors unique to the protein–membrane system that justify the use of such a simplistic assumption. The equilibrium behaviour of the system is dominated by the membrane-mediated protein–protein interaction dictated by R rather than by direct protein–protein interactions (which is constituted by van der Waals, electrostatic, hydrogen-bond terms) dictated by a₀. To support these claims, Figure 1 shows that the membrane-mediated interaction is dominated by repulsion at range R, while Figure 2 shows that, owing to this repulsion, the distance of closest approach between two protein molecules on the membrane is R and not a₀. Thus, the nature of the short-range potential is not expected to dictate the thermodynamic behaviour, as long as there is no overwhelming short-range attraction through specific interactions between two proteins. The fact that curvature-inducing proteins such as epsins have no specific interactions with each other (i.e. no overwhelming attraction at short range) was established by a prior experiment that reported that these proteins act as monomers [30]. Together, these facts justify the use of the hard-sphere potential, as they imply that the system behaviour at the mesoscale is impervious to the nature of direct short-range protein–protein interactions at the nanoscale.

Figure 1.

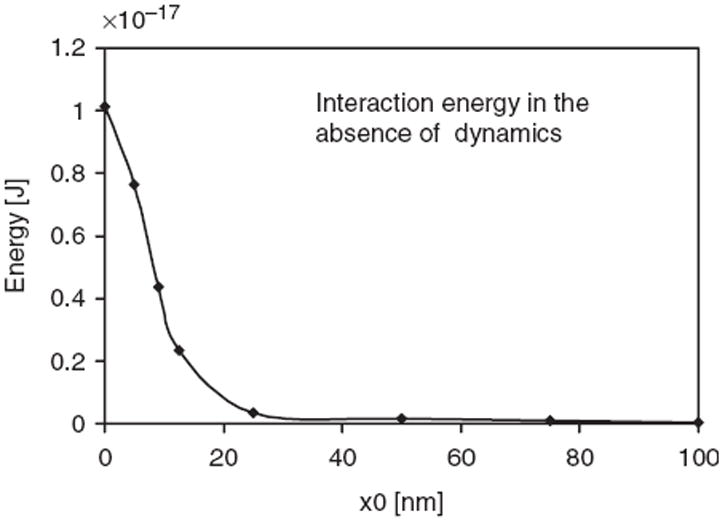
Interaction energy (total energy when two membrane-bound proteins are separated by a distance r minus twice the energy of the membrane with one protein bound) between two membrane-bound stationary proteins at different distances of relative separation, r. Each protein induces curvature according to the H₀ function in Equation (4); here C₀ = 20 m⁻¹ and R = 40 nm.

Figure 2.

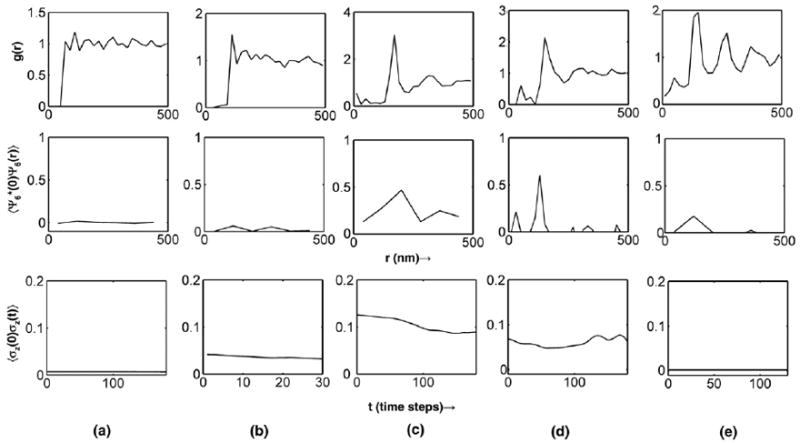
(Top row): Radial distribution functions showing liquid-like order with the packing determined by the range R. (Middle row): Orientational correlation functions up to 4R. (Bottom row): Height correlation functions showing the relaxation time associated with the dominant membrane undulation mode. (a) ρ* = 0.03, R/nm = 40, C₀ × μm = 15; (b) ρ* = 0.008, R/nm = 60, C₀ × μm = 60; (c) ρ* = 0.016, R/nm = 100, C₀ × μm = 20; (d) ρ* = 0.012, R/nm = 80, C₀ × μm = 30; (e) ρ* = 0.03, R/nm = 80, C₀ × μm = 5.

2.3. Model for protein diffusion

Our model for sampling different protein conformations is via the simulation of probabilistic hopping between discrete ‘lattice’ sites. The hopping steps are generated via a kinetic Monte Carlo (KMC) scheme [32] on the discretized lattice, in which each hop of each protein (or diffusion) to a neighbouring lattice site is treated as an elementary chemical reaction with an associated rate prescribed by

$$\mathit{rate},a_{\mu }=\frac{4D}{a_0^2(1+{(\nabla z)}^2)}\exp (-\frac{\Delta E}{k_{B}T}).$$ (3)

Here, $4D/a_0^2$ is the bare hopping rate (due to free diffusion in a planar manifold in two dimensions), the term 1 + (∇z)² corrects for the curvilinear manifold due to membrane deformation to the first-order approximation, and the exponential factor accounts for the protein diffusion in an energy landscape. The energy term in the exponential represents the work done as the protein drags the intrinsic curvature field to the neighbouring lattice location for the fixed membrane configuration, where the term ΔE (for protein hop along the x-direction) is given by

$$\begin{array}{lll}\mathrm{\Delta }E& =& \frac{\partial E}{\partial x_{0i}}\mathrm{\Delta }{x}_{0i}=\frac{4\kappa C_0\mathrm{\Delta }{x}_{0i}}{R^2}{\displaystyle \mathit{\int }{\displaystyle {\mathit{\int }}_A{\mathrm{e}}^{-2\{[{(x-x_{0i})}^2+{(y-y_{0i})}^2]/R^2\}}}}\times (H_0+\frac{H_0{(\nabla z)}^2}{2}-{\nabla }^{2}z)(x-x_{0i})\mathrm{d}x\mathrm{d}y,\\ H_0& =& {\displaystyle \sum _i{C}_0{\mathrm{e}}^{-2\{[{(x-x_{0i})}^2+{(y-y_{0i})}^2]/R^2\}}}.\end{array}$$ (4)

The term ΔE in Equation (4) prescribes the energy landscape for the diffusion of curvature-inducing proteins in the linearized elastic model and summarizes the two-way coupling present in this model, which is not present in the related continuum elastic membrane models in the literature. Through the ΔE and the 1 + (∇z)² terms, the membrane deformation influences protein diffusion. Through the H₀ function (which depends on the positions of all membrane-bound curvature-inducing proteins i, namely x_0i, y_0i), the proteins influence membrane relaxation in Equation (2). Together, these effects summarize the two-way coupling between protein motion and membrane motion on the equilibrium behaviour.

The bulk and lateral membrane-bound diffusion coefficients (D) for translation are taken from experimental data [28,33,34] (bulk diffusion coefficient D = 10 μm² s⁻¹, membrane-bound bare diffusion coefficient D = 1 μm² s⁻¹). The initial distribution of proteins on the membrane surface is random, consistent with size exclusion. We carry out KMC simulations for $N~\mathrm{\Delta }t/(a_0^2/D)$ steps (such that the total time elapsed in the KMC simulations is equal to Δt, the time-step of TDGL integration, we choose Δt = 10⁻³ s) and we determine the steady-state profiles 〈H₀〉_N (by time-averaging over the course of the N steps of the KMC simulations) at every time-step of integration involving the membrane dynamics (TDGL) equations. Thus, the TDGL equations are propagated in time, based on time-averaged interactions dictated by 〈H₀〉_N resulting from the KMC simulations. The temperatures T in the TDGL and KMC schemes are made equal to ensure thermal equilibrium. Details of the complete model, numerical simulation, implementation, and stability analysis associated with our KMC-TDGL simulations are available in our recent publication [23]. The simulation results in the propagation of the protein as well as membrane degrees of freedom in the canonical ensemble (see Movie S1 of the Supplementary Material for the visualization of the KMC-TDGL integrated membrane and protein dynamics (available on the online article webpage)).

2.4. Spatial and temporal correlation functions

To capture and quantify the emergent response of the membrane dynamics under the influence of the proteins, we compute several correlation functions.

1. Radial distribution function (see Figure 2, top row). The spatial organization of the proteins bound to the membrane is recorded by calculating the radial distribution function g(r) = ρ*(r)/〈ρ*〉, where the quantity in the numerator is the surface density of membrane-bound proteins at a particular location and that in the denominator is its spatial average.

2. Orientational correlation function [35] (see Figure 2, middle row). This is defined as $\langle {\mathrm{\Psi }}_6^{\ast }(0){\mathrm{\Psi }}_6(r)\rangle$, where Ψ₆(r) is given by Σ_j exp(i6θ_j(r)). Here, i = (−1)^1/2, the index j runs from 1 to the number of nearest neighbours to any given membrane-bound protein at location r, and θ_j(r) is the angle formed by the projection of the line joining the nearest neighbours (termed the nearest neighbour bond) on the xy plane with the x axis. Nearest neighbour pairs are identified as those pairs of molecules separated by a distance that falls in the range of the first peak of the g(r) function. The quantity $\langle {\mathrm{\Psi }}_6^{\ast }(0){\mathrm{\Psi }}_6(r)\rangle$, therefore, measures the persistence of bond-orientational correlations (or hexagonal ordering) among the membrane-bound proteins.

3. Dynamical correlation functions (see Figure 2, bottom row). These yield the membrane relaxation times and reflect the dynamical state of the system. The membrane height autocorrelation function (see Figure 2, bottom row) is defined as 〈σ_z(0)σ_z(t)〉, where σ_z(t) (see Figure 3) is the standard deviation of the height profile z(x, y) of the membrane at each spatial location. In our definition, the average of the height is always 0, i.e. the global translation is removed from the trajectories at time t. The membrane height autocorrelation function is sensitive to any global rearrangement in membrane geometry and yields the relaxation time associated with such reorganization. Again, we note that time t is fictitious as we ignore hydrodynamic interactions and the calculation of correlation functions is merely a numerical tool to assess convergence.

Figure 3.

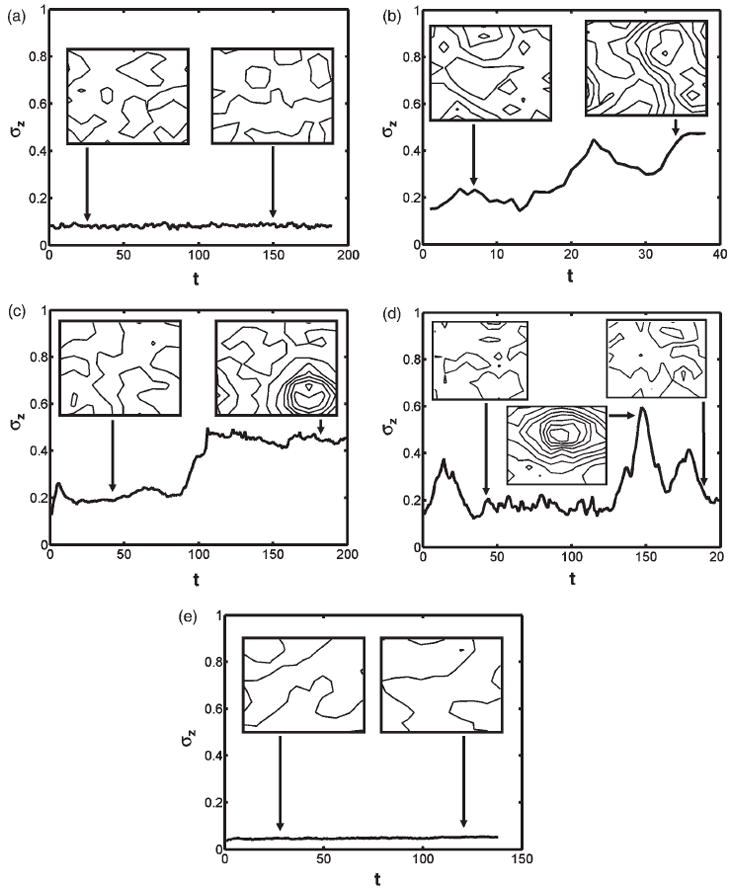
Standard deviation of the height profile as a function of simulation time, t. (a)–(e) correspond to cases (a)–(e) of Figure 2. Insets in each panel depict the contours of the membrane height profile (as well as a snapshot of the membrane profile) at the indicated simulation time. Adjacent contour lines have a height difference of 0.5 Å.

Even though it is more traditional to perform a Fourier analysis and compute the spectral intensity function 〈|z(q)|²〉 – here z(q) is the Fourier transform of the membrane surface z(x, y) – such a scaling function is only available when the curvature-inducing proteins act independent of one another and not coupled to membrane dynamics [36] and is not available from theory for the case we are considering, namely when the curvature-inducing functions are themselves diffusing and coupled to membrane motion through Equation (4). In the absence of curvature-inducing functions, 〈|z(q)|²〉 scales as [37] k_BT/[κq⁴ + γq²], and we have indeed verified this scaling by performing the TDGL of the free membrane and subsequently the Fourier analysis (data not shown); in fact, the successful reproduction of this scaling was taken as an indication of the correctness of the implementation of our numerical TDGL code. We also note that the KMC code was validated by ensuring that the mean-squared displacement of the bound proteins on the flat membrane under zero intrinsic curvature followed a linear relationship with time.

3. Results and discussion

3.1. Potential of mean force between two membrane-bound proteins

Most of the previous analyses have shown that membrane-deformation-mediated energies tend to be repulsive and should prevent, rather than promote, the formation of protein dimers or clusters. Aranda-Espinoza et al. have previously calculated the membrane-mediated interaction between curvature-inducing proteins [38]. The authors used a combination of integral equation theory to describe the spatial distribution of the membrane-bound proteins and the linearized elastic free energy model (considered in this work) and reported that the interaction between two membrane-bound curvature-inducing proteins is dominated by a repulsive interaction. Consistent with these published reports, the calculated binding energy between two membrane-bound proteins (see Figure 1) from our model is also dominated by repulsive interactions governed by the range of the curvature-inducing function R. The profile for the interaction energy in Figure 1 closely matches the calculations of Aranda-Espinoza et al. [38]; this agreement serves as a validation of our model and calculations.

Recently, Kozlov has discussed how the effect of fluctuations can change the repulsive nature of the interactions [39]. The author’s discussion is based on the premise that any membrane protein locally restrains thermal undulations of the lipid bilayer. Such undulations are favoured entropically, and so this increases the overall free energy of the bilayer. Neighbouring proteins collaborate in restricting the membrane undulations and reduce the total free energy costs, yielding an effective (membrane-mediated) protein–protein attraction. Indeed, for the linearized free energy model, we can compute the second variation of energy (note that, at equilibrium, the first variation is zero, while the second variation governs the stiffness of the system against fluctuations) to explicitly show that the presence of a protein (or, equivalently, a curvature-inducing function) leads to a localized suppression of membrane fluctuations. Namely,

$${\delta }^{2}E(z,\eta )=\frac{{\mathrm{d}}^2}{\mathrm{d}{\epsilon }^2}\left[\mathit{\int }\mathit{\int }\mathrm{d}x\mathrm{d}y\frac{\kappa }{2}{\{{\nabla }^2(z+\epsilon \eta )-H_0\}}^2,+(\frac{\gamma }{2}+\frac{\kappa }{2}{H}_0^2){\{\nabla (z+\epsilon \eta )\}}^2\right],$$

which reduces to

$${\delta }^{2}E(z,\eta )=\mathit{\int }\mathit{\int }\mathrm{d}x\mathrm{d}y\kappa {\{{\nabla }^2\eta \}}^2+(\gamma +\frac{\kappa }{2}{H}_0^2){\{\nabla \eta \}}^2.$$ (5)

For any real-valued function η, the integrand is always positive and, hence, the second variation of energy is positive, which implies that, at equilibrium, the energy is indeed minimized. Equation (5) also suggests that the second variation of energy increases with increasing H₀, thus a larger spontaneous curvature leads to higher stiffness of the membrane and would result in smaller height fluctuations. This provides for the possibility that our linearized free energy model can support an entropically mediated protein–protein attraction. The outcome of the interplay between the attractive entropic forces and the repulsive energetic forces is context specific as both have the same dependence on the protein–protein distance, and their absolute values differ only by coefficients with similar values. Thus, based on Equations (1b) and (5), we expect that the potential of mean force between membrane-bound proteins (which is governed by this balance) will be strongly dependent on the magnitude and range of the curvature-inducing function (i.e. C₀ and R) as well as on the density ρ*; in particular, for a certain regime spanned by these parameters (for which entropic effects dominate over the energetics) we can expect a net attractive force favouring protein clustering (see Section 3.3). We emphasize that these results are not new to our work and have been discussed before [2,38,39] in other contexts and we have taken the agreement in trends between our calculations and these prior works as a validation of our model and simulations. It is also worth mentioning for completeness that Chou et al. [40] have extended the energetic analysis to membrane-bound proteins that have a non-circular cross-sectional shape and to local membrane deformation with a saddle shape (negative Gaussian curvature) and have shown that, in such cases, the interactions can be attractive even without considering fluctuations.

3.2. Emergent membrane response to curvature-inducing proteins

Exploring a range of values of ρ*, R (a lower valued range mimics the curvature induced by an individual protein or protein multimers, while a higher valued range mimics the curvature induced by a clathrin coat assembly) and C₀ in a series of KMC-TDGL simulations (other parameters, namely γ, κ, M, and T, are fixed at values corresponding to a cytoskeleton-fortified phospholipid bilayer membrane at T = 300 K), we find varying system behaviour with respect to the membrane-height fluctuations; see Figures 3(a)–(e) and Movies S2–S5 of the Supplementary Material (available on the online article webpage), which we use to delineate regions in parameter space with markedly different emergent behaviour.

The parameter regime [0.0 ≤ ρ* ≤ 0.03, 20 ≤ R/nm ≤ 80, 10 ≤ C₀ × μm ≤ 40] represents the conditions under which regular thermal undulations of the membrane are captured and no nucleation of a vesicle-bud is observed. The evolution of the standard deviation in membrane height, i.e. σ_z(t) typical of the emergent membrane-height fluctuations in this regime, is provided in Figure 3(a). The insets depict the membrane-height profile as a contour plot (points along a contour have the same height z and adjacent contours differ by 0.5 Å in z) at a single snapshot of the simulation time indicated by the corresponding arrows. In particular, the insets show regular undulations and no systematic patterns in the membrane-height profile. In contrast, the membrane-height profiles in the parameter regime [0.008 ≤ ρ* ≤ 0.016, 40 ≤ R/nm ≤ 100, 40 ≤ C₀ × μm ≤ 60] show patterns of systematic vesicle-bud formation even under a low density of membrane-bound proteins; a profile of the emergent membrane response typical of this regime is depicted in Figure 3(b); in particular, the system evolves from a state of low σ_z in which no vesicle-bud is formed (left inset) to one of high σ_z in which a vesicle-bud appears (right inset). Thus tracking the transition of the σ_z value appears to be a reasonable indicator (order parameter) in identifying regimes that support vesicle-bud formation (see also Movie S2). The parameter regime [0.012 ≤ ρ* ≤ 0.024, 80 ≤ R/nm ≤ 100, 10 ≤ C₀ × μm ≤ 30] also supports vesicle-bud formation (see a typical scenario in Figure 3(c) and Movie S3), but at lower values of C₀ and higher values of R, ρ* relative to the previous case discussed. However, in contrast to the previous case (namely, Figure 3(b) and Movie S2), the relatively higher density of membrane-bound proteins needed to elicit the transition (Movie S3) is suggestive of a cooperative process leading to vesicle-bud formation (see Section 3.3). We note that the simulations in the regime [0.008 ≤ ρ* ≤ 0.012, R/nm = 80, 20 ≤ C₀ × μm ≤ 30] also supported vesicle-bud formation, but unlike the previous two cases discussed (in which the vesicle-bud once formed was stable for the rest of the simulation), the bud was only metastable, suggestive of a metastable state. The typical profile of this behaviour is depicted in Figure 3(d) and Movie S4. Finally, in the parameter regime [0.024 ≤ ρ* ≤ 0.03, 60 ≤ R/nm ≤ 80, 0 ≤ C₀ × μm ≤ 10] (see a typical profile in Figure 3(e) and Movie S5), the evolution of the membrane-height profile suggested a state of repressed membrane undulations at a high density of membrane-bound proteins.

3.3. Cooperativity in protein–protein interaction

In order to relate the context-dependent nature of the membrane-mediated protein–protein interaction (discussed in Section 3.1) on the emergent membrane-height profile evolution (Section 3.2), we further investigate the form of the potential of mean force (i.e. effective free energy of membrane-mediated interaction) between two membrane-bound curvature-inducing proteins by calculating the two-dimensional radial distribution functions (see Figure 2 (top row) for the range of parameters ρ*, R, and C₀ explored in Section 3.2). The radial distribution functions are characterized by repulsion between membrane-bound proteins at distances of R at which the range of the intrinsic curvature functions overlap. This parameter sets the dominant scale for the spatial localization and packing of the proteins on the membrane, and in a density-dependent fashion we observe liquid-like structuring. We note that, at very short distances (equal to the protein exclusion diameter a₀), there is repulsion due to protein–protein overlap; however, due to the repulsion at R, which is greater than a₀, this regime is seldom explored in protein conformations (see Figures 2(a) and (b)). However, at moderate-to-high densities and moderate values of C₀ (Figures 2(c)–(e)), the g(r) is non-zero for r < R and the repulsive energetic barrier is overcome to localize the protein molecules at these short distances: for these cases, we observe correlations between proteins at two length scales, namely that of the exclusion diameter a₀ and that of the range of interaction R.

It is notable that, under the conditions of Figure 2(b), which support stable vesicle-bud formation, the localization of proteins at distances less than R is not a necessity. Moreover, the vesicle-bud formation is sustained even without any significant clustering of proteins, as evidenced by the lack of structure in the g(r) function. These characteristics suggest that the vesicle-bud formation under these conditions does not require any significant degree of cooperativity in protein–protein interaction and that, in fact, the large curvature (C₀) induced by each individual protein is the primary driver of vesicle-bud formation. Hence, we term this mode of nucleation ‘NWC’ or nucleation without cooperativity.

In contrast to the NWC regime, it is clear that the nucleation of the vesicle-bud in Figures 2(c) and (d) is accompanied by significant spatial correlations, as evidenced by the peaked g(r) functions, suggesting protein–protein cooperativity as the orchestrator of the nucleation events. In order to determine if the induction of spatial ordering leads to spatial patterning of the membrane-bound protein molecules, we calculate the orientational correlation functions (see middle row of Figure 2). Intriguingly, the orientational correlations are pronounced and significant only for Figures 2(c) and (d) and are practically absent in Figures 2(a), (b), and (e). It is clear that the presence of orientational correlations under the regime of moderate C₀ and ρ* correlates with the induction of vesicle-bud nucleation. Moreover, the nucleation event leads to the formation of a stable bud only if the orientational correlation persists beyond r₀, the location of the first peak in g(r) (Figure 2(c) and Movie S3), but the nucleated bud is only metastable and the system returns to the undulating membrane phase when this persistence is absent (Figure 2(d) and Movie S4). We therefore conclude that, in addition to protein co-localization, spatial patterning that sustains short-range orientational order beyond the first coordination shell is a necessary condition for the stabilization of the nucleated vesicle-bud. We term this regime of vesicle-bud nucleation as nucleation via orientational ordering or ‘NVOO’. The requirement of sustained spatial and orientational correlations, which necessitates the involvement of multiple membrane-bound proteins, is indeed suggestive of a cooperative phenomenon associated with the NVOO nucleation event. We note that this notion of cooperativity emerging from our simulations is consistent with the analysis of Kim et al. [41], who have shown using an energetic analysis that, in the zero temperature limit, clusters of larger than five membrane-bound curvature-inducing proteins can be arranged in energetically stable configurations. Among the regimes exhibiting no orientational correlations (namely, Figures 2(a), (b), and (e)), the regime associated with Figure 2(e) is unique because the orientational correlations are absent despite the strongest manifestation of spatial correlations. Moreover, at the high density of membrane-bound proteins in this regime, the membrane-height fluctuations are repressed (see Figure 3(e) and Movie S5), and the membrane autocorrelation function is flat, suggesting a suppressive behaviour in membrane undulations (see Figure 2, bottom row). We term this state of membrane fluctuations as ‘RU’ for repressed undulation.

4. Conclusion

The trace of short-range positional and orientational order in response to parameter variation is plotted in Figure 4(a): the plot depicts the values of g(r = r₀) and Ψ₆(r = r₀), where r₀ is the location of the first peak of g(r). The different symbols represent different manifestations of membrane dynamics; the unfilled circles [0.012 ≤ ρ* ≤ 0.024, 80 ≤ R/nm ≤ 100, 10 ≤ C₀ × μm ≤ 30] correspond to NVOO, squares [0.008 ≤ ρ* ≤ 0.012, R/nm = 80, 20 ≤ C₀ × μm ≤ 30] to NVOO with only a metastable bud, and the filled hexagons [0.008 ≤ ρ* ≤ 0.016, 40 ≤ R/nm ≤ 100, 40 ≤ C₀ × μm ≤ 60] correspond to NWC. The diamonds [0.0 ≤ ρ* ≤ 0.03, 20 ≤ R/nm ≤ 80, 10 ≤ C₀ × μm ≤ 40] represent conditions under which no nucleation (or ‘NoN’) is observed, and the triangles [0.024 ≤ ρ* ≤ 0.03, 60 ≤ R/nm ≤ 80, 0 ≤ C₀ × μm ≤ 10] correspond to RU. The traces in Figure 4(a) further support the previously stated trend that the induction of spatial correlation at larger densities of membrane-bound proteins [0.012 ≤ ρ* < 0.024] leads to the induction of short-range orientational ordering only under certain conditions (see unfilled circles and squares) and that, for large values of curvature induction (i.e. C₀ × μm ≥ 40), vesicle budding occurs even in the absence of positional and orientational order (filled hexagons in Figure 4(a)).

Figure 4.

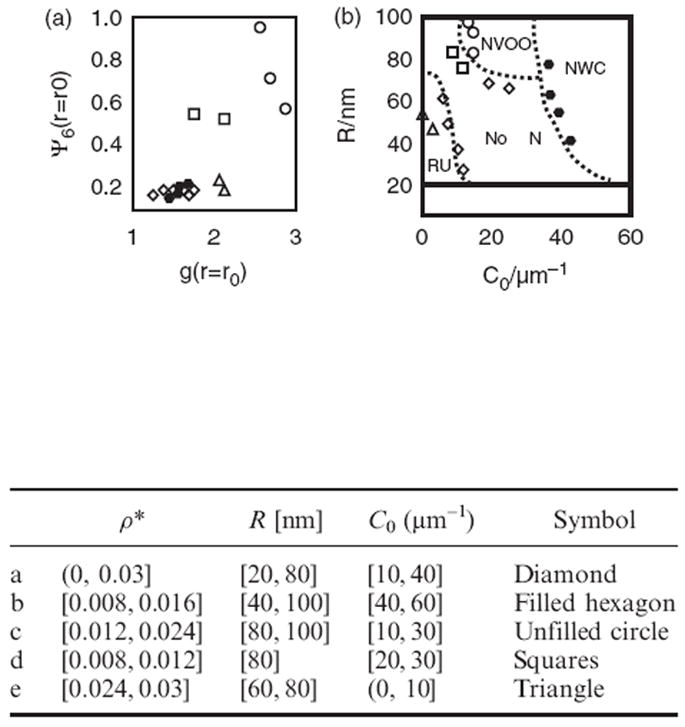
(a) Trace of spatial and orientational correlations in response to changes in tunable system parameters ρ*, R, and C₀. (b) Global state diagram for classifying membrane state behaviour based on the observations recorded in (a).

Subject to the well appreciated approximations of the linear elastic model (described in Section 2), the analysis of the collective behaviour of protein-mediated membrane-height profile fluctuations leads to the development of a global state diagram when classified and plotted in terms of the tunable parameters, namely C₀, R, and ρ* (see Figure 4(b)). The state boundaries (dotted lines) are drawn approximately to separate symbols (regions) of distinct emergent dynamic behaviour. The different symbols in Figure 4(b) have a one-to-one correspondence with those in Figure 4(a) and the dotted lines are a guide to the eye rather than representing co-existence lines; free energy estimates or the challenging task of equating chemical potentials have not been carried out. The state diagram depicts two regimes showing nucleation of vesicle-buds via distinct mechanisms (NVOO and NWC), the regime showing repressed undulations of the membrane at high protein density (RU), and an intervening regime showing no nucleation (NoN) with only regular thermal undulations in the membrane.

Several measures for experimental validation of the reported palette of membrane behaviour and the predicted state diagram are possible. In particular, the surface density ρ* can be tuned by varying the protein concentration, and C₀ and R by studying different protein variants (wildtype vs. mutants) of epsin, AP180. The physical characteristics of the protein–membrane interaction (i.e. C₀ and R values) may be characterized by a combination of microscopy and diffraction experiments [42,43]. In addition to the C₀ and R values, the frequency response of the system can be obtained from dielectric relaxation spectroscopy [44,45]. Direct observation of membrane undulation and vesicle budding can also be obtained via defocusing microscopy [46,47]. Collectively, these measures can yield an experimental phase diagram analogous to Figure 4(b).

In future work, we plan to address the case of extreme curvatures by relaxing the linearization assumption in the elastic free energy and also extend our methodology to simulate the dynamics by including hydrodynamic interactions. These extensions will facilitate the application of our methodology to study the bioenergetics of cellular biochemical processes such as receptor internalization via clathrin-mediated endocytosis [48], where it is well established that the curvature-inducing proteins associate with a hexagonal-lattice forming protein clathrin to orchestrate vesicle formation, however, the precise sequence of events and mechanism remain unknown.