The Role of Stretching in Slow Axonal Transport

Abstract

Axonal stretching is linked to rapid rates of axonal elongation. Yet the impact of stretching on elongation and slow axonal transport is unclear. Here, we develop a mathematical model of slow axonal transport that incorporates the rate of axonal elongation, protein half-life, protein density, adhesion strength, and axonal viscosity to quantify the effects of axonal stretching. We find that under conditions where the axon (or nerve) is free of a substrate and lengthens at rapid rates (>4 mm day⁻¹), stretching can account for almost 50% of total anterograde axonal transport. These results suggest that it is possible to accelerate elongation and transport simultaneously by increasing either the axon's susceptibility to stretching or the forces that induce stretching. To our knowledge, this work is the first to incorporate the effects of stretching in a model of slow axonal transport. It has relevance to our understanding of neurite outgrowth during development and peripheral nerve regeneration after trauma, and hence to the development of treatments for spinal cord injury.

Introduction

Slow axonal transport and axonal elongation occur at approximately the same velocity, and many have suspected that these two processes are closely related. It is intuitive that axonal elongation cannot occur at a rate that exceeds the transport of the materials that make up the axon. Although proteins associated with organelles are moved by fast transport at average velocities of up to 400 mm day⁻¹, cytoskeletal proteins (e.g., neurofilament proteins, tubulin, and actin) are transported by slow axonal transport at velocities in the range 0.2–8 mm day⁻¹ (1–6). A series of recent articles have demonstrated that axonal stretching is linked to axonal elongation (7–11). A particularly exciting finding is that when forces are applied to axons, in a process called extreme stretch growth, the axons can elongate at a rate of 8 mm day⁻¹ for sustained periods of time without thinning (7,12). Together these results imply that under certain conditions stretching contributes to slow axonal transport.

The physical properties of the axon and substrate significantly modulate axonal stretching. For example, when axons are tightly bound to the substrate, stretching will not occur along the axon. This mode of elongation is called tip growth (Fig. 1 B) and is exemplified by the elongation of Xenopus neurons on the sticky substrate concanavalin A. In contrast, when an axon (or a nerve) is unattached to the substrate and axial forces cause it to lengthen, stretching will occur along the length of the axon. This mode of elongation is called towed growth (Fig. 1 D) and is seen in vivo during body growth after synapse formation (8,13,14). Towed growth has been examined in vitro by plating neurons on platforms with a gap between them and moving them apart over the course of days. Because high rates of elongation can be achieved, this is called extreme stretch growth. Between the bounds of towed growth and tip growth are situations where stretching occurs along a portion of the axon. An example of this is observed when chick sensory neurons are grown on laminin. Here, forces generated by the growth cone cause low-velocity transport and stretching of the distal axon (15). Our previous work suggests that stretching is limited to the distal axon because forces generated by the growth cone are dissipated by axonal interactions with the substrate (Fig. 1 C) (16). In terms of modeling the impact of stretching on slow axonal transport, we consider three situations to be of the greatest interest: towed growth in vivo, extreme stretch growth in vitro, and growth-cone-mediated elongation in vitro on laminin.

Figure 1.

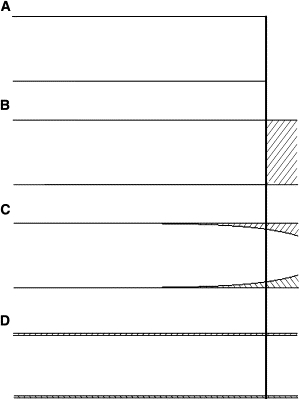
Three models of mass addition during axonal elongation. The vertical line denotes the initial position of the distal tip. (A) Diagram of an axon before elongation. (B) Elongation by tip growth. The shaded area denotes the location of the addition of new mass. (C) Elongation by stretching in the presence of adhesions. Forces generated at the growth cone are dissipated because of interactions with the substrate. The force gradient results in nonuniform thinning of the axon. The unshaded area distal to the vertical line shows the portion of the axon that has been pulled forward by stretching. (D) Towed growth and extreme stretch growth. Axial tension is the same at all points, so that thinning and mass addition occur uniformly along the axon.

During natural development, axons first lengthen as a result of the actions of their growth cones. Forces generated by growth-cone dynamics cause elongation until the neurite reaches its target. After synapse formation, axons become longer through natural body growth. In addition, there is abundant evidence that axons and nerves increase in diameter. For example, the cross-sectional area of the human sural nerve is ∼0.25 mm² in infants and increases to ∼0.6 mm² in adults (17). Increases in axonal diameter have also been observed in rat, chick, and Drosophila neurons (18–20). The need for slow axonal transport to add mass to the axon depends on protein demand and mode of elongation. Demand for new protein can be created by changes in axonal length, changes in axonal caliber, and degradation of proteins along the length of the axon. Each of these creates a need for anterograde flux of new material (20). At an intuitive level, stretching can contribute to transport during lengthening, but without additional modes of transport, it will cause axons to thin. It is well accepted that active-kinesin-based transport underlies slow axonal transport and is needed for addition of new material to the axon. Even without mathematical analysis, it is clear that active-kinesin-based transport will be highest when axons are rapidly lengthening, diameter is increasing, and protein half-life is short. Likewise, axonal stretching will be high when the axons are free from the substrate and axonal length is rapidly increasing. The interesting problem is to determine quantitatively the contribution of stretching to slow axonal transport under physiological conditions.

In this article, we develop a set of equations to analyze the role of stretching in slow axonal transport. We do this in the contexts of growth-cone-mediated axonal elongation, towed growth in vivo after synapse formation, and conditions of extreme stretch growth (i.e., towed growth at a high rate in vitro). In our model, we consider the influences of rate of axonal elongation, protein half-life, protein density, adhesion strength, and axonal viscosity. We find that when axons are free of a substrate and lengthen at rapid rates, stretching can account for ∼50% of total slow axonal transport.

Results

Flux equations

The flux profile J(x,t) that is necessary to support a constant velocity of axonal elongation is

$$J\left(x,t\right)=-\left[\frac{P\left(t\right)}{\tau }+\alpha \right]x+\frac{P\left(t\right)L\left(t\right)}{\tau }+\gamma P\left(t\right)+\alpha L\left(t\right),$$ (1)

where P is the density of materials in the axon, L is the length of the axon, α is the rate of change of the density of materials, γ is the rate of lengthening, and τ is the characteristic time constant of decay (defined by half-life = $\ln 2\times \tau$) (20). Based on data from experiments where axonal diameter and mitochondrial density were analyzed along nerves in vivo (18,20), we treat the density P as uniform with respect to distance along the axon, but note that this does not hold in all cases. It has been reported that axonal diameter tapers (from an average diameter of 10.8 μm to 9.77 μm, by our calculations) over a distance of 4 cm in the soleus nerve of rabbits (21). In addition, axonal caliber increases with distance in a stepwise manner along the mouse optic nerve (22). Length and density increases in elongating axons have also shown a linear trend based on experimental data over defined developmental time windows. This leads to the equations L(t) = L₀ + γt and P(t) = P₀ + αt (20). Although it is clear that there are nonlinear variations in the rate of axonal elongation and the rate of change in axon diameter over the course of development (17), here we use linear models for the sake of simplicity.

In our model, we discuss protein density (P) in terms of unit length of the axon (i.e., g/μm). In general, there is a tight regulation between cell volume, protein density, and osmotic control (23,24). This leads to the assumption that an increase in P can be interpreted as an increase in axonal diameter, as opposed to an increase in protein concentration. In mature vertebrate axons, neurofilaments are the most abundant protein, and they are particularly important in controlling axonal diameter. Nonetheless, the relationship between P and axonal diameter is complex, because axonal diameter is a function of both neurofilament concentration and composition and is influenced by other factors, such as distance along the axon (25,26).

Total flux in Eq. 1 will be satisfied by the combined effects of multiple transport processes (2). We separate the contribution of stretching from other processes using the formula

$$J_{Total}\left(x,t\right)=J_{Stretch}\left(x,t\right)+J_{Other}\left(x,t\right).$$ (2)

The form of the equation for stretch flux will depend on the rate at which the axon is elongating, the strength of adhesions along the length of the axon, and the density of materials. Processes including active-kinesin-based transport and diffusion comprise the other flux in the axon.

When tension is initially applied to an axon it acts for several seconds like a spring or viscoelastic solid. In contrast, over minutes to hours, an axon acts like a dashpot or viscoelastic fluid that exhibits a constant growth rate for a given level of force (27): $\text{Force}=\text{constant × velocity}$. Since we model elongation over long time periods, we treat the axon as a series of dashpots. The viscoelastic response of an axon to pulling forces is dependent on both the axon's axial viscosity and the level of adhesions that exist between the axon and a possible substrate (16). In terms of modeling slow axonal transport, we consider two cases: one where there are no adhesions and one where there are adhesions uniformly distributed along the length of the axon. It is worth noting that axons in nerves are fasciculated (i.e., have attachments along their length), yet the nerve itself is typically free from attachments along its length. Thus, we treat individual axons and nerves that are free from the substrate equivalently. In the case where the axon or nerve is unattached, the axial force is felt equally along the length of the axon. Since the cell body (or spinal cord) is chosen to be the stationary point of reference, the velocity of materials will decrease linearly from the end of the axon (Fig. 2) so that stretch flux J_U(x,t) in this regime can be approximated by

$$J_{\text{Stretch}}\left(x,t\right)=J_{\text{U}}\left(x,t\right)=\gamma \frac{x}{L\left(t\right)}P\left(t\right),$$ (3)

where the rate of elongation, γ, a function of the force applied and axonal viscosity G, is assumed to be constant, as discussed above (7,27).

Figure 2.

Flux during towed growth in vivo when adhesions are absent. Transport profiles are shown at 0 (A), 1 (B), and 5 (C) days of elongation. The rate of axonal elongation is set to $\alpha =$9.24 μm h⁻¹. Dimensionless values characterizing the rate of axonal elongation (A = 1.98) and the rate of mass addition along the axon (C = 1.00) are based on experimental data shown in Table 1. Solid lines denote the flux profile necessary to fulfill protein demand (Eq. 6). The position along the x axis where the stretch-transport (Eq. 7) and other-transport lines intersect is $x_{1/2}/L$. Stretching accounts for more than half of the anterograde transport in the region: $x_{1/2}/L<x\le 1$. As the axon elongates, this value increases toward 1. The size of the region is significant in the absence of adhesions.

If adhesions are present, then the decrease in velocity of materials is nonlinear in x and is dependent on the viscosity of the axon, G, and the strength of the adhesions, η (16). In this case, the flux of materials can be approximated by

$$J_{\text{Stretch}}\left(x,t\right)=J_{\text{Ad}}\left(x,t\right)=\frac{F_0}{{\left(\eta G\right)}^{1/2}}\frac{\sinh \left(x{\left(\eta /G\right)}^{1/2}\right)}{\cosh \left(L\left(t\right){\left(\eta /G\right)}^{1/2}\right)}P\left(t\right),$$ (4)

where F₀ is the magnitude of the generated axial force (Fig. 3). Here, we assume that the axon is long enough so that the flux at the growth cone is $J_{\text{Ad}}\left(L\left(t\right),t\right)\approx \left[F_0/{\left(\eta G\right)}^{1/2}\right]P\left(t\right)$ where the velocity of elongation $F_0/{\left(\eta G\right)}^{1/2}$ is constant. We thus equate this value to the growth rate, γ.

Figure 3.

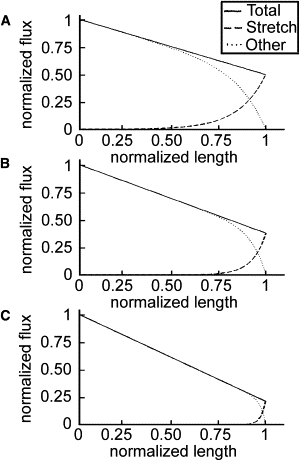
Flux during growth-cone-mediated stretching in the presence of adhesions. Transport profiles are shown at 0 (A), 1 (B), and 5 (C) days of elongation. The rate of axonal elongation is set to 9.24 μm h⁻¹. Dimensionless values characterizing axonal elongation (A = 1.98), viscoelastic properties (B = 7.06), and rate of mass addition (C = 1.00) were calculated from the parameters listed in Table 1. Solid lines denote the flux profile necessary to fulfill protein demand (Eq. 6). The position along the x axis where the stretch-transport (Eq. 8) and other-transport curves intersect is $x_{1/2}/L$. Stretching accounts for more than half of the anterograde transport in the region: $x_{1/2}/L<x\le 1$. As the axon elongates, this value increases toward 1. The presence of adhesions along the length of the axon decreases the significance of stretching.

There are several simplifications inherent in our equations that model stretching along the axon. In Eq. 3, we model the situation where the cell body and the tip of the axon (or nerve) are associated with points that are moving apart and where the axon is free of external associations. The underlying assumption is that the movement is the net result of internal and external forces (28,29), the result being that when an axon lengthens, stretching occurs equally at all points along it. We think a model that includes the actions of forces along the axon would be useful, but at this point the experimental data needed to model those parameters are too limited.

Nondimensionalization

As the magnitudes of variables and parameters will vary based on the system to be studied, it is necessary to redefine them in dimensionless form. We start with the following choices for the variables:

$$\tilde{x}=\frac{x}{L_0}\tilde{t}=\frac{\gamma }{L_0}t\tilde{P}=\frac{P}{P_0}\tilde{L}=\frac{L}{L_0}\tilde{J}=\frac{\tau }{P_0{L}_0}J$$ (5)

L₀ and P₀ represent the initial values of the axon length and protein density, respectively. Because we are studying the case of minimal protein decay (τ large), we avoid using $\tilde{t}=\frac{t}{\tau }$. The nondimensional flux equations can then be written as

$$\tilde{J}(\tilde{x},\tilde{t})=-\left[\tilde{P}+C\right]\tilde{x}+\tilde{P}\tilde{L}+A\tilde{P}+C\tilde{L},$$ (6)

$${\tilde{J}}_{\text{U}}(\tilde{x},\tilde{t})=A\frac{\tilde{x}}{\tilde{L}}\tilde{P},$$ (7)

and

$${\tilde{J}}_{\text{Ad}}\left(\tilde{x},\tilde{t}\right)=AD\frac{\sinh \left(B\tilde{x}\right)}{\cosh \left(B\tilde{L}\right)}\tilde{P},$$ (8)

where the four dimensionless parameters A, B, C, and D are defined as

$$A=\frac{\gamma \tau }{L_0}B=L_0{(\eta /G)}^{1/2}C=\frac{\alpha \tau }{P_0}D=\frac{F_0}{\gamma {\left(\eta G\right)}^{1/2}}.$$ (9)

These parameters can be defined as follows: A, the axonal elongation parameter; B, the binding adhesion/viscosity parameter; C, the cytosolic density parameter; and D, the velocity ratio. Expressions for the scaled length and density are $\tilde{L}\left(\tilde{t}\right)=1+\tilde{t}$ and $\tilde{P}\left(\tilde{t}\right)=1+\left(C/A\right)\tilde{t}$, respectively. Our assumption that the velocity of stretch elongation is constant will be considered safe if $\tanh \left(B\tilde{L}\right)>0.99$, which requires that $B\tilde{L}>2.7$. If this is the case, then γ can be equated with the velocity of stretch elongation and we can set D = 1.

It is to be noted that $B\tilde{L}$ will be <2.7 during the first hours of axonal elongation, when the axon is very short. In the case of chick sensory neurons grown on laminin, $B\tilde{L}$ = 2.7 when the length of the axons is $\sim 90$μm. In this situation, forces and axonal stretching will be at significant levels along the length of the axon reaching back to the cell body. Mathematically, this minimizes the impact of adhesion. As the axon grows longer, the effect of adhesions increases to steady-state behavior (i.e., BL > 2.7). It is possible to model this situation with short axons, but it is beyond the scope of this manuscript.

At this point, we eliminate the tildes, keeping in mind that we are dealing with dimensionless variables.

Region of stretch dominance and anterograde momentum

In our model, the total-flux profile is decreasing and the stretch-flux profiles are increasing along the axon, so that for each value of t there will be a unique point, $x_{1/2}\left(t\right)$, at which the stretch-induced flux will equal half of the total flux. Between that point and the terminal end of the axon, stretching will account for more than half of anterograde flux of material (Figs. 2 and 3). In the case of no adhesions, we solve the equation $J_{\text{U}}\left(x,t\right)=J(x,t)/2$ for x and divide by L to obtain

$$\frac{x_{1/2}}{L}=\frac{PL+AP+CL}{PL+2AP+CL},$$ (10)

which is between 0 and 1. The evolution of this point of equality is shown in Fig. 4 A for four conditions: 1), wild-type, 2), constant axonal diameter, 3), no protein degradation, and 4), constant diameter and no degradation. In more detail, in Condition 1, the wild-type condition, protein is normally degrading and the cytosolic density of proteins along the axon is normally increasing, with the parameters set at A =1.98 and C = 1.00 (wild-type). The theoretical situation in Condition 2 is that protein degradation is normal but axonal diameter is constant, with parameters A = 1.98 and C = 0; here, C = 0 is interpreted as a constant diameter with α = 0, and thus P(t) = P₀ for all t. In Condition 3, where net mass addition is occurring along the axon but protein degradation is undetectable, the parameters are A >> 1 and C >> 1; since τ is in both A and C, both of these parameters are large. In Condition 4, where diameter is constant and protein degradation is undetectable, the parameters are A >> 1 and C = 0; here, A is large because τ is large and C = 0 because α = 0. In general, increasing C pushes $x_{1/2}\left(t\right)/L$ toward 1 (decreases the impact of stretching), whereas increasing A pushes $x_{1/2}\left(t\right)/L$ toward 0.5 (increases the impact of stretching). We note here that 0.5 is not the absolute lower bound; when the level of active transport is insufficient to maintain axonal caliber, $x_{1/2}\left(t\right)/L$ can be <0.5 and approaches zero as active transport declines.

Figure 4.

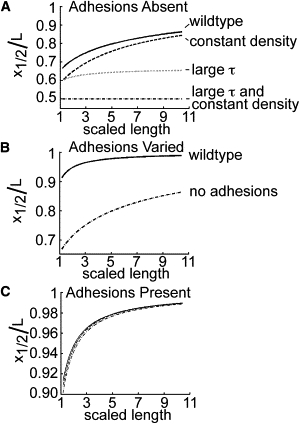
Contribution of stretching changes during elongation. As an axon elongates, the fraction of the axon where stretching is the dominant form of transport decreases. (A) The lines show $x_{1/2}/L$ as a function of increasing axonal length (Eq. 10). In the absence of adhesions, when axonal diameter remains constant and protein half-life is extremely high (A >> 1, C = 0), the only source of protein demand is axonal elongation. Thus, $x_{1/2}/L$ remains fixed at 0.5. When the effect of increasing protein density is added (A, C >> 1), $x_{1/2}/L$ increases slowly to a limiting value of 2/3. Under conditions of a physiological protein half-life and constant axonal diameter (A = 1.98, C = 0), the contribution due to stretching is diminished. When proteins degrade and caliber increases (A = 1.98 and C = 1.00), the role of stretching is further reduced. (B) Comparison of the evolution of $x_{1/2}/L$ in the presence (solid line; solution of Eq. 14) and absence (dash-dotted line; Eq. 10) of adhesions. A = 1.98 and C = 1.00 in both cases, and B = 7.06 when adhesions are present. (C) In the presence of adhesions (B = 7.06), $x_{1/2}/L$ is affected only slightly for varying levels of protein half-life and diameter increase (solution of Eq. 14).

Another measure of the effect of stretching is how much it contributes to the total anterograde momentum of the system. Momentum, p(t), is calculated as the integral of flux over the length of the axon and is a measure of total transport in the axon.

$$p\left(t\right)=\underset{0}{\overset{L\left(t\right)}{\int }}J\left(x,t\right)dx=\frac{L}{2}\left(PL+2AP+CL\right).$$ (11)

The momentum due to stretching is calculated in a similar way (here in the absence of adhesions):

$$p_U\left(t\right)=\underset{0}{\overset{L\left(t\right)}{\int }}{J}_U\left(x,t\right)dx=\frac{1}{2}APL.$$ (12)

The fraction of anterograde momentum that is accounted for by stretching is $p_U\left(t\right)/p\left(t\right)$. In the case of no adhesions, the contribution of stretching to total anterograde momentum and the point where stretching accounts for half of the total flux are related by

$$\frac{p_U\left(t\right)}{p\left(t\right)}=\frac{AP}{PL+2AP+CL}=1-\frac{x_{1/2}}{L}.$$ (13)

When adhesions are present along the length of the axon, we find $x_{1/2}/L$ by solving the equation $J_{Ad}\left(x,t\right)=J\left(x,t\right)/2$, which is transcendental. Multiplying this equation by 2 and setting D = 1 gives

$$2A\frac{\sinh \left(Bx\right)}{\cosh \left(BL\right)}P=-\left[P+C\right]x+PL+AP+CL.$$ (14)

For the case of constant protein density and undetectable protein degradation (C = 0 and A >> 1), the asymptotic solution is

$$\frac{x_{1/2}}{L}=\frac{{\sinh }^{-1}\left[\frac{\cosh \left(BL\right)}{2}\right]}{BL}+O\left(A^{-1}\right),$$ (15)

where the smaller-order terms have been omitted and the first term is a good approximation. In the general case, the solution may be well approximated using Newton's method. Fig. 4 B compares the evolution of $x_{1/2}/L$ in the presence (solid line) to that in the absence (dash-dotted line) of adhesions. Fig. 4 C shows that in the presence of adhesions, the region of stretch dominance is much less sensitive to the parameters involving axonal elongation (A) and changes in cytosolic density (i.e., axonal diameter) (C).

To most effectively increase the role of stretching in slow axonal transport, we need to know which parameter to modify to cause the greatest reduction in $x_{1/2}/L$. Fig. 5 shows the dependence of $x_{1/2}/L$ on parameters A–C when $t=0$ (the qualitative results are similar for other values of t). Dotted lines represent the value of $x_{1/2}/L$ for $A=1.98$, $B=7.06$, and $C=1.00$, which is derived using data from previous experiments (see Table 1). In each graph, one parameter is allowed to vary while the other two are held fixed at the values listed above. Values for B are restricted to those >2.7, as is required for the use of this model. The sensitivity of $x_{1/2}/L$ with respect to each parameter is estimated as the derivative of each of these curves at $\left(\overline{A},\overline{B},\overline{C}\right)=\left(1.98,7.06,1.00\right)$. Those estimates are

$$\frac{\partial }{\partial A}{\left(\frac{x_{1/2}}{L}\right)|}_{\left(\overline{A},\overline{B},\overline{C}\right)}=-5.01\times {10}^{-3},\frac{\partial }{\partial B}{\left(\frac{x_{1/2}}{L}\right)|}_{\left(\overline{A},\overline{B},\overline{C}\right)}=-1.12\times {10}^{-2},\frac{\partial }{\partial C}{\left(\frac{x_{1/2}}{L}\right)|}_{\left(\overline{A},\overline{B},\overline{C}\right)}=-4.97\times {10}^{-3},$$ (16)

which shows that at this set of parameter values, $x_{1/2}/L$ is about twice as sensitive to adhesion/viscosity (B) as to the other two parameters. In Fig. 5, we see that the greatest reduction in $x_{1/2}/L$ can be achieved by decreasing B.

Figure 5.

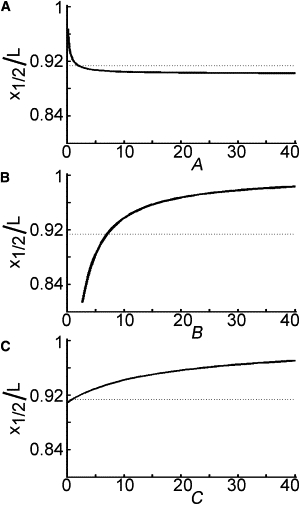
Sensitivity of the stretch-dominated region in the presence of adhesions. The location of x_1/2/L (Eq. 14) is plotted for varying values of the dimensionless parameters when t = 0. Dotted lines represent the value of x_1/2/L = 0.913 for wild-type parameter values A = 1.98, B = 7.06, and C = 1.00. The contribution of stretching to transport is increased when x_1/2/L is lowered. In the presence of adhesions, varying A = γτ/L₀ or C = ατ/P₀ does little to decrease x_1/2/L (A and C). Decreasing adhesions (lowering B = L₀(η/G)^1/2), however, can significantly decrease x_1/2/L (B).

Table 1.

Parameters used to calculate baseline values of nondimensional parameters

Parameter	Value	System	Source
α	4.49 × 10−3 mito μm−1 h−1	Drosophila larvae	(20)
γ	9.24 μm h−1	Drosophila larvae	(20)
τ	50.8 h	Drosophila larvae	(20)
L0	237 μm	Drosophila larvae	(20)
P0	.229 mito μm−1	Drosophila larvae	(20)
G	3.9 × 107 g μm h−1	Embryonic chick	(16)
η	3.5 × 104 g μm−1 h−1	Embryonic chick	(16)

A = $\frac{\gamma \tau }{L_0}$= 1.98, B = $L_0{\left(\eta /G\right)}^{1/2}$= 7.06, and C = $\frac{\alpha \tau }{P_0}$= 1.00.

Anterograde momentum is calculated in the same way as above:

$$p_{\text{Ad}}\left(t\right)=\underset{0}{\overset{L\left(t\right)}{\int }}{J}_{\text{Ad}}\left(x,t\right)dx=AP\frac{1-\text{sech}\left(BL\right)}{B}.$$ (17)

The fraction of anterograde momentum that is accounted for by stretching in the presence of adhesions is p_Ad(t)/p(t) and can be expressed as

$$\frac{p_{Ad}\left(t\right)}{p\left(t\right)}=\frac{2AP}{PL+2AP+CL}\frac{1-\text{sech}\left(BL\right)}{BL}.$$ (18)

Fig. 6 shows the sensitivity of this ratio to the parameters $A,B,\text{and C}$ when t = 0. As with the region of stretch dominance, the greatest increase in the stretching contribution to anterograde momentum can be achieved by decreasing adhesion/viscosity (B). Unlike $x_{1/2}/L$, however, the contribution of stretching to anterograde momentum is about equally sensitive to each parameter at $\left(\overline{A},\overline{B},\overline{C}\right)=\left(1.98,7.06,1.00\right)$:

$$\frac{\partial }{\partial A}{\left(\frac{p_{\text{Ad}}}{p}\right)|}_{\left(\overline{A},\overline{B},\overline{C}\right)}=-1.59\times {10}^{-2},\frac{\partial }{\partial B}{\left(\frac{p_{\text{Ad}}}{p}\right)|}_{\left(\overline{A},\overline{B},\overline{C}\right)}=-1.31\times {10}^{-2},\frac{\partial }{\partial C}{\left(\frac{p_{\text{Ad}}}{p}\right)|}_{\left(\overline{A},\overline{B},\overline{C}\right)}=-1.58\times {10}^{-2}.$$ (19)

These partial derivatives can be determined directly from Eq. 18. Note that this equation has a local maximum with respect to B, but this is an artifact, since it occurs in the region $0<B<2.7$ (when axons are just beginning elongation) for all t ≥ 0. In a similar way, $x_{1/2}/L$ has a local minimum with respect to B, but this also occurs for $0<B<2.7$ for all t ≥ 0.

Figure 6.

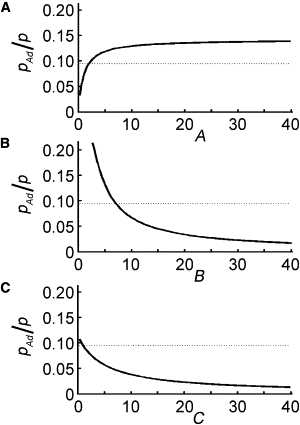
Sensitivity of the relative contribution of stretching to momentum in the presence of adhesions. The proportion of transport that is due to stretching, p_Ad(t)/p(t), is plotted for varying values of the dimensionless parameters when t = 0. Dotted lines represent the value p_Ad(t)/p(t) = .094 for wild-type parameter values A = 1.98, B = 7.06, and C = 1.00. The contribution of stretching to transport is increased when p_Ad(t)/p(t) is elevated. In the presence of adhesions, increasing A can cause a moderate increase in p_Ad(t)/p(t), but decreasing C does little (A and C). Decreasing B leads to the greatest increase in p_Ad(t)/p(t) (B).

All figures in this article were created using MATLAB (The MathWorks, Natick, MA) and Photoshop (Adobe, San Jose, CA).

Discussion

This work is the first that we know of to incorporate the effects of axonal stretching in a model of slow axonal transport. We analyze this problem taking into consideration axonal viscosity (G), adhesions (η), protein degradation (τ), the rate of elongation (γ), and the rate of mass addition along the axon (α).We focus on three different situations as examples. The first is in vivo towed growth in Drosophila larvae. Here, synapse formation has occurred, the nerves are free of attachments along their lengths, and the nerves are elongating as the result of body growth. In the second example, we examine the contribution of stretching to slow axonal transport during the outgrowth of neurons grown on laminin/polyornithine. In this situation, there are attachments along the length of the axon, and stretching occurs most prominently in the distal axon. In the final case, we model the extreme stretch growth of neurons elongating in vitro as the result of externally applied forces. Here, the cell bodies and growth cones are on separate platforms that are moved apart, and the axons are free of adhesions. We find that stretching makes the most significant contribution to transport when the rate of elongation is rapid, adhesions are absent, and the rate of protein degradation is low. In the case of the extreme stretch growth, we estimate that stretching accounts for almost 50% of total slow axonal transport.

We start with the assumption that multiple modes of transport are making contributions to the slow-axonal-transport flux (Eq. 1). Minimally, these include Stop-and-Go transport of polymers, active-kinesin-mediated transport of soluble proteins, diffusion, and stretching (2). To simplify this problem, we divide total transport into two groups; stretch transport and other transport (Eq. 2). We have chosen two means by which to consider the effects of stretching. The first is to compare the contribution of stretching to the flux of materials at different points along the axon. When this contribution is greater than half of the total flux, we say that stretching is the dominant form of transport at that point. As the total-flux profile is decreasing and the stretch-flux profile is increasing, there will be a unique point along the axon, $x_{1/2}\left(t\right)$, where stretching will account for half of the anterograde flux (Eq. 10). Between this point and the distal end, stretching is the dominant form of transport. The fraction of the axon where stretching is the dominant form of transport, then, is $1-x_{1/2}/L$. The strength of this approach is that it is straightforward and obvious from the graphs. The second way in which we view the contribution of stretching to transport is in terms of anterograde momentum, which is the integral of anterograde flux over the length of the axon. Whereas flux is a measure of transport at a single point, anterograde momentum is a measure of total anterograde transport in the axon. The fraction of total anterograde transport that occurs by stretching is given by the ratio $p_U\left(t\right)/p\left(t\right)$ when adhesions are absent (Eq. 13) and $p_{\text{Ad}}\left(t\right)/p\left(t\right)$ when adhesions are present (Eq. 18). Of these two methods of analysis, we think momentum has the greatest utility, because it represents in a single number the total flux along the length of an axon. Ultimately, we would like to know the momentum of each mode of transport (i.e., Stop-and-Go, soluble transport, diffusion, and stretching) and how momentum changes when proteins important for axonal transport are altered (e.g., cytoplasmic dynein and the various members of the kinesin and myosin families).

Our nondimensional model introduces three main parameters that play a role in the contribution of axonal stretching: the axonal elongation parameter, $A=\gamma \tau /L_0$; the cytosolic density parameter, $C=\alpha \tau /P_0$; and the adhesion/viscosity binding parameter, $B=L_0{\left(\eta /G\right)}^{1/2}$. In the case of no adhesions, only the elongation and density parameters, A and C, respectively, are present in Eqs. 6 and 7, and their values dictate both the size of the stretch-dominated region and the fraction of anterograde momentum due to stretching. Contributing to each of these dimensionless quantities is the degradation time constant, τ, so that a change in the half-life of the protein would change both A and C. In particular, in situations where protein degradation is very low, A and C will both be large. A change in A or C alone would be interpreted as a change in γ or α, respectively. Fig. 4 A shows that a slower rate of protein density increase, α (decreased C), and/or an increase in protein half-life, τ (increased A and C), elevate the relative contribution of stretch-induced transport. Both of these changes result in a decrease in the overall demand for new protein, leaving the demand at the distal tip and the actual flux contribution of stretching unchanged (see Eq. 1 and 3). This part of the model best describes the cases of nerve elongation due to bodily growth and instances where axons are towed while unattached to a substrate.

One such example of this type of elongation is the extreme stretch-grown axons engineered by Pfister et al. (7,12). In these experiments, innervated rat axons were elongated to a length of 5 cm over the course of 14 days. During the first 2 days the rate of elongation was increased from 1 to 4 mm day⁻¹, and for the final 12 days, the rate of elongation was held at 4 mm day⁻¹ (7). Using their data for microtubule density and axonal caliber before and after the elongation process, we can estimate the contribution that stretching makes to slow axonal transport in these experiments. The values used to determine parameters A and C are given in Table S1 in the Supporting Material.

Fig. 7 shows the contribution of stretching to overall transport in extreme stretch-grown axons. We have assumed, here, that the velocity of elongation is constant, but the elongation steps were actually made in a stepwise fashion. However, our assumption seems reasonable as the 0.5-μm steps were made approximately every 10.8 s and this elongation rate (4 mm day⁻¹) was held constant for 12 days. We observe that under conditions of extreme stretch growth, stretching accounts for 49.1% of anterograde momentum at the beginning of the third day of stretch growth (t = 0, the beginning of the 4 mm day⁻¹ elongation rate). At the end of the 12-day span (t = 13.7) at this elongation rate, the percentage of anterograde momentum that is accounted for by stretching has only dropped to 41.1%. This is due to the fact that the elongation parameter based on the experimental data is much greater than the density parameter (Table S1; A = 84.1, C = 1.96). The studies of Pfister et al. showed that axons are able to grow at remarkable rates. Our model suggests that when axons elongate at high rates in this manner, stretching makes a significant contribution to the transport of axonal materials.

Figure 7.

Contribution of stretching to slow axonal transport in extreme stretch-grown axons. We applied our model to the study of Pfister et al. (7) to see how much stretching contributed to anterograde transport in cases of extreme stretch growth. In the study, axons were elongated at a rate of γ = 4 mm day⁻¹ for 12 days. These axons were free of adhesions along the length, so Eqs. 6 and 7 were applied. Parameter values A = 84.1 and C = 1.96 were derived using values listed in Table S1. (A) Flux profiles of anterograde transport at the beginning of the 12-day elongation period. Since A is much greater than C, the slope of the total flux profile is close to zero, and stretching is the dominant form of transport in the majority of the distal axon (x_1/2/L = 5.09). (B) After 12 days, stretching is still the dominant form of transport in the distal 41% (20 mm) of the axon (x_1/2/L = 5.89). (C) The relative contribution of stretching to anterograde momentum is given by the ratio p_U/p. Over the course of 12 days of elongation at 4 mm day⁻¹, this ratio declines from .491 to .411, showing that stretching accounts for a significant amount of anterograde transport (>40%) when axons are elongated by extreme stretch growth.

During growth-cone-mediated axonal elongation, both the growth cone and the length of the axon are typically associated with a substrate. In vivo, this is typically the basal lamina. In vitro, it is often coverslips coated with adhesion factors. The adhesion/viscosity parameter, B, enters in Eq. 8 when adhesions are present along the axon. Its effect on the point where stretching accounts for half of the total transport $\left(x_{1/2}/L\right)$ is much more pronounced than varying the rate of axonal elongation, A, or rate of that cytosolic density increases, C. When the adhesion/viscosity parameter is set to conditions typical for the outgrowth of neurons or polyornithine/laminin-coated coverslips (B = 7.06), stretching is dominant in the distal 10% of the axon (Figs. 3 and 4 B). In this case, there is almost no effect on the time evolution of $x_{1/2}/L$ when the rate of axonal elongation, A, and/or the rate of increase in cytosolic density, C, take extreme values (Fig. 4 C). Altering the value of adhesion/viscosity parameter, B, while keeping the other parameters constant amounts to modifying the ratio η/G, where η describes the strength of focal adhesions and G describes the viscosity of the axon. Axial forces are quickly dissipated by strong axonal adhesions, so when this ratio is large, there will be limited stretching of the axon. High axonal viscosity will lower force dissipation and a larger portion of the distal axon will experience stretching (assuming the same velocity of elongation). This part of the model best describes when axons are engaged in growth-cone-mediated elongation along sticky substrates.

To determine how the main parameters of our model influence axonal stretching, we systematically varied the rate of axonal elongation, the binding strength of the adhesions, and the rate of change in axonal cytoplasmic density (A, B, and C, respectively) and then determined the point where stretching accounted for half of the total transport (x_1/2/L). Fig. 5 shows the sensitivity of the system to variations in the three parameters when P = L = 1 (i.e., when t = 0). From previous work, we consider wild-type dimensionless parameter values A = 1.98, B = 7.06, and C = 1.00 (Table 1). At this set of parameters the axon is elongating, adhesions are present, and net mass addition is occurring at wild-type levels. Then, keeping two of these values fixed, we allow the third parameter to vary to study its effect on $x_{1/2}/L$ (note that to increase the size of the region where flux is dominated by stretching, x_1/2/L must be lowered). We found that the contribution of stretching to total transport increases as the rate of axonal elongation increases (Fig. 5 A). In contrast, the contribution of stretching decreases when the strength of the adhesions increases (Fig. 5 B) and also decreases as the rate of mass addition along the axon increases (Fig. 5 C). At a more detailed level, our model also shows that in the presence of adhesions, increasing A or decreasing C only produces mild reductions in $x_{1/2}/L$. In contrast, reducing B can lead to as much as a doubling of the size of the stretch-dominated region. Thus, decreasing adhesions along the length of the axon is the most effective single method of increasing the contribution of stretching during elongation.

Anterograde momentum due to flux exhibits a similar dependence on the rate of growth, adhesion strength, and rate of density change. The key difference is that it is in terms of the net mass that is moving along the axon. We think this is more intuitive. For example, in Fig. 6 A, we show the effect of increasing the rate of axonal elongation. When A = 1.98 in the graph (i.e., the rate of elongation is 9.24 μm h⁻¹ (Table 1)), stretching accounts for ∼9% of the total transport (Fig. 6, dashed lines). When A = 10, the elongation rate is ∼47 μm h⁻¹ and the impact of stretching increases by ∼50% to ∼13%. This result is satisfying in that it speaks to the older debate about the role of axonal stretching in axonal elongation. In particular, many previous studies observed axonal stretching in Xenopus neurons which can grow at rates up to 100 μm h⁻¹ (30). Several studies subsequently suggested that stretching was the result of the high rate of growth (31). Our analysis suggests that indeed fast rates of elongation are coupled with increased stretching of the axon. Likewise, it is well accepted that adhesion strength is inversely associated with axonal stretching. For example, axonal stretching is obvious when Xenopus neurons are grown on laminin, whereas stretching does not appear to occur along the axon shaft when the same neurons are grown on the sticky substrate ConA (32). Likewise, in our model, we see that as adhesions increase, the impact of stretching drops sharply (Fig. 6 B). Perhaps the most interesting aspect of momentum is the impact of the mass addition along the axon. In this case, we model the net accumulation of material along the axon that has been reported during development in terms of increases in axonal width. In Fig. 6 C, we see that the contribution of stretching decreases when the rate of net mass addition along the axon is high. Our understanding of this is that net mass addition along the axon is the result of active-kinesin-based transport. When mass addition is high, kinesin-based transport is high and the relative contribution of stretching is reduced.

There are other possible patterns of bulk transport worthy of note. For example, new material could be added at the base of the axon and bulk transport could occur at a constant velocity along the axon. This scenario has been proposed in the structural hypothesis (2). Although this is a formal possibility, there is currently no strong experimental support for this mode of growth. Alternatively, more complicated patterns could exist where force generation occurs at the cell body and or along the axon. This might result in retrograde bulk low-velocity transport toward the cell body or contraction in some regions and stretching in other regions of the axon. Nonetheless, because there are no detailed experimental data sets supporting these modes of elongation, we do not consider them in our analysis.

One important aspect of stretch-induced elongation that we have not addressed here is short-term axonal thinning. In their extreme stretch-growth experiments, Pfister et al. demonstrated that stretching axons at very high strain rates leads to rupture. However, when these tracts were properly conditioned, they were able to sustain elongation rates of up to 8 mm day⁻¹ (7). Although our current model would suggest that in the absence of adhesions, increasing the elongation parameter A as much as possible would increase both the rate of elongation and the contribution of stretching to anterograde transport, there is certainly a limit as to how much stretching an axon or a nerve can support. A theoretical analysis of this limitation is required for optimal rates of axon/nerve regeneration to be determined.

It has long been thought that the rate of axonal regeneration is linked to the speed of slow axonal transport. When an axon elongates by axially oriented forces, much of the necessary transport in the axon occurs by stretching, reducing the demand for microtubule-motor-mediated transport. A way to increase regeneration rates in the presence of adhesions may be to condition the nerves to be more susceptible to stretching (33,34). In this way, transport due to stretching would increase slow axonal transport and allow faster rates of regeneration. We have shown that the stretch-dominated region and anterograde momentum of an axon/nerve are sensitive to the ratio of adhesions to axonal viscosity, and that influence of stretching can be increased by controlling this ratio. It may be possible to achieve this increase by modulating the expressions of cell-adhesion molecules (to decrease η) and/or cytoskeletal components (to increase G).

Discovery of a drug that would drastically increase the rates of both axonal elongation and slow axonal transport would be a major advance in the field of nerve regeneration. Stretching, a purely physical mechanism, has the ability to simultaneously accomplish both tasks. With advances in technology, axonal winches (cables embedded in the body to stretch damaged nerves) and miniature robots that tow nerves will be possible. A combination of physical and cellular approaches (e.g., growth factors, gene therapy, and neuronal stem cells) has the promise to yield phenomenal rates of exquisitely controlled nerve regeneration.