Cluster Analysis of Time-Dependent Crystallographic Data: Direct Identification of Time-Independent Structural Intermediates

Abstract

The initial output of a time-resolved macromolecular crystallography experiment is a time-dependent series of difference electron density maps that displays the time-dependent changes in underlying structure as a reaction progresses. The goal is to interpret such data in terms of a small number of crystallographically refinable, time-independent structures, each associated with a reaction intermediate; to establish the pathways and rate coefficients by which these intermediates interconvert; and thereby to elucidate a chemical kinetic mechanism. One strategy toward achieving this goal is to use cluster analysis, a statistical method that groups objects based on their similarity. If the difference electron density at a particular voxel in the time-dependent difference electron density (TDED) maps is sensitive to the presence of one and only one intermediate, then its temporal evolution will exactly parallel the concentration profile of that intermediate with time. The rationale is therefore to cluster voxels with respect to the shapes of their TDEDs, so that each group or cluster of voxels corresponds to one structural intermediate. Clusters of voxels whose TDEDs reflect the presence of two or more specific intermediates can also be identified. From such groupings one can then infer the number of intermediates, obtain their time-independent difference density characteristics, and refine the structure of each intermediate. We review the principles of cluster analysis and clustering algorithms in a crystallographic context, and describe the application of the method to simulated and experimental time-resolved crystallographic data for the photocycle of photoactive yellow protein.

Introduction

Despite the wide success of traditional macromolecular crystallography in determining static, time-independent structures, mechanism is much more difficult to establish by crystallographic means. A mechanism involves a series of distinct structural intermediates lying between the reactant and product states. The structural differences that distinguish reactant from intermediates from product can be purely local, confined to an active site, or global, involving most of the protein. Such structural changes can occur over a wide range of timescales, from picoseconds to seconds or even longer. To establish a chemical mechanism it is necessary to identify these short-lived intermediate structures and the complex pathways by which they interconvert.

Such structural changes and mechanisms can be studied to a limited extent with traditional crystallographic trapping methods (1,2). However, they are particularly suited to analysis by time-resolved crystallography (3–5). The immediate goal of a time-resolved crystallographic experiment is to measure the variation with time of the structure amplitudes |F(hkl,t)|, spanning the entire time range of the structural reaction being considered from initiation at t = 0 to completion. By making use of the known phases ϕ₀ at t = 0, the data from such an experiment is typically presented as a series of time-dependent difference electron density maps (TDED, hereafter also referred to as the density) Δρ(r,t) = ρ(r,t) − ρ(r,0) which display the changes of the average electron density with time as a biochemical reaction progresses. A close approximation to Δρ(r,t) is obtained by Fourier transformation of ΔF(hkl,t) = {|F(hkl,t)| − |F(hkl,0)|, ϕ₀}.

The interactions between molecules in the lattice of a biological crystal are weak, unlike those between molecules in crystals of small organic and inorganic species. Hence biological molecules tend to behave independently of one another as if they were in dilute solution, in the specific sense that if one molecule adopts, e.g., a reaction intermediate state B, the probability that adjacent molecules in the crystal lattice will adopt state B (or state A or state C, etc.) is unaffected. The transitions between intermediates are then uncorrelated in time from molecule to molecule in the crystal lattice, and the variation with time of the average structure arises from the variation in population of the underlying intermediate structures. The intermediate structures themselves do not vary; they are time-independent (3). Hence

$$\rho \left(\mathbf{r},\text{t}\right)=\sum {\text{C}}_{\text{j}}\left(\text{t}\right){\rho }_{\text{j}}\left(\mathbf{r}\right),$$ (1)

and

$$\Delta \rho \left(\mathbf{r},\text{t}\right)=\sum {\text{C}}_{\text{j}}\left(\text{t}\right)\Delta {\rho }_{\text{j}}\left(\mathbf{r}\right),$$ (2)

where ρ_j(r) denotes the electron density at location r for species j, Δρ_j(r) denotes the difference electron density at location r between species j and species 0 (identical to the reactant ρ(r,0)), and C_j(t) is the fractional concentration of species j at time t. Although 0 ≤ C_j(t) ≤ 1, Δρ(r,t) and Δρ_j(r) may be either positive or negative.

This may be illustrated by a simple kinetic mechanism involving four states I₀, I₁, I₂, and I₃:

$$I_0\stackrel{k_{01}}{\to }{I}_1\stackrel{k_{12}}{\to }{I}_2\stackrel{k_{23}}{\to }{I}_3.$$ (3)

The fractional concentration of each state as a function of time is presented in Fig. 1. At nearly all time points the average structure is heterogeneous and contains a significant population of two or more states. The problem that time-resolved crystallography faces is given ρ(r,t), identify the number and nature of the distinct short-lived intermediate states, refine the structure of each state, and determine the reaction mechanism(s), and rate coefficients for the interconversion of these states (3–5).

Figure 1.

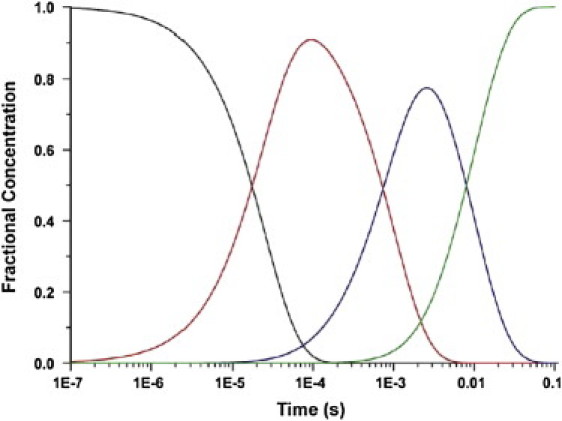
Time course of the population of each intermediate in the chemical kinetic mechanism of Eq. 2. This mechanism is used in all subsequent figures for the simulated data. The time course is derived using the rate constants in Table 1: I₀ (black), I₁ (red), I₂ (blue), and I₃ (green).

The experimental techniques for successful conduct of time-resolved Laue crystallography are now largely in place in systems in which a reaction can be initiated by light, as recent examples show (6–10). A substantial remaining problem is that of data analysis and interpretation. The major difficulties arise from the low signal/noise ratio. The signal is weak because the level of reaction initiation in the crystal may be as low as 10%–20%. Even in those molecules that do react, most atoms do not move as the reaction progresses and those that do move may not move very far (i.e., Δρ(r,t) << ρ(r,t) for most values of r and t).

The noise contains both random and systematic contributions. Spatial and temporal random noise can arise from error in measurement of the time-dependent structure factor amplitudes. Phase errors may produce spatially random errors that have no temporal component and are constant from time point to time point. Systematic contributions arise from the use of the difference Fourier approximation, from the fact that an entire time series is often pieced together from data in which only one or a few time points are acquired on the same crystal, and from significant crystal-to-crystal, or experiment-to-experiment, variation in the extent of reaction initiation.

Several strategies to minimize the noise have been developed. One strategy (11) is to make repeated measurements of |F(hkl,t)| containing at least 10 observations, which yields precise values of both its mean and its standard deviation. Knowledge of the latter allows the application of weighting schemes that reduce error (12). An effective strategy to minimize experiment-to-experiment errors is to collect data in the four-dimensional data space (hkl,t) with time as the fast variable, by acquiring only a subset of |F(hkl)| values on a single crystal, for all values of t (13). Singular value decomposition (SVD) acts both as a powerful noise filter and is also effective in identifying the number of distinct intermediates present (14–17).

Even when these strategies are applied, the data analysis stages remain very demanding. Thus, unscrambling or deconvoluting the time-independent, heterogeneous mixture of structures from the very noisy time-dependent data is the essential challenge we consider here. This approach has been termed analytical trapping, by which time-independent structures are analytically trapped from time-dependent data. The term parallels the more widely used chemical trapping and physical trapping of intermediate structures (2,18,19).

In this study, we present what we believe is a novel analytical trapping strategy—cluster analysis. This technique originated in statistics but has been used widely in many areas of science including analysis of gene microarrays (20,21), protein dynamics simulations (22), and functional magnetic resonance imaging (23). With the exception of our prior brief communication (24), we believe this is the first application of cluster analysis to crystallography. In the following text, we review the basic principles and algorithms of cluster analysis, and apply cluster analysis to simulated data with different levels of noise and to noisy real data. This is followed by a discussion.

Computational Methods

The TDED maps are described by the time profile of the density Δρ(r,t) over a set of time points spanning the time domain of interest at a discrete set of grid points {r_i} over the space occupied by the asymmetric unit, which we refer to as voxels. The fundamental rationale for our approach is that the TDED for each individual voxel r follows a pattern which is determined by the concentration profile (shape) in time of the structural intermediate(s) j to which the density at this particular voxel is sensitive. Thus, the TDED at a voxel that is sensitive to a single intermediate will be similar in shape to the unknown concentration profile of this intermediate. In this case, Eq. 2 consists of a single term, e.g., j = J. Conversely, if the density at a voxel r is not sensitive to any intermediate, then Δρ(r,t) ≈ 0 for all t. A more complicated but also more common case arises when the density at a voxel is sensitive to more than one intermediate. Then Δρ(r,t) will exhibit a more complex time dependence over the time interval when the concentration of those intermediates is nonzero (Fig. 1). Thus, if voxels could be classified or clustered into groups such that each group corresponds to one intermediate (or combination of intermediates) then the number of intermediates present can be inferred from the number of such groups. Further, the common shape of the TDED at the voxels in each group yields the time profile of their concentration changes and hence the relaxation rates associated with their interconversion. If these time profiles can be represented by a simple sum of exponentials, then a chemical kinetic mechanism may hold.

Two key ingredients are the existence of voxels whose TDED is indeed sensitive to the presence of only one intermediate; and for those voxels whose TDED depends on more than one intermediate, the ability to separate the individual contributions of each intermediate to the total TDED. This separation would allow refinement of the structures of each intermediate. We show that such a separation is indeed possible, at least in the case of a simple sequential kinetic mechanism where only two intermediates overlap in time.

Cluster analysis

The computational grouping of objects based on their similarity as defined by a suitable mathematical measure is referred to in statistics as cluster analysis (25,26). The basic problem in cluster analysis may be formulated as: given N objects (here, the voxels in the electron density map) the difference density at which is measured in each of p variables (here, the time points), devise a scheme for grouping the objects into g classes or clusters. The number of clusters g in the general case is not known a priori. If this number were known the grouping would simply involve categorization of the objects.

The application of cluster analysis to time-resolved crystallographic data requires three questions to be addressed. Is there any initial transformation of the raw data that will better distinguish the groupings? What is the appropriate mathematical measure of similarity between the data? Once a similarity measure is chosen, what kind of clustering algorithm should be used? The correct answers to these questions are interconnected and require careful analysis.

Data transformation

The initial data to be clustered consists of Δρ(r,t). The data may be replaced by w(r,t) T(Δρ(r,t)), where w(r,t) is an appropriate weighting function and T denotes a mathematical transformation. We explored various transformations T such as |Δρ(r,t)| and (Δρ(r,t))² and conclude (data not shown) that it is best to use Δρ(r,t) as is. The weighting function w(r,t) may depend explicitly on factors such as t or r; and implicitly on the quality of the data, or the magnitude of Δρ(r_i,t). In the simplest weighting scheme w(r_i,t) is either 0 or 1 depending on whether some criterion is met. Thus a time point t_m that contains large systematic noise can be excluded from the analysis by setting w(r, t_m) = 0 for that time point. Likewise attention can be restricted to the region of space containing the protein molecule, or only the active site, by applying a spatial mask and setting w(r_i, t) = 0 outside the mask. To initially identify the number of clusters present, we found it useful to consider only a subset of the voxels that have the strongest signal. This corresponds to using a weighting factor that depends on the magnitude of Δρ(r_i,t) and is zero whenever |Δρ(r_i,t)| does not reach a specified magnitude at any time during the reaction. Initially focusing on only the few hundred voxels with largest magnitudes of the TDED instead of all voxels present in the map, typically ∼10⁵, both greatly accelerates the computations that are otherwise quite unwieldy, and more importantly, allows more accurate identification of the clusters.

Choice of similarity measure

The choice of metric (25) used to quantify whether the TDEDs at two voxels in the density maps are similar to each other is of primary importance. The values of the electron density for a given voxel at n different times define an n-dimensional vector. We tested the most commonly used similarity measures: the Euclidean distance (the distance between two points in the n-dimensional space sensitive to both the direction and the magnitude of the electron density vectors); the Pearson correlation coefficient (the dot product of two normalized vectors that captures the directional similarity in space (or shape along the time axis) with no emphasis on magnitude); and Kendall's Tau (that measures the tendency of TDEDs at two voxels to vary in the same direction with time). The performance of each of these similarity metrics is discussed in the supplemental materials. Because we aim to distinguish the TDED profiles based on shape similarities and not on absolute magnitude we expect that the Pearson correlation coefficient measure will perform best.

The choice of similarity measure is complicated by the fact that Δρ(r_i,t) can be both positive (an atom moving into a region of space) and negative (an atom moving out of a region). There exist voxels whose TDEDs have similar time profiles that are mirror images of each other across the time axis, but are sensitive to the same intermediate or group of intermediates. Most similarity measures would classify such voxels as belonging to different clusters, whereas in the present context they should be grouped together. This may be addressed by using a variant of the Pearson similarity measure—Pearson squared—that clusters together both positively and negatively correlated voxels.

Clustering algorithms

We find that the most appropriate methods for analysis of time-resolved crystallographic data are those that divide the data into a predetermined number of homogeneous groups by optimizing some predefined criterion, usually attempting to minimize the within-groups dispersion matrix (the objects in the groups are tight) or maximizing the between-groups dispersion matrix (the groups are well separated). One such widely used method is k-means clustering, in which the number of partitions M to be sought is chosen in advance (26). In this approach, each of the M partitions has a reference vector, which is initialized randomly. Each voxel is then partitioned to its most similar reference vector. Next, each reference vector is recalculated as the average of all vectors assigned to it. These steps are repeated until all electron density vectors map to the same partition on consecutive iterations. It should be noted that k-means clustering is nondeterministic due to the random initialization (although deterministic versions exist) and therefore different k-means runs on the same data can and do produce slightly different outcomes.

An important consideration in k-means clustering is choosing the number of partitions. In the analysis of time-resolved crystallography data, this task is aided by the available experimental evidence that usually places restrictions on the number of possible intermediates and hence of partitions. If there are N intermediates (i.e., states distinguishable from the reactant state) then there are 2^N – 1 partitions. For the simulated data analyzed here the number of intermediates is known in advance. Even in this case, it is not always obvious how many partitions to specify to display the underlying structure in the data. Due to the imperfect similarity measures and the noise and complexity of the data, if the number of partitions is set too low, voxels that should belong to the same cluster are often grouped into two or more separate clusters at the expense of voxels that should belong in a separate cluster. Thus it seems that the number of clusters specified in k-means clustering should be overdetermined by trial and error, something that is more difficult to do when the number of intermediates is not known in advance.

We explored several other clustering algorithms using k-means clustering as a reference point. These include k-means support, Pavlidis template matching, self-organizing maps, and quality clustering (QTC). The results using these methods are reviewed in the supplemental materials. Although many of these alternatives have attractive features they contain equally important drawbacks. The arbitrary specification of the number of clusters in k-means clustering is substituted by equally arbitrary criteria such as the cluster diameter in QTC. The choice of the number of clusters in k-means clustering is guided by the anticipated number of intermediates and is a discrete parameter that can be systematically explored, unlike some of the continuous parameters needed in the other methods.

These considerations and our computational results presented in the next section show that k-means clustering with the Pearson squared similarity measure produces the best results.

Results

Simulated data

The clustering computations were carried out with the TMeV program developed by The Institute for Genomic Research for the analysis of gene microarray data (27), customized to include additional similarity measures. This program was chosen because it contains a large number of clustering algorithms and similarity measures.

We first analyze simulated crystallographic data representing structural intermediates in the photocycle of photoactive yellow protein (PYP). The data consist of a time series of difference electron density maps generated for different noise levels as described in Schmidt et al. (15) and subjected there to SVD analysis. Briefly, the intermediates are derived from several structures of PYP deposited in the Protein Data Bank: the entry 2phy represents the dark state structure and the entries 3pyp, 2pyr, and 2pyp the structures of three intermediates. A sequential kinetic mechanism is used in which the three intermediates have the concentration profiles shown in Fig. 1, generated with the rate coefficients in Table 1. The time-dependent structure factor for the crystal as a whole is calculated by the vector addition of time-independent structure factors of the intermediates to the dark-state structure factor, each weighted by its time-dependent concentration. Values of time are chosen equidistant in logarithmic time to cover the entire time course of the photocycle. Noise on the structure amplitudes is based on the experimental standard deviations σ measured for an experimental data set on a PYP crystal in the dark. A spatial mask is applied to the difference maps that includes one PYP molecule and contains ∼82,000 voxels; complete details are provided in Schmidt et al. (15). We retain the notation of that study, e.g., 5 s/3 s denotes simulated data that has a noise level of 5σ in the light state and 3σ in the dark state.

Table 1.

Comparison of input and fitted rate coefficients

Data	k01	k12	k23
Input	40,000	1000	100
No noise data	40,177	1006	100
2 s/1 s noise	33,557	1444	69
5 s/3 s noise	34,733	1416	61

Rate coefficients (s⁻¹) used to generate the simulated data according to the mechanism in Fig. 1, and the coefficients obtained from the global fitting of the cluster analysis results at each of the three levels of noise.

We found that for the simulated data, applying a weighting function of zero for voxels with a TDED below 5σ at any time point t_m, where σ represents the standard deviation of Δρ(r,t) for all voxels in the asymmetric unit, allows us to initially focus on those voxels most representative of the clusters in the data and produces the best trade-off between computational speed and reliable identification of all intermediates.

Simulated data without noise

Two of the similarity measures analyzed, Euclidean and Kendall's Tau (see Fig. S1 in Supporting Material), frequently produce clusters that are not homogeneous and contain mixtures of voxels that are sensitive to more than one intermediate. This undesirable effect is minimized when using the Pearson correlation coefficient that best captures the differences in shapes of the TDED that we seek (Fig. S1 c). In particular, Pearson squared groups together both positively and negatively correlated voxels, as shown in Fig. 2 a where the number of clusters was chosen to be 12. This permits voxels with TDEDs that are mirror images of each other along the time axis to be grouped into the same cluster, a clustering that is physically correct. The data is partitioned into clusters that can be associated with the time course followed by the concentration of the each of the three intermediates separately (Fig. 2 a, D, A, and H; compare with Fig. 1) and with combinations of two of the intermediates, or all three intermediates (for example, Fig. 2 a, E, J, and L). Plotting of the electron density features associated with each of these clusters (Fig. 2 a, A, D, and H) shows that they are spatially contiguous as would be chemically expected.

Figure 2.

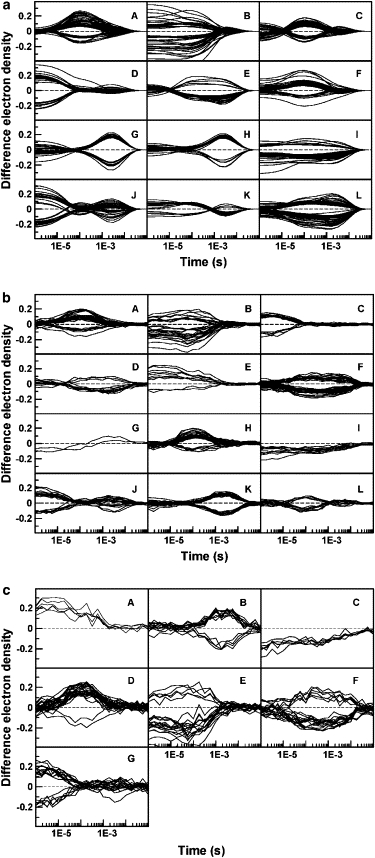
Clusters of voxels at which the TDED exceeds 5σ, obtained by applying the k-means clustering algorithm with the Pearson squared similarity measure to simulated data. Each panel represents a different cluster. The number of voxels in each cluster is shown in parentheses: (a) no added noise: A(54), B(44), C(51), D(50), E(32), F(39), G(36), H(37), I(36), J(43), K(18), L(65), (b) intermediate (2 s/1 s) noise level: A(40), B(33), C(21), D(14), E(10), F(48), G(2), H(38), I(12), J(21), K(33), L(15), and (c) high (5 s/3 s) noise level: A(5), B(14), C(6), D(27), E(22), F(22), G(20).

Identification of other clusters is aided by analyzing zero crossings. Any cluster for which certain TDEDs cross zero (e.g., Fig. 2 a, C, E, G, J, and K) must arise from more than one intermediate. One zero crossing implies two intermediates; two zero crossings imply three intermediates, and so forth. This follows from the fact that Δρ_j(r) in Eq. 2 may be positive or negative.

We note also that each TDED in a cluster arising from a combination of two (or more) intermediates is a weighted sum of the TDEDs of the two (or more) clusters arising from each intermediate separately. The combination is a linear combination of the individual clusters, a fact that aids in its identification. For example, the cluster in Fig. 2 a, G resembles that in Fig. 2 a, H, but both the zero crossings and the larger values at the lowest times in Fig. 2 a, G suggest that it contains both the first and third intermediates, rather than simply the third intermediate as in Fig. 2 a, H.

Noisy simulated data

Fig. 2, b and c, depicts the clusters obtained when using simulated data at the 2 s/1 s and 5 s/3 s noise levels. As with the no noise data, the resulting clusters can clearly be associated with each of the intermediates present in the simulated data. For example, Fig. 2 c, B, D, and G, correspond to each of the three intermediates separately, whereas Fig. 2 c, E, corresponds to a mixture of the first two intermediates. Clustering at the highest noise level provides the most convincing partition of the data. This apparent paradox may be explained by the small number of voxels selected for the initial clustering by applying the 5σ noise cut-off criterion. Smaller data sets are mathematically easier to cluster into distinct groups. Only 7 clusters yielded a clear partitioning as opposed to the 12 clusters necessary at the lower noise levels. We verified that the initial clusters obtained are homogeneous by attempting to subcluster each of the clusters into two or more clusters (data not shown). No new clusters or time profiles were observed.

After data partitioning, we then determine the contribution of each intermediate to the TDEDs of voxels in the clusters that are sensitive to more than one intermediate. First, we take the clusters that correspond to each of the three intermediates and globally fit the TDEDs of each voxel with a sum of three exponentials, in which the relaxation rates are fit with the constraint to be the same for each voxel, whereas the pre-exponential factors are allowed to vary for each voxel. The initial values of the rates in the fit were those used to generate the simulated data (Table 1). Fig. 3 a depicts such a fit for a voxel sensitive to the second intermediate. This process yields the relaxation rates R₁, R₂, and R₃; their values for the different noise levels are shown in Table 1. Using these rates we fit the remaining voxels in the density maps using the following expression:

$$\Delta \rho ({\text{r}}_{\text{i}},\text{t}){=\text{A}}_{\text{i}}\text{exp}\left(-{\text{R}}_1\text{t}\right){+\text{B}}_{\text{i}}\text{exp}\left[\left(-{\text{R}}_2\text{t}\right)-\text{exp}\left(-{\text{R}}_1\text{t}\right)\right]{+\text{C}}_{\text{i}}\left[\text{exp}\left(-{\text{R}}_3\text{t}\right)-\text{exp}\left(-{\text{R}}_2\text{t}\right)\right].$$ (4)

Figure 3.

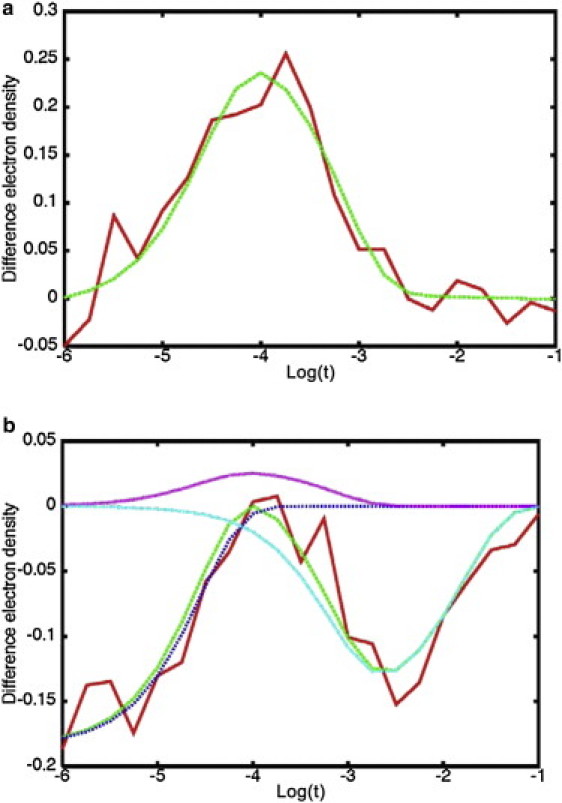
Fits using a sum of exponentials with rates from Table 1 of two voxels selected from the 5 s/3 s data set. The red (solid) line is the input data and the green (dashed) line represents the fit, (a) voxel sensitive to the second intermediate only, (b) voxel sensitive to the first and third intermediates. The contributions of each exponential term to the total fit are shown with purple, light blue, and dark blue dotted lines.

The first term in the above equation represents the decay of the first intermediate, whereas the second and third terms account for, respectively, the rise and decay of the second and third intermediates. An example of such a fit is presented in Fig. 3 b (see also Fig. S3) for a voxel that depends on two intermediates. The pre-exponential coefficients A_i, B_i, and C_i vary for each voxel and represent the time-independent contribution of each intermediate to the TDED at voxel i. By generating a set (A_i, B_i, C_i) for each voxel in the asymmetric unit, the TDEDs maps are deconvoluted into three time-independent density maps, each corresponding to a single intermediate j. Fig. 4 compares the input density maps (first row) for the three intermediates (columns) with those obtained from the fitting procedure at each of the three noise levels (second through fourth rows). The excellent agreement between the maps obtained via clustering and the input maps is apparent. The clustering maps even reproduce artifacts in the input maps such as features outside the asymmetric unit (black arrows) and side-chain density differences arising from the crystal structure used to construct I₁ (blue arrow). Fig. 4 demonstrates that the clustering results are robust to the presence of even large levels of noise that do not appreciably influence the main features of the resulting time-independent maps.

Figure 4.

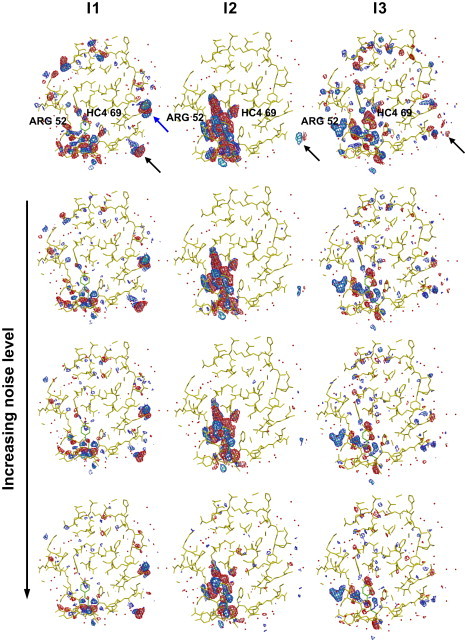
Comparison of the input difference density map for the three intermediates, I₁, I₂, and I_3, with output maps obtained by clustering at the three different noise levels. Maps contoured at −4σ (pink), −3σ (red), 3σ (blue), and 4σ (cyan). Each column represents one intermediate. The first row is the input difference density map, the second through fourth rows are the difference density maps derived from clustering of simulated data with no noise, with 2 s/1 s noise, and with 5 s/3 s noise, respectively.

Because an irreversible kinetic mechanism is simulated here, fitting of pre-exponential coefficients and apparent rates readily derives the intermediates. It remains to be explored whether this approach will be applicable to more complicated mechanisms with reversible steps or with more intermediates.

Experimental data

The experimental time-resolved data for wild-type PYP spans the microsecond to second time range (6). We omit the last seven time points from our analysis due to their low signal/noise. We also removed the sixth point for which the mean value of |Δρ(r,t)| across the asymmetric unit deviates markedly from the values for adjacent time points. Removal is based on the premise that concentration profiles in real reactions vary smoothly with time (Eq. 2) and that a spike can only arise from systematic noise such as a scaling error (see also Rajagopal et al. (17)). The results of clustering the TDED at voxels exceeding 6σ using the k-means and the Pearson squared similarity measure are shown in Fig. 5. The clusters reveal the presence of two intermediates: one early intermediate (cluster F) and one late intermediate (clusters A and C). The other clusters contain voxels that depend on both intermediates. This initial result is confirmed by varying the number of clusters and by attempting to recluster each cluster (data not shown). In neither case does any new cluster corresponding to additional intermediates emerge. These results differ from the interpretation of the same data using SVD analysis by Ihee et al. (4), who find evidence of more intermediates in this time range. One possibility for this discrepancy is that the intermediates with similar and closely overlapping concentration profiles identified in (6) may not be readily discernible by the Pearson similarity measure used in the present computations, particularly at the high noise levels inherent in experimental data. A discussion of cluster analysis and SVD is presented below.

Figure 5.

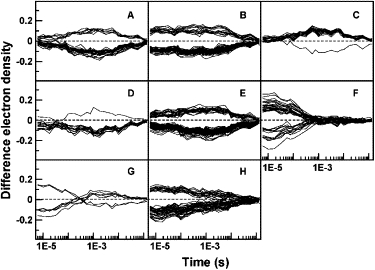
Clusters of voxels at which the TDED exceeds 6σ, obtained by applying k-means clustering and the Pearson squared similarity measure to experimental data for PYP spanning the microsecond to second time range. Each panel represents a different cluster. The number of voxels in each cluster is shown in parentheses: A(30), B(57), C(20), D(15), E(81), F(38), G(7), H(54).

We then applied the two-step voxel time course fitting procedure described above to the experimental data. First, all voxels in the clusters corresponding to only the first and second intermediates were fitted separately to a sum of two exponentials with the same relaxation rates for each voxel. The values obtained for the two relaxation rates R₁ and R₂ are 4400 s⁻¹ and 30 s⁻¹, close to the values of 3030 s⁻¹ and 100 s⁻¹ determined by SVD (6). Next, these relaxation rates were used to fit all voxels in the density map with

$$\begin{array}{l}\Delta \rho \left({\text{r}}_{\text{i}},\text{t}\right){=\text{A}}_{\text{i}}\text{exp}\left(-4400\text{t}\right){+\text{B}}_{\text{i}}\left[\text{exp}\left(-30\text{t}\right)-\text{exp}\left(-4400\text{t}\right)\right],\end{array}$$ (5)

where the first term represents the decay of the first intermediate whereas the second term represents the rise and decay of the second intermediate. The time-independent electron density maps corresponding to each of the two intermediates are shown in Fig. 6. As expected, the density features are spatially contiguous and concentrated around the chromophore. Each intermediate displays distinct density features.

Figure 6.

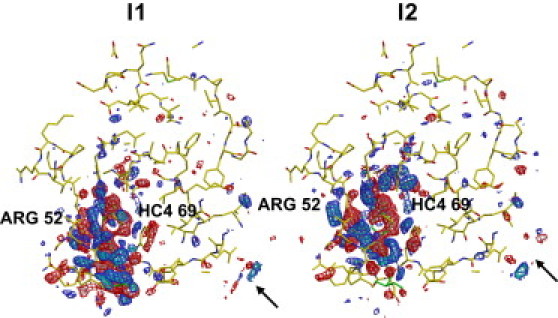
Difference density maps for the two intermediates identified by clustering of the experimental PYP data. Maps are contoured at −4σ (pink), −3σ (red), 3σ (blue), and 4σ (cyan), where σ here denotes the root mean-square value of the difference electron density across the asymmetric unit.

Discussion

Potential of clustering

For cluster analysis to be successful in analyzing time-resolved x-ray crystallographic data it must address three problems: 1), be able to handle the large amount of data generated by time-resolved experiments, typically hundreds of thousands of voxels spanning the asymmetric unit, over tens of time points; 2), be robust with respect to the significant noise present in each TDED; and 3), be able to accurately identify voxels whose TDED is sensitive to one intermediate only and those whose TDED is sensitive to more than one intermediate.

The first problem is surmounted by our finding that it is not necessary to cluster all voxels to identify the clusters corresponding to the intermediates present in the data. Initially analyzing only those few hundred voxels that contain the strongest signal is sufficient. However, care must be taken not to omit all voxels belonging to a given intermediate when none of those voxels exhibits a strong enough signal. This can be addressed by clustering the sets of voxels at decreasing signal levels, say first 6σ, then 5σ and 4σ, and noting if the inclusion of voxels with progressively lower signal levels leads to the appearance of new clusters.

With respect to the second problem, none of the similarity measures currently used in statistics is fully satisfactory for the clustering of the inherently noisy, time-resolved crystallographic data. Yet, as the clusters of the simulated data with increasing levels of noise indicate, the results are sufficiently stable to the presence of high levels of noise (Fig. 2 and Fig. 4). The number of unique clusters and their characteristics remain unchanged. Thus, the results with the noisy simulated data gave us the confidence to apply cluster analysis to experimental data.

The third problem is more complicated at first sight but turns out to have a simple solution. Our results for both the simulated and the real data indicate that by using the fitting procedure described above it is only necessary to identify those clusters that correspond to a single intermediate. All other voxels are then fit to a sum of exponentials with relaxation rates determined from the fit to the single-intermediate clusters, a process that allows establishing the contributions of the peak populations of each intermediate to the difference density of the remaining voxels. We show that this is possible in the case of a simple sequential mechanism where the intermediates are relatively well separated in time. Of course, this fit can be preceded by further refinement of the relaxation rates against all voxels, not just those associated with a single intermediate or whose TDED exceeds the sigma cutoff.

The third problem has a second, more general geometrical aspect: will voxels always exist whose TDED arises from each single intermediate? We believe the answer is “yes” as in the simulated and experimental data analyzed here, but lack a formal proof.

Cluster analysis using k-means does not have any inherent assumptions that bias the method toward a particular number of intermediates. In practice, in the initial clustering we use only those voxels with the largest magnitude of TDED to identify the number of intermediates. Authentic intermediates may exist with features that have weaker signal, especially if an intermediate contains more delocalized structural changes with weaker signal. Such intermediates would not be captured in the initial analysis. In principle, it is possible to include in the initial clustering voxels with weaker signal/noise ratio or even all voxels in the difference map. However, such an approach results in poor clustering and worse reproducibility; therefore in Fig. 2 and Fig. 5 the substantial number of voxels whose TDEDs have values near zero at all times were eliminated with the 5σ weighting function. Initially, we expected that voxels containing primarily noise would be clustered into a separate noise cluster. This proved to be only partially true. The reason lies in the mathematical nature of clustering that is based on a minimax algorithm. This algorithm attempts both to minimize the intracluster difference between the clustered objects and maximize the intercluster differences. When the number of voxels to be clustered becomes too large or if many of their TDEDs do not contain strong features, the quality of the resulting clusters is reduced because many noise voxels are incorrectly allocated to clusters associated with one of more of the structural intermediates. Even when the voxels whose TDED is near zero throughout are eliminated, many voxels remain whose TDEDs contain signal at some time points but only noise at others. Due to a smaller minimax penalty, the clustering algorithm might group such partially noisy voxels together with others that are somewhat similar in TDED, rather than segregating them into a separate cluster. An example is in Fig. 2, c, G, where one voxel stands out at long times. The clustering algorithms and similarity measures currently used in statistics are not designed to deal with complex and noisy data where a large number (and in fact the great majority) of the objects to be grouped do not contain the features sought. At the same time, the signal/noise in the data is not large enough (unlike data from time-resolved spectroscopy) to provide a clear-cut distinction between the TDEDs containing signal and those containing only noise.

The robustness of the cluster analysis results is validated by three key findings. First, the clusters are homogeneous and no new time courses are revealed by reclustering any of the clusters associated with a single intermediate. Second, the features in the single-intermediate density maps obtained with cluster analysis for both simulated and real data are spatially contiguous as would be chemically expected. If the candidate single-intermediate maps were in fact heterogeneous due to a failure in clustering, then they would not be refinable by a single intermediate structure. Finally, for the simulated data the input density maps are accurately reproduced.

Comparison with singular value decomposition

For a review of the principles of SVD analysis see Henry and Hoftrichter (14). The application of the method to simulated and real data for PYP is presented in Ihee et al. (6) and Schmidt et al.(15,16). Both cluster analysis and SVD are able to correctly identify the number of intermediates and their interconversion rates in the simulated data, a case where these quantities are known in advance (see Table 1). However, SVD analysis of the experimental data for wild-type PYP (6) identifies more intermediates than does cluster analysis. Two general reasons why cluster analysis may miss an intermediate were discussed above: omitting all voxels belonging to a given intermediate if they do not have a strong enough signal and difficulty in discerning species with similar and closely overlapping concentration profiles. An additional reason is that difference density maps obtained by cluster analysis have not been refined. The pB₂ late intermediate identified by SVD as present in very low fractional concentrations was only discovered during the refinement process (6). The SVD analysis also contains uncertainties. Although the initial matrix decomposition is an exact mathematical operation the subsequent determination of the number of significant singular values and vectors is more subjective. Previous studies (6,15,16) have adopted a comprehensive set of criteria for the selection of the relevant singular values, criteria designed to eliminate subjectivity to the greatest possible extent. Nonetheless it remains possible that the number of intermediates may be overestimated. Such a possibility has already been discussed with respect to spectroscopic data (28) where a simple weighting made the distinction much clearer between singular values that contain information from those that contain noise. Because spectroscopy data are typically of much higher signal/noise than our time-resolved crystallography data, the spectroscopic analysis was able to identify the significant singular values only on the basis of their magnitude, and did not require any additional criteria such as those used in the SVD analysis of time-resolved data.

A critical distinction between cluster analysis and SVD is that cluster analysis is able to directly identify the voxels in the density maps that are sensitive to each of the time-independent intermediates, separately. In contrast, SVD analysis produces a set of time-independent density maps consisting of the left singular vectors, each of which is a linear combination of the individual maps corresponding to each intermediate. The individual maps can be derived from the left singular vectors after fitting the right singular vectors with a candidate kinetic model. Once the structures of the intermediates are known, the kinetic mechanism can further be validated and the rate coefficients refined by posterior analysis (15). The ability of cluster analysis to derive the intermediate time-independent density maps directly from the TDED maps is a substantial advantage as it eliminates an analysis step that may introduce subjectivity and inaccuracy. Certain steps in cluster analysis at first glance appear entirely subjective: choice of σ cutoff, number of partitions, and identification of particular clusters with single intermediates. These can be made at least partially objective by varying e.g., the σ cutoff and number of partitions, and by reclustering to demonstrate the homogeneity of all clusters including those provisionally identified with single intermediates.

Conclusions

Applied individually, SVD and cluster analysis represent powerful analytical methods that enable the deconvolution of time-resolved crystallographic data to extract information on enzymatic reaction intermediates, mechanisms, and time courses that is impossible to obtain via simple observation of electron density maps. We demonstrate that cluster analysis is a viable alternative and complement not only to SVD but to other methods for the analysis of time-resolved crystallographic data such as data averaging of adjacent time points (11). The joint application of these techniques promises to become a useful analytical tool for the analysis of complex biological reactions.

Future work will explore the possibility of finding an optimal signal/noise cutoff that would allow the inclusion of any intermediates that are manifested with weaker signal while at the same time maintaining clusters of high quality that enable those intermediates to be readily distinguished. Future work should also formulate new clustering algorithms and/or similarity measures that are capable of effectively segregating the noise time courses from complex data in situations where such time courses constitute a significant fraction of the data. Ideally, new similarity measures would be able to distinguish between time profiles with similar shapes that are nearly overlapping in time. Such advances will allow applying the clustering analysis to more complex mechanisms and resolve any remaining discrepancies between SVD and cluster analysis for the experimental PYP data.