A Simple Thermodynamic Model of the Liquid-Ordered State and the Interactions between Phospholipids and Cholesterol

Abstract

A theoretical model is proposed to describe the heat capacity function and the phase behavior of binary mixtures of phospholipids and cholesterol. The central idea is that the liquid-ordered state (L_o) is a thermodynamic state or an ensemble of conformations of the phospholipid, characterized by enthalpy and entropy functions that are intermediate between those of the solid and the liquid-disordered (L_d) states. The values of those thermodynamic functions are such that the L_o state is not appreciably populated in the pure phospholipid, at any temperature, because either the solid or the L_d state have much lower free energies. Cholesterol stabilizes the L_o state by nearest-neighbor interactions, giving rise to the appearance of the L_o phase. The model is studied by Monte Carlo simulations on a lattice with nearest-neighbor interactions, which are derived from experiment as much as possible. The calculated heat capacity function closely resembles that obtained by calorimetry. The phase behavior produced by the model is also in agreement with experimental data. The simulations indicate that separation between solid and L_o phases occurs below the melting temperature of the phospholipid (T_m). Above T_m, small L_d and L_o domains do exist, but there is no phase separation.

Introduction

Our understanding of the interactions between phospholipids and cholesterol (Chol) is still incomplete, as demonstrated by the continuous work on the problem in recent years (1–5). The effect of cholesterol on the excess heat capacity (ΔC_p) associated with the main phase transition of phosphatidylcholines (PC) has intrigued researchers for a long time (6–10). Fig. 1 shows typical changes in ΔC_p of dipalmitoylphosphatidylcholine (DPPC) caused by incorporation of cholesterol in the bilayer, determined by differential scanning calorimetry (DSC) (8). When cholesterol is added to PC multilamellar vesicles (MLVs), ΔC_p decreases substantially and the main phase transition temperature (T_m) decreases slightly; at still higher cholesterol concentrations, a significant broadening of ΔC_p is observed, and the maximum moves to higher temperatures. Eventually, the phase transition becomes extremely broad and hard to detect.

Figure 1.

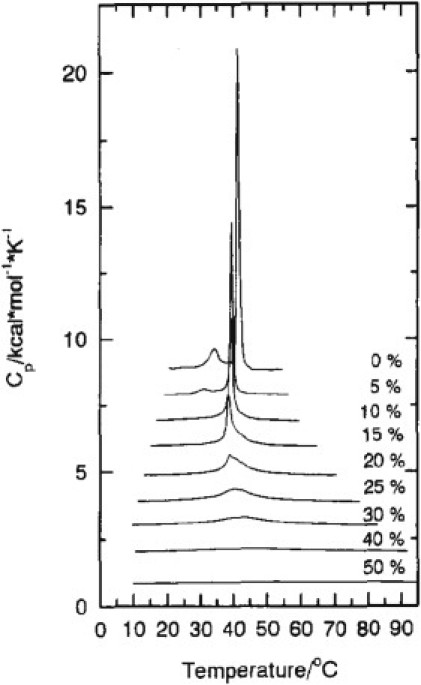
Effect of increasing amounts of cholesterol on the excess heat capacity function of DPPC MLVs. (Reprinted with permission from Huang et al. (8). Copyright 1993 American Chemical Society.)

Ipsen et al. (11) proposed a model that became the standard description of the phase behavior in PC/Chol mixtures. In pure DPPC, the main phase transition occurs at T_m = 41.5°C, between a solid and a liquid-disordered (L_d) phase. At high cholesterol content, however, the phospholipid exists in a state of high chain order, akin to the solid, but with fast long-range mobility, akin to the liquid, which was called a liquid-ordered phase (L_o). The model yielded ΔC_p functions for DPPC/Chol mixtures (12) that closely resembled those obtained experimentally by DSC. The broad, high-temperature melting at Chol ≥ 20 mol % was reproduced, which was associated with an L_o→L_d phase transition. Furthermore, based on this model Ipsen et al. (11,12) calculated a phase diagram that subsequently received significant experimental corroboration (9,13,14). The canonical phase diagram for DPPC/Chol is shown in Fig. 2 A (4).

Figure 2.

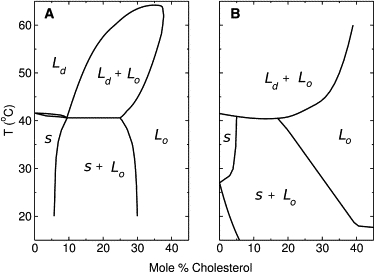
(A) Canonical phase diagram for DPPC/Chol, based on theory and several lines of experimental data. (B) Variation based also on the ¹³C-NMR signal of the lipid carbonyl group (8). In these diagrams, S represents a solid phase.

In recent years, interest in PC/Chol mixtures has resurged, motivated mainly by two developments. First, an alternative view, the idea that interactions between phospholipids and cholesterol can be described by formation of condensed complexes with defined stoichiometry was proposed by McConnell et al. (15,16). The broad, high-temperature shoulder in ΔC_p (Fig. 1) was interpreted as thermal dissociation of the complexes, and was qualitatively reproduced by calculations (17). Although formation of complexes between PC and Chol is an old and criticized idea, the new concept does not require highly specific and well-defined chemical interactions, but rather transient associations between PC and cholesterol (18).

Second, developments in fluorescence microscopy, combined with the ability to produce giant unilamellar vesicles with diameters ≥10 μm, allowed direct visualization of liquid-liquid phase separation in phospholipid/cholesterol mixtures (19–24). L_d/L_o phase separation was observed in ternary mixtures of cholesterol with two phospholipids, one of which is typically saturated, with a high T_m (ordered), and the other is unsaturated (or has short acyl chains), with a low T_m (disordered). However, in binary mixtures of PC/Chol, no micron-size phase separation was observed (19), and it now appears that no L_d/L_o phase separation occurs in DPPC/Chol (25). This is contrary to a strict interpretation of the immiscibility in PC/Chol systems in terms of the phase diagram of Fig. 2 A, which includes a large region of L_d/L_o phase coexistence. The condensed complex model, on the other hand, predicted a closed loop in ternary mixtures of a high-melting and a low-melting PC with cholesterol in the liquid state (18,26), which means that no L_d/L_o phase separation would exist in the PC/Chol binary mixtures.

Recently, we investigated domain formation in ternary mixtures of a high- and a low-melting PC with cholesterol by Monte Carlo simulations (27). A simple lattice model of the membrane was used, with phospholipids and cholesterol interacting only with nearest neighbors. The unlike nearest-neighbor interaction Gibbs free energies were represented by a parameter designated by ω_AB, which is equivalent to the Flory parameter in polymer physics (28,29),

$${\omega }_{AB}=g_{AB}-\frac{1}{2}\left(g_{AA}+g_{BB}\right),$$ (1)

where g_AA and g_BB are the Gibbs energies of interaction between two A or two B molecules, and g_AB is the Gibbs energy of interaction between one A and one B molecule. The simulations showed that phase separation occurs in the ternary mixture, but not in any of the three binary mixtures (27). This result requires that a favorable interaction exist between the ordered lipid and cholesterol (ω_AB < 0) combined with unfavorable interactions (ω_AB > 0) of the disordered lipid with both the ordered lipid and cholesterol. This is all that is necessary for a closed loop to exist in the ternary phase diagram, with no need to invoke formation of complexes (1,27).

However, the model we used does not account for phase transitions, which is a serious limitation. That model cannot describe the fundamental behavior of mixtures containing cholesterol over the phospholipid phase transition, which may be biologically relevant because sphingomyelins have T_m close to 37°C. A model that includes the phase transition is necessary and useful, but it must be simple to be extended to ternary mixtures, which are of greater biological interest. The model used by Ipsen et al. (12), which combines the 10-state Pink and q-state Potts models, is too complicated for this purpose. The condensed complex model, on the other hand, results in a ΔC_p that exhibits a large spurious transition at high cholesterol content, below the lipid main phase transition (17). In addition, its energetic parameters are much too large (1).

This report describes an attempt to fill this gap, using a simple thermodynamic model that is approximate but tractable. This model is applied to DPPC/Chol binary mixtures and is investigated using Monte Carlo simulations on a triangular lattice. The lipid interactions are represented by parameters that are consistent with experiment. The calculated ΔC_p(T) is in fairly good agreement with that obtained experimentally by DSC. The model correctly produces phase separation in DPPC/Chol, or not, in agreement with the experimental observations.

The Model

The central idea of the model is that the L_o state is a thermodynamic state of the phospholipid characterized by an enthalpy and an entropy that are intermediate between the L_d and solid states (Fig. 3 A). The values of those thermodynamic functions are such that the L_o state is not appreciably populated in pure DPPC. Below T_m, the free energy of the solid lies much below those of the L_d and L_o states (Fig. 3 B); above T_m, the free energy of L_d is much lower than those of L_o and solid states. Therefore, the transition of pure DPPC occurs from the solid to the L_d phase (Fig. 3 C). The L_o state is scarcely populated, except in the region of the main phase transition, where it stabilizes solid/L_d interfaces (but even at T_m, L_o < 7 mol %). In the presence of cholesterol, however, the free energy of the L_o state is lowered by preferential nearest-neighbor interactions with cholesterol, and its population increases. This is qualitatively illustrated in Fig. 3 C where the addition of ≈20 mol % Chol brings the L_o line (dashed) close to the solid, which is the reference state (horizontal axis).

Figure 3.

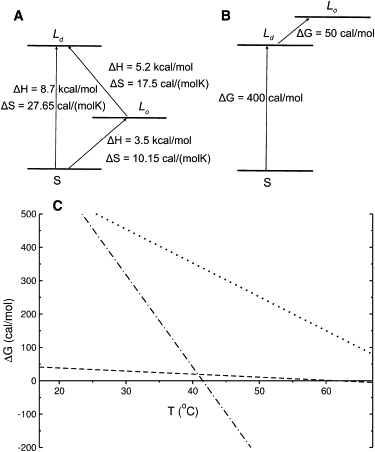
Thermodynamic model used in the simulations. (A) Enthalpy of the three states of DPPC, solid (S), L_o, and L_d.. (B) Gibbs free energy of the three states close to room temperature (300 K). (C) Qualitative illustration of the temperature dependence of the free energy for the solid, which is the reference state (solid line at ΔG = 0), the L_d state (dash-dotted line), and the L_o state of the phospholipid in the absence (dotted line) and in the presence of ∼20% Chol (dashed line).

The concept proposed is fundamentally similar to the classical model of Monod et al. (30) for oxygen binding to hemoglobin. Hemoglobin was assumed to exist in two states, T and R, which interconvert through a conformational change. The T state dominates in the absence of oxygen and has low affinity for it. The R state is not appreciably populated in the absence of oxygen, but has high affinity for it. Thus, binding of oxygen stabilizes the R state, increasing its population. In the DPPC/Chol model, cholesterol plays a role similar to that of oxygen: it stabilizes the L_o state. The classical alternative for binding of oxygen to hemoglobin is the model of Koshland et al. (31), in which the R state does not exist in the absence of oxygen, but is formed concomitant with ligand binding to the protein (induced fit). The analogous model in DPPC/Chol would not allow for L_o to exist in the absence of cholesterol. But in this case, the implementation of the model is much more complicated because numerous restrictions must be imposed in the various moves and transitions in the Monte Carlo simulations. In the case of hemoglobin, binding of oxygen is described similarly well by both models. I expect that both models would work well in DPPC/Chol, but the model chosen is much simpler to implement. It also seems to me that the PC conformations that prefer to interact with cholesterol should be possible in its absence.

The DPPC/Chol binary system was studied with this model. A leaflet of the lipid bilayer is represented by a triangular lattice with periodic boundary conditions. Each site represents a phospholipid (in the solid, L_o, or L_d states) or a cholesterol molecule. The free energy of each lattice site is determined by its interactions with nearest neighbors, represented by the ω_AB parameters, and, in the case of DPPC, by the enthalpy of its state. Monte Carlo simulations were performed to obtain the equilibrium properties of the lattice, such as the excess heat capacity (ΔC_p) and the phase behavior. A complete description of simulation methods is given in the Supporting Material.

For the main transition of DPPC, T_m = 41.5°C (32,33) and ΔH = 8.7 kcal/mol (34). The solid→L_o transition enthalpy was set to ΔH₁ = 3.5 kcal/mol, from which follows that ΔH = 5.2 kcal/mol for L_o→L_d transition (ΔH₁ + ΔH₂ = ΔH). The corresponding entropies of the transitions are then determined by the imposed conditions that ΔG₁ = 450 cal/mol (solid→L_o) at 300 K and ΔS₁ + ΔS₂ = ΔS, which equals 27.65 cal/mol/K for the solid→L_d transition of pure DPPC (Fig. 3, A and B).

The work of Regen et al. (35,36) using the nearest-neighbor recognition method constitutes one of the major sources of experimental data for lipid-lipid interaction parameters. Values of ω_AB derived from those data were recently compiled and vary between −350 and +400 cal/mol (1). Several other experimental approaches yield ω_AB of similar magnitudes (27,37–46). In DPPC/Chol, the van 't Hoff enthalpy was determined from the temperature dependence of ω_AB (47), providing an estimate of the interaction enthalpy, ΔH_AB. In the L_d phase, both ω_AB and ΔH_AB ≈ 0 for DPPC/Chol (47). In the L_o phase, the interaction is favorable, with a significant temperature dependence, reflected in ΔH_AB = −2.1 kcal/mol (47), which was included in the simulations. For example, at 60°C, ω_AB = −100 cal/mol, but at 20°C, ω_AB = −340 cal/mol. In the solid, the PC/Chol interaction is unfavorable, judging from distearoylphosphatidylcholine (DSPC)/Chol mixtures (48), with ω_AB ≈ +370 cal/mol (1).

In pure DPPC, ω_AB for the L_d/solid interaction was assigned by matching the excess heat capacity maximum (ΔC_p,max) obtained in the simulations to the value known from experiment. In DPPC MLVs, ΔC_p,max = 10–70 kcal/mol/K have been reported using DSC (6,7,40,49–51). In choosing ω_AB = 360 cal/mol for L_d/solid in the simulations, a value of ΔC_p,max = 33 kcal/mol/K, in the midrange of the experimental values, is obtained. A simplifying assumption was to use the same value of ω_AB = 330 cal/mol for both the L_o/solid and L_o/L_d interactions, because otherwise T_m would depend on those interaction parameters, with either the solid or the L_d state being stabilized relative to the other. Table 1 lists the complete set of parameters used in the calculations.

Table 1.

Lipid-lipid interaction parameters, transition enthalpies, and transition entropies used in the Monte Carlo simulations

Lipid pair (A/B)	ωAB (cal/mol)	ΔH (kcal/mol)	ΔS (cal/mol/K)
Solid/Ld	+360	8.7	27.65
Solid/Lo	+330	3.5	10.15
Lo/Ld	+330	5.2	17.5
Chol/Ld	+20	—	—
Chol/Lo	−340∗	—	—
Chol/solid	+350	—	—

^∗Value at 20°C. This parameter is temperature-dependent, with ω_AB = −2120 + 6.07 T cal/mol (T in K).

Results

Approximately 180 Monte Carlo simulations were performed, each with 5 × 10⁵ to 5 × 10⁶ Monte Carlo cycles, in pure DPPC and in DPPC/Chol mixtures containing 10, 15, 20, 25, and 30 mol % Chol, as a function of temperature. Those simulations were used to obtain the equilibrium configuration of the membrane, represented by a 100 × 100 triangular lattice, from which observable, average properties were calculated. Of particular interest were the heat capacity and the phase behavior of the mixtures.

Heat capacity

The excess heat capacity functions of DPPC/Chol mixtures were calculated from the Monte Carlo simulations through the fluctuation-dissipation theorem (28),

$$C_p=\frac{\langle H^2\rangle -{\langle H\rangle }^2}{R{T}^2},$$ (2)

where 〈H²〉 − 〈H〉² denotes the fluctuations in enthalpy. The results are shown in Fig. 4. As the cholesterol content in DPPC increases, ΔC_p,max initially moves to lower temperatures, consistent with the freezing point depression observed experimentally. When cholesterol reaches 20 mol %, the curve also broadens significantly, and on further increase in concentration the broad maximum moves to higher temperatures. This is consistent with the DSC data (Fig. 1). In the simulations, ΔC_p(T) depends on the parameters chosen, both in the terms of position of the maximum and the width of the transition, but there are no dramatic qualitative changes when the parameters change slightly.

Figure 4.

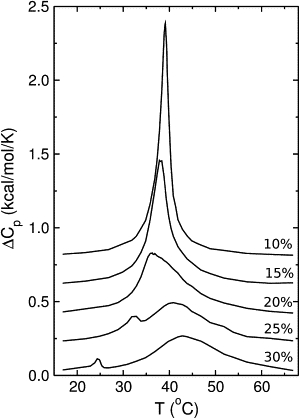
Excess heat capacity function calculated from the Monte Carlo simulations for different concentrations of Chol in DPPC, indicated next to each curve in mol % Chol. The parameters used are listed in Table 1.

A small, local maximum in ΔC_p is observed in DPPC/Chol 75:25 at 32°C, and in DPPC/Chol 70:30 at 25°C. This has not been observed by DSC at 30 mol % Chol, but some studies do show a slight local maximum at 25 mol % Chol in DSC scans (5). The occurrence of this local maximum in the simulations depends on the choice of ΔH₁ (solid→L_o). If ΔH₁ is reduced, the small maximum decreases and shifts to lower temperatures, and when ΔH₁ < 2 kcal/mol, this transition becomes essentially indiscernible in the heat capacity.

Phase behavior

The phospholipid transition is conveniently followed by a plot of the fractions of DPPC in each of the three states as a function of temperature (Fig. 5). In DPPC/Chol 80:20 (Fig. 5 A), as in pure DPPC, the main transition occurs from the solid (dotted line) to the L_d state (solid line). The population of the L_o state (dashed line) reaches a maximum at the transition midpoint. (This is also true in pure DPPC, in this model, but the L_o state does not even reach 7 mol %.) In DPPC/Chol 70:30 (Fig. 5 B) there is an initial solid→L_o transition, which is completed at ≈25°C, followed by a broad L_o→L_d transition.

Figure 5.

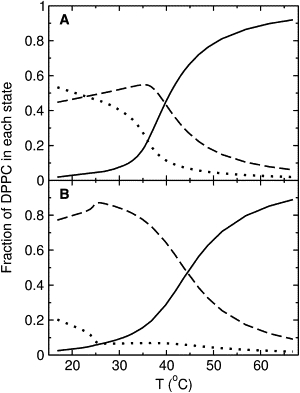
Fractions of DPPC molecules in each state in mixtures of DPPC/Chol 80:20 (A) and 70:30 (B): L_d (solid line), L_o (dashed), and solid states (dotted line).

Fig. 6 shows snapshots of the lattice along the course of the transition in DPPC/Chol 80:20. Below T_m, clear solid/L_o phase separation is observed (Fig. 6 A, 29°C), but as the temperature increases, the large domains disappear (Fig. 6, B and C, 36 and 39°C). Above T_m of DPPC, where the phase diagram indicates L_d/L_o phase coexistence, only small domains are actually observed (Fig. 6 D, 43°C).

Figure 6.

Snapshots of the Monte Carlo simulations of DPPC/Chol 80:20 at four different temperatures along the transition: (A) 29, (B) 36, (C) 39, and (D) 43°C. The different colors represent Chol (red) and DPPC in L_d (black), L_o (green), and solid states (white).

Distribution functions of the domain sizes in DPPC/Chol 80:20 are shown in Fig. 7 A for the solid state at 29°C (gray) and 36°C (black), and in Fig. 7 B for the L_d state at 39°C (black) and 43°C (gray). Thus, well-defined solid domain sizes are observed in the solid/L_o coexistence region, indicative of phase separation (Figs. 6 A and 7 A). But in the L_d/L_o coexistence region, the domain distribution is very broad, indicating that no true phase separation occurs (Figs. 6 D and 7 B).

Figure 7.

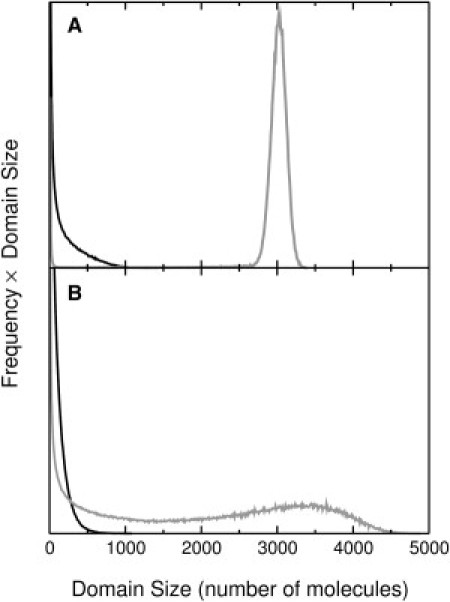
Distributions of domain sizes in DPPC/Chol 80:20 (10⁷ mcc). (A) Solid domains at 29°C (gray) and 36°C (black). At 29°C there are ≈3400 DPPC solid molecules, which corresponds to ∼42% of the DPPC. (B) Liquid-disordered (L_d) domains at 39°C (black) and 43°C (gray). At 43°C there are ≈4800 DPPC L_d molecules, which corresponds to ∼60% of the DPPC. The ordinate scale is the same in both panels.

It is also interesting to consider the mixture DPPC/Chol 70:30. Here, the main transition occurs from L_o→L_d (Fig. 5 B). The snapshots of the lattice show what is occurring. At low temperatures, solid/L_o phase separation exists (Fig. 8, A and B), but it disappears abruptly above 25°C, when the system becomes entirely L_o phase (Fig. 8 C). This solid→L_o transition corresponds to the weak local maximum in ΔC_p (Fig. 4). At high temperatures, in the L_d/L_o coexistence region, no phase separation exists but only small clusters (Fig. 8 D, 44°C).

Figure 8.

Snapshots of the Monte Carlo simulations of DPPC/Chol 70:30 at four different temperatures along the transition: (A) 17, (B) 22, (C) 27, and (D) 44°C. The colors represent Chol (red) and DPPC in L_d (black), L_o (green), and solid states (white).

In summary, the solid→L_o transition is sharp but the L_o→L_d transition is continuous.

Discussion

The L_d–L_o phase separation model

The canonical DPPC/Chol phase diagram shown in Fig. 2 A results from a combination of the original proposal of Ipsen et al. (11,12) with DSC, ²H-NMR, and electron paramagnetic resonance (EPR) data (4,9,13,52). Ipsen et al. (12) provided a compelling interpretation of ΔC_p of PC/Chol mixtures using a microscopic interaction model. The PC conformations were represented by the 10-state Pink model, where one state corresponds to the liquid and the other nine, to the solid. One of the solid states is the all-trans, ground-state, and the other eight are excited conformations containing gauche isomers (53–55). In addition, the q-state Potts model was used to represent the crystallinity of the lipid states. The variable q takes a value between 1 and ≈30 (55), which accounts for matching domain boundaries in the solid (crystalline) state; but q is lost in the liquid state. In the absence of cholesterol, the Pink/Potts states are coupled, and the phase transition occurs from an ordered solid to a disordered liquid (L_d). In the presence of cholesterol, however, the transitions are decoupled, as cholesterol prefers to interact with ordered acyl chains without crystalline order. Above T_m of the phospholipid, “this leads to massive phase separation” (12) between two liquids, L_d and L_o (Fig. 2 A).

The shape of ΔC_p calculated by Ipsen et al. (12) was in good agreement with DSC measurements. Namely, the broad high-temperature melting region at Chol ≈ 20 mol % is very nicely reproduced, and this broadening increases with cholesterol content, until the transition becomes virtually undetectable at Chol ≈ 40 mol %. A problem of the model, however, is its very large number of parameters, which render it unwieldy to extension to ternary mixtures. Also, it is not clear whether the agreement with DSC is quantitative because ΔC_p was reported in arbitrary units (12). Finally, the parameters of the microscopic interaction model correspond to ω_AB ≈ 1 kcal/mol in absolute value (11), which are ≈3 × larger than typical experimental values (1).

Does phase separation occur?

Several features of the phase diagram of Fig. 2 A are not consensual.

First, as pointed out by Marsh (4), the phase boundary between the solid/L_o and the all-L_o regions, which is drawn almost vertical in the canonical PC/Chol phase diagram, has been proposed to be much more slanted, even by Ipsen et al. (11,12), and to extend to higher cholesterol content (Fig. 2 B), both for DPPC/Chol and DSPC/Chol, based on the ¹³C-NMR signal of the lipid carbonyl group (8).

Second, fluorescence microscopy of giant unilamellar vesicles has shown that L_d/L_o phase separation occurs in ternary mixtures of cholesterol with a high- and a low-melting phospholipid, but not in binary mixtures of PC/Chol (19–24).

In the end, however, the criterion for phase separation needs to be thermodynamic, not a limit of resolution, which could be the case when light is used to visualize domains.

How large must domains be to be considered a phase and not just compositional fluctuations?

For the energy of a phase to be well defined, the contribution of the interface to the energy of a domain must be small (1,56). In very rough terms, a two-dimensional system with N molecules is large if the ratio of the boundary, of order N^1/2, to the interior, of order N, is small (57). If by small we mean <1%, then for a system to be large in two dimensions, N^1/2/N < 0.01, or N > 10⁴. In fluorescence microscopy the detectable domain size is ∼1 μm, so that each domain contains ≈10⁶ lipids, which is clearly large and corresponds to phase separation by this criterion. ²H-NMR is particularly well suited to assess phase separation because, if two-component spectra are observed (not just line broadening), then the domains must be larger than ≈100 nm (4). Domains of 100 nm contain ≈10⁴ lipids, which is the threshold between small domains and phase separation. Indeed, by this criterion, phase separation has been observed in the solid/L_o region of the DPPC/Chol phase diagram (Fig. 2 A), not only by fluorescence microscopy, but also by two-component ²H-NMR spectra (58).

In the L_d/L_o region, however, no such two-component spectra have been produced, except—but much less clearly—in DPPC/Chol 75:25, in a small region of the phase diagram, just 1–2°C above the three-phase, horizontal line (59). Other measurements largely rule out L_d/L_o phase separation (25). At 60°C, using a biradical spin-label, two-component spectra were observed by EPR in DPPC/Chol (52) and in sphingomyelin/Chol mixtures (60). But two-component spectra are expected in this case, even if only very small L_d and L_o domains exist, because in EPR the exchange is slow on the magnetic timescale (4).

The condensed complex model and ternary mixtures

McConnell and collaborators proposed to describe interactions between phospholipids and cholesterol by formation of condensed complexes, and provided a new interpretation for many experimental observations (15–18,26,61–64). However, the condensed complex model does not perform well in calculating ΔC_p(T) of PC/Chol mixtures. It correctly yields freezing point depression and a broad high-temperature shoulder in ΔC_p, which is interpreted as thermal dissociation of the complexes (17,63). But a very large transition is predicted at high cholesterol concentrations and low temperatures, which is not observed experimentally. Moreover, the shape of ΔC_p(T) is quite different from that obtained by DSC. Furthermore, ΔC_p was reported in arbitrary units (17), which precludes a quantitative comparison with experiment.

The free energies of interaction between lipids (ω_AB) estimated from experiments are of the order of a few hundred calories per mole in absolute value (1). Typically, ω_AB are positive (repulsive), which is normally expected (29). Remarkably, they are negative between PC and cholesterol in the L_o phase, indicating a favorable interaction (1,47,48). The condensed complex model is consistent with this favorable interaction, but the values of free energy and enthalpy used are approximately one order-of-magnitude too large. For example, formation of a PC/Chol 1:1 complex is associated with a Gibbs free energy change of ≈−2 to −3 kcal/mol (18,26,65), and an enthalpy of ≈−10 kcal/mol (18,65). This is larger than ΔH for the phase transition of DPPC from L_d to solid, where the acyl chains must be more ordered than in the complex. In addition, the experimental van 't Hoff enthalpy associated with ω_AB in the L_o phase of DPPC/Chol is ΔH_AB = −2 kcal/mol (47), not −10 kcal/mol.

The condensed complex model correctly predicts the existence of a closed loop in ternary phase diagrams of cholesterol with a high- and a low-melting phospholipid. However, a closed loop does not require the existence of complexes. Monte Carlo simulations of a simple lattice model with nearest-neighbor interactions demonstrated that phase separation occurs in this type of ternary mixture (27), but not in any of the three binary mixtures, provided that the Chol/L_o interaction be sufficiently attractive, and the Chol/L_d and L_o /L_d interactions be sufficiently repulsive.

None of the ω_AB parameters that specify those interactions need be much larger than 300 cal/mol in absolute value (27). Subsequently, two other studies also demonstrated that the minimal requirements for the observation of phase separation in ternary mixtures, but not in binary mixtures, are sufficiently strong interactions of cholesterol, favorable with ordered and unfavorable with disordered phospholipids. This was shown by a combination of Monte Carlo simulations with mean-field theory (66), and by a simple, but very illuminating, phenomenological model that assumes first-order transitions and a free energy expanded in the acyl-chain order parameter (67).

Mean-field models

The interactions and phase behavior of DPPC/Chol mixtures have also been investigated using self-consistent mean-field approaches. Elliott et al. (68) modeled the lipid chain conformations using Flory's rotational isomers. The free energy is then determined by the area and orientation of the lipid chains. Cholesterol interacts more favorably with chain segments oriented perpendicular to the membrane, hence preferring ordered chains. If the interaction between cholesterol molecules is comparable to the interaction between phospholipids, the model generates a phase diagram with the same topology as that shown in Fig. 2 A; however, it is significantly displaced to high cholesterol concentrations, with first-order transitions between lipid phases.

In a different mean-field model (69,70) the bilayer was represented as a continuous field of DPPC acyl-chain order, onto which cholesterol molecules were superimposed. The order at each point depends on order at neighboring points and on interactions with cholesterol. The order parameter is derived from a library of acyl-chain conformations obtained from molecular dynamics simulations, instead of using Flory's isomeric states. The interaction between DPPC and cholesterol was considered anisotropic (70), reflecting the smooth and rough faces of the cholesterol molecule, the former interacting more favorably with DPPC. The model produces regions of low and high order, the latter increasing with cholesterol concentration. In some cases, a broad distribution of order parameters is observed, but no phase separation. A phase diagram representing the amounts of ordered states was generated, which is similar to that of Fig. 2 A, but no sharp transitions actually occur. The model also yields ΔC_p(T) curves whose main features and magnitudes resemble those obtained experimentally by DSC (Fig. 1).

A simple thermodynamic model

The model proposed here to understand ΔC_p(T) and the phase behavior of DPPC/Chol incorporates nearest-neighbor, lipid-lipid interactions and the phase transition of the phospholipid. The L_o state is considered a thermodynamic state of the phospholipid, characterized by enthalpy and entropy functions that are intermediate between those of the L_d and solid states, which is consistent with an intermediate acyl-chain order. In pure DPPC, the L_o state essentially does not exist, because its free energy is much larger than those of the solid and L_d states (Fig. 3 C). Cholesterol, however, stabilizes the L_o state by preferential nearest-neighbor interactions, thus increasing its population.

Monte Carlo simulations of the model, using interaction parameters consistent with experiment, reproduce the main features of ΔC_p(T) of DPPC/Chol mixtures. Addition of cholesterol initially lowers the phase transition temperature, decreases ΔC_p,max, and broadens the transition slightly. When Chol ≥ 20 mol %, the model correctly reproduces the broadening of the transition and its shift to higher temperatures. Quantitatively, however, the value of ΔC_p,max in the simulations of DPPC/Chol mixtures is smaller than in experiment. In the simulations, ΔC_p,max drops from 33 kcal/mol/K in pure DPPC to 1.6 kcal/mol/K in the presence of 10 mol % Chol, and to 0.43 kcal/mol/K in the presence 20% Chol. Experimentally, in MLVs containing 10 and 20 mol % Chol, ΔC_p,max drops to ≈5 kcal/mol/K and ≈1 kcal/mol/K, respectively (6–8,10).

Two points may be noted. First, if the phase transition of DPPC is simulated using a simple two-state, solid/liquid model, inclusion of 10 mol % Chol strictly as an impurity (ω_AB=0 between Chol and both phospholipid states) already decreases ΔC_p,max to ≈2 kcal/mol/K.

Second, in the model proposed here the Chol/L_o interaction is isotropic, whereas its anisotropy appears to be important in the model of Pandit et al. (70). Even though our results are in good agreement with experiment without any anisotropy, its inclusion may improve the agreement—a possibility that will be explored in the future.

At low temperatures, solid/L_o phase separation clearly occurs in DPPC/Chol 80:20 and 70:30 mixtures (Figs. 6 A and 8, A and B). Thus, this Monte Carlo simulation result is in agreement with experiment (58). As noted above, the small local maximum in ΔC_p(T) apparent at 25°C in the simulations of DPPC/Chol 70:30 (Fig. 4), which corresponds to a solid→L_o transition (Fig. 5 B), has never been observed by DSC. The phase diagram of Fig. 2 B, on the other hand, predicts the occurrence of this transition, as the system is heated across the slanted phase boundary from the solid/L_o region to the all-L_o region, at 28°C (8). This transition temperature is close to that observed in the simulations, although no particular effort was made to obtain a match by adjusting the solid→ L_o enthalpy change. The reason phase separation occurs in the solid/L_o region is the combination of the two unfavorable interactions, Chol/solid (ω_AB = +340 cal/mol) and solid/L_o (ω_AB = +330 cal/mol), with the favorable Chol/L_o interaction (ω_AB = −340 cal/mol, at 20°C). This situation is similar to what occurred in the ternary mixture we simulated previously (27).

As the temperature increases, in the DPPC/Chol 80:20 mixture the solid state is progressively converted to L_d, whereas the amount of L_o state remains fairly constant, but all three phospholipid states are appreciably populated (Figs. 5 A and 6 B). Above 40°C, the solid disappears and the system enters the L_d/L_o coexistence region (Fig. 6, C and D). The DPPC/Chol 70:30 mixture had entered the all-L_o phase just above 25°C (Figs. 5 B and 8 C) and, on further increase in temperature, leaves this one-phase region and also enters the L_d/L_o coexistence region.

These results are in agreement with the phase diagram of Fig. 2, but with one important difference. In the simulations, only small L_d and L_o domains are observed in this coexistence region (Figs. 6, C and D, and 8 D). No massive phase separation actually occurs, in agreement with experiment (19,25). That is, the transition is of a continuous nature. The reason only small domains occur in the L_d/L_o region is that the favorable Chol/L_o interaction is weakened to ω_AB = −200 cal/mol at high temperatures, and although the L_d/L_o interaction is still +330 cal/mol, the Chol/L_d interaction is essentially zero. Therefore, the combination of the three interactions does not result in phase separation.