Bidentate RNA–magnesium clamps: On the origin of the special role of magnesium in RNA folding

Abstract

Magnesium plays a special role in RNA function and folding. Although water is magnesium's most common first-shell ligand, the oxyanions of RNA have significant affinity for magnesium. Here we provide a quantum mechanical description of first-shell RNA–magnesium and DNA–magnesium interactions, demonstrating the unique features that characterize the energetics and geometry of magnesium complexes within large folded RNAs. Our work focuses on bidentate chelation of magnesium by RNA or DNA, where multiple phosphate oxyanions enter the first coordination shell of magnesium. These bidentate RNA clamps of magnesium occur frequently in large RNAs. The results here suggest that magnesium, compared to calcium and sodium, has an enhanced ability to form bidentate clamps with RNA. Bidentate RNA–sodium clamps, in particular, are unstable and spontaneously open. Due to magnesium's size and charge density it binds more intimately than other cations to the oxyanions of RNA, so that magnesium clamps are stabilized not only by electrostatic interactions, but also by charge transfer, polarization, and exchange interactions. These nonelectrostatic components of the binding are quite substantial with the high charge and small interatomic distances within the magnesium complexes, but are less pronounced for calcium due to its larger size, and for sodium due to its smaller charge. Additionally, bidentate RNA clamps of magnesium are more stable than those with DNA. The source of the additional stability of RNA complexes is twofold: there is a slightly attenuated energetic penalty for ring closure in the formation of RNA bidentate chelation complexes and elevated electrostatic interactions between the RNA and cations. In sum, it can be seen why sodium and calcium cannot replicate the structures or energetics of RNA–magnesium complexes.

INTRODUCTION

Magnesium plays a special role in folding of large globular RNAs (Draper 2008; Hsiao et al. 2008). These RNAs are closely associated with magnesium ions, many of which can be visualized by X-ray diffraction. One hundred and eighteen magnesium ions associate with the 23S rRNA in the large ribosomal subunit (LSU) of Haloarcula marismortui (PDB entry 1JJ2) (described in Ban et al. 2000; Klein et al. 2004). Although magnesium's most common first-shell ligand is water, the oxyanions of RNA phosphates (i.e., the nonbridging phosphate oxygens) have significant affinity for magnesium. Ninety-eight of the magnesium ions associated with the LSU of H. marismortui contain phosphate oxyanions within their first coordination shells (characterized by Mg²⁺–OP distances < 2.4 Å). Other RNAs show the same trend. Seventy-one magnesium ions are observed to associate with the P4–P6 domain of the tetrahymena Group 1 intron (PDB 1HR2) (described in Cate et al. 1997; Juneau et al. 2001). Twenty-six of these contain phosphate oxyanions within their first coordination shell.

Our work here focuses on bidentate chelation of magnesium by RNA phosphates (Fig. 1A), where two oxyanions enter the first coordination shell of a magnesium ion. These complexes are rigid with well-defined geometry because the first coordination shell of magnesium is a well-packed octahedron (Brown 1992; Bock et al. 1999). Tight packing and crowding is a hallmark of first-shell magnesium ligands, leading to highly restrained geometry and strong ligand-ligand interactions. Bidentate chelation of magnesium by RNA is associated with noncanonical conformation states of the backbone (Klein et al. 2004; Hsiao et al. 2008; Hsiao and Williams 2009).

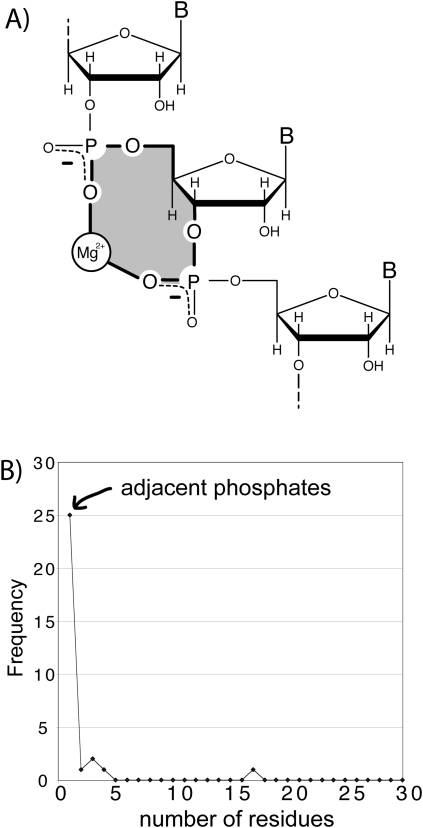
FIGURE 1.

(A) A schematic diagram of a bidentate RNA clamp of magnesium, formed when adjacent phosphate groups enter the first coordination shell of a common magnesium ion. A 10-membered ring (shaded yellow) characterizes these bidentate RNA clamps. (B) Adjacent phosphate groups enter the first coordination sphere of a common phosphate more commonly than nonadjacent phosphates. A bidentate RNA clamp of magnesium corresponds to one residue in the frequency graph below (frequency from the H. marismortui 23S rRNA, PDB entry 1JJ2). Extending the horizontal axis (not shown) reveals local phosphates enter the first shell of a common magnesium ion preferentially over remote phosphates.

The most frequent mode of bidentate chelation of magnesium by large RNAs involves oxyanions of adjacent nucleotides (Fig. 1B; Hsiao et al. 2008; Hsiao and Williams 2009). An example of such a bidentate RNA–magnesium complex, extracted from the LSU of H. marismortui is shown in Figure 2A. One observes these bidentate “clamps” of adjacent phosphates on a magnesium ion 25 times in the H. marisortui LSU (Ban et al. 2000), twice in the P4–P6 domain of the tetrahymena Group 1 intron (Cate et al. 1997; Juneau et al. 2001), once in a self-splicing group II intron from Oceanobacillus iheyensis (PDB entry 3IGI) (described in Toor et al. 2008), and once in the L1 ligase (PDB entry 2OIU) (described in Robertson and Scott 2007). The folding and function of each of these RNAs is magnesium-dependent. These bidentate clamps appear to be elemental units of RNA folding and assembly. Tri- and tetradentate RNA–magnesium complexes nearly always contain at least one of these bidentate clamps (Hsiao et al. 2008). A magnesium ion is clamped twice, by both the mRNA and the rRNA, in the assembled Thermus thermophilus ribosome (PDB entry 2J01, described in Selmer et al. 2006). These bidentate clamps are characterized by 10-membered ring systems (Mg²⁺–O⁻–P–O5′–C5′–C4′–C3′–O3–P–O⁻) (Figs. 1B, 2A).

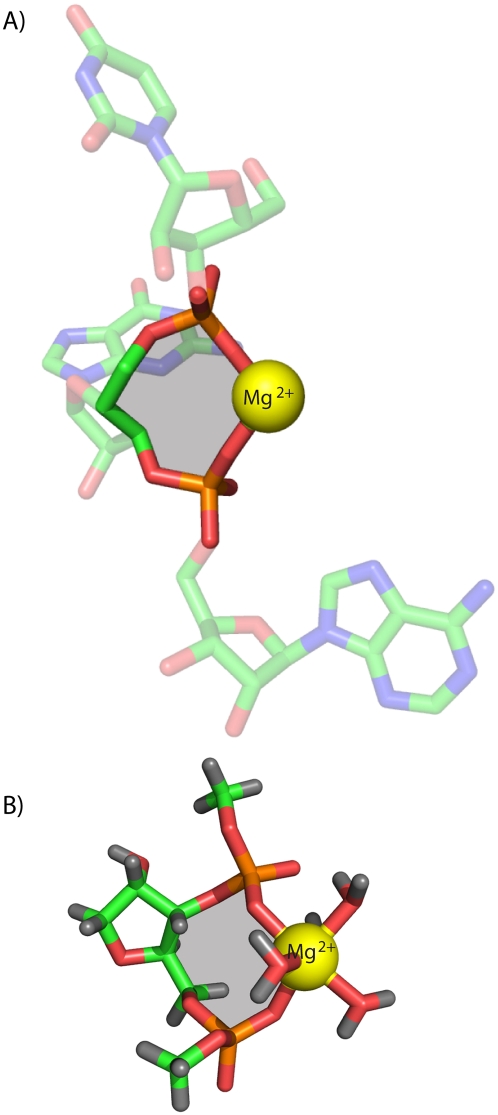
FIGURE 2.

(A) A bidentate RNA clamp of magnesium observed in the H. marismortui ribosomal LSU crystal structure (Mg 8003 from PDB entry 1JJ2). (B) The RNA²⁻–Mg²⁺•(H₂O)₄ complex used here for QM calculations. The base has been replaced by a hydrogen atom and the chain is terminated with methyl groups. Ten-membered rings are shaded yellow.

For association of RNA with diffuse ions, the continuum approaches of Draper have been successful (Misra and Draper 2001; Grilley et al. 2007; Draper 2008). Westhof and co-workers used molecular dynamics simulations to investigate binding of magnesium ions to phosphate oxyanions of a bacterial 5S rRNA and characterized Mg complexes containing a mixed binding mode (with both inner and outer shell coordination) (Auffinger et al. 2003). However, prediction of the binding geometries and especially energies of directly coordinated cations remains a serious challenge (Tsui and Case 2001; Draper 2008). The net binding energy of the first-shell complexes is an intricate balance between generally favorable electrostatic and “nonelectrostatic” components, opposed by unfavorable desolvation. The nonelectrostatic components, including polarization, charge transfer and exchange correlation (as defined by Natural Energy Decomposition Analysis [NEDA]) (Glendening 1996; Schenter and Glendening 1996), are related to the specific nature of the cation and the geometry of the coordination complex. These ion-specific effects are most important for small, high-charged cations like magnesium (Rulisek and Sponer 2003; Petrov et al. 2004; Ditzler et al. 2010). Unlike electrostatics, nonelectrostatic effects are not severely attenuated in water. Ion-specific nonelectrostatic components of the binding energy cause continuum approaches such as the Nonlinear Poisson-Boltzmann theory (NLPB) or the Generalized Born approach with solvent accessible surface area, and conventional molecular dynamics force fields to fail in their prediction of geometries and energetics of complexes of directly coordinated magnesium ions (Petrov et al. 2005a; Ditzler et al. 2010).

However, the energetics of cation association with nucleic acids and other ligands can be accurately characterized by the application of high-level theory using ab initio (Trachtman et al. 1998; Munoz et al. 2001; Gresh et al. 2003; Rulisek and Sponer 2003) and density functional methods (Murashov and Leszczynski 1999; Petrov et al. 2004, 2005b). The requirement for high-level theory is indicated by a study of the ff99 Amber forcefield (Wang et al. 2000), which was shown to give incorrect energies for formation of guanine–Mg²⁺ (Petrov et al. 2002) and dimethylphosphate–Mg²⁺ complexes (Petrov et al. 2005a), as well as for RNA–Mg²⁺ complexes (Petrov et al. 2004, 2005b). By contrast, the use of the quantum mechanical (QM) theory for small complexes or combined QM/NLPB approaches for larger RNA–Mg structures (Petrov et al. 2004, 2005b) provide satisfactory results, with the association energies in general agreement with, for example, the experimental data of Colmenarejo and Tinoco (1999).

Here QM theory explains the specific energetic and conformational fingerprints of bidentate RNA magnesium clamps. We compare the QM predictions to observed three-dimensional structures. The combined results show at a fundamental level why magnesium ions can induce specific conformational and electronic states of RNA that are inaccessible with other biological cations. The interactions, geometries, and stabilities of bidentate RNA clamps with cations are seen to be dependent on cation type, position, and coordination. Only with magnesium do the complexes have significant polarization, charge-transfer, and exchange components.

We have dissected the conformations and energetics of bidentate RNA and DNA clamps of magnesium, calcium, or sodium, in an aqueous environment. A prototypical bidentate RNA clamp of magnesium (Fig. 2A) extracted from within the LSU of H. marismortui (PDB entry 1JJ2) was used to build a template clamp containing phosphates attached to both the O3′ and O5′ atoms of a ribose. The 5′ and 3′ phosphates were capped with methyl groups in lieu of the remainder of the RNA polymer (Fig. 2B).

RESULTS

An RNA^2-–Mg²⁺•(H₂O)₄ clamp, consisting of a ribose, 5′ and 3′ phosphates, and a tetrahydrated magnesium ion, is shown in Figure 2B. We considered the following reaction:

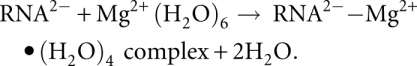This reaction proceeds in three steps, starting with free RNA and Mg²⁺•(H₂O)₆. In step 1 the geometry of the RNA changes from open to closed. The conformation of the RNA in the open state, in which the phosphate groups are not in close proximity, was obtained by optimization in the absence of magnesium. The RNA in the open state is relaxed, with bond angles and rotamers centered within the primary frequency envelopes (Hershkovitz et al. 2003). In step 2 the magnesium partially dehydrates, releasing two water molecules. In step 3 the RNA closes on the partially dehydrated magnesium ion to form a bidentate clamp. Two oxyanions of the closed RNA bind directly to the magnesium ion. The conformation of the RNA in the closed state is obtained by optimization of the bidentate clamp, and is very similar to that observed in crystal structures of bidentate RNA clamps of magnesium.

We created analogous reactions with sodium and calcium, allowing for differences in ionic radii. The geometry of each clamp is thus cation-dependent. For DNA clamps the 2′ hydroxyl group was replaced with a hydrogen atom. The methods by which the calculations were performed are described in detail in the Materials and Methods section.

Affinities

Bidentate clamps are specific to RNA and magnesium in terms of geometry and affinity. RNA clamps tightly to magnesium with an energy of −31.9 kcal/mol in aqueous phase (Table 1). The other ions form less stable bidentate clamps with RNA. The absolute value of the interaction energies for RNA with cations decreases in the series Mg²⁺ > Ca²⁺ > Na⁺. The interaction energies, including the basis set superposition error (BSSE), calculated as the differences between the energies of products and reactants, are given in Table 1. Bidentate DNA clamps with magnesium are ∼10 kcal/mol less stable than RNA clamps.

TABLE 1.

Interaction energies for RNA and DNA complexes with cations in the gas and aqueous phases

Geometries

Bidentate clamp geometry is cation-dependent. The ligands are closer to the magnesium than to other cations, as expected from known coordination chemistry. The oxyanions contained within the magnesium first shell are closer together than those associated with the other cations. It can be seen that the repulsive interaction between adjacent oxyanions distorts the first-shell octahedron of magnesium (Fig. 3), forcing the oxyanions apart. The resulting geometries (Table 2) are fully consistent with known coordination chemistry (Brown 1992).

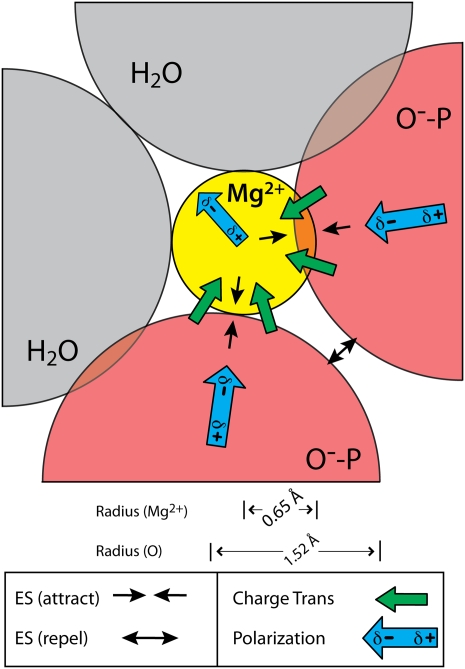
FIGURE 3.

Interactions of a hexacoordinated magnesium ion with two anionic oxygen atoms and four water molecules (only the two in-plane water molecules are shown). Illustrated distances and angles are based on the QM calculations. Arrows represent electrostatic, polarization, and charge transfer components of the interaction energy as obtained by NEDA and given in Table 2. Only the major components of the interaction energy are shown. The exchange term, which is favorable but significantly weaker than the corresponding charge transfer and polarization terms, is omitted from the schematic diagram for clarity.

TABLE 2.

Cation–oxygen distances (Å) in RNA clamps

Bending stress

In converting from the open to closed form, RNA accumulates moderate bending stress. The extent of bending stress was inferred by replacement of ribose with a flexible trimethylene backbone (retaining C3′, C4′, and C5′), followed by optimization, and calculation of the interaction energy. Comparison of the energetics of bidentate clamps of native RNA and this flexible analog indicate that bending stress destabilizes the native RNA clamp with magnesium by 4.9 kcal/mol (Table 1).

Electrostatic repulsion between phosphate groups

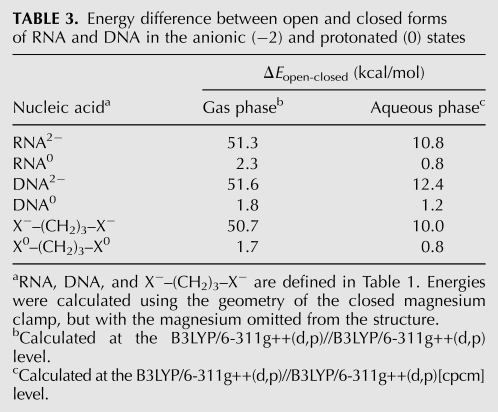
There is a significant electrostatic penalty for converting from the open to closed form, bringing oxyanions into proximity to form a bidentate clamp with magnesium. The energy difference between RNA alone in the open and closed states is 10.8 kcal/mol in aqueous phase and 51.3 kcal/mol in the gas phase (Table 3). The closing penalty is seen to be electrostatic in nature by a comparison of the closing costs of native (anionic) and neutral RNA. Neutralizing the RNA (by protonating the phosphates) reduces the penalty for closing the bidentate RNA clamp by 10.0 kcal/mol: from 10.8 to 0.8 kcal/mol in the aqueous phase (Table 3). The values are slightly higher for DNA. Neutralizing DNA reduces the penalty for closing a DNA clamp by 11.2 kcal/mol: from 12.4 to 1.2 kcal/mol in the aqueous phase.

TABLE 3.

Energy difference between open and closed forms of RNA and DNA in the anionic (−2) and protonated (0) states

Sodium does not form stable bidentate clamps

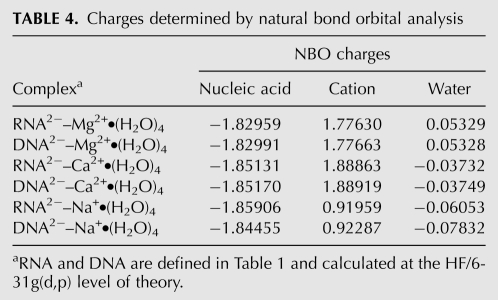
Formation of an RNA clamp with a cation requires that favorable interactions of the oxyanions with the cation are sufficient to overcome the repulsive interactions. If not, the ring opens. RNA ring opening is observed for sodium: sodium was found after optimization to remain directly coordinated to only one oxyanion (see Table 4, where only one oxyanion remains in the sodium first shell after optimization).

TABLE 4.

Charges determined by natural bond orbital analysis

Nonelectrostatic effects

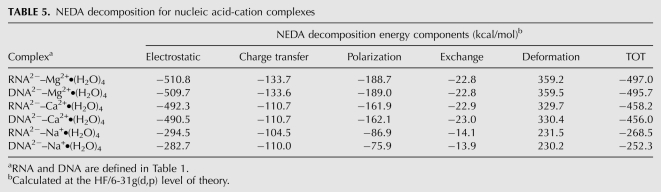
In all of the bidentate clamps studied here, cations draw anionic charge from the lone pairs of oxyanions. The resulting reduction in charge on the cation depends on the cation type, and is most pronounced for magnesium (Mg²⁺: 0.223 electrons > Ca²⁺: 0.111 > Na⁺: 0.081, for RNA clamps). This charge transfer along with other nonelectrostatic components of the interaction energy, such as polarization and exchange enhances stability. These effects were investigated here with Natural Bond Orbital (NBO) and NEDA as implemented in NBO5.0 (Glendening 1996; Schenter and Glendening 1996). Table 4 summarizes the NBO charges on the RNA, DNA, cations and water molecules. The energies associated with the charge transfer from RNA or DNA to the cation correlate well with the total stability of the complexes: Mg²⁺ > Ca²⁺ > Na⁺. The full energy decomposition is presented in Table 5 and summarized in Figure 3.

TABLE 5.

NEDA decomposition for nucleic acid-cation complexes

DISCUSSION

Magnesium, from the origin of life, has been closely associated with some of the central players in biology—phosphates and phosphate esters (Westheimer 1987). Here we show how magnesium shares a special geometric and energetic relationship with the phosphates of RNA. Adjacent RNA phosphates form bidentate clamps selectively with magnesium ions (Fig. 2). The ionic radius of Mg²⁺ is small (0.65 Å), the charge density is high, the coordination geometry is strictly octahedral (the average observed coordination number is 5.98), the preferred ligands are charged or neutral oxygens, and the hydration enthalpy is large (−458 kcal/mol) (Rashin and Honig 1985; Brown 1988, 1992; Bock et al. 1999). In comparison with group I ions, calcium, or polyamines (Feuerstein et al. 1991), magnesium has a greater affinity for phosphate oxygens, and binds to them with well-defined geometry. Unlike other biological cations, magnesium can bring phosphate oxygens in its first shell into direct proximity.

Here we demonstrate with QM calculations why neither sodium nor calcium can replicate the three-dimensional structures or the energetics of bidentate RNA–magnesium clamps, which contain adjacent phosphate oxygens within the first shell of the magnesium ion. RNA forms more stable bidentate clamps with magnesium, with tighter packing of phosphate oxyanions, than with calcium or sodium. Clamps with sodium in particular are unstable, and spontaneously open. Magnesium forms closer contacts than other cations to oxyanion ligands, and so magnesium clamps are stabilized not only by electrostatic interactions but also by charge transfer, polarization, and exchange. Those components of the energy are quite substantial at short range, and in a shielding solvent like water can dominate electrostatic interactions. These effects are less pronounced for calcium due to its larger size and for sodium due to its smaller charge. Only magnesium, not sodium or calcium, enforces close contacts between first-shell ligands. The QM calculations described here are supported by experimental three-dimensional structures, which contain RNA–magnesium clamps at high frequency, and closely packed oxyanions only when directly coordinated to magnesium.

Bidentate clamps are specific to RNA in that ribose clamps are more stable than deoxyribose clamps. The nature of the extra stabilizing energy of RNA clamps is twofold: (1) RNA has a slightly attenuated electrostatic penalty of ring closure (10.0 kcal/mol for RNA vs. 11.0 kcal/mol for DNA) (Table 3) and (2) RNA has slightly more favorable electrostatic interactions than DNA with cations (−510.8 kcal/mol for RNA vs. −509.7 kcal/mol for DNA), as seen from NEDA decomposition (Table 5). The greater favorability of electrostatic interactions in RNA complexes is related to through-space effects of the polar 2′-OH group in the ribose. Thus, the results here allow us to understand fundamental differences between RNA and DNA.

Clamp formation is anti-cooperative. The energy for forming an RNA clamp of magnesium (−31.9 kcal/mol) (Table 1) is less than for the independent formation of two isolated first-shell magnesium complexes with dimethyl-phosphate (−19.2 kcal/mol per contact) (Petrov et al. 2005a), which yields a total energy of −38.4 kcal mol. The anti-cooperativity is predominantly associated with the electrostatic penalty of closing, which is ∼10 kcal/mol.

MATERIALS AND METHODS

The geometric optimization of complexes and individual monomers, as well as calculations of interaction energies, were performed using density functional theory (DFT) at the B3LYP level, which combines the GGA exchange three-parameter hybrid functional developed by Becke (1988) and the correlation functional of Lee et al. (1988) as implemented in the Gaussian 03 (Frisch et al. 2004) suite of programs.

Geometries of complexes and monomers (including individual water molecules in reactions involving dehydration) were obtained in a gas phase by using the 6-311G(d,p)++ basis set with one set of polarization and diffusion functions on all atoms. All complexes and monomers were treated within the restricted approximation.

Interaction energies were calculated in a gas phase and in water using the gas phase optimized geometries of monomers and complexes. The COSMO-PCM (CPCM) approach (Andzelm et al. 1995; Barone et al. 1997) was used to account for the effect of a polar solvent. Additional details of computational methods are given elsewhere (Petrov et al. 2004, 2005a). The molecular cavity was formed by interlocking spheres centered on the solute atoms with radii taken from the Universal Force Field model. The BSSE in the dimer-centered basis set was obtained by applying the counterpoise procedure of Boys and Bernardi (Boys and Bernardi 1970). The corrected interaction energies were calculated by taking into account deformational energies of monomers according to a scheme proposed by van Duijneveldt-van de Rijdt and van Duijneveldt (1997):

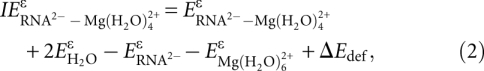where 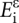are the energies of the RNA²⁻–Mg²⁺.•(H₂O)₄ complex and its monomers and 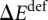accounts for the deformation of monomers in the complex compared to their geometries in isolated states in the gas phase.

Natural atomic charges were calculated at the HF/6-31(d,p) level of theory using the NBO5.0 (Reed et al. 1985) program implemented in the GAMESS package (Schmidt et al. 1993; Gordon and Schmidt 2005). The Natural Energy Decomposition Analysis (Glendening and Streitwieser 1994) was performed at the same level of theory for the complexes, in which the sugar–diphosphate backbone and hydrated cations were considered as monomers.

SUPPLEMENTAL MATERIAL

Supplemental material includes coordinates of all complexes described here and can be found at http://www.rnajournal.org.