Abstract
Human pancreatic glucokinase is a monomeric enzyme that displays kinetic cooperativity, a feature that facilitates enzyme-mediated regulation of blood glucose levels in the body. Two theoretical models have been proposed to describe the non-Michaelis-Menten behavior of human glucokinase. The mnemonic mechanism postulates the existence of one thermodynamically favored enzyme conformation in the absence of glucose, whereas the ligand-induced slow transition model (LIST) requires a pre-existing equilibrium between two enzyme species that interconvert with a rate constant slower than turnover. To investigate whether either of these mechanisms is sufficient to describe glucokinase cooperativity, a transient state kinetic analysis of glucose binding to the enzyme was undertaken. A complex, time-dependent change in enzyme intrinsic fluorescence was observed upon exposure to glucose, which is best described by an analytical solution comprised of the sum of four exponential terms. Transient state glucose binding experiments conducted in the presence of increasing glycerol concentrations demonstrate that three of the observed rate constants decrease with increasing viscosity. Global fit analyses of experimental glucose binding curves do not support the glucose binding component of the mnemonic mechanism, the simplified LIST mechanism or a mechanism that includes three unliganded enzyme species. Instead, our experimental data are consistent with a LIST kinetic model that includes two additional glucose-bound binary complexes. The kinetic model presented herein suggests that glucokinase samples multiple conformations in the absence of ligand and that this conformational heterogeneity persists even after the enzyme associates with glucose.
Keywords: Human Pancreatic Glucokinase, Transient-State Kinetics, Global Fit, Monomeric Cooperativity
INTRODUCTION
Glucokinase (HK-IV, hexokinase D) catalyzes the ATP-dependent phosphorylation of glucose in the first step of glycolysis, a transformation that repressents the rate-limiting reaction of glucose metabolism in the liver and pancreas (1–3). Heterozygous inactivating mutations in the glucokinase gene cause maturity onset diabetes of the young 2 (MODY2), whereas homozygous inactivating lesions produce a more severe condition known as permanent neonatal diabetes mellitus (PNDM) (4, 5). Under steady-state conditions, glucokinase activity displays a sigmoidal response to increasing glucose concentrations that is characterized by a Hill equation with a coefficient of 1.7. While kinetic cooperativity is observed with respect to glucose, traditional Michaelis-Menten kinetics are observed when the concentration of the second substrate, MgATP2−, is varied in the presence of saturating glucose levels (6). The existence of kinetic cooperativity in human glucokinase is intriguing because the enzyme functions exclusively as a monomer under physiological conditions (7, 8). Although a number of mechanisms for kinetic cooperativity in monomeric enzymes have been proposed in the literature, the mnemonic and the ligand-induced slow transition (LIST) models have received the most attention in recent studies of glucokinase (9–14).
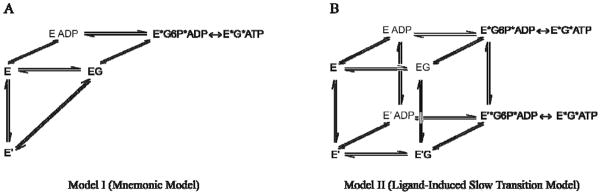
Ricard, Meunier and Buc first formulated the mnemonic model for cooperativity in monomeric enzymes in 1974. (13, 15–17). It was based upon earlier conceptual work by Rabin and Frieden, who postulated that the conformation of an enzyme following product release could be different from the initial state (18, 19). The mnemonic model postulates that an enzyme is capable of oscillating between two conformationally distinct species – a low-affinity state (E′) and a high-affinity state (E) (Figure 1A). According to the mnemonic mechanism, only the low-affinity conformation exists in the absence of substrate. The catalytic cycle begins when glucose binds to the low-affinity state and induces a conformational change to the high-affinity state. This conformational transition is slow, presumably because the conversion involves significant structural rearrangements. Upon reaching the high-affinity state, glucokinase rapidly binds ATP to generate the ternary complex, where catalysis occurs. Release of products ADP and glucose 6-phosphate is permitted from the high-affinity state. If substrate glucose is abundant, the high-affinity state can rapidly undergo a second round of catalysis without formation of the slowly realized, low-affinity conformation. If glucose concentrations are low, however, sufficient time exists for the enzyme to relax to the low-affinity conformation before another molecule of glucose binds. According to the mnemonic model this slow relaxation step prevents conformational equilibration from being reached during the catalytic cycle, a condition that results in cooperativity.
Figure 1.
Two previously proposed kinetic models for cooperativity in monomeric human glucokinase. The mnemonic model (A) postulates the existence of a single thermodynamic favored state in the absence of ligand, E′, whereas the ligand-induced slow transition (LIST) model (B) postulates the existence of two catalytic cycles involving two conformationally distinct species. In both models, the rate of interconversion of E and E′ is slower than kcat.
The ligand-induced slow transition (LIST) model developed by Neet and coworkers provides a more general mechanism to explain kinetic cooperativity in monomeric enzymes (14, 20–23). Similar to the mnemonic model, the LIST mechanism involves the existence of two distinct enzyme conformations, E and E′. In the LIST model, however, the enzyme is characterized by a pre-existing equilibrium that involves two conformationally distinct species in the absence of substrate (Figure 1B). These two conformations possess different affinities for substrate glucose, and the equilibrium between these states is controlled by the concentration of glucose. Similar to the mnemonic model, the LIST mechanism requires that the conformational equilibration between enzyme states is slower than catalysis. In the LIST mechanism two separate catalytic cycles are possible, whereas the mnemonic model requires only one catalytically active enzyme species. According to the LIST model, the steady state velocity of the glucokinase reaction is the sum of the rates of the two cycles.
Support for both the mnemonic and LIST mechanisms can be found within experimental data collected on glucokinase over the last 40 years (20–29). For example, the observation of decreased glucose cooperativity under limiting MgATP2− concentrations, or when a poorly reacting nucleotide replaced MgATP2−, was judged to support the mnemonic model prediction that cooperativity depends upon the ability of the second substrate to react rapidly with the binary enzyme-glucose complex (25). More recently, Kamata and coworkers succeeded in determining the three dimensional structure of human pancreatic glucokinase both in the unliganded state and in the presence of glucose and a synthetic small molecule activator (30). The ability of these investigators to isolate and structurally characterize a single unliganded enzyme species was interpreted in terms of the mnemonic model. Evidence in support of the LIST mechanism includes the observation of a Hill coefficient less than 1 under low MgATP2− concentrations, a condition that requires more than one catalytic cycle (22).
In recent years, a number of transient state kinetic investigations of glucose binding to the human enzyme have also produced conflicting reports regarding the mechanism of glucokinase cooperativity. The first of these studies was conducted by Heredia and coworkers, who reported a biphasic response of glucokinase intrinsic fluorescence upon glucose association (31). The resulting kinetic data fit best to a reversible two-step mechanism, which was consistent with the mnemonic model. In a subsequent study, Kim et al. reported that the intrinsic fluorescence of the enzyme displayed a monophasic response to glucose association, although the associated kobs showed a biphasic dependence upon glucose concentrations (32). These authors interpreted their data in terms of the LIST model, whereby the pre-existing equilibrium involves a high affinity species that displays a glucose Kd value of 90 μM, while the low affinity state is characterized by a glucose Kd value of 73 mM. The most recent report on glucose binding using transient state kinetic methods was published by Antoine and colleagues, who found that glucose binding traces take a long period of time to reach equilibrium (>100 seconds) and are best described by a sum of four exponential terms (33). The phase with the highest amplitude, kobs3, exhibited the same biphasic behavior as the observed rate constant previously described by Kim. Antoine simulated the dependence of kobs3 upon increasing glucose concentrations and used these results to predict the existence of at least two unliganded conformations with different glucose affinities and two slowly interconverting binary enzyme-glucose complexes.
In this study, we report the results of our own investigations into the transient state kinetic behavior of human pancreatic glucokinase. In contrast to the aforementioned studies, we employed high enzyme concentrations and conducted viscosity and temperature variation studies to investigate glucose binding kinetics. Our experimental glucose binding curves were fit to a variety of mechanistically distinct models using numerical integration of the relevant rate equations. The results of these global fit analyses provided a poor fit to previously proposed models, including simplified versions of both the mnemonic and ligand-induced slow transition (LIST) mechanisms. Instead, the present kinetic data require a minimal kinetic mechanism that includes two conformationally distinct ligand free species and four structurally unique binary enzyme-glucose complexes. Our global fit analysis also provides an estimate for individual microscopic rate constants describing the glucose binding process – data that afford useful benchmarks for future experimental investigations into glucokinase kinetic cooperativity.
MATERIALS AND METHODS
Protein Expression and Purification
Recombinant human pancreatic glucokinase was produced as an N-terminal hexa-histidine tagged polypeptide in the glucokinase-deficient E. coli strain BM5340(DE3). Bacterial cultures were inoculated to an initial OD600 nm of 0.01 and were grown at 37°C in Luria-Bertani broth supplemented with ampicillin (150 μg/ml), kanamycin (40 μg/ml) and chloramphenicol (25 μg/ml). When the OD600 nm reached 0.85, IPTG (1 mM) was added to induce gene expression and the temperature was reduced to 20°C, where growth was continued for 20 hours. Cells were harvested by centrifugation at 8,000g and 5 g of wet cell pellet was resuspended in 17 ml of buffer A containing HEPES (50 mM, pH 7.6), KCl (50 mM), imidazole (40 mM), dithiothreitol (10 mM) and glycerol (25% w/v). Cells were lysed using a French Press and subjected to centrifugation at 25,000g at 4°C for 1 hour. The supernatant was immediately loaded onto a 5 ml HisTrap Fast Flow Affinity Column (GE Healthcare) previously equilibrated in buffer A. Following loading, the column was washed with 10 column volumes of buffer A followed by 5 columns of buffer A containing 65 mM imidazole. Glucokinase was eluted with buffer A containing 250 mM imidazole and the enzyme was dialyzed overnight at 4°C against 1L of buffer containing HEPES (50 mM, pH 7.6), KCl (50 mM) and dithiothreitol (10 mM). To validate the performance of our enzyme in transient state kinetic experiments, we purified a sample of recombinant human glucokinase using an additional size exclusion chromatography step following affinity column purification. For these experiments, dialyzed glucokinase was injected onto a Superose 6 10/300 gel filtration column (Amersham-Pharmacia) pre-equilibrated in a buffer containing HEPES (50 mM, pH 7.6), KCl (50 mM) and dithiothreitol (10 mM). The gel filtration column was ran at a flow rate of 0.02 ml/min and fractions containing the highest A280 nm readings were pooled and retained for further analysis. We detected no difference in the transient state kinetic data when the size-exclusion chromatography step was included. Thus, to maximize the enzyme concentration and the signal-to-noise ratio of transient fluorescence data, affinity column purified recombinant glucokinase that was judged to be > 95% pure based on SDS-PAGE analysis was used in transient state binding experiments. We observed that the enzyme obtained after just affinity chromatography is less active than the one obtained after the size-exclusion chromatography step was introduced in the purification. However, the impurities do not seem to interfere with the glucose binding capabilities of glucokinase, not seem to display significant fluorescence signal.
Equilibrium Binding and Transient State Kinetic Experiments
For equilibrium glucose binding studies, proteins were purified as described above and were dialyzed against HEPES (50 mM, pH 7.6), NaCl (50 mM), DTT (10 mM) and glycerol (5 %, w/v) prior to data collection. Binding affinities were determined by monitoring the change in fluorescence at 335 nm that occurred in the presence of varying glucose concentrations (0.010–100 mM) following excitation of glucokinase (10 μM) at 280 nm using a 5 nm slit width, as previously described. Briefly, enzyme and glucose were mixed in 0.5 mL, 1.0 cm pathlength cuvettes in a buffer containing sodium phosphate (5 mM, pH 7.6), KCl (25 mM), and DTT (10 mM). Equilibrium binding experiments were performed on a Cary Eclipse Fluorescence Spectrometer housed in the Physical Biochemistry Laboratory in the Institute for Molecular Biophysics. Data were collected in duplicate, averaged, and fitted to the following equation:
Transient state binding data were collected on an Applied Photophysics SX20 stopped-flow spectrometer housed in the Protein Biophysics Laboratory in the Institute for Molecular Biophysics at Florida State University. Sample syringes were maintained at the appropriate temperature by a circulating water bath. The intrinsic fluorescence of human glucokinase was excited at 280 nm and the emission spectrum was monitored using a 320 nm cutoff filter. A minimum of five transient fluorescence traces were obtained at each glucose concentration and the multiple traces were averaged prior to analysis using the curve-fitting program of the instrument. Fluorescence traces were collected for a total of 250 seconds using a log scale to obtain the fast phase kinetics. At time frames above 250 seconds a drop in protein fluorescence signal was observed, presumably due to photobleaching of the sample. A variety of enzyme concentrations (1–39 μM) were investigated to maximize the fluorescence signal. To verify the existence of multiple exponentials terms in the binding traces, several control experiments were conducted. Enzyme was pre-incubated with glucose and mixed with buffer in the stopped-flow instrument to measure the dissociation rates. These experiments showed the same number of exponential terms as the binding experiments, indicating that the number of transitions observed during glucose binding was authentic. The hexa-histidine tag was removed via insertion of a specific seven amino acids sequence, Glu-Asn-Leu-Phe-Tyr-Gln-Ser, followed by cleavage between Gln and Ser with TEV protease. Transient state glucose binding curves using the cleaved enzyme showed the same number of exponential terms as the His-tagged version of the protein.
Technical optimizations were needed to eliminate a random artifact signal observed when enzyme was initially mixed with buffer, the amplitude of which was significant enough to interfere with the amplitude of the fastest transient observed. These optimizations included increasing the number of drives between acquisitions from one to four, decreasing the slit width (from 2 nm down to 0.165 nm), decreasing the mixing pressure (from 60 psi to 20 psi) and increasing the incubation time at the appropriate temperature prior to acquisition (from 5 min up to 40 min). The observed artifact appeared to be associated with the mixing pressure. Indeed, exposing the enzyme to high pressures (60 psi) such as those routinely used to mix reagents in the stopped-flow loop caused an 80% loss in the enzymatic activity of human glucokinase. A maximum mixing pressure of 30 psi allowed the preservation of the full enzymatic activity. Since the traces were recorded on the order of minutes, photobleaching was initially observed as a decrease in the fluorescence signal. To eliminate this effect, we decreased the slit width (0.165 nm) until a straight baseline was observed up to 250 seconds after mixing enzyme and buffer. The kinetic rate constants and amplitudes as a function of ligand concentration were determined from the time dependent change in fluorescence intensity by fitting the binding curves to a quadruple exponential equation of the form:
where I(t) is the intensity of fluorescence signal at time t, n is the number of exponentials, Ai is the amplitude of the ith exponential, kobsi is the observed rate constant for ith exponential, and C is a constant corresponding to the asymptotic signal limit.
Pre-Steady State Viscosity and Temperature Variation Experiments
To assess the degree to which viscosity affected the number and rates of the observed transients, different glycerol concentration were added to the stopped-flow buffers. Addition of glycerol caused alterations in the kobs values associated with glucose binding, without affecting the overall number of exponential terms needed to fit the data. Solutions containing 5%, 10%, 20%, and 40% glycerol (w/v) were used to equilibrate the enzyme and to prepare 2x stock solutions of the appropriate glucose concentration. Relative viscosities of glycerol solutions were measured using a Cannon-Fenske Viscometer. For temperature variation experiments, the temperature was set to either 25°C or 10°C on the water bath unit of the Applied Photophysics SX20 stopped-flow spectrometer and samples from ice were allowed to equilibrate for at least 10 minutes prior to data acquisition.
Global Fit Analysis of Glucose Binding Curves
The transient state kinetics of glucose binding and dissociation were best described by an analytical solution comprised of the sum of four exponential terms. To gain insight into the significance of the observed rate constants, we attempted to fit the experimental traces to different kinetic models. Glucose binding traces were averaged, normalized and imported into the Pro-KII software from Applied Photophysics (34). To actively fit the glucose binding family of curves we have normalized the fluorescence axes. This normalization was achieved by dividing the signal by a constant number. Since the value of the initial intrinsic glucokinase fluorescence is the same (because the concentration of the enzyme is constant) we divided the signal by the initial value of fluorescence at time 0. Additionally this normalization is done to avoid any fluctuations in the signal due to the changes in the detector’s voltage. The Pro-KII program allows the simultaneous fitting of glucose binding curves to a unique kinetic mechanism via numerical integration. Data collected during the first 5 milliseconds were eliminated from each binding trace prior to fitting. Glucose concentrations used in the experiment (3–96 mM) were introduced as initial parameters in the program along with estimated concentration values for individual enzyme species. Initially, we considered a simplified kinetic model containing only a single enzyme conformation in the absence of ligand. Other mechanistic variations that were considered included the glucose binding component of LIST and mnemonic models, as well as models that included more than two enzyme conformations. Initial values for individual microscopic rate constants were chosen arbitrarily, and each parameter was allowed to vary until the optimal sum of squares value was obtained. At this stage, a visual inspection of the observed microscopic rate constants was performed to identify reasonable rate constants with low errors value. These values were fixed, while the remaining rate constants were refined in a second simulation step to produce a completed fit. For kinetic models that involved more than one enzyme conformation, different concentrations of E and E′ were investigated.
We wished to investigate the extent to which the values of the fitted microscopic rate constants were constrained by our experimental data within the context of the final kinetic model. To do so, we fixed individual rate constants, one at a time, to values that were either 10-fold higher or 10-fold lower than the best-fit value. The remaining 13 rate constants were permitted to vary and the simulation was allowed to proceed through a single iteration. If the resulting sum of squares value changed by greater than 10-fold as compared to the best-fit sum of squares value, the microscopic rate constant was considered constrained.
RESULTS
Equilibrium Binding of Glucose to Human Pancreatic Glucokinase
Equilibrium binding of glucose to glucokinase was monitored by measuring the change in the enzyme’s intrinsic fluorescence at increasing concentrations of glucose. Consistent with earlier reports, cooperativity was not observed in our equilibrium measurements. The dissociation constant for glucose determined from these experiments was 5 mM. Interestingly, this thermodynamic constant is not significantly different from the glucose K0.5 value (8.1 mM) determined from steady-state kinetic assays. Based on our experimentally determined glucose KD value, we chose to conduct transient state binding experiments over a glucose concentration range of 0.35–96 mM.
Transient State Binding of Glucose to Glucokinase
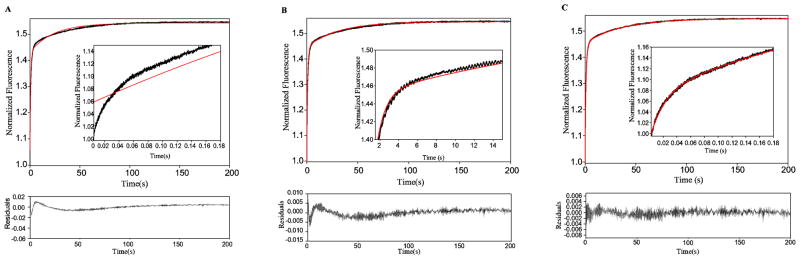
Transient state binding experiments were conducted by mixing a range of glucose concentrations with high concentrations of recombinant enzyme using a stopped-flow spectrometer. Binding curves were obtained at 9 different glucose concentrations and were collected over a time ranging from 5 msec to 250 seconds (Figure 2). The resulting traces were fit to a variety of exponential functions in an attempt to arrive at an analytical solution that best described each curve. At glucose concentrations below 1 mM an analytical solution consisting of the sum of two exponential terms was sufficient to describe the binding curves. The addition of a third exponential term to the analytical solution was necessary to accurately represent binding transients at glucose concentrations between 1 and 3 mM. At higher glucose concentrations, however, a triple exponential function correlated poorly with the experimental data in both the fast and intermediate time regimes. Thus, a fourth exponential term was required to fit glucose binding curves at glucose concentrations above 3 mM (Figure 3A–C). Because of the differential number of observable events detected at low glucose concentrations, we only considered binding curves for glucose concentrations at or above 3 mM in our subsequent global fit analyses. Transient state dissociation kinetics conducted at high glucose concentrations confirmed the existence of four kinetically distinguishable events (Figure S1). Similarly, four exponential terms were required to accurately fit binding curves obtained at saturating concentrations of the non-cooperative substrate 2-deoxyglucose (Figure S2).
Figure 2.
(A) Pre-steady state kinetics of glucose (0.35–96 mM) binding to human pancreatic glucokinase (39 μM). (B) A pre-steady state burst is observed within the first 50 msec after enzyme and glucose are mixed. (C) Fluorescence signal of enzyme alone is unchanged during the time course of observation, demonstrating negligible photobleaching of the sample.
Figure 3.
Glucose binding curves require an analytical solution comprised of the sum of four exponential terms for glucose concentrations above 3 mM. Attempt to fit the 96 mM glucose binding curve (black) to an analytical solution (red) comprised of the sum of two exponential terms (A), three exponential terms (B) and four exponential terms (C). The quality of the fit in the fast regime is shown in the inset and the residuals associated with each fit are shown below the binding curves.
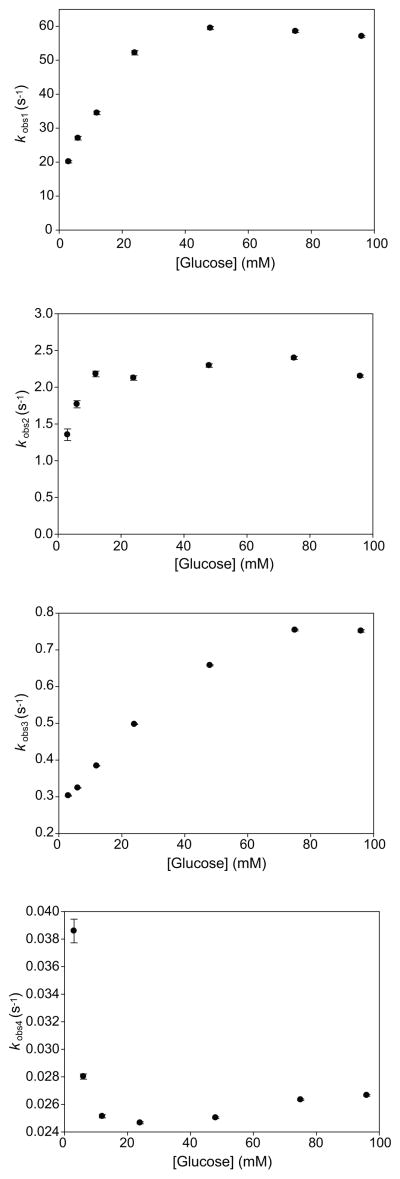
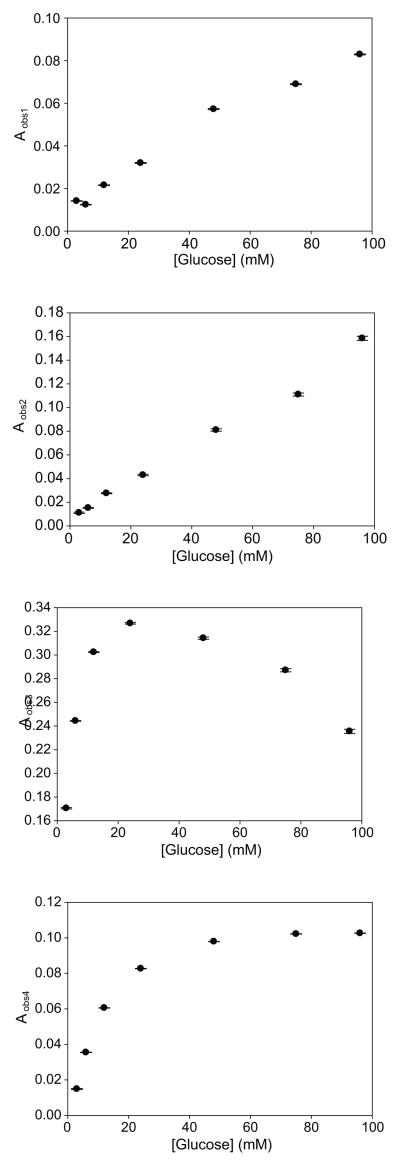
The observed amplitudes and rate constants of the four kinetically distinguishable events detected in our transient state experiments displayed a complex behavior as a function of increasing glucose concentrations (Figures 4 and 5). The two fastest observable rate constants, kobs1 and kobs2, appear to display hyperbolic dependencies upon glucose concentration. The value of kobs2 appears to be more steeply dependent upon glucose concentrations, reaching a maximum value near 10 mM, whereas the value of kobs1 does not reach a maximum until 50 mM glucose. The normalized amplitudes of both kobs1 and kobs2 increase linearly as a function of increasing glucose concentrations. The third observable rate constant, kobs3, appears to display a sigmoidal dependence upon glucose concentration. The amplitude of kobs3 increases sharply with increasing glucose concentrations up to 24 mM, and then it decreases as glucose levels are raised to 96 mM. The value of the slowest rate constant, kobs4, initially decreases with increasing glucose concentrations up to 24 mM. A slight increase in the value of this rate constant can be observed at glucose concentrations between 24–96 mM. The amplitude of kobs4 displays a hyperbolic dependence upon glucose.
Figure 4.
The magnitude of the four observed rate constants as a function of glucose concentrations. The kobs values were obtained by fitting the data to an analytical solution comprised of four exponential terms. Error bars represent the goodness of fit between the experimental data and the analytical solution.
Figure 5.
The amplitudes of the four observed transient signals as a function of glucose concentration. The amplitudes were obtained by fitting the data to an analytical solution comprised of four exponential terms. Error bars represent the goodness of fit between the experimental data and the analytical solution.
Glycerol and Temperature Effects on Glucose Binding
To provide insight into the physical basis of the four kinetically distinguishable events observed in our transient state glucose binding curves, we altered both the viscosity and temperature at which binding occurred. Increasing the relative viscosity of the solution via the addition of glycerol caused a decrease in the values of kobs1, kobs2 and kobs3 without altering the number of exponential terms required in the analytical solution used to fit each binding curve (Table 1). In contrast, the value of kobs4 was largely unaffected by increasing solution viscosity. At 3 mM glucose (the lowest concentration analyzed) there was a high degree of variability in the values of several rate constants, a fact that may be attributable to the low amplitude of this signal at diminishing glucose concentrations.
Table 1.
Observed rate constants associated with glucose binding at different viscosities.
| [Glucose] (mM) | % Glycerol (w/v) (relative viscosity) | kobs1 | kobs2 | kobs3 | kobs4 |
|---|---|---|---|---|---|
| 96 | 0 (1.0) | 57 ± 0.3 | 2.2 ± 0.02 | 0.75 ± 0.003 | 0.027 ± 0.0001 |
| 5 (1.2) | 44 ± 0.2 | 2.2 ± 0.01 | 0.77 ± 0.002 | 0.029 ± 0.0001 | |
| 10 (1.4) | 43 ± 0.2 | 2.1 ± 0.01 | 0.70 ± 0.002 | 0.028 ± 0.0001 | |
| 20 (1.9) | 35 ± 0.2 | 1.5 ± 0.01 | 0.54 ± 0.003 | 0.025 ± 0.0001 | |
| 40 (4.3) | 16 ± 0.1 | 0.9 ± 0.01 | 0.20 ± 0.001 | 0.022 ± 0.0001 | |
| 75 | 0 (1.0) | 58 ± 0.4 | 2.4 ± 0.02 | 0.75 ± 0.002 | 0.026 ± 0.0001 |
| 5 (1.2) | 59 ± 0.3 | 2.6 ± 0.02 | 0.76 ± 0.002 | 0.028 ± 0.0001 | |
| 10 (1.4) | 43 ± 0.2 | 2.2 ± 0.01 | 0.66 ± 0.001 | 0.026 ± 0.0001 | |
| 20 (1.9) | 27 ± 0.2 | 1.5 ± 0.01 | 0.51 ± 0.001 | 0.024 ± 0.0001 | |
| 40 (4.3) | 17 ± 0.2 | 0.9 ± 0.01 | 0.25 ± 0.001 | 0.020 ± 0.0001 | |
| 48 | 0 (1.0) | 59 ± 0.5 | 2.3 ± 0.02 | 0.66 ± 0.002 | 0.025 ± 0.0001 |
| 5 (1.2) | 38 ± 0.2 | 2.1 ± 0.02 | 0.62 ± 0.001 | 0.028 ± 0.0001 | |
| 10 (1.4) | 35 ± 0.2 | 2.1 ± 0.01 | 0.56 ± 0.001 | 0.026 ± 0.0001 | |
| 20 (1.9) | 27 ± 0.3 | 1.5 ± 0.02 | 0.44 ± 0.001 | 0.022 ± 0.0001 | |
| 40 (4.3) | 17 ± 0.3 | 0.9 ± 0.02 | 0.22 ± 0.001 | 0.019 ± 0.0001 | |
| 24 | 0 (1.0) | 52 ± 0.7 | 2.1 ± 0.03 | 0.49 ± 0.001 | 0.025 ± 0.0001 |
| 5 (1.2) | 42 ± 0.3 | 2.5 ± 0.03 | 0.47 ± 0.001 | 0.027 ± 0.0001 | |
| 10 (1.4) | 48 ± 0.3 | 2.4 ± 0.02 | 0.39 ± 0.001 | 0.025 ± 0.0001 | |
| 20 (1.9) | 15 ± 0.2 | 1.2 ± 0.02 | 0.29 ± 0.001 | 0.022 ± 0.0001 | |
| 40 (4.3) | 19 ± 0.2 | 0.9 ± 0.01 | 0.14 ± 0.001 | 0.018 ± 0.0001 | |
| 12 | 0 (1.0) | 34 ± 0.5 | 2.2 ± 0.04 | 0.38 ± 0.001 | 0.025 ± 0.0001 |
| 5 (1.2) | 45 ± 0.6 | 2.7 ± 0.03 | 0.35 ± 0.001 | 0.028 ± 0.0001 | |
| 10 (1.4) | 36 ± 0.5 | 2.4 ± 0.02 | 0.27 ± 0.001 | 0.026 ± 0.0001 | |
| 20 (1.9) | 7.0 ± 0.3 | 1.2 ± 0.05 | 0.18 ± 0.001 | 0.021 ± 0.0001 | |
| 40 (4.3) | 9.0 ± 0.2 | 0.6 ± 0.01 | 0.09 ± 0.001 | 0.017 ± 0.0001 | |
| 6 | 0 (1.0) | 27 ± 0.5 | 1.8 ± 0.05 | 0.32 ± 0.001 | 0.028 ± 0.0002 |
| 5 (1.2) | 20 ± 0.3 | 1.6 ± 0.05 | 0.28 ± 0.001 | 0.031 ± 0.0002 | |
| 10 (1.4) | 16 ± 0.3 | 1.6 ± 0.03 | 0.21 ± 0.001 | 0.028 ± 0.0001 | |
| 20 (1.9) | 16 ± 0.4 | 1.3 ± 0.03 | 0.14 ± 0.001 | 0.024 ± 0.0001 | |
| 40 (4.3) | 14 ± 0.7 | 0.8 ± 0.02 | 0.06 ± 0.001 | 0.015 ± 0.0001 | |
| 3 | 0 (1.00) | 20 ± 0.4 | 1.4 ± 0.08 | 0.30 ± 0.001 | 0.039 ± 0.001 |
| 5 (1.2) | 22 ± 0.6 | 1.5 ± 0.08 | 0.26 ± 0.001 | 0.046 ± 0.001 | |
| 10 (1.4) | 3.0 ± 0.3 | 0.7 ± 0.34 | 0.18 ± 0.002 | 0.051 ± 0.001 | |
| 20 (1.9) | 19 ± 0.8 | 1.0 ± 0.04 | 0.11 ± 0.001 | 0.035 ± 0.001 | |
| 40 (4.3) | 18 ± 0.3 | 0.6 ± 0.014 | 0.05 ± 0.001 | 0.015 ± 0.0001 | |
In an attempt to obtain a better separation of the individual signals observed during glucose binding, the temperature was decreased to 10 °C. Under these conditions, the analytical solution that provided the best fit to the experimental data requires three or fewer exponential terms at glucose concentrations below 12 mM. At glucose concentrations above this value, the decreased temperature produced lower values for kobs1 and kobs3, while having only modest effects upon kobs2 and kobs4 (Table 2).
Table 2.
Temperature dependence of the observed rate constants. Traces collected below 12 mM glucose at 10°C were not included due to their failure to be fitted to a four exponential function.
| [Glucose] (mM) | Temperature (°C) | kobs1 | kobs2 | kobs3 | kobs4 |
|---|---|---|---|---|---|
| 96 | 25 | 57 ± 0.3 | 2.2 ± 0.1 | 0.75 ± 0.003 | 0.027 ± 0.001 |
| 10 | 20 ± 3.4 | 2.2 ± 0.5 | 0.20 ± 0.003 | 0.015 ± 0.001 | |
| 75 | 25 | 59 ± 0.4 | 2.4 ± 0.1 | 0.75 ± 0.002 | 0.026 ± 0.001 |
| 10 | 22 ± 3.6 | 2.8 ± 0.5 | 0.20 ± 0.002 | 0.017 ± 0.002 | |
| 48 | 25 | 59 ± 0.5 | 2.3 ± 0.1 | 0.66 ± 0.002 | 0.025 ± 0.001 |
| 10 | 20 ± 2.9 | 2.7 ± 0.7 | 0.17 ± 0.002 | 0.021 ± 0.003 | |
| 24 | 25 | 52 ± 0.6 | 2.1 ± 0.1 | 0.49 ± 0.001 | 0.025 ± 0.001 |
| 10 | 24 ± 2.6 | 2.7 ± 0.4 | 0.14 ± 0.003 | 0.048 ± 0.009 | |
| 12 | 25 | 34 ± 0.5 | 2.2 ± 0.1 | 0.38 ± 0.001 | 0.025 ± 0.001 |
| 10 | 22 ± 0.9 | 3.7 ± 1.1 | 0.47 ± 0.17 | 0.102 ± 0.015 | |
Global Fit Analyses of Transient Glucose Binding Kinetics
The Pro-Kineticist II program from Applied Photophysics was used to fit the glucose binding data collected at 25°C, in the absence of added glycerol, to a variety of mechanistic postulates (34). The Pro-Kineticist II program enables one to perform a global fit analysis of kinetic data obtained under a variety of experimental concentrations to a user specified model. The resulting fit provides an assessment of how well the experimental data can be fit to a given kinetic model, as reflected in the sum of squares value. The fit also provides an estimate of the microscopic rate constants for individual events described in the specified model. In the present study, we investigated a variety of kinetic pathways for glucose binding to human glucokinase, two of which are shown in Figure 1 and four of which are depicted in Figure 6. Binding curves obtained at glucose concentrations below 3 mM were not included in the global fit analyses due to their failure to require four exponential terms to accurately describe them. We have only considered the data above 3 mM for the global fitting because we believe that below this value the fluorescence of all the discrete glucokinase species is too low to be detectable even at the highest concentration of enzyme used in this study (39 μM).
Figure 6.
Experimental glucose binding curves were fit to different kinetic models (A–D) using numerical integration of the rate equations via global fit analysis. The best-fit model, Model VI, produce a sum of squares value of 0.98.
The glucose binding component of the mnemonic model (Model I, Figure 1A) and the LIST mechanism (Model II, Figure 1B) failed to provide a good fit to our experimental data, as judged by their respective sum of squares values, 49 and 3.1. Next, we explored whether the inclusion of additional unliganded enzyme species or additional binary enzyme-glucose complexes improved the fit. The sum of squares value obtained for Model III (Figure 6A), which includes three distinct enzyme-glucose complexes was 690. The sum of squares values for Models IV and V (Figure 6B, C), which contain multiple ligand free species and multiple interconverting glucose bound states, were 5.1 and 1.7, respectively. Only kinetic Model VI (Figure 6D) produced a fit to our experimental glucose binding data that was characterized by a sum of squares value below 1. A comparison of the fit to the experimental data for each model tested is available in Supporting Information (Figures S3–S8).
The global fit analysis for Model VI also provided an estimate for the values of the microscopic rate constants, which are detailed in Table 3. To evaluate whether the fitted values of the microscopic rate constants are well constrained by our experimental data, error analysis was performed. We investigated the reliability of both the upper and lower limits for each rate constant value by exploring the sensitivity of the sum of squares value to variations in individual rate constants, as described in Material and Methods. These studies demonstrate that several of the microscopic rate constants are underrepresented by the glucose binding traces. For example, the upper limits of k1, k6 and k7 are poorly constrained, as are the lower limits for the values of k−1, k−2, k−6 and k−7. The values of k2 are poorly constrained in both directions. Rate constants that were judged to be ill defined in any direction are denoted with an asterisk in Table 3.
Table 3.
The sensitivity of the sum of squares values (SSQ) to variations in the microscopic rate constants around the best-fit value. Poorly constrained rate constants are denoted with an asterisk. Sum of squares values that are not significantly perturbed upon varying the microscopic rate constants are indicated with a (P).
| Rate constant | Best-fit value of rate constant | SSQ of best-fit | SSQ upon fixing rate constant at 0.1k | SSQ upon fixing rate constant at 10k |
|---|---|---|---|---|
| *k1 | (1407) (M−1 s−1) | 0.98 | 24 | 3.6 (P) |
| *k−1 | 1.1 (s−1) | 0.98 | 3.7 (P) | 23 |
| *k2 | 0.04 (s−1) | 0.98 | 7.7 (P) | 3.5 (P) |
| *k−2 | 0.34 (s−1) | 0.98 | 4.9 (P) | 14 |
| k3 | 0.015 (s−1) | 0.98 | 21 | 20 |
| k−3 | 0.009 (s−1) | 0.98 | 21 | 49 |
| k4 | (202) (M−1 s−1) | 0.98 | 65 | 240 |
| k−4 | 23 (s−1) | 0.98 | 220 | 78 |
| k5 | 2.9 (s−1) | 0.98 | 54 | 268 |
| k−5 | 0.2 (s−1) | 0.98 | 130 | 22 |
| *k6 | 0.012 (s−1) | 0.98 | 23 | 7.9 (P) |
| *k−6 | 0.11 (s−1) | 0.98 | 2.2 (P) | 55 |
| *k7 | 0.053 (s−1) | 0.98 | 11 | 2.7 (P) |
| *k−7 | 0.003 (s−1) | 0.98 | 1.6 (P) | 9.9 |
DISCUSSION
Four previous investigations have been conducted into the transient state kinetics of glucose binding to human glucokinase (23, 31–33). Surprisingly, the results of these studies failed to produce a consensus regarding the mechanism of glucokinase kinetic cooperativity. In each of the prior studies low concentrations of enzyme were used. As a result, several low amplitude fluorescence signals associated with glucose binding were difficult or impossible to detect. In the present work, we employed high enzyme concentrations and long acquisition times to obtain the most complete description of glucose binding kinetics reported to date. We observed four kinetically distinguishable events at glucose concentrations ranging from 3–96 mM. At lower glucose concentrations, or at temperatures below 25°C, one or more of these events became undetectable, as evidenced by the lower number of exponential terms required to fit binding curves collected under these conditions. Our results are consistent with the findings of Antoine et al., (33) who also detected four kinetically distinguishable events associated with glucose binding; however in their studies only the value of kobs3 was obtained with sufficient certainty to allow kinetic modeling (33). By comparison, our experiments afforded the acquisition of accurate rate constant and fluorescence amplitude data for all four observable events at a total of 7 different glucose concentrations.
Viscosity and temperature variation studies provided insight into the nature of the events described by individual transient signals. The addition of the microviscogen glycerol produced a decrease in the magnitude of kobs1, kobs2 and kobs3. The viscogen dependencies of kobs1 and kobs3 were particularly strong for all glucose concentrations investigated. Since diffusional processes are expected to be most sensitive to solution viscosity, it seems reasonable to postulate that kobs1 and kobs3 describe, in part, the formation of the initial enzyme-glucose complex(es). Consistent with this speculation is the observation that both rate constants decrease in magnitude when the temperature is reduced from 25°C to 10°C. The value of kobs2 displays a more moderate response to increasing viscosity, making it more difficult to assign to a specific physical process to this event. One possibility is that kobs2 describes a multitude of processes, one of which is associated with a diffusion-dependent event. Alternatively, kobs2 may reflect a conformational change that occurs after the initial association of the enzyme with glucose, the rate of which is only slightly affected by the presence of glycerol. The extent to which the rates of conformational change might be altered in the presence of added viscogen is unclear, although the response would likely depend upon both the nature and magnitude of the associated structural rearrangements. Similar to previous observations by Neet and coworkers, we observed that the slowest process associated with glucose binding, kobs4, is largely independent of glycerol concentration (23). This fact, combined with the unique glucose dependence of kobs4, complicates efforts to identify the process or processes that generate this signal. Control experiments conducted in this study exclude the possibility that kobs4 is caused by photobleaching.
Our ability to obtain accurate amplitude and rate constant data for each transient at a variety of glucose concentrations afforded the opportunity to apply global fit techniques to investigate the validity of specific kinetic models (35). We tested a number of potential mechanisms including the glucose binding section of mnemonic and LIST models. In each case, we attempted to fit our data to a minimal mechanism comprised of the smallest number of microscopic rate constants and the fewest number of enzyme species. A mechanism that included the presence of two unliganded species, E and E′, and four binary enzyme-glucose complexes produced a reasonable level of agreement with our experimental binding curves. It is worth noting that the various enzyme species present in our proposed model are capable of interconversion at all stages of the reaction coordinate. This model is similar to the initial LIST model put forth by Neet, except that it includes the formation of two intermediate enzyme-glucose complexes (E1G and E′1G) (22).
Although previous transient state investigations have extracted microscopic rate constants based on a particular kinetic model, these approaches were often incomplete. Two studies failed to detect four kinetically distinguishable events associated with glucose binding (31, 32), while a third neglected amplitude data associated with the transient state binding curves (33). Our study represents the first attempt to globally fit glucose binding curves to a variety of kinetic models using the totality of rate constant and amplitude data obtained at a variety of glucose concentrations. The resulting values for the individual microscopic rate constants presented in Table 3 are derived from fitting fourteen unknown variables, with limited constraints, to a kinetic model using transient state binding data collected at 7 different glucose concentrations. Based on this fact, caution should be used when considering the values of these microscopic rate constants (36). Indeed, we found that the values of several microscopic rate constants presented here are poorly constrained by our experimental data. To verify
Nevertheless, our results provide strong qualitative support for the kinetic pathway shown in Figure 6D.
Further refinement of individual microscopic rate constant values awaits additional experimental investigation.
Human glucokinase is an attractive model to study the role of conformational changes in enzyme action. The unique non-Michaelis-Menten kinetics observed in the steady state velocity is intriguing because the enzyme functions exclusively as a monomer (7, 8). Based upon the transient state glucose binding curves presented herein, we propose a minimal kinetic model in which the enzyme samples more than one conformationally distinct state, both in the absence and presence of glucose.
The possibility that glucokinase continues to sample a rugged free-energy landscape even after substrate association provides a wealth of opportunities for posttranslational regulation of the activity of this important metabolic enzyme.
Supplementary Material
Acknowledgments
This work was supported, in part, by grants from the James and Ester King Biomedical Research Program (09KN08) and from the National Institute of Diabetes and Digestive and Kidney Diseases (DK081358).
ABBREVIATIONS
- GK
glucokinase
- OD
optical density
- TCEP
tris(2-carboxyethyl)phosphine
- LIST
ligand-induced slow transition model
- HEPES
4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid
- MODY2
maturity onset diabetes of young 2
- HI
Hyperinsulinemia of Infancy
Footnotes
SUPPORTING INFORMATION AVAILABLE
References
- 1.Pilkis JS. Identification of human hepatic glucokinase and some properties of the enzyme. Proceedings of the Society for Experimental Biology and Medicine Society for Experimental Biology and Medicine (New York, NY) 1968;129(3):681–684. doi: 10.3181/00379727-129-33396. [DOI] [PubMed] [Google Scholar]
- 2.Matschinsky FM. Glucokinase as glucose sensor and metabolic signal generator in pancreatic β-cells and hepatocytes. Diabetes. 1990;39:647–652. doi: 10.2337/diab.39.6.647. [DOI] [PubMed] [Google Scholar]
- 3.Bell GI, Polonsky KS. Diabetes mellitus and genetically programmed defects in β-cell function. Nature. 2001;414:788–791. doi: 10.1038/414788a. [DOI] [PubMed] [Google Scholar]
- 4.Vionnet N, Scoffel M, Takeda J, Yasuda K, Bell GI, Zouali H, Lesage S, Velho G, Iris F, Passa P, Froguel P, Cohen D. Nonsense mutation in the glucokinase gene causes early-onset non-insulin dependent diabetes mellitus. Nature. 1992;356:721–722. doi: 10.1038/356721a0. [DOI] [PubMed] [Google Scholar]
- 5.Golyn A. Glucokinase (GCK) mutations in hyper-and hypoglycemia: maturity-onset diabetes of young, permanent neonatal diabetes and hyperinsulinemia of infancy. Hum Mut. 2003;22:353–362. doi: 10.1002/humu.10277. [DOI] [PubMed] [Google Scholar]
- 6.Holroyde MJ, Allen MB, Storer ACA, Warsy AS, Chesher JME, Trayer JP, Cornish-Bowden A, Walker DG. The purification in high yield and characterization of rat hepatic glucokinase. Biochem J. 1976;153:163–373. doi: 10.1042/bj1530363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Storer A, Cornish-Bowden A. Kinetics of rat liver glucokinase. Co-operative interactions with glucose at physiological significant concentrations. Biochem J. 1976;159:7–14. doi: 10.1042/bj1590007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cardenas ML, Rabajille E, Niemeyer H. Maintenance of the monomeric structure of glucokinase under reacting conditions. Arch Biochem Biophysic. 1978;190:142–148. doi: 10.1016/0003-9861(78)90261-8. [DOI] [PubMed] [Google Scholar]
- 9.Moulay AM, Van Schaftingen E. Analysis of the cooperativity of human β-cell glucokinase through the stimulatory effect of glucose on fructose phosphorylation. J Biol Chem. 2001;276:3872–3878. doi: 10.1074/jbc.M008722200. [DOI] [PubMed] [Google Scholar]
- 10.Gregoriou M, Trayer IP, Cornish-Bowden A. Isotope-exchange evidence for an ordered mechanism for rat-liver glucokinase, a monomeric cooperative enzyme. Biochemistry. 1981;20:499–506. doi: 10.1021/bi00506a009. [DOI] [PubMed] [Google Scholar]
- 11.Pettersson G. Mechanistic origin of the sigmoidal rate behaviour of glucokinase. Biochem J. 1986;233:347–350. doi: 10.1042/bj2330347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Monasterio O, Cardenas ML. Kinetic studies of rat liver hexokinase D (‘glucokinase’) in non-cooperative conditions show an ordered mechanism with MgADP as the last product to be released. Biochem J. 2003;371:29–38. doi: 10.1042/BJ20020728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Richard J, Meunier JC, Buc J. Regulatory behavior of monomeric enzymes: The mnemonical enzyme concept. Eur J Biochem. 1974;49:195–208. doi: 10.1111/j.1432-1033.1974.tb03825.x. [DOI] [PubMed] [Google Scholar]
- 14.Ainslie GR, Jr, Shill JP, Neet KE. Transients and cooperativity. A slow transition model for relating transients and cooperative kinetics of enzymes. J Biol Chem. 1972;247:7088–7096. [PubMed] [Google Scholar]
- 15.Ricard J, Buc J, Meunier J-C. Enzyme memory. A transient kinetic study of wheat-germ hexokinase LI. Eur J Biochem. 1977;80:581–592. doi: 10.1111/j.1432-1033.1977.tb11915.x. [DOI] [PubMed] [Google Scholar]
- 16.Buc J, Ricard J, Meunier JC. Enzyme memory 2. Kinetics and thermodynamics of the slow conformation changes of wheat-germ hexokinase LI. Eur J Biochem. 1977;80:593–601. doi: 10.1111/j.1432-1033.1977.tb11916.x. [DOI] [PubMed] [Google Scholar]
- 17.Meunier JC, Buc J, Ricard J. Enzyme memory effect of glucose 6-phosphate and temperature on the molecular transition of wheat-germ hexokinase LI. Eur J Biochem. 1979;97:573–583. doi: 10.1111/j.1432-1033.1979.tb13146.x. [DOI] [PubMed] [Google Scholar]
- 18.Rabin BR. Co-operative effects in enzyme catalysis: a possible kinetic model based on substrate-induced conformation isomerization. Biochem J. 1967;102(2):22C–23C. doi: 10.1042/bj1020022c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Frieden C. Kinetic aspects of regulation of metabolic processes. The hysteretic enzyme concept. J Biol Chem. 1970;245:5788–5799. [PubMed] [Google Scholar]
- 20.Neet KE. Cooperativity in enzyme function: equilibrium and kinetic aspects. In: Purich DL, editor. Contemporary Enzyme Kinetics and Mechanism. Academic Press; New York: 1983. pp. 267–320. [Google Scholar]
- 21.Neet KE, Ainslie GR., Jr Hysteretic enzymes. Methods Enzym. 1980;64:192–226. doi: 10.1016/s0076-6879(80)64010-5. [DOI] [PubMed] [Google Scholar]
- 22.Neet KE, Keenan RP, Tippett PS. Observation of a kinetic slow transition in monomeric glucokinase. Biochemistry. 1990;29:770–777. doi: 10.1021/bi00455a026. [DOI] [PubMed] [Google Scholar]
- 23.Lin SX, Neet KE. Demonstration of a slow conformational change in liver glucokinase by fluorescence spectroscopy. J Biol Chem. 1990;265(17):9670–9675. [PubMed] [Google Scholar]
- 24.Storer AC, Cornish-Bowden A. Kinetic evidence for a ‘mnemonical’ mechanism for rat liver glucokinase. Biochem J. 1977;165(1):61–69. doi: 10.1042/bj1650061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pollard-Knight D, Cornish-Bowden A. Kinetics of hexokinase D (‘glucokinase’) with inositne triphosphate as phosphordonor; loss of co-operativity with respect to glucose. Biochem J. 1987;245:625–629. doi: 10.1042/bj2450625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Niemeyer H, Cardenas ML, Rabajille E, Ureta T, Clark-Turri L, Pefnaranda J. Sigmoidal kinetics of glucokinase. Enzyme. 1975;20:321–333. doi: 10.1159/000458957. [DOI] [PubMed] [Google Scholar]
- 27.Cornish-Bowden A, Storer AC. Mechanistic origin of the sigmoidal rate behaviour of rat liver hexokinase D (‘glucokinase’) Biochem J. 1986;240:293–296. doi: 10.1042/bj2400293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Parry MJ, Walker DG. Further properties and possible mechanism of action of adenosine 5′-triphosphate-D-glucose 6-phosphotransferase from rat liver. Biochem J. 1967;105(2):473–482. doi: 10.1042/bj1050473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gonzalez C, Ureta T, Babul J, Rabajille E, Niemeyer H. Characterization of isoenzymes of adenosine triphosphate: D-hexose 6-phosphotransferase from rat liver. Biochemistry. 1967;6(2):460–468. doi: 10.1021/bi00854a014. [DOI] [PubMed] [Google Scholar]
- 30.Kamata K, Mitsuya M, Nishimura T, Eiki J, Nagata Y. Structural basis for allosteric regulation of the monomeric allosteric enzyme human glucokinase. Structure. 2004;12:429–438. doi: 10.1016/j.str.2004.02.005. [DOI] [PubMed] [Google Scholar]
- 31.Heredia VV, Thomson J, Nettleton D, Sun S. Glucose-induced conformational changes in glucokinase mediate allosteric regulation: transient kinetic analysis. Biochemistry. 2006;45:7553–7562. doi: 10.1021/bi060253q. [DOI] [PubMed] [Google Scholar]
- 32.Kim YB, Kalinowski SS, Marcinkeviciene J. A pre-steady state analysis of ligand binding to human glucokinase: evidence for a preexisting equilibrium. Biochemistry. 2007;46:1423–1431. doi: 10.1021/bi0617308. [DOI] [PubMed] [Google Scholar]
- 33.Antoine M, Boutin JA, Ferry G. Binding kinetics of glucose and allosteric activators to human glucokinase reveal multiple conformational states. Biochemistry. 2009;48(23):5466–5482. doi: 10.1021/bi900374c. [DOI] [PubMed] [Google Scholar]
- 34.Puxty G, Maeder M, Neuhold YM, King P. Pro-Kineticist II. Applied Photophysics Ltd; Leatherhead, England: 2005. http://www.photophysics.com/prokii.php. [Google Scholar]
- 35.Johnson KA, Simpson ZB, Blom T. Global Kinetic Explorer: A new computer program for dynamic simulation and fitting of kinetic data. Anal Biochem. 2009;387:20–29. doi: 10.1016/j.ab.2008.12.024. [DOI] [PubMed] [Google Scholar]
- 36.Johnson KA, Simpson ZB, Blom T. FitSpace Explorer: An algorithm to evaluate multidimensional parameter space in fitting kinetic data. Anal Biochem. 2009;387:30–41. doi: 10.1016/j.ab.2008.12.025. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.