A Poisson model for random multigraphs

Abstract

Motivation: Biological networks are often modeled by random graphs. A better modeling vehicle is a multigraph where each pair of nodes is connected by a Poisson number of edges. In the current model, the mean number of edges equals the product of two propensities, one for each node. In this context it is possible to construct a simple and effective algorithm for rapid maximum likelihood estimation of all propensities. Given estimated propensities, it is then possible to test statistically for functionally connected nodes that show an excess of observed edges over expected edges. The model extends readily to directed multigraphs. Here, propensities are replaced by outgoing and incoming propensities.

Results: The theory is applied to real data on neuronal connections, interacting genes in radiation hybrids, interacting proteins in a literature curated database, and letter and word pairs in seven Shaskespearean plays.

Availability: All data used are fully available online from their respective sites. Source code and software is available from http://code.google.com/p/poisson-multigraph/

Contact: klange@ucla.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Random graph theory has proved vital in modeling the internet and constructing biological and social networks. In the original formulation of the theory by Erdös and Rényi (1959, 1960), there are three key assumptions: (a) a graph exhibits at most one edge between any two nodes; (b) the formation of a given edge is independent of the formation of other edges; and (c) all edges form with the same probability. There is a general agreement that this simple model is too rigid to capture many real-world networks (Albert and Barabasi, 2002; Strogatz, 2001). The surveys (Barabasi and Albert, 1999; Durrett, 2006; Newman et al., 2001) summarize some of the elaborations and applications of two generations of scholars, with emphasis on power laws, phase transitions and scale-free networks. In the current article, we study a multigraph extension of the Erdös–Rényi model appropriate for very large networks. Our model specifically relaxes assumptions (a) and (c). With appropriate alternative assumptions in place, we derive and illustrate a novel maximum likelihood algorithm for estimation of the model parameters. With these parameters in hand, we are then able to find statistically significant connections between pairs of nodes.

In practice many graphs are derived from multigraphs. To simplify analysis, the multiple edges between two nodes of a multigraph are collapsed to a single edge. The movie star example in reference (Newman et al., 2001) is typical. In the movie star graph, two actors are connected by an edge when they appear in the same movie. Some actor pairs will appear in a movie mostly by chance. Other actor pairs will be connected by multiple edges because they are intrinsically linked. Classic pairs such as Abbot and Costello, Loy and Powell, and Lewis and Martin come to mind.

The well-studied neural network of Caernorhabditis elegans is a prime biological example. Here neuron pairs are connected by multiple synapses. Because collapsing edges wastes information, it is better to tackle the multiplicity issue directly. Thus, we will deal with random multigraphs. For our purposes, these exclude loops and fractional edge weights. Instead of a Bernoulli number of edges between any two nodes as in the Erdös and Rényi model, we postulate a Poisson number of edges. This choice can be viewed as unnecessarily restrictive, but it is worth recalling that a Poisson distribution can approximate a binomial or normal distribution. Furthermore, the Poisson assumption allows an arbitrary mean number of edges.

In relaxing assumption (c) above, we want to introduce as few parameters as possible but still capture the capacity of some nodes to serve as hubs. Thus, we assign to each node i a propensity p_i to form edges. The random number of edges X_ij between nodes i and j is then taken to be Poisson distributed with mean p_ip_j. Node pairs with high propensities will have many edges, pairs with low propensities will have few edges, and pairs with one high and one low propensity will have intermediate numbers of edges. Later, we will show that these choices promote simple and rapid estimation of the propensities. Another virtue of the model is that it generalizes to directed graphs where arcs replace edges. For directed graphs, we postulate an outgoing propensity p_i and an incoming propensity q_i for each node i. The number of arcs X_ij from i to j is taken to be Poisson distributed with mean p_iq_j. In the directed version of the model, the two random variables X_ij and X_ji are distinguished. In accord with assumption (b), the random counts X_ij in either model are taken to be independent.

Protein and gene networks can involve tens of thousands of nodes. Estimation of propensities under the Poisson multigraph model for such networks is consequently problematic. Standard algorithms for parameter estimation such as least squares, Newton's method and Fisher scoring require computing, storing and inverting large Hessian matrices. Such actions are not really options in high-dimensional problems. One of the biggest challenges in the present article is crafting an alternative estimation algorithm that remains viable in high dimensions. Fortunately, the MM (minorize–maximize) principle (Lange, 2004; Lange et al., 2000) allows one to design a simple iterative algorithm for the random multigraph model. Large matrices are avoided and convergence is reasonably fast. In the appendix, we prove that the new MM algorithm converges to the global maximum of the likelihood.

Another strength of the model is that it permits assessment of statistical significance. In other words, it helps distinguish random connectivity from functional connectivity. The basic idea is very simple. Every edge count X_ij is Poisson distributed with a parameterized mean. If we substitute estimated propensities for theoretical propensities, then we can estimate the mean and therefore approximate the tail probability p = Pr(X_ij ≥ x_ij) associated with the observed number of edges x_ij between two nodes i and j. The smaller this probability, the less likely these edges occur entirely by chance. For instance, in the movie star example, the actor pair Abbot and Costello would be flagged as significant in any representative dataset of their era. In less obvious examples, discerning functionally connected pairs is more challenging. In the appendix (Supplementary Material), we show how to approximate very low P-values under the Poisson distribution.

To test the model, we analyze five real datasets. Three of these are biological and involve undirected graphs. The first is the neural network of C.elegans (Watts and Strogatz, 1998; White et al., 1986) already mentioned. The second is a network obtained by subjecting a panel of radiation hybrids to gene expression measurements (Ahn et al., 2009; Park et al., 2008). In the network two genes are connected by an edge if a marker significantly regulates the expression levels of both genes in the clones of the panel. Our third biological example involves interacting proteins taken from the curated Human Protein Reference Database (Keshava Prasad et al., 2009). For directed graphs, we turn to literary analysis of a subset of Shakespeare's plays. Here, we look at letter pairs and word pairs. Every time the first letter of a pair precedes the second letter of a pair in a word, we introduce an arc between them. Likewise, every time the first word of a pair precedes the second word of a pair in a sentence, we introduce an arc between them. Other applications such as monitoring internet traffic come immediately to mind but will not be treated here.

Let us stress the exploratory nature of the Poisson multigraph model. Its purpose is to probe large datasets for hidden structure. Identifying hub nodes and node pairs with excess edges are primary goals. The fact that the model is at best, a cartoon does not eliminate these possibilities. For example, even if we do not take the P-values generated by the model seriously, they can still serve to rank important node pairs for further investigation and experimentation. Computational biology is full of compromises between realistic models and computational feasibility.

Before tackling these specific examples, we will briefly review the MM principle and lay out the details of the model. Once this foundation is in place, we show how a simple inequality drives the optimization process. The MM principle is designed to steadily increase the log-likelihood of the model given the data. This ascent property is the key to understanding how the algorithm operates.

2 BACKGROUND ON THE MM ALGORITHM

As we have already emphasized, the MM algorithm is a principle for creating algorithms rather than a single algorithm. There are two versions of the MM principle, one for iterative minimization and another for iterative maximization. Here, we deal only with the maximization version. Let L(p) be the objective function we seek to maximize. An MM algorithm involves minorizing L(p) by a surrogate function g(p ∣ pⁿ) anchored at the current iterate pⁿ of a search. Minorization is defined by the two properties

(1)

(2)

In other words, the surface p ↦ g(p ∣ pⁿ) lies below the surface p ↦ L(p) and is tangent to it at the point p = pⁿ. Construction of the surrogate function g(p ∣ pⁿ) constitutes the first M of the MM algorithm.

In the second M of the algorithm, we maximize the surrogate function g(p ∣ pⁿ) rather than L(p). If pⁿ⁺¹ denotes the maximum point of g(p ∣ pⁿ), then this action forces the ascent property L(pⁿ⁺¹) ≥ L(pⁿ). The straightforward proof

reflects definitions (1) and (2) and the choice of pⁿ⁺¹. The ascent property is the source of the MM algorithm's numerical stability. Strictly speaking, it depends only on increasing g(p ∣ pⁿ), not on maximizing g(p ∣ pⁿ).

The celebrated EM algorithm (Dempster et al., 1977) is a special case of the MM algorithm (Lange, 2004; Lange et al., 2000). The EM algorithm always relies on some notion of missing data. Discerning the missing data in a statistical problem is sometimes easy and sometimes hard. In our Poisson graph model, it is unclear what constitutes the missing data. In contrast, derivation of a reliable MM algorithm is straightforward but ad hoc. Readers wanting a more systematic derivation are apt to be disappointed. In our defense, it is possible to codify several successful strategies for constructing surrogate functions (Hunter and Lange, 2004; Lange, 2004; Lange et al., 2000).

3 METHODS

Consider a random multigraph with m nodes labeled 1, 2,…, m. A random number of edges X_ij connects every pair of nodes {i, j}. We assume that the X_ij are independent Poisson random variables with means μ_ij. As a plausible model for ranking nodes, we take μ_ij = p_ip_j, where p_i and p_j are non-negative propensities. The log-likelihood of the observed edge counts x_ij = x_ji amounts to

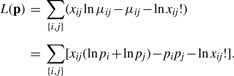Inspection of L(p) shows that the parameters are separated except for the products p_ip_j. To achieve full separation of parameters in maximum likelihood estimation, we employ the majorization

with the superscript n indicating iteration. Observe that equality prevails when p = pⁿ. This majorization leads to the minorization

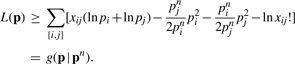Maximization of g(p ∣ pⁿ) can be accomplished by setting

The solution

(3)

is straightforward to implement and maps positive parameters to positive parameters. When edges are sparse, the range of summation in ∑_j≠ix_ij can be limited to those nodes j with x_ij > 0. Observe that these sums need only be computed once. The partial sums ∑_j≠ip_jⁿ = ∑_jp_jⁿ − p_iⁿ require updating the full sum ∑_jp_jⁿ once per iteration.

A similar MM algorithm can be derived for a Poisson model of arc formation in a directed multigraph. We now postulate a donor propensity p_i and a recipient propensity q_j for arcs extending from node i to node j. If the number of such arcs X_ij is Poisson distributed with mean p_iq_j, then under independence we have the log-likelihood

With directed arcs, the observed numbers x_ij and x_ji may differ. The minorization

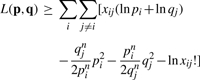now yields the MM updates

Again these are computationally simple to implement and map positive parameters to positive parameters. It is important to observe that the log-likelihood L(p, q) is invariant under the rescaling cp_i and c⁻¹q_j for a positive constant c and all i and j. This fact suggests that we fix one propensity and omit its update.

To derive a reasonable starting value in the undirected multigraph model, we maximize L(p) under the assumption that all p_i coincide. This gives the initial values

The same conclusion can be reached by equating theoretical and sample means. In the directed multigraph model, we maximize L(p, q) subject to the restriction that all p_i and q_j coincide. Now we have

Note that the fixed parameter is determined by this initialization.

4 RESULTS

4.1 Caernorhabditis elegans neural network

The neural network of C.elegans is a classic dataset first studied by White et al. (1986) and later by Watts and Strogatz (1998). In their paper, White et al. were able to obtain high-resolution electron microscopic images. This allowed them to identify all the synapses, map all the connections and to work out the entire neuronal network of the worm. To use all known connections in our analysis, we add as edges the electric junctions and neuromuscular junctions observed by Chen et al. (2006). For consistency, we disregard the directionality of the chemical synapses. In our opinion, the flexibility of the model in accepting different definitions of edges should be viewed as a strength. We declare a connection between two neurons i and j to be functionally significant when Pr(X_ij ≥ x_ij) ≤ 10⁻⁶. Figure 1 in the Appendix (Supplementary Material) depicts the network.

Fig. 1.

Graph of a cluster of the radiation hybrid network with significant connections (P < 10⁻⁹). In this graph, node size is proportional to a node's estimated propensity. Also, the darker the edge, the more significant the connection; red lines highlight the most significant connections. Edges between this cluster and the rest of the network were removed for clarity.

As recorded in Table 1, many of the most significant connections extend between motor neurons. The model also captures the bilateral symmetry between the right and left sides of the worm. Thus, the connections between the pairs RIPR-IL2VR and RIPL-IL2VL and between OLLL-AVEL and OLLR-AVER are all significant. Note that an L or an R at the end of a neuron's name signifies the left and right side, respectively. The right neuron PDER appears twice on the top 50 list and its left counterpart PDEL is missing, but both have the same number of significant edges overall. Although these dual connections are highlighted as about equally significant in our analysis, the corresponding propensity estimates show a left–right imbalance. The cause of these slight departures from bilateral symmetry is obscure. In any event, the model is subtle enough to distinguish between high edge counts and significant edge counts. Thus, even though one pair of nodes may have more edges than another pair, it does not necessarily imply that the first pair is more significantly connected than the second pair.

Table 1.

List of the 20 most significant connections of the C.elegans dataset

Rank	Neuron1	Neuron2	Obs.	Exp.	−Log P
1	VB03	DD02	37	0.7967	47.1265
2	VB08	DD05	30	0.382	45.1218
3	VB06	DD04	30	0.4653	42.5846
4	VB05	DD03	27	0.6609	33.1679
5	VD03	DA03	24	0.5834	29.6503
6	VA06	DD03	24	0.6495	28.5599
7	VA08	DD04	21	0.4289	27.6046
8	VD05	DB03	23	0.6934	26.3561
9	VA04	DD02	21	0.6325	24.1455
10	PDER	AVKL	16	0.2738	22.4316
11	VB02	DD01	20	0.6488	22.4101
12	RIPR	IL2VR	14	0.1702	21.7724
13	VA09	DD05	15	0.2934	20.2217
14	PDER	DVA	16	0.3972	19.8949
15	OLLL	AVER	18	0.6434	19.5152
16	VD03	AS03	14	0.2599	19.2348
17	VD03	DB02	16	0.4868	18.5184
18	VD01	DA01	14	0.3102	18.1794
19	RIPL	IL2VL	11	0.1136	18.0317
20	VA03	DD01	18	0.7851	18.0170

To the right of each pair appear the observed number of edges, the expected number of edges and minus the log base 10 P-value.

4.2 Radiation hybrid gene network

Radiation hybrids were originally devised as a tool for gene mapping (Goss and Harris, 1975) at the chromosome level. The detailed physical maps they ultimately provided (Cox et al., 1990) served as a scaffolding for sequencing the entire human genome. To construct radiation hybrids, one irradiates cells from a donor species. This fragments the chromosomes and kills the vast majority of cells. A few donor cells are rescued by fusing them with cells of a recipient species. Some of the fragments, say 10%, get translocated or inserted into the chromosomes of the recipient species. The hybrid cells have no particular growth advantage over the more numerous unfused recipient cells. However, if cells from the recipient cell line lack an enzyme such as hypoxanthine phosphoribosyl transferase (HPRT) or thymidine kinase (TK), both the unfused and the hybrid cells can be grown in a selective medium that eliminates the unfused recipient cells. This selection process leaves a few hybrid cells, and each of the hybrid cells serves as a progenitor of a clone of identical cells. Each clone contains a random subset of the genome of the donor species. The presence or absence of a particular short region can be assayed by testing for a donor marker in that region. A given donor marker is present in a given clone in 0, 1 or 2 copies.

It turns out that one can exploit radiation hybrids to map QTLs (quantitative trait loci). We measured the log intensities of 232 626 aCGH (array comparative genomic hybridization) markers and 20 145 gene expression levels in each of 99 mouse–hamster radiation hybrids (Ahn et al., 2009; Park et al., 2008). In this case, a mouse served as the donor and a hamster as the recipient. We then regressed the mouse gene expression levels on the mouse copy numbers recorded for each of the mouse markers. Altogether this amounts to about 5 × 10⁹ separate linear regressions. We constructed a multigraph from the data by analogy with the movie star example, with genes corresponding to actors and markers to movies. An edge is added between two genes if both genes showed statistically significant dependence on the marker at the level P ≤ 10⁻⁹. This strict P-value cutoff was chosen to produce an easily visualized graph. Because the aCGH markers densely cover the mouse genome, a quasi-peak finding algorithm was used to delete the excess edges occurring under a common linkage peak. Figure 2 in the Appendix (Supplementary Material) depicts the full network. Here, node size is proportional to estimated propensity and edge darkness is proportional to significance. Red edges are the most significant. Even with a very stringent significance level and elimination of edges by peak finding, there are still 729 169 significant connections.

Fig. 2.

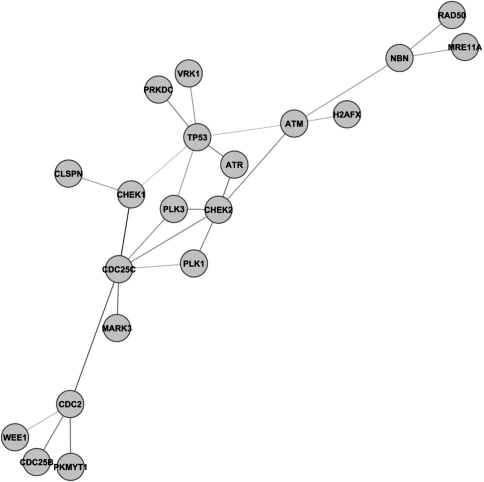
Graph of a disjoint cluster of the HPRD dataset after analysis with our method using a cutoff of P < 10⁻⁶. Note that this cluster is featured in the BiNGO analysis results displayed in Table 4.

Figure 1 shows an interesting subnetwork with highly significant edges, genes (nodes) of large propensity, and genes with related functions. The Dishevelled 1 (Dvl1) member of this subnetwork is part of the wingless/Int (Wnt) signaling pathway. The Wnt pathway has a reciprocal signaling relationship with the hedgehog pathway, which requires oxysterols for optimal function (Corcoran et al., 2009). The Wnt hedgehog connection is important in stem cell renewal. Interestingly, oxysterol binding protein-like 3 (Osbpl3) is a member of the subnetwork as well as Dvl1. Furthermore, the subnetwork contains two membrane-associated proteins: mucolipin 3 (Mcoln3), a cation channel protein (Cuajungco and Samie, 2008) and aquaporin 2 (Aqp2), a water channel protein (Carbrey and Agre, 2009). An emerging theme in cancer research is the notion of evolving genetic networks (Maxwell et al., 2008). Networks constructed using the Poisson multigraph model can robustly identify unexpected connections with known oncogene pathways such as the Wnt pathway. These connections may ultimately suggest novel therapeutic strategies.

4.3 Protein interactions via literature curation

With the advent of high-throughput experimentation, an enormous mass of information on protein interactions has accumulated. Because there was initially no universal format for presenting interactions, many of the early discoveries were useful only to the originating labs. This bottleneck forced coordination and eventually the construction of unified databases with fixed formats combining all of the published information. A notable example of this process of curation is the Human Protein Reference Database (Keshava Prasad et al., 2009). We downloaded Release 7 of the database and analyzed it with the random multigraph model.

Several interesting features of the data emerge under a P-value cutoff of 10⁻⁶. For instance, the protein with the most observed edges, TP53, turns out to be different from the protein with the most significant edges, Stat3. In fact, none of the top five proteins ranked by the most observed edges are in the top five proteins ranked by the most significant edge counts. Thus, the hub nodes of the raw data differ sharply from the hub nodes of the processed data. The two most extreme cases, YWHAG and CREBBP, have no significant edge counts despite being ranked fourth and fifth based on observed edges (Tables 2 and 3). One should be cautious in interpreting such results because molecular experiments are hypothesis driven and generate very biased data. The value of looking for significance is that it turns up hidden structure, not that it calls into question known structure.

Table 2.

Top 20 proteins with the most observed connections in the literature-curated protein database

Rank	Protein	Obs.	Sig.	Prop.
1	TP53	358	6	1.2515
2	GRB2	291	3	1.0164
3	SRC	277	5	0.9674
4	YWHAG	249	0	0.8693
5	CREBBP	231	0	0.8063
6	EGFR	231	5	0.8063
7	EP300	231	0	0.8063
8	PRKCA	229	4	0.7993
9	MAPK1	213	4	0.7433
10	CSNK2A1	207	1	0.7223
11	FYN	205	4	0.7153
12	PRKACA	202	2	0.7048
13	ESR1	200	1	0.6978
14	SHC1	195	5	0.6803
15	SMAD3	193	0	0.6733
16	STAT3	190	10	0.6628
17	SMAD2	183	1	0.6384
18	RB1	169	2	0.5894
19	TRAF2	168	2	0.5859
20	SMAD4	166	0	0.5789

To the right of each protein is the observed number of connections, the number of significant connections using P-value of 10⁻⁶, and the estimated propensity.

Table 3.

The 20 proteins with the most significant connections (P < 10⁻⁶) in the literature-curated protein database

Rank	Protein	Obs.	Sig.	Prop.
1	STAT3	190	10	0.6628
2	STAT1	162	9	0.565
3	MAPT	127	9	0.4427
4	PCNA	114	8	0.3973
5	RPS6KA1	59	7	0.2055
6	TP53	358	6	1.2515
7	MAPK3	148	6	0.5161
8	PTPN6	144	6	0.5021
9	DLG4	132	6	0.4602
10	MAPK14	107	6	0.3729
11	BTK	100	6	0.3485
12	HCK	82	6	0.2857
13	CREB1	59	6	0.2055
14	CDC25C	58	6	0.202
15	F2	57	6	0.1985
16	COPS4	31	6	0.1079
17	SRC	277	5	0.9674
18	EGFR	231	5	0.8063
19	SHC1	195	5	0.6803
20	LCK	156	5	0.544

To the right of each protein is the observed number of connections, the number of significant connections, and the estimated propensity.

When we cluster proteins by significant edge counts, the TP53 protein is especially interesting. Consider the small component containing TP53 shown in Figure 2. We analyzed this cluster using the BiNGO addition to Cytoscape (Maere et al., 2005). BiNGO computes the probability that x or more genes in a given set of genes shares the same GO (gene ontology) category. Altogether we found 30 significant GO categories with P < 10⁻⁶; most of these categories are listed in Table 4. These results dramatically illustrate the role of TP53 in regulating the cell cycle by (a) activating DNA repair proteins; (b) arresting the cell cycle at the G₁/S checkpoint to permit repair; and (c) initiating apoptosis in extreme circumstances.

Table 4.

BiNGO results of the small detached component around TP53 (Fig. 2) in the literature-curated protein database (Maere et al., 2005)

GO-ID	−Log P	GO term
7049	15.8761	Cell cycle
6974	12.6819	Response to DNA damage stimulus
279	12.2596	M phase
6281	12.1261	DNA repair
22 403	11.5544	Cell-cycle phase
22 402	11.5421	Cell-cycle process
6259	11.4597	DNA metabolic process
43 283	9.3883	Biopolymer metabolic process
43 687	8.9393	Post-translational protein modification
6796	8.2857	Phosphate metabolic process
6793	8.2857	Phosphorus metabolic process
7126	8.0123	Meiosis
51 327	8.0123	M phase of meiotic cell cycle
51 321	7.9706	Meiotic cell cycle
6464	7.6440	Protein modification process
6302	7.6216	Double-strand break repair
6310	7.5607	DNA recombination
43 170	7.5607	Macromolecule metabolic process
43 412	7.5186	Biopolymer modification
6468	7.5171	Protein amino acid phosphorylation
74	7.4559	Regulation of cell cycle
42 770	7.3665	DNA damage response, signal transduction

Note here that the P-values reported in the column labeled −Log P are the BiNGO P-values for clustering, not the P-values delivered by the Poisson model.

4.4 Word pairs and letter pairs

Identifying frequently used word pairs in literary texts can be useful in problems of literary attribution and in the identification of word fossils. Vocabulary richness and frequencies of sets of words have been studied in many different literary contexts using a variety of methods, including, for example, Bayesian analysis and machine learning to determine authorship of the Federalist papers (Holmes and Forsyth, 1995; Mosteller and Wallace, 1984), and likelihood ratio tests to study the Pearl poems (McColly and Weier, 1983). Recent investigations of long texts (Bernhardsson et al., 2009) have called into question Zipf's law (Zipf, 1932), which postulates that the frequency of any word is inversely proportional to its rank in usage. Here, we apply the Poisson model of graph connectivity to study pairs of words used consecutively in a set of Shakespeare's plays.

Our version of word pair analysis begins by scanning a literary work and creating a dictionary of words found in the text. An arc is drawn between two consecutive words, from the first word to the second word of the text, provided the words are not separated by a punctuation mark. The number of arcs between an ordered pair of words is counted and stored in a square matrix with dimensions equal to the number of unique words in the text. We chose seven of Shakespeare's plays, All's Well that Ends Well, As You Like It, Julius Caesar, King Lear, Macbeth, Measure for Measure and Titus Andronicus, concatenated them, and analyzed them as a whole. Contractions such as ‘o'er’ and ‘ta'en’ were replaced by the corresponding full words, ‘over’ and ‘taken’, respectively. We retained in our analysis word pairs constituting character names.

We calculated the observed frequency of each word pair. Based on the directed random multigraph model described in Section 3, we estimated the outgoing and incoming propensities for each word along with expected frequencies and P-values for each word pair. Table 5 lists the most connected word pairs in the text ranked by their P-values. This set is dominated by phrases that are commonly used in the language of the day, such as ‘I am’ and ‘my lord’, and by character names, such as ‘Lady Macbeth’ and ‘Second Lord’, in each play.

Table 5.

Most significantly connected word pairs

Rank	−Log P	Obs.	Exp.	Pair
1	391.3236	355	10.7509	i am
2	332.9314	293	8.2031	my lord
3	220.4243	337	30.4288	i have
4	195.8137	286	23.9518	i will
5	173.4930	73	0.1179	lady macbeth
6	163.1923	105	1.1239	thou art
7	160.2825	215	15.5290	it is
8	159.2199	399	70.5448	in the
9	146.6971	111	2.0425	no more
10	128.5489	51	0.0600	re enter
11	124.9406	160	10.6422	i know
12	110.9513	109	4.1161	let me
13	107.6928	151	11.8937	you are
14	107.3818	66	0.6054	second lord
15	95.2465	168	19.1548	i do
16	94.4514	80	2.0708	they are
17	94.0240	83	2.4030	pray you
18	93.8222	61	0.6902	thou hast
19	93.6175	137	11.6537	i would
20	88.9511	43	0.1446	first soldier

Preceding each word pair is its minus log P-value, the observed number of edges, and the expected number of edges.

One can identify several word pairs whose members almost never occur separately by examining the ratio 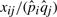of observed to expected word pair frequencies. Table 6 lists several examples ranked by this index. These word pair fossils are dominated by a few phrases still in common use such as ‘pell mell’ and ‘tick tack’ as well as various Latin and Italian phrases, such as ‘et tu Brute’, and other strange phrases specific to the context of particular plays, such as ‘boarish fangs’ and ‘rustic revelry’.

Table 6.

Words observed as a pair and never as singletons

Pair	Pair
hysterica passio	ordered honorably
bosko chimurcho	stinkingly depending
oscorbidulchos volivorco	facit monachum
boblibindo chicurmurco	stench consumption
suit's unprofitable	rustic revelry
quietly debated	fellowships accurst
tu brute	du vinaigre
ovid's metamorphoses	nec arcu
sectary astronomical	penthouse lid
boarish fangs	sun's uprise
curvets unseasonably	remained unscorched
cullionly barbermonger	clothier's yard
aves vehement	parallels nessus
downfallen birthdom	et tu
threateningly replies	mort du
tick tack	kerely bonto
kneaded clod	whoop jug
brethren's obsequies	fa sol
revania dulche	mastiff greyhound
tempestuous gusts	throca movousus

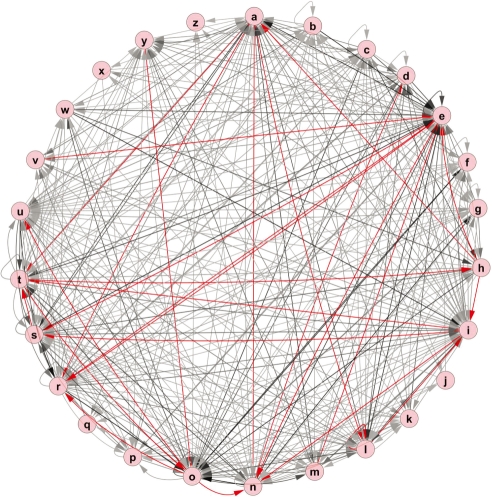
In addition, we studied pairs of letters encountered consecutively in the combined text of the Shakespearean plays. Figure 3 depicts the letter pair connections using a very stringent P-value of 10⁻¹⁹ for display purposes. Table 7 lists the same results in tabular form. The two most significant pairs are ‘th’ and ‘he’. One would expect much more stability over time of letter pair usage than word pair usage. This contention is borne out by our separate analysis of the novel Jane Eyre by Charlotte Bronte.

Fig. 3.

Graph of the significant connections (P < 10⁻⁹) in the letter pair network. In this graph, a darker edge implies a more significant connection, with the red edges highlighting the most significant connections.

Table 7.

Most significantly connected letter pairs

Pair	−Log P	Obs.	Exp.
th	10042	20308	2739
ou	3444	10452	2230
nd	3358	8125	1366
ll	2747	5404	703
yo	2257	4488	592
he	2098	15227	6085
ng	1974	3790	477
an	1775	10 554	3769
ve	1717	5138	1082
in	1469	8825	3172
ow	1365	3113	489
er	1283	10 264	4312
of	1186	3273	636
ha	1167	7665	2902
st	1069	5555	1823
my	999	2221	339
wi	835	3336	907
us	825	4134	1324
is	821	6346	2622
wh	778	3127	854
hi	692	5924	2573
ma	672	3585	1198
ur	659	4331	1641
fo	640	2855	843
om	619	2896	886

To the right of each pair appear the minus log P-value, the observed number of connections, and the expected number of connections.

5 CONCLUSIONS

Multigraphs are inherently more informative than ordinary graphs, and random multigraphs offer rich possibilities for modeling biological, social and communication networks. Our applications are meant to be illustrative rather than exhaustive. Graphical models will surely grow in importance as research laboratories and corporations gather ever larger datasets and hire ever more computer scientists and statisticians to mine them. The Poisson model has many advantages. It is flexible enough to capture hub nodes and functional connectivity, generalizes to directed graphs, and sustains an MM estimation algorithm capable of handling enormous numbers of nodes. It is also very quick computationally as measured by total iterations and total time until convergence. A glance at Table 1 of the Appendix (Supplementary Material) suggests that 20–30 iterations suffice for convergence. To thrive, data mining must balance model realism with model computability. In our opinion, the Poisson model achieves this end. Of course, other distributions for edge counts could be tried, for instance the binomial or the negative binomial, but they would be even less well motivated and less adapted to fast estimation.

It is natural to place our advances in the larger context of applied random graph theory. For instance, early on social scientists married latent variable models and random networks (Holland and Leinhardt, 1981). Stochastic blockmodels assign nodes either deterministically or stochastically to latent classes (Airoldi et al., 2008; Holland et al., 1983; Newman and Leicht, 2007; Nowicki and Snijders, 2001; Wang and Wong, 1987). Alternatively, a latent distance model sets up a social space and estimates the distances between node pairs in this space (Hoff et al., 2002). It is possible to combine features of both latent class and latent distance models in a single eigenmodel (Hoff, 2008). The ‘attract and introduce’ model is another helpful elaboration (Fowler et al., 2009). None of these models focuses on multigraphs. Furthermore, most classical applications involve networks of modest size. However, under the stimulus of large internet datasets, the field of random networks is in rapid flux. Going forward it will be a challenge to turn the rising flood of data into useful information. Importing more of the social science contributions into biological research may pay substantial dividends.

In practice, most large networks contain an excess of weak interactions. The radiation hybrid data are typical in this regard. To sift through the data, it is helpful to focus on hub nodes and strong interactions. The Poisson multigraph model provides a rigorous way of doing so. The model's flexibility in allowing different sorts of edges is appealing if not taken to extremes. When confidence in edge assignment varies widely across edge definitions, a weighted graph model might be a better modeling device than a multigraph model. However, converting a multigraph to a weighted graph has its own problems. For instance, there is more than one way to make the conversion. An even bigger disadvantage of weighted graph models is their tendency to ignore the stochastic nature of node formation. This is a hindrance in assessing functional connections and suggests an opportunity for more nuanced modeling. To be competitive with Poisson multigraphs, a good stochastic model for weighted graphs should support fast estimation of parameters. One substitute for Poisson randomness is to condition on the degree of each node (Chung and Lu, 2002). Within these constraints, one can randomize edge placement. This perspective lends itself to permutation testing but not to parameter estimation (Maslov and Sneppen, 2002). Unfortunately, the computational cost of generating the required permutations limits the chances for approximating very small P-values and hence ranking connections by P-values.

The random multigraph model raises as many questions as it answers. How closely is it tied to the Poisson distribution? How closely is it tied to the propensity parameterization of edge means? Can predictors be incorporated that determine propensities? More importantly, what applications would benefit from this sort of modeling? We are content to raise these issues, with the hope that other computational and mathematical scientists can be enlisted over time to resolve them and related problems beyond our current understanding.

Funding: United States Health Service grants (GM53275 and MH59490 to K.L.); Stein Oppenheimer Endowment Award, UCLA (to D.J.S.).

Conflict of Interest: none declared.