Imaging electrical resonance in hair cells

Abstract

The mechanosensory hair cells of many auditory receptor organs are tuned by an electrical resonance that increases their responses to stimulation over a narrow band of frequencies. The small oscillations of membrane potential characteristic of this phenomenon have previously been detectable only through intracellular electrode measurements, which are laborious and preclude analysis at the level of an entire sensory organ. We used a voltage-sensitive dye to image hair-cell electrical resonance in an intact preparation of the bullfrog's sacculus, a receptor organ sensitive to low-frequency seismic and auditory stimuli. Imaging revealed distinct populations of hair cells whose resonant response varied with the frequency of transepithelial electrical stimulation. Most of the hair cells in the saccular epithelium in vitro were electrically tuned to stimulation at 25–50 Hz. The frequency dependence of the fluorescence signal was sensitive to pharmacological blockade of large-conductance Ca²⁺-sensitive K⁺ channels and to enzymatic digestion. At an elevated concentration of Ca²⁺, we observed transient fluorescence signals that probably represented action potentials. The stroboscopic imaging and analysis techniques described here present a general approach for studying subthreshold oscillations in electrically excitable cells.

Animals identify complex sounds by decomposing them into their constituent frequency components. This resolution is achieved in vertebrates through selective tuning of mechanosensory hair cells. An array of hair cells tuned to different frequencies thus accounts for an animal's hearing range. The tuning curves of individual afferent auditory nerve fibers are very sharp, a result suggesting that signals are subject to multiple stages of filtering (1). Although acoustic dispersion within a hearing organ provides some of this tuning, hair cells also make a significant contribution.

One mechanism of frequency tuning intrinsic to hair cells is electrical resonance. When stimulated at its resonant frequency, a hair cell responds with membrane-potential oscillations of maximal amplitude; these oscillations, in turn, elicit the release of more neurotransmitter at its synapses. Observed in the hair cells of fishes (2) and in nonmammalian tetrapods such as frogs (3–5), turtles (6), lizards (7), and birds (8), electrical resonance is an important tuning mechanism for frequencies up to 1 kHz. Resonance originates from an interplay between L-type voltage-gated Ca²⁺ channels and large-conductance Ca²⁺-activated K⁺ (BK) channels whereby kinetic differences between the opposing currents cause the system to oscillate when perturbed electrically (5, 9).

Measurements of electrical resonance have heretofore been performed by intracellular recording, most often from isolated cells (4, 6). Recordings from hair cells along the frog's amphibian papilla (10), the turtle's basilar papilla (11), and the chick's basilar papilla (8) indicated that the tonotopic map of electrical resonance accords with the tuning gradients observed in measurements from auditory nerve fibers. Owing to the laborious nature of the measurement technique, however, electrical resonance was assayed in these studies at only a few locations along the tonotopic axis. It is therefore difficult to establish a map of electrical tuning for an individual animal. A parallelized technique that provides a snapshot of electrical tonotopy would help to elucidate the role played by this tuning mechanism. Moreover, although electrical oscillation is a widespread phenomenon among neurons in the central nervous system (12, 13), there is currently no efficient means of simultaneously observing these low-amplitude signals from many individual cells.

In response to membrane-potential changes, voltage-sensitive dyes produce optical signals that are detectable as shifts in absorption and emission spectra. Experimental measurements typically illuminate and detect at fixed wavelengths; the signals thus represent changes in fluorescence intensity. When combined with fluorescence imaging, these signals allow electrical activity to be monitored from many cells simultaneously (14–16). The chief limitation of this approach is the small signal size: Typical emission-based responses to a 100-mV voltage change are 1–5% of the baseline fluorescence. Given the low intensity of fluorescence images, averaging is often required to produce detectable signals. Because systematic readout noise in cameras increases with the speed of data acquisition, imaging fast electrical activity, such as electrical resonance in hearing organs, exacerbates this problem. In addition, acoustic frequencies can exceed even the highest frame rates for sensitive cameras. For periodic measurements, however, stroboscopic illumination offers an alternative method for imaging fast activity. A relatively slow camera with a large dynamic range can resolve fast activity by using a rapidly switched source of illumination. Although averaging is still required for measuring small signals, stroboscopic imaging reduces noise and is therefore attractive for the detection of small, high-frequency signals that are periodic.

Isolated hair cells of the bullfrog's sacculus, an otolithic receptor organ sensitive to low-frequency seismic and acoustic stimuli (17, 18), exhibit electrical resonance at frequencies between 10 and 250 Hz (3, 4, 19, 20). In an intact sacculus, however, the hair cells are mechanically coupled by an otolithic membrane. This coupling, combined with loading by a large overlying otoconial mass, presumably forces the saccular hair cells to resonate collectively at frequencies that are at the lower end of the range for electrical resonance in isolated cells. It remains unclear to what frequencies hair cells in intact saccular maculae are tuned. To address this question, we used a voltage-sensitive dye to measure the electrical responses of hair cells to the transepithelial application of sinusoidal current.

Results

Simulated Optical Signals.

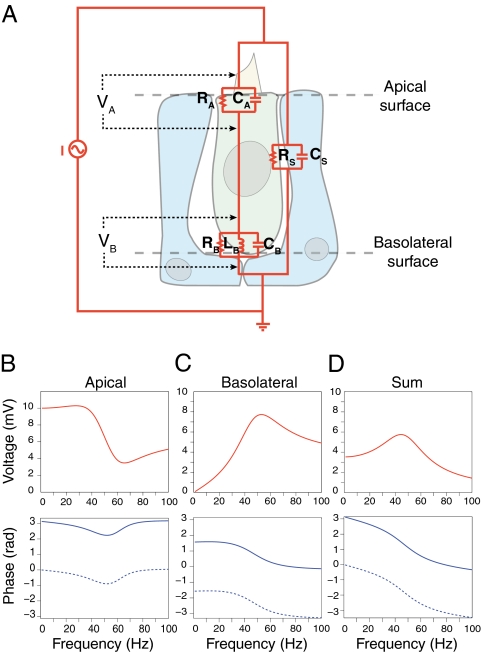
Under physiological conditions, acoustic stimulation of a saccular hair cell causes current to flow through mechanotransduction channels, eliciting equal membrane-potential changes over all aspects of the cell. During transepithelial stimulation of the bullfrog's sacculus, however, current passes through the hair cell's apical and basolateral surfaces in series and through a shunt comprising cell–cell junctions and other leakage pathways (Fig. 1A). The apical and basolateral membranes of a hair cell thus experience differing voltage changes and should therefore elicit distinct optical signals from membrane-bound voltage-sensitive dyes. We modeled the voltage response of both apical and basolateral membranes to help interpret the experimental results.

Fig. 1.

A model of electrical resonance and fluorescence signals in saccular hair cells. (A) The equivalent circuit for the saccular epithelium includes three membranes that impede transepithelial current: the hair cell's apical and basolateral membranes (indicated by subscripts A and B) and a shunt pathway (indicated by subscript S) through supporting cells and the extracellular space. We calculated the voltage changes V_A across the hair cell's apical membrane and V_B across its basolateral membrane. (B) Numerical simulation predicts the voltage change across the apical membrane during sinusoidal current stimulation with an amplitude of 0.5 μA. (Upper) The modulus and (Lower) phase of the response as a function of the stimulus frequency. The dotted line represents the corresponding fluorescence signal; a factor of π rad has been added because the polarity of the optical signal is opposite that of the voltage change. (C) The corresponding data for the voltage change across the basolateral membrane reveals a resonant response. (D) The sum of the two responses, weighted by the relative membrane areas, represents the fluorescence signal expected in the absence of noise.

In response to a sinusoidal current stimulus of fixed amplitude but varying frequency, the basolateral membrane potential of hair cells displays a broadly tuned resonant peak (Fig. 1 B and C). The resonant frequency lies 10 Hz lower than 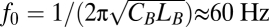, the resonant frequency expected for a typical isolated hair cell with basolateral capacitance C_B and phenomenological inductance L_B. Assuming that the fluorescence signal includes both apical and basolateral responses, and recognizing that the polarity of the fluorescence signal is opposite that of the membrane-potential change, we simulated a voltage signal that incorporated the two weighted by the relative membrane surface areas (Fig. 1D). At the peak of resonance, which occurred at 45 Hz, this signal displayed an amplitude of only 6 mV. In contrast, the phase of the summed response featured a dramatic shift of almost 2 rad at resonance. This result implies that the response's phase change can serve as a criterion for identifying resonant features in noisy voltage measurements.

Stroboscopic Fluorescence Imaging.

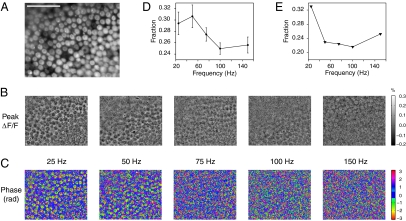
The voltage-sensitive naphthyl styryl-pyridinium dye di-3-ANEPPDHQ labels hair cells strongly (Fig. 2A). We separated fluorescence changes that were induced by electrical stimulation of the sacculus from unrelated intensity fluctuations by subtracting background images acquired in the absence of stimulation. Over multiple repetitions of the stimulus waveform, we averaged the fluorescence of every pixel at each of eight equally spaced phases (SI Appendix). The time course of each pixel's value across the resulting image stack was fit to a sinusoid with free parameters of amplitude and phase.

Fig. 2.

The spatial distribution of resonance-related fluorescence signals. (A) A fluorescence image shows hair cells stained with a voltage-sensitive dye in an intact saccular macula. The cells are most clearly distinguished as hair cells by their brightly stained mechanosensory hair bundles. (Scale bar: 100 μm; all images are presented with the same field of view.) (B) Images of the peak relative fluorescence changes (ΔF/F) for the indicated stimulus frequencies delineate hair cells. The scale bar is shown at the right. (C) Hair cells are readily apparent in images showing the phase of the fluorescence response based on a least-squares fit. The pixels with phases between −π/8 and π/8 are colored dark blue to visually threshold the images; the color axis wraps around at ±π rad. (D) At each frequency of stimulation, the phase information was used to generate an image that displays, for every pixel, the SD of the phase values among the eight neighboring pixels. The fraction of pixels with a spatial variance of less than π/5 is plotted with the SEM as a function of stimulus frequency. (E) The presence of 100 nM iberiotoxin shifted the relation between stimulus frequency and pixel conglomeration to lower frequencies.

We analyzed the spatial features of both the peak relative fluorescence changes (ΔF/F) and fitted phases of the fluorescence signal elicited by transepithelial current stimulation. The stimulation frequencies were chosen from the range over which electrical resonance has been observed in saccular hair cells. Both responses varied with the stimulus frequency (Fig. 2 B and C). In the phase images, contours that corresponded to dye-labeled cells were prominent at 25 and 50 Hz, but disappeared at higher frequencies of stimulation. Furthermore, it was evident from both sets of images that distinct populations of cells displayed resonance at those two stimulus frequencies.

The spatial patterns of the fitted phase parameter provided striking evidence of electrical resonance (Fig. 2C). Whereas pixels that contained mostly background fluorescence yielded random phase fits that were widely distributed about zero phase, pixels featuring genuine intensity fluctuations at the stimulus frequency displayed a more restricted phase distribution and delineated cellular boundaries. The response's sinusoidal amplitude, which is intuitively the parameter most indicative of voltage oscillations, did not localize resonant signals well. The low signal-to-noise ratio of the measurements, compounded with the sparse temporal sampling, caused pixels with large noise amplitudes—but no underlying sinusoidal component at the frequency of stimulation—to display high amplitudes when fitted to a sinusoid.

Phase of the Fluorescence Response.

Because the phase images yielded the clearest depiction of resonant cells, we quantified the relation between the stimulus frequency and the appearance of cellular patterns by measuring the proportion of phase-image pixels with low spatial variance (Fig. 2D). Although our models, which did not include noise, predicted a phase shift at resonance, our most salient observation was the emergence of cellular contours whose response had a well-defined phase. Our spatial metric was indicative of resonance because cells that oscillated electrically with large amplitudes yielded optical signals that exceeded the noise, causing cell contours to appear. Averaged over six positive control experiments, the data showed a peak in pixel-value conglomeration at 50 Hz. This trend closely resembled that of the simulated amplitude of driven voltage oscillations in hair cells for a weighted sum of apical and basolateral membrane signals (Fig. 1D Upper). Application of 100 nM iberiotoxin, a blocker of large-conductance Ca²⁺-activated K⁺ channels, dramatically reduced pixel conglomeration and shifted the resonance to 25 Hz (Fig. 2E). This effect accords with reports that iberiotoxin eliminates outward K⁺ currents and thus precludes high-frequency resonance (10, 19).

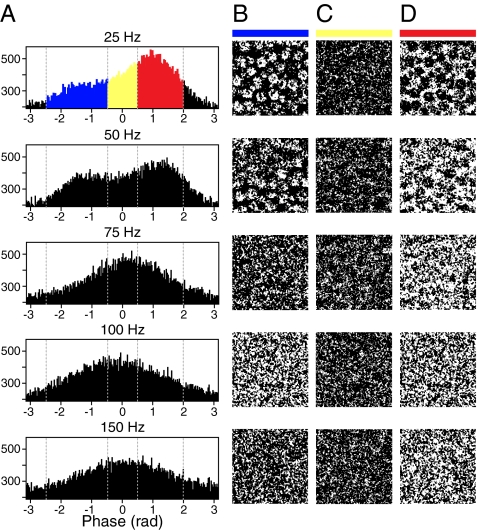
Tabulating the pixels from phase-fit images in histograms identified distinct populations responsive to stimulation at 25 and 50 Hz (Fig. 3A). The responses disappeared at higher stimulus frequencies. To identify the portions of the macula represented by these populations, we created binary images in which pixels were assigned a value of 1 if their phase lay within a specific range. Highlighting pixels that had phases between −2.5 and −0.5 rad clearly delineated hair cells (Fig. 3B). Furthermore, these highlighted regions appeared to be confined to the cells' upper surfaces; this observation is consistent with the phase predicted for signals that originated from voltage-sensitive dye in the apical membranes (Fig. 1B). Pixels that displayed phases near 0 rad were scattered diffusely throughout the field of view (Fig. 3C). Highlighting pixels with phases between 0.5 and 2.0 rad delimited the areas between hair cells, presumably the sites of supporting cells (Fig. 3D). At stimulus frequencies above 50 Hz, pixels from all phase bins were scattered diffusely.

Fig. 3.

Spatial patterns of activity as a function of stimulus frequency and phase. (A) Histograms tabulate the phases for all pixels in one representative experiment with five frequencies of electrical stimulation. (B) A binary map of the spatial locations of pixels whose response phases fell between −2.5 and −0.5 rad clearly delineates the hair cells. (C) A similar map displays pixels with phases from −0.5 to 0.5 rad. (D) The pixels with phases from 0.5 to 2.0 rad are concentrated between the hair cells. The phase ranges are color-coded by the horizontal bars atop the columns; matching colors highlight data points in the phase histograms of A. The width of each image in B–D is 80 μm.

Analysis of Phase Statistics.

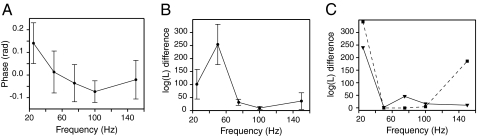
Fitting the phase histograms to a single von Mises distribution, the analog of a normal distribution for angular data, allowed us to relate the mean phase to the frequency of stimulation (Fig. 4A). This trend resembled the modeled phase response of the combined apical and basolateral membranes for an individual hair cell (Fig. 1D, Lower), albeit on a compressed ordinate scale.

Fig. 4.

Statistical analysis of the phase behavior of electrically resonant sacculi. (A) The mean phase (±SEM) of the fluorescence response to transepithelial electrical stimulation at various frequencies was averaged over six control experiments. The mean was extracted from a unimodal von Mises fit to each phase histogram. (B) The log-likelihood values provide a means of comparing the fits of unimodal and bimodal models to phase histograms. For each frequency of stimulation, the value of ln(m_a/m_b) (±SEM) was averaged over six control experiments; m_a and m_b are the maximized likelihoods that the data were represented by respectively a bimodal or a unimodal model. Values of less than 3, the difference in the number of parameters of the uni- and bimodal models, suggest that a bimodal model does not provide a significantly better representation of the data. (C) The log-likelihood differences for preparations treated with 100 nM iberiotoxin (continuous line) and proteinase type XXIV (dotted line) display shifts of bimodality to lower frequencies. The preparation treated with the proteinase additionally displayed an increase in bimodality at 150 Hz.

Histograms of phase exhibited stereotyped bimodality as a function of stimulus frequency, a finding consistent with our simulations predicting different phases at resonance for a hair cell's apical and basolateral surfaces. To quantify this visually apparent finding, we fit each histogram both with a unimodal von Mises distribution with two parameters and with a bimodal model consisting of a combination of two von Mises distributions with five parameters. To assess the preference for each model, we then examined the log-likelihood, the probability that the model and the fitted parameters would have generated the observed data. An information criterion whereby a model is excluded if the log-likelihood difference between it and a competing model is less than the difference in the number of model parameters (3 in this instance) provided a reference value for our analysis (21). When the difference between the log-likelihoods of bimodal and unimodal models was plotted as a function of stimulus frequency, a bimodal model was highly preferable at 25 and 50 Hz (Fig. 4B). At higher frequencies the log-likelihood difference declined dramatically, falling below 3 in some experiments. This analysis effectively captured the evolution of bimodality (Fig. 3A) and confirmed that electrical resonance produced responses at two well-defined phases.

In a preparation treated with iberiotoxin, the preference for a bimodal model peaked at 25 Hz, fell below the information criterion at 50 Hz, and remained low for still greater frequencies (Fig. 4C). This bimodality trend matched that of pixel conglomeration and of the visual appearance of cells at 25 Hz in the preparation treated with iberiotoxin.

Subjection of frog saccular hair cells to enzymatic digestion increases their frequency of electrical resonance to 150–200 Hz (19). When we performed stroboscopic imaging on a preparation treated with proteinase, cells were apparent in phase images for stimulation at both 25 and 150 Hz. This effect was mirrored in the occurrence of bimodality in the phase histograms and confirmed by log-likelihood analysis (Fig. 4C).

Putative Ca²⁺ Action Potentials.

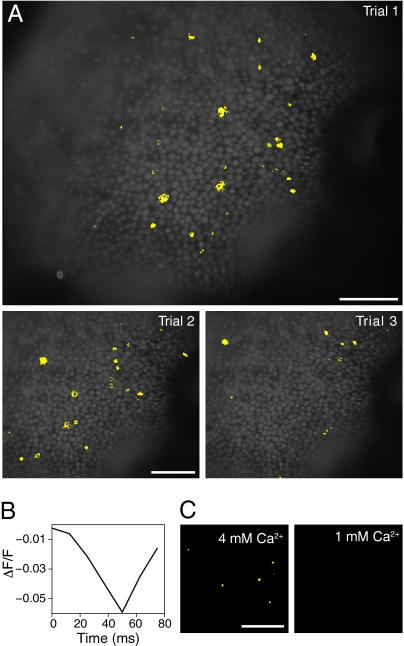
In imaging experiments performed at an elevated Ca²⁺ concentration of 4 mM, we observed large transient changes in the fluorescence signal, 5% of the baseline value, in individual hair cells during single-trial records. These events were most prominent within the first 10 imaging records and occurred at variable intervals in scattered hair cells. The transients likely represented Ca²⁺ action potentials, which have been described in isolated saccular hair cells as 40- to 75-mV depolarizing spikes (22, 23). In response to 10-Hz electrical stimulation, evidence for spiking was apparent in images of the extracted sinusoidal amplitude superimposed on a background fluorescence image (Fig. 5A). Each transient event represented a decrease in fluorescence, which at the excitation and emission wavelengths used implied a membrane depolarization. The fluorescence signals were asymmetric, negative spikes lasting 50–60 ms (Fig. 5B), a duration similar to that of action potentials observed electrophysiologically in frog hair cells (22). Sacculi bathed in 1 mM Ca²⁺ did not exhibit spike-related signals (Fig. 5C).

Fig. 5.

Putative Ca²⁺ action potentials. (A) Images showing high values for the sinusoidal component of the fluorescence response to electrical stimulation at 10 Hz are superimposed on a fluorescence image of a sacculus stained with di-3-ANEPPDHQ. The three images represent the initial trials of this recording in the presence of 4 mM Ca²⁺; the latter two images are displayed with a cropped field of view. Pixels whose extracted sinusoidal components exceeded a value of 150 are displayed in yellow. All single-trial images were spatially filtered by applying a 3 × 3-pixel sliding-window average. (B) A plot of the relative fluorescence change (ΔF/F) against time reveals the time course of a single depolarization in a hair cell in the final panel of A. (C) In these binary images, yellow pixels represent values exceeding 600 for the sinusoidal fit coefficients from single-trial recordings at 50 Hz in the presence of 4 mM (Left) and 1 mM (Right) Ca²⁺. (Scale bar: 100 μm in all micrographs, including those in A.)

Discussion

We used optical imaging of electrical activity to confirm the presence of a heterogeneous population of resonating hair cells in intact saccular maculae. The bullfrog's sacculus is electrically tuned to frequencies in the range of 25–50 Hz, a result that is consistent with in situ measurements from individual saccular hair cells in a preparation that had been furrowed and denuded of its otolithic membrane (19). Applying iberiotoxin lowered the resonant frequency, an effect consistent with the toxin's function as a blocker of Ca²⁺-sensitive K⁺ channels. In addition, electrical tuning was sensitive to enzymatic digestion, consistent with the finding that papain increases the frequency of electrical resonance (19).

Although our measurements accord with the electrical tuning observed in frog saccular hair cells spared exposure to enzymes, it should be noted that we removed the otolithic membranes to reduce optical blurring owing to scattering. This manipulation largely destroys the hair cells' mechanotransduction apparatus, producing a change in conductance that might affect both the resting membrane potential and electrical tuning (24).

Imaging electrical resonance yielded signals at several distinct phases. Although the exact populations varied between experiments and shifted somewhat as a function of frequency, pixels in the averaged images fell into three distinct populations centered approximately at 0, −1, and 1 rad. Pixels whose temporal response did not contain a significant sinusoidal component nonetheless displayed shot noise; when fit to a sinusoid, these pixels yielded phases scattered about zero. This phenomenon was probably an artifact of the electrical stimulation whereby dye bound to the membranes of cells other than hair cells, particularly supporting cells, responded in phase with the current stimulus. Because these pixels were distributed diffusely throughout the field of view and were found in all recordings regardless of stimulus frequency, we attributed this unresponsive population to background fluorescence. Pixels whose sinusoidal response component had a phase centered near −1 rad occurred primarily within the confines of hair-cell bodies. This population, which was confined to resonant frequencies, exhibited a phase close to that simulated for a voltage-sensitive dye in a hair cell's apical membrane.

The anatomical origin of the population of pixels centered near 1 rad is less clear. Our imaging system lacked optical-sectioning capability, so these signals might correspond to the summed voltage signals from multiple membranes. Moreover, the saccular surface was uneven, and the pooled data therefore contained phase information from various depths. One possible explanation for the positive phase population is that the modeled shunt pathway, represented by the measured resistance and a generic membrane capacitance scaled to half the macular area, is unduly simplistic. This model does not encompass, for example, the layer of supporting cells beneath the hair cells. These additional membrane surfaces certainly experience voltage changes, and it is possible that their fluorescence signals contributed to the population at 1 rad. Another possibility is that electrical stimulation directly excited nerve fibers that synapse onto hair cells and that their responses occurred at a phase different from that of the basolateral membranes. Any of these signals, either alone or in combination, could have contributed to the positive-phase population.

The multimodality of the optical response's phase implies that the mean phase cannot be compared directly with our simulations. Tracking the mean phase as a function of stimulus frequency revealed a trend similar in shape and initial value to those predicted by the simulation, but whose overall modulation of 0.2 rad was only 10% as great. One plausible explanation for this compression is that the average was weighted toward zero by pixels representing background fluorescence. These pixels, which were not included in our simulation, had phase fits widely distributed about zero phase; adding a static fluorescence signal centered about zero phase to the model readily reproduced the observed compression.

When exposed to sinusoidal transepithelial current, the hair bundles in the bullfrog's sacculus oscillate at the frequency of stimulation (25, 26). Although mechanical responses might contribute to the fluorescence signals, several factors—foremost among them optical considerations—make this improbable. The microscope system's total magnification was only 12.6×, which permitted us to image the entire sacculus. Each pixel therefore represented an area of 512 nm × 512 nm. Because current-induced hair-bundle motions rarely exceed 100 nm, it is unlikely that this effect propagated beyond a single pixel. Furthermore, the depth of field extended several micrometers, a distance that would have reduced the contrast of optical signals from lateral bundle movements. To determine whether current stimulation elicited vertical motion artifacts, we used heterodyne laser vibrometry to measure any vertical displacements in the sacculus during sinusoidal electric stimulation. No oscillations were observed at the stimulus frequency.

What is the behavioral relevance of the electrical tuning that we observe in bullfrog sacculi at 25–50 Hz? Seismic and airborne waves at these low frequencies have large wavelengths that make their sources difficult to locate but concomitantly reduce the attenuation owing to obstacles (27). The bullfrog, whose broad-spectrum vocalizations are modulated at frequencies below 100 Hz (28), takes advantage of this frequency regime for communication. The female bullfrog's territorial call, for example, is modulated steadily at 30 Hz, then ends with an abrupt upward glissando to 90 Hz. It is possible that the bullfrog's sacculus, which features a wealth of hair cells tuned in the range of 25–50 Hz, is specialized for the detection of these communication signals.

Whereas electrical resonance tunes the sacculus to frequencies in the range of 25–50 Hz, Ca²⁺ action potentials may provide a mechanism for hair cells to respond distinctly to very low frequencies or static deflections related to head orientation (23). In a subpopulation of saccular hair cells, we observed putative Ca²⁺ action potentials in response to low-frequency stimulation and at an extracellular Ca²⁺ concentration of 4 mM. Our measurements in single trials with a high signal-to-noise ratio show that action potentials can be detected optically without the use of stroboscopic imaging. This approach could be used to test hypotheses concerning the utility of spiking behavior. It should be straightforward, for instance, to study the large-scale spiking response in an intact sacculus during static deflections of the otolithic membrane.

Voltage-sensitive dyes permit optical measurement of fast electrical activity in neurons and other electrically excitable cells. The technique has facilitated voltage measurements in systems ranging from action potentials in individual nerve terminals (29) and dendritic spines (30) to large-scale dynamics in the cerebral cortex (31). The detection of small voltage signals is limited by noise. Considering only shot noise, the signal-to-noise ratio predicted for a 2-mV signal measured with the sensitive potentiometric dye di-3-ANEPPDHQ is only 0.2. The other major source of noise in our measurements, camera readout noise, arises during the transfer and measurement of photoelectron signals. Readout noise increases in proportion to the square root of the measurement's bandwidth, so fast measurements are noisier. Stroboscopic illumination effectively reduces the measurement's bandwidth by shifting the burden of speed to the light source. When driven by a stable and rapidly switched current supply, stroboscopic imaging permits fast, periodic signals to be measured at low frame rates, reducing the readout noise. This systematic source of noise can be effectively eliminated by using cameras with low intrinsic readout noise. This strategy, which enabled us to image signals estimated at 5 mV from electrically resonant hair cells, can facilitate the detection of electrical resonance in other cell types. For example, the stroboscopic technique could be used to quantify the receptor potentials in hair cells of the mammalian cochlea during electrical or near-threshold acoustic stimulation. More broadly, many neurons in the thalamus, hippocampus, and cerebral cortex exhibit subthreshold oscillatory potentials that filter the cells' inputs and synchronize distant neuronal assemblies (12, 13). The imaging and data-analysis techniques described here provide a means of studying the extent and consequences of these intrinsic cellular resonances.

Materials and Methods

Summary of Experimental Procedure.

To help interpret the voltage-sensitive–dye fluorescence signals that originate from saccular hair cells in situ, we numerically simulated the cells' electrical response to sinusoidal current stimulus. The simulations modeled the current that passed through equivalent circuit representations of the hair cells' apical and basolateral membranes and through an additional parallel circuit element that represented a low-resistance shunt pathway between cells and through supporting cells. To account for the kinetic differences between voltage-gated Ca²⁺ channels and Ca²⁺-activated K⁺ channels, we included a phenomenological inductance in the basolateral membrane's equivalent circuit.

For the physiological preparation, we excised each saccular macula from an adult bullfrog (Rana catesbeiana) and carefully removed its otolithic membrane with an eyelash. After being stained with the voltage-sensitive dye di-3-ANEPPDHQ, the preparation was encased in low-melting-point agarose to minimize mechanical motion during image acquisition. The sacculus was then mounted in a recording chamber in which each side of the preparation contacted saline solution in an electrically isolated compartment. The chamber therefore permitted access for both optical imaging and transepithelial electrical stimulation.

A computer controlled electrical stimulation, data acquisition, and strobed illumination. The stained preparation was illuminated by a green light-emitting-diode array, and the orange fluorescence from the dye was filtered by a long-pass absorption filter before being collected by a 16-bit charge-coupled device camera. For each stimulus frequency, the camera's electronic shutter was opened and the intact sacculus was illuminated by a series of short square pulses, equal to one-eighth of the stimulus period, that were phase-locked to the electrical stimulus. This procedure generated a single image representing the fluorescence from a particular phase of the stimulus cycle; during subsequent exposures, the illuminating pulses were delivered at other phases. For each frequency of current stimulus, we generated a stack of eight images that depicted the sacculus's voltage-dependent fluorescence activity through a full cycle of stimulation.

Summary of Data Processing.

To extract the sinusoidally varying component of the fluorescence response, we fit the time course of each pixel to a function that contained constant, linear, cosine, and sine terms. The magnitude and phase of the sinusoidal component of the response were calculated from the coefficients of the fitted cosine and sine terms. Images depicting the extracted phase clearly highlighted saccular hair cells. We quantified this spatial clustering by measuring the proportion of pixels that had low spatial variances from maps of pixel SDs created with matlab's stdfilt.m function.

Histograms of phase were frequently bimodal. To quantify this bimodality, we compared the log-likelihood that unimodal and bimodal von Mises functions would have yielded the observed data. The data were fit to these distributions with the aid of functions from the Circular Statistics Toolbox for matlab (32). For the bimodal distributions, we used a method-of-moments algorithm (33). Data manipulation and image processing were performed in matlab.