Analysis of Untyped SNPs: Maximum Likelihood and Imputation Methods

Abstract

Analysis of untyped single nucleotide polymorphisms (SNPs) can facilitate the localization of disease-causing variants and permit meta-analysis of association studies with different genotyping platforms. We present two approaches for using the linkage disequilibrium structure of an external reference panel to infer the unknown value of an untyped SNP from the observed genotypes of typed SNPs. The maximum-likelihood approach integrates the prediction of untyped genotypes and estimation of association parameters into a single framework and yields consistent and efficient estimators of genetic effects and gene-environment interactions with proper variance estimators. The imputation approach is a two-stage strategy, which first imputes the untyped genotypes by either the most likely genotypes or the expected genotype counts and then uses the imputed values in a downstream association analysis. The latter approach has proper control of type I error in single-SNP tests with possible covariate adjustments even when the reference panel is misspecified; however, type I error may not be properly controlled in testing multiple-SNP effects or gene-environment interactions. In general, imputation yields biased estimators of genetic effects and gene-environment interactions, and the variances are underestimated. We conduct extensive simulation studies to compare the bias, type I error, power, and confidence interval coverage between the maximum likelihood and imputation approaches in the analysis of single-SNP effects, multiple-SNP effects, and gene-environment interactions under cross-sectional and case-control designs. In addition, we provide an illustration with genome-wide data from the Wellcome Trust Case-Control Consortium (WTCCC) [2007].

INTRODUCTION

The rapid improvement of high-throughput genotyping technology and the precipitous drops of genotyping cost have led to the widespread use of genome-wide association studies (GWAS) in elucidating the genetic basis of complex human diseases. Because the current genotyping platforms assay only a small fraction of single nucleotide polymorphisms (SNPs) in the human genome, many disease-susceptibility loci will inevitably be untyped (i.e. not genotyped). Thus, it is highly desirable to conduct association analysis at untyped SNPs. Such analysis can help localize causal variants and facilitate selection of SNPs for follow-up studies. Such analysis also allows investigators to compare or combine results from studies that use different genotyping chips. As untyped SNPs are not measured on any study subject, the missing information cannot be recovered from the study data alone. Fortunately, the linkage disequilibrium (LD) structure observed in an external reference panel, such as the HapMap [The International HapMap Consortium, 2005], can be used to predict untyped variants from typed variants.

A variety of methods have been developed for the statistical analysis of untyped SNPs. In particular, de Bakker et al. [2005#x0005D;, Nicolae [2006], and Zaitlen et al. [2007] used the haplotype frequencies of tag SNPs to estimate the allele frequencies of the untyped SNP for cases and controls. This strategy, although simple and intuitive, is not statistically efficient and is confined to case-control comparisons without environmental factors.

In a similar spirit of tagging, Lin et al. [2008] proposed a likelihood-based method for the analysis of untyped SNPs in case-control studies with or without environmental factors. The likelihood integrates the study data and external data while reflecting the biased sampling nature of the case-control design. This method yields consistent and efficient estimators of genetic effects and gene-environment interactions, and the variance estimators fully account for the uncertainties in inferring the unknown variants.

A simpler approach is to impute the unknown values of the untyped SNPs for each subject and then use the imputed values in a downstream association analysis. Statistically speaking, this two-stage strategy, which is called single imputation in the missing data literature, is less satisfactory than the maximum likelihood because of its bias and inefficiency [Little, 1992]. However, single imputation has a practical advantage: once the missing data are imputed, the association analysis can be readily carried out (for any traits and study designs) in standard software packages.

Given the operational convenience of (single) imputation and the statistical optimality of maximum likelihood, comprehensive comparisons of these two approaches are sorely needed. This article provides such comparisons under cross-sectional and case-control designs. We expand the approach of Lin et al. [2008] to encompass both cross-sectional and case-control studies. In addition, we develop a tagging-based imputation strategy. We establish the theoretical properties of the proposed imputation method and conduct extensive simulation studies to evaluate the performance of the imputation and maximum-likelihood methods in testing/estimating genetic effects and gene-environment interactions. We apply the two methods to the GWAS data from the Wellcome Trust Case-Control Consortium (WTCCC).

METHODS

IMPUTATION

Suppose that we are interested in a particular untyped SNP, whose genotype is denoted by G_u. Let Y denote the phenotype of interest, which can be quantitative or qualitative. Also, let X denote a set of environmental factors. We characterize the effects of genetic and environmental factors on the phenotype through the conditional density function P_α,β,ξ(Y|G_u, W), where W consists of X and the genotypes of the typed SNPs, and α, β and ξ pertain to the intercept, regression parameters, and nuisance parameters (e.g. error variance), respectively. (If we are interested in the marginal effect of G_u, then W is an empty set.) We formulate P_α,β,ξ(Y|G_u, W) through a generalized linear regression model with linear predictor α+β^T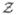(G_u, W), where 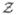(G_u, W) is a vector-function of G_u and W under a particular mode of inheritance. We assume the additive mode of inheritance in this article, although all the formulas can be easily modified to accommodate other modes of inheritance. For a quantitative trait, we specify the linear regression model:

$$Y=\alpha +{\mathbf{\beta }}^{\text{T}}\mathcal{Z}(G_u,\mathbf{W})+\epsilon ,$$

where ε is zero-mean normal with variance σ². For a binary trait, it is natural to use the logistic regression model:

$$Pr(Y=1\mid G_u,\mathbf{W})=\frac{{\text{e}}^{\alpha +{\mathbf{\beta }}^{\text{T}}\mathcal{Z}(G_u,\mathbf{W})}}{1+{\text{e}}^{\alpha +{\mathbf{\beta }}^{\text{T}}\mathcal{Z}(G_u,\mathbf{W})}}.$$ (1)

We use the LD information from a reference panel to select a set of (M−1) typed SNPs that provides the most accurate prediction of the untyped SNP, where M is a small number, which is set to five in this article. The accuracy of prediction is measured by R² of Stram [2004]. The M-locus genotype G consists of G_u and G_t, where G_t is the genotype of the (M−1) typed SNPs. Suppose that the M SNPs have a total of K haplotypes. For k = 1, …, K, let h_k denote the kth haplotype, and π_k denotes the frequency of h_k. Assume that the Hardy-Weinberg equilibrium (HWE) holds. For a reference panel of ñ trios, the likelihood for π = (π₁, …, π_K)^T is

$$L_R(\mathbf{\pi })=\prod _{j=1}^{\stackrel{\sim }{n}}\sum _{(h_k,h_l,h_{k^{\prime }},h_{l^{\prime }})\sim G_j}{\pi }_k{\pi }_l{\pi }_{k^{\prime }}{\pi }_{l^{\prime }},$$ (2)

where G_j = (GF_j, GM_j, GC_j) is the genotype data for the jth trio with the M-locus genotypes GF_j, GM_j and GC_j for the father, mother and child, respectively, and (h_k, h_l, h_k′, h_l′) ~ G_j means that (h_k, h_l) is compatible with GF_j, (h_k′, h_l′) is compatible with GM_j, and (h_k, h_k′), (h_k, h_l′), (h_l, h_k′), or (h_l, h_l′) is compatible with GC_j.

By maximizing L_R(π) given in Equation (2) via the EM algorithm, we obtain the maximum-likelihood estimator (MLE) π̃ = (π̃₁, …, π̃_K)^T. Assuming that the haplotype frequencies are the same between the study population and the external panel, we can estimate the probability distribution of G_u from the observed values of G_t for each study subject according to the formula

$$Pr(G_u=g\mid G_t;\stackrel{\sim }{\mathbf{\pi }})=\frac{{\sum }_{(h_k,h_l)\sim (G_t,G_u=g)}{\stackrel{\sim }{\pi }}_k{\stackrel{\sim }{\pi }}_l}{{\sum }_{g^{\prime }=0,1,2}{\sum }_{(h_k,h_l)\sim (G_t,G_u=g^{\prime })}{\stackrel{\sim }{\pi }}_k{\stackrel{\sim }{\pi }}_l},g=0,1,2,$$ (3)

where (h_k, h_l) ~ (G_t, G_u = g) means that (h_k, h_l) is compatible with (G_t, G_u = g). We use this (estimated) probability distribution to impute the unknown value of G_u, either as the expected count (i.e. dosage) or the most likely value of G_u. We replace the unknown values of G_u by the imputed values for all study subjects to create a “complete” data set, which is then analyzed by standard regression methods.

In the Appendix A, we prove that the above imputation method yields a valid test of the null hypothesis H₀:β_G = 0 under the linear predictor $\alpha +{\beta }_{G_u}{G}_u+{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}}\mathbf{W}$, where β_Gu and β_W pertain to the effects of G_u and W, respectively, provided that G_t is independent of Y conditional on W. This result holds for both cross-sectional and case-control studies, even when the reference panel and the study sample are drawn from different underlying populations. However, the estimator of β_Gu is generally biased with underestimated variance when β_Gu ≠ 0, and type I error may not be properly controlled for other hypotheses.

MAXIMUM LIKELIHOOD

Let H denote the diplotype associated with the M-locus genotype G. We write H = (h_k, h_l) if the diplotype consists of haplotypes h_k and h_l. In the previous subsection, we formulate the effects of G and X through the conditional density function P_α,β,ξ(Y|G_u, W), where W consists of G_t and X. In this subsection, we represent the same regression model in the form of P_α,β,ξ(Y|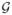(h_k, h_l), X), where 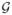(h_k, h_l) denote the genotype G induced by the diplotype (h_k, h_l). We assume that H and X are independent.

Let n denote the total number of study subjects. For i = 1, …, n, let Y_i, G_ti, and X_i denote the values of Y, G_t, and X on the ith subject. For a cross-sectional study, the likelihood for θ = (α, β^T, ξ^T)^T and π takes the form

$$L_S(\mathbf{\theta },\mathbf{\pi })=\prod _{i=1}^n\sum _{(h_k,h_l)\sim G_{ti}}{P}_{\alpha ,\mathbf{\beta },\mathbf{\xi }}(Y_i\mid \mathcal{G}(h_k,h_l),{\mathbf{X}}_i){\pi }_k{\pi }_l$$ (4)

where (h_k, h_l) ~ G_ti means that the diplotype (h_k, h_l) is compatible with genotype G_ti.

For case-control studies, we assume the logistic regression model given in (1) with the linear predictor α+β^T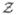((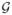h_k, h_l), X). Because the sampling is conditional on the case-control status, the likelihood takes the retrospective form ${\prod }_{i=1}^{n}P(G_{ti},{\mathbf{X}}_i\mid Y_i)$. If there are no environmental factors and the disease is rare, then this likelihood becomes

$$L_S(\mathbf{\theta },\mathbf{\pi })=\prod _{i=1}^n\frac{{\sum }_{(h_k,h_l)\sim G_{ti}}{\text{e}}^{Y_i{\mathbf{\beta }}^{\text{T}}\mathcal{Z}(\mathcal{G}(h_k,h_l))}{\pi }_k{\pi }_l}{{\sum }_{k,l}{\text{e}}^{Y_i{\mathbf{\beta }}^{\text{T}}\mathcal{Z}(G(h_k,h_l))}{\pi }_k{\pi }_l}$$ (5)

where θ = β. In the presence of X, the retrospective likelihood involves the unknown distribution of X, which is high-dimensional. We eliminate the distribution of X by the profile-likelihood approach [Lin and Zeng, 2006] and replace (5) with the following profile likelihood:

$$L_S(\mathbf{\theta },\mathbf{\pi })=\prod _{i=1}^n\frac{{\sum }_{(h_k,h_l)\sim G_{ti}}{\text{e}}^{Y_i\{\mu +{\mathbf{\beta }}^{\text{T}}\mathcal{Z}(\mathcal{G}(h_k,h_l),{\mathbf{X}}_i)\}}{\pi }_k{\pi }_l}{{\sum }_{k,l,y}{\text{e}}^{y\{\mu +{\mathbf{\beta }}^{\text{T}}\mathcal{Z}(\mathcal{G}(h_k,h_l),{\mathbf{X}}_i)\}}{\pi }_k{\pi }_l},$$

where θ = (μ,β^T)^T, μ is an unknown constant, and the summation in the denominator is taken over k, l = 1, …, K and y = 0,1.

The likelihood that combines the study data and the reference panel is L_C(θ,π) = L_S(θ,π)L_R(π), where L_R(π) is given in Equation (2). We maximize this combined likelihood via the Newton-Raphson algorithm. We set the initial value of π at π̃, the maximizer of L_R(π). To improve numerical stabilities, we exclude the haplotypes whose estimated frequencies are 0 or very close to 0, i.e. less than max(2/n, 0.001). The MLE of (θ, π) is consistent, asymptotically normal, and asymptotically efficient.

Note that the likelihood for case-control studies was previously given in Lin et al. [2008] and is reformulated in this section to conform with the notation for the imputation method. The likelihood for cross-sectional studies is new.

RESULTS

SIMULATION STUDIES

We carried out extensive simulation studies to evaluate the performance of the MLE and imputation methods in realistic settings. We generated genotype data for various sets of five SNPs according to the LD patterns observed in the HapMap CEU sample. For each SNP set, we chose one SNP to be untyped in the study data. For some SNP sets, we picked more than one SNP to be untyped, one at a time, each representing a different scenario. Table I lists the nine scenarios used in the simulation studies, with R² [Stram, 2004] ranging from 0.41 to 0.98.

TABLE I.

Haplotype frequencies for the scenarios used in simulation studies

Haplotype	S1: R2 = 0.41, MAF = 0.39		S2: R2 = 0.59, MAF = 0.28		S3: R2 = 0.70, MAF = 0.15
	UTTTT	Frequency	TTTUT	Frequency	TTUTT	Frequency
h1	00011	0.0513	00100	0.3171	00000	0.0513
h2	00100	0.0260	00101	0.0988	00100	0.1460
h3	01011	0.0855	00111	0.2027	01000	0.6958
h4	01100	0.3094	01001	0.1518	10011	0.1069
h5	01101	0.1377	10100	0.1059
h6	11011	0.0085	10101	0.0209
h7	11100	0.1775	10111	0.0793
h8	11101	0.0247	11001	0.0235
h9	11111	0.1794
Haplotype	S4: R2 = 0.81, MAF = 0.33		S5: R2 = 0.84, MAF = 0.24		S6: R2 = 0.93, MAF = 0.15
	UTTTT	Frequency	TTUTT	Frequency	TTUTT	Frequency
h1	00011	0.2846	01101	0.2852	00011	0.0513
h2	00101	0.0128	10100	0.2510	00100	0.0260
h3	00111	0.0342	11000	0.2393	01011	0.0855
h4	10101	0.2374	11100	0.0321	01100	0.3094
h5	10111	0.1917	11101	0.0963	01101	0.1377
h6	11110	0.2393	11110	0.0961	11011	0.0085
h7					11100	0.1775
h8					11101	0.0247
h9					11111	0.1794
Haplotype	S7: R2 = 0.95, MAF = 0.09		S8: R2 = 0.98, MAF = 0.28		S9: R2 = 0.98, MAF = 0.29
	UTTTT	Frequency	TTUTT	Frequency	TTTTU	Frequency
h1	00111	0.3809	01000	0.4231	01000	0.4231
h2	01110	0.2350	01010	0.1154	01010	0.1154
h3	01111	0.2900	01011	0.0043	01011	0.0043
h4	11001	0.0897	01111	0.2821	01111	0.2821
h5	11111	0.0044	10010	0.1751	10010	0.1751

“U” and “T” indicate the untyped and typed SNP positions, respectively. R² is the squared correlation between the expected and true allele counts [Stram, 2004]. MAF is the minor allele frequency of the untyped SNP.

We explored three types of association: (1) single-SNP effects, (2) gene-environment interactions, and (3) multi-SNP effects. For each type of model, we considered both cross-sectional and case-control designs. Since the case-control design naturally requires a binary trait, we focused on quantitative traits for cross-sectional studies. Thus, there were six series of simulation studies. For each setup, we simulated 10,000 data sets with 2,000 study subjects and 60 trios. Under the case-control design, we set the overall disease rate to be approximately 1% and selected an equal number of cases and controls. We chose 60 trios for the reference panel so as to approximate the CEU sample in the current version (i.e. phase 3) of the HapMap database, which consists of 44 trios, 8 duos, and 17 singletons. For each simulated data set, we applied the MLE and imputation approaches. For the latter approach, we imputed the unknown genotype by both the dosage and the most likely genotype, which are referred to as the IMP-DOS and IMP-MLG methods, respectively. All the analysis was based on the Wald statistic.

Our first series of simulation studies was concerned with the (marginal) effect of an untyped SNP on a quantitative trait in a cross-sectional study. We generated the trait value from the linear regression model

$$Y=\alpha +\beta G_u+\epsilon ,$$

where ε is standard normal and α = 0. Table II displays the results for various values of β. As expected, the MLE is virtually unbiased in all cases. IMP-DOS also shows negligible bias, which is not surprising because conditional mean imputation is known to yield consistent estimators of regression parameters under the linear model [Little, 1992]. The estimator of β produced by IMP-MLG is seriously biased toward zero and the bias can be as much as 25% of the true parameter value. For non-zero β, both IMP-DOS and IMP-MLG tend to underestimate the variances, so their confidence intervals have poor coverage probabilities. Under scenario S8, in which R² = 0.98, the coverage probability of the 99% confidence interval of IMP-DOS is only 98% when β = 0.9. IMP-MLG is much worse than IMP-DOS because it suffers from both biased estimation of parameter and underestimation of variance; see S1–S3. As predicted by our theory, both IMP-DOS and IMP-MLG have appropriate type I error. In some cases (i.e. S2, S3, and S5), IMP-DOS is slightly more powerful than MLE. This phenomenon is attributed to the underestimation of variance by IMP-DOS. When R² is large (e.g. S7–S9), all methods have the same power.

TABLE II.

Simulation results for studying the effect of an untyped SNP on a quantitative trait under the cross-sectional design

	β	MLE					IMP-DOS					IMP-MLG
		Bias	SE	SEE	CP	PW	Bias	SE	SEE	CP	PW	Bias	SE	SEE	CP	PW
S1	0.0	0.000	0.051	0.051	0.989	0.011	0.000	0.051	0.051	0.990	0.010	0.000	0.041	0.041	0.989	0.011
	0.1	0.000	0.051	0.051	0.990	0.274	−0.001	0.051	0.051	0.990	0.267	−0.031	0.041	0.041	0.965	0.190
	0.2	0.000	0.052	0.051	0.990	0.905	−0.002	0.051	0.051	0.990	0.903	−0.062	0.042	0.041	0.857	0.781
	0.6	0.000	0.053	0.052	0.990	1.00	−0.007	0.056	0.053	0.987	1.00	−0.185	0.047	0.043	0.063	1.00
	0.9	−0.002	0.054	0.052	0.988	1.00	−0.010	0.061	0.056	0.982	1.00	−0.277	0.053	0.046	0.001	1.00
S2	0.0	0.000	0.046	0.046	0.991	0.009	0.000	0.046	0.046	0.990	0.010	0.000	0.036	0.036	0.991	0.009
	0.1	0.000	0.046	0.047	0.991	0.325	0.000	0.046	0.046	0.990	0.336	−0.026	0.036	0.036	0.965	0.309
	0.2	0.000	0.048	0.048	0.992	0.960	0.000	0.048	0.046	0.988	0.963	−0.051	0.038	0.036	0.843	0.937
	0.6	0.001	0.057	0.057	0.988	1.00	−0.001	0.061	0.047	0.954	1.00	−0.154	0.048	0.037	0.151	1.00
	0.9	0.000	0.060	0.060	0.985	1.00	−0.001	0.077	0.049	0.903	1.00	−0.231	0.060	0.038	0.059	1.00
S3	0.0	0.000	0.055	0.054	0.992	0.008	0.000	0.055	0.054	0.991	0.009	0.000	0.041	0.041	0.990	0.010
	0.1	0.000	0.055	0.055	0.992	0.217	0.001	0.055	0.054	0.989	0.237	−0.025	0.041	0.041	0.977	0.233
	0.2	0.001	0.057	0.057	0.991	0.856	0.001	0.058	0.054	0.986	0.871	−0.050	0.042	0.041	0.907	0.863
	0.6	0.001	0.070	0.070	0.987	1.00	0.004	0.078	0.055	0.936	1.00	−0.149	0.046	0.041	0.172	1.00
	0.9	0.000	0.074	0.073	0.987	1.00	0.006	0.100	0.056	0.863	1.00	−0.224	0.051	0.042	0.033	1.00
S4	0.0	0.000	0.037	0.037	0.989	0.011	0.000	0.037	0.037	0.989	0.011	0.000	0.035	0.035	0.989	0.011
	0.1	0.000	0.037	0.037	0.989	0.544	0.000	0.037	0.037	0.989	0.544	−0.007	0.035	0.035	0.986	0.540
	0.2	0.000	0.038	0.037	0.989	0.998	−0.001	0.037	0.037	0.988	0.998	−0.013	0.035	0.035	0.983	0.997
	0.6	0.000	0.038	0.038	0.988	1.00	−0.002	0.039	0.038	0.986	1.00	−0.039	0.036	0.036	0.929	1.00
	0.9	0.000	0.039	0.038	0.989	1.00	−0.003	0.041	0.038	0.984	1.00	−0.059	0.036	0.036	0.829	1.00
S5	0.0	0.000	0.041	0.040	0.991	0.009	0.000	0.041	0.040	0.991	0.009	0.000	0.036	0.036	0.991	0.009
	0.1	0.000	0.041	0.041	0.991	0.456	0.000	0.041	0.040	0.990	0.463	−0.012	0.036	0.036	0.985	0.463
	0.2	0.001	0.042	0.042	0.991	0.991	0.001	0.042	0.040	0.988	0.991	−0.023	0.036	0.036	0.971	0.991
	0.6	0.001	0.048	0.048	0.988	1.00	0.001	0.050	0.041	0.966	1.00	−0.071	0.036	0.036	0.722	1.00
	0.9	0.001	0.052	0.051	0.987	1.00	0.002	0.060	0.041	0.929	1.00	−0.106	0.037	0.036	0.365	1.00
S6	0.0	0.000	0.050	0.050	0.990	0.010	0.000	0.050	0.050	0.990	0.010	0.000	0.048	0.047	0.990	0.010
	0.1	0.000	0.050	0.050	0.990	0.286	0.000	0.050	0.050	0.990	0.284	−0.008	0.048	0.047	0.988	0.266
	0.2	0.000	0.050	0.050	0.990	0.919	−0.001	0.050	0.050	0.990	0.918	−0.015	0.048	0.047	0.985	0.904
	0.6	0.000	0.050	0.050	0.990	1.00	−0.003	0.050	0.050	0.990	1.00	−0.046	0.048	0.048	0.943	1.00
	0.9	0.000	0.050	0.049	0.989	1.00	−0.004	0.051	0.051	0.991	1.00	−0.069	0.049	0.049	0.876	1.00
S7	0.0	0.000	0.056	0.056	0.990	0.010	0.000	0.056	0.056	0.990	0.010	0.000	0.055	0.055	0.990	0.010
	0.1	0.000	0.056	0.056	0.990	0.215	0.000	0.056	0.056	0.990	0.214	0.000	0.055	0.055	0.990	0.215
	0.2	0.000	0.056	0.056	0.990	0.844	0.000	0.056	0.056	0.990	0.844	−0.001	0.055	0.055	0.990	0.845
	0.6	0.000	0.056	0.056	0.990	1.00	0.000	0.056	0.056	0.990	1.00	−0.003	0.055	0.055	0.990	1.00
	0.9	0.000	0.056	0.056	0.990	1.00	0.000	0.056	0.056	0.990	1.00	−0.004	0.056	0.056	0.990	1.00
S8	0.0	0.000	0.036	0.036	0.990	0.010	0.000	0.036	0.036	0.990	0.010	0.000	0.035	0.035	0.990	0.010
	0.1	0.000	0.036	0.036	0.990	0.590	0.000	0.036	0.036	0.990	0.590	−0.002	0.035	0.035	0.991	0.590
	0.2	0.000	0.036	0.036	0.991	0.999	0.000	0.036	0.036	0.990	0.999	−0.003	0.035	0.035	0.991	0.999
	0.6	0.000	0.037	0.037	0.990	1.00	0.000	0.037	0.036	0.987	1.00	−0.009	0.035	0.035	0.988	1.00
	0.9	0.000	0.038	0.038	0.989	1.00	0.000	0.038	0.036	0.982	1.00	−0.014	0.035	0.035	0.984	1.00
S9	0.0	0.000	0.036	0.035	0.990	0.010	0.000	0.036	0.035	0.990	0.010	0.000	0.035	0.035	0.990	0.010
	0.1	0.000	0.036	0.035	0.990	0.599	0.000	0.036	0.035	0.990	0.599	−0.001	0.035	0.035	0.990	0.598
	0.2	0.000	0.036	0.035	0.990	0.999	0.000	0.036	0.035	0.990	0.999	−0.001	0.035	0.035	0.990	0.999
	0.6	0.000	0.036	0.035	0.990	1.00	0.000	0.036	0.035	0.990	1.00	−0.004	0.035	0.035	0.991	1.00
	0.9	−0.001	0.036	0.035	0.990	1.00	−0.001	0.036	0.035	0.989	1.00	−0.005	0.035	0.035	0.990	1.00

S1–S9 denote the nine scenarios listed in Table I. Bias and SE are the bias and standard error of the parameter estimator. SEE is the mean of the standard error estimator. CP is the coverage probability of the 99% confidence interval. PW is the type I error/power for testing zero parameter value at the 0.01 nominal significance level. Each entry is based on 10,000 replicates.

In our second series of studies, we simulated case-control data under the logistic regression model

$$Pr(Y=1\mid G_u)=\frac{{\text{e}}^{\alpha +\beta G_u}}{1+{\text{e}}^{\alpha +\beta G_u}},$$

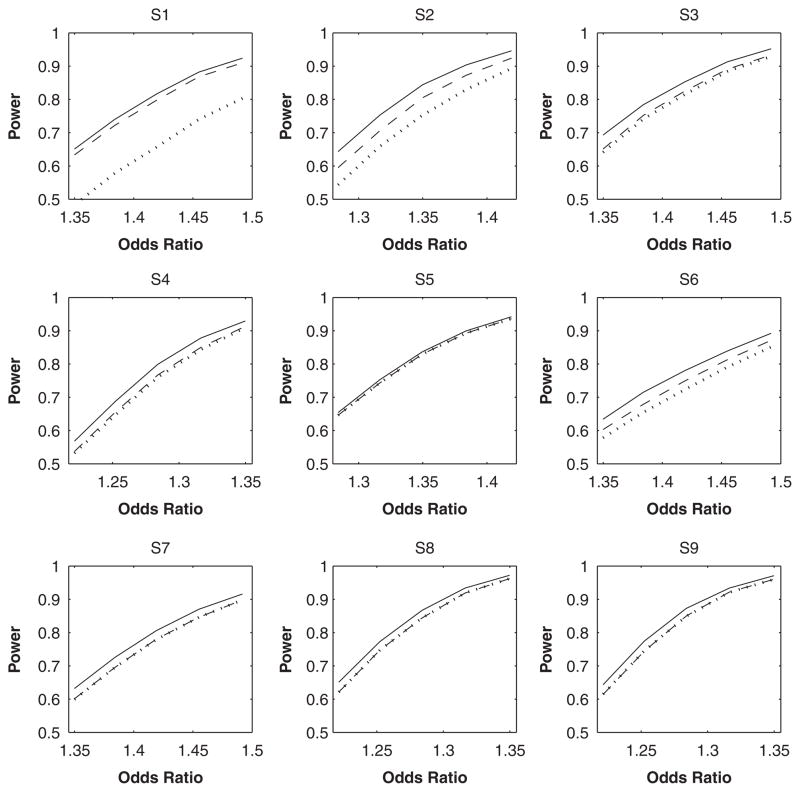
where α was set to −4.6 to yield disease rates of approximately 1%. The results are summarized in Table III. Unlike linear regression, IMP-DOS can produce substantial bias under logistic regression; see S1–S3 and S5. MLE is now uniformly more powerful than both IMP-DOS and IMP-MLG; this feature can be seen more clearly in Figure 1. The power gain of MLE over imputation persists as R² approaches 1 because MLE exploits the HWE assumption, whereas imputation does not. When R² is low, the bias of imputation (under non-linear models) also affects its power. Again, all three methods have accurate control of type I error. As in cross-sectional studies, both IMP-DOS and IMP-MLG tend to underestimate the variances (for non-zero β) and thus yield poor confidence interval coverage, especially when β is large and R² is low.

TABLE III.

Simulation results for studying the effect of an untyped SNP on the risk of disease under the case-control design

	β	MLE					IMP-DOS					IMP-MLG
		Bias	SE	SEE	CP	PW	Bias	SE	SEE	CP	PW	Bias	SE	SEE	CP	PW
S1	0.0	0.001	0.100	0.099	0.989	0.011	0.001	0.101	0.101	0.990	0.010	0.001	0.082	0.082	0.990	0.010
	0.3	0.000	0.103	0.101	0.990	0.651	−0.010	0.101	0.100	0.989	0.633	−0.093	0.082	0.081	0.922	0.483
	0.6	0.000	0.108	0.106	0.989	0.999	−0.031	0.102	0.099	0.984	0.999	−0.190	0.082	0.081	0.580	0.993
	0.9	−0.008	0.115	0.113	0.986	1.00	−0.070	0.104	0.100	0.961	1.00	−0.297	0.083	0.082	0.156	1.00
S2	0.0	−0.002	0.091	0.090	0.991	0.009	−0.001	0.093	0.092	0.989	0.011	−0.001	0.073	0.072	0.988	0.012
	0.3	0.000	0.085	0.084	0.989	0.844	0.012	0.094	0.091	0.987	0.805	−0.067	0.075	0.072	0.934	0.753
	0.6	−0.002	0.084	0.082	0.990	1.00	0.046	0.103	0.092	0.971	1.00	−0.117	0.083	0.073	0.757	1.00
	0.9	−0.009	0.084	0.083	0.989	1.00	0.093	0.115	0.094	0.919	1.00	−0.157	0.097	0.075	0.566	1.00
S3	0.0	−0.002	0.106	0.106	0.992	0.008	−0.001	0.109	0.108	0.989	0.011	0.000	0.082	0.082	0.989	0.011
	0.3	−0.001	0.099	0.098	0.991	0.693	0.012	0.110	0.105	0.987	0.651	−0.067	0.081	0.079	0.953	0.641
	0.6	0.000	0.096	0.096	0.990	1.00	0.047	0.120	0.103	0.969	1.00	−0.116	0.082	0.078	0.841	1.00
	0.9	−0.003	0.096	0.097	0.989	1.00	0.096	0.136	0.103	0.915	1.00	−0.153	0.087	0.078	0.682	1.00
S4	0.0	0.000	0.073	0.073	0.990	0.010	0.000	0.075	0.074	0.989	0.011	0.000	0.071	0.070	0.989	0.011
	0.3	0.001	0.075	0.074	0.990	0.929	0.002	0.078	0.077	0.990	0.913	−0.016	0.074	0.073	0.986	0.909
	0.6	0.000	0.077	0.077	0.989	1.00	0.007	0.082	0.081	0.990	1.00	−0.028	0.077	0.077	0.984	1.00
	0.9	−0.006	0.082	0.081	0.990	1.00	0.011	0.088	0.087	0.989	1.00	−0.039	0.083	0.082	0.979	1.00
S5	0.0	0.000	0.079	0.079	0.989	0.011	0.000	0.082	0.081	0.989	0.011	0.000	0.072	0.071	0.989	0.011
	0.3	0.001	0.086	0.087	0.990	0.837	−0.005	0.085	0.084	0.988	0.830	−0.040	0.074	0.074	0.977	0.830
	0.6	0.002	0.103	0.102	0.989	1.00	−0.023	0.093	0.088	0.980	1.00	−0.092	0.078	0.077	0.912	1.00
	0.9	0.009	0.130	0.127	0.988	1.00	−0.051	0.102	0.093	0.961	1.00	−0.154	0.082	0.081	0.744	1.00
S6	0.0	0.000	0.096	0.097	0.991	0.009	0.000	0.100	0.100	0.991	0.009	0.000	0.095	0.095	0.991	0.009
	0.3	0.001	0.102	0.103	0.990	0.634	0.000	0.105	0.106	0.989	0.603	−0.022	0.100	0.101	0.989	0.578
	0.6	−0.002	0.112	0.112	0.989	0.999	−0.007	0.114	0.114	0.990	0.997	−0.049	0.108	0.108	0.981	0.996
	0.9	−0.004	0.122	0.121	0.989	1.00	−0.014	0.125	0.123	0.987	1.00	−0.077	0.118	0.117	0.964	1.00
S7	0.0	0.000	0.109	0.108	0.991	0.009	0.000	0.112	0.111	0.992	0.008	0.000	0.112	0.111	0.992	0.008
	0.3	−0.001	0.103	0.102	0.989	0.632	−0.001	0.106	0.106	0.991	0.601	−0.002	0.106	0.105	0.991	0.599
	0.6	0.000	0.097	0.098	0.990	1.00	0.001	0.102	0.102	0.990	1.00	−0.002	0.101	0.101	0.990	1.00
	0.9	−0.003	0.096	0.095	0.989	1.00	−0.001	0.101	0.100	0.989	1.00	−0.005	0.100	0.099	0.989	1.00
S8	0.0	0.000	0.070	0.069	0.989	0.011	0.000	0.072	0.071	0.989	0.011	0.000	0.071	0.070	0.989	0.011
	0.3	0.000	0.066	0.067	0.990	0.972	0.002	0.069	0.070	0.990	0.962	−0.003	0.068	0.069	0.989	0.962
	0.6	−0.001	0.066	0.066	0.990	1.00	0.004	0.071	0.070	0.990	1.00	−0.006	0.069	0.069	0.989	1.00
	0.9	−0.006	0.066	0.066	0.990	1.00	0.005	0.072	0.071	0.990	1.00	−0.008	0.070	0.070	0.991	1.00
S9	0.0	0.000	0.069	0.069	0.988	0.012	0.000	0.071	0.071	0.989	0.011	0.000	0.071	0.070	0.989	0.011
	0.3	0.000	0.067	0.067	0.992	0.971	0.000	0.069	0.069	0.991	0.960	−0.001	0.069	0.069	0.991	0.960
	0.6	−0.002	0.066	0.066	0.991	1.00	−0.001	0.069	0.069	0.992	1.00	−0.004	0.069	0.069	0.992	1.00
	0.9	−0.007	0.067	0.066	0.989	1.00	−0.002	0.072	0.071	0.989	1.00	−0.007	0.071	0.070	0.988	1.00

S1–S9 denote the nine scenarios listed in Table I. Bias and SE are the bias and standard error of the parameter estimator. SEE is the mean of the standard error estimator. CP is the coverage probability of the 99% confidence interval. PW is the type I error/power for testing zero parameter value at the 0.01 nominal significance level. Each entry is based on 10,000 replicates.

Fig. 1.

Power of testing the effect of an untyped SNP at the 1% nominal significance level under the case-control design. The solid, dashed, and dotted curves pertain to MLE, IMP-DOS and IMP-MLG, respectively. SNP, single nucleotide polymorphism; MLE, maximum-likelihood estimator.

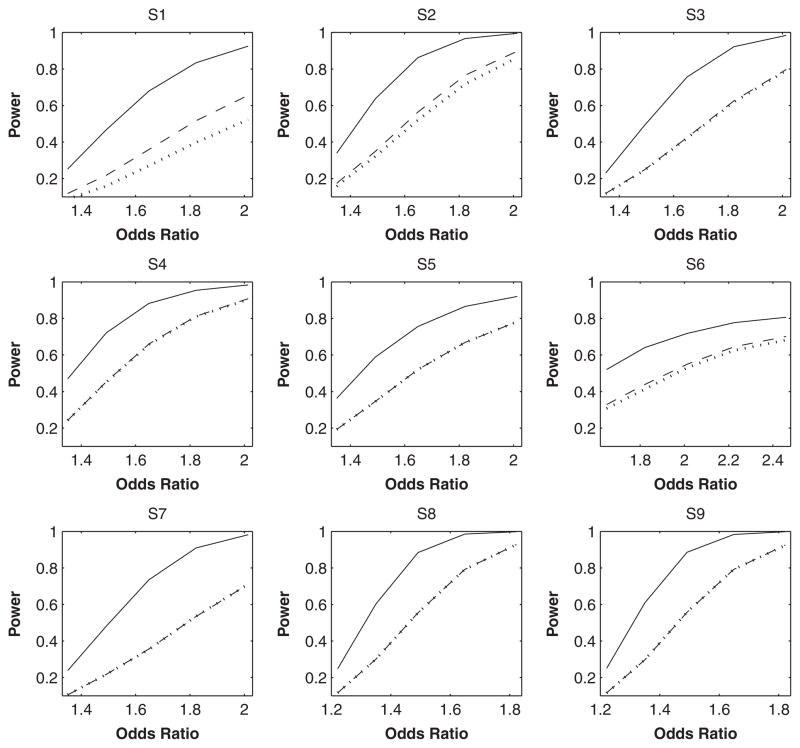
Our third and fourth series of studies were focused on gene-environment interactions under the cross-sectional and case-control designs, respectively. We generated data from the same models as in the first two series but with the linear predictors α+β₁G_u+β₂X+β₃G_uX, where X is Bernoulli with Pr(X = 1) = 0.4. The results for cross-sectional studies are displayed in Table IV. For detecting interactions, both IMP-DOS and IMP-MLG produce confidence intervals with poor coverage probabilities, especially when the effects are large and the LD is low; see S1–S6. Both may lose control of type I error and are substantially less powerful than MLE. The power gain of MLE is largely attributed to its incorporation of gene-environment independence. The power difference decreases as R² increases. In the extreme case of R² = 1, the summation in (4) disappears and MLE is equivalent to imputation. The results for case-control studies are shown in Table V. Both imputation methods yield biased estimates, poor confidence interval coverage, and diminished power. The power difference between MLE and imputation is further illustrated in Figure 2. The power gain of MLE is again largely attributed to its use of gene-environment independence. If we analyzed the imputed genotypes (either the dosage or the most likely genotype) by the method of Chatterjee and Carroll [2005], which also exploits gene-environment independence, then the power gain of MLE was reduced considerably (results not shown).

TABLE IV.

Simulation results for studying gene-environment interactions under the cross-sectional design with a quantitative trait

	β1	β3	MLE					IMP-DOS					IMP-MLG
			Bias	SE	SEE	CP	PW	Bias	SE	SEE	CP	PW	Bias	SE	SEE	CP	PW
S1	0.5	0.0	0.000	0.097	0.096	0.990	0.010	−0.002	0.107	0.107	0.991	0.009	−0.001	0.087	0.087	0.990	0.010
	0.5	0.2	0.000	0.095	0.094	0.990	0.328	−0.004	0.108	0.109	0.991	0.210	−0.063	0.088	0.089	0.970	0.150
	0.5	0.3	0.000	0.094	0.093	0.990	0.740	−0.005	0.108	0.111	0.992	0.531	−0.094	0.089	0.090	0.943	0.385
	0.5	0.9	0.000	0.092	0.091	0.990	1.00	−0.012	0.115	0.121	0.993	1.00	−0.279	0.098	0.100	0.409	1.00
	1.2	0.0	0.000	0.085	0.084	0.991	0.009	−0.002	0.116	0.123	0.994	0.006	−0.001	0.099	0.102	0.992	0.008
S2	0.5	0.0	−0.001	0.092	0.092	0.991	0.009	−0.002	0.097	0.096	0.990	0.010	−0.001	0.076	0.075	0.991	0.009
	0.5	0.2	−0.001	0.092	0.091	0.990	0.352	−0.002	0.098	0.097	0.989	0.303	−0.053	0.077	0.076	0.964	0.273
	0.5	0.3	−0.001	0.092	0.091	0.990	0.763	−0.002	0.100	0.098	0.989	0.682	−0.078	0.078	0.076	0.926	0.633
	0.5	0.9	−0.001	0.091	0.090	0.991	1.00	−0.003	0.118	0.103	0.977	1.00	−0.232	0.092	0.081	0.377	1.00
	1.2	0.0	0.000	0.087	0.087	0.989	0.011	−0.002	0.107	0.105	0.989	0.011	−0.001	0.083	0.083	0.992	0.009
S3	0.5	0.0	0.000	0.110	0.110	0.991	0.009	0.000	0.113	0.112	0.989	0.011	0.000	0.085	0.084	0.989	0.011
	0.5	0.2	0.001	0.110	0.110	0.990	0.224	0.001	0.115	0.112	0.987	0.223	−0.050	0.086	0.085	0.974	0.218
	0.5	0.3	0.000	0.111	0.111	0.989	0.560	0.002	0.118	0.113	0.986	0.541	−0.075	0.087	0.085	0.951	0.533
	0.5	0.9	0.000	0.110	0.111	0.991	1.00	0.006	0.144	0.116	0.964	1.00	−0.224	0.094	0.087	0.487	1.00
	1.2	0.0	0.000	0.108	0.108	0.990	0.010	−0.001	0.124	0.116	0.984	0.017	0.000	0.093	0.088	0.984	0.016
S4	0.5	0.0	−0.001	0.077	0.076	0.988	0.012	−0.001	0.077	0.077	0.990	0.010	−0.001	0.073	0.072	0.989	0.011
	0.5	0.2	−0.001	0.077	0.076	0.988	0.516	−0.002	0.077	0.077	0.990	0.496	−0.014	0.073	0.073	0.988	0.488
	0.5	0.3	−0.001	0.077	0.076	0.988	0.913	−0.002	0.078	0.077	0.991	0.901	−0.021	0.073	0.073	0.987	0.895
	0.5	0.9	−0.001	0.076	0.075	0.988	1.00	−0.004	0.079	0.080	0.990	1.00	−0.060	0.074	0.076	0.966	1.00
	1.2	0.0	−0.001	0.076	0.075	0.988	0.012	−0.001	0.080	0.080	0.990	0.010	−0.001	0.076	0.076	0.990	0.010
S5	0.5	0.0	−0.001	0.084	0.083	0.990	0.011	−0.001	0.084	0.083	0.989	0.011	−0.001	0.074	0.073	0.989	0.011
	0.5	0.2	−0.001	0.084	0.083	0.989	0.432	−0.001	0.085	0.083	0.988	0.432	−0.025	0.075	0.073	0.985	0.432
	0.5	0.3	−0.001	0.085	0.084	0.989	0.842	−0.001	0.086	0.084	0.988	0.840	−0.036	0.075	0.074	0.978	0.840
	0.5	0.9	−0.001	0.085	0.084	0.989	1.00	0.000	0.097	0.085	0.978	1.00	−0.108	0.077	0.075	0.872	1.00
	1.2	0.0	−0.001	0.084	0.083	0.988	0.012	−0.001	0.089	0.086	0.987	0.013	−0.001	0.078	0.076	0.987	0.013
S6	0.5	0.0	−0.001	0.102	0.101	0.989	0.011	0.000	0.102	0.102	0.990	0.010	−0.001	0.097	0.098	0.990	0.010
	0.5	0.2	−0.001	0.102	0.101	0.989	0.277	−0.001	0.102	0.103	0.990	0.261	−0.016	0.098	0.098	0.990	0.245
	0.5	0.3	−0.001	0.101	0.101	0.989	0.649	−0.002	0.102	0.103	0.990	0.621	−0.024	0.098	0.098	0.989	0.591
	0.5	0.9	−0.001	0.101	0.100	0.989	1.00	−0.005	0.103	0.105	0.991	1.00	−0.070	0.099	0.100	0.973	1.00
	1.2	0.0	−0.001	0.099	0.099	0.989	0.011	0.000	0.103	0.105	0.991	0.009	−0.001	0.100	0.101	0.991	0.009
S7	0.5	0.0	−0.002	0.114	0.114	0.991	0.009	−0.002	0.114	0.114	0.991	0.009	−0.002	0.114	0.113	0.991	0.009
	0.5	0.2	−0.002	0.114	0.114	0.991	0.202	−0.002	0.114	0.114	0.991	0.202	−0.003	0.114	0.113	0.991	0.201
	0.5	0.3	−0.002	0.114	0.114	0.990	0.515	−0.002	0.114	0.114	0.991	0.512	−0.004	0.114	0.113	0.991	0.512
	0.5	0.9	−0.004	0.114	0.114	0.990	1.00	−0.003	0.114	0.114	0.991	1.00	−0.007	0.114	0.114	0.991	1.00
	1.2	0.0	−0.002	0.114	0.114	0.990	0.010	−0.002	0.115	0.114	0.991	0.009	−0.002	0.114	0.114	0.991	0.009
S8	0.5	0.0	0.001	0.073	0.073	0.989	0.011	0.001	0.074	0.073	0.989	0.011	0.001	0.072	0.072	0.989	0.011
	0.5	0.2	0.001	0.074	0.073	0.989	0.572	0.001	0.074	0.073	0.989	0.572	−0.002	0.072	0.072	0.989	0.572
	0.5	0.3	0.001	0.074	0.073	0.989	0.939	0.001	0.074	0.073	0.990	0.939	−0.004	0.072	0.072	0.989	0.939
	0.5	0.9	−0.001	0.074	0.073	0.989	1.00	0.001	0.075	0.073	0.989	1.00	−0.013	0.073	0.072	0.987	1.00
	1.2	0.0	0.001	0.074	0.073	0.990	0.011	0.001	0.074	0.073	0.989	0.011	0.001	0.073	0.072	0.989	0.011
S9	0.5	0.0	0.001	0.073	0.072	0.990	0.010	0.001	0.073	0.072	0.990	0.010	0.001	0.073	0.072	0.990	0.010
	0.5	0.2	0.001	0.073	0.072	0.990	0.579	0.001	0.073	0.072	0.990	0.577	0.000	0.073	0.072	0.990	0.577
	0.5	0.3	0.000	0.073	0.072	0.990	0.943	0.001	0.073	0.072	0.990	0.942	−0.001	0.073	0.072	0.990	0.943
	0.5	0.9	−0.001	0.073	0.072	0.990	1.00	0.000	0.073	0.073	0.990	1.00	−0.005	0.073	0.072	0.989	1.00
	1.2	0.0	0.001	0.073	0.072	0.990	0.010	0.001	0.073	0.073	0.990	0.011	0.001	0.073	0.072	0.990	0.010

β₂ = 0.2. S1–S9 denote the nine scenarios listed in Table I. Bias and SE are the bias and standard error of the parameter estimator. SEE is the mean of the standard error estimator. CP is the coverage probability of the 99% confidence interval. PW is the type I error/power for testing zero parameter value at the 0.01 nominal significance level. Each entry is based on 10,000 replicates.

TABLE V.

Simulation results for studying gene-environment interactions under the case-control design

	β3	MLE					IMP-DOS					IMP-MLG
		Bias	SE	SEE	CP	PW	Bias	SE	SEE	CP	PW	Bias	SE	SEE	CP	PW
S1	0.0	0.000	0.151	0.149	0.990	0.010	−0.002	0.210	0.209	0.990	0.010	−0.002	0.169	0.169	0.991	0.009
	0.5	−0.008	0.165	0.163	0.988	0.679	−0.021	0.218	0.216	0.988	0.359	−0.157	0.175	0.175	0.952	0.270
	0.9	−0.025	0.188	0.187	0.987	0.985	−0.065	0.233	0.231	0.985	0.859	−0.295	0.187	0.187	0.840	0.751
S2	0.0	0.000	0.136	0.135	0.992	0.008	−0.001	0.189	0.189	0.991	0.009	−0.001	0.148	0.147	0.991	0.009
	0.5	−0.006	0.140	0.139	0.991	0.863	0.032	0.198	0.194	0.989	0.565	−0.103	0.157	0.152	0.965	0.521
	0.9	−0.023	0.153	0.153	0.989	1.00	0.098	0.216	0.204	0.978	0.990	−0.153	0.174	0.160	0.927	0.980
S3	0.0	0.002	0.162	0.160	0.992	0.008	0.001	0.226	0.223	0.991	0.009	0.000	0.170	0.168	0.990	0.010
	0.5	−0.002	0.160	0.158	0.990	0.756	0.034	0.232	0.223	0.987	0.424	−0.100	0.171	0.168	0.973	0.421
	0.9	−0.016	0.167	0.166	0.987	1.00	0.099	0.247	0.227	0.977	0.968	−0.152	0.177	0.171	0.948	0.967
S4	0.0	−0.002	0.110	0.109	0.988	0.012	−0.002	0.154	0.153	0.990	0.010	−0.002	0.145	0.144	0.990	0.010
	0.5	−0.011	0.130	0.129	0.989	0.882	0.004	0.169	0.169	0.990	0.660	−0.026	0.160	0.159	0.989	0.657
	0.9	−0.036	0.157	0.158	0.990	0.996	0.007	0.193	0.194	0.990	0.977	−0.044	0.182	0.183	0.989	0.977
S5	0.0	−0.001	0.118	0.118	0.992	0.008	0.001	0.166	0.166	0.991	0.009	0.001	0.146	0.146	0.991	0.009
	0.5	−0.011	0.150	0.150	0.991	0.756	−0.014	0.187	0.185	0.989	0.521	−0.072	0.163	0.163	0.982	0.521
	0.9	−0.031	0.200	0.199	0.991	0.963	−0.056	0.221	0.216	0.987	0.904	−0.157	0.191	0.190	0.965	0.904
S6	0.0	−0.003	0.146	0.146	0.990	0.010	−0.003	0.205	0.206	0.992	0.008	−0.003	0.196	0.195	0.993	0.007
	0.5	−0.017	0.186	0.185	0.991	0.521	−0.005	0.238	0.235	0.990	0.329	−0.041	0.226	0.223	0.988	0.307
	0.9	−0.049	0.243	0.241	0.993	0.806	−0.023	0.282	0.280	0.991	0.701	−0.087	0.268	0.266	0.989	0.682
S7	0.0	0.003	0.165	0.163	0.991	0.009	0.000	0.230	0.230	0.990	0.010	0.000	0.229	0.229	0.990	0.010
	0.5	−0.004	0.157	0.156	0.991	0.735	−0.001	0.227	0.226	0.988	0.356	−0.003	0.226	0.225	0.989	0.354
	0.9	−0.015	0.157	0.156	0.990	1.00	0.000	0.225	0.226	0.992	0.926	−0.004	0.224	0.225	0.991	0.926
S8	0.0	0.001	0.104	0.104	0.991	0.009	0.000	0.146	0.146	0.991	0.009	0.000	0.144	0.144	0.991	0.009
	0.5	−0.007	0.107	0.107	0.990	0.985	0.005	0.149	0.149	0.991	0.792	−0.003	0.147	0.147	0.991	0.792
	0.9	−0.025	0.116	0.116	0.986	1.00	0.008	0.159	0.157	0.989	0.999	−0.006	0.156	0.155	0.989	0.999
S9	0.0	0.001	0.104	0.103	0.991	0.009	0.000	0.146	0.145	0.990	0.010	0.000	0.145	0.145	0.990	0.010
	0.5	−0.007	0.108	0.107	0.989	0.983	0.002	0.148	0.149	0.989	0.792	−0.001	0.147	0.148	0.990	0.792
	0.9	−0.026	0.117	0.116	0.986	1.00	0.000	0.158	0.157	0.991	0.999	−0.006	0.157	0.156	0.990	0.999

β₁ = 0.0, β₂ = 0.1. S1–S9 denote the nine scenarios listed in Table I. Bias and SE are the bias and standard error of the parameter estimator. SEE is the mean of the standard error estimator. CP is the coverage probability of the 99% confidence interval. PW is the type I error/power for testing zero parameter value at the 0.01 nominal significance level. Each entry is based on 10,000 replicates.

Fig. 2.

Power of testing gene-environment interactions at the 1% nominal significance level under the case-control design. The solid, dashed, and dotted curves pertain to MLE, IMP-DOS and IMP-MLG, respectively. MLE, maximum-likelihood estimator.

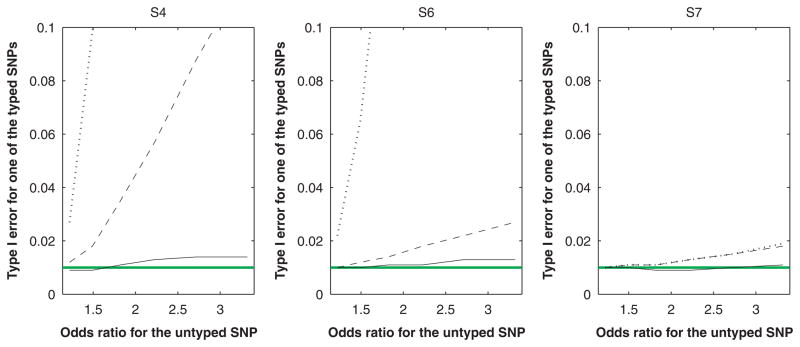
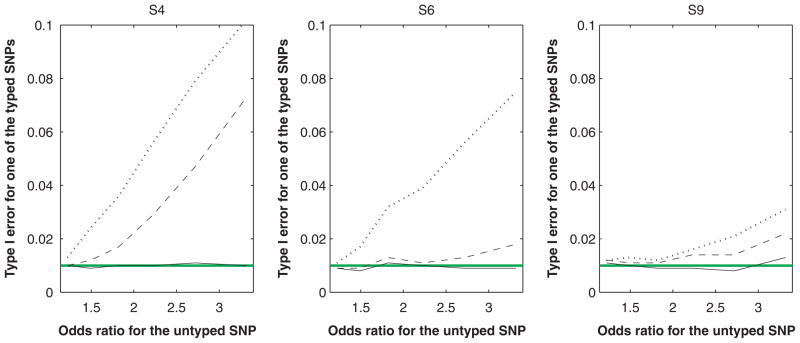
Our last two series of studies dealt with multi-SNP effects. We set the untyped SNP to be causal and included all five SNPs in the joint analysis. For making inference on the effect of the untyped SNP, the performance of IMP-DOS and IMP-MLG is similar to the first two series of studies (results not shown). In particular, type I error is properly controlled. This is not surprising because our theory indicates that imputation yields a valid test of the untyped SNP even when there are environmental factors or typed SNPs in the model. On the other hand, if the untyped SNP is associated with the trait, the bias in the estimation of its effect can cause bias in estimating the null effects of the typed SNPs. Indeed, both IMP-DOS and IMP-MLG can have inflated type I error in testing the effects of the typed SNPs and the inflation of type I error becomes more severe as the effect of the untyped SNP increases. Figures 3 and 4 display these results for cross-sectional and case-control studies, respectively. As before, MLE has accurate control of type I error.

Fig. 3.

Type I error for testing the null effect of a typed SNP on a quantitative trait at the 1% nominal significance level in the joint analysis involving a causal, untyped SNP under the cross-sectional design. The solid, dashed, and dotted curves pertain to MLE, IMP-DOS and IMP-MLG, respectively. SNP, single nucleotide polymorphism; MLE, maximum-likelihood estimator.

Fig. 4.

Type I error for testing the null effect of a typed SNP at the 1% nominal significance level in the joint analysis involving a causal, untyped SNP under the case-control design. The solid, dashed, and dotted curves pertain to MLE, IMP-DOS and IMP-MLG, respectively. SNP, single nucleotide polymorphism; MLE, maximum-likelihood estimator.

WTCCC DATA

We considered WTCCC data on type 1 diabetes (T1D). The database contains 1,963 subjects with T1D and 2,938 controls. For the typed SNPs, we applied the standard Armitage trend test. For the untyped SNPs that are cataloged in the HapMap phase 3 database, we applied both MLE and IMP-DOS, with the phase 3 HapMap CEU sample as the reference panel. For each untyped SNP, we first identified the typed SNPs within 100 kb and then found a set of four that yields the largest R². If there were fewer than eight SNPs within 100 kb, we enlarged the window until a minimum of eight SNPs were located. If there were more than 20 SNPs within 100 kb, we restricted our attention to the closest 20 SNPs so as to reduce computation time.

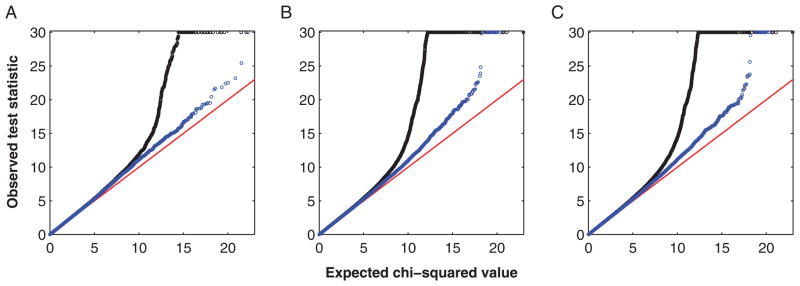
As shown in Figure 5, MLE and IMP-DOS produce nearly identical quantile-quantile (Q-Q) plots for the untyped SNPs, which are similar to that of the typed SNPs. The deviations of the test statistics from the null distribution are minor except in the extreme tails, which correspond to significant associations. The over-dispersion parameter (i.e. the genomic control λ) was estimated at approximately 1.05 for all three plots. These results illustrate that, for single-SNP analysis, both MLE and imputation have correct type I error.

Fig. 5.

Q-Q plots for the single SNP analysis of the T1D data from the WTCCC study: (A) Armitage trend test for typed SNPs, (B) MLE for untyped SNPs, and (C) IMP-DOS for untyped SNPs. Chi-squared statistics exceeding 30 are truncated. The black curve in (A) pertains to 392,746 typed SNPs that pass the standard project filters, have MAF >1% and missing data rates <1%, and have good cluster plots. The black curves in (B) and (C) pertain to 819,727 untyped SNPs that are cataloged in Phase 3 of HapMap with MAF >1%. The Q-Q plots, which exclude all SNPs located in the regions of association listed in Table III of the WTCCC [2007] paper, are superimposed in blue. The blue curves show that departures in the extreme tails of the distributions of test statistics are due to regions with strong signals for association. WTCCC, Wellcome Trust Case-Control Consortium; SNP, single nucleotide polymorphism; T1D, type 1 diabetes; MAF, minor allele frequencies; MLE, maximum-likelihood estimator; Q-Q, quantile-quantile.

Figure 6 displays the results of the association tests for both typed and untyped SNPs on chromosomes 1, 6, and 12, which have the strongest evidence of association. Both MLE and IMP-DOS were able to identify untyped SNPs that are more strongly associated with the disease than typed SNPs, but MLE picked out those SNPs more clearly. This is not surprising since MLE is expected to be more powerful than imputation.

Fig. 6.

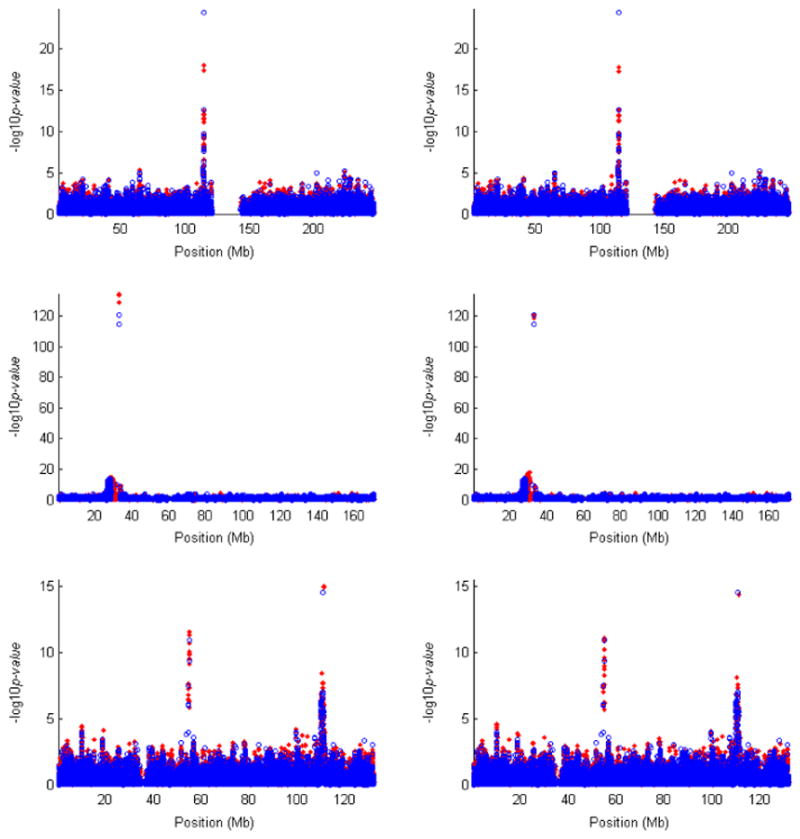
Results of single-SNP association tests for the WTCCC study of T1D. The log₁₀ P-values for typed SNPs and untyped SNPs are shown in blue circles and red dots, respectively. The three rows correspond to chromosomes 1, 6 and 12, which have the strongest evidence of association. The left column corresponds to the trend test for the typed SNPs and the MLE method for the untyped SNPs. The right column corresponds to the trend test for the typed SNPs and the IMP-DOS method for the untyped SNPs. All typed SNPs pass the standard project filters, have MAF >1% and missing data rate <1%, and have good cluster plots. All untyped SNPs have MAF >1% in HapMap. WTCCC, Wellcome Trust Case-Control Consortium; SNP, single nucleotide polymorphism; T1D, type 1 diabetes; MLE, maximum-likelihood estimator.

DISCUSSION

We have presented two approaches to the analysis of untyped SNPs and investigated their properties both theoretically and numerically. The maximum-likelihood approach yields approximately unbiased parameter estimators, proper confidence intervals, and accurate control of type I error. It tends to be more powerful than the imputation approach, especially for case-control studies and in testing gene-environment interactions. The maximum-likelihood method requires the study sample and reference panel be generated from the same underlying population and may be numerically unstable when the haplotype frequencies are low.

We have assumed gene-environment independence in the maximum-likelihood approach. This assumption is satisfied in most applications and can substantially improve the efficiency of association analysis, especially in case-control studies [Chatterjee and Carroll, 2005]. It is possible to allow gene-environment dependence, but the analysis will be more complicated and less efficient.

The imputation approach has some advantages over the maximum-likelihood approach. Numerically, the former is more stable than the latter. For single-SNP tests, imputation has proper control of type I error even if the reference panel does not match the study population. For testing other hypotheses, however, imputation may have inflated type I error. In general, imputation yields biased parameter estimators and incorrect variance estimators. Because the bias can be upward and the variance is underestimated, imputation can sometimes be more powerful than maximum likelihood. Thus, maximum likelihood and imputation are complementary to each other. One possible strategy is to use imputation (with the dosage as the imputed value) in the initial single-SNP tests and to use maximum likelihood for more complex analysis once a region of disease association has been identified.

For cross-sectional studies, Xie and Stram [2005] showed that the score test based on the dosage of the risk haplotype is asymptotically valid. We have shown that imputation is asymptotically valid for single-SNP tests under both cross-sectional and case-control designs whether the untyped SNP is imputed by the dosage or the most likely genotype. Note that the haplotype analysis does not involve external data, whereas the analysis of untyped SNPs does.

Because it ignores the random variation of the reference panel, the imputation approach generally underestimates the variances of the parameter estimators. As the size of the reference panel increases, the underestimation of variance becomes less severe and thus confidence intervals have better coverage probabilities. The size of the reference panel, however, has little influence on the bias of imputation. On the other hand, increasing the size of the reference panel reduces the variance of the MLE. Indeed, the power of maximum likelihood improves at a faster rate than imputation as the reference panel becomes larger, especially under the case-control design (results not shown).

Both MLE and imputation are computationally fast, and the relevant software is available at our website. It took about 8 hr on a 64-bit, 30-GHz Intel Xeon machine (Chapel Hill, NC) to perform the MLE analysis on chromosome 1 of the WTCCC GWAS data. Imputation was slightly faster. The computational savings of imputation will be more substantial if there are multiple traits of interest because the untyped SNPs only need to be imputed once.

For computational expediency, we used the significance level of 0.01 in our simulation studies. The relatively small number of replicates required for obtaining accurate summary statistics at this significance level allowed us to explore a very wide variety of scenarios. It would be formidable to conduct extensive simulation studies at the significance level of 10⁻⁴ or lower, which would require at least 1 million replicates. We repeated some of our simulation studies using the significance level of 10⁻⁴, and the basic conclusions regarding the relative merits of MLE and imputation remained the same.

We have focused on tagging-based imputation. An alternative approach is to use hidden-Markov models (HMM) [Browning and Browning, 2007; Marchini et al., 2007; Li et al., 2008, submitted]. The latter approach, which explores the LD information over a larger region and incorporates population genetics knowledge, can yield more accurate prediction of untyped genotypes in certain situations. We chose tagging over HMM in this article for several reasons: (1) using the same amount of information to infer missing genotypes ensures that the maximum likelihood and imputation methods are compared on equal footing; (2) an investigation by the imputation working group of GAIN [The GAIN Collaborative Research Group, 2007] revealed that tagging is nearly as accurate as HMM (unpublished data); and (3) tagging is much simpler and faster than HMM and can handle much larger studies. We are currently trying to incorporate HMM into the maximum-likelihood framework. The conclusions of this article regarding the relative merits of the maximum likelihood versus imputation approaches are expected to hold when tagging is replaced by HMM.

APPENDIX A: THEORETICAL PROPERTIES OF IMPUTATION

We are interested in the effect of the untyped SNP genotype G_u on the phenotype Y adjusted for the effects of covariates W (if there are any). The covariates, which are required to be fully observed, may include environmental factors and typed SNPs and are allowed to be correlated with the untyped SNP. The linear predictor is assumed to take the form of $\alpha +{\beta }_{G_u}{G}_u+{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}}\mathbf{W}$, where β_Gu and β_W represent the regression effects of G_u and W, respectively. Write $\mathbf{\beta }={({\beta }_{G_u},{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}})}^{\text{T}}$. We are particularly interested in testing the null hypothesis H₀: β_Gu = 0.

Let n denotes the total number of study subjects. For i = 1, …, n, let Y_i, G_ui, and W_i denote the values of Y, G_u, and W on the ith subject. We replace G_ui by Ĝ_ui, where Ĝ_ui is the imputed value of G_ui based on Equation (3), and then apply standard likelihood methods to the imputed data set (Y_i, Ĝ_ui, W_i) (i = 1, …, n). The validity of such analysis does not follow from the standard likelihood theory because the n imputed values {Ĝ_ui}(i = 1, …, n) are correlated due to the presence of the estimator π̃ in them.

We first consider cross-sectional studies. The “likelihood” for θ = (α, β^T, ξ^T)^T based on the imputed data set takes the form $L(\mathbf{\theta })={\prod }_{i=1}^n{P}_{\alpha ,\mathbf{\beta },\xi }(Y_i\mid {\widehat{G}}_{ui},{\mathbf{W}}_i)$. Denote the resulting estimator by θ̂. As mentioned above, standard likelihood theory is not applicable to θ̂ because the n terms in L(θ) are not independent.

Under H₀: β_Gu = 0, Y is related to W only and is independent of G_u given W. Assume that G_t is independent of Y given W. (This assumption holds if G_t is independent of Y or is part of W.) Then Ĝ_u, which is a function of G_t and π̃, is also independent of Y given W, regardless of the value of π̃. In other words, the regression effects of Ĝ_u and W on Y are the same as those of G_u and W under H₀. Denote the reference panel by R. Conditional on R, the imputed values are uncorrelated, so that, under H₀, the random vector I^1/2(θ̂)(θ̂ − θ) converges to a multivariate normal distribution with mean zero and identity covariance matrix, where I(θ) = −∂² log L(θ)/∂θ². Because the limiting distribution does not depend on R, the convergence also holds unconditionally. Thus, standard likelihood methods can be used to test H₀ (even if the study sample and reference panel are drawn from different populations).

The above result hinges critically on the null hypothesis H₀: β_Gu = 0 under the linear predictor $\alpha +{\beta }_{G_u}{G}_u+{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}}\mathbf{W}$, which ensures that θ̂ converges to the true value of θ conditional on R. If β_Gu ≠ 0, then the asymptotic distribution of θ̂ conditional on R depends on R, so that the inverse information matrix I⁻¹(θ̂), which ignores the variability in the reference panel, will underestimate the true variation of θ̂. Thus, the confidence intervals for β_Gu will not have proper coverage probabilities unless β_Gu = 0. It should also be pointed out that the validity of association testing is not guaranteed if the linear predictor does not take the form of $\alpha +{\beta }_{G_u}{G}_u+{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}}\mathbf{W}$.

We now consider the analysis of case-control data under the logistic regression model

$$Pr(Y=1\mid G_u,\mathbf{W})=\frac{{\text{e}}^{\alpha +{\beta }_{G_u}{G}_u+{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}}\mathbf{W}}}{1+{\text{e}}^{\alpha +{\beta }_{G_u}{G}_u+{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}}\mathbf{W}}}.$$

Write $\mathbf{\theta }={(\alpha ,{\beta }_{G_u},{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}})}^{\text{T}}$. If G_u were observed on all study subjects, then the maximum-likelihood estimator of θ (based on the prospective likelihood) would converge to θ^* and its covariance matrix would be consistently estimated by the inverse information matrix, where θ^* is the same as θ except that α is replaced by a different constant [Prentice and Pyke, 1979]. Let θ̂ be the maximizer of the (prospective) likelihood based on the imputed data:

$$L(\mathbf{\theta })=\prod _{i=1}^n\frac{{\text{e}}^{Y_i(\alpha +{\beta }_{G_u}{\widehat{G}}_{ui}+{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}}{\mathbf{W}}_i)}}{{\text{1}+\text{e}}^{\alpha +{\beta }_{G_u}{\widehat{G}}_{ui}+{\mathbf{\beta }}_{\mathbf{W}}^{\text{T}}{\mathbf{W}}_i}}.$$

It then follows from the above arguments for cross-sectional studies that, under H₀: β_Gu = 0, the random vector I^1/2(θ̂)(θ̂ − θ^*) converges to a multivariate normal distribution with mean zero and identity covariance matrix, where I(θ) = −∂²log L(θ)/∂θ². Thus, the association testing is valid. Again, the variance is underestimated by the inverse information matrix if β_Gu ≠ 0, and the association testing may not be valid for other types of hypotheses.