Semiparametric Transformation Models with Random Effects for Joint Analysis of Recurrent and Terminal Events

Summary

We propose a broad class of semiparametric transformation models with random effects for the joint analysis of recurrent events and a terminal event. The transformation models include proportional hazards/intensity and proportional odds models. We estimate the model parameters by the nonparametric maximum likelihood approach. The estimators are shown to be consistent, asymptotically normal, and asymptotically efficient. Simple and stable numerical algorithms are provided to calculate the parameter estimators and to estimate their variances. Extensive simulation studies demonstrate that the proposed inference procedures perform well in realistic settings. Applications to two HIV/AIDS studies are presented.

1. Introduction

Data on recurrent events arise in longitudinal follow-up studies when each subject may experience a particular event repeatedly over time. Medical examples of recurrent events include tumor recurrences, multiple infection episodes, and repeated hospitalizations. In such studies, investigators are typically interested in evaluating the effects of covariates (e.g., treatment assignments and demographic characteristics) on the recurrent event times and in predicting the development of future events given the past event history of an individual.

In practice, recurrent event times are subject to censoring. If censoring is caused by the end of the study or random loss to follow-up, then the censoring time can be regarded as independent or noninformative of the recurrent event times. In many applications, especially in medical studies, the observation on recurrent events may be terminated by the subject's withdrawal from the study (because of deteriorating health or some other reasons) or the subject's death. Then the censoring time (i.e., time to the terminal event) is likely to be correlated with the recurrent event times. Most of the existing methods on recurrent events (e.g., Prentice, Williams, and Peterson, 1981; Andersen and Gill, 1982; Wei, Lin, and Weissfeld, 1989) require noninformative censoring and may yield misleading results when recurrent event times are informatively censored.

Marginal models have been proposed to analyze recurrent event data in the presence of a terminal event; see Cook and Lawless (1997) and Ghosh and Lin (2000, 2002). These models cannot be used to predict the development of future events given an individual's past event history. In addition, it is difficult to construct efficient estimators under marginal models.

An attractive alternative approach is to formulate the joint distribution of recurrent and terminal events through shared frailty or random-effects models. Wang, Qin, and Chiang (2001) and Huang and Wang (2004) studied a shared frailty model with proportional intensity and proportional hazards assumptions for recurrent events and the terminal event, respectively. The model allows an unknown distribution for the shared frailty but requires covariates to be time independent. The proposed estimators do not appear to be (statistically) efficient. Liu, Wolfe, and Huang (2004) considered the same model but assumed a gamma frailty distribution and allowed time-dependent covariates. They developed a Monte Carlo expectation–maximization (EM) algorithm to calculate the nonparametric maximum likelihood estimators (NPMLEs), but did not provide theoretical justifications.

In this article, we present a broad class of transformation models with shared random effects for recurrent and terminal events. Examples of transformation models include proportional hazards/intensity and proportional odds models. We allow time-dependent covariates and various (possibly multivariate) random-effects distributions. We propose to estimate the model parameters by the NPMLEs and establish their theoretical properties. In addition, we provide simple and efficient numerical algorithms to implement the proposed inference procedures.

2. Methods

Let N*(t) denote the number of recurrent events the subject has experienced by time t, let T denote the time to the terminal event, and let Z(t) be a vector of (external) possibly time-dependent covariates. Let b denote the subject-specific random effects with (multivariate) density function f (b; γ) indexed by a set of parameters γ. We assume that N*(·) and T are independent conditional on b and Z. We specify that, conditional on the covariates Z and random effects b, the cumulative intensity function of the recurrent event process N*(t) and the cumulative hazard function of the terminal event time T take the forms

$${\mathrm{\Lambda }}_R\left(t\mid Z;b\right)=H\left({\int }_0^t{e}^{{\alpha }^{T}Z(s)+b^T\stackrel{\sim }{Z}(s)}dA(s)\right),$$ (1)

and

$${\mathrm{\Lambda }}_T\left(t\mid Z;b\right)=G\left({\int }_0^t{e}^{{\beta }^{T}Z(s)+b^T(\phi \circ \stackrel{\sim }{Z}(s))}d\mathrm{\Lambda }(s)\right),$$ (2)

respectively, where H and G are specific transformation functions, Z͂(t) is a subset of Z(t) plus the unit component, α and β are regression parameters, A(·) and Λ(·) are arbitrary increasing functions, ϕ is a set of unknown constants, and ϕ ∘ Z͂(s) denotes the component-wise product of ϕ and Z͂(s).

Our formulation allows very flexible dependence structures, including negative correlations between recurrent event times. The variance component in the random-effects distribution characterizes the dependence among recurrent event times while the parameter ϕ characterizes the dependence between recurrent event process N*(·) and terminal event time T attributed to the unobserved random effects. Zero value of ϕ implies that the dependence between N* and T can be fully explained by the (observed) covariates. When the variance component is zero, N* and T would also be independent even if ϕ is nonzero. On the other hand, if the variance component is nonzero and ϕ is also nonzero, then the variance component not only accounts for the correlations among recurrent events, but also represents the dependence between recurrent and terminal events.

Let C denote the noninformative censoring time, which is assumed to be independent of T, N*, and b conditional on Z. For a random sample of n subjects, the data consist of {Y_i, Δ_i, $N_i^{\ast }(t)$, Z_i (t); t ≤ Y_i} (i = 1, …,n), where Y_i = min(T_i, C_i), Δ_i = I (T_i ≤ C_i), and I(·) is the indicator function. The (observed-data) log-likelihood function for parameters (α, β, ϕ, γ, A, Λ) is

$$\begin{array}{l}\sum _{i=1}^n\text{log}{\int }_b\left[\prod _t{\left\{a(t)e^{{\alpha }^T{Z}_i(t)+b^T{\stackrel{\sim }{Z}}_i(t)}H\prime \times \left({\int }_0^t{e}^{{\alpha }^T{Z}_i(s)+b^T{\stackrel{\sim }{Z}}_i(s)}dA(s)\right)\right\}}^{R_i(t)\mathrm{\Delta }{N}_i^{\ast }(t)}\times \text{exp}\left\{-H\left({\int }_0^{Y_i}{e}^{{\alpha }^T{Z}_i(t)+b^T{\stackrel{\sim }{Z}}_i(t)}dA(t)\right)\right\}\right]\\ \times \left[{\left\{\lambda (Y_i)e^{{\beta }^T{Z}_i(Y_i)+b^T(\phi \circ {\stackrel{\sim }{Z}}_i(Y_i))}G\prime \times \left({\int }_0^{Y_i}{e}^{{\beta }^T{Z}_i(t)+b^T(\phi \circ {\stackrel{\sim }{Z}}_i(t))}d\mathrm{\Lambda }(t)\right)\right\}}^{{\mathrm{\Delta }}_i}\times \text{exp}\left\{-G\left({\int }_0^{Y_i}{e}^{{\beta }^T{Z}_i(t)+b^T(\phi \circ {\stackrel{\sim }{Z}}_i(t))}d\mathrm{\Lambda }(t)\right)\right\}\right]f\left(b;\gamma \right)db,\end{array}$$

where R_i(t) = I(Y_i ≥ t), $\mathrm{\Delta }{N}_i^{\ast }(t)$ denotes the jump size of $N_i^{\ast }(t)$ at t, a(t) = A′(t), and λ(t) = Λ′(t). Here and in the sequel, g′ denotes the derivative of g. The dependence of b on i is suppressed.

We propose to use nonparametric maximum likelihood estimation. In this approach, we consider A as a step function with jumps only at the observed recurrent event times and Λ as a step function with jumps only at the observed terminal event times. In addition, a(t) and λ(t) in the likelihood function are replaced by the jump sizes of A(t) and λ(t) at time t, denoted by A{t} and Λ{t}, respectively. Thus, we maximize the following modified log-likelihood function

$$\begin{array}{l}\sum _{i=1}^n\text{log}{\int }_b\left[\prod _t{\left\{A\left\{t\right\}{e}^{{\alpha }^T{Z}_i(t)+b^T{\stackrel{\sim }{Z}}_i(t)}H\prime \times \left({\int }_0^t{e}^{{\alpha }^T{Z}_i(s)+b^T{\stackrel{\sim }{Z}}_i(s)}dA(s)\right)\right\}}^{R_i(t)\mathrm{\Delta }{N}_t^{\ast }(t)}\times \text{exp}\left\{-H\left({\int }_0^{Y_i}{e}^{{\alpha }^T{Z}_i(t)+b^T{\stackrel{\sim }{Z}}_i(t)}dA(t)\right)\right\}\right]\\ \times \left[{\left\{\mathrm{\Lambda }\left\{Y_i\right\}{e}^{{\beta }^T{Z}_i(Y_i)+b^T(\phi \circ {\stackrel{\sim }{Z}}_i(Y_i))}G\prime \times \left({\int }_0^{Y_i}{e}^{{\beta }^T{Z}_i(t)+b^T(\phi \circ {\stackrel{\sim }{Z}}_i(t))}d\mathrm{\Lambda }(t)\right)\right\}}^{{\mathrm{\Delta }}_i}\times \text{exp}\left\{-G\left({\int }_0^{Y_i}{e}^{{\beta }^T{Z}_i(t)+b^T(\phi \circ {\stackrel{\sim }{Z}}_i(t))}d\mathrm{\Lambda }(t)\right)\right\}\right]f(b;\gamma )db.\end{array}$$ (3)

The maximization is taken over α,β,ϕ,γ, and the jump sizes of A and Λ. The resulting NPMLEs are denoted by α̂, β̂, ϕ̂, γ̂, Â (·), and Λ̂ (·).

We may use quasi-Newton or other optimization algorithms to obtain the NPMLEs. In Web Appendix A, we provide a simple EM algorithm that regards subject-specific random effects b_i as missing data. In the E-step, we evaluate the conditional expectations of certain functions of b_i given the observed data through numerical approximations. In the M-step, we maximize the conditional expectation of the complete-data log-likelihood function given the observed data. Although the parameters of interest include the jump sizes of A and Λ at all observed event times, which can be a large number, we derive simple recursive formulae such that the maximization is taken over α,β, ϕ,γ, and two or four additional parameters only.

In Web Appendix B, we show that the NPMLEs α̂, β̂, ϕ̂, γ̂,Â(·), and Λ̂(·) are consistent and asymptotically normal. In addition, the estimators α̂, β̂, ϕ̂, and γ̂ are asymptotically efficient in that their limiting covariance matrix attains the semiparametric efficiency bound. It is also shown in Web Appendix B that the variances and covariances can be estimated by inverting the observed information matrix for all the parameters, including α,β,ϕ,γ, and the jump sizes of A and Λ. The observed information matrix can be calculated via the Louis (1982) formula.

3 Simulation Studies

We conducted extensive simulation studies to examine the performance of the proposed methods in practical settings. We generated recurrent and terminal events from models (1) and (2) in which Z consists of a Bernoulli variable with 0.5 success probability and a uniform (−1, 1) variable, α = β = (1, 0.5)^T, Z͂ = 1, b is normal with mean 0 and standard derivation 0.5, A(t) = ξ₁t, and Λ(t) = ξ₂t², where ξ₁ and ξ₂ are some constants. We generated the noninformative censoring time from a uniform [0, 5] distribution. We set ϕ to 1, 0, or −1, corresponding, respectively, to positive, zero, and negative dependence between recurrent and terminal events. We considered H(x) = x or log (1 + x) and G(x) = x or log (1 + x). We varied the values of ξ₁ and ξ₂ to obtain 35% censoring rate for the terminal event and to keep the average number of observed recurrent events in the range of 0.5 to 2.

We obtained the NPMLEs through the EM algorithm given in Web Appendix A. We set the initial values of the regression parameters to 0 and the initial value of the variance of the random effect ${\sigma }_b^2$ to 1. We estimated the variances of the NPMLEs by the Louis formula. It took approximately 8 hours and 24 hours on an IBM HS40 machine to complete 1000 repetitions with n = 200 and n = 400, respectively.

Tables 1–3 summarize the results of the simulation studies. Clearly, the proposed methods perform well in all cases. The parameter estimators are virtually unbiased, the standard error estimators reflect accurately the true variations, and confidence intervals have reasonable coverage probabilities.

Table 1. Summary statistics for the simulation studies under H(x) = G(x) = x.

n		ϕ = 1				ϕ = 0				ϕ = −1
		Bias	SE	SEE	CP	Bias	SE	SEE	CP	Bias	SE	SEE	CP
200	α1	−0.009	0.183	0.183	0.95	−0.000	0.176	0.170	0.93	0.000	0.204	0.203	0.94
	α2	−0.003	0.160	0.154	0.94	−0.006	0.148	0.143	0.95	0.007	0.175	0.171	0.95
	A(τ/4)	0.003	0.100	0.099	0.94	0.005	0.111	0.108	0.94	0.006	0.071	0.070	0.95
	A(τ/2)	0.001	0.129	0.130	0.95	0.007	0.148	0.143	0.94	0.009	0.094	0.093	0.95
	A(3τ/4)	−0.009	0.206	0.209	0.95	0.012	0.231	0.224	0.94	0.018	0.146	0.145	0.95
	β1	0.005	0.244	0.245	0.96	0.025	0.189	0.194	0.95	0.016	0.240	0.254	0.96
	β2	0.018	0.192	0.198	0.96	0.029	0.160	0.161	0.95	0.024	0.195	0.202	0.96
	Λ(τ/4)	0.002	0.067	0.067	0.96	−0.007	0.050	0.051	0.96	0.002	0.062	0.065	0.96
	Λ(τ/2)	0.004	0.104	0.106	0.96	−0.005	0.081	0.083	0.97	0.003	0.098	0.098	0.96
	Λ(3τ/4)	0.036	0.264	0.257	0.96	0.007	0.171	0.180	0.96	0.009	0.224	0.224	0.96
	ϕ	0.034	0.359	0.377	0.96	0.003	0.211	0.213	0.95	−0.013	0.405	0.462	0.95
	${\sigma }_b^2$	−0.017	0.136	0.144	0.98	−0.021	0.119	0.123	0.97	−0.021	0.172	0.169	0.97
400	α1	−0.000	0.133	0.130	0.94	−0.000	0.122	0.120	0.94	0.005	0.139	0.144	0.96
	α2	0.004	0.112	0.109	0.95	0.002	0.100	0.101	0.96	0.004	0.122	0.121	0.94
	A(τ/4)	−0.000	0.070	0.070	0.95	0.000	0.079	0.076	0.94	0.000	0.047	0.049	0.96
	A(τ/2)	−0.002	0.092	0.092	0.95	0.001	0.106	0.100	0.94	0.001	0.062	0.065	0.96
	A(3τ/4)	−0.013	0.154	0.147	0.95	0.006	0.165	0.158	0.94	0.004	0.096	0.102	0.96
	β1	0.009	0.168	0.171	0.96	0.015	0.136	0.134	0.95	0.008	0.178	0.178	0.95
	β2	0.011	0.138	0.138	0.95	0.012	0.111	0.111	0.96	0.008	0.145	0.141	0.95
	Λ(τ/4)	−0.001	0.046	0.047	0.95	−0.004	0.037	0.036	0.95	0.001	0.045	0.046	0.95
	Λ(τ/2)	−0.002	0.174	0.074	0.95	−0.005	0.060	0.058	0.95	0.000	0.070	0.069	0.95
	Λ(3τ/4)	−0.002	0.170	0.171	0.95	0.001	0.126	0.125	0.96	0.005	0.171	0.157	0.94
	ϕ	0.007	0.239	0.249	0.97	0.001	0.139	0.141	0.95	0.014	0.293	0.305	0.94
	${\sigma }_b^2$	−0.002	0.101	0.103	0.96	−0.005	0.088	0.087	0.96	−0.006	0.118	0.121	0.97

Note: Bias and SE are the bias and standard error of the parameter estimator, SEE is the mean of the standard error estimator, and CP is the coverage probability of the 95% confidence interval. The confidence intervals for A(·) and Λ(·) are constructed on the basis of the log transformation, while the confidence intervals for ${\sigma }_b^2$ are based on the Satterthwaite approximation: $\left(\nu {\widehat{\sigma }}_b^2/{\chi }_{\nu ,0.975}^2,\nu {\widehat{\sigma }}_b^2/{\chi }_{\nu ,0.025}^2\right)$, where $\nu =2{\left\{{\widehat{\sigma }}_b^2/\widehat{\text{se}}\left({\widehat{\sigma }}_b^2\right)\right\}}^2$, and ${\chi }_{\nu ,\alpha }^2$ is the α-quantile of the χ²-distribution with ν degrees of freedom.

Table 3. Summary statistics for the simulation studies under H(x) = G(x) = log(1 + x).

n		ϕ = 1				ϕ = 0				ϕ = −1
		Bias	SE	SEE	CP	Bias	SE	SEE	CP	Bias	SE	SEE	CP
200	α1	−0.008	0.253	0.258	0.95	0.004	0.241	0.247	0.96	0.009	0.260	0.262	0.95
	α2	−0.003	0.228	0.222	0.95	−0.006	0.209	0.212	0.95	0.003	0.233	0.224	0.94
	A(τ/4)	−0.006	0.297	0.301	0.94	0.005	0.478	0.477	0.95	0.003	0.314	0.310	0.95
	A(τ/2)	−0.007	0.413	0.414	0.95	0.010	0.679	0.661	0.95	0.008	0.436	0.427	0.94
	A(3τ/4)	−0.002	0.719	0.695	0.94	0.024	1.141	1.114	0.95	0.012	0.707	0.712	0.95
	β1	−0.007	0.297	0.314	0.96	0.023	0.275	0.289	0.97	0.006	0.298	0.313	0.96
	β2	0.020	0.255	0.261	0.96	0.040	0.239	0.244	0.96	0.023	0.254	0.260	0.96
	Λ(τ/4)	0.005	0.148	0.149	0.96	−0.004	0.118	0.121	0.96	0.002	0.151	0.155	0.97
	Λ(τ/2)	0.011	0.278	0.267	0.96	0.007	0.218	0.216	0.96	0.005	0.284	0.281	0.97
	Λ(3τ/4)	0.043	0.765	0.733	0.95	0.055	0.537	0.572	0.97	0.027	0.826	0.780	0.95
	ϕ	−0.019	0.651	0.872	0.93	−0.028	0.692	0.775	0.95	0.029	0.667	0.920	0.93
	${\sigma }_b^2$	0.020	0.254	0.319	0.94	−0.017	0.254	0.310	0.96	0.014	0.271	0.327	0.95
400	α1	−0.005	0.182	0.181	0.96	−0.005	0.175	0.175	0.95	−0.004	0.183	0.184	0.96
	α2	−0.004	0.149	0.155	0.95	0.010	0.147	0.150	0.96	0.002	0.160	0.158	0.95
	A(τ/4)	0.004	0.217	0.214	0.94	0.015	0.350	0.340	0.94	0.011	0.215	0.220	0.96
	A(τ/2)	0.002	0.296	0.293	0.95	0.026	0.482	0.470	0.94	0.020	0.299	0.304	0.95
	A(3τ/4)	−0.010	0.498	0.486	0.95	0.071	0.852	0.797	0.94	0.042	0.503	0.508	0.95
	β1	0.008	0.227	0.227	0.96	0.010	0.202	0.200	0.95	0.003	0.217	0.223	0.96
	β2	0.015	0.183	0.186	0.96	0.013	0.167	0.169	0.96	0.008	0.180	0.184	0.96
	Λ(τ/4)	−0.005	0.107	0.105	0.95	−0.001	0.089	0.084	0.94	−0.000	0.111	0.110	0.95
	Λ(τ/2)	−0.002	0.192	0.187	0.95	−0.000	0.151	0.149	0.95	−0.001	0.206	0.198	0.95
	Λ(3τ/4)	−0.003	0.488	0.513	0.95	0.024	0.392	0.389	0.95	0.000	0.551	0.549	0.95
	ϕ	−0.055	0.561	0.668	0.93	0.014	0.454	0.433	0.95	−0.012	0.521	0.667	0.93
	${\sigma }_b^2$	0.002	0.193	0.227	0.95	−0.003	0.187	0.225	0.96	0.011	0.207	0.235	0.95

Note: See the Note to Table 1.

4. Examples

4.1 The AIDS Links to Intravenous Experiences Study

We applied the proposed methods to the AIDS Links to Intravenous Experiences (ALIVE) cohort study (Vlahov et al., 1991). The study collected data on HIV infection, in-patient admissions, and other variables from a group of intravenous drug users in the city of Baltimore, Maryland, United States. We considered the hospitalization data collected between August 1, 1993 and December 31, 1997 on 652 subjects. In this study, the terminal event was death. There were, on average, 2.5 hospital admissions per subject, and there were 93 deaths. The investigators were interested in assessing the effects of baseline covariates, such as age, gender, race, and HIV status, on recurrent hospital admissions and death.

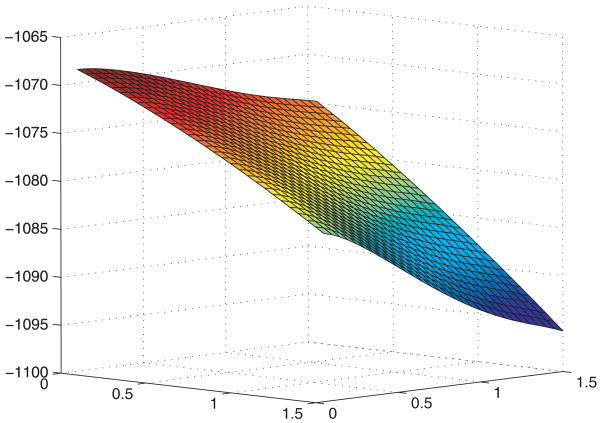
We considered the class of logarithmic transformations r⁻¹ log (1 + rx) (r ≥ 0) for H and G. This class includes the proportional intensity/hazards and proportional odds models. We used the Akaike information criterion to choose the best transformations. Figure 1 shows the surface of the log-likelihood function for different combinations of H and G. The combination of H and G with the largest log-likelihood value corresponds to the proportional intensity model for hospitalizations and the proportional hazards model for death. We also considered the class of Box–Cox transformations ρ−¹{(1 + x)^ρ − 1}, and the log-likelihood surface pointed to the same combination of H and G.

Figure 1.

Log-likelihood function surface under the logarithmic transformations for the ALIVE study: the x- and y-axes correspond to the transformation parameter r for recurrent events and terminal event, respectively.

Table 4 summarizes the estimation results under the selected model. There does not appear to be any race or gender effect on hospitalizations or death. Not surprisingly, the subjects who were HIV positive tended to be hospitalized more frequently and to die earlier. Even after adjusting for the patients' demographics and HIV status, there appears to be some positive association between hospitalizations and death due to unknown factors.

Table 4. Estimation results for the ALIVE study.

	Death		Hospital admissions
	Estimate	Std. error	Estimate	Std. error
Black versus nonblack	0.500	0.603	−0.076	0.139
Female versus male	−0.404	0.258	0.044	0.075
HIV+ versus HIV−	1.737	0.287	0.299	0.069
Age	0.024	0.018	0.014	0.005
ϕ	1.161	0.326
σ2	0.284	0.035

The cumulative rate of hospitalizations conditional on covariates, i.e., E[N*(t) ∣ T > t, Z], can be expressed as

$$\frac{{\int }_{b}H\left({\int }_0^t\text{exp}\{{\alpha }^{T}Z(s)+b^T(\phi \circ \stackrel{\sim }{Z}(s))\}dA\right)\text{exp}\left\{-G\left({\int }_0^t\text{exp}\{{\beta }^{T}Z(s)+b^T(\phi \circ \stackrel{\sim }{Z}(s))\}d\mathrm{\Lambda }\right)\right\}f\left(b;\gamma \right)db}{{\int }_b\text{exp}\left\{-G\left({\int }_0^t\text{exp}\{{\beta }^{T}Z(s)+b^T(\phi \circ \stackrel{\sim }{Z}(s))\}d\mathrm{\Lambda }\right)\right\}f\left(b;\gamma \right)db}.$$

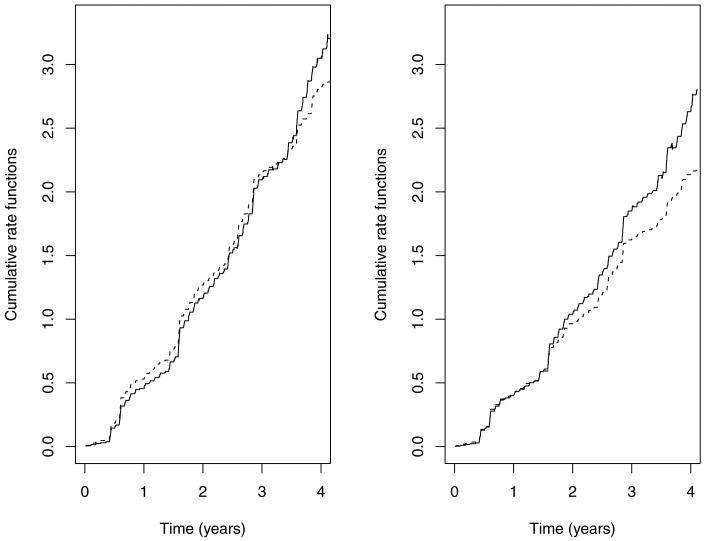
We estimate this function by replacing the unknown parameters by their NPMLEs. Figure 2 displays the predicted functions versus their nonparametric counterparts for the HIV-positive versus HIV-negative subjects. The nonparametric estimator takes the form of ${\sum }_{i=1}^{n}I(Y_i\ge t)N_i(t)/{\sum }_{i=1}^{n}I\times (Y_i\ge t)$. The two sets of curves are close to each other (except at the right tails), supporting the choice of the model.

Figure 2.

Estimated cumulative rate functions of hospitalizations for the ALIVE Study: the left and right panels correspond to the HIV-positive and HIV-negative subjects, respectively; the solid and dashed curves pertain to the nonparametric and model-based estimates, respectively.

4.2 Community Programs for Clinical Research on AIDS

We also applied our methods to data from the Terry Beirn Community Programs for Clinical Research on AIDS (CPCRA) (Abrams et al., 1994; Neaton et al., 1994). The main interest lied in the effects of diadanosine (ddI) as compared to zalcitabine (ddC) on both the survival and the opportunistic infections in the HIV-infected subjects who previously received zidovudine and had 300 or fewer CD4 cell per cubic centimeter. Out of the 467 subjects enrolled in the study, 230 were randomized to the ddI treatment and the remaining 237 to the ddC treatment. A total of 100 patients in the ddI group and 88 patients in the ddC group died during the follow-up period of 21 months. There were 172 confirmed or probable opportunistic infections in the ddI group and 191 in the ddC group. The censoring rate was 60% and the average number of infections per patient was 0.78, with a range of 0 to 5.

We considered the two classes of transformations used in Section 4.1 but restricted the values of r and ρ to be between 0 and 1. The combination of H(x) = log (1 + x) and G(x) = x, i.e., the proportional “odds” model for recurrent infections and the proportional hazards model for death, yielded the largest likelihood value. Table 5 summarizes the corresponding estimation results. There is no treatment difference in opportunistic infections. Although ddC reduces the risk of death as compared to ddI, the reduction is not statistically significant. There is strong association between the two types of events due to unknown factors.

Table 5. Estimation results for the CPCRA study.

	Death		Opportunistic infections
	Estimate	Std. error	Estimate	Std. error
ddC versus ddI	−0.368	0.244	−0.002	0.197
ϕ	1.481	0.509
σ2	1.422	0.380

5. Discussion

Recently, Zeng and Lin (2007) studied nonparametric maximum likelihood estimation for several classes of semiparametric regression models with censored data. They did not consider joint models for recurrent and terminal events. In Web Appendix B, we use the general asymptotic theory of Zeng and Lin (2007) to establish the asymptotic properties of the NPMLEs for our joint models by showing that the regularity conditions of Zeng and Lin (2007) hold under a set of conditions specific to our problem.

We can extend our models to multiple sequences of recurrent events, such as clustered recurrent events (Schaubel, 2005). We can also extend our models to deal with multiple types of terminal events (e.g., death versus voluntary withdrawal). The inference procedures described in Section 2 can be modified accordingly.

The proposed class of joint transformation models is very broad and thus allows accurate prediction in a variety of situations. In each application, one would need to determine which model best fits the data. We used the Akaike information criterion to select the best transformations in the two examples. We also showed in the first example the use of model-predicted versus nonparametric estimates of event processes to check the fit of the model. It is worthwhile developing additional methods for model selection and model checking.

Table 2. Summary statistics for the simulation studies under H(x) = x and G(x) = log(1 + x).

n		ϕ = 1				ϕ = 0				ϕ = −1
		Bias	SE	SEE	CP	Bias	SE	SEE	CP	Bias	SE	SEE	CP
200	α1	−0.009	0.168	0.162	0.95	−0.003	0.192	0.184	0.93	−0.013	0.177	0.172	0.94
	α2	0.010	0.138	0.138	0.95	−0.003	0.159	0.156	0.95	−0.012	0.154	0.146	0.93
	A(τ/4)	0.009	0.139	0.138	0.95	0.006	0.103	0.101	0.95	0.012	0.118	0.114	0.94
	A(τ/2)	0.006	0.189	0.184	0.95	0.008	0.138	0.136	0.95	0.020	0.159	0.154	0.95
	A(3τ/4)	0.005	0.290	0.290	0.96	0.017	0.220	0.215	0.95	0.032	0.251	0.239	0.94
	β1	−0.009	0.295	0.306	0.96	0.014	0.271	0.282	0.97	0.019	0.300	0.308	0.95
	β2	0.022	0.254	0.259	0.96	0.034	0.235	0.239	0.95	0.034	0.257	0.259	0.96
	Λ(τ/4)	0.005	0.148	0.147	0.95	−0.001	0.133	0.135	0.96	−0.000	0.152	0.155	0.97
	Λ(τ/2)	0.010	0.270	0.165	0.95	0.011	0.247	0.245	0.96	0.009	0.288	0.284	0.97
	Λ(3τ/4)	0.048	0.732	0.704	0.95	0.066	0.626	0.656	0.96	0.067	0.850	0.771	0.96
	ϕ	0.005	0.428	0.447	0.95	0.010	0.432	0.437	0.93	−0.007	0.454	0.459	0.95
	${\sigma }_b^2$	−0.023	0.116	0.116	0.97	−0.019	0.141	0.140	0.97	−0.014	0.146	0.130	0.95
400	α1	−0.002	0.111	0.115	0.96	0.003	0.132	0.130	0.94	−0.001	0.124	0.122	0.94
	α2	−0.000	0.096	0.098	0.95	0.002	0.109	0.110	0.95	−0.002	0.106	0.104	0.94
	A(τ/4)	0.002	0.099	0.097	0.94	0.002	0.073	0.071	0.94	0.003	0.084	0.081	0.95
	A(τ/2)	−0.001	0.133	0.130	0.94	0.002	0.097	0.096	0.94	0.005	0.112	0.108	0.95
	A(3τ/4)	−0.008	0.213	0.205	0.94	0.004	0.153	0.151	0.94	0.013	0.177	0.169	0.93
	β1	0.002	0.214	0.215	0.95	0.005	0.199	0.196	0.95	0.008	0.221	0.216	0.94
	β2	0.010	0.183	0.181	0.95	0.012	0.165	0.167	0.96	0.012	0.182	0.181	0.95
	Λ(τ/4)	−0.003	0.105	0.102	0.95	−0.001	0.098	0.094	0.95	0.000	0.112	0.109	0.94
	Λ(τ/2)	−0.003	0.191	0.184	0.95	−0.002	0.172	0.169	0.95	0.001	0.205	0.197	0.95
	Λ(3τ/4)	0.020	0.479	0.477	0.94	0.020	0.447	0.448	0.96	0.011	0.547	0.522	0.95
	ϕ	−0.003	0.304	0.304	0.95	−0.001	0.283	0.288	0.95	0.005	0.305	0.309	0.96
	${\sigma }_b^2$	−0.008	0.082	0.083	0.96	−0.007	0.095	0.099	0.97	−0.004	0.099	0.093	0.94

Note: See the Note to Table 1.