Spin Coupling in Roussin’s Red and Black Salts

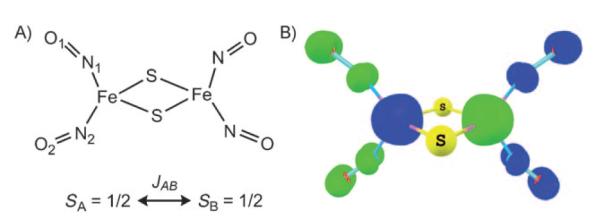
Abstract

Although DFT calculations have provided a first-order electronic-structural description for Roussin’s red and black salts, a detailed study of spin coupling in these species has yet to be reported. Such an analysis is presented here for the first time, based on broken-symmetry density functional theory (DFT, chiefly OLYP/STO-TZP) calculations. Both the Noodleman and Yamaguchi formulas were used to evaluate the Heisenberg coupling constants (J). Three nitrosylated binuclear clusters were studied: [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺ (1; Et-HPTB=N,N,N’,N’ -tetrakis-(N-ethyl-2-benzimidazolylmethyl)-2-hydroxy-1,3-diaminopropane), [Fe(NO)₂{Fe(NO)(NS₃)}-S,S’] (2), and Roussin’s red salt anion [Fe₂(NO)₄(μ-S)₂]²⁻ (3). Although the Heisenberg J for 1 is small (≈10² cm⁻¹), 2 and 3 exhibit J values that are at least an order of magnitude higher (≈ 10³ cm⁻¹), where the J values refer to the following Heisenberg spin Hamiltonian: $\mathscr{H}=J{S}_{\mathrm{A}}\cdot S_{\mathrm{B}}$. For Roussin’s black salt anion, [Fe₄(NO)₇(μ₃-S)₃]⁻ (4), the Heisenberg spin Hamiltonian describing spin coupling between the {FeNO}⁷ unit (S_A=3/2) and the three {Fe(NO)₂}⁹ units (S_B=S_C=S_D=1/2) in [Fe₄(NO)₇(μ₃-S)₃]⁻ was assumed to have the form: $\mathscr{H}=J_{12}(S_{\mathrm{A}}\cdot S_{\mathrm{B}}+S_{\mathrm{A}}\cdot S_{\mathrm{C}}+S_{\mathrm{A}}\cdot S_{\mathrm{D}})+J_{22}(S_{\mathrm{B}}\cdot S_{\mathrm{C}}+S_{\mathrm{B}}\cdot S_{\mathrm{D}}+S_{\mathrm{C}}\cdot S_{\mathrm{D}})$, in which J₁₂ corresponds to the interaction between the apical iron and a basal iron, and J₂₂ refers to that between any two basal iron centers. Although the basal–basal coupling constant J₂₂ was found to be small (≈ 10² cm⁻¹), the apical–basal coupling constant J₁₂ is some forty times higher (≈ 4000 cm⁻¹). Thus, the nitrosylated iron–sulfur clusters feature some exceptionally high J values relative to the non-nitrosylated {2Fe2S} and {4Fe4S} clusters. An analysis of spin-dependent bonding energies shed light on this curious feature. In essence, the energy difference between the high-spin (i.e., ferromagnetically coupled iron sites) and low-spin (i.e., maximum spin coupling) states of Roussin’s salts are indeed rather similar to those of analogous non-nitrosylated iron– sulfur clusters. However, the individual Fe(NO)_x (x=1, 2) site spins are lower in the nitrosylated systems, resulting in a smaller denominator in both the Noodleman and Yamaguchi formulas for J, which in turn translates into the very high J values.

Introduction

Widely prevalent in inorganic chemistry, ligand-bridged transition-metal clusters are also of great importance in biology and in areas such as molecular magnetism. Iron–sulfur clusters and oxo-bridged di-iron sites thus rank among the best-known nonheme biometal sites. These sites are responsible for a variety of single- and multielectron redox processes, including the reduction of dinitrogen to ammonia by the MoFe cluster of nitrogenase,[1] electron-transfer processes involving Rieske {2Fe2S} centers,[2] and the reduction of ribonucleotides to deoxyribonucleotides by a complex proton-coupled electron-transfer (PCET) mechanism within the R2 subunit of Class 1 ribonucleotide reductase (RNR).[3,4] Understanding the electronic structures of these clusters is clearly important for an appreciation of their biological functions. A key step in developing such an understanding is to analyze the spin couplings among the individual metal centers. Such analyses have been carried out in considerable detail for iron–sulfur and oxo-bridged di-iron clusters.[5–9]

Against this context, the electronic structures of nitrosylated iron–sulfur clusters, notably the iconic Roussin’s red and black salt anions, remain little explored.[10] Long known as stable, thermodynamic sinks in Fe/S/NO chemistry,[11,12] Roussin’s salts have been studied in recent years as light-activated, anticancer NO donor drugs.[13–15] Although the toxicity of Roussin’s salts precludes their use as systemic drugs, intratumoral application might be possible.[13] Broken-symmetry DFT calculations have resulted in first-order molecular orbital pictures for the binuclear red and tetranuclear Roussin’s salt anions.[16–18] In particular, DFT calculations from one of our laboratories have indicated substantial energy gaps between the fully spin-coupled (diamagnetic) ground states and excited states in which the iron atoms are all ferromagnetically aligned, emphasizing the need for detailed analyses of the metal–metal spin couplings.[18,19] Such analyses are reported here for the first time for Roussin’s red and black salt anions, along with similar analyses for two structurally related synthetic iron–sulfur complexes. The computed Heisenberg J coupling constants are evaluated in relation to other relevant iron–sulfur complexes.

Computational Details

All calculations are based on broken-symmetry (BS) DFT methods. The BS state captures the essential physics of spin-coupled systems and provides a practical approach to estimations of trends in experimental coupling constants.[6,20,21] There is some evidence that hybrid functionals provide a more accurate description of antiferromagnetically (AF) coupled states than pure functionals, owing to the more spin-polarized nature of the unrestricted wavefunction with the former.[18] Hybrid functionals, however, generally yield somewhat poorer geometries, including unduly long metal–metal and metal–ligand bonds, relative to pure functionals (such as PW91[22]).[18,23] The latter, however, overestimate metal–ligand covalencies, and exhibit an undue preference for lower spin states.[24] In this context, pure functionals such as OLYP,[25,26] based on the OPTX exchange functional, have emerged as a good compromise, providing reasonable descriptions of both geometric and electronic structures for spin-coupled systems.[18,24,27–29]

These considerations led us to employ OLYP to analyze the molecular structures and spin coupling of four polyiron nitrosyls (1–4, Table 1). Initial geometries obtained from crystallographic coordinates were optimized in vacuum and in methanol (COSMO,[30] dielectric constant 32.6) with Slater-type triple-ζ plus polarization basis sets (STO-TZP) (Amsterdam Density Functional Theory program system (ADF) 2007).[31] For 2, additional calculations were carried out with the PW91 functional, because OLYP seriously overestimated the length of the Fe–N bond trans to the strong Fe–NO bond (such inaccurate descriptions of trans effects have been observed for other complexes as well).[32] In addition, for complex 3, the very strong coupling between the metal centers results in a collapse of the OLYP wavefunction to a spin-restricted solution. To describe the antiferromagnetic coupling in this complex, we carried out B3LYP[26,33] (Gaussian 03,[34] 6-311G(d,p), COSMO) calculations, which led to the expected BS wavefunction.

Table 1.

Details of optimized broken-symmetry states.^[a]

Com- plex	ST[b]	Symm[c]	Iron center[d]		Spin population
				Fe	N	O
1	0	C 1	{FeNO}7	3.47	−0.51	−0.40
			{FeNO}7	−3.47	0.51	0.40
2	1	C 1	{FeNO}7	2.35	−0.08	−0.11
			{Fe(NO)2}9	−1.15	0.19/0.19[f]	0.15/0.15[f]
3	0	C 1	{Fe(NO)2}9	2.47	−0.36/−0.36[f]	−0.32/−0.33[f]
			{Fe(NO)2}9	−2.47	0.36/0.36[f]	0.32/0.33[f]
4	0	C3V[e]	{FeNO}7	−1.18	0.16	0.13
			3*{Fe(NO)2}9	0.62	−0.09/−0.10[f]	−0.07/−0.07[f]

^[a]OLYP/TZP/COSMO except for 3 (B3LYP/6-311(d,p)/COSMO electronic structure at OLYP/TZP/COSMO geometry) and 2 (OLYP/TZP/COSMO electronic structure at PW91/TZP/COSMO geometry).

^[b]S_T=total spin.

^[c]Symmetry constraint employed.

^[d]Number of chemically equivalent centers is indicated with N*.

^[e]C_S symmetry employed for Heisenberg coupling constant calculations.

^[f]Spin populations on the two NO groups in each {Fe(NO)₂}⁹ unit.

To obtain broken-symmetry states for spin-zero complexes, an appropriate high-spin state was optimized, followed by flipping of the spin on selected atoms to generate an antiferromagnetically coupled state. The spin-flipped electronic structure was then used as a starting guess for geometry optimization of the M_S=0 broken-symmetry states.

Heisenberg J coupling constants were computed for optimized broken-symmetry geometries (ADF, OLYP). The Heisenberg spin Hamiltonian shown in Equation (1) was employed in our analysis, in which S_A and S_B are spin operators for the interacting sites A and B.[35]

$$\mathscr{H}=J{S}_{\mathrm{A}}\cdot S_{\mathrm{B}}$$ (1)

The J constants were computed from the energy difference between a high-spin state (HS, S=S_A+S_B) and the broken-symmetry state (BS, S=S_A–S_B). In the Noodleman formalism, J is given by Equation (2).[5,36]

$$J=(E_{\mathrm{HS}}-E_{\mathrm{BS}})∕2S_{\mathrm{A}}{S}_{\mathrm{B}}$$ (2)

Equation (2) is considered to be valid in the weak-coupling limit only, and an alternative expression has been put forward by Yamaguchi and co-workers, shown in Equation (3), in which <S²>_HS and <S²>_BS are the expectation values of the HS and BS S² operators. Both expressions for J have been employed here.[37]

$$J=2(E_{\mathrm{HS}}-E_{\mathrm{BS}})∕({<{\mathrm{S}}^2>}_{\mathrm{HS}}-{<{\mathrm{S}}^2>}_{\mathrm{BS}})$$ (3)

Unrestricted corresponding orbital (UCO) analyses[38] were performed with the ORCA[39] program (vacuum, OLYP or B3LYP with the TZVP basis set[40]), using the OLYP (ADF) optimized broken-symmetry geometries. A UCO analysis involves unitary transformations of the MOs to generate α and β orbitals with maximum overlap. An overlap value of one is considered to be a covalent interaction, whereas orbital pairs with overlap values significantly less than one are considered magnetic orbitals.[38] Overlap values of 0 are obtained for singly occupied orbitals (SOMOs).

Results and Discussion

Broken-symmetry states, Heisenberg J coupling constants, and unrestricted corresponding orbitals were calculated for four polynuclear nonheme iron nitrosyls. These include three binuclear complexes, [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺ (1]; Et-HPTB=N,N,N’,N’-tetrakis-(N-ethyl-2-benzimidazolylmethyl)-2-hydroxy-1,3-diaminopropane), [Fe(NO)₂{Fe(NO)-(NS₃)}-S,S’] (2), and Roussin’s red salt anion [Fe₂(NO)₄(μ-S)₂]²⁻ (3), and one tetranuclear complex, Roussin’s black salt anion [Fe₄(NO)₇(μ₃-S)₃]⁻ (4, Table 1). Detailed results for each species are discussed below. Complexes 1–3, the cores of which may be viewed as partial models of that of 4, were essentially chosen as preludes to an analysis of the much more electronically complicated 4, the ultimate objective of this study.

A bis-{FeNO}⁷ complex

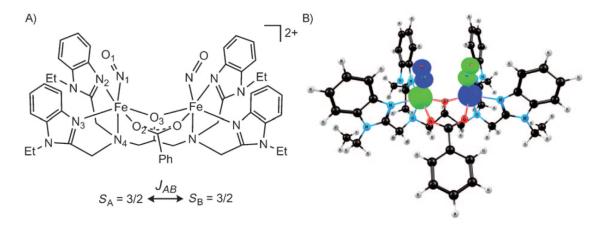
The binuclear complex 1 (Figure 1 A) is a synthetic analogue of the NO-bound state of the di-iron active site complex of ribonucleotide reductase (RNR) subunit R2.[4,41] The reduced form of R2 (RNR_red) reacts with nitric oxide to form an antiferromagnetically coupled pair of {FeNO}⁷ centers.[41] Magnetic susceptibility studies of 1-(BF₄)₂ indicated a site spin of S=3/2 for each {FeNO}⁷ unit.[41] We have optimized the antiferromagnetically coupled broken-symmetry state of [Fe₂(NO)₂(Et-HPTB)-(O₂CPh)]²⁺ (OLYP, ADF) (Figure 1 B, Table 2). The computed iron–ligand distances are slightly overestimated, and in particular the iron–iron distance is about 0.11 Å longer than in the experimental structure (Table 2). The spin density (Figure 1 B) shows oppositely aligned spin populations on iron and NO, of 3.47 and −0.91, respectively (opposite signs for the second iron center, Table 1). The cylindrical[42] NO spin density is in agreement with a suggested Fe³⁺–_NO⁻ description of the {FeNO}⁷ units.[43]

Figure 1.

Selected OLYP/TZP/COSMO (ADF) results on 1. A) Structure, atom numbering, and Heisenberg J_AB between the two S=3/2 {FeNO}⁷ centers; B) broken-symmetry M_S=0 spin density (contour value 0.03 eÅ⁻³).

Table 2.

Structural parameters and Heisenberg coupling constants of [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺.

Bond length [Å]/ Angle [°][a]	Vacuum BS-OLYP[b]	COSMO BS-OLYP[b]	Experimental[c]
Fe–Fe	3.55	3.56	3.44
Fe–N1	1.77	1.78	1.75/1.75
N1–O1	1.17	1.18	1.15/1.16
Fe-N1-O1	159.8/160.0	157.6	166.6/168.2
Fe–O2	2.16	2.22	2.12/2.13
Fe–O3	2.08	2.05	2.02/2.01
Fe–N2	2.21	2.19	2.12/2.14
Fe–N3	2.18	2.18	2.12/2.12
Fe–N4	2.40	2.33	2.29/2.28

J[d][cm−1]	Vacuum	COSMO	Experimental[b]
Noodleman[e]	95	184	46
Yamaguchi[f]	95	184

^[a]See Figure 1 A for atom numbering.

^[b]OLYP/TZP (ADF) broken-symmetry geometry. Only one value is given if values are identical for both FeNO units.

^[c]Ref. [41].

^[d]Based on $\mathscr{H}=J{S}_{\mathrm{A}}{S}_{\mathrm{B}}$.

^[e]Equation (2).

^[f]Equation (3).

The experimentally determined magnetic coupling between the iron centers is weak, with a fitted J_AB of −23 cm⁻¹ (with $\mathscr{H}=-2J{S}_{\mathrm{A}}{S}_{\mathrm{B}}$, S_A=S_B=3/2).[41] The weak coupling is probably due to the nature of the bridging groups, an alkoxide and a carboxylate anion (Figure 1). Here, we have calculated J_AB for the optimized broken-symmetry geometry (M_S=0). The corresponding ferromagnetically coupled state (M_S=3) was calculated by assuming parallel spins on both {FeNO}⁷ units. By treating the FeNO units as single sites with site-spin 3/2, we evaluate only the strength of the interaction between the sites, whereas the extremely strong antiferromagnetic coupling between iron and NO does not enter the calculated Heisenberg constant. The Noodleman [Eq. (2), S_A=S_B=3/2, $\mathscr{H}=J{S}_{\mathrm{A}}{S}_{\mathrm{B}}$] and Yamaguchi approaches [Eq. (3), <S²>_Ms=3=13.21, <S²>_Ms=0=4.25, ADF, OLYP, COSMO] give essentially identical results, with J_AB=95 cm⁻¹ for the vacuum optimized geometry, and 184 cm⁻¹ for the COSMO geometry (Table 2). Both values are overestimated relative to the experimental coupling constant (46 cm⁻¹ by employing $\mathscr{H}=J{S}_{\mathrm{A}}{S}_{\mathrm{B}}$). Errors of this magnitude are understandable, given that the calculations are based on a small difference in energy between the broken-symmetry M_S=0 and the M_S=3 states (ΔE_vacuum=0.05 eV and ΔE_COSMO=0.1 eV, OLYP; the equivalent ΔE based on the experimental J value is 0.026 eV).

The J for this complex is similar to those for oxidized, diferric ribonucleotide reductase (RNR_ox R2) and oxidized diferric methane monooxygenase (MMO_ox) (see summary of experimental data in Tables 3 and 5 of Han et al.[44]). Both contain high-spin Fe³⁺, with AF coupling of the two Fe sites. The bridging ligands are different for oxidized RNR_ox and MMO_ox. In addition to a carboxylate bridge, which is ineffective in mediating spin coupling, MMO_ox contains a hydrogen-bonded dihydroxyl (OH)₂ bridge, whereas RNR_ox contains a single oxo-bridge. The experimental J values (with the Heisenberg spin Hamiltonian above) are J_exp=8–20 cm⁻¹ for MMO_ox, and J_exp=180–216 cm⁻¹ for RNR_ox.The calculated J values (PW91) for model systems are in qualitative agreement with the experimental values: 78 cm⁻¹ (MMO_ox), and 480 cm⁻¹ (RNR_ox). Despite the difference in the functional used as well as chemical differences, these values bracket that obtained here for 1.

Table 3.

Structural parameters and Heisenberg coupling constants of [Fe(NO)₂{Fe(NO)(N(CH₂CH₂S)₃)}-S,S’].

Bond length Å/ Angle [°][a]	BS-OLYP- (vacuum)//PW91- (vacuum)[b]	BS-OLYP (COSMO)//PW91- (COSMO)[b]	Experimental[c]
Fe1–Fe2	2.72	2.71	2.77
Fe1–N1	1.72	1.72	1.74
N1–O1	1.18	1.20	1.15A/1.17B
Fe1–S1	2.29	2.27	2.31
Fe1–S2	2.34	2.33	2.36
Fe1–S3	2.22	2.23	2.23
Fe1–N4	2.31	2.25	2.23
Fe2–N2	1.67	1.66	1.67
Fe2–N3	1.65	1.65	1.66
N2–O2	1.18	1.19	1.13A/1.23B
N3–O3	1.19	1.19	1.16
Fe2–S1	2.28	2.28	2.30
Fe2–S2	2.27	2.27	2.29
Fe1-N1-O1	148.68	145.81	145.0A/151.7B
Fe2-N2-O2	162.92	162.18	161.6A/170.0B
Fe2-N3-O3	175.53	173.64	173.2

J[d][cm−1]	Vacuum	COSMO
Noodleman[e]	3599	3733
Yamaguchi[f]	2967	3055

^[a]See Figure 4 A for atom numbering.

^[b]OLYP/TZP single-point calculations at PW91/TZP geometries.

^[c]Ref. [49]. The X-ray structure is disordered for two NO units. Two different conformations are given here, denoted A and B.

^[d]Based on $\mathscr{H}=J{S}_{\mathrm{A}}{S}_{\mathrm{B}}$.

^[e]Equation (2).

^[f]Equation (3).

Table 5.

Structural parameters and Heisenberg coupling constants of 4.

Bond length [Å]/ Angle [°][a]	Vacuum BS-OLYP[b]	COSMO BS-OLYP[b]	Experimental[c]
Fe1–Fe2	2.70	2.70	2.70
Fe2–Fe3	3.63	3.63	3.57–3.59
Fe1–N1	1.64	1.65	1.66
Fe2–N2	1.65	1.65	1.67
Fe3–N3	1.65	1.65	1.67
N1–O1	1.19	1.19	1.16
N2–O2	1.19	1.19	1.16–1.17
N3–O3	1.19	1.19	1.16
Fe1–S1	2.19	2.19	2.21
Fe2–S1	2.25	2.25	2.25–2.27
Fe1-N1-O1	180.0	180.0	178.3
Fe2-N2-O2	162.4	163.1	163.6–168.1
Fe2-N3-O3	164.4	164.5	166.9–167.3

J[d][cm−1]	Vacuum	COSMO
J22, Noodleman[e]	78–182	147–214
J12, Noodleman[e]	5027–5050	4668–4683
J12, Yamaguchi[f]	3739–3804	3539–3577

^[a]See Figure 10 A for atom labels.

^[b]Broken-symmetry state optimized with OLYP/TZP, ADF.

^[c]Ref. [55].

^[d]Based on $\mathscr{H}=J{S}_{\mathrm{A}}{S}_{\mathrm{B}}$. See also Scheme 1.

^[e]Equation (2).

^[f]Equation (3).

It is also instructive to compare the calculated J for 1 to that in 2Fe ferredoxin-type systems. For example, in a {2Fe2S} synthetic complex [Fe₂S₂(S₂-o-xyl)₂]²⁻ containing two Fe³⁺ sites, the previously calculated J values (OLYP, ORCA, vacuum) are J=618 and 602 cm⁻¹ ($\mathscr{H}=J{S}_{\mathrm{A}}{S}_{\mathrm{B}}$) with the Noodleman and Yamaguchi formalisms, respectively,[20] whereas J_exp=(296±16) cm⁻¹.[45] Clearly, the experimental J for 1 is much smaller: J=95 cm⁻¹ (OLYP, vacuum), and J_exp=46 cm⁻¹ ($\mathscr{H}=J{S}_{\mathrm{A}}{S}_{\mathrm{B}}$).[41] The magnetic susceptibility properties of the binuclear complexes are governed by the energetics of the low-lying spin states, which are given by the Landé interval rule, E(S)–E(S–1)=JS [see also Eq. (4)], and the various spin state energy ladders resulting therefrom (and depicted in the various figures to follow). The tetranuclear Roussin’s black salt spin state diagram is more complicated, as expected (see below). The J values for the [Fe₂S₂(S₂-o-xyl)₂]²⁻ complex are good reference values for comparisons with the binuclear nitrosyl complexes, as we will show later.

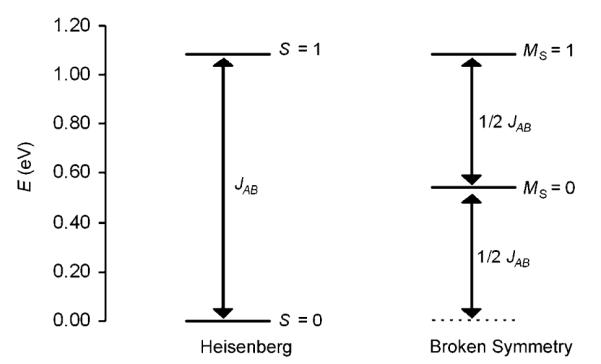
The computed J_AB for 1 was used to calculate the spin-projected energies of the pure spin states on the Heisenberg ladder (Figure 2). The relative energy of each pure spin state is given by Equation (4), and the spin-projected energy of the pure ground state S_min by Equation (5).

$$E\left(S\right)=(J_{\mathrm{A}\mathrm{B}}∕2)S(S+1)$$ (4)

$$E\left(S_{\min }\right)=E\left(S_{\max }\right)-(J_{\mathrm{AB}}∕2)\left[S_{\max }\right(S_{\max }+1)-S_{\min }(S_{\min }+1\left)\right]$$ (5)

Figure 2.

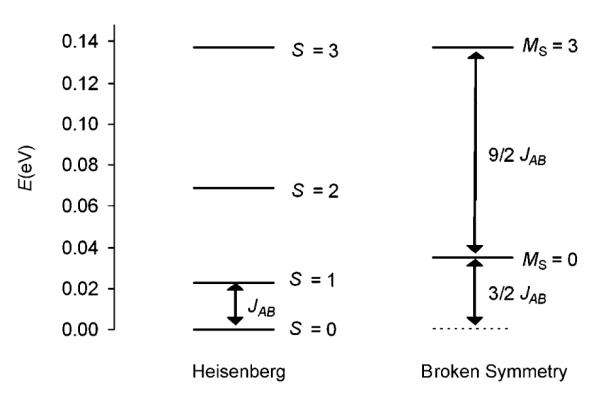
Heisenberg spin ladder for 1 showing the relative positions of the pure and broken-symmetry spin states (J_AB=184 cm⁻¹).

Here the energy of the ferromagnetically coupled, M_S=3 state was equated to that of the S_max state. The resulting Heisenberg spin ladder (based on J_AB=184 cm⁻¹ from OLYP with COSMO energies) is shown in Figure 2.

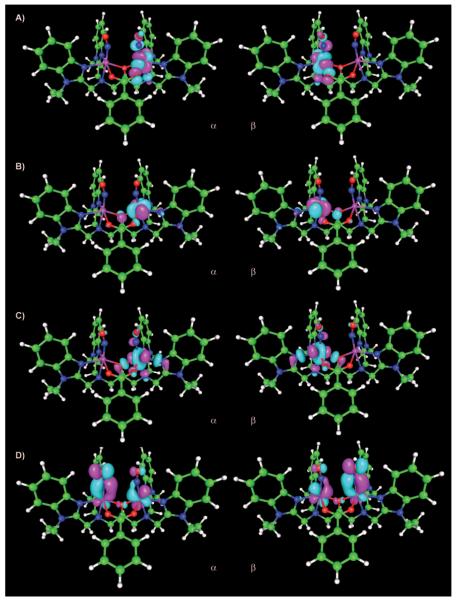
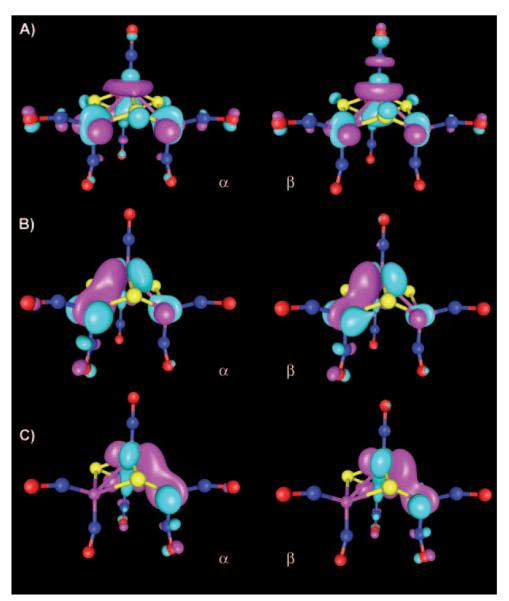
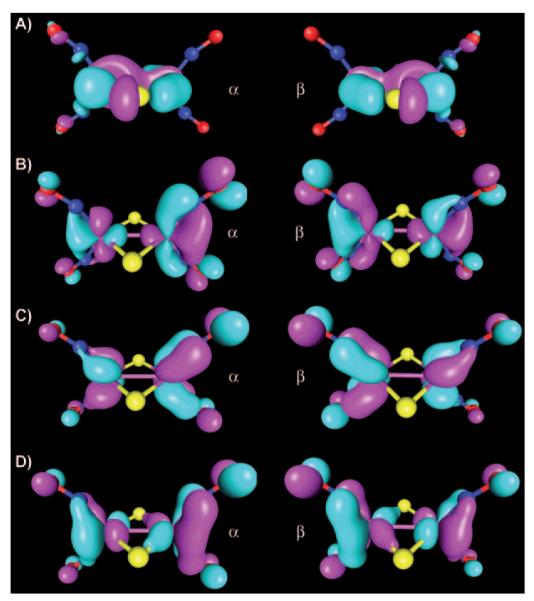
The magnetic orbitals involved in the antiferromagnetic coupling in 1 were analyzed in terms of unrestricted corresponding orbitals (UCOs, ORCA).[38] UCO analysis involves a unitary transformation of the BS orbitals to sort them into pairs with maximum overlap, with the goal of identifying orbital pairs that correspond to covalent and magnetic interactions.[46] Broken-symmetry calculations (OLYP, ORCA, vacuum) on the optimized geometry (OLYP, ADF) resulted in an electronic structure similar to that described above (Table 1), with Fe spin populations of ±3.55 and oppositely aligned NO spin densities of ±0.92. The computed J values are 116 and 117 cm⁻¹ (OLYP, ORCA, vacuum) with the Noodleman and Yamaguchi formalisms, respectively, in agreement with that mentioned above (95 cm⁻¹, OLYP, ADF, vacuum). The UCO analysis shows seven magnetic orbital pairs, with overlap values of <0.001, 0.076, 0.092, 0.758, 0.825, 0.848, and 0.882. The first three pairs correspond to the interaction between the two S=3/2 units and show very small overlap values (<0.001 to 0.092), in agreement with the small coupling constant (Figure 3A–C). The remaining four magnetic orbital pairs show high overlap values (0.758 to 0.882), and correspond to the antiferromagnetic interaction between iron and NO (Figure 3D). This interaction involves two SOMO d_π electrons on each iron and two π* electrons on each NO, leading to two strongly coupled orbital pairs on each {FeNO}⁷ unit. Although the four UCOs obtained here are consistent with this picture, all four orbital pairs are delocalized over both {FeNO}⁷ units (Figure 3D), as opposed to there being two pairs of magnetic orbital pairs on each unit.[47,48]

Figure 3.

Magnetic orbital pairs in 1 (OLYP, ORCA, four of seven magnetic pairs are shown, contour value 0.035). Overlap values: A) <0.001 (orbital pair no. 263); B) 0.076 (no. 262); C) 0.092 (no. 261); D) 0.758 (no. 260).

A binuclear {FeNO}⁷–{Fe(NO)₂}⁹ complex

The [Fe(NO)₂{Fe(NO)(N(CH₂CH₂S)₃)}-S,S’] complex (2) has an asymmetric di-iron core, involving one {FeNO}⁷ and one {Fe(NO)₂}⁹ unit bridged by two thiolate sulfur atoms (Figure 4).[49] This arrangement may be viewed as a substructure of the tetranuclear Roussin’s black salt anion (see below). Complex 2 has a magnetic moment of μ_eff=2.81 (293 K), which indicates a triplet ground state.[49] B3LYP calculations at the experimental structure support an S=1 ground state, arising from antiferromagnetic coupling between the S=3/2 {FeNO}⁷ and S=1/2 {Fe(NO)₂}⁹ units.[50] Attempts at geometry optimization of 2 (BLYP or B3LYP, 6-311G*) yielded poor agreement with the experimental structure, in particular an overestimation of the metal–metal distance by 0.15 Å (BLYP; this is due to spin contamination effects, as discussed above).[50] Optimization with OLYP (STO-TZP, COSMO) resulted in significant improvement in the Fe–Fe distance (calculated 2.78 Å versus X-ray crystallography values 2.77 Å), but also an unduly long Fe₁–N₄ bond (trans to the strong Fe–NO bond, Figure 4), which is overestimated by 0.18 Å and 0.10 Å in COSMO and in vacuum, respectively (see the Supporting Information, Table S1). The best agreement with the experimental structure was obtained by employing PW91 (STO-TZP, COSMO) for geometry optimization, which resulted in geometric errors of only 0.01–0.06 Å (Table 3). Given that the Heisenberg J is rather sensitive to geometry, we have evaluated it for 2 at both the PW91 and the OLYP geometries (Table 3, and Table S1 in the Supporting Information).

Figure 4.

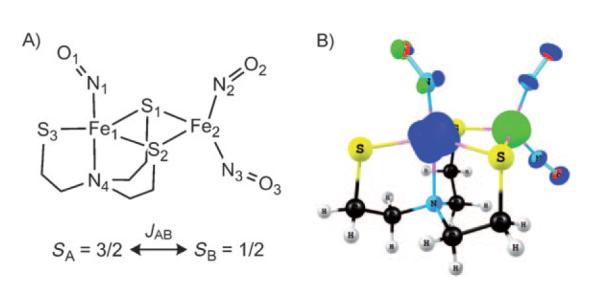
The [Fe(NO)₂{Fe(NO)(N(CH₂CH₂S)₃)}-S,S’] complex. A) Scheme showing atom numbering and J_AB coupling constant for interaction between {FeNO}⁷ (S_A=3/2) and {Fe(NO)₂}⁹ unit (S_B=1/2); B) Spin density for the M_S=1 state (ADF, OLYP//PW91, TZP, COSMO, contour value 0.03 eÅ⁻³).

The Fe spin populations are 2.35 and −1.15 for the {FeNO}⁷ and {Fe(NO)₂}⁹ units, respectively (OLYP//PW91, Table 1, Figure 4). The nitrosyl spin populations are relatively small, ranging from 0.19 to 0.34 (Table 1). For the OLYP geometry, slightly larger Fe spin populations were obtained (2.61 and −1.31). Overall, the absolute values of the spin populations of 2 are smaller than those for 1 discussed above, which may be explained by the much stronger spin coupling in 2 (see below).

The vacuum OLYP//PW91 Heisenberg J_AB for AF coupling between the Fe(NO)_x (x=1, 2) centers in 2 was found to be 3599 cm⁻¹ with Equation (2) (S_A=3/2, S_B=1/2, H=JS_AS_B), and somewhat less, 2967 cm⁻¹, with the Yamaguchi approach [Eq. (3)] (<S²>_HS=6.44, <S²>_BS=2.80). For the COSMO geometry, both values are slightly higher: 3733 and 3055 cm⁻¹, respectively (Table 3, OLYP//PW91). If the OLYP geometry is employed, the corresponding values in solvent are 2911 and 2485 cm⁻¹ (see the Supporting Information, Table S1, OLYP//OLYP), underlining the sensitivity of the computed J to the geometry. Overall, we may conclude that the antiferromagnetic coupling in 2 is significantly stronger (by about an order of magnitude) than in the carboxylate/alkoxide-bridged bis-{FeNO}⁷ complex 1. The thiolate bridges in 2 evidently contribute to the stronger coupling. Spin-projected energies were computed by assuming that the ferromagnetically coupled M_S=2 state corresponds to the S_max state, and OLYP/COSMO energies (J_AB=3733 cm⁻¹) were employed to generate the Heisenberg spin ladder, shown in Figure 5. To the best of our knowledge, the J value for 2 has not been determined experimentally. Figure 5 shows that the energy gap between the ground and excited states is fairly large, which makes it unlikely that magnetic susceptibility studies can shed light on the magnitude of J, except for the fact that it is large.

Figure 5.

Heisenberg spin ladder for 2, showing relative positions of pure and broken-symmetry spin states (J_AB=3733 cm⁻¹).

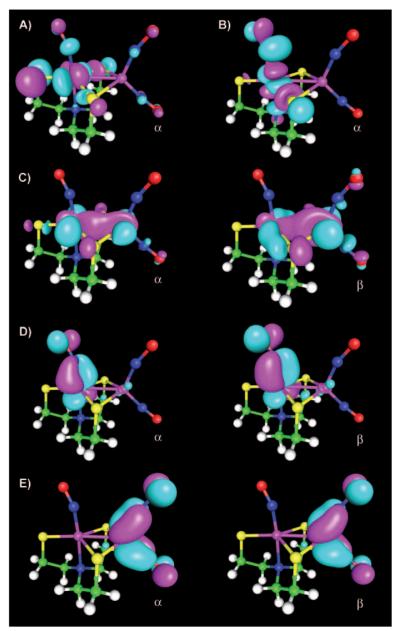
Single-point vacuum OLYP/TZVP calculations with ORCA on the optimized geometry (ADF, OLYP/TZP, COSMO) yielded spin populations in close agreement with those mentioned above (ADF electronic structure, Table 1). UCO analysis revealed one magnetic orbital pair with relatively large overlap (0.748, OLYP), related to antiferromagnetic coupling between the iron centers (Figure 6C). These magnetic orbitals describe a σ interaction along the Fe–Fe axis, but do not involve the NO π* systems. The two unpaired electrons are expected to be located on the {FeNO}⁷ unit, consistent with the two SOMOs (Figure 6A and B). In addition to these magnetic orbitals, six orbital pairs with small deviations from unity are observed, corresponding to antiferromagnetic coupling within the FeNO units (OLYP overlap 0.947, 0.975, 0.978, 0.984, 0.986, and 0.988, Figure 6D and E). The large overlap values indicate an almost spin-restricted description for both Fe(NO)_x units. The strong spin coupling is responsible for the small Fe spin population for the {Fe(NO)₂}⁹ unit (−1.15). The {FeNO}⁷ unit, which harbors the two SOMO electrons, exhibits a higher Fe spin population (2.35, Table 1).[51]

Figure 6.

UCO analysis of 2 (OLYP/TZVP, ORCA, three of seven magnetic orbital pairs are shown, contour value 0.035). A, B) SOMOs (orbital no. 99,100); C) magnetic orbital pair for antiferromagnetic coupling between iron centers (no. 98, overlap 0.748); D) orbital pair on {FeNO}⁷ unit (no. 97, overlap 0.947); E) orbital pair on {Fe(NO)₂}⁹ unit (no. 92, overlap 0.988).

Roussin’s red salt anion, a bis-{Fe(NO)₂}⁹ complex

Roussin’s red salt anion, [Fe₂(NO)₄(μ-S)₂]²⁻ (3), is made up of two S=1/2 {Fe(NO)₂}⁹ units (Figure 7), which couple antiferromagnetically to give a diamagnetic ground state.[16,52] The OLYP-optimized geometry of [Fe₂(NO)₄(μ-S)₂]²⁻ agrees well with the X-ray crystal structure,[52] with only a slight overestimation of the Fe–Fe distance (Table 4). However, due to the very strong coupling between the metal centers in 3, the OLYP wavefunction collapses to a spin-restricted solution, as opposed to a broken-symmetry state (this is a general characteristic of pure functionals; see the computational details section). The antiferromagnetic coupling in 3 was therefore analyzed with B3LYP. The Fe spin populations of the B3LYP broken-symmetry state of 3 are ±2.47 on the two iron centers; as expected, the spin densities on the NO groups are aligned oppositely relative to the iron atoms to which they are bound (Table 1).

Figure 7.

Selected results on 3. A) Atom numbering and J_AB coupling constant for the two S=1/2 {Fe(NO)₂}⁹ units; B) spin density for the B3LYP broken-symmetry state (M_S=0, Gaussian 03, COSMO, contour value 0.03 eÅ⁻³).

Table 4.

Structural parameters and Heisenberg coupling constants for 3.

Bond length [Å]/ Angle [°][a]	Vacuum BS-B3LYP// OLYP[b]	COSMO BS- B3LYP//OLYP[b]	Experimental[c]
Fe–Fe	2.75	2.76	2.70
Fe–N1	1.65	1.64	1.66
Fe–N2	1.64	1.65	1.66
N1–O1	1.21	1.20	1.16
N2–O2	1.21	1.21	1.16
Fe–S	2.25	2.25	2.24
Fe1-N1-O1	160.0	160.8	165.9
Fe2-N2-O2	163.7	163.6	165.9

J[d][cm−1]	Vacuum	COSMO
Noodleman[e]	7462	8773
Yamaguchi[f]	3476	4322

^[a]See Figure 7 A for atom numbering.

^[b]Broken-symmetry electronic structure optimized with B3LYP (Gaussian/6-311G(d,p)) at OLYP geometry (ADF/TZP).

^[c]Ref. [52]. Reported values are averages.

^[d]Based on $\mathscr{H}=J{S}_{\mathrm{A}}{S}_{\mathrm{B}}$.

^[e]Equation (2).

^[f]Equation (3).

Calculation of the Heisenberg coupling constant yields J_AB=3476 cm⁻¹ with Equation (3) (<S²>_HS=5.02, <S²>_BS=2.87), and a value of 7462 cm⁻¹ with Equation (2) (S_A=S_B=1/2) (B3LYP/6-311G(d,p)/Gaussian at vacuum OLYP/TZP/ADF geometry, Table 4). For the COSMO geometries, the values are 4322 and 8773 cm⁻¹, respectively (Table 4). Note that the magnitude of the computed J_AB values is fairly basis-set-dependent. At the same geometry (OLYP/TZP, ADF, vacuum), the J_AB values obtained for 3 with the Ahlrichs TZVP basis set (B3LYP, Gaussian, vacuum) are 8459 cm⁻¹ with the Noodleman approach [Eq. (2)], and 6837 cm⁻¹ with the Yamaguchi approach [Eq. (3)]. These values are significantly higher than those obtained with the 6-311G(d,p) basis set (7462 cm⁻¹ with Eq. (2) and 3476 cm⁻¹ with Eq. (3), Table 4).[53] The large difference between the Noodleman and the Yamaguchi approaches is mainly due to the fact that Equation (2) is valid only in the weak coupling regime. Thus, the strong coupling in [Fe₂(NO)₄(μ-S)₂]²⁻ is not described correctly by the Noodleman approach. Still, both <S²>_HS and <S²>_BS reflect considerable spin mixing (spin contamination). However, the difference <S²>_HS–<S²>_BS=2.15 is close to that expected between the pure S_HS=1 and S_BS=0 states, for which <S²>_HS–<S²>_BS=2. The spin-projected energies of 3 were computed by assuming that the ferromagnetically coupled state (M_S=1) corresponds to the S_max state, and B3LYP COSMO energies (J_AB=8773 cm⁻¹) were employed to generate the Heisenberg spin ladder, shown in Figure 8.

Figure 8.

Heisenberg spin ladder for 3 showing the relative positions of pure and broken-symmetry spin states (J_AB=8773 cm⁻¹).

Evidently, the computed J values for both 2 and 3 are much higher than those found for {2Fe2S} ferredoxin-type systems, as represented by the values quoted above for [Fe₂S₂(S₂-o-xyl)₂]²⁻.[20, 45] A valuable alternative comparison is provided by examining the spin-dependent bonding energy (SDBE), which analyzes the contribution of spin coupling to the overall bonding interaction between fragments. In this respect, non-nitrosylated ferredoxin-type systems behave differently compared to ligand-bridged iron nitrosyl complexes. The SDBE is defined as the energy stabilization of the spin ground state with respect to the barycenter of all pure spin states E(SDBE)=E(BAR-J)–E(S_min), with E(BAR-J) given by Equation (6), in which E(S) is defined as in Equation (4) and the degeneracy is D(S)=2S+1.

$$E\left(\mathrm{BAR}\text{-}\mathrm{J}\right)=\sum _{S=S\min }^{S=S\max }D\left(S\right)E\left(S\right)∕\sum _{S=S\min }^{S=S\max }D\left(S\right)$$ (6)

This stabilization energy is positive according to the definition above, which was first developed by Mouesca et al.[5] (see Table 4 in this reference), who called it the spin barycenter energy difference. By using the same methods as these authors,[5] we find E(SDBE) values of 3.75, 1.25, and 0.75 J for 1, 2, and 3, respectively. By employing the respective computed vacuum J values (Noodleman formalism, Tables 2, 3, and 4) for these complexes, we obtain E(SDBE) values of 0.04 eV for 1, 0.56 eV for 2, and 0.69 eV for 3. By comparison, for [Fe₂S₂(S₂-o-xyl)₂]²⁻ and oxidized {2Fe2S} ferredoxins, the E(SDBE) is 8.75 J, which translates to 0.67 eV for J=618 cm⁻¹ (OLYP, ORCA).[20] Thus, based on typical J values and E(SDBE), the spin bonding energies for {2Fe2S} ferredoxins are more or less comparable in strength to those for 2 and 3, whereas for 1 the spin bonding energy is much smaller.[54]

Analysis of the unrestricted corresponding orbitals (B3LYP/TZVP, ORCA, at the OLYP/TZP/COSMO ADF geometry) of 3 reveals nine orbital pairs, for which the overlap deviates from unity. The magnetic orbital pair with the smallest overlap (0.555) describes antiferromagnetic coupling between the two S=1/2 {Fe(NO)₂}⁹ centers (Figure 9A). The other eight magnetic orbital pairs show high overlap values (0.782, 0.787, 0.810, 0.821, 0.827, 0.828, 0.848, and 0.864, Figure 9) and are topologically similar to those describing the antiferromagnetic coupling in the {Fe(NO)₂}⁹ unit of 2 (Figure 6). All eight orbital pairs show significant delocalization over both {Fe(NO)₂}⁹ units (three of these orbital pairs are shown in Figure 9B–D).

Figure 9.

Magnetic orbital pairs of 3 (B3LYP, ORCA, four of nine pairs are shown, contour value 0.035). Overlap values: A) 0.555 (orbital no. 72); B) 0.828 (no. 66); C) 0.848 (no. 65); D) 0.864 (no. 64).

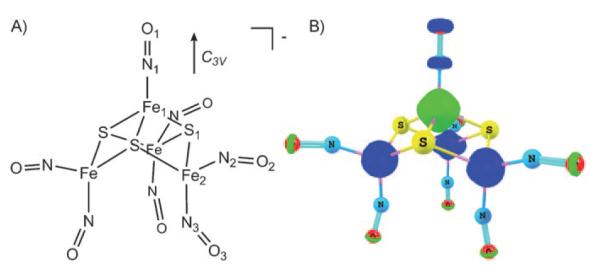
Roussin’s black salt anion, [Fe₄(NO)₇(μ₃-S)₃]⁻

Roussin’s black salt anion (4, Figure 10)[17,52,55,56] exhibits C_3v symmetry, with one apical {FeNO}⁷ unit and three basal {Fe(NO)₂}⁹ units. Antiferromagnetic coupling between the apical S=3/2 and the three basal S=1/2 units results in an overall diamagnetic ground state. The spin-density plot of the optimized broken-symmetry geometry is shown in Figure 10 (ADF, OLYP, COSMO). The OLYP broken-symmetry geometry agrees very well with the X-ray crystal structure,[55] with only a slight overestimation of the basal iron–iron distances (Table 5). In contrast, B3LYP broken-symmetry geometries showed severe deviations from the experimental structure.[17,18] The better OLYP geometries may be related to less spin-polarized descriptions, reflecting less contamination by higher S excited states. Thus, for OLYP/TZP, 4 shows Fe spin populations of only −1.18 for the apical iron and 0.62 for each basal iron (Table 1).

Figure 10.

Roussin’s black salt anion (4). A) Atom numbering and symmetry axis; B) spin density for the broken-symmetry M_S=0 geometry (ADF, OLYP/TZP, COSMO, C_3v, contour value 0.02 eÅ⁻³).

The Heisenberg spin Hamiltonian describing the coupling between the {FeNO}⁷ unit (S_A=3/2) and the three {Fe(NO)₂}⁹ units (S_B=S_C=S_D=1/2) in [Fe₄(NO)₇(μ₃-S)₃]⁻ is assumed to have the form of Equation (7), in which J₁₂ corresponds to the interaction between the apical iron and a basal iron, and J₂₂ that between any two basal iron centers (Scheme 1).

$$\begin{array}{cc}\hfill \mathscr{H}& =J_{12}(S_{\mathrm{A}}\cdot S_{\mathrm{B}}+S_{\mathrm{A}}\cdot S_{\mathrm{C}}+S_{\mathrm{A}}\cdot S_{\mathrm{D}})\hfill \\ \hfill & +J_{22}(S_{\mathrm{B}}\cdot S_{\mathrm{C}}+S_{\mathrm{B}}\cdot S_{\mathrm{D}}+S_{\mathrm{C}}\cdot S_{\mathrm{D}})\hfill \end{array}$$ (7)

Scheme 1.

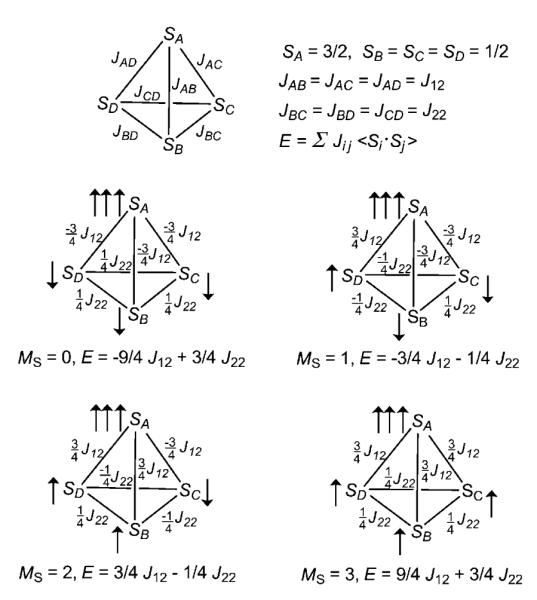
Schematic representation of Heisenberg coupling constants in 4 and of the four broken-symmetry states (M_S=0, 1, 2, 3).

Determination of J₁₂ and J₂₂ involved SCF optimization of multiple broken-symmetry states (M_S=0, M_S=1, M_S=2, M_S=3, Scheme 1) at the M_S=0 geometry. This required a lowering of the symmetry from C_3v to C_s (the C_s geometry, however, is exceedingly close to C_3v).

The energies of the broken-symmetry states can be expressed by Equation (8) (Scheme 1).

$$E=\Sigma J_{\mathrm{i}\mathrm{j}}<S_{\mathrm{i}}\cdot S_{\mathrm{j}}>$$ (8)

Thus, for S_i=3/2 and S_j=1/2, Equation (8) yields ±3/4 J₁₂, and for S_i=S_j=1/2, Equation (8) yields ±1/4 J₂₂, for which the plus sign is for parallel spin alignment and the minus sign is for antiparallel alignment. The values of J₁₂ and J₂₂ can be determined from the energy differences between different broken-symmetry states, as shown in the example in Equation (9), which results in J₁₂=5027 cm⁻¹ based on the Noodleman formalism (Table 5).

$$\begin{array}{cc}\hfill E(M_{\mathrm{s}}=3)-E(M_{\mathrm{s}}=0)& =(2.25J_{12}+0.75J_{22})\hfill \\ \hfill & -(-2.25J_{12}+0.75J_{22})=4.5J_{12}\hfill \end{array}$$ (9)

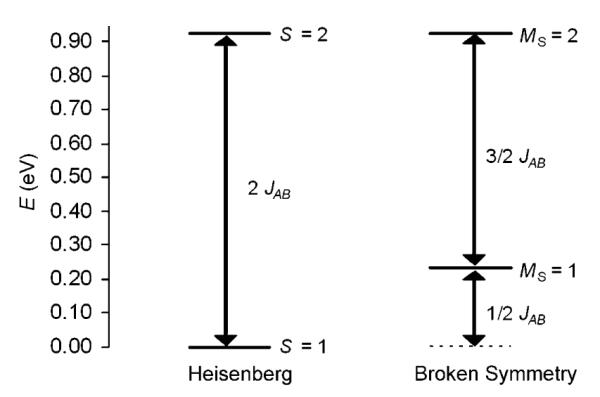
The energy difference between the two alternative broken-symmetry states, M_S=1 and M_S=2, yields J₁₂=5050 cm⁻¹. The magnitude of J₂₂ can then be evaluated as 78–182 cm⁻¹ (Table 5). For COSMO geometries, we obtained values of J₁₂=4668–4683 and J₂₂=147–214 cm⁻¹ (Table 5). The coupling constant J₁₂ is somewhat larger than the J describing the analogous interaction between the {FeNO}⁷ and {Fe(NO)₂}⁹ units in 2 (3733 cm⁻¹, ADF/COSMO, Table 3). In contrast, J₂₂ is small and antiferromagnetic, almost negligible compared to J₁₂. This system thus exhibits only slight spin frustration due to the parallel alignment of the basal irons. Similarly, the effect of J₂₂ on the predicted spin ladder (Figure 11) is very small.

Figure 11.

Heisenberg spin ladder for 4, showing relative positions of pure and broken-symmetry spin states (J₁₂=4668, J₂₂=147 cm⁻¹).

Determination of both J₁₂ and J₂₂ is not possible within the Yamaguchi approach. However, because Equation (9) shows that E(M_s=3)–E(M_s=0) results in a cancellation of J₂₂, these two states can be employed to determine J₁₂ within the Yamaguchi formalism. A J₁₂ value of 3539 cm⁻¹ was obtained (<S²>_Ms=0=0.838, <S²>_Ms=3=12.710, OLYP, COSMO, ADF). Also E_(Ms=2) – E_(Ms=1) results in a cancellation of J₂₂, resulting in a value of 3577 cm⁻¹ for J₁₂ (<S²>_Ms=1=3.025, <S²>_Ms=2=6.952, OLYP, COSMO, ADF). For the vacuum-optimized geometry, the J₁₂ values, as obtained by these two methods, are 3739 and 3804 cm⁻¹. The two energy differences thus give remarkably consistent values for J₁₂. Also, the Yamaguchi-based method has a broader range of applicability than Equation (9), due to the fact that the M_S=0 broken-symmetry state differs from M_S=3 only in the relative alignment of the apical spin (S_A) to the basal spins (S_B, S_C, S_D). Similarly, the M_S=2 broken symmetry state differs from M_S=1 only in the relative alignment of S_A to (S_B, S_C, S_D).

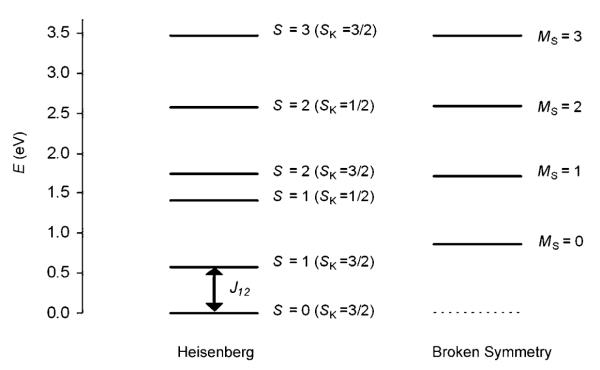
Based on Equation (7), the expression for the spin-projected energy becomes that given in Equation (10), in which S_K=S_B+S_C+S_D and S_T=S_A+S_K.

$$\begin{array}{cc}\hfill E(S_{\mathrm{T}},S_{\mathrm{K}})& =J_{12}∕2\left[S_{\mathrm{T}}\right(S_{\mathrm{T}}+1)-S_{\mathrm{K}}(S_{\mathrm{K}}+1\left)\right]\hfill \\ \hfill & +J_{22}∕2\left[S_{\mathrm{K}}\right(S_{\mathrm{K}}+1\left)\right]\hfill \end{array}$$ (10)

The Heisenberg spin ladder was calculated by assuming that the energy of the M_S=3 state corresponds to the pure S=3 state (Figure 11, J₁₂=4668, J₂₂=147 cm⁻¹). The ladder contains six unique pure spin states between S=0 and S=3. There are two S=1 and two S=2 states, which differ in the magnitude of S_K (Figure 11).

It is constructive to contextualize the main Heisenberg spin coupling parameter (J₁₂) in relation to the J of {4Fe4S} ferredoxin protein active sites.[5] Evaluation of the comparative spin bonding energies should be similarly illuminating. A simple but relevant computational model for {4Fe4S} complexes is [Fe₄S₄(SR)₄]²⁻, in which R=CH₃. The Fe sites are delocalized mixed-valence, and can be decomposed into two mixed-valence {Fe₂S₂} rhombs (with the delocalized 2Fe pair, 2Fe^2.5+, parallel spin within a rhomb), with opposite spin alignment for the alternate {Fe₂S₂} rhombs (layers) of the cubane. Then the effective spin Hamiltonian is $\mathscr{H}=J_{\mathrm{m}}{S}_{12}\cdot S_{34}$ with S₁₂=9/2, S₃₄=9/2, which correspond to delocalized pairs of spins S₁₂=S₃₄=5/2+2. The delocalization energy within each rhomb is large enough to force parallel spin alignment, so that this is a reasonable Hamiltonian and effective for computation. Calculations on [Fe₄S₄(SR)₄]²⁻ with a Vosko–Stoll exchange correlation potential and a Becke perturbative correction (VS+B) (vacuum) gave J_m=645 cm⁻¹.[5] Related experimental values from analysis of NMR paramagnetic shifts in synthetic {4Fe4S} complexes are J_m=295–413 cm⁻¹[57] and 261–397 cm⁻¹[58] from magnetic susceptibility studies. These experimental values are about 40–60 % of those calculated, which is fairly typical. Clearly, Table 5 shows that the J₁₂ for 4 greatly exceeds the interlayer J_m for {4Fe4S} complexes.

However, once again, the spin bonding energy tells a different story. For 4, the spin bonding energy is E(SDBE)=3.75 (J₁₂) (neglecting the much smaller J₂₂ terms), whereas for [Fe₄S₄(SR)₄]²⁻, E(SDBE)=24.75 (J_m). Numerically, these give comparable SDBEs.[59,60] Thus, with J₁₂=3804 cm⁻¹ (OLYP) for 4, we obtain an E(SDBE) of 1.77 eV, which is comparable to the value of 1.98 eV calculated for [Fe₄S₄(SR)₄]²⁻. Although both of these values are likely to be larger than the experimentally determined values, these spin bonding energies in the two cases should still be fairly high and comparable in magnitude. Further, in the {4Fe4S} complexes, the total spin-dependent delocalization energy is also large: E(SDDE)=10B for the two rhombs, for which B=645 cm⁻¹ (VS+B, calculated) and 699–787 cm⁻¹ (estimated from the position of absorption bands in the near infrared). These translate to E(SDDE)=0.78 eV (VS+B) versus about 0.91 eV (experiment). Overall, the much higher J values in Roussin’s red and black salts are compensated by smaller site spins, resulting in spin bonding energies similar to those in the non-nitrosylated {2Fe2S} and {4Fe4S} ferredoxins (and related synthetic complexes), which feature smaller J values, but also higher site spins and higher numbers of coupled magnetic orbitals.

The magnetic orbitals of 4 were analyzed through UCO analysis (OLYP/TZVP, ORCA, vacuum). The UCO calculations yielded an electronic structure consistent with that described above (Table 1). The apical S=3/2 {FeNO}⁷ unit formally has three unpaired electrons, located in the d_z², d_x²–y², and d_xy orbitals (where the d_xz and d_yz electrons are involved in π-bonding interactions with NO). Coupling of these SOMO electrons to the d_z²-based SOMOs of the basal irons leads to three magnetic orbital pairs with overlap values of 0.909, 0.946, and 0.946 (Figure 12A–C). The antiferromagnetic coupling between iron and nitrosyl in the four FeNO units is expected to involve 14 magnetic pairs (four electron pairs for each {Fe(NO)₂}⁹ unit and two pairs for the {FeNO}⁷ unit). The OLYP description gives overlap values of 0.987 to 0.997 for these 14 orbital pairs. The deviations from unity are so small that these orbital pairs can be considered to represent covalent interactions.[61]

Figure 12.

Magnetic orbital pairs in 4 (OLYP/TZVP, ORCA, contour value of 0.035). Overlap values: A) 0.909 (orbital pair no. 128); B) 0.946 (no. 127); C) 0.946 (no. 126).

Spin-density and magnetic orbital isovalue plots for complexes 1–4 show how the Fe–NO bond interacts with the remaining spin density in the overall broken-symmetry picture. In several cases, as a result of strong Fe(d_π)–NO(π*) interactions, the magnetic orbitals (UCOs) of a fragment trans to a given Fe–NO bond are oriented so they can engage in bridge-mediated interactions with other fragment magnetic orbitals. Thus, the apical Fe–NO interaction in 4 directs the fragment spin density toward the basal fragments, and the basal Fe(NO)₂ fragments direct their spin densities upward toward the Fe2-S-Fe1, as well as toward the trigonal axis (Figures 10 and 12), which explains the strong spin coupling in Roussin’s black salt. Further support for this analysis comes from calculations probing the effects of bending the apical FeNO angle in 4 from 180° to 120°. This change increases the local spin density on the apical FeNO group, while weakening the trans-directing ability of the apical NO, resulting in a substantial reduction in the apical/basal coupling strength. Thus J₁₂(180°)=3661 cm⁻¹ and J₁₂(120°)=2972 cm⁻¹ (by using Eq. (3), vacuum, OLYP/TZP (ADF), C₁ symmetry). The strong Heisenberg spin coupling predicted for 2 (Figures 4 and 6) and 3 (Figures 7 and 9) may be rationalized in a similar manner. By contrast, the situation in 1 is different. As can be seen in Figures 1 and 3, directing the Fe spin density trans to the FeNO groups (for both Fe–NO groups) leads to very weak Fe–Fe coupling, mediated by the alkoxy bridging oxygen (O3). The bridging carboxylate group provides even weaker mediation of spin coupling between the two iron centers, as shown in Figure 3.

Conclusion

Roussin’s red and black salts are iconic structures in iron– sulfur–NO chemistry, a field that is currently undergoing a renaissance, thanks to its biological relevance. A detailed understanding of the electronic structures and properties of these complexes may engender significant biomedical advances, particularly in the form of light-activated NO donor drugs. With their complex spin-coupled electronic structures, Roussin’s salts are also of exceptional theoretical interest, as evidenced by multiple studies from the early days of quantum chemistry, when the methods available were hardly equal to the task.[62] In recent years, we and others have applied broken-symmetry DFT methods to these systems, and such efforts have led to a first-order electronic-structural description of Roussin’s salts.[17,18,20] Somewhat surprisingly, in view of the importance of the problem, a detailed analysis of spin coupling in these systems has not been reported until now. We have provided such an analysis here, based on broken-symmetry DFT methods.

We have studied three nitrosylated binuclear clusters: [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺ (1), [Fe(NO)₂{Fe(NO)-(NS₃)}-S,S’] (2), and Roussin’s red salt anion [Fe₂(NO)₄ (μ-S)₂]²⁻ (3). Although the Heisenberg J for 1 is small (≈10² cm⁻¹), 2 and 3 exhibit J values that are at least an order of magnitude higher (≈10³–10⁴ cm⁻¹), in which the J values refer to the Heisenberg spin Hamiltonian H=JS_AS_B. Both the original Noodleman and the more general Yamaguchi formalisms were used to calculate the J values. For Roussin’s black salt anion, [Fe₄(NO)₇(μ₃-S)₃]⁻ (4), the Heisenberg spin Hamiltonian describing the coupling between the {FeNO}⁷ unit (S_A=3/2) and the three {Fe(NO)₂}⁹ units (S_B=S_C=S_D=1/2) in [Fe₄(NO)₇(μ₃-S)₃]⁻ was assumed to have the form of Equation (11), in which J₁₂ corresponds to the interaction between the apical iron and a basal iron, and J₂₂ to that between any two basal iron centers.

$$\begin{array}{cc}\hfill \mathscr{H}& =J_{12}(S_{\mathrm{A}}\cdot S_{\mathrm{B}}+S_{\mathrm{A}}\cdot S_{\mathrm{C}}+S_{\mathrm{A}}\cdot S_{\mathrm{D}})\hfill \\ \hfill & +J_{22}(S_{\mathrm{B}}\cdot S_{\mathrm{C}}+S_{\mathrm{B}}\cdot S_{\mathrm{D}}+S_{\mathrm{C}}\cdot S_{\mathrm{D}})\hfill \end{array}$$ (11)

Although the basal–basal coupling constant J₂₂ was found to be small (≈10² cm⁻¹), the apical–basal coupling constant J₁₂ is some forty times higher (≈4000 cm⁻¹). In other words, the nitrosylated iron–sulfur clusters feature some exceptionally high J values relative to non-nitrosylated {2Fe2S} and {4Fe4S} clusters.

An analysis of spin-dependent bonding energies provided crucial insight into this phenomenon. Shorn of technical details (which are described above), the energy difference between the high-spin (i.e., ferromagnetically coupled iron sites) and low-spin (i.e., maximum spin coupling) states of Roussin’s salts are indeed rather similar to those of analogous non-nitrosylated iron–sulfur clusters. However, the individual site spins are lower in the nitrosylated systems, resulting in a smaller denominator in both the Noodleman and Yamaguchi formulas [Eqs. (2) and (3)], which translates into the high J values.

Finally, unrestricted corresponding orbital analysis provided an MO rationale for the strong spin couplings in Roussin’s red and black salts. Not only are the bridging sulfide groups more effective in mediating spin coupling than oxo, alkoxo, and carboxylate groups, the trans-directing effects of the NOs on fragment spin densities also play a major role in enhancing inter-site spin coupling in complexes 2–4.