Abstract
The study of collective or group-level movement patterns can provide insight regarding the socio-ecological interface, the evolution of self-organization and mechanisms of inter-individual information exchange. The suite of drivers influencing coordinated movement trajectories occur across scales, resulting from regular annual, seasonal and circadian stimuli and irregular intra- or interspecific interactions and environmental encounters acting on individuals. Here, we promote a conceptual framework with an associated statistical machinery to quantify the type and degree of synchrony, spanning absence to complete, in pairwise movements. The application of this framework offers a foundation for detailed understanding of collective movement patterns and causes. We emphasize the use of Fourier and wavelet approaches of measuring pairwise movement properties and illustrate them with simulations that contain different types of complexity in individual movement, correlation in movement stochasticity, and transience in movement relatedness. Application of this framework to movements of free-ranging African elephants (Loxodonta africana) provides unique insight on the separate roles of sociality and ecology in the fission–fusion society of these animals, quantitatively characterizing the types of bonding that occur at different levels of social relatedness in a movement context. We conclude with a discussion about expanding this framework to the context of larger (greater than three) groups towards understanding broader population and interspecific collective movement patterns and their mechanisms.
Keywords: circadian rhythm, coherence, elephant, movement ecology, time-series analysis, wavelets
1. Introduction
Swarms of insects, flocks of birds and the long-distance ungulate migrations provide stunning examples of self-organizing collective movements, the study of which has proved relevant for many branches of science. Empirical studies of movement across multiple individuals have provided important insight regarding the influence of social interactions on the spatial structure of populations [1], mechanisms of sexual segregation [2], movement synchronization in relation to group position and size [3] and connections between aggregate level patterns and rules governing behavioural switching and interactions at the individual level [4,5]. Whether group-level patterns provide evolutionary or ecological advantage or are merely the consequence of individual-based decisions has also been discussed [4,6].
In wildlife systems, combined analysis of multiple trajectories has provided insight into population-level movement parameters [7], yet the direct comparison between two or more individual movement paths for investigating social interactions and collective movement has received comparatively little attention (but see [8]). By contrast, individual-based simulation models have provided considerable advances in determining how individual decision rules can affect group-level collective patterns from relatively parsimonious rules, e.g. movement depends only on other neighbouring individuals, but not spatial heterogeneity in relevant landscape features [6,9]. A recent work by Getz & Saltz [10] that incorporates social and ecological processes illustrates how rapidly complexity can emerge in the design and study of collective movement models. Directly testing collective movement models with empirical data has remained challenging because experimental manipulation is sometimes (e.g. see the collection of papers based on experiments in Dyer et al. [11]) but often not possible, and likelihood functions for highly detailed models are very complex. The approach emphasized here relies on the use of statistical ‘probes’ as one essential component to robust data analysis [12–14], and complements both experimental work and fitting of phenomenological or mechanistic models.
From data on an individual time series of geographical locations, several candidate univariate time series can be obtained (figure 1) to which standard time-series tools such as those used here can be applied to characterize movement. A fully comprehensive analysis of collective movement will simultaneously include step length, turning angle, absolute heading and relative position, but the descriptors of movement data that are most informative or relevant to collective patterns are potentially system specific. As elaborated on by Gurarie et al. [15], persistence and turning angle velocities often meld step length and turning angle information into useful (i.e. approx. normally distributed random variables) movement descriptors from which descriptive statistics with standard tools can be obtained. Here, analyses based on either persistence velocity or step length yielded practically identical results, while correlation between turning velocity data was consistently weak and uninformative about coherence across all individuals. For groups in which individuals do not maintain consistent position relative to other members, correlations in turning velocity or turning angle may not characterize subtle similarities or differences in movement. Thus, we use step length as an initial probe (although the simulation studies below may be more generally interpreted as a study on either step length or persistence velocity time series) with subsequent analysis of the other descriptors of collective movement conditioned on these results.
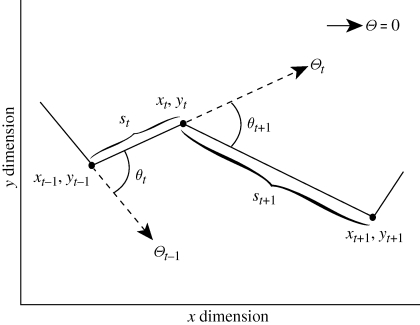
Figure 1.
Schematic of potential movement time-series data: step length (net displacement between sequential locations) S; absolute direction Θ; and turning angle θ, defined to lie between (−π, π]—derived from time-indexed location data (xt, yt) typically collected from animal telemetry. In this paper, step-length time series SN from multiple individuals are analysed in the context of socio-ecological and spatial information to understand properties of collective movement. Alternatively, the persistence and turning velocities at time t, defined as pt = St cos(θt) and Tt = St sin(θt), respectively, could be studied with the methods of this paper.
In a previous study, Polansky et al. [8] applied wavelet coherence to characterize movement relatedness of a wild African buffalo (Syncerus caffer) population whose member groups form and separate over time, referred to as fission–fusion societies [16]. In this system, individuals typically showed step-length distributions similar to a random walk, resulting in somewhat simple presence or absence of synchrony between individuals. However, in many animal systems, strong circadian rhythms in movement are also common in addition to random movements [8,12,17,18]. Here, we build on the baseline provided by the buffalo example by exploring the occurrence of alternative classes of movement synchrony based on coordination in both circadian rhythms and stochastic processes.
In this paper, we develop a conceptual framework for synchrony classification based on the degree to which two individuals share random movement properties and circadian activity patterns (referred to as deterministic structure here). Conceptual descriptions of different types of synchrony and examples are initially presented without technical details. A stochastic movement model that produces practically continuous space–time trajectories based on circadian rhythms (deterministic) and noise (stochastic) processes in the step-length data that can be correlated across individuals is then introduced. We present the methods used to quantitatively define the degree of synchrony outlined in our framework, with a review of the statistical and mathematical details provided in the electronic supplementary material, appendix A. Simulation experiments with the model indicate that these tools can effectively differentiate the extent of synchrony between two individuals with differing degrees of deterministic and stochastic similarity. Applying the conceptual framework and related analytical approaches to empirical movement data from African elephants (Loxodonta africana), we illustrate the emergence of several types of movement synchrony and show how the classification is most likely to be both a function of social relatedness and a shared environment that induces circadian activity cycles. Finally, we discuss some broader contributions of this framework to collective movement studies and movement ecology in general. We use the freely available R programming environment [19] to carry out all simulations and analyses, and thus coherence tools for assessing synchrony classification are readily available.
2. Pairwise movement synchrony and a movement coherence spectrum
For many species, the behaviours and underlying mechanisms that give rise to collective movement are variable and complex, being derived from internal states and external cues in the context of organismal biology [20,21]. That individual movement trajectories represent an amalgamation of different behavioural states is increasingly recognized [22]. A useful biological characterization of a particular behavioural state is the mean (determinism) and variance (stochasticity) of step lengths, which can serve to characterize foraging strategies [23] or spatial location probability distributions [24,25]. The consistency or variation of time spent in each behavioural state provides a second opportunity for both determinism and stochasticity to influence patterns in data. Empirical data across many different wildlife systems demonstrate this, i.e. that the sequence of behavioural states and associated time durations are often periodic at circadian scales (see [7,8,12,17] and our own additional unpublished analyses).
Motivated by the somewhat abstract yet intuitive notion that movement consists of both cyclic determinism and stochasticity, we can conceptualize movement synchrony between individuals along a spectrum from none to complete that is a function of both deterministic and stochastic properties of movement trajectories. The contribution of these features to the degree of synchrony along this continuum can be measured by squared coherence and delineated as follows.
— No synchrony. At one extreme, deterministic properties are unrelated and stochastic correlation is absent between two movement trajectories.
— Intermediate synchrony. A variety of states varying from strong deterministic similarity coupled with weak stochastic similarity to strong stochastic similarity coupled with weak deterministic similarity. Activity oscillation waves may be in phase with differences near 0 (e.g. elephants ‘close’ in space–time but not completely pair bonded, wildebeest and zebra migrating together) or out of phase with absolute values of phase difference near π (e.g. temporal niche partitioning around a shared resource [26]). In the examples postulated, shared ecological or environmental determinants of movement between individuals may generate co-oscillations in movement activity at similar frequencies even if there is no inter-individual relationship, e.g. temperature fluctuations can initiate coordination in circadian rhythms (the deterministic component), while sudden rain showers may drive stochastic correlation.
— Strong synchrony. Characterized by identical deterministic properties and high correlation in stochasticity so that the movement path of one individual strongly predicts the movement path of another. This synchronous relationship reflects tight coupling in the ecological/environmental rules determining behaviour as well as a high degree of inter-individual coordination. An interesting special case includes strong correlation in a random walk where the ‘deterministic’ contribution is often 0 (e.g. buffalo herds [8]).
— Complete synchrony. The extreme case whereby deterministic rules of movement are exactly coordinated and stochastic correlation is 1, likely to occur for relatively brief moments of time (e.g. close-knit groups: schools of fish, flocks of birds, family groups of ungulates).
To underpin this conceptual framework with analytical methods that allow the quantification of the degree of synchrony between movement trajectories, we apply Fourier and wavelet transforms, standard statistical tools from physical and statistical sciences, to assess pairwise synchrony states in a movement ecology context. The following analyses focus on step lengths, but other movement properties integrating information on turning angle such as movement persistence or turning velocity (figure 1) [15] are equally applicable. We note that the following approaches alone cannot strictly distinguish between synchrony induced by sociality or synchrony induced by shared environment or ecology. As we illustrate with our case studies, however, comparing types of synchrony in the context of spatial separation and other covariate data allows plausible hypotheses to be made (and others to be rejected) about the mechanisms underlying a particular synchrony classification.
3. A movement model
Basic elements of movement data in isolation of any knowledge about covariate data are step length, turning angle between three successive locations and the absolute direction (heading) between successive locations. We denote the continuous position of an animal at time t in the plane R2 by r(t) = (x(t), y(t)). The data are discretely sampled locations r(tj) = (x(tj), y(tj)), j = 0,1,…,N, at a constant sampling interval Δt = tj+1 – tj for all j, with absolute heading from r(tj−1) to r(tj) denoted by Θj. The time series SN = {S1, …, SN} of each individual is used to construct N step lengths, where Sj = |r(tj) − r(tj−1)|/Δt, j = 1, …, N, and the turning angle obtained from three sequential positions r(tj−1), r(tj) and r(tj+1) is θj = Θj+1 − Θj (figure 1). The methods applied here to define categories of coherence rely on SN, while comparison of θj and Θj are presented corroboratively.
To explore the utility of frequency-based coherence analysis in distinguishing across the categories of movement coherence outlined above, we created a model that can accommodate the different conceptual categories. The model starts by describing the continuous space–time position r(t) of an animal at time t with the stochastic differential equation
| 3.1 |
where μ is the drift representing the deterministic component of incremental movement, σ is a scalar function of time controlling the stochastic contribution to incremental movement, B is a Wiener process and r(0) is the initial location. A detailed explication on spatial movement models such as equation (3.1) and their simulation can be found in Brillinger [27]. To model movement in the x–y plane R2, μ and B, and hence r, are defined as 2 × 1 matrices representing the abscissa (e.g. longitude) and ordinate (e.g. latitude) dimensions. This model closely matches movement models in Brillinger et al. [12], Preisler et al. [17] and Polansky et al. [8]; however, when carrying out the simulations, we included a correlation parameter ρ to control the stochastic similarity in the incremental move values between locations of two different individuals. For ρ = 0, the two movement paths are unrelated with respect to their stochastic features (e.g. straight-line path of a predator versus a tortuous path of prey), and as ρ approaches 1, the two individuals increasingly share a similar response to ‘environmental noise’ (alternatively, ρ near 1 could be interpreted as a mimicking between individuals). We could not think of a biologically plausible reason to explore negative values of ρ (conspecific avoidance would be better modelled as negative correlation in the deterministic component μ of movement), so analyses of such scenarios are not presented.
For simplicity, we modelled only two distinct canonical behavioural modes of activity (e.g. foraging and taxis) by assuming that μ and σ switch among two sets of values 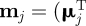 , σj) for j = 1 or 2, where
, σj) for j = 1 or 2, where 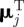 is the transpose of μj. Parameter values for μj(t) and σj(t) were set to be different by an order of magnitude with
is the transpose of μj. Parameter values for μj(t) and σj(t) were set to be different by an order of magnitude with 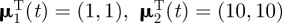 , σ1(t) = 2 and σ2(t) = 5, for all t. Other choices of parameter values providing relatively distinct behavioural states with respect to step-length values resulted in similar conclusions, reflecting the insensitivity of coherence methods to changes in the amplitude of step length. Let
, σ1(t) = 2 and σ2(t) = 5, for all t. Other choices of parameter values providing relatively distinct behavioural states with respect to step-length values resulted in similar conclusions, reflecting the insensitivity of coherence methods to changes in the amplitude of step length. Let 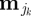 be the kth behavioural state in the sequence
be the kth behavioural state in the sequence 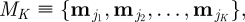 where K − 1 is the total number of state switches during a single day, and let EK ≡ {τ1, τ2, …, τK} be the expected temporal duration for each
where K − 1 is the total number of state switches during a single day, and let EK ≡ {τ1, τ2, …, τK} be the expected temporal duration for each 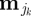 . Assigning values to the τk in units of hours such that
. Assigning values to the τk in units of hours such that 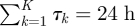 , together with the state sequence MK, defines a behavioural sequence determining the circadian pattern of behaviour.
, together with the state sequence MK, defines a behavioural sequence determining the circadian pattern of behaviour.
We considered three basic types of circadian patterns that are relevant to a wide range of taxa whose movements regularly cycle between distinct behavioural modes: deterministic type 1—1 cycle d−1 dominates, reflecting one period of relative activity and one period of relative inactivity such as might be found in central-place foraging organisms, and modelled by setting K = 2 and M2 ≡ {m1, m2} with τ1 = 4 and τ2 = 20; deterministic type 2—2 cycles d−1 dominates, reflecting two periods of relative activity separated by two periods of relative inactivity such as might be found in crepuscular organisms, and modelled by setting K = 4 and M4 ≡ {m1, m2, m1, m2} with τ1 = 4, τ2 = 8, τ3 = 4 and τ4 = 8; and, as a null model to independently explore the influence of the correlation across individuals in the absence of deterministic movement components, we also generated movement labelled here as deterministic type 0—0 cycles d−1, modelled by setting K = 1 and M1 ≡ {m1} with τ1 = 24; individual movement is modelled as a single type of random walk. Additionally, implementation of the latter allows comparison of movement patterns with deterministic components against those without. For each simulation day, the actual amount of time spent in each behavioural state 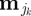 can be made stochastic by selecting a uniform random variable distributed on the interval [τk − τmin, τk + τmax], where τmin, τmax ≥ 0.
can be made stochastic by selecting a uniform random variable distributed on the interval [τk − τmin, τk + τmax], where τmin, τmax ≥ 0.
Summarizing the movement model, its main deterministic feature is the regularly oscillating changes between distinct canonical behavioural modes, while its main stochastic feature allows correlation in noise across individuals by controlling the correlation ρ between two individuals, which may be interpreted as representing shared responses to noise or a degree of inter-individual attraction. Using the Euler-based method [28] to simulate trajectories from equation (3.1) allows a practically continuous space–time trajectory from which to sample locations at user-specified sampling intervals in simulation experiments. To match the empirical data analysed, we use Δt = 1 h with simulation time steps set at 1 min (see electronic supplementary material, appendix A, figure S1, for the results of different sampling intervals).
4. Time-series coherence
In general, analysis of SN can be accomplished using either time-domain (regression using difference equations) or frequency-domain (regression on periodic functions) statistics [29,30]. For movement, frequency-domain approaches are often naturally suited for studying collective movements whose members engage in fairly regular oscillations between behavioural states across a range of temporal scales (e.g. diurnal to seasonal-based cycles). We note that for many frequency-domain models, there exists an exact counterpart in the time domain [29], but the approach taken here is often more economical for quantifying pairwise movement owing to the underlying oscillatory quality of behavioural sequences and their subsequent reflection in the signal SN. The key tool of frequency-domain statistics that we employ is the squared coherence function, which measures the strength of relatedness across two time series (though it is possible to expand it to multiple series) based on computing estimates of spectral densities of the component time series and their cross-spectra (electronic supplementary material, appendix A). This metric can quantitatively place pairwise movement along a synchrony spectrum ranging from absent to complete. Furthermore, the use of wavelet analysis provides time-localized information on the strength of coherence between the SN of different individuals so that changes in synchronous states can be identified with respect to temporal or spatial covariate information. Wavelet analysis is a valuable and increasingly standard tool for studying ecological time series [31], and the capacity for time-localized quantification of synchrony is essential given the transient nature and spatio-temporal dependence in behavioural states [7,8,15,18].
A descriptive summary of Fourier and wavelet analysis as applied in this study is provided here, with a more detailed review of the statistical machinery and directions to further literature of spectral coherence for both approaches provided in the electronic supplementary material, appendix A. Coherence captures the correlation between two time series, indexed by frequency. Squared coherence measures the strength of the linear association between the SN of two individuals with values between 0 (absent) and 1 (complete) at different frequencies. Shared activity is reflected by significant coherence values, which can be used to place pairwise movement coherence along the synchrony spectrum described above. When movement stochasticity is highly correlated between individuals, squared coherence will also be significant at frequencies not related to larger scale patterns of movement; i.e. there will be significance across all frequency values. Deviations in the squared coherence value from 1 indicate uncorrelated noise, the presence of nonlinearity or differentiation in determinants influencing the movement of the two individuals. Thus, for individuals that are unrelated, on average we will not expect significant squared coherence at any frequency.
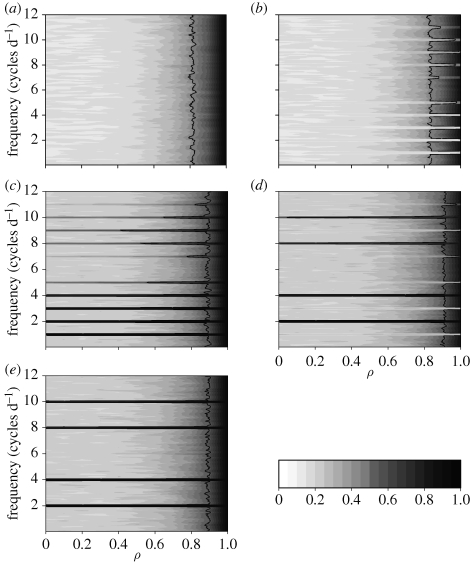
Figure 2 illustrates expected patterns of (Fourier) cross-coherence for movement trajectories undergoing similar or different deterministic circadian patterns across a range of correlation ρ values driving the incremental stochastic contributions to step lengths. For movement trajectories in which both individuals do not show any circadian pattern (i.e. there is no strong deterministic component to their movement pattern), coherence emerges only for the correlation parameter ρ at values approximately ≥0.8 with the result of complete synchrony between individuals (figure 2a) as ρ tends towards 1. When individuals show a mismatch between their deterministic movement properties (figure 2b,d), on average, individuals will show significant coherence only with high step-length correlation or at frequencies for which both movements oscillate. Given that both movement trajectories are reflecting non-trivial (i.e. not type 0) and identical circadian activity patterns (figure 2c,e), two movement trajectories typically show coherency at frequencies related to their circadian nature of movement even when their incremental step-length correlation ρ ≈ 0 (intermediate synchrony). As ρ approaches 1, coherency becomes significant across the remaining frequencies, capturing the stochastic properties of movement data and movement becomes completely synchronous. The significant coherence at frequencies unrelated to the circadian patterns of movement appearing in figure 2c–e, and in general how patterns of coherence relate to sampling interval, is discussed in the electronic supplementary material, appendix A, figure S1. However, we have found that such spurious results are easily identified in practice by direct examination of data (e.g. box plots of step length arranged by time of day [8]). Rather, the transience in the strength of coherence tends to limit the usefulness of Fourier-based coherence in practice, and to solve this problem, we turn to wavelet-based coherence analysis.
Figure 2.
Contours of averaged-squared coherence values of 100 pairs of simulated trajectories based on equation (3.1) sampled at hourly intervals, presented for different combinations of circadian oscillations in activity and strengths in stochastic correlation ρ. All panels have the same colour-value map, shown at the bottom right, with white corresponding to squared coherency values of 0 and black to values of 1. Each panel represents the pair of circadian patterns used (§3): (a) deterministic type 0,0; (b) deterministic type 0,1; (c) deterministic type 1,1; (d) deterministic type 1,2; (e) deterministic type 2,2. For all figure panels, the common range of ρ values is shown below (e); the y-axis shows the frequency of step-length co-oscillation. The line is contoured at the level corresponding to the asymptotic 95th percentile for the null hypothesis that the squared coherency is absent (i.e. is 0 for all ω). To restrict the different types of stochasticity so that the value of ρ = 1 corresponds to identical time-series values in the SN, we set τmin = τmax = 0. Electronic supplementary material, appendix A, figure S1, shows similar results for shorter sampling intervals.
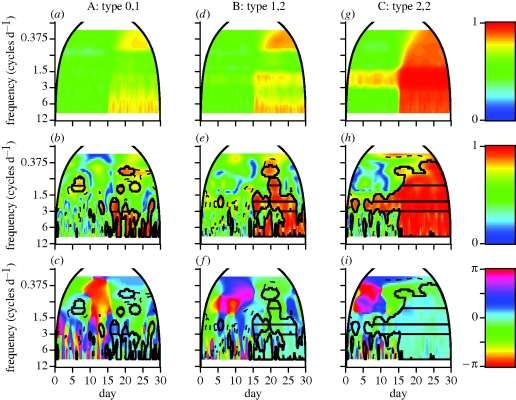
Figure 3 illustrates the time-localized information provided through wavelet coherence regarding the synchrony classification between two individuals. In all simulations, the stochastic correlation parameter ρ changes from 0.05 to 0.95 on day 15, and we have set τmin = τmax = 30 min to move towards a more realistic situation in which individuals do not change their behavioural states at exactly the same time each day. Unreported exploration of varying this parameter in the model confirms intuition: as the component signals increasingly differ owing to this additional component of randomness, the profile of coherence strength diminishes for both important and spuriously significant frequencies. The deterministic rules and results of figure 3 are as follows: column A shows when one of a pair of individuals does not contain any deterministic movement, coherence is typically absent (top panel, based on values typically associated with coherence in the lower panel rows) when ρ is near 0, indicating no synchrony. Larger coherence values at noise frequencies related to stochastic correlation in incremental movement after day 15 cannot override the differences between the presence versus absence of deterministic circadian rhythms, resulting in a horizontal green band during the second half of the simulation at 1 cycle d−1. However, patches of coherence can emerge with a range of phase differences (bottom two panels; electronic supplementary material, appendix A, equation (A 4)) during times when the stochasticity is highly correlated with ρ near 1, indicating a form of intermediate synchrony. Column B shows when individuals share similar but not exact deterministic features of movement (in this example, both individuals cycle on a circadian scale, but with differing dominant frequencies), no synchrony is the prevailing relationship when ρ is near 0. When the correlation ρ is high under these circumstances, intermediate synchrony is exhibited where coherence occurs across a limited number of frequencies (top panel) related to the underlying deterministic frequencies of movement. Under these conditions, co-oscillations may occur across a limited temporal range (middle panel) with phase differences possibly away from 0. Column C shows individuals that share exactly the same deterministic rules show coherence at frequencies related to the circadian nature of movement throughout the entire time series (top panel). When ρ is near 0 under these circumstances, coherence is not necessarily constant for any one pair (middle panel, first 15 days) and phase differences can be away from 0, resulting in an intermediate synchrony classification. When the stochastic element of movement is also highly correlated, this is reflected by a high proportion of significantly coherent frequencies between the Nyquist frequency ω = 1/2Δt through ω < 1 cycle d−1, with phase differences near 0. The temporal accuracy of transitions between these types of coherence is accurately delineated by the methods employed, though the transition to larger coherence values at lower frequencies lags in relation to the length of time needed for coherence to manifest at these frequencies.
Figure 3.
Wavelet analyses of simulated movement trajectories provide estimates of the modulus and phase differences with colour-value maps on the right. The column title of each panel column, labelled A, B and C, denotes the pair of circadian patterns used with τmin = τmax = 30 min (§3). (a,d,g) Averaged squared cross-wavelet modulus values for 100 pairs of simulations. (b,e,h) Representative squared wavelet coherence values of a single pair of step-length values driven by the deterministic movement types identified in the column label; (c,f,i) the corresponding phase differences. For each simulation, the correlation ρ across individuals in the stochastic component of incremental movement changed from 0.05 to 0.95 on day 15. Solid arched lines denote the cone-of-influence, outside of which wavelet calculations are unreliable owing to the finiteness of the data. Dashed lines are drawn at the 0.95 quantile values using a white noise null model and indicate significant co-oscillation according to the ‘pointwise’ test. Solid lines within the dashed lines indicate values that are ‘areawise’ significant. Horizontal lines within the solid lines indicate significant patches that are longer than 95% of the coherent regions defined as ‘areawise’ significant, obtained from 100 wavelet-based surrogate datasets.
In summary and with consideration of the above cautionary caveats, spectral coherence allows identification of shared deterministic or stochastic properties of circadian-based movement step-length trajectories and indicates that synchrony classification may be reasonably based on coherence analysis. In practice, the step-length time series SN of each individual may require a separate analysis to facilitate interpretation of the results of coherence analysis (e.g. to identify active frequencies at which cycling occurs during complete synchrony). Distinguishing the contribution of deterministic and stochastic influences when stochastic correlation is weak, ρ approximately <0.5, was not possible at the sampling interval considered here. Identification of periods of high correlation (ρ > 0.8) in the presence or absence of deterministic cycling in behavioural modes, however, was straightforward.
5. Results
The socio-ecology of the free-ranging elephants of Samburu, Kenya, has been extensively characterized based on multiple years of study [1,32], revealing complex intraspecific social structure that includes: (i) tight affiliation at the familial level, (ii) fission–fusion relationships demonstrating regular close affiliation and successive complete separation at the extended familial level, (iii) ephemeral bonding that is temporally irregular or seasonal at the clan level, and (iv) non-affiliating or unrelated individuals. Previous analyses of movement paths by Wittemyer et al. [18] of individuals within this population show that their movement is typified by both randomness and circadian cycling between different behavioural states. Positions of these individuals were recorded each hour.
We begin by examining coherence for elephant pairs belonging to family and extended family categories of relatedness (one adult female representing a family totalling 9–13 individuals in size is collared). For a closely associating familial pair, movement synchrony remains consistently strong (electronic supplementary material, appendix B, figure S2a), providing an illustrative example that consistently strong movement synchrony reflects the strongest level of pair bonding in this system. Figure 4 shows the results for an extended family pair (two adult females from different family units that regularly associate) over a time span that covers multiple fission–fusion events (figure 4a). Strong synchrony, characterized by significant squared coherence values near one with phase difference values near 0 (figure 4b,c), was demonstrated during periods of close spatial bonding while intermediate or no synchrony was manifested during periods of spatial dissociation (figure 4d).
Figure 4.
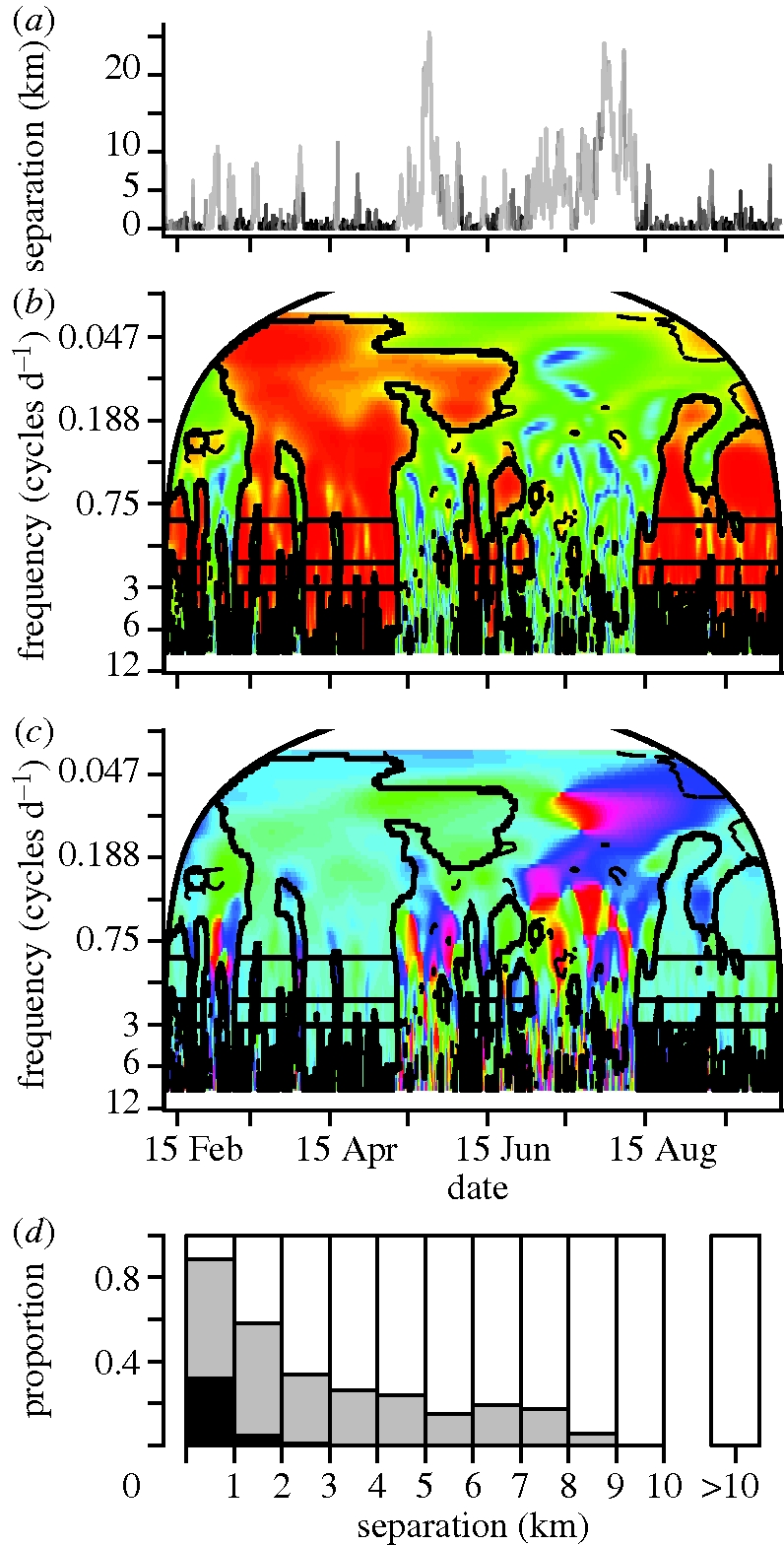
The extended family elephant pair of Monsoon and Stratus demonstrates classic fission–fusion behaviour over time, shown in (a) by the inter-individual distances calculated across a period of coordinated tracking; the line is coloured to indicate the proportion of frequencies ≥1 cycle d−1 at each time step that are significant compared with random walk-type movement, where light grey = 0 and black = 1. Wavelet analysis squared coherence (b) and phase difference (c) values with associated colour maps and the inset lines outlining significant regions as defined in figure 3. (d) A bar plot of the proportion of movement synchrony classifications for different separation distance bins: black denotes strong synchrony, defined by times where ≥80% of wavelet coherence values for frequencies ≥1 cycle d−1 are significant and phase differences are ≤π/8; grey denotes intermediate synchrony, defined by times with significant wavelet coherence at any of the frequency values 1, 2 or 3 cycles d−1 (corresponding to detectable circadian movement patterns of individuals), regardless of the phase difference but without strong synchrony also being present; and white denotes no synchrony, defined by times with no significant co-oscillations at 1, 2 or 3 cycles d−1. Strong synchrony occurs during times of extended pair bonding and relatively close spatial proximity and is associated with high correlation between values of the additional movement data (step lengths, turning angles and absolute direction heading—figure 5). Intermediate synchrony occurs across the range of close to intermediate spatial separation values, with less correlation in the additional movement data. No synchrony is present for maximal separation values but can occur even for very close separation values, and is associated with no correlation in movement data. Fission–fusion transitions in the bonding between the two elephants are clearly delineated by the wavelet analysis.
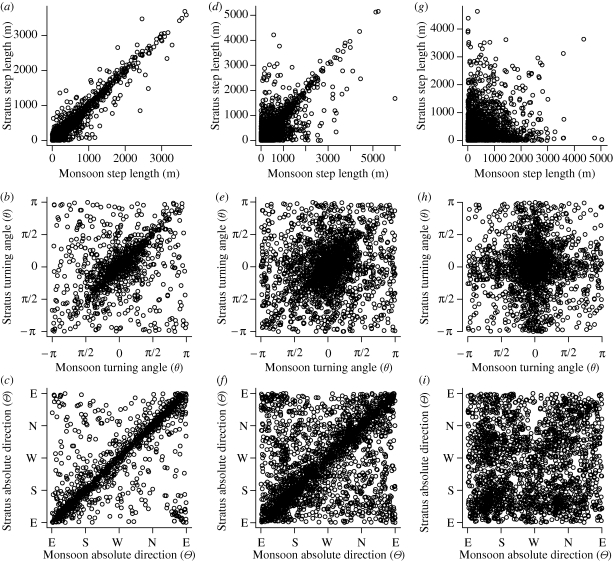
As noted above, our coherence analysis focuses on measures of step length. Additional analysis of turning velocity indicated an absence of any within-individual temporal autocorrelation and no significant across-individual coherence and therefore was disregarded as a starting point for this analysis. However, turning angle is of obvious importance in understanding cohesions, therefore further analyses were conducted regarding synchrony in directional changes. Figure 5 shows the relationship between step length, turning angle and absolute direction conditioned on their synchronous state, indicating that the wavelet coherence analysis is sorting out times of increasing similarity across all elemental movement properties in this system.
Figure 5.
Based on the wavelet coherence analysis of Monsoon and Stratus (figure 4), data were partitioned into times of strong synchrony (a–c), intermediate synchrony (d–f) and no synchrony (g–i), as defined in figure 4. Plotting step length (a,d,g), turning angle (b,e,h) and absolute direction (c,f,i) values given these partitions confirms that wavelet-based step-length analyses isolate different types of group cohesion. For step length, the squared sample correlation coefficient (R2) and significance (p) between the two variables, and for angle plots the circular version of Pearson's product moment correlation (r) and significance values (p), are as follows: (a) R2 = 0.91, p = 0; (b) r = 0.46, p = 0; (c) r = 0.74, p = 0; (d) R2 = 0.53, p = 0; (e) r = 0.22, p = 0; (f) r = 0.50, p = 0; (g) R2 = 0.02, p = 0; (h) r = 0.04, p = 0; (i) r = 0.09, p = 0. Absolute direction axes are labelled W, west (0 rad); S, south (−π/2 rad); E, east (π rad); N, north (π/2 rad).
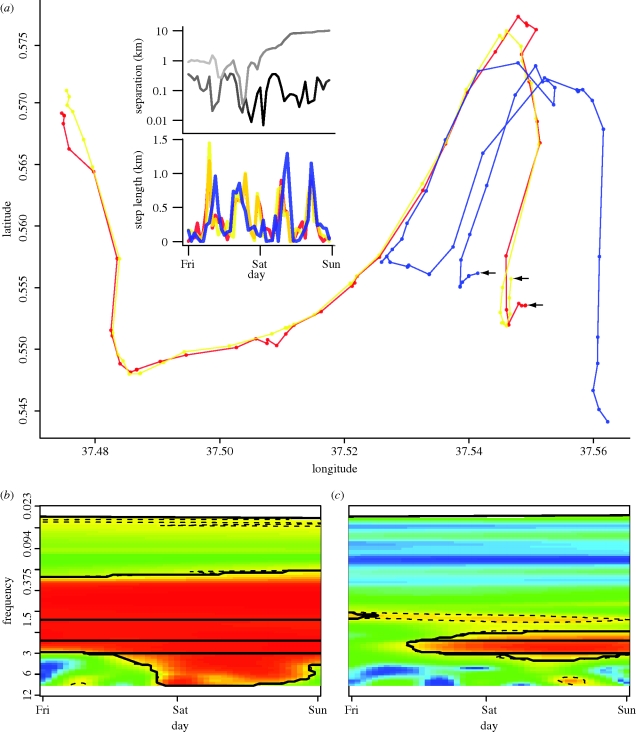
Between Friday, 24 August 2001, 0 h, and Saturday, 26 August 2001, 23.00 h, the extended family pair analysed in figures 4 and 5 merged with other individuals to form a larger herd that included members of socially unaffiliated individuals (figure 6). Isolating the squared wavelet coherence values during a 48 h period (figure 6b), the extended family pair Monsoon–Stratus demonstrates relatively strong movement synchronization. In contrast, Monsoon and the socially distant individual (Goya) have low levels of synchrony, despite qualitative similarity in movement trajectories during the first 24 h period (figure 6a,c, and inset panels). As Goya and Monsoon separate, intermediate synchrony emerges between them driven by common 2 cycle d−1 co-oscillations (figure 6a,c, and bottom inset panel), probably driven by shared physiological or ecological drivers of movement that occur when in the same locale, such as rest and movement, related to shade availability and diurnal temperature fluctuations. Interestingly, shared properties among the socially disparate pairs formed by Goya and the other individuals were disrupted during periods of close association, indicating a possible cost of social interaction among weakly bonded animals [33]. Examining wavelet coherence values for Stratus–Goya shows similar results as Monsoon–Goya, but with less common intermediate synchrony possibly in relation to greater intra-individual separation distances (electronic supplementary material, appendix B, figure S2b,c).
Figure 6.
A moment when the three individuals Monsoon, Stratus and Goya converge in space–time shows differences in movement coordination irrespective of separation distance. (a) The spatial trajectories of Monsoon, Stratus and Goya represented by the colours red, yellow and blue, respectively; the black arrows point to the starting position of this sequence of moves for each individual. The top panel of the two inset figures shows separation distances on a log10 scale between individuals of each pair, with the top line corresponding to the Monsoon–Goya pair, and the bottom line corresponding to the Monsoon–Stratus pair; the line is coloured to indicate the degree of coherence as described in figure 4. The bottom panel of the two inset figures shows step-length values, where the colours are as in the spatial trajectories, and the colour orange shows high overlap between Monsoon (red) and Stratus (yellow). (b,c) Colour contour plots of squared wavelet coherence between the two pairs, where the colour values and significance lines are as in figure 3: (b) Monsoon–Stratus (extended family); (c) Monsoon–Goya (unaffiliated). Coherence analyses for the remaining pairwise combinations are reported in the electronic supplementary material, appendix B, figure S2.
This application of our framework demonstrates that the social network structure derived from long-term (5 years) point-based data on social interactions is represented by short periods (as short as 48 h) of movement as captured through relatively continuous temporally monitored location data. In contrast to point observations, movement analyses are able to capitalize on data that are not restricted spatially or temporally. The ephemeral group containing these three individuals contained nuanced differences (i.e. synchrony between pairs was not always similar irrespective of separation distance) in movement synchrony between members that appeared to be a function of the complete suite of processes affecting elephant movements (social, environmental and physiological). Usefully, differentiated degrees of synchrony identified using the presented framework were congruous with the strength of social bonds among these individuals as defined in Wittemyer et al. [32].
6. Discussion
Patterns at the group level represent one key source of information scientists have for understanding rules determining movement, particularly those influenced by their social context. As predicted by Couzin & Krause [20], the influence of stochasticity, and in particular its correlation across individuals, is important in determining coherence for the simulation and empirical studies discussed here. Further, identifying relatively repeated, shared deterministic cycles in movement data refines understanding about collective movement at larger spatio-temporal scales and provides clues to the relative roles of physiological, social and ecological factors determining a movement path. This is exemplified by contrasting the type of movement synchrony found in elephants (presented here) and African buffalo fission–fusion social structures, where movements of both were sampled at hourly intervals. The underlying movement patterns of buffalo are dominated by random walk-type movements and synchrony between individuals was either absent (when separated) or strong (when in close proximity) simply as a function of the degree of coordination in movement stochasticity [8]. In the context of our framework, these buffaloes show only the extremes of the synchrony continuum. By contrast, the elephants show a richer collection of synchronous states, driven by stronger circadian structure in individual movement trajectories. Different kinds of social interactions and foraging strategies probably cause this contrast, where elephants show greater complexity in both diet and sociality that appears to drive the emergence of a diverse range of synchronous states found between individuals.
Quantifying time–space-specific synchrony using wavelet coherence in conjunction with other social and environmental data allows novel insight regarding the influence of social and ecological processes on group-level behaviours, a critical arena for garnering understanding of the architecture of collective movements. Moreover, these calculations can show clear evidence of when collective movement models can assume constant rules of interaction across all members (e.g. [34]) and when rules differ across individuals (e.g. [35]). Emergent properties of group structure may result from an array of factors [6], including population size and number of influential neighbours [36], a shared target [34] or noise [5]. As such, discerning the degree to which coordination is a manifestation of sociality versus shared environmental stimuli (e.g. travel to water holes, easiest path away from a predator or fire etc.) requires additional information beyond simply identifying the structure of coherence between two individuals. Coherence analysis is best viewed as a complementary probe for providing guidance on within-group heterogeneity in movement rather than a strict test between competing mechanisms.
The quantification of movement synchrony dynamics can offer insight into the mechanistic drivers of collective movements. For example: (i) the relative similarities and differences between the cohesion of adjacent (nearest neighbours) and non-adjacent group members can serve to elucidate whether group-level properties are manifested by global or local cueing, and can be applied to assess how and at what rate information exchange occurs across a group, (ii) grouping properties and rules can be identified by quantitative characterization of group movement during dissolution/formation (i.e. fission–fusion), measured by classifying synchrony across all pairs in relation to the timing and location of perturbations (e.g. the level of synchrony among group members during a predator attack will probably be a function of the relative position of group members and the location of the attack, influencing the manner in which a group disassociates during the disturbance and the time until divided group components return to their pre-disturbance state), and (iii) synchrony classification within pack-hunting groups may refine understanding of predation events by identifying common modes of activity during extended chases, elucidating the differential roles among group members or rules governing coordinated behaviours during each mode (i.e. when and where to break or join in the coordinated activity); such an analysis may complement the use of space–time clustering algorithms and state-space models for identifying kill sites [37,38]. The very high-resolution data necessary for quantifying fast-paced events in group structure dynamics are likely to not be a limitation in the near future (increasingly, data at much less than 1 h sampling intervals are available, with 1 min interval data already appearing in the published literature [39]).
Emphasizing pairwise comparisons, as done here, allows identification of the time-specific switching across levels of synchrony that can facilitate identification of fine-scale and event-specific covariate triggers for maintenance or changes in synchronous states. For more than a handful of individuals, a group- or a population-level measure of synchrony may be desirable, yet organizing the myriad of resulting pairwise analyses will be challenging. The framework presented here can be scaled for analyses of large group collective movements in the same manner that inter-individual interactions are used to assess population-level social structure (e.g. [40]). Likely directions for scaling to group-level analyses include averaging the amount of time spent in specific synchrony states over all unique pairs for each synchrony class or using the spectral information in each time series to obtain information theoretic based measures of disparity [41]. The latter may offer a more objective approach for discrimination and hierarchical classification in a manner that remains faithful to the time-series nature of movement. Recent statistical work has extended discrimination and classification techniques for grouping time series to be based on time–frequency representations of the data [42,43] and provides possible avenues to approach wavelet-based population-level classification schemes based on movement data. It should be noted, however, that the space–time specific information obtained from pairwise analyses will get lost in such averaging and grouping approaches. As such, the analysis approach taken will probably be somewhat system or question specific.
We have emphasized a statistical framework to quantitatively compare the degree of movement synchrony between concomitant movement trajectories. This framework connects quintessential aspects of movement data (combined determinism and stochasticity) shown by many wildlife species with a means for localizing temporally dynamic patterns in space–time. As such, this framework enables investigation of the mechanistic rules governing collective movements and individual interactions. However, this framework as developed here does not attempt to solve the very difficult problems associated with using trajectory data alone to quantify specific behavioural states [15,44] and possible related optimization strategies connecting resource distribution to movement [23,45], or the influence of sampling interval on such conclusions [46,47]. Statistical tests of mechanisms of movement drivers (e.g. social versus ecological) will ultimately require a multitude of covariate data. But, as we have shown here, by remaining flexible with the data, location time series can be used to begin to disentangle some of the relevant processes and suggest areas of future data collection, opening lines of inquiry that are just beginning to be approached in movement ecology.
Acknowledgements
We would like to thank W. M. Getz and several anonymous reviewers for helpful comments on early versions of this manuscript, and Alice R. Schlein for help with figures. This research was supported by start-up funds given to G.W. from Colorado State University. Movement data came from Iain Douglas-Hamilton and the Save the Elephants Tracking Animals for Conservation Programme. We thank the Kenyan Office of the President, the Kenya Wildlife Service (KWS) and the Samburu and Buffalo Springs National Reserve's County Council, wardens and rangers for their support of our work.
References
- 1.Wittemyer G., Getz W. M., Volllrath F., Douglas-Hamilton I. 2007. Social dominance, seasonal movements, and spatial segregation in African elephants: a contribution to conservation behavior. Behav. Ecol. Sociobiol. 61, 1919–1931 10.1007/s00265-007-0432-0 (doi:10.1007/s00265-007-0432-0) [DOI] [Google Scholar]
- 2.Ruckstuhl K. E., Heuhaus P. 2001. Behavioral synchrony in ibex groups: effects of age, sex, and habitat. Behaviour 138, 1033–1046 10.1163/156853901753286551 (doi:10.1163/156853901753286551) [DOI] [Google Scholar]
- 3.Focardi S., Pecchioli E. 2005. Social cohesion and foraging decrease with group size in fallow deer (Dama dama). Behav. Ecol. Sociobiol. 59, 84–91 10.1007/s00265-005-0012-0 (doi:10.1007/s00265-005-0012-0) [DOI] [Google Scholar]
- 4.Parrish J. K., Edelstein-Keshet L. 1999. Complexity, pattern, and evolutionary trade-offs in animal aggregation. Science 284, 99–101 10.1126/science.284.5411.99 (doi:10.1126/science.284.5411.99) [DOI] [PubMed] [Google Scholar]
- 5.Yates C. A., Erban R., Escudero C., Couzin I. D., Buhl J., Kevrekidis I. G., Maini P. K., Sumpter D. J. T. 2009. Inherent noise can facilitate coherence in collective swarm motion. Proc. Natl Acad. Sci. USA 106, 5464–5469 10.1073/pnas.0811195106 (doi:10.1073/pnas.0811195106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Parrish J. K., Viscido S. V., Grünbaum D. 2002. Self-organized fish schools: an examination of emergent properties. Biol. Bull. 202, 296–305 10.2307/1543482 (doi:10.2307/1543482) [DOI] [PubMed] [Google Scholar]
- 7.Forester J. D., Ives A. R., Turner M. G., Anderson D. P., Fortin D., Beyer H. L., Smith D. W., Boyce M. S. 2007. State-space models link elk movement patterns to landscape characteristics in Yellowstone National Park. Ecol. Monogr. 77, 285–299 10.1890/06-0534 (doi:10.1890/06-0534) [DOI] [Google Scholar]
- 8.Polansky L., Wittemyer G., Cross P., Tambling C. J., Getz W. M. 2010. From moonlight to movement, and synchronized randomness: Fourier and wavelet analyses of animal location time series data. Ecology 91, 1506–1518 10.1890/08-2159.1 (doi:10.1890/08-2159.1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Couzin I. D., Krause J., Franks N. R., Levin S. A. 2005. Effective leadership and decision-making in animal groups on the move. Nature 433, 513–516 10.1038/nature03236 (doi:10.1038/nature03236) [DOI] [PubMed] [Google Scholar]
- 10.Getz W. M., Saltz D. 2008. A framework for generating and analyzing movement paths on ecological landscapes. Proc. Natl Acad. Sci. USA 105, 19 066–19 071 10.1073/pnas.0801732105 (doi:10.1073/pnas.0801732105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dyer J. R. G., Ioannou C. C., Morrell L. J., Croft D. P., Couzin I. D., Waters D. A., Krause J. 2008. Consensus decision making in human crowds. Anim. Behav. 75, 461–470 10.1016/j.anbehav.2007.05.010 (doi:10.1016/j.anbehav.2007.05.010) [DOI] [Google Scholar]
- 12.Brillinger D. R., Preisler H. K., Ager A. A., Wisdom M. J. 2004. An exploratory data analysis (EDA) of the paths of moving animals. J. Stat. Plann. Infer. 122, 43–63 10.1016/j.jspi.2003.06.016 (doi:10.1016/j.jspi.2003.06.016) [DOI] [Google Scholar]
- 13.Kendall B. E., Briggs C. J., Murdoch W. W., Turchin P., Ellner S. P., McCauley E., Nisbet R. M., Wood S. N. 1999. Why do populations cycle? A synthesis of statistical and mechanistic modeling approaches. Ecology 80, 1789–1805 10.1890/0012-9658(1999)080[1789:WDPCAS]2.0.CO;2 (doi:10.1890/0012-9658(1999)080[1789:WDPCAS]2.0.CO;2) [DOI] [Google Scholar]
- 14.Tukey J. W. 1980. We need both exploratory and confirmatory. Am. Stat. 34, 23–25 10.2307/2682991 (doi:10.2307/2682991) [DOI] [Google Scholar]
- 15.Gurarie E., Andrews R. D., Laidre K. L. 2009. A novel method for identifying behavioural changes in animal movement data. Ecol. Lett. 12, 395–408 10.1111/j.1461-0248.2009.01293.x (doi:10.1111/j.1461-0248.2009.01293.x) [DOI] [PubMed] [Google Scholar]
- 16.Cross P. C., Lloyd-Smith J. O., Getz W. M. 2005. Disentangling association patterns in fission–fusion societies using African buffalo as an example. Anim. Behav. 69, 499–506 10.1016/j.anbehav.2004.08.006 (doi:10.1016/j.anbehav.2004.08.006) [DOI] [Google Scholar]
- 17.Preisler H. K., Ager A. A., Johnson B. K., Kie J. G. 2004. Modeling animal movements using stochastic differential equations. Environmetrics 15, 643–657 10.1002/env.636 (doi:10.1002/env.636) [DOI] [Google Scholar]
- 18.Wittemyer G., Polansky L., Douglas-Hamilton I., Getz W. M. 2008. Disentangling the effects of forage, social rank, and risk on movement autocorrelation of elephants using Fourier and wavelet analyses. Proc. Natl Acad. Sci. USA 105, 19 108–19 113 10.1073/pnas.0801744105 (doi:10.1073/pnas.0801744105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.R Development Core Team 2008. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing [Google Scholar]
- 20.Couzin I. D., Krause J. 2003. Self-organization and collective behavior in vertebrates. Adv. Study Behav. 32, 1–75 10.1016/S0065-3454(03)01001-5 (doi:10.1016/S0065-3454(03)01001-5) [DOI] [Google Scholar]
- 21.Nathan R., Getz W. M., Revilla E., Holyoak M., Kadmon R., Saltz D., Smouse P. E. 2008. A movement ecology paradigm for unifying organismal research. Proc. Natl Acad. Sci. USA 105, 19 052–19 059 10.1073/pnas.0800375105 (doi:10.1073/pnas.0800375105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Barraquand F., Benhamou S. 2008. Animal movements in heterogeneous landscapes: identifying profitable places and homogeneous movement bouts. Ecology 89, 3336–3348 10.1890/08-0162.1 (doi:10.1890/08-0162.1) [DOI] [PubMed] [Google Scholar]
- 23.Bartumeus F., Catalan J. 2009. Optimal search behavior and classic foraging theory. J. Phys. A 42, 434002. 10.1088/1751-8113/42/43/434002 (doi:10.1088/1751-8113/42/43/434002) [DOI] [Google Scholar]
- 24.Codling E. A., Plank M. J., Benhamou S. 2008. Random walk models in biology. J. R. Soc. Interface 5, 813–834 10.1098/rsif.2008.0014 (doi:10.1098/rsif.2008.0014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Turchin P. 1998. Quantitative analysis of movement: measuring and modeling population redistribution in animals and plants. Sunderland, MA: Sinauer Associates [Google Scholar]
- 26.Kronfeld-Schor N., Dayan T. 1999. The dietary basis for temporal partitioning: food habits of coexisting Acomys species. Oecologia 121, 123–128 10.1007/s004420050913 (doi:10.1007/s004420050913) [DOI] [PubMed] [Google Scholar]
- 27.Brllinger D. R. 2010. Modeling spatial trajectories. In Handbook of spatial statistics (eds Gelfand A. E., Diggle P., Guttorp P., Fuentes M.), pp. 465–477 Boca Raton, FL: Chapman & Hall/CRC Press [Google Scholar]
- 28.Iacus S. M. 2008. Simulation and inference for stochastic differential equations: with R examples. New York, NY: Springer [Google Scholar]
- 29.Brillinger D. R. 1981. Time series: data analysis and theory. San Francisco, CA: Holden-Day [Google Scholar]
- 30.Shumway R. H., Stoffer D. S. 2000. Time series analysis and its applications. New York, NY: Springer [Google Scholar]
- 31.Cazelles B., Chavez M., Berteaux D., Menard F., Vik J. O., Jenouvrier S., Stenseth N. C. 2008. Wavelet analysis of ecological time series. Oecologia 156, 287–304 10.1007/s00442-008-0993-2 (doi:10.1007/s00442-008-0993-2) [DOI] [PubMed] [Google Scholar]
- 32.Wittemyer G., Douglas-Hamilton I., Getz W. M. 2005. The socioecology of elephants: analysis of the processes creating multitiered social structures. Anim. Behav. 69, 1357–1371 10.1016/j.anbehav.2004.08.018 (doi:10.1016/j.anbehav.2004.08.018) [DOI] [Google Scholar]
- 33.Wittemyer G., Getz W. M. 2007. Hierarchical dominance structure and social organization in African elephants. Anim. Behav. 73, 671–681 10.1016/j.anbehav.2006.10.008 (doi:10.1016/j.anbehav.2006.10.008) [DOI] [Google Scholar]
- 34.Codling E. A., Pitchford J. W., Simpson S. D. 2007. Group navigation and the ‘many-wrongs principle’ in models of animal movement. Ecology 88, 1864–1870 10.1890/06-0854.1 (doi:10.1890/06-0854.1) [DOI] [PubMed] [Google Scholar]
- 35.Romey W. L. 1996. Individual differences make a difference in the trajectories of simulated schools of fish. Ecol. Model. 92, 65–77 10.1016/0304-3800(95)00202-2 (doi:10.1016/0304-3800(95)00202-2) [DOI] [Google Scholar]
- 36.Viscido S. V., Parrish J. K., Grünbaum D. 2005. The effect of population size and number of influential neighbors on the emergent properties of fish schools. Ecol. Model. 183, 347–363 10.1016/j.ecolmodel.2004.08.019 (doi:10.1016/j.ecolmodel.2004.08.019) [DOI] [Google Scholar]
- 37.Franke A., Caelli T., Kuzyk G., Hudson R. J. 2006. Prediction of wolf (Canis lupus) kill-sites using hidden Markov models. Ecol. Model. 197, 237–246 10.1016/j.ecolmodel.2006.02.043 (doi:10.1016/j.ecolmodel.2006.02.043) [DOI] [Google Scholar]
- 38.Web N. F. W., Hebblewhite M., Merrill E. H. 2008. Statistical methods for identifying wolf kill sites using global positioning system locations. J. Wildl. Manage. 72, 798–807 [Google Scholar]
- 39.Amano T., Katayama N. 2009. Hierarchical movement decisions in predators: effects of foraging experience at more than one spatial and temporal scale. Ecology 90, 3536–3545 10.1890/08-1910.1 (doi:10.1890/08-1910.1) [DOI] [PubMed] [Google Scholar]
- 40.Krause J., Lusseau D., James R. 2009. Animal social networks: an introduction. Behav. Ecol. Sociobiol. 63, 967–973 10.1007/s00265-009-0747-0 (doi:10.1007/s00265-009-0747-0) [DOI] [Google Scholar]
- 41.Kakizawa Y., Shumway R. H., Taniguchi M. 1998. Discrimination and clustering for multivariate time series. J. Am. Stat. Assoc. 93, 328–340 10.2307/2669629 (doi:10.2307/2669629) [DOI] [Google Scholar]
- 42.Huang H.-Y., Ombao H., Stoffer D. S. 2004. Discrimination and classification of nonstationary time series using the SLEX model. J. Am. Stat. Assoc. 99, 763–774 10.1198/016214504000001105 (doi:10.1198/016214504000001105) [DOI] [Google Scholar]
- 43.Ringo Ho M.-H., Ombao H., Edgar J. C., Cañive J. M., Miller G. A. 2008. Time–frequency discriminant analysis of MEG signals. Neuroimage 40, 174–186 10.1016/j.neuroimage.2007.11.014 (doi:10.1016/j.neuroimage.2007.11.014) [DOI] [PubMed] [Google Scholar]
- 44.Patterson T. A., Thomas L., Wilcox C., Ovaskainen O., Matthiopoulos J. 2008. State-space models of individual animal movement. Trends Ecol. Evol. 23, 87–94 10.1016/j.tree.2007.10.009 (doi:10.1016/j.tree.2007.10.009) [DOI] [PubMed] [Google Scholar]
- 45.Edwards A. M., et al. 2007. Revisiting Levy flight search patterns of wandering albatrosses, bumblebees and deer. Nature 449, 1044–1048 10.1038/nature06199 (doi:10.1038/nature06199) [DOI] [PubMed] [Google Scholar]
- 46.Codling E. A., Hill N. A. 2005. Sampling rate effects on measurements of correlated and biased random walks. J. Theor. Biol. 233, 573–588 10.1016/j.jtbi.2004.11.008 (doi:10.1016/j.jtbi.2004.11.008) [DOI] [PubMed] [Google Scholar]
- 47.Plank M. J., Codling E. A. 2009. Sampling rate and misidentification of Lévy and non-Lévy movement paths. Ecology 90, 3546–3553 10.1890/09-0079.1 (doi:10.1890/09-0079.1) [DOI] [PubMed] [Google Scholar]