Bayesian models for multiple outcomes nested in domains

Summary

We consider the problem of estimating the effect of exposure on multiple continuous outcomes, when the outcomes are measured on different scales and are nested within multiple outcome classes, or “domains”. Our Bayesian model extends the linear mixed models approach to allow the exposure effect to differ across domains and across outcomes within domains. Our model can be parameterized to allow shrinkage of the effects within the different levels of nesting, or to allow fixed domain-specific effects with no shrinkage. Our model also allows covariate effects to differ across outcomes and domains. Our methodology is applied to data on prenatal methylmercury exposure and multiple outcomes in four domains measured at 9 years of age on children enrolled in the Seychelles Child Development Study. We use three different priors and found that our main conclusions were not sensitive to the choice of prior. Simulation studies examine the model performance under alternative scenarios. Our results demonstrate that a sizeable increase in power is possible.

1 Introduction

There is a need for more powerful methodologies to detect small but potentially important effects of low-dose exposure on multiple correlated outcomes, such as those that characterize childhood thinking, remembering, language, and behavior. Typically, studies that aim to assess exposure effects on multiple outcomes estimate these effects from models fit separately to each outcome. However if the effects are similar across outcomes, separate models lack power to detect an overall exposure effect. Another complication is that the multiple outcomes may be manifestations of a smaller number of broad outcome classes, or “domains”. For example a neurodevelopmental test battery typically contains multiple tests, some of which measure motor function, while others measure cognition, sensory or perceptual functions or other aspects of human behavior. Estimation of the global and domain-specific exposure effects may also be of interest. Ours is the first paper to introduce a general and flexible methodology for directly modeling domain-specific effects on multiple outcomes. A related approach using structural equation models is taken by Budtz-Jorgensen and colleagues [2].

A number of papers have addressed multiple correlated outcomes within a single model. In these papers, the outcomes are typically treated as belonging to a single group or “domain”. These papers have generally adopted one of two general approaches. In one approach, one or more latent variables are introduced and the outcomes are viewed as multiple manifestations of the latent variables [21, 10, 2, 3, 23]. This approach can be extended to model a mixture of continuous and categorical outcomes [16, 10], but results can be very sensitive to model misspecification [22]. The second general approach uses generalized linear mixed models to model the effect of exposure on the outcomes directly [21, 15, 19, 7]. Correlations between outcomes measured on the same subject are induced through the random subject-specific effects. When the multiple outcomes are continuous and are measured on different scales, the outcomes require rescaling so that the estimated overall effect is not dominated by outcomes with the largest scales [21].

Our approach to modeling multiple outcomes uses the second general approach, but we also incorporate information about the clustering of outcomes within domains. This clustering is also handled by Budtz-Jorgensen and colleagues in their application [2], using the first general approach. We develop a Bayesian model to allow the exposure effects to differ across outcomes within domains and also across domains, by introducing domain-specific and outcome-specific deviations. Using frequentist terminology, our model can treat these deviations either as “random” or “fixed” effects, although in both cases the deviations have a prior distribution since we use a fully Bayesian approach. When treated as “random” effects, we assume that the deviations arise from a common distribution and we specify a prior distribution on their common variance component. This hierarchical structure results in a borrowing of strength of the effects across levels of nesting and can increase power. When treated as “fixed” effects, each deviation has an independent and diffuse prior so there is no borrowing of strength by shrinkage towards a common value. Treatment of the covariate effects can be as flexible as treatment of the exposure effects.

We apply our model to data from the Seychelles Child Development Study (SCDS). We investigate the relationship between prenatal exposure to methylmercury (MeHg) and multiple neurodevelopmental outcomes measured on children at 9 years of age [17]. Estimates of the prenatal MeHg effect on neurodevelopmental outcomes are often small with large standard errors. The significance of the estimated MeHg effect varies not only across outcomes [17], but also across studies using the same outcomes [1]. Being able to estimate these effects with more precision may be important for future policy decisions concerning MeHg and fish consumption.

The outcomes in the SCDS cluster into several broad neurodevelopmental domains, and the effect of prenatal MeHg exposure is believed to be similar both within and across domains. Our primary focus here is to estimate the overall MeHg effect and the outcome-specific effects, from a model that allows for a similarity of MeHg effects and takes advantage of the correlation between outcomes, within and across domains. Using an alternative prior structure our model is well-suited to address questions such as “Does MeHg affect motor function?”, or “Is the effect of MeHg on motor function different than its effect on sustained attention?” Our Bayesian model is easily extended to handle missing outcome data, thereby allowing exposure effect comparisons on the same subjects. We illustrate this in the SCDS application.

In Section 2 we describe a model for multiple outcomes, first for a single domain and then for multiple domains. In Section 3 we discuss the SCDS and give results from fitting our model to this dataset. Simulation results are presented in Section 4. We conclude with some discussion in Section 5.

2 Our models

2.1 Model for a single domain

Our model for multiple continuous outcomes in a single domain resembles models used by Sammel et al. [21], Lin et al. [15] and Roy et al. [19]. When the outcomes are not on a common scale, this linear mixed model (LMM) approach divides each observed outcome by an outcome-specific scale factor, so that the scale of the common exposure effect is meaningful. We also center the outcomes. The scale factors used in these papers are the marginal outcome-specific standard deviation (SD) [21], the outcome-specific SD conditional on covariates and random effects [15], or the outcome-specific SD conditional only on covariates [19].

We use the marginal outcome-specific SD as scale factors. We also center and scale the exposure and all covariates. The scaling implies that the regression coefficients are partial correlation coefficients and that the variances of the residual errors are partial variances. The centering affects the intercepts, which we treat as nuisance parameters, but not the slopes. Centering all variables implies that the overall intercept and all domain-specific and outcome-specific deviations are zero. An advantage of a model without intercepts is that fewer model parameters (that are not of particular interest) need to be estimated. When necessary, the sign of some outcomes should be reversed so that larger values of all outcomes are associated with better (or worse) performance, allowing a common exposure effect that is interpretable. Our model is not appropriate if subjects with better performance on one outcome tend to have worse performance on other outcomes. When it is reasonable to model all outcome-specific deviations as random effects, our model for the single domain case is

$$y_{i,j}^{\ast }=({\beta }_x+b_{j,x})x_i+({\beta }_S^T+{\mathbf{b}}_{j,S}^T){\mathbf{S}}_i+r_i+{\in }_{i,j},$$ (1)

where $y_{i,j}^{\ast }$ is the scaled and centered jth outcome for the ith subject, for i = 1, …, n, and j = 1, …, J. Here x_i is the scaled and centered exposure, and S_i are the p covariates (also centered and scaled, and not including exposure). The “x” and “S” subscripts refer to the slope for exposure, and slope for covariates. Also β_x is the overall effect of exposure on the scaled outcomes, and b_{j, x}, j = 1, …, J are the outcome-specific deviations from the overall exposure effect. Similarly β_S is the vector of covariate-specific effects and b_{j, S} is the vector of outcome-specific deviations from the overall covariate-specific effects. The r_i, i = 1, …, n are the subject-specific random effects, which reflect the fact that some individuals tend to perform better on most outcomes than predicted by the model, while others tend to perform less well. Finally, ∊_{i, j} are the residual errors, i.e. the differences in the scaled outcomes from those predicted from the model.

We assume that the outcome-specific deviations, ${\mathbf{b}}_j={\left(b_{j,x}{\mathbf{b}}_{j,S}^T\right)}^T$, subject-specific random effects, r_i and residual errors, ∊_i,1, …, ∊_i,J are mutually independent and are normally distributed. These are typical assumptions for LMMs, and are also assumed by Lin et al. [15] and Roy et al. [19]. The treatment of b_j as random effects implies that it is reasonable to assume a similarity of exposure effects and covariate effects across the multiple outcomes after scaling. Our model is complete upon specifying priors for β and all variance components. Of note, we allow Var(∊_i,j) to differ across outcomes, which is not a typical feature of scaled multiple outcome models. However the set of partial correlations between an outcome and the model covariates can differ across outcomes, implying that the partial variances of the residual errors will also differ. Var(∊_i,j) will be almost one for outcomes that are essentially uncorrelated with the covariates, and substantially smaller for outcomes that are highly correlated with the model covariates. In our application the partial variances from separate regression models varied substantially between outcomes, necessitating this model expansion.

2.2 Model for multiple domains

Model (1) can be expanded to allow domain-specific effects and outcomes-specific effects within domains. We assume that the J outcomes are grouped in D domains such that each outcome is nested in a single domain. Because individual subjects may do better on some domains than others, in addition to the overall subject-specific random effects r_i, our model includes domain-specific random subject effects, $r_{\mathcal{D},d,i}$, for d = 1, …, D. For clarity we sometimes refer to $r_{\mathcal{D},d,i}$ as $r_{\mathcal{D},d\left(j\right),i}$ where d(j) is the domain to which the jth outcome belongs. The “$\mathcal{D}$” and “$\mathcal{O}$” in subscripts indicate “domain-level effct” and “outcome-level effect” respectively. Assuming it is reasonable to model both domain-specific and outcome-specific covariate effects and exposure effects as random, model (1) becomes

$$y_{i,j}^{\ast }=({\beta }_x+b_{\mathcal{D},d\left(j\right),x}+b_{\mathcal{O},j,x})x_i+({\beta }_S^T+{\mathbf{b}}_{\mathcal{D},d\left(j\right),\mathbf{S}}+b_{\mathcal{O},j,\mathbf{S}}){\mathbf{S}}_i+r_i+r_{\mathcal{D},d\left(j\right),i}+{\in }_{i,j}$$ (2)

for i = 1, …, n and j = 1, …, J, where $b_{\mathcal{D},d\left(j\right),x}$ and $b_{\mathcal{D},d\left(j\right),\mathbf{S}}$ are adjustments to the overall exposure effect and covariate effects respectively, for domain d, and $b_{\mathcal{O},j,x}$ and $b_{\mathcal{O},j,\mathbf{S}}$ are further adjustments specific to the jth outcome, which is in domain d(j). The jth outcome-specific slope, (${\beta }_x+b_{\mathcal{D},d\left(j\right),x}+b_{\mathcal{O},j,x}$), can easily be converted to the original scale by multiplying it by s_yj/S_x, for comparison with the separate regression on the original scale.

Model (2) gives one version of our model for multiple domains, but our model encompasses many model variants. If the outcome-specific covariate effects are not needed, $b_{\mathcal{O},j,\mathbf{S}}$ can be deleted from the model. In some applications it may be more reasonable to model the domain-specific covariate effects and/or exposure effects as fixed effects. If all domain-specific covariate effects are treated as fixed effects, $b_{\mathcal{D},d\left(j\right),\mathbf{S}}$ in (2) would not be present, and instead the definition of S_i would be expanded to allow domain-specific slopes for each covariate. Our model allows some domain-specific covariate effects to be treated as fixed and others as random. Fixed domain-specific covariate or exposure effects may differ among sets of outcomes within a domain, with a further expansion of the definition of S_i.

Model (2) and all model variants mentioned above can be expressed for all subjects and outcomes together using a more general model formulation:

$${\mathbf{Y}}^{\ast }={\mathbf{F}}_{(\otimes )}\beta +{\mathbf{Z}}_{\mathcal{D}}{\mathbf{b}}_{\mathcal{D}}+{\mathbf{Z}}_{\mathcal{O}}{\mathbf{b}}_{\mathcal{O}}+\mathbf{R}+R_{\mathcal{D}}+\in$$ (3)

where F_(⊗) denotes the fixed effects for exposure and covariates, ${\mathbf{Z}}_{\mathcal{D}}$ the domain-specific random effects, ${\mathbf{Z}}_{\mathcal{O}}$ the outcome-specific random effects, R the overall subject-specific random effects, and ${\mathbf{R}}_{\mathcal{D}}$ the domain-specific random subject effects. We define this notation more specifically in Web Appendix A.

Our model assumptions imply a positive correlation structure between the outcomes conditional on model covariates. In (3), we have also assumed that the overall and domain-specific random subject effects are sufficient to capture the correlations between the multiple outcomes measured on the same subject. However our model can be expanded to allow further flexibility. If a subset of outcomes within a domain are more highly correlated with each other than model (3) implies, another random subject effect can be added which is non-zero only for this cluster of outcomes.

2.3 Model assumptions

We assume that all the random effects, ${\mathbf{b}}_{\mathcal{D}}$, ${\mathbf{b}}_{\mathcal{O}}$, ${\mathbf{r}}_{\mathcal{D}}$, and r, are independent, are independent of β and ε, and are normally distributed. Specifically for d = 1, …, D, j = 1, …, J, and i = 1, …, n, we assume ${\mathbf{b}}_{\mathcal{D},d,x}\sim N(0,{\Sigma }_{b,\mathcal{D}})$, ${\mathbf{b}}_{\mathcal{O},j,x}\sim N(0,{\Sigma }_{b,\mathcal{O}})$, $r_i\sim N(0,{\sigma }_r^2)$, ${\mathbf{r}}_{\mathcal{D},i}\sim N(0,{\Sigma }_{r,\mathcal{D}})$, and ∊_i ~ N(0,Σ_∊), where ${\Sigma }_{r,\mathcal{D}}=\text{diag}({\sigma }_{r,\mathcal{D},1}^2,\dots ,{\sigma }_{r,\mathcal{D},\mathcal{D}}^2)$, ${\Sigma }_{\in }=\text{diag}({\sigma }_{∊,1}^2,\dots ,{\sigma }_{∊,J}^2)$, and in our application ${\Sigma }_{b,\mathcal{D}}={\sigma }_{b,\mathcal{D},x}^2$ and ${\Sigma }_{b,\mathcal{O}}={\sigma }_{b,\mathcal{O},x}^2$. As will be explained in Section 3.1, in our application we did not have ${\mathbf{b}}_{\mathcal{D},d,\mathbf{S}}$ or ${\mathbf{b}}_{\mathcal{O},d,\mathbf{S}}$. Should these terms be necessary they would be treated in the same way as ${\mathbf{b}}_{\mathcal{D},d,x}$ and ${\mathbf{b}}_{\mathcal{O},j,x}$.

Our priors are β ~ N(β₀, Σ₀), ${\sigma }_{d,\mathcal{D},x}^2\sim \text{IG}(A_{0,b,\mathcal{D}},B_{0,b,\mathcal{D}})$, ${\sigma }_{d,\mathcal{O},x}^2\sim \text{IG}(A_{0,b,\mathcal{O}},B_{0,b,\mathcal{O}})$, ${\sigma }_r^2\sim \text{IG}(A_{0,r},B_{0,r})$, ${\sigma }_{r,\mathcal{D},1}^2,\dots ,{\sigma }_{r\mathcal{D},\mathcal{D}}^2\sim \text{IG}(A_{0,r,\mathcal{D}},B_{0,r,\mathcal{D}})$, and ${\sigma }_{∊,1}^2,\dots ,{\sigma }_{∊,J}^2\sim \text{IG}(A_{0,∊},B_{0,∊})$, where IG denotes the inverse gamma distribution. We use hyperparameter values that correspond to weakly informative priors. We use three different priors to examine the sensitivity of model results to the prior choise. For our primary prior, “Prior A”, we take β₀ = 0, ${\Sigma }_0^{-1}=\text{diag}\left\{0.00001\right\}$, $A_{0,b,\mathcal{D}}=A_{0,b,\mathcal{O}}=A_{0,r}=A_{0,r,\mathcal{D}}=A_{0,∊}=0.5$, $B_{0,b,\mathcal{D}}=B_{0,b,\mathcal{O}}=B_{0,r}=B_{0,r,\mathcal{D}}=0.00005$ and B_0,∊ = 0.0005. “Prior B” differs from “prior A” is using 0.1 for all shape hyperparameters. “Prior C” is an improper uniform prior on all the standard deviations. This prior is suggested by Gelman [12], is the same as an IG(−0.5, 0) prior on the variances, and requires J > 2 and D > 2 in order for the posteriors to be proper [12]. Further discussion of the inverse gamma prior is given in Appendix E.

2.4 Sampling from the joint posterior, missing data, and model checking

We use Markov Chain Monte Carlo (MCMC) to sample from the joint posterior distribution of all model parameters. We do this using Gibbs sampling, in which we sample iteratively from the conditional posterior distribution of each model parameter (or group of model parameters), conditional on the data and on all other model parameters, thereby obtaining samples from the joint posterior distribution of all parameters. We give the conditional posterior distributions of model parameters in Web Appendix B. We programmed the MCMC algorithm in Matlab.

Missing outcome data were handled using data augmentation [24], which adds an additional step to the Gibbs sampler. In this step we draw a sample of missing outcome values from their posterior distribution, conditional on the observed data and on the most recent draws of all model parameters. These sampled values are then treated as fixed for the next MCMC draw of the model parameters. We give further details in Web Appendix D.

For each prior (“A”, “B”, and “C”), we ran 10 MCMC chains using overdispersed starting values (Appendix E). The MCMC samples were read into R for assessing convergence of the 77 parameters. Our diagnostics for multiple chains included (a) visual examination of all traceplots; (b) the Gelman-Rubin diagnostic $\widehat{R}$ [11], and (c) mcgibbsit [28]; and for single chains the Raftery-Lewis diagnostic [18]. Model results are reported using every 5th draw from all 10 chains (10,000 draws total). We also examined the posterior predictive distribution to assess whether our model was consistent with the observed data (Appendix E).

3 Seychelles Child Development Study (SCDS) and model results

3.1 Background and descriptive data analysis

The SCDS was begun in 1989 to examine the possible effects of low level prenatal MeHg exposure on childhood cognition, memory, language and behavior among a cohort for whom the source of MeHg was primarily fish consumption. Average maternal hair MeHg during pregnancy was used as a biomarker for fetal brain MeHg level. For the observations used in this paper, MeHg averaged 6.83 ppm (range: 0.54 to 23.09 ppm). In the primary paper reporting on the 9-year outcomes, Myers et al. [17] used separate regression models to examine the covariate-adjusted MeHg effects on 21 outcomes. MeHg exposure was associated with a significantly worse performance for one outcome, better performance for another, and no significant relationships were found for the remaining outcomes.

Exposure to high doses of MeHg during the in utero period is known to cause damage throughout the brain [27]. The nature of the damage, as seen in autopsies from Iraq [5], suggests that cellular functions associated with very basic brain development are altered by in utero MeHg exposure [6]. Therefore a similarity of prenatal MeHg exposure effects on outcomes in different domains is to be expected, motivating our treatment of domain-specific exposure effects as random. In contrast, there is no a priori reason to expect covariates to have a similarity of effects across domains. Our models adjusted for six covariates that were significant in more than one of the separate regression models: sex (1=male, 0=female), maternal age, HOME score (a measure of the home environment), K-BIT (a measure of the mother's IQ), Hollingshead socio-economic status, and the child's test age. We treated all model covariates except sex as continuous variables.

Our model was fit using 20 SCDS outcomes nested within four broad developmental or behavioral domains: cognition, memory, motor, and social behavior. The nesting of outcomes within domains was determined a priori by the third author. The 20 outcomes were chosen from a longer list of outcomes, from which we excluded one domain containing only two outcomes each of which was subject to substantial missingness, one domain in which a substantial fraction of subjects were missing data on all three outcomes, and two outcomes that were uncorrelated with all other outcomes within their domain. Five subjects who had measurements of only one outcome in a domain were deleted. Our final sample consisted of 533 eligible subjects with complete covariate data and measurements of two or more outcomes in each of the four domains. Three hundred ninety-one of the subjects had complete outcome data, 128 were missing one outcome, 12 were missing two outcomes, and 2 were missing 4 outcomes. Before fitting our model we fit separate regression models for each outcome and checked regression assumptions. Six outcomes were log-transformed in order to better satisfy regression assumptions. A linear relationship between MeHg and all outcomes was reasonable. Based on subject-matter knowledge of the outcomes by the third author, the sign of seven outcomes was reversed so that a larger outcome value always implies a better performance.

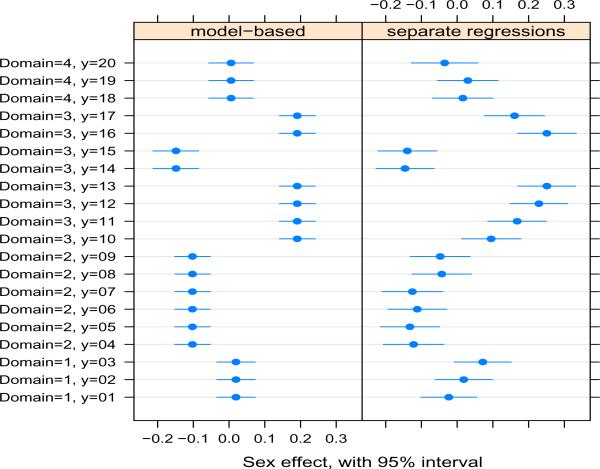
Table 1 lists the 20 outcomes, their nesting within domains, and some summary statistics. Several conclusions emerge. First, correlations between MeHg and outcomes are generally close to zero, and the sign of the correlations is inconsistent even within domains. This suggests that (a) the MeHg effects are small, and (b) we have no empirical evidence that these correlations or the MeHg effects are of the same sign. Secondly, the regression coefficients for MeHg in separate scaled models are generally very similar to the correlations, suggesting that the covariates did not strongly modify the MeHg effect. Third, the residual variances from the separate scaled regressions varied substantially, underscoring the importance of allowing the residual error to vary across outcomes. Finally, the pattern of covariate effects was generally similar within domains, but differed across domains. However, not evident in this table is the fact that the sign of the sex effect was inconsistent within the motor domain (see Figure 1).

Table 1.

Grouping of outcomes within domains with key properties of each outcome. An asterisk superscript indicates the sign of the original outcome has been reversed, and an “L” subscript indicates the outcome was log-transformed.. Var(y_obs) gives the variance of the unscaled outcomes, and n_mis gives the number of subjects out of 533 who were missing the outcome. The columns labeled “Scaled $\widehat{\beta }$” and “Residual variance” give the regression coefficient for MeHg and the residual variance from separate regressions of the scaled outcomes on the scaled MeHg and covariates. Covariates are: 1=sex, 2=maternal age, 3=HOME score, 4=Kbit (mother's IQ), 5=Hollingshead SES, and 6=child's test age.

						From separate scaled regressions
Domain		Outcome name	Var(yobs)	nmis	Corr w/ Hg	Scaled $\widehat{\beta }$	Residual variance	Important Covariates
1 - Cognition	y 1	WISC verbal IQ	9.6	0	0.02	0.01	0.83	3,4,5,6
	y 2	WISC performance IQ	13.6	0	−0.02	−0.04	0.86	2,3,4,5
	y 3	Boston naming test: no cues	4.1	4	0.01	0.00	0.85	3,4,5,6
2 - Memory	y 4	CVLT: recognition	0.4	3	0.02	0.02	0.98	1
	y 5	CVLT: immediate recallL	1.0	1	0.06	0.06	0.93	1,6
	y 6	CVLT: short delay recall	1.0	1	0.08	0.08	0.93	1,3,6
	y 7	CVLT: long delay recall	1.0	33	0.09	0.08	0.93	1,3,6
	y 8	WISC-R digit span	2.5	0	0.03	0.03	0.94	5
	y 9	WRAML: design memory	2.9	0	−0.01	−0.02	0.95	3
3 - Motor	y 10	grooved pegboard: dominant hand*,L	0.2	0	−0.01	−0.02	0.94	1,3,6
	y 11	grooved pegboard: non-dominant hand*,L	0.2	0	0.00	−0.01	0.91	1,3,6
	y 12	finger tapping: dominant hand	5.5	1	−0.01	−0.02	0.88	1,3,6
	y 13	finger tapping: non-dominant	4.4	1	0.04	0.03	0.88	1,3,6
	y 14	trail making A*,L	0.4	3	0.00	−0.01	0.90	1,3,6
	y 15	trail making B*,L	0.5	15	−0.01	−0.02	0.90	1,3,4,6
	y 16	Bruinincks-Oseretsky	6.0	2	0.09	0.10	0.92	1,5
	y 17	Beery-Buktenica	11.8	8	0.02	0.01	0.94	1,3
4 - Behavior	y 18	CBCL: internal T score*	10.1	0	0.02	0.01	0.97	2
	y 19	CBCL: external T score*	10.0	0	0.01	−0.00	0.97	2,3
	y 20	CTRS hyperactivity index*,L	0.2	88	0.11	0.11	0.98	none

Figure 1.

A comparison of the sex effect on outcomes within domains. The left panel shows the posterior means and 95% posterior intervals from the Bayesian model, and the right panel shows the point estimate and 95% confidence interval from separate scaled regressions for each outcome. Domain and outcome numbers are shown in Table 1.

In the motor domain, being a male was associated with significantly better performance on nearly all outcomes, except for trailmaking A and B (y₁₄ and y₁₅). These outcomes measure time to accurately draw connecting lines between sequential numbers (trailmaking A) or alternating sequential numbers and letters (trailmaking B). The component of number and letter recognition is not part of other motor domain outcomes, which may explain why these two outcomes are different.

We modified our multiple outcomes model for the Seychelles data to allow the effect of sex on trailmaking A and B to differ from its effect on the other outcomes in the motor domain, by expanding the definition of S_i (see Web Appendix A). The dissimilarity of covariate effects across domains and similarity within domains (except for sex), suggests that domain-specific covariate effects should be modeled as fixed effects, and that outcome-specific deviations within a domain for covariates are less important. Therefore our model, as expressed generally in (3), differs from model (2) by not including $b_{\mathcal{D},d\left(j\right),\mathbf{S}}$ or $b_{\mathcal{O},j,\mathbf{S}}$.

3.2 Model results

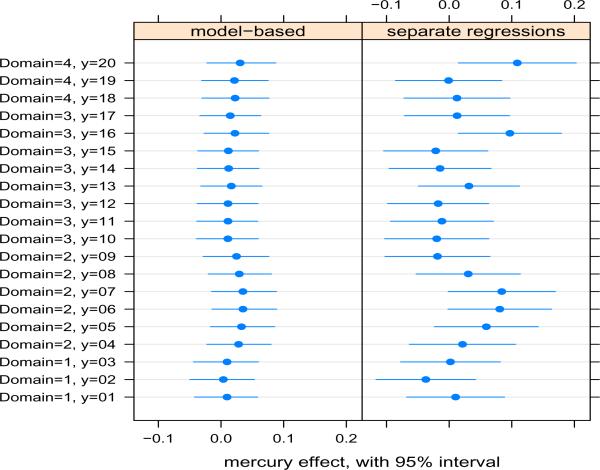
Our results are given in Table 2 under the “Prior A” column. The mean overall exposure effect was 0.02, and Pr(β_x > 0 | data) = 0.81, giving some evidence for a small beneficial MeHg effect. Because we had reason to treat the domain-specific deviations as random effects, thus shrinking them towards each other, estimation of these effects and their differences are not of as much interest as they would have been had we treated them as fixed effects. Of more interest in this application are each of the J outcome-specific exposure effects (${\beta }_x+b_{\mathcal{D},d\left(j\right),x}+b_{\mathcal{O},j,x}$). Figure 2 shows that the 95% posterior intervals for these effects are substantially smaller than the corresponding 95% confidence intervals from separate regressions, demonstrating a considerable increase in power. Shrinkage of the effects towards the domain-specific average, and towards the overall effect are also evident. Figure 1, which shows the sex effects, also demonstrates some increase in power from our model, despite our treatment of these as fixed effects. The similarity of outcome-specific exposure effects is also reflected in the extremely small posterior variances of the domain-specific and outcome-specific deviations (Table 2), and suggests that a model with a common slope for MeHg might be adequate. However we did not consider such a model here, because we are specifically interested in allowing the exposure effects to differ across domains and outcomes, while borrowing strength across the two levels of nesting.

Table 2.

Posterior means (MeHg effects) or medians (standard deviations) and associated 95% posterior intervals for key parameters as applied to the Seychelles Child Development Study. Residual standard deviations are given for the first outcome in each domain. Prior A is IG(0.5, 0.00005), prior B is IG(0.1, 0.00005), and prior C is IG(−0.5, 0), which is a uniform prior on the standard deviations.

		Posterior means (MeHg effects) or medians (SDs) and 95% posterior intervals
		Prior A		Prior B		Prior C
	parameter description	estimate	95% interval	estimate	95% interval	estimate	95% interval
β x	overall MeHg effect	0.020	(−0.025, 0.065)	0.020	(−0.031, 0.072)	0.020	(−0.045, 0.087)
$b_{\mathcal{D},1}$	MeHg: domain 1 deviation	−0.009	(−0.050, 0.015)	−0.013	(−0.063, 0.021)	−0.016	(−0.090, 0.036)
$b_{\mathcal{D},2}$	MeHg: domain 2 deviation	0.010	(−0.015, 0.046)	0.012	(−0.022, 0.059)	0.015	(−0.038, 0.082)
$b_{\mathcal{D},3}$	MeHg: domain 3 deviation	−0.005	(−0.038, 0.021)	−0.007	(−0.051, 0.027)	−0.008	(−0.072, 0.048)
$b_{\mathcal{D},4}$	MeHg: domain 4 deviation	0.004	(−0.024, 0.040)	0.005	(−0.031, 0.051)	0.008	(−0.051, 0.079)
${\sigma }_{b,\mathcal{D},x}$	SD(domain deviation)	0.013	(0.004, 0.049)	0.018	(0.006, 0.077)	0.027	(0.002, 0.163)
${\sigma }_{b,\mathcal{O},x}$	SD(outcome deviation)	0.011	(0.004, 0.030)	0.014	(0.005, 0.036)	0.013	(0.000, 0.040)
σ r	SD(overall subject effect)	0.418	(0.387, 0.451)	0.418	(0.388, 0.452)	0.419	(0.388, 0.453)
${\sigma }_{r,\mathcal{D},1}$	SD(subject effect: 1st domain)	0.198	(0.176, 0.221)	0.198	(0.177, 0.222)	0.199	(0.178, 0.222)
${\sigma }_{r,\mathcal{D},2}$	SD(subject effect: 2nd domain)	0.224	(0.203, 0.247)	0.224	(0.203, 0.247)	0.225	(0.204, 0.248)
${\sigma }_{r,\mathcal{D},3}$	SD(subject effect: 3rd domain)	0.219	(0.200, 0.241)	0.220	(0.200, 0.241)	0.220	(0.201, 0.242)
${\sigma }_{r,\mathcal{D},4}$	SD(subject effect: 4th domain)	0.197	(0.172, 0.226)	0.198	(0.172, 0.226)	0.199	(0.174, 0.228)
σ ε,1	Residual SD(outcome 1)	0.728	(0.680, 0.781)	0.729	(0.680, 0.780)	0.730	(0.682, 0.782)
σ ε,4	Residual SD(outcome 4)	0.851	(0.798, 0.908)	0.852	(0.800, 0.911)	0.853	(0.801, 0.911)
σ ε,10	Residual SD(outcome 10)	0.817	(0.766, 0.872)	0.818	(0.766, 0.874)	0.819	(0.767, 0.876)
σ ε,18	Residual SD(outcome 18)	0.960	(0.901, 1.026)	0.962	(0.903, 1.028)	0.964	(0.904, 1.029)

Figure 2.

A comparison of the mercury effect on outcomes within domains. The left panel shows the posterior means and 95% posterior intervals from the Bayesian model, and the right panel shows the point estimate and 95% confidence interval from separate scaled regressions for each outcome. Domain and outcome numbers are shown in Table 1.

The large posterior median for ${\sigma }_r^2$ (see Table 2, which gives posterior SDs) reflects the substantial overall within-subject correlations between outcomes. Also ${\sigma }_{r,\mathcal{D},1}^2,\dots ,{\sigma }_{r,\mathcal{D},4}^2$, are relatively large, indicating greater correlation between outcomes on a single subject within domains than across domains. The residual variances from the model, ${\sigma }_{∊,1}^2,\dots ,{\sigma }_{∊,20}^2$, (Table 2, which gives SDs) are all smaller than from separate regressions (second to last column in Table 1), indicating that the subject-specific effects can reduce the residual error in our Bayesian model as compared to separate regressions.

The posterior means and medians under priors “B” and “C” (Table 2, last two columns) were extremely similar to those under “prior A”. The only noticeable differences were (a) the domain-specific deviations for the exposure effect were somewhat farther from zero under priors “B” and “C” than under “prior A”, and consequently the median of ${\sigma }_{d,\mathcal{D},x}^2$ was larger; and (b) the posterior intervals for the fixed effects and domain- and outcome-specific random effects were somewhat wider under priors “B” and “C” than “A”. In summary, as the prior became less informative the posterior intervals for effects of interest became wider, but the overall conclusions about these model parameters were essentially the same.

A comparison of summary statistics from the posterior predictive distribution (Appendix E) to the corresponding SCDS values suggests that our treatment of outcomes within a domain as exchangeable (except for sex effects in the motor domain) is an oversimplification. Including additional random subject effects for subsets of outcomes within domains might provide a more accurate representation of the data. Nonetheless, we anticipate that this adjustment would not have much effect on the exposure effect estimates in this application.

4 Simulations

We present results from two small simulations. Each uses “prior A” and sets true parameter values to their posterior means (or medians for variance components) from the MCMC on the SCDS data but uses different values for slopes relating exposure to the outcomes. Both simulations take β_x = 0.05. The first simulation (Web Table 1) uses relatively large domain-specific deviations of ${\mathbf{b}}_{\mathcal{D},x}={(-0.03,0.03,-0.15,0.15)}^T$ and outcome-specific deviations that are all zero. The second simulation (Web Table 2) uses small domain-specific deviations of ${\mathbf{b}}_{\mathcal{D},x}={(-0.01,0.01,-0.01,0.01)}^T$, and small outcome-specific deviations of ±0.005 or ±0.01.

We sampled 50 datasets of size 533 × 20 for each simulation, conditional on the observed values of MeHg and covariates from the SCDS data. We used a single MCMC chain with reasonable starting values. We ran the MCMC 6,000 times for each simulated dataset, saved the last 5000 draws for inference, and present results averaged over datasets within a simulation. The overall slope for exposure was estimated well under both simulations. Shrinkage of the domain-specific effects towards each other is evident from these simulations, with more shrinkage for the model with smaller domain-specific deviations (Web Table 2). For both simulations, posterior intervals for outcome-specific slopes are noticeably smaller and have smaller MSE under our model as compared to the 95% intervals based on separate regressions, showing an increase in power under our model.

5 Discussion

We modeled the effect of exposure on multiple correlated outcomes nested within domains using a Bayesian framework, motivated by data from the SCDS. Our model allows shrinkage of the outcome-specific exposure effects within a domain towards each other, and shrinkage of the domain-specific effects towards an overall effect. As motivated by our application, covariate effects were treated as fixed effects which were allowed to differ across domains. Our model also includes overall and domain-specific random subject effects. As expected from the exploratory analysis, the overall, domain-specific and outcome-specific exposure effects for the scaled outcomes were all very small. Results from our application and two simulations showed that a substantial increase in power is possible under our model as compared to separate models for each outcome.

Our model is appropriate for situations in which nesting of outcomes within domains is known in advance. In our application similar domain-specific exposure effects are expected. By treating domain-specific exposure effects as random, our model allows a borrowing of strength across outcomes and domains. However this shrinkage of effects means that their differences will be shrunk towards zero. If estimation of the domain-specific effects and their differences is a primary focus, it may be more reasonable to treat these as fixed effects.

Our model for multiple outcomes nested in domains resembles and extends the LMM approach for multiple outcomes within a single domain as discussed in [21, 15, 19]. However we take a Bayesian approach in which we use MCMC to iteratively sample from the conditional posterior distributions of all model parameters. It would be impossible to estimate the model parameters non-iteratively. To do so would require inverting (Z^TZ), where $\mathbf{Z}=\left({\mathbf{Z}}_{\mathcal{D}}{\mathbf{Z}}_{\mathcal{O}}\right)$, but (Z^TZ) is not invertible (Web Appendix F).

Although not significantly different from zero, our results suggest that there is slightly beneficial overall effect of MeHg exposure on neurodevelopmental outcomes at age 9 in the Seychelles Islands, consistent with earlier results [17]. However MeHg is a known neurotoxicant, and results from a cohort of children in the Faeroe Islands have consistently indicated adverse MeHg effects [13, 14]. Two recent papers used Bayesian hierarchical random-effects models on the regression coefficients and their standard errors to relate MeHg to multiple IQ outcomes from Seychelles, Faeroe Islands, and New Zealand cohorts [1, 20]. The model includes random effects for studies and endpoints, which assumes shrinkage of these effects is reasonable. A similarity of estimated exposure effects on IQ across studies was seen. These effects were small and were significant for the Faeroe Island cohort, but not the SCDS [1]. This illustrates the importance of being able to estimate small, but important, effects with greater precision, such as can potentially be achieved with the methods presented in this paper.

The major difference between the Seychelles and Faeroes cohorts is the primary dietary source of MeHg, which is pilot whale in the Faeroes [13] and fish in Seychelles. Fish contain many beneficial nutrients including long chain polyunsaturated fatty acids (LCPUFA), which are essential to fetal brain growth and development [8, 25]. Pilot whales are not a rich source of LCPUFA, and often contain PCBs and pesticides. A more recent cohort of Seychelles children included measurements of pregnancy LCPUFA levels [9, 26], and results from this cohort indicated an adverse MeHg effect after adjusting for LCPUFA. A more detrimental MeHg effect after adjustment for fish consumption has also been reported in the Faeroes cohort [4]. We could not adjust for LCPUFA in this dataset, and the estimated MeHg effects here may represent a combination of a direct, presumed adverse, MeHg effect, and an indirect, presumed beneficial, effect of LCPUFA. The models presented in this paper would work well for the more recent Seychelles cohort dataset, when LCPUFA are included as additional covariates.

Our model shares many features with a structural equations model (SEM) fit using data from the Faeroe Islands. Budtz-Jorgensen and colleagues [2] examined the effect of MeHg on multiple outcomes within two neurobehavioral functions: motor and verbal. Their inclusion of standardized latent variables for each function allows estimation of the MeHg effect on the functions directly, as our model does for multiple domains. Factor loadings in the SEM relate the scaled latent variable to the outcomes on the original scale, and allow different exposure effects. Unlike our model approach as illustrated for the SCDS data, these factor loadings are not shrunk towards each other. Results from either the SEM or our LMM approach may be sensitive to model misspecification. By taking a Bayesian approach we can check for model misspecification by comparing summary statistics of the posterior predictive distribution to their corresponding values in the data. Substantial discrepancies may suggest different model variants, or possibly model improvements. Further comparisons of an SEM model and a multiple outcomes model based on the LMM such as our model will be of interest, especially when the model contains multiple domains or functions.