From moonlight to movement and synchronized randomness: Fourier and wavelet analyses of animal location time series data

Abstract

High-resolution animal location data are increasingly available, requiring analytical approaches and statistical tools that can accommodate the temporal structure and transient dynamics (non-stationarity) inherent in natural systems. Traditional analyses often assume uncorrelated or weakly correlated temporal structure in the velocity (net displacement) time series constructed using sequential location data. We propose that frequency and time–frequency domain methods, embodied by Fourier and wavelet transforms, can serve as useful probes in early investigations of animal movement data, stimulating new ecological insight and questions. We introduce a novel movement model with time-varying parameters to study these methods in an animal movement context. Simulation studies show that the spectral signature given by these methods provides a useful approach for statistically detecting and characterizing temporal dependency in animal movement data. In addition, our simulations provide a connection between the spectral signatures observed in empirical data with null hypotheses about expected animal activity. Our analyses also show that there is not a specific one-to-one relationship between the spectral signatures and behavior type and that departures from the anticipated signatures are also informative. Box plots of net displacement arranged by time of day and conditioned on common spectral properties can help interpret the spectral signatures of empirical data. The first case study is based on the movement trajectory of a lion (Panthera leo) that shows several characteristic daily activity sequences, including an active–rest cycle that is correlated with moonlight brightness. A second example based on six pairs of African buffalo (Syncerus caffer) illustrates the use of wavelet coherency to show that their movements synchronize when they are within ∼1 km of each other, even when individual movement was best described as an uncorrelated random walk, providing an important spatial baseline of movement synchrony and suggesting that local behavioral cues play a strong role in driving movement patterns. We conclude with a discussion about the role these methods may have in guiding appropriately flexible probabilistic models connecting movement with biotic and abiotic covariates.

Introduction

The study of movement provides links among behavior, foraging strategies, population dynamics, community ecology, landscape characteristics, and disease (Nathan et al. 2008, Patterson et al. 2008). As such, movement ecology offers a promising approach for understanding the interplay among different levels of ecologically significant biological organization. Theoretical models and their fitting to data facilitate our understanding of ecological patterns driven by movement and dispersal. Both spatial (e.g., home range) and temporal (e.g., correlated random walk) methods of analysis exist. We focus on the latter but note that the results of time-resolved analyses can be interpreted in a spatial context (e.g., Wittemyer et al. 2008).

Among the most common null hypotheses of movement is the class of uncorrelated random-walk models; they are applied to a wide variety of research areas including foraging strategies (Bartumeus et al. 2005, Edwards et al. 2007, Reynolds and Rhodes 2009), dispersal kernels (Nathan 2006), and rates of invasion (McCulloch and Cain 1989, Turchin 1998). Many models that incorporate temporal dependency, including relatively complex state–space models, have focused on first-order autocorrelation as the extent of temporal structure in current net displacement (Anderson-Sprecher and Ledolter 1991, Jonsen et al. 2003, 2005, Forester et al. 2007) or on directional persistence (Kareiva and Shigesada 1983, Root and Kareiva 1984, Bovet and Benhamou 1988, Turchin 1991, 1998). More recent efforts using modern statistical techniques to study models based on difference equations tend to focus on estimating behavioral states and behavioral mode changes (Patterson et al. 2008, Web et al. 2008, Gurarie et al. 2009), but do not focus on the regularity in which these changes may occur.

Animal location data are being collected at increasingly high resolutions (0.25–4.0 hour sampling intervals of large mammals are now quite common) over several seasons. For such data, first-order autoregressive (hereafter abbreviated by AR(1)) and random-walk models may miss important features of the data. Regular temporal oscillations of light and temperature, spatio-temporal resource variation (e.g., plant phenology), changing internal physiological states (e.g., hunger, the need for water, and reproduction), long-term memory, and dynamic inter- and intraspecific population densities are a few likely contributors to movement patterns. Resulting movement patterns may have a high degree of temporal correlation operating at multiple scales and with changing statistical properties (i.e., movement is likely to be nonstationary at one or several temporal scales) relating to scale-specific factors affecting movement. For example, evidence of temporal dependence in net displacement operating at multiple scales has been documented for two different elephant systems (Cushman et al. 2005, Wittemyer et al. 2008).

Given the propensity for many plausible movement mechanisms to operate on fairly regular but different frequencies, with the relative contribution of each driver potentially changing over time, Fourier and wavelet methods (also referred to as frequency and time–frequency methods, respectively) are natural methods to analyze the cyclicity of animal movement and behavior (Wittemyer et al. 2008). The nonparametric nature of these methods makes them particularly useful as initial statistical probes for detecting and understanding transient relationships among movement and physiological, ecological, climatic, and landscape factors.

While Fourier transforms have been increasingly applied in movement studies (Brillinger 2003, Brillinger et al. 2004, 2008), wavelet transforms are less common in movement studies (but see Wittemyer et al. 2008). Wavelet methods have been productive in other areas of ecology, including disease (Grenfell et al. 2001, Cazelles et al. 2007) and population dynamics (Cazelles et al. 2008). However, neither frequency nor time–frequency methods have been evaluated in a systematic manner on movement data with known properties (i.e., simulated data) or presented in a general way. The purpose of this paper is to first evaluate the utility of applying Fourier and wavelet transforms to time series of individual animal movement velocity data (defined as the net displacement from one observation to the next) by using an advection–diffusion based simulation model to generate synthetic movement data. In addition, we discuss and present evaluation of crucial issues related to significance testing; in particular, we examine the role that the “areawise” test (Maraun et al. 2007) can play in addressing intrinsic correlation in the wavelet signal before moving on to empirical studies. Then, we present several empirical examples that illustrate how ecological insight can be gained from Fourier- and wavelet-based analyses.

We begin by briefly reviewing Fourier and wavelet methods. Next we introduce and expand a general stochastic differential equation previously used to analyze and simulate movement (see Brillinger 2003, Brillinger et al. 2004, 2008, Wittemyer et al. 2008), performing simulation studies to test and illustrate these methods. In particular, we focus on how different mixtures of behavior and changes among these mixtures affect the statistical signatures and consider which of several simplistic null hypotheses and significance testing methods most accurately detect behavioral changes. Additional sampling interval considerations are relegated to the Appendix. We illustrate these methods in practice using movement tracks from a single lion (Panthera leo) and six African buffalo (Syncerus caffer). Despite the lack of high-resolution covariate data from which to build mechanistic models, our analyses yield new ecological insights regarding the influence of moon phase on rest cycles in lions and the synchronizing influence of herding behavior in buffalo beyond the effects of local landscape features. Software and computational strategies described in the methods are highly developed and publicly available; all analyses here were done in the freely available R environment (R Development Core Team 2008) making such approaches quite accessible. We conclude by elucidating how the statistical probes presented here may contribute to research using mechanistic movement models that rely on likelihood-based statistical inference.

Methods

Fourier and wavelet transforms

We provide a brief overview of Fourier and wavelet analysis, with greater detail and further references provided in the Appendix (Section A1). Useful starting references include Carmona et al. (1998), Torrence and Compo (1998), Cazelles et al. (2008), and Maraun et al. (2004, 2007). To introduce notation, we start with the continuous position of an animal at time t in the plane R² by the spatial coordinates r(t) = (x(t), y(t)). The data are discretely sampled locations r(t_j) = (x(t_j), y(t_j)), j = 0, 1, …, N, at a constant sampling interval Δt = t_j+1 − t_j for all j. The time series X^N = {X₀, …, X_N−1} is used to construct N approximate velocities X_j = |r(t_j) − r(t_j−1)|/Δt.

Fourier analysis is a ubiquitous tool throughout science, inter alia, allowing estimation of the strength of frequencies ω making up the spectral density f(ω) of a stationary stochastic process. Given the data X^N, the periodogram estimates the spectral density and will show peaks in its power at frequencies most correlated with the data. In addition, the exact analytic relationship between independent and identically distributed (i.i.d.) normal distributions (white noise) and AR(1) (red noise) models and their spectral densities is known (Gilman et al. 1963, Shumway and Stoffer 2000). This relationship provides a convenient approach for comparing empirical movement data against null random-walk models.

Several broad remarks can be made about the choice of the periodogram as a means to probe movement data for temporal structure. Plotting the autocorrelation function, which describes the linear relationship between X_t, and X_t−h, for different lags h, may be a more familiar tool for ecologists. This approach, however, requires a choice on the number of lags that can be realistically included, and estimates of the linear relationship as a function of lag h will be sinusoidal in nature for data with cyclic switches between behavioral modes, making them less efficient for summarizing the correlation structure (Fig. 1). In contrast, Fourier analysis can more sharply identify dominant frequency patterns in movement data, and due to its close connection with the machinery and output of a wavelet analysis, facilitate the application of this tool for detecting non-stationarity in movement.

Fig. 1.

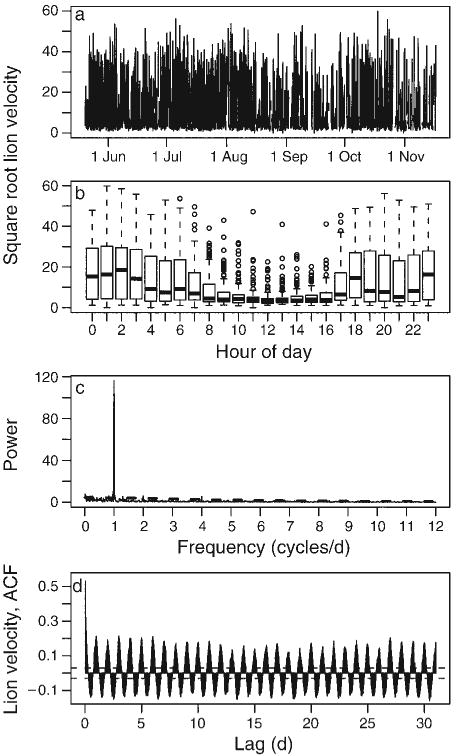
Square-root transformed lion (Panthera leo) velocity (m/h before transformation) shown (a) as a time series and (b) as box plots of velocity by time of day where the thick line denotes the median value, the box extends from the 25th to the 75th percentiles, and the whiskers extend to 1.5 times this interquartile range. (c) Fourier periodogram normalized so that the theoretical white-noise spectrum is at the constant power value of 1; the theoretical spectrum of a red-noise data model is shown by the dashed line. The strong peak at 1 cycle/day reflects an overall daily behavioral sequence of resting during the day with increased activity at night. For comparison with time domain methods, panel (d) shows the estimated autocorrelation function (ACF), with the horizontal lines drawn at $\pm 1.96/\sqrt{\mathit{\text{N}}-1}$ corresponding to the approximate 95% confidence intervals for a white-noise data model.

Continuous wavelet transforms solve some of the limitations of Fourier analysis by decomposing X^N into a function of both time and scale. First, a wavelet function is chosen, which will have a periodic quality and whose period changes for different analyzing scales. We chose the Morlet wavelet, a damped complex exponential, and set its oscillation parameter to preserve an approximate relationship between the scale of the wavelet analysis and the frequency in a Fourier analysis (Appendix); subsequent discussion will hence refer to the time–frequency plane. The wavelet transform of X^N using the Morlet wavelet produces an array of complex numbers in the time–frequency domain from which the estimated wavelet power spectrum (scalogram) can be computed as the squared modulus of these numbers. Relatively large scalogram values identify points in time where the frequency content of X^N matches closely that of the Morlet wavelet for a specific frequency, while small scalogram values identify a mismatch. Another useful tool, based on a wavelet Parseval formula, is the calculation of the proportion of the variance of X^N explained by a band of frequencies through time (Blatter 1998, Torrence and Compo 1998). We will use this tool to categorize movement by its dominant frequency of interest at each time step.

Several features of the scalogram are necessary to consider when evaluating the significance of scalogram values. First, estimating significance of scalogram values relies initially on bootstrapping (Torrence and Compo 1998). For example, to test if a velocity time series is different from white or red noise, one would estimate the white or red noise parameters from X^N, generate a large number of replicate velocity time series, and estimate quantiles for each modulus value. Second, because neighboring times and scales in a scalogram contain intrinsic correlation (Maraun and Kurths 2004, Maraun et al. 2007), this correlation must be taken into consideration. To address this, Maruan et al. (2007) have developed an “areawise” test that removes spurious area of significant scalogram values deemed significant by a bootstrapping test. The areawise test as implemented in Maruan et al. (2007) and employed here, considers the size and geometry of each significant patch, comparing it with that expected from the reproducing kernel of the Morlet wavelet, removing ∼90% of the spuriously significant area defined from bootstrapped quantile estimates of the null model. Third, the cone of influence (the region of the scalogram where edge effects resulting from the finiteness of the data are present) must be calculated (Torrence and Compo 1998). Modulus values outside this cone of influence have been influenced by the finiteness of the data and should be used with caution in biological or statistical inference.

With two contiguous time series, cross wavelet analysis can aid in comparing the time-specific features of movement data between two individuals. This cross wavelet analysis, when based on the Morlet wavelet, produces an array of complex numbers that provide the time-resolved correlation between the two individuals (wavelet coherence), the values of which range from 0 to 1, with 1 denoting perfect linear correlation and 0 denoting no relationship. In addition, the phase lag between them (measured in radians from −π to π) can be estimated. Smoothing in the time and scale dimensions is essential when computing wavelet coherency and phase differences (for details, see Maraun and Kurths 2004). After applying both the bootstrapping and an areawise tests for identification of significant co-oscillation between two movement time series, some consideration should be given to the expected duration, frequency, and phase difference at which synchrony occurs for randomly related movement trajectories with similar spectral properties (e.g., two individuals both take extended midday and midnight rests, but are otherwise unrelated); options include simulations or bootstrapping based on surrogate data produced with similar Fourier spectral (Schreiber and Schmitz 1996) or wavelet properties (Maraun et al. 2007).

Stochastic movement model

In this section, we present a model of animal movement based on a stochastic diffusion process (see Iacus [2008] for a general introduction to this branch of statistics) that has been previously used in several movement studies (Brillinger 2003, Brillinger et al. 2004, 2008, Wittemyer et al. 2008). The continuous position r(t) of an animal at time t is modeled by the stochastic differential equation

$$\mathbf{\text{r}}\left(t\right)=\mathbf{\text{r}}\left(0\right)+{\int }_0^t\mathbf{\mu }\left(\mathbf{\text{r}}\left(s\right),s\right)ds+{\int }_0^t\mathbf{\sigma }\left(\mathbf{\text{r}}\left(s\right),s\right)d\mathbf{\text{B}}\left(s\right)$$ (1)

where μ is the drift representing the deterministic component of movement, σ is a parameter controlling the stochastic contribution to movement, B is a Wiener process (Iacus 2008), and r(0) is the initial location, all of which are vectors or functions in the x−y plane R².

Movement trajectories of arbitrary spatial and temporal complexity can be simulated using Eq. 1 through complicated assignments for μ and σ as functions of space and time. For example, assignments may be motivated by organisms known to be crepuscular or nocturnal/diurnal, with μ and σ periodic in time. The general recipe we use for simulation is described next, and specific details on simulating solutions to models such as Eq. 1 may be found in the Appendix (Section 2) and Iacus (2008). By assuming μ and σ to be constant over discrete intervals of time, Eq. 1 models movement as a locally memoryless diffusion process, but can accommodate different canonical activities when μ and σ are switched over time. The intent of our exposition in this paper, motivated by the results of the empirical studies, is to present methods for analyzing systems where μ and σ switch back and forth over consecutive discrete intervals of time.

In our simulations, we represent three canonical behavioral modes of activity (e.g., resting, feeding, and moving among patches), by assuming that μ and σ switch among three sets of distinct pairs m_i = (μ_i, σ_i), i = 1, 2, or 3 (note μ_i and σ_i are themselves two-dimensional vectors). Let m_ik be the kth behavioral mode (in this example, either of type 1, 2, or 3) in the sequence S_K = {m_i1, m_i2, …, m_iK} where K − 1 is the total number of mode switches, and let E_K ≡ {τ₁, τ₂, …, τ_K} be the expected temporal durations for each m_ik. Assigning values to the τ_k in units of hours such that ${\sum }_{k=1}^K$ τ_k = 24 hours, together with the mode sequence S_K, defines an expected daily behavioral sequence.

By changing the sequence of modes in S_K, the values of τ_k, and the value of K itself, we can simulate different null models of movement according to different expected daily behavioral sequences. In the simulations we present below, we set μ₁ = μ₂ = (0, 0)^⊤, μ₃ = (10, 10)^⊤, σ₁ = (0, 0)^⊤, σ₂ = (2, 2)^⊤, and σ₃ = (2, 2)^⊤, where ⊤ is the transpose of the matrix for all positions r(t). The latter assumption that the switch of values does not depend on position in space, but will only depend on time, is equivalent to assuming the process takes place in a spatially homogeneous environment. To help with conceptual clarity, we classify the behavioral modes m_1k as “rest,” m_2k as “feed,” and m_3k as “taxis” but do not bother to specify the actual units since it is only the relative differences among modes that determine the inherent pattern for a single individual. Additionally, one assumption easily relaxed is that the actual amount of time spent in each behavioral mode m_ik from one day to the next will likely be stochastic. We include this feature in the model by selecting a uniform random variable distributed on the interval [τ_k − 0.5h, τ_k + 0.5h], where h denotes hours, during each simulation day for the amount of time spent in mode m_ik. Choosing sufficiently broad intervals from which to select a realized time in each behavioral mode will remove the regularity of the daily behavioral sequence and therefore the temporal structure in the daily movement, but other reasonable choices for the width of this interval did not appreciably alter the results. A representative example of a simulated movement path and associated velocity time series is shown in the Appendix: Fig. A1.

Fourier and wavelet transforms in practice

Transforming the velocity X^N by its square root can help improve the utility of spectral analyses in several ways. For the Fourier transforms, this helps identify the cyclic nature of velocity time series by stabilizing the variance. The square-root transform also improves the ability of the wavelet analysis to identify temporal structure across a range of temporal scales by diminishing the effect of singular, large velocity values; inordinately large velocity values, while potentially informative about movement ecology in their own right, are associated with high wavelet power across a range of frequencies at a specific point in time and obscure other information in the scalogram. Also, we normalized all Fourier transforms by the variance X^N to facilitate comparison with theoretical Fourier spectrums of modeled white and red noise (the choices for smoothing parameters when implementing Fourier and wavelet transforms are given in the Appendix: Table A1).

Missing data values in X^N, such as those originating from missed GPS fixes, require an appropriate fix that does not artificially create time-dependent signals nor abandon all notion of time dependence in the data. For both empirical studies, we estimated missing latitudinal coordinates using the Kalman smoother (Shumway and Stoffer 2000) obtained from the state–space model lat_obs(t) = lat_true(t) + w_t, lat_true(t + 1) = lat_true(t) + v_t, where w_t and v_t are each independent, identically distributed normal random variables both with mean 0 and variance ${\mathit{\sigma }}_{\text{obs}}^2$ and ${\mathit{\sigma }}_{\text{proc}}^2$, respectively. Longitudinal positions were estimated similarly. Another closely related option would be to use linear interpolation between missing values, but the state–space approach here conditions on all observed data and provides a step toward implementing more sophisticated process models. (Unreported analyses indicate that this choice does not change the conclusions of this paper.) Either of these approaches would clearly fail to address any potential spatio-temporal movement complexity, but we do not wish at this stage of analysis to construct the complexity which we are trying to detect. In the Discussion section, we outline how the methods discussed in this paper may be used in conjunction with movement process models that incorporate relevant complexity (e.g., behavioral switching, covariate data) to produce models and subsequent estimates of missing spatial positions that more completely incorporate movement complexity.

Results

Simulated examples

Our first use of the movement model discussed here is to introduce minimal behavioral mode switching to a random-walk model and explore how the frequency spectrum evolves from the theoretical flat line. Setting K = 2, where K− 1 denotes the number of changes between behavioral modes, and Δt = 1 hour, we varied the ratio τ₂/τ₁ from 0 (random walk) to 1 (τ₁ = τ₂ = 12 hours; a condition producing time symmetric bimodal behavior). In Fig. 2 we see how, as the ratio τ₂/τ₁ increases, the power at ω = 1 cycle/day becomes dominant, while for τ₂/τ₁ = 0, no single frequency is strongly differentiated, as expected from a stochastic random walk. This analysis in insensitive to relatively large Δt, with the same basic result holding at the coarser sampling interval of Δt = 4 hours (Appendix: Fig. A2). We examine how the spectral signatures of crepuscular activity, another biologically common daily movement pattern, differs from a random or bimodal activity pattern. Increasing the value of K to a minimum of 4 in our movement model produces two active periods each day separated by less active periods. For such a movement pattern, strong peaks in the periodogram occur at the frequency ω = 2 cycles/day (Fig. 3). Again, the basic pattern holds when Δt = 4 hours (Appendix: Fig. A3). Regardless of the movement complexity, the periodogram provides a good indication of when temporal dependency exists, but both frequency aliasing and spurious peaks at higher frequencies may limit the ability to map a specific periodogram to a specific daily behavioral sequence.

Fig. 2.

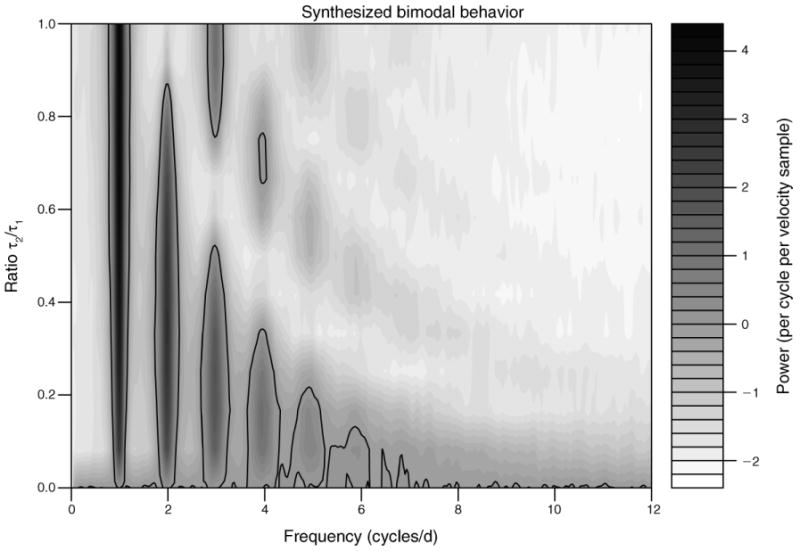
Contour plot of log_e-transformed, averaged normalized periodogram values (power) from 100 simulated movement trajectories consisting of daily bimodal behavior. The daily behavioral sequence is given by the movement mode set S_K = {m₂, m₃} with the values of m_i as defined in Methods: Stochastic movement model. The expected time spent in mode 2 was varied among {0, 1, …, 12} to span a movement complexity of no behavioral switching (τ₂ = 0, i.e., a random walk), to evenly partitioned switching (τ₂ = τ₁ = 12 hours, i.e., symmetric bimodal behavior). For each ratio we simulated 100 continuous movement paths and sampled locations each hour for 30 days. Lines are contoured at the levels of log_e(1) = 0 and enclose regions of frequencies with power larger than that expected by white noise. S_K is the number of distinct movement modes; m₂ is movement mode 2, and m₃ is movement mode 3, as defined in Methods: Stochastic movement models; τ₁ and τ₂ are expected temporal durations for m₁ and m₂, respectively. Grayscale units are in power per cycle per velocity sample, where power is the periodogram value.

Fig. 3.

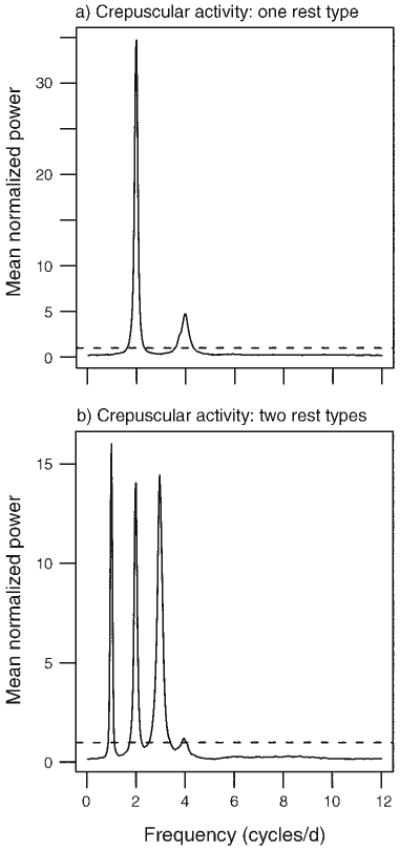
Periodograms for two kinds of simulated crepuscular activity sampled every hour. (a) For the “one rest type” activity, the daily behavioral sequence was defined by S_K = {m₁, m₃, m₁, m₃} and E_K = {4, 8, 4, 8} (the expected temporal durations for each movement mode m_ik) interpreted as alternating between rest and taxis. (b) The “two rest types” activity was defined by S_K = {m₁, m₃, m₂, m₃} and E_K = {4, 4, 12, 4}, interpreted as the sequence rest, taxis, feed, taxis. The power spectrum in each figure panel represents the mean of 100 normalized periodograms. Horizontal dashed lines are drawn at the value of a theoretical white-noise spectrum.

Our second use of the movement model is to evaluate and illustrate frequency and time–frequency methods in the presence of movement non-stationarity. We simulated a path where the daily behavioral sequence was bimodal for an expected 20 days, random for an expected 10 days, and crepuscular for a final expected 20 days (the sample movement path and velocity for the time series analyzed here is shown in Appendix: Fig. A1). As expected, a Fourier analysis provides indication of temporal dependency (Fig. 4a), but only the wavelet transform detects the behavioral shifts (Fig. 4b–d). A white-noise model, combined with an areawise test of significant modulus patches, appears to provide the most accurate delineation of changes between daily behavioral sequence patterns (Fig. 4b), while the random-walk portion of this movement trajectory remains characterized by spurious patches of significant modulus values scattered across a range of frequencies. These basic patterns hold for the coarser sampling interval Δt = 4 hours (Appendix: Fig. A4). Though generated from a single realization of the model, the example result presented in Fig. 4 is a very good representation of the “true” scalogram, estimated by averaging results over many simulations (Appendix: Fig. A5).

Fig. 4.

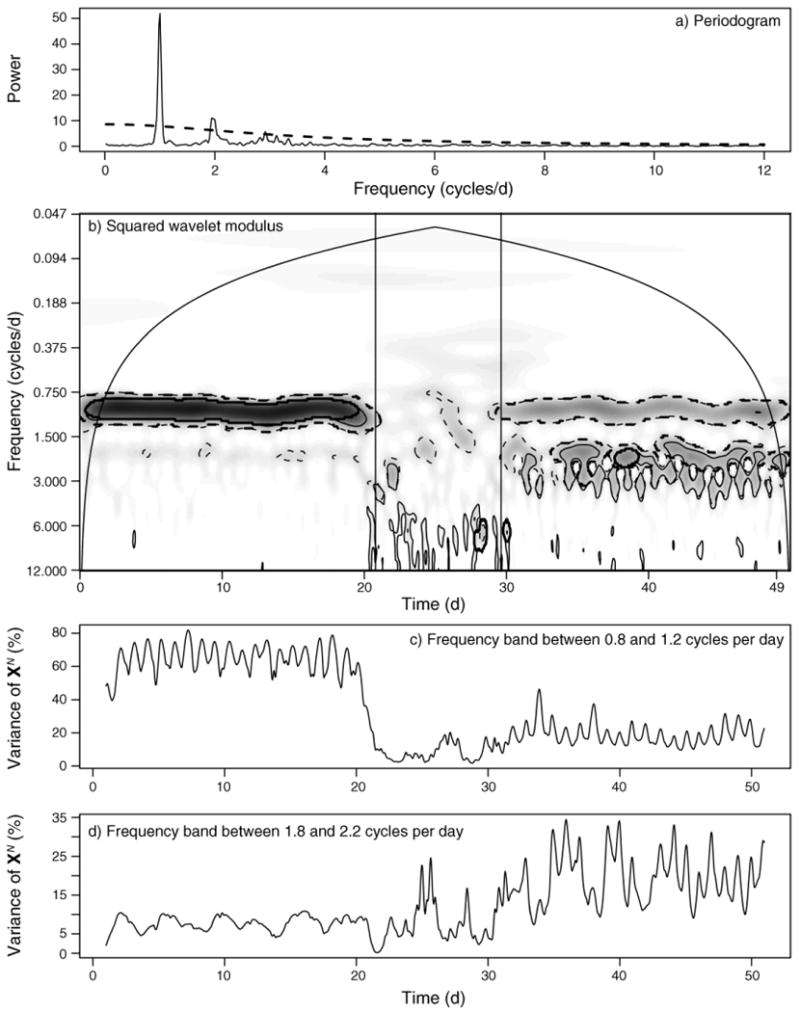
Frequency and time–frequency analyses of a simulated individual movement trajectory over 50 days sampled at Δt = 1 hour. The daily behavioral sequence (with m_i defined in Methods: Stochastic movement model) was S_K = {m₁, m₂, m₃, m₂} and E_K = {6, 6, 6, 6}, corresponding to equal times of rest, feed, taxis, feed for the first 20 days, followed by randomly chosen behavioral modes with expected temporal duration τ_k = 1 hour for the middle 10 days, and ending with crepuscular activity defined as S_K = {m₁, m₃, m₂, m₁, m₂, m₃} with E_K = {4, 4, 4, 4, 4} corresponding to equal expected durations of rest, taxis, walk, rest, walk, taxis, during the final 20 days. (a) The normalized smoothed periodogram shows peaks different from white (constant value of 1) or red (dashed line) noise null models, suggesting cyclic behavior. (b) Contoured squared wavelet modules values (smaller values are given by whiter colors and larger values by darker colors). Using 1000 simulated step-length time series based on the white and red noise null models, we calculated the bootstrapped 95th percentile significant patches, delineated by thin dashed and solid lines, respectively; significant patches remaining from an areawise test (see Methods: Fourier and wavelet transformation) are delineated by thick dashed and solid lines for the white and red noise null models, respectively. The cone of influence is delineated by the arched solid black line. Panels (c) and (d) show the time series of the percentage variance explained by frequency bands around (c) ω = 1 cycle/day and (d) ω = 2 cycles/day, where X^N is the length N time series of movement velocities, defined in Methods: Fourier and wavelet transforms.

Summarizing the simulation study, dominant modes of behavior, e.g., one or two rest periods, are reflected in the periodogram by strong peaks at ω = 1 or ω = 2 cycles/day, respectively. However, there does not appear to be an exact one-to-one relationship between the location of significant peaks in the spectral signature and behavioral modes for realistic sampling intervals and noise. For example, simulations of both bimodal and crepuscular activity produced significant frequencies at ω = 1, 2, and 3 cycles/day (Figs. 2–4 and Appendix: Figs. A2–A4). Wavelet analyses proved useful for distinguishing changes in the frequency content but also produce spurious patches of significant scalogram values. Finally, the correlation of modulus values across both the time and frequency dimensions, and choice of smoothing parameters, will obscure precise identification of changes in the daily behavioral sequence.

Case study: Panthera leo

The first case study investigates the location time series of an individual female lion in the Kruger National Park (KNP), South Africa, with a sampling interval Δt = 1 hour from 19 May 2005 through 16 November 2005. The periodogram of this data has a dominant peak at a frequency of ω = 1 cycle/day (Fig. 1c), reflecting a daily behavioral sequence arising from relatively small daytime (e.g., resting) and high nighttime (e.g., hunting) velocity values (Fig. 1b). The smaller peaks at ω = 2 and ω = 4 cycles/day also indicate possible deviations from a random-walk model, but may also reflect spectral harmonics, and bear further investigation given the slight decline in median values at around 21:00 hours and 04:00 hours (Fig. 1b); further investigation of the data related to ω = 4 did not reveal a strong alternative behavior type, and we subsequently focus on significance at the ω = 1 or 2 cycles/day.

A wavelet analysis (Fig. 5a) confirms information from the Fourier spectrum (Fig. 1c), but indicates the existence of additional structure: the bimodal behavior waxes and wanes somewhat irregularly, and significant time–frequency patches around ω = 2 cycles/day do not appear to be related to the primary bimodal behavior. Using the percentage variance explained at each time step and a white-noise null model of movement to partition the data into subsets for which ω = 1 cycle/day is significant and dominant, ω = 2 cycle/day is significant and dominant, or for which neither ω = 1 cycle/day or ω = 2 cycles/day is significant (random-walk type behavior at a daily time scale) provides a more interpretable understanding of the different behavioral modes engaged in by this lion (Fig. 5b–d, Table 1): the primary signature of ω = 1 cycle/day reflects a bimodal activity, the strength at ω = 2 cycles/day reflects several nights during which additional rest periods take place, while time for which random walk occurs is typified by overall less activity throughout a 24-hour period. The results of the wavelet analysis further partition the lion data in a useful manner not readily obvious from either random-walk assumptions or Fourier analyses.

Fig. 5.

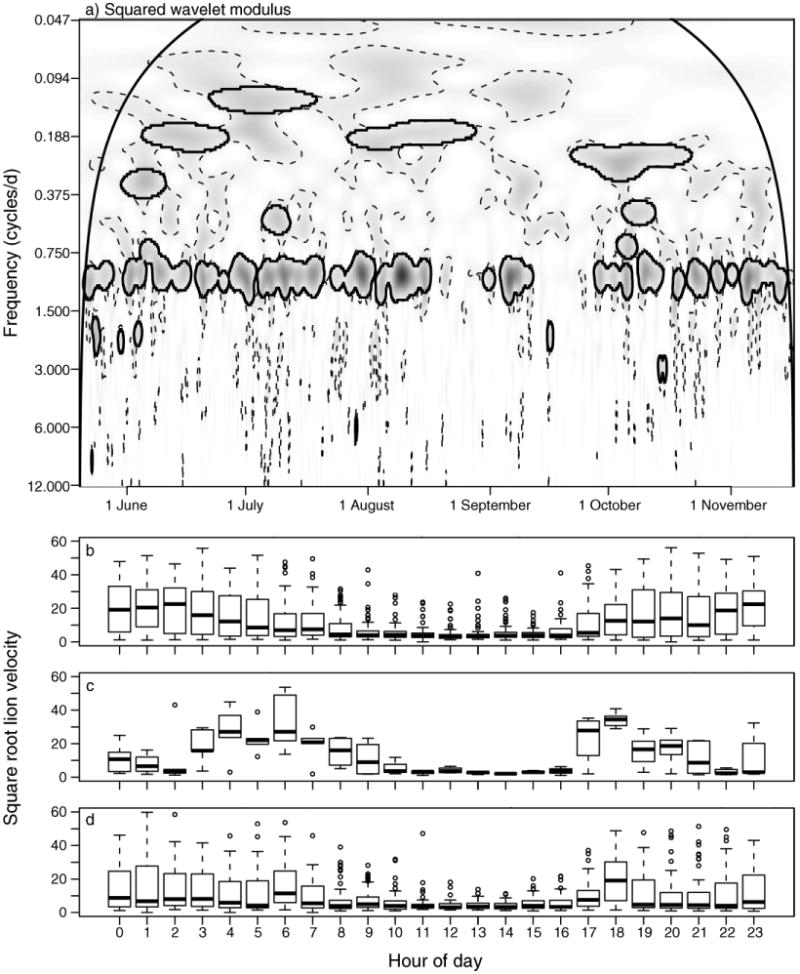
(a) Wavelet analysis of lion velocity data (smaller values are given by lighter colors and larger values by darker colors) shows a dominant, yet transient, 1, 2, or no cycles/day behavior. Significant patches are defined as those that lie inside the solid black closed lines, which delineate patch area remaining from an areawise test of patches defined by 95th estimated percentiles obtained from 1000 bootstrapped white-noise null-model time series, delineated by dashed lines. The cone of influence is delineated by the smooth, arched solid black line. (b–d) Tukey box plots, where the thick line denotes the median value, the box extends from the 25th to the 75th percentiles, and the whiskers extend to 1.5 times this interquartile range, of square-root transformed velocity (m/h before transformation) grouped by hour of day for different partitions of the data: (b) times during which scalogram values at 1 cycle/day are significant and explain a greater proportion of the variance than scalogram values at 2 cycle/day, indicating a basic active–rest cycle; (c) times during which scalogram values at 2 cycles/day are significant and explain a greater proportion of the variance than scalogram values at 1 cycle/day, identifying several active nights during which a secondary rest period occurs; (d) box plots without significant scalogram values at 1 or 2 cycles/day, identifying nights with less activity.

Table 1.

For each time series, a wavelet analysis was used to partition velocity sample times according to one of several characteristic daily behavioral sequences as identified by peaks in the Fourier transform of velocity data.

Daily behavioral sequence type	Time spent in each type (%)
Lion (Panthera leo)
1 cycle/day	63
2 cycles/day	3
Random walk	34
Buffalo (Syricerus caffer)
T7
1 cycle/day	17
2 cycles/day	17
3 cycles/day	2
Random walk	64
T12
1 cycle/day	5
2 cycles/day	16
3 cycles/day	6
Random walk	73
T13
1 cycle/day	4
2 cycles/day	14
3 cycles/day	9
Random walk	73
T15
1 cycle/day	12
2 cycles/day	14
3 cycles/day	4
Random walk	69
T16
1 cycle/day	<1
2 cycles/day	20
3 cycles/day	7
Random walk	72
T17
1 cycle/day	6
2 cycles/day	5
3 cycles/day	9
Random walk	80

Notes: Random walk was defined as the time for which no cycling activity was present. Percentages indicate the amount of time the sequence type is representative of the data. T7, T12, and so on, are individual buffalo.

Explaining the cause of these changes in the daily behavioral sequence is the natural next step in any ecological study. Here, the primary reason for deviation from the bimodal active–rest daily behavioral sequence is reduced nighttime movement, of which there are several possible explanations, including suboptimal hunting conditions resulting from too much light or recent feeding events. Nighttime darkness has been shown to be a significantly important variable in predicting lion hunting success (Funston et al. 2001) and is important in the development of models used to predict lion kill sites from hourly GPS data (C. J. Tambling, unpublished data). A cross-correlation between velocity and moonlight luminosity showed a negative correlation at the 0 lag and a positive correlation at a two week lag, while the cross-correlation between scalogram values at the frequency ω = 1 cycle/day and moonlight luminosity indicates that nighttime darkness predicts increased velocity cycling by several days (Appendix: Fig. A6). The negative correlation of velocity and cycling with moonlight luminosity, and associated decline in median velocities during nights associated with no cycling, suggests that an increase in activity occurs during darker nights associated with the new moon. We also investigated the role of known kills on lion movements in an effort to detect possible triggers for additional rest periods or days during which more movement occurred, but no obvious patterns were present. This may be a function of unknown kills eroding the differences between days with and without known kills as well as the influence of kill size relative to the size of the lion pride on movements (larger kills may elicit longer rest periods). Our analyses suggest several areas where data collection efforts could be focused, including cloud cover, reproductive activity, predation success, prey abundance, or failed-kill attempts, all of which are likely to impact the continuity of repetitive movement by lions.

Case study: Syncerus caffer

The second case study analyzes the time–frequency properties and synchronicity in movement velocity of six female African buffalo, also located in KNP. Locations were sampled at an interval Δt = 1 hour for all six individuals, with a mean length of 131 days (see Appendix: Table A1). Like many ruminants, African buffalo in KNP make multiple behavioral switches throughout the day (e.g., ruminating and foraging), which are often related to temperature and resource availability. The buffalo examined here exhibit a set of behaviors that are typified by several (two or three) relatively active periods each day, while the wavelet transforms show that the strength of this activity pattern is irregular in time (Appendix: Figs. A7–A12). Table 1 summarizes the amount of time spent in different daily behavioral sequences based on the results of wavelet analyses.

The fission–fusion social structure of buffalo in the KNP (Cross et al. 2005) provides an opportunity to illustrate the use of a wavelet coherence analysis to investigate a connection between social proximity (i.e., grouped or separate) and synchronicity in movement patterns, thereby isolating potential scales of movement influencing factors and establishing a baseline measure of synchrony between individuals. Here we focus on two individuals with temporally overlapping data from 15 July 2005 through 29 October 2005, with wavelet coherence analyses of other pairs producing similar results and presented in the Appendix (Section 4).

A wavelet coherence analysis (Fig. 6 and Appendix: Figs. A13–A17) coupled with an estimate of the distance threshold at which significant coherence dissipates (Appendix: Figs. A19–A22) shows that individual velocity time series have a strong linear relationship across their dominant periodogram frequencies at daily scales and are highly synchronized in phase when the individuals are within a distance of ∼1 km, the approximate diameter of a large herd. (Simulation studies using the movement model suggest that the coherence shown between the velocity time series for individuals separated by <1 km is highly unlikely to be a result of random synchrony; see Appendix: Fig. A18.) The scale at which this synchrony drops off suggests herd-level behavioral cues have an important role for movement relative to environmental cues. While landscape features are often one basis for models of movement patterns (sensu foraging strategy literature) and useful predictors of movement (e.g., location of water in arid ecosystems), tradeoffs between foraging and predation risk may be more salient to movement behavior than typically recognized (Getz and Saltz 2008, Hay et al. 2008). The results of our wavelet coherence analyses suggest that investigation of behavioral hypotheses in addition to those driven by foraging strategy (Ruckstuhl and Neuhaus 2002) are merited. Coupled with more context-specific data, further analysis could test environmental (predation risk or variation in forage quantity and quality among neighboring patches) or social (herd sex ratio and size) variables that explain the coherence or lack thereof among individuals.

Fig. 6.

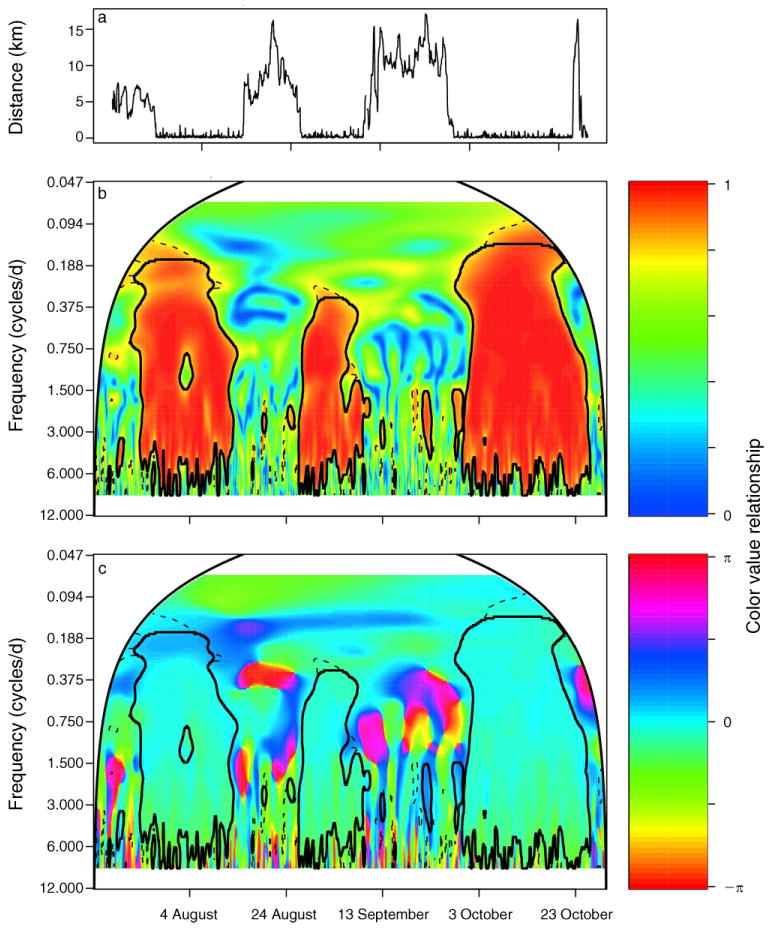
Analyses of two African buffalo (Syncerus caffer; T12 and T13 in Table 1) in July through October 2005: (a) the distance between them, (b) their wavelet coherency, and (c) wavelet coherency phase differences, where the color-value relationship is shown by the color bars to the right of each contour. Wavelet coherence values <1 indicate uncorrelated noise, a nonlinear relationship between the velocity of T12 and T13, or that the processes influencing T12's or T13's velocity are not identical. In panels (b) and (c), significant patches are defined as those that lie inside the solid black closed lines, which delineate patch area remaining from an areawise test of patches defined by 95th estimated percentiles obtained from 1000 bootstrapped white-noise null-model time series, delineated by dashed lines, while the cone of influence is delineated by the smooth, arched solid black line.

Discussion

Frequency and time–frequency methods have several strengths and limitations for better understanding movement data. On the one hand, ecological interpretation of significance in the frequency or time–frequency domain is not always straightforward, and correlation in the time and frequency dimensions challenges the identification of hard boundaries at which the daily behavioral sequence changes. However, motivated by the positive results of our simulation study indicating that the wavelet method is able to identify the timing and extent of behavioral patterns not detectable by a Fourier transform, autocorrelation function, or treatment of data as independently and idenically distributed (i.i.d.), we were able to extract new insights from several rich, but statistically challenging, empirical GPS animal-location data sets. Applied to the lion data, wavelet methods provide an objective, quantitative basis for partitioning data in a way other approaches assuming stationarity in the data do not. This facilitated the detection of a connection between nighttime brightness and activity patterns. By incorporating wavelet approaches to identify temporal switches in cycling behavior, such analyses can contribute to models for kill-site determination (e.g., Franke et al. 2006, Webb et al. 2008) by facilitating model development and suggesting informative priors in estimating posterior densities of complex models. Applied to the buffalo data, the suite of analyses presented here reveals regular within-day switching of behavioral modes and suggests a role for social cues within herds as a mechanism for synchronizing the movement of individuals separated by up to 1 km. Time–domain and time–frequency analyses can clearly contribute to a more nuanced understanding of movement patterns than a priori assumptions of i.i.d. random or low order correlated random-walk models, and stimulate discussion about what poses as an appropriate null model of movement.

Assessment of the spatial organization of wavelet modulus values in both case studies failed to reveal obvious unique locations associated with significant scalogram values; developing techniques for assessing spatio-temporal patterns based on the results of wavelet analyses represent one area of possible future research. However, the failure to identify locations uniquely associated with significant scalogram values at biologically interpretable frequencies highlights an important irony: as long-term, high-resolution data are gathered, quantification of relationships between ecological covariates and movement will often require equally detailed data on other individuals (both within and across species), environment, immune status, or physiology.

The ability to identify time-dependent structure at increasingly higher resolutions should be a cause for encouragement and suggestion about which possible covariates need closer examination. Recently, a wavelet-based time-series-discrimination method has been developed by Rouyer et al. (2008) which classifies multiple (more than two) time series which offer a method for clustering groups of individuals based on shared time–frequency properties. As further data become available, we anticipate wavelet based approaches can be used to improve understanding about the nature of interspecific interactions, e.g., herbivores and plant phenology, predator–prey, or predator–scavenger interactions.

Incorporating frequency and time–frequency based methods into movement analyses has the potential to contribute to future studies in several broader, complementary ways. Recent research (e.g., Jonsen et al. 2005, Patterson et al. 2008) has included the use of state–space models with parameter switching, a likelihood-based statistical model that can accommodate behavioral mode switching, important for testing the role of spatially and temporally dependent covariates. By using the statistical probes evaluated in this paper as a guide, coupled with box plots of activity, ecologists may increase their chances of proposing suitably flexible models and computational strategies (e.g., parameter bounds, informative priors) necessary to successfully conduct statistical inference based on models with complex likelihood functions. Random-walk models connect theoretical mechanisms with patterns (Reynolds and Rhodes 2009), and the use of time-series tools may improve the accuracy of these models by providing data partitioning based on statistically rigorous criteria. Multiple methods of data analysis and presentation may be the most useful approach for a robust analysis of the emerging high-resolution empirical animal location data.