Colloidal quasicrystals with 12-fold and 18-fold diffraction symmetry

Abstract

Micelles are the simplest example of self-assembly found in nature. As many other colloids, they can self-assemble in aqueous solution to form ordered periodic structures. These structures so far all exhibited classical crystallographic symmetries. Here we report that micelles in solution can self-assemble into quasicrystalline phases. We observe phases with 12-fold and 18-fold diffraction symmetry. Colloidal water-based quasicrystals are physically and chemically very simple systems. Macroscopic monodomain samples of centimeter dimension can be easily prepared. Phase transitions between the fcc phase and the two quasicrystalline phases can be easily followed in situ by time-resolved diffraction experiments. The discovery of quasicrystalline colloidal solutions advances the theoretical understanding of quasicrystals considerably, as for these systems the stability of quasicrystalline states has been theoretically predicted for the concentration and temperature range, where they are experimentally observed. Also for the use of quasicrystals in advanced materials this discovery is of particular importance, as it opens the route to quasicrystalline photonic band gap materials via established water-based colloidal self-assembly techniques.

Micelles are the simplest type of self-assembly structure found in nature. They are formed by the association of amphiphilic molecules in solution. Micelles are ubiquitous colloids being used in washing detergents, for the solubilization of pharmaceuticals as well as for the preparation of advanced materials (1). Above concentrations of about 10%, there is an order–disorder transition, where micelles self-assemble into liquid crystalline structures. In the case of spherical micelles, the most common structure types are of cubic symmetry with space groups 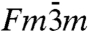(fcc) or 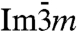(body-centered cubic).

We were investigating the liquid crystalline phase behavior of polymeric micelles in this concentration range in greater detail. For this investigation we used block copolymer micelles that have a well-defined micellar core containing the hydrophobic polymer blocks, surrounded by a relatively large shell consisting of the hydrophilic polymer blocks. As block copolymers we used poly(isoprene-b-ethylene oxide), PI_n-PEO_m, with different degrees of polymerization n and m of the respective polymer blocks. By shear orientation using plate–plate or Searle-type rheometers, large monodomain samples of centimeter dimension can be prepared that allows one to determine the liquid crystalline structure by using small-angle X-ray scattering (SAXS) and small-angle neutron scattering (SANS) (2).

Results

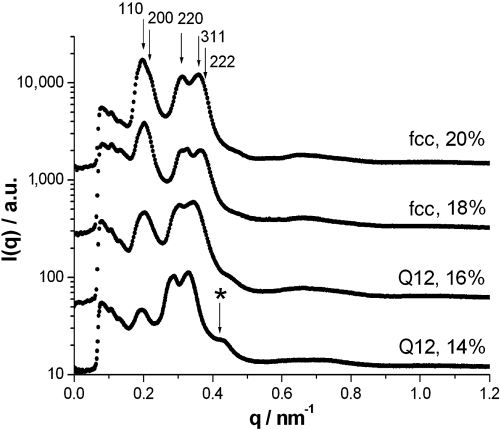
When investigating the phase behavior of PI₃₀-PEO₁₂₀ micelles near the order–disorder transition with synchrotron SAXS and SANS, we discovered phases with diffraction patterns of 12- (Q12) and 18-fold (Q18) diffraction symmetry (Fig. 1). With increasing concentration we find at a temperature of 20 °C a sequence of phases Disordered |13%|Q12|18%| Cubic (fcc). In the concentration range between 13 and 18%, we observe the Q12-phase to be stable at intermediate temperatures (15° and 20 °C), the Q18 phase to be stable at lower temperatures (10 °C), and the fcc phase to be stable at temperatures equal to and above 25 °C. In the scattering curves of isotropic samples in the concentration range between 14–20% at 20 °C the phase transition fcc → Q12 is evident only from the suppression of the 110 reflection and the development of a weak maximum at q = 0.45 nm^-1 (see Fig. 2). Each of the scattering curves in Fig. 2 has been measured at a synchrotron beamline (BW4, DESY) by successive exposures of 30-min duration (to check for possible beam damage) using a Pilatus 300-k detector. Measurements over a broader concentration range between 10–25% have been performed with lower resolution and are shown in SI Text. From the peak positions and the positions of the form factor oscillations in the scattering curve of the fcc phase, we calculate a unit cell dimension of 52.2 nm and a radius of the micellar core of 8.1 nm.

Fig. 1.

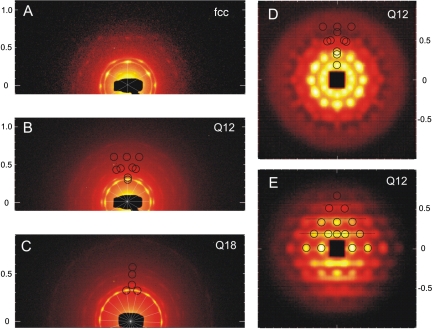
Synchrotron SAXS (A, B, and C) and SANS (D and E) diffraction patterns of the fcc phase (A) and the quasicrystalline phases Q12 (B, D, and E) and Q18 (C). The SANS patterns have been recorded parallel (D) and normal (E) to the 12-fold rotation axis The circles and lines indicate the position of the reflections that are compared to the calculated positions for a quasicrystal in Fig. 6. The scattering vector q is given in nm^-1; the intensity is displayed on a logarithmic scale.

Fig. 2.

Series of synchrotron small-angle X-ray scattering curves for isotropic samples in a concentration range between 14 and 20%. At concentrations of 18 and 20%, the observed peak positions are in good agreement with an fcc structure (space group 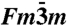). The scattering curves at lower concentrations are characterized by a suppression of the intensity of the 110 reflection and the development of a peak at q^∗ = 0.45 nm^-1, which for the dodecagonal structure corresponds to the 20100 reflection.

Fig. 1 shows the diffraction patterns of shear-oriented samples for the Q12, Q18, and fcc phases. For the Q12 phase we observe a diffraction pattern with 12-fold symmetry (Fig. 1B), for the Q18 phase with 18-fold symmetry (Fig. 1C). The diffraction pattern of the fcc phase is characterized by a 6-fold diffraction symmetry with pronounced 220 reflections (Fig. 1A). The full diffraction pattern of the Q12 phase measured with a larger area detector is shown in SI Text. The Q12 phase was also studied by SANS, and the diffraction pattern with the characteristic 12-fold diffraction symmetry is shown in Fig. 1D. In addition, the diffraction in the orthogonal direction was determined and is shown in Fig. 1E. The Q12 and Q18 phases are stable after shearing. When scanning with the beam (20 × 40 μm) through the sample (30-mm diameter), the same diffraction patterns are found. We reproduced the results by synthesizing further block copolymers with similar block lengths, i.e., PI₃₀-PEO₁₂₄ and PI₃₂-PEO₁₂₀ that showed exactly the same behavior.

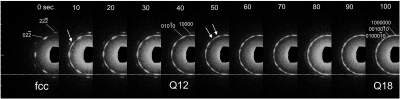
To get insight into the topological changes during the phase transition from fcc into the Q12 and Q18 phase, we performed time-resolved microfocus synchrotron SAXS experiments. The sample, a micellar PI₃₀-PEO₁₂₀ solution at 15%, was cooled under oscillatory shear to induce phase transitions from a fcc monodomain into the Q12 and the Q18 phase. Diffraction patterns were recorded in 10-s frames and are shown in Fig. 3. At the beginning we observe the characteristic diffraction pattern of the fcc phase with its 6-fold diffraction symmetry. The strong 220 reflections, but also the weak 222 reflections, are observed. In the second diffraction pattern, measured after 10 s, a second set of six strong reflections (6₂) has appeared between the six 220 reflections (6₁), indicated by the arrow. This signals the transition into the Q12 phase. After 40 s the Q12 phase has fully developed. After 50 s the transition into the Q18 phase has started indicated by the splitting of the six (6₁) reflections (see arrows in Fig. 3), which subsequently develop into two peaks separated by an azimuthal angle of 20°. The position of the six (6₂) reflections remains unchanged during this rearrangement. This results in the diffraction pattern of the Q18 phase with its 18-fold diffraction symmetry. During phase transitions there is a significant increase in forward scattering due to the heterogeneities of the biphasic regions.

Fig. 3.

Time-resolved microfocus synchrotron SAXS experiment showing the temperature-induced transition from the fcc phase to the Q12 and Q18 phases. The diffraction patterns were recorded in 10-s frames. The dotted line indicates that the involved length scale during the phase transition remains constant. The transition into the Q12 phase proceeds by appearance of an additional set of six reflections after 10 s and subsequently into the Q18 phase by the splitting into further six reflections after 50 s, as indicated by the arrows.

The observed crystallographically “forbidden” diffraction patterns with 12-fold and 18-fold diffraction symmetry could be the result of the formation of a quasicrystalline phase, but could also be due to the presence of a twinned fcc polydomain structure. The time-resolved experiments suggest that the transition from the fcc phase (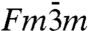) to the Q12 and Q18 phases proceeds via rearrangements of micelles in the (111) layers of the fcc phase. Such rearrangements could result in a 30° rotation of the (111) layers. For a multidomain structure consisting of the same number of 30°-rotated and -unrotated layers this would give rise to diffraction patterns with 12-fold rotational symmetry in the [111] direction. To be consistent with the mirror symmetry of the diffraction pattern observed in the perpendicular direction (Fig. 1E), domains of layers with ABCA… stacking as well as domains with the corresponding twinned ACBA… stacking should be present with equal probability. To calculate the corresponding diffraction patterns we considered a multidomain structure consisting of sequences (ABC)_n(A^′B^′C^′)_n(ACB)_n(A^′C^′B^′)_n of layers that contain the structural features of equal numbers of twinned and 30°-rotated/-nonrotated layers. This layer stacking is shown in Fig. 4E. The subscript n denotes the number of layer repetitions and the primes indicate 30°-rotated layers. We find that the diffraction patterns for n = 2, parallel and perpendicular to the (111) layers, are very similar to the diffraction patterns calculated for other stacking sequences.

Fig. 4.

Micellar packing in the fcc phase (A and D), in a multidomain 0°/30°-rotated, twinned fcc phase (n = 2) with 12-fold symmetry (B and E), and in a multidomain 0°/20°/40°-rotated twinned fcc phase (n = 1) with 18-fold symmetry (C and F). (Upper) A view normal to the micellar layers; (Lower) a view perpendicular to the layers.

Because of the sixfold symmetry the stacking of alternate 0°,30°,0°,…-rotated domains is equal to a stacking of 0°,30°,60°,…-rotated domains, which would be conceptually very similar to the structure of smectic twisted grain boundary (TGB) phases. The TGB phase consists of smectic grains separated by twisted grain boundaries. If the angle α between the layer normals in adjacent slabs is a rational number P/Q, then the TGB phase is quasicrystalline (3). For these phases diffraction patterns with up to 18-fold symmetry or higher have been reported (4, 5). Although this structural similarity suggests a possible stabilizing mechanism for the proposed rotated (111) layers, we note that in the TGB phases the layers are rotated about an in-plane rotation axis, whereas for the multidomain fcc phase the layer stacks are rotated about a rotation axis normal to the layer plane (Fig. 4B). An in-plane rotation such as in the TGB phase would give rise to diffraction patterns that differ considerably from the experimentally observed patterns in Fig. 1.

Similar considerations can be made for the structure with 18-fold diffraction symmetry. Here, a multidomain fcc structure can be proposed that consists of equal numbers of twinned, nonrotated, 20°-rotated, and 40°-rotated (111) layers. To be specific, we calculated the diffraction pattern of a (ABC)_n(A^′B^′C^′)_n(A^′′B^′′C^′′)_n(ACB)_n(A^′C^′B^′)_n(A^′′C^′′B^′′)_n sequence. Also in this case, the subscript n denotes the number of layer repetitions, the primes indicate 20°-rotated layers, and the double primes indicate 40°-rotated layers. By construction, this diffraction pattern possesses an 18-fold diffraction symmetry. The schematic structure for n = 1 is shown in Fig. 4 C and F. The calculated diffraction pattern for n = 2 is shown in Fig. 6F.

Fig. 6.

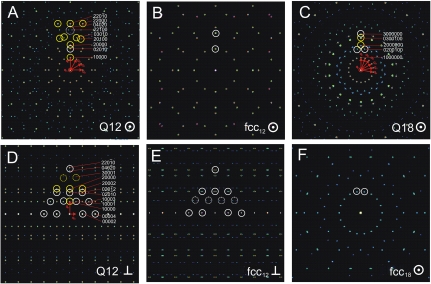
Diffraction patterns of the dodecagonal phase (A and D), the 0°/30°-rotated multidomain fcc phase (B and E), the enneagonal phase (C), and the 0°/20°/40°-rotated multidomain fcc phase (F). A and C are calculated for the h₁h₂h₃h₄0 reciprocal space layer, D perpendicular to it. The encircled reflections are observed experimentally. The reflections encircled in white occur for both the quasicrystalline and the mixed fcc structure. The reflections encircled in yellow occur only for the quasicrystalline structures and are observed experimentally. The reflections for the quasicrystals are indexed based on a set of five reciprocal base vectors for the Q12 phase and on a set of seven reciprocal base vectors for the Q18 phase.

For comparison we have constructed models for quasicrystalline phases such that their diffraction patterns have 12-fold and 18-fold rotational symmetry with the positions of the reflections being in good agreement with the experimentally observed diffraction patterns in Fig. 1. To proceed we note that the projection of the (111) layers in the [111] direction can be represented by a periodic tiling of rhomboedric tiles having a 6-fold diffraction symmetry (Fig. 5D). On this tiling one can generate nonperiodic tilings with 9-fold (enneagonal) (Fig. 5G) and 12-fold (dodecagonal) symmetry (Fig. 5F). The scaling factor between the bases of the 6-fold, 9-fold, and 12-fold tiles can be deduced from their hexagonal periodic average structures (PAS) (Fig. 5E) to be 1.485 and 0.536 (6). The full layer structure is then generated by decorating the tiles with micelles. The tiles and their respective tilings are shown in Fig. 5F for the 12-fold, and in Fig. 5G for the 9-fold tiling. Because of the common PAS, only small rearrangements of the position of the micelles are required for the transition from the FCC to the dodecagonal and enneagonal structure (see Fig. 5 B and C). From the coordinates of the micelles the diffraction patterns are calculated and are shown in Fig. 6.

Fig. 5.

Schematic representation of a layer of hexagonally packed polymer micelles (A), an overlay showing the structural relation between an fcc (111) layer and the corresponding layers of the enneagonal and dodecagonal quasicrystals (B and C), a periodic tiling and the tile representing the [111] projection of the fcc phase (D), the tiling and the tiles of the dodecagonal Q12 phase (F) and the enneagonal Q18 phase (G), and an overlay showing the structural relation between the fcc crystal and the enneagonal and dodecagonal quasicrystals with their respective PAS (E). Different colors represent different layers.

We note that the calculated diffraction patterns of the dodecagonal quasicrystal exhibits reflections, marked in yellow in Fig. 6A, that are not present in the diffraction pattern of the fcc multidomain twinned/30°-rotated structure. The appearance of these reflections in the dodecagonal phase is related to the loss of the 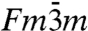ABC stacking and its glide plane upon the transition into the Q12 phase. As these reflections are observed experimentally, they are a strong indication for the formation of a quasicrystalline phase. Further, the position of the reflections observed in the perpendicular direction (Fig. 1E) cannot be reproduced by assuming an fcc structure, whereas the calculated diffraction pattern of the dodecagonal quasicrystalline structure shows good agreement, allowing one to index each of the observed reflections. Also the calculated diffraction pattern of the enneagonal quasicrystal exhibits reflections that are not present in the diffraction pattern of the fcc multidomain twinned/20°-/40°-rotated structure. The appearance of these reflections in the experimentally measured diffraction patterns of the Q18 phase are a further strong indication for the formation of a quasicrystalline phase. A peculiarity of the SAXS diffraction patterns is a suppression of the innermost reflections of the Q12 and the Q18 phase, which is related to the opposite X-ray contrast of the micellar core and shell with respect to the solvent. This is different for the neutron contrast, so that the reflections are visible.

Discussion

The observation of additional reflections and the agreement between calculated and observed diffraction patterns parallel and perpendicular to the n-fold rotation axis strongly suggest the formation of quasicrystalline structures. The diffraction patterns of soft lyotropic phases generally do not show many higher-order reflections due to structural imperfections. For example, there is a considerable horizontal smearing of the 1000n and 2000n reflections observed in the experimental diffraction pattern in Fig. 1E, which indicates that the micelles on the tile vertices are not exactly located in plane with the other micelles. The large width and small number of reflections limit the available structural information. We have in detail considered plausible alternative structures such as multidomain TGB-type phases that would give rise to 12- and 18-fold symmetric diffraction patterns, but in all cases we found that the proposed quasicrystalline structures give the best agreement with the observed diffraction patterns. We cannot completely rule out the possibility that a yet unknown structure with a very large unit cell, a rather complex, hitherto unknown multidomain fcc (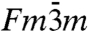) structure, or the coexistence of a yet unknown phase could similarly explain the observed diffraction patterns. However, we have so far no indications for their existence, and all available experimental data can be well explained by the formation of the proposed quasicrystalline structures.

Quasicrystals were first discovered about 25 years ago (7, 8) and are most commonly found in binary and ternary metallic alloys (9), and recently also in binary nanoparticle mixtures (10). They have also been discovered in soft materials such as polyether dendrons (11) and terblock star copolymers (12, 13). This report describes quasicrystals that are spontaneously formed by self-assembly in colloidal solutions. As they are water-based one-component quasicrystals, they are physically and chemically very simple systems. Quasicrystals with 18-fold diffraction symmetry have previously been unreported for any material.

The existence of colloidal quasicrystals has been theoretically predicted for colloids with soft interaction potentials (14). They were predicted to be stable at low temperatures in a range of concentrations between the disordered state and close-packed crystals of fcc or hcp type, which is in agreement with our experimental observations. The stability was traced to a competition between packing efficiency, favoring the fcc or hcp crystal, and nearest neighbor coordination, favoring quasicrystalline order. Lifshitz and Diamant (15) explained the stability of soft one-component quasicrystals with the existence of two natural length scales together with the presence of three-body interactions. Block copolymer micelles exhibit a soft interaction potential, are inherently characterized by two length scales, i.e., the dimensions of the micellar core and the micellar shell (see Fig. 5A), and exhibit interpenetration of polymer chains in adjacent shells making three-body interactions significant. They thus represent an ideal model system to develop a theoretical understanding of quasicrystalline structure and stability.

The unusual symmetry of quasicrystals has been exploited in recent years for the fabrication of photonic band gap arrays (16, 17). Owing to their high symmetry, two-dimensional quasiperiodic structures induce and widen the photonic band gap, preventing light within a range of wavelengths from propagating in any direction. To produce photonic quasicrystals, elaborate electron beam lithographic techniques are currently used. As colloidal quasicrystals are water-based, this opens the way to use established colloidal self-assembly wet chemistry routes to generate photonic quasicrystals (18).

Materials and Methods

Polymer Synthesis and Sample Preparation.

PI-PEO was synthesized by sequential living anionic polymerization of isoprene and ethylene oxide in THF (19). For the present study, three samples were synthesized and investigated: PI₃₀-PEO₁₂₅, PI₃₀-PEO₁₂₀, and PI₃₂-PEO₁₂₀, where the subscripts denote the degrees of polymerization. The degrees of polymerization and polydispersities were determined by MALDI-TOF-mass spectrometry, size exclusion chromatography (chloroform), and ¹H NMR. The polydispersities M_w/M_n were < 1.08. The samples were prepared by directly dissolving the polymers in water for the SAXS measurements and in D₂O for the SANS measurements.

Small-Angle Neutron Scattering.

The experiments were performed at the instrument D11 at the Institut Laue–Langevin. The neutron wavelength was λ = 0.6 nm with Δλ/λ = 9%. Data were collected with a ³He-filled area detector of overall size 96 cm × 96 cm with a spatial resolution 0.75 cm × 0.75 cm per detection element. The sample-to-detector distance was 5.0 m. The collimation distance was 20.5 m, and a 0.3-mm slit was used as the sample aperture to maximize real space and reciprocal space resolution. Details of the instrumentation and data reduction can be found elsewhere (20).

The sample (10 mL) was filled into a quartz shear cell consisting of a stationary outer cup with temperature control and a rotating inner cylinder (Searle geometry) with a 1.0-mm gap, set up in a Bohlin CVO stress-controlled rheometer. The sample stage with the rheometer could be translated to capture all beam positions from the “radial” to the “tangential” position and with the neutron beam hitting the sample perpendicular with respect to the axis of rotation. The quartz cell was thermostated at temperatures of 15, 20, 25, and 30 °C.

The samples were shear-oriented by oscillating shear at amplitudes of 0.5–1 and frequencies of 5–20 s^-1. The structure and orientational state of the shear-oriented samples were stable in time after cessation of shear.

Small-Angle X-Ray Scattering.

Synchrotron SAXS experiments were performed at the BW4-beamline HASYLAB/DESY. The beamlines were equipped with either a two-dimensional CCD detector (MAR Research) or a Pilatus 100-k detector and operated at a wavelength of λ = 0.138 nm. The sample-detector distance was varied between 1.25 and 2.10 m for optimum coverage of the q range, with a moderately focused microbeam of 20 μm × 40 μm (vertical × horizontal) diameter (21). The rotating anode setup consists of a rotating Cu anode, a Göbel mirror, and image plate detectors (Fuji) with a sample-detector distance of 1.00 m. The beam diameter was 1.0 mm. The sample was shear-oriented using a Linkam rheometer with plate–plate geometry and a gap of 0.3 mm using oscillating shear at amplitudes of 0.5–1.0 and frequencies between 5–20 s^-1.

Calculation of Diffraction Patterns.

The diffraction patterns were calculated from the coordinates of the micelles in the tiling models in Fig. 3 C and D according to 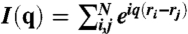with typically a number of N > 1,000 micelles.