Determining biological noise via single cell analysis

Abstract

Single cell analysis techniques describe the cellular heterogeneity that originates from fundamental stochastic variations in each of the molecular processes underlying cell function. The quantitative description of this set of variations is called biological noise and includes intrinsic and extrinsic noise. The former refers to stochastic variations directly involved with a given process, while the latter is due to environmental factors associated with other processes. Mathematical models are successful in predicting noise trends in simple biological systems, but it takes single cell techniques such as flow cytometry and time lapse microscopy to determine and dissect biological noise. This review describes several approaches that have been successfully used to describe biological noise.

Biological noise

Biological systems are intrinsically heterogeneous. Underlying their heterogeneity are stochastic fluctuations of each molecular process (e.g., the production of RNA molecules from DNA transcription, the production of peptides from RNA translation, the degradation of RNA molecules, etc.) needed for cell function. The quantitative description of such fluctuations is termed biological noise [1, 2].

Biological noise is divided into intrinsic and extrinsic noise [3]. Intrinsic noise usually refers to the combination of stochastic variations associated with each of the molecular processes directly involved with the production of a gene product (i.e., a protein) or the biological function associated with the gene product (e.g., enzymatic activity). In contrast, extrinsic noise refers to the variations caused by other molecular processes such as cell-to-cell and cell-to-extracellular matrix contacts, mechanical stress, thermal stress, or variations in the concentrations of other surrounding molecules (e.g., regulators, inhibitors, or metabolites) that do not directly participate in gene expression, but have the potential to modify gene expression via molecular interactions. It is the combined effects of intrinsic and extrinsic noise that lead to cellular heterogeneity or phenotypic variation.

The emergence of single cell analysis techniques has made possible the description of heterogeneity (e.g., phenotypic variations) in biological systems. Comprehensive reviews on single cell analysis have recently appeared [4–8], and some examples of single cell techniques are listed in Table 1. However, the emphasis of this review is on those single cell techniques that have been used as tools for investigating biological noise. More specifically, this review provides examples of how mathematical models, flow cytometry and time-lapse fluorescence microscopy have been used to describe biological noise.

Table 1.

Examples of single cell analysis techniques

Technique	Single cell measurement	Cellular system	References
Flow cytometry	Noise in abundances of GFP-fusion proteins	Sacharomyces cerevisiae	[31]
Optical well arrays	Kinetics of recA and lacZ gene expression using GFP reporter	Escherichia coli	[33]
Fluorescence microscopy	Intracellular calcium release to identify subpopulations differing in expression of P2 receptors	Human osteoblasts	[34]
Electrochemical detection	Time profile of bursts of insulin secretion	Rat and human pancreatic beta cells	[35]
Raman microspectroscopy	Changes in Raman spectra indicating coexisting cell types	Clostridium beijerinckii in an acetone–butanol fermentation reactor	[36]
CE-LIF biomolecules	Two-dimensional separation of proteins that are fluorescently labeled on-line	Cultured MC3T3-E1 osteoprogenitor and MCF-7 breast cancer cells	[37]
CE-LFI organelles	Separation and detection of mitochondria labeled with DsRed2	Cultured 143B osteosarcoma cells	[38]
MALDI-MS	Identification of neuropeptides	Neuron cells isolated from Aplysia Californica	[39]
LCM and cDNA microarray analysis	Gene expression profiling pointing to two subpopulations	CA1 neurons from rat hippocampus	[40]
Multiplexed, real-time RT-PCR	Quantification of 20 different mRNAs	Human small intestine cells selected by FACS	[41]

GFP, green fluorescent protein; CE-LIF, capillary electrophoresis with laser-induced fluorescence detection; MALDI-MS, matrix-assisted laser desorption/ionization mass spectrometry; LCM, laser capture microdissection; RT-PCR, reverse transcriptase polymerase chain reaction; FACS, fluorescence-activated cell sorting

Defining biological noise

An analysis of biological noise begins by taking into account the stochastic variations associated with each of the processes along the path of genomic information flow, a.k. a. gene regulation function (GRF) [9]. Thus, stochastic variations in a GRF will include those associated with (i) gene activation through the binding of a transcription factor to a promoter site in the DNA; (ii) DNA transcription into RNA; (iii) RNA translation into a peptide; (iv) peptide maturation into a functional protein; (v) mRNA degradation; (vi) protein degradation; (vii) molecular autoregulation; (viii) segregation due to cell division, and; (ix) incorrect transcription [3, 10, 11].

Ideally, the stochastic variation in the output from each of these processes is expected to have a Poisson distribution. For example, if the mean number of protein molecules is <p>, the variance δp² equals <p> [3]. Thus,

$$\nu =\delta p^2∕\langle p\rangle$$ (1)

where ν is known as the Fano factor and represents noise strength. Similarly, the coefficient of variation, CV = δp/<p>, is also used to represent noise. For ideal Poisson behavior, ν =1 and CV² = 1/<p>.

As expected for Poisson distributions, molecular processes involving few molecules result in high noise levels. However, processes with large numbers of molecules do not necessarily have reduced noise levels [9, 12], because extrinsic noise or global noise also contributes to the total noise in the GRF output. In fact, this is the main source of phenotypic variation in E. coli and S. cerevisiae [13, 14].

In order to take the various noise sources into account, total biological noise is calculated as

$${\mathrm{CV}}_{\text{tot}}^2={\mathrm{CV}}_{\text{in}}^2+{\mathrm{CV}}_{\text{ex}}^2$$ (2)

where the subscripts “tot,” “in,” and “ex” in each coefficient of variation represent the total, intrinsic and extrinsic noise, respectively [12]. This expression makes it possible to determine the extrinsic noise after measuring the total biological noise (e.g., CV_tot) and the intrinsic noise (e.g., CV_in).

GRF outputs are usually time-dependent. It is the temporal variation in the GRF outputs that ultimately defines cell size, cell cycle frequency or status, developmental cell-fate decisions [15], the production of biomolecules such as mRNA [16], and the release of species such as Ca²⁺ [17]. The form of the GRF output varies among biological systems and they may appear as a steady function, a gradual change, on–off switching [15, 18], bursts [19], oscillations [20, 21], or circadian clocks [22, 23]. Therefore, the noise associated with each GRF output is similarly time-dependent. Some of the examples listed below will demonstrate the importance of the time dependence of biological noise.

Examples of biological noise measurements

Most studies investigating biological noise have used either microscopy or flow cytometry to monitor variants of green fluorescent protein [12, 24–26]. This review describes four approaches used to characterize biological noise. These approaches are: numeric simulations, the regulation of two reported genes by equivalent promoters, the simultaneous monitoring of a gene regulator and the corresponding gene product, and high-throughput biological noise analysis.

Numeric simulations

Following earlier simulations [27–29], Thattai et al. used a numeric simulation to predict the production of proteins from the expression of the lacZ and lacA genes [3]. In this simulation, the authors incorporated reaction rates and the concentrations of species involved in transcription, translation, RNA degradation and protein degradation, and used kinetic constant values previously reported in the literature for the molecular processes. Their simulations predicted Fano factors for protein expression under conditions of steady state, nonequilibrium, autoregulation, and cell division. The reader is referred to the original article for a detailed explanation of the mathematical derivations that were needed [3]. Here, only key features are discussed.

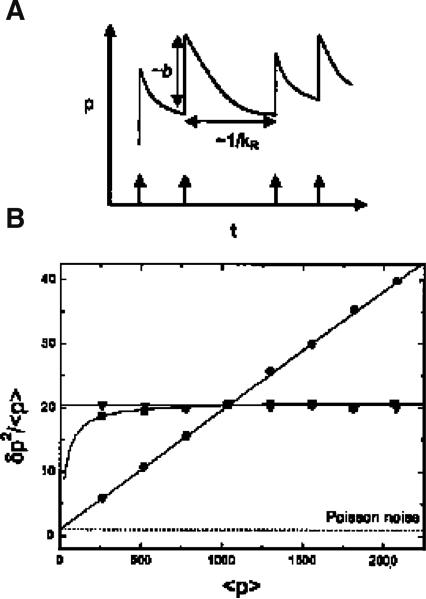
The first simulation assumed a steady state number of mRNA molecules having a Poisson distribution with <r>= k_R/γ_R and ν = δ²/<r> = 1 (c.f. Eq. 1), where <r> is the average number of mRNA molecules, k_R is the mRNA production rate, andγ_R is the mRNA degradation rate. The simulation predicted bursts of protein expression every time an mRNA molecule is transcribed (indicated by the vertical arrows along the time axis in Fig. 1A). When the rate of protein degradation is much smaller than that of mRNA degradation, each burst has on average b protein molecules, with a predicted Fano factor larger than that of a Poisson distribution (i.e., ν~b + 1; c.f. Eq. 1). For the genes lacZ and lacA, the bursts consist of 40 and 5 protein molecules and the predicted Fano factors are ~ 41 and ~ 6, respectively.

Fig. 1A–B.

Numerical simulation of protein production as a function of mRNA translation. A Each transcription initiation event (indicated by an arrow) causes the production of a burst of proteins of average size b; the proteins decay between bursts. B Fano factor (δp²/<p>) as a function of mean protein abundance <p> resulting from varying only the protein burst size (circles), transcript initiation rate (triangles), or the protein half-life (squares). When not varied, the mRNA half life is 2 min; the average protein burst size is 20; the transcript initiation rate is 0.01 s⁻¹, and the protein half life is 1 h. Other conditions of the model are described in [3]; copyright National Academy of Sciences, USA

Figure 1B shows the expected Fano factor (y-axis; c.f. Eq. 1) as a function of the average protein expression (x-axis) when all of the parameters are kept constant except for one of protein burst size (circles), transcription rates (inverted triangles), or protein half-life (squares). As seen from this graph, the transcription rates and protein degradation have constant noise contributions (i.e., ~ constant Fano factors; y-axis) across most of the <p> range, while the noise contribution from the protein burst size (i.e., translation) increases as <p> increases, indicating that the noise in this system is translationally regulated.

The second and third simulations predicted protein production in nonequilibrium systems and in dividing cells, respectively. When the time-dependent degradation of a protein is taken into consideration (i.e., exponential decay after each burst in Fig. 1B), the Fano factor is ν~2b + 1, for short times. Thus, noise levels are higher than in the respective steady-state system [3]. During cell division, the Fano factor changes as a function of cell age. It is predicted that ν~1.33b + 1 just before and ν~0.67b + 1 just after cell division. Thus, noise levels tend to increase as the cell progresses through the cell cycle [3].

The fourth simulation presented by Thattai and co-workers described an autoregulatory system, which is a common motif in biological systems. In autoregulatory systems, the transcription initiation rate (k_R) decreases as the mean gene product (i.e., protein) concentration <p> increases. This system is usually represented by a nonlinear Hill function,

$$k_{\mathrm{R}}=\frac{k_{\mathrm{R},\text{max}}}{1+{\left(\frac{\langle p\rangle }{k_{\mathrm{d}}}\right)}^n}$$ (3)

where k_R,max is the uninhibited transcription initiation rate, <p> is the mean protein concentration, K_d is the dissociation constant between the protein and the interaction site in the transcription machinery, and n is the Hill coefficient. When <p> is low, (i.e., autoregulation is occurring), the Fano factor (c.f. Eq. 2) becomes

$$\nu =\left(\frac{1-k_1∕{\gamma }_{\mathrm{p}}}{1+b{k}_1∕{\gamma }_{\mathrm{p}}}\right)\left(\frac{b}{1+{\gamma }_{\mathrm{p}}∕{\gamma }_{\mathrm{R}}}\right)+1$$ (4)

where the burst of protein molecules per mRNA molecule is b (c.f. Fig. 1), the rate of mRNA degradation is γ_R, the rate of protein degradation is γ_P, and k₁ is inversely proportional to K_d. As an example of autoregulation, the authors simulated the CL repressor protein (i.e., gene product) acting on the promoter P_R (i.e., regulator site) of the bacteriophage λ, which has a K_d value of 50 nM. They also represented a similar system in which CL repressor protein acts on the promoter P_RM, which has a K_d value of 1000 nM. They convincingly demonstrated that the noise strength decreases as the K_d values decrease, pointing to the importance of autoregulation in noise reduction (c.f. Fig. 3 in [3]).

Regulation of two reporter genes by equivalent promoters

An example of this approach is the work by Elowitz et al. [12]. They used time correlation between the expression of two reporter proteins, cyan fluorescent protein (CFP) and yellow fluorescent protein (YFP), each controlled by separate equivalent promoter sites (i.e., two P_Llac_O1 promoter sites located equidistantly in opposite directions from the origin of replication). LacI is a repressor that, when binding to this promoter, increases the production of both CFP and YFP. Therefore, by controlling the expression of LacI (e.g., by changing the concentration of isopropyl β-d-thiogalactopyranoside, which inactivates the expression of LacI), different levels of CFP and YFP expression were attained.

In the absence of intrinsic biological noise, it was expected that CFP and YFP expressions would track each other with time, even in the presence of extrinsic noise that results in temporal variations in protein abundance (Fig. 2A). On the other hand, when intrinsic noise is present, in addition to variations in protein amounts due to extrinsic noise, it was expected that the proportions of CFP and YFP would also vary with time, indicating a loss of time correlation (Fig. 2B). The predicted observations for such systems were that, in the absence and presence of intrinsic noise, bacteria expressing these proteins would all look the same color (right, Fig. 2A) or display color variations (right, Fig. 2B), respectively.

Fig. 2A–B.

Evaluation of biological noise using YFP and CFP expression regulated by equivalent regulatory sequences. The abundances of both proteins are monitored by their respective fluorescence (shown as red and green traces on the left, respectively) versus time; the relative abundances of YFP and CFP determine the observed color (right panels). A In a hypothetical case in which there is no intrinsic noise, the relative abundances of YFP and CFP are constant (i.e., the same color on the right panel), while their individual abundances fluctuate as a result of extrinsic noise. B When intrinsic noise is present, it causes changes to the relative abundance of the two proteins as a function of time. At a given time, the proportion of the two proteins will cause a change in the observed color (right panel). From [12], reprinted with the permission of the AAAS

In the work by Elowitz and coworkers [12], expression of both CFP and YFP in E. coli cells was monitored by fluorescence microscopy, and computerized image analysis was used to create plots of normalized mean fluorescence intensities. As seen in Fig. 3A, a plot of normalized YFP versus normalized CFP values tends to describe a diagonal with a slope of 1. Deviations perpendicular to the diagonal represent intrinsic noise (i.e., changes in the proportions of CFP and YFP). Dispersion along the diagonal represents extrinsic noise (i.e., changes in the amounts of CFP and YFP). This approach worked well for twelve different examples using four different E. coli strains and different variations in promoter regulation (Table 2). In the various scenarios described in this work, the intrinsic noise (η_in = CV_in; e.g., red triangles in Fig. 3) decreased as the number of fluorescent molecules produced increased (Fig. 3B). On the other hand, the dominant extrinsic noise reached a maximum at an intermediate value of fluorescence intensity (η_ex =CV_ex in Fig. 3B). It is believed that the observed maxima were dependent on cell-to-cell variations in the LacI concentration resulting from using a plasmid to express LacI [12].

Fig. 3A–B.

Quantification of noise in a dual gene expression system regulated by equivalent promoters. A Plot of normalized mean fluorescence intensities for the YFP reporter (y-axis) versus the CFP reporter (x-axis). Each marker represents either one M22 (inverted blue triangle) or one D22 (green triangle) E. coli cell. Intrinsic noise is calculated from the deviations perpendicular to a diagonal with slope 1, while extrinsic noise is represented by the dispersion along the diagonal. The total noise is calculated using Eq. 2. B The total (blue diamond), intrinsic (red triangle), and extrinsic (green inverted triangle) noise levels in D22 E. coli as a function of relative fluorescence. The coefficient of variation (CV) is represented by η. As expected, the intrinsic noise decreases as the relative fluorescence increases. Surprisingly, the extrinsic noise, which dominates, has a maximum at 0.3 relative fluorescence. From [12], reprinted with the permission of the AAAS

Table 2 Model systems and strategies used to investigate biological noise

Molecules	System features	Biological noise	Reference
LacZ product	Mathematical model, single gene	ν~41a	[3]
		ν~81b
LacA product	Mathematical model, single gene	ν~6a	[3]
		ν~11b
CL repressor	Autoregulation system of PR promoter (Kd=50 nM)	ν~4a	[3]
CL repressor	Autoregulation system of PRM promoter (Kd=1000 nM)	ν~6a	[3]
Ara product	On–off response	– c	[3]
Lac product	On–off response	– c	[3]
Promoter PR, phage λ	Simultaneous monitoring of two gene products under the same regulation in E. coli	<mi></mi> <mi></mi>	[9]
PLlacO1	Simultaneous monitoring of two gene products under the same regulation in E. coli	<mi></mi> <mi></mi>	[12]
p53–Mdm2	Simultaneous monitoring of protein and suppressor in MCF7 and H1299 cells	– c	[19]
NfκB–lκB	Simultaneous monitoring of protein and suppressor in mice stem cells	– c	[42]
HSF1–hsp70 or hsp90	Simultaneous monitoring of protein and suppressor in mammalian cells	– c	[43]
Smo–Ptc	Simultaneous monitoring of protein and suppressor in Drosophila embryos	– c	[44]
Ime1–Ime2 σH–dnaK or dnaJ	Simultaneous monitoring of protein and suppressor in yeast	– c	[45]
>2500 proteins	Flow cytometry, selection of yeast cells defining intrinsic noise based on scattering	CVtot ~ 0.05–0.45	[31]

^aIntrinsic noise, steady state, ν~b + 1

^bIntrinsic noise, nonequilibrium, ν~2b + 1

^cNot reported

In summary, Elowitz and coworkers found that the production of large and low amounts of CFP and YFP (e.g., in LacI⁻ and Lac⁻ strains) had low and high intrinsic noise, respectively [12]. These results are in agreement with previous studies which indicate that intrinsic noise in these systems is a function of transcription rate, regulatory dynamics, and genetic factors [14].

Simultaneous monitoring of a gene regulator and the gene product

Rosenfeld et al. simultaneously monitored the amounts of CL repressor of the P_R promoter that controlled the expression of the CFP in E. coli lineages [9]. The amount of CL repressor could be monitored by fluorescence microscopy, because this repressor was expressed as the fusion protein CL-YFP construct. This fusion protein was not typically expressed, but when it was transiently induced, it repressed the P_R promoter and the production of CFP. Thus, following induction, the abundance of CL-YFP was high and CFP abundance was low. The investigators monitored cell division and tracked the abundances of CL-YFP and CFP in the cell lineages as a function of time. They observed that CL-YFP was diluted out as cells divided, which removed the repression of the P_R promoter, which in turn led to increased CFP (c.f. Fig. 1 in [9]).

The data nicely fitted Hill functions of the form f(R)= β/[1 + (R/K_d)ⁿ, where f(R) is the protein (CFP) concentration, R is the repressor (CL-YFP) concentration, β is the maximal production rate, K_d is the repressor concentration that gives half-maximal expression, and n is the degree of effective cooperativity in the repression (c.f. Eq. 3). From the deviations from the fit, they determined that the total noise was high (i.e., CV_tot ~ 0.55) and that the CV_tot decreased slightly to ~ 0.4 after correcting for the cell cycle.

In order to further dissect the total noise, the authors carried out a separate experiment in which they regulated two identical genes by the same promoter [12]. This experiment used concepts similar to those outlined in Fig. 2 and made it possible to determine the intrinsic biological noise (i.e., CV_in ~ 0.2). From the total noise and the intrinsic noise (c.f. Eq. 2), they determined that extrinsic noise predominated in this system (i.e., CV_ex ~ 0.350). This extrinsic noise was attributed to differences in the micro-environment for each cell [30], and the various sources of noise caused by other cellular processes [12].

High-throughput biological noise analysis

Flow cytometry was used to investigate the architecture of biological noise in >2500 unique yeast proteins, each tagged with GFP to its c-terminus and expressed from its endogenous promoter and its natural chromosomal position [31]. This was the most comprehensive and systematic study of biological noise to date, and included: (i) the dissection of the observed fluctuations into the extrinsic and intrinsic noise of each yeast strain containing a unique protein; (ii) the identification of gene products deviating from the noise-abundance trends in the entire library of yeast strains, and; (iii) the correlation of deviant gene products in the library with Gene Ontology parameters that contribute to noise.

In flow cytometry, the total noise (i.e., CV_tot) can be determined from the widths of the fluorescence intensity histograms resulting from the analysis of cells expressing the GFP constructs. As shown in Fig. 4A, two different protein constructs may have similar mean fluorescence intensities but different CV_tot values, as shown in the inset. In order to identify the intrinsic and extrinsic noise, the investigators used the concept of gating in 2D plots of forward scattering (FSC), which is a measurement of size, and side scattering (SSC), which is a measurement of cellular granularity. In these plots, they determined the average FSC and SSC, and used these coordinates to define radial regions (gates) in the 2D scattering plots. These gates were then used to select the cells used in the GFP fluorescence intensity distributions (c.f. Fig. 4A). As the gate radius decreased (right to left in Fig. 4B), the CV decreased (black line) until it practically flattened out (indicated by the dashed vertical line). This flat CV value in Fig. 4B suggests that extrinsic noise (blue line) has basically been eliminated, and what remains is intrinsic noise (red line) and instrumental artifacts (gray line), which can be easily corrected. Both the intrinsic and instrumental noise are uncorrelated, and thus can be represented as flat lines in the CV versus gate radius plot. By subtracting the instrument noise and the intrinsic noise from the total noise over the entire gate radius range, one obtains the extrinsic noise (blue line). The two examples in Fig. 4B demonstrate different levels of intrinsic noise (i.e., CV_in) associated with the His4 gene (left) and the Rps25A gene (right).

Fig. 4A–D.

Using flow cytometry to determine the nature of biological noise in yeast. A Example of two flow cytometry results measuring two separate genes expressing GFP-fusion products with similar protein abundances (x-axis) but different distribution widths (i.e., CVs). The strains expressing Rp135A-GFP (red) and Nop8-GFP (blue) have CVs of 11.8 and 38.6, respectively. After sorting and reanalysis, their CVs remain unchanged (see inset), suggesting that flow cytometry is a suitable technique for investigating biological noise. B Dissecting biological noise based on the use of gated forward and side scattering measurements in flow cytometry. The gate, defined as the circular region in a forward versus side scattering plot centered on the average forward and side scattering measurements, is used to select the cells used to determine the CVs of the fluorescence measurements (see A). As the gate is decreased, the CVs of the fluorescence distributions decrease until they plateau (vertical dashed line). This CV represents the intrinsic noise (red trace) after correction for instrumental noise (gray trace). The extrinsic noise (blue trace)is then calculated using Eq. 2. The left and right panels correspond to His4 and Rps25A genes, respectively. C Global noise trends in the expression of all of the yeast genes included in this study. Without gating (top panel), the running median (orange line) shows that there is little dependence of total noise [represented as log₁₀(CV²)] as a function of protein abundance [represented as log₁₀(abundance)]. On the other hand, the intrinsic noise (i.e., when gating is used) is inversely related to protein abundance. In fact, for low-abundance proteins, the slope is ~ −1, which is in agreement with Poissonian behavior (c.f. Eq. 1). D Deviations of CVs from the running median in part C are represented as DMs and plotted versus the square root of protein abundance. The plot shows that some biological processes (e.g., ATP synthesis and the TCA cycle) are noisy. From [31], reprinted with the permission of Macmillan Publishers Ltd.

A plot of log₁₀(CV²) versus log₁₀(abundance) is shown in Fig. 4C for all of the GFP constructs that were investigated in this study [31]. In this figure, CV² shows no correlation with abundance for the ungated results. On the other hand, the use of the gate radii, as indicated by a vertical line in Fig. 4B, results in a plot in which CV² tends to be inversely proportional to protein abundance. In Fig. 4C, the running median (orange line) of low-abundance proteins (e.g., <1000) have a slope ~ −1, which corresponds to a Fano factor of ~1 (c.f. Eq. 1). This is consistent with ideal Poisson behavior.

One unique feature of the study by Newman et al. is that it provides the intrinsic noise values (i.e., gated CVs) for a large number of gene products [31]. These investigators compared the distance of individual CV values from the mean CV value (DM) when the CVs are plotted as a function of protein abundance. As shown in Fig. 4D, gene products displaying an average trend were mainly associated with stochastic noise, while those displaying deviations from that trend suggest the involvement of other parameters, such as the regulation required to maintain low noise (e.g., transcription factors Fl1, Rap1, and Abf1), or high noise (e.g., factors SAGA, SWI/SNF, Ino80, Isw2, and Swr1).

Furthermore, by correlating intrinsic noise with Gene Ontology terms, Newman and coworkers found that proteins involved in the translation, proteolysis and acidification of vesicles in the secretory pathway are associated with low noise levels, suggesting that these processes are highly regulated [31]. Another particularly interesting observation was that proteins involved in oxidative phosphorylation, heat shock, stress, and amino acid synthesis are associated with high noise. The fact that these proteins are associated with organelles that are distributed to the two cells resulting from cell mitosis suggests that subcellular localization is another contributor to intrinsic biological noise.

Concluding remarks

The roles of biological noise in different biological systems cannot be underscored enough. For example, high biological noise may introduce diversity into populations, thus making their evolution possible under conditions of natural selection. In other instances, such as in embryonic development, low levels of or high tolerance to biological noise may be needed. The characterization of noise in such systems is only possible with suitable single-cell analysis techniques.

Flow cytometry and time lapse microscopy have made it possible to observe individual cell behavior and extract information about the origins of biological noise in yeast and E. coli. It is envisioned that other single cell techniques (c.f. Table 2) could use strategies similar to those described in this review to identify the intrinsic noise and extrinsic noise resulting from cellular microenvironments.