Theoretical and empirical quality assessment of transcription factor-binding motifs

Abstract

Position-specific scoring matrices (PSSMs) are routinely used to predict transcription factor (TF)-binding sites in genome sequences. However, their reliability to predict novel binding sites can be far from optimum, due to the use of a small number of training sites or the inappropriate choice of parameters when building the matrix or when scanning sequences with it. Measures of matrix quality such as E-value and information content rely on theoretical models, and may fail in the context of full genome sequences. We propose a method, implemented in the program ‘matrix-quality’, that combines theoretical and empirical score distributions to assess reliability of PSSMs for predicting TF-binding sites. We applied ‘matrix-quality’ to estimate the predictive capacity of matrices for bacterial, yeast and mouse TFs. The evaluation of matrices from RegulonDB revealed some poorly predictive motifs, and allowed us to quantify the improvements obtained by applying multi-genome motif discovery. Interestingly, the method reveals differences between global and specific regulators. It also highlights the enrichment of binding sites in sequence sets obtained from high-throughput ChIP-chip (bacterial and yeast TFs), and ChIP–seq and experiments (mouse TFs). The method presented here has many applications, including: selecting reliable motifs before scanning sequences; improving motif collections in TFs databases; evaluating motifs discovered using high-throughput data sets.

BACKGROUND

Position-specific scoring matrices (PSSM) are commonly used to describe the binding specificity of a transcription factor (TF) to DNA. Such matrices can be built from collections of experimentally characterized binding sites (1–7), or result from pattern discovery algorithms (8–12). TF-binding motifs are generally short in length and moderately informative, so searching for motif instances over a sequence can return many false positives. In addition, annotated binding sites and motifs are of variable quality. It is thus essential for biologists to evaluate the ability of a PSSM to discover functional binding sites in genome sequences.

Several theoretical measures have been proposed to estimate intrinsic properties of a PSSM: information content (13,14), E-value (14) α- and β-risk distributions (15). However, all of these rely on some theoretical model without any guarantee of their adequacy for predicting binding sites in practice. A precise example of this conflict was shown when comparing matrices designed to predict sigma70 promoters, where information content was not, surprisingly, the best indicator of predictive capacity (16).

In order to estimate the capability of a PSSM to distinguish bona fide binding sites from genome background, we propose a method that relies on the combined analysis of theoretical and empirical score distributions in positive and negative control sets. Importantly, positive sets are analyzed using matrices rebuilt with a Leave-One-Out (LOO) procedure, to reduce over-fitting biases. As an additional negative control, we compare empirical distributions of the original matrix with those of column-permuted PSSM.

Beyond quantifying the reliability of a matrix, score distributions reveal interesting biological properties of TFs, distinguishing global from specific regulators. We illustrate the pragmatic interest of the method by applying it to 60 motifs annotated in RegulonDB (17), and show that multi-genome pattern discovery can significantly improve the quality of problematic motifs. Furthermore, we analyze the enrichment of binding sites in sequences obtained from a ChIP-chip experiments characterizing bacterial and yeast TFs (18), as well as ChIP–seq experiments for 13 mouse TFs (19).

MATERIALS AND METHODS

Sequence analysis

Except for matrix building (done with MEME and consensus), all the sequence retrieval and analysis tasks were performed using the Regulatory Sequence Analysis Tools (RSAT) (36–38).

Sequence retrieval

The tool ‘retrieve–seq’ was used to retrieve upstream sequences of all the protein-coding genes of Escherichia coli K12. Sequence lengths were computed to collect all non-coding sequence up to the first upstream gene, with a maximal distance of 400 bp.

For multi-genome analysis, putative orthologs were collected with ‘get-orthologs’ on the basis of the reciprocal best-hit criterion, and upstream sequences were collected for each organism using the tool ‘retrieve–seq-multigenome’.

Computation of weight scores

The weight score (W_S) of a site is computed according to (14).

(1)

where S is a sequence segment of the same length as the matrix (w), P(S|M) is the probability of S given the motif M, and P(S|B) the probability of S given the background model B.

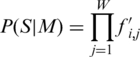(2)

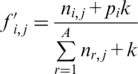(3)

where i is the residue of sequence S aligned with the j^th column of the matrix, 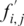is the frequency of this residue at the j^th position of the PSSM, corrected by a pseudo-count k (14). The background probability of the sequence 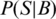, can be estimated using either a Bernoulli schema, or a higher order Markov chain (21).

Theoretical score distribution

The program ‘matrix-distrib’, available as part of the RSAT suite of programs, is able to compute the theoretical distribution of WS for a given PSSM with either Bernoulli (39) or Markovian (21) background models. For each possible weight score (W_S), the program computes its P-value, defined as the probability to observe a score of at least W_S under the background model.

Validation statistics

Sensitivity (Sn) is defined as

(4)

where TP is the number true positives (i.e. annotated sites with W_S above a threshold), and FN is the number of false negatives (i.e. annotated sites scoring below that threshold).

The False Positive Rate (FPR) is defined as

(5)

where FP is the number of false positives (i.e. non-binding sites scoring above the threshold) and TN is the number of true negatives (i.e. non-binding sites below the threshold).

Matrix building

PSSMs were collected from RegulonDB in February 2008 (2,17). We only retained matrices built from TFs having at least four binding sites reported in the literature. The motifs stored in RegulonDB were initially built with the program consensus (8). Motif width is set manually for each TF depending on the sizes of the binding sites reported in the literature.

In addition to the RegulonDB matrices, we derived new collections of matrices using two alternative matrix-building programs: MEME (10) and consensus (14). For building this new collection, redundant sites were filtered out by eliminating sites whose positions overlap by at least 8 bp. We also tested the impact of various parameters on the resulting matrices: (1) motif width varied form 8 to 42; (2) The background Markov was estimated either from the complete genome of E. coli K12 or from the subset of upstream non-coding sequences; (3) for MEME, we tested Bernoulli and first-order Markov models (consensus only accepts Bernoulli models).

ChIP-chip data

LexA ChIP-chip detected binding sequences were obtained from the Supplementary Material of Wade et al. (30).

RESULTS

Overview of the method

The method, implemented in the software tool ‘matrix-quality’, consists of comparing a series of score distributions that characterize various properties of a PSSM:

1. The ‘theoretical distribution’ provides an estimate of the expected FPR at each possible weight score (W_S), based on the prior choice of a relevant background model.

2. The ‘empirical score distribution in all upstream non-coding sequences’ of the organism of interest. These sequences are essentially composed of non-binding sites (the non-coding genomic background), interspersed with a few functional binding sites. The empirical distribution typically fits the theoretical distribution for small W_S values (the background), but separates at high W_S values, most likely corresponding to functional TF-binding sites.

3. The ‘separation between the right tails of the empirical and theoretical distributions’ indicates the capability of the matrix to identify a set of high-scoring putative binding sites in the collection of promoters. We capture this separation by computing normalized weight difference (NWD) curves.

4. An empirical estimate of the FPR is obtained by scanning all upstream non-coding sequences with column-permuted matrices, which supposedly do not correspond to any TF in the organism under consideration. If the background model has been chosen correctly, the ‘empirical distribution of the permuted matrices’ should fit the theoretical distribution.

5. The ‘empirical score distribution in the annotated binding sites’ indicates the sensitivity of the matrix, i.e. its capability to recover binding sites above a given W_S threshold. Matrices are rebuilt and annotated sites are scored using a LOO procedure to reduce over-fitting biases when estimating the capability to detect novel sites.

6. ‘Receiver Operating Characteristic (ROC) curves’ are drawn to indicate the tradeoff between sensitivity and FPR. These curves provide a direct way to estimate the expected cost (in terms of false positives) for achieving a desired sensitivity, or, reciprocally, the sensitivity that can be expected for a given FPR.

7. Optionally, empirical distributions can be measured in any other sequence set, e.g. sequences pulled down in ChIP-chip or ChIP–seq experiments. The comparison with the theoretical distribution indicates the enrichment of these collections in putatively functional binding sites.

Study cases

As our main study case we apply ‘matrix-quality’ to the PSSM for the E. coli K12 tryptophan repressor (TrpR), obtained from RegulonDB. We also discuss the quality of six other representative TFs: CRP, FNR, LexA, CysB, HipB and NanR. We then extend our analysis to all TFs annotated in RegulonDB and further apply it to several high-throughput datasets from bacteria, yeast and mouse.

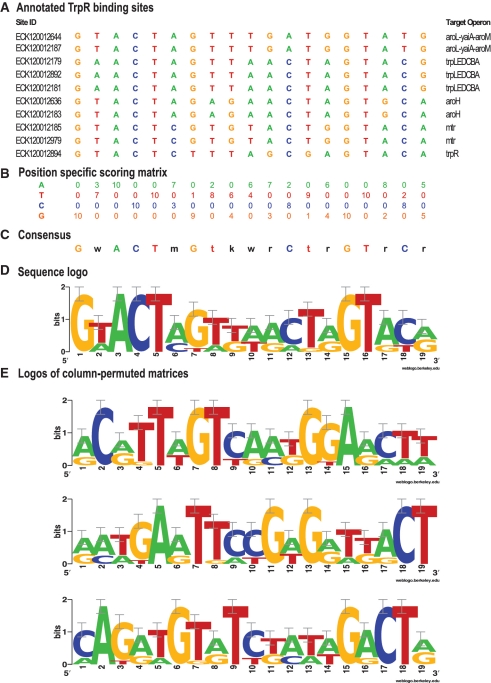
The tryptophan repressor (TrpR) is a specific TF involved in regulating tryptophan biosynthesis. RegulonDB holds information on 10 binding sites associated with five operons in the genome of E. coli K12 (Figure 1A). The database also contains a PSSM built from the aligned binding sites (Figure 1B). Position-specific residue conservation can be summarized either by a degenerate consensus (Figure 1C) or as a sequence logo (Figure 1D) (20).

Figure 1.

TrpR PSSM annotated in RegulonDB and permutation examples. (A) Collection of experimentally characterized binding sites for the TF TrpR of E. coli K12. (B) Count matrix, indicating the occurrences of each residue (row) at each position (column) of the aligned binding sites. (C) Degenerate consensus derived from the matrix (obtained with the RSAT program ‘convert-matrix’). (D) Sequence logo obtained with the program ‘seqlogo’ (40). (E) Three examples of column-permuted matrices used for the negative controls (logo representation).

Theoretical score distribution provides an estimate of the FPR

To detect putative binding sites with a PSSM, the Regulatory Sequence Analysis Tools (RSAT) program ‘matrix-scan’ (21) computes various statistics, including the weight score (W_S) defined by Hertz and Stormo (14) (‘Materials and Methods’ section). However, W_S can be misleading, because its range depends on the matrix width and information content. A more interpretable score is the P-value, i.e. the probability of observing by chance a site scoring above a given W_S, which gives an estimate of the FPR. The theoretical distribution indicates the P-value associated to each possible W_S (Figure 2A and B), and corresponds to the distribution that would be expected when scoring a random sequence of infinite length generated according to the background model.

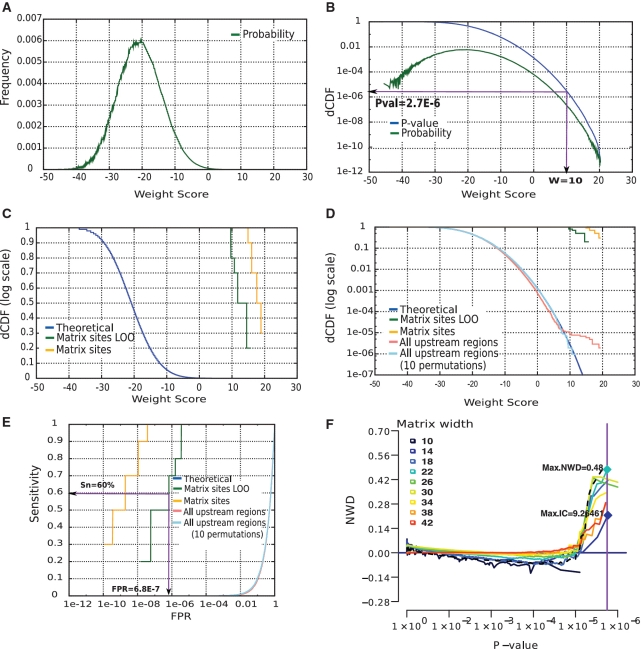
Figure 2.

Theoretical and empirical score distributions for the TrpR matrix. (A) Theoretical density function showing the probability (ordinate) associated to each W_S value (abscissa). In this figure, the theoretical score distribution was estimated with a Bernoulli model calibrated using the whole set of upstream non-coding sequences of E. coli K12. (B) Decreasing cumulative distribution function (dCDF, blue curve) derived from the density function (green curve in A). Abscissa represents the W_S assigned by the matrix. Note that the Y-axis is in log-scale, in order to emphasize small frequencies. (C) Score distributions in the annotated binding sites. Orange: biased scores assigned by the matrix to the annotated binding sites. Green: unbiased scores obtained with a LOO procedure. Blue: theoretical distribution (P-value). (D) Empirical score distribution observed in the whole set of upstream non-coding sequences for the TrpR matrix (pink) and 10 matrices randomized by column permutations (cyan). The logarithmic Y-axis highlights the relevant range of P-values (small values). (E) The ROC curve shows the difference between the biased and LOO validations. The ordinate indicates the sensitivity (fraction of sites detected), the abscissa shows the corresponding FPR. Note the logarithmic X-axis, which is essential to highlight the relevant FPR range (small values). (F) NWD curves for matrices of different widths built from annotated TrpR-binding sites. The dotted line corresponds to the RegulonDB matrix.

The theoretical frequency of all possible W_S for the TrpR matrix is shown in Figure 2A. This is a discrete distribution, because the weight is obtained by computing products from two finite sets of probabilities, respectively defined by the matrix and the background model. The decreasing cumulative distribution function (dCDF, Figure 2B) indicates the P-value, i.e. the probability to obtain by chance a W_s higher than or equal to a given value. This curve is displayed with a logarithmic axis; the arrows show that, in this curve, a W_S of 10 has a P-value of 2.7 × 10⁻⁶, which initially seems excellent. However, even with this quite restrictive cutoff value, we would expect about 23 false positives when scanning the whole genome of E. coli K12 (4.2 Mb) on both strands, and three false positives if the search is restricted to the upstream sequences of all the genes (579 kb × 2 strands).

When the same analysis is applied to other TFs (Figure 3), each PSSM shows a specific theoretical P-value distribution, depending on the particular frequency of each residue in each column of the matrix. Remarkably, NanR shows a step-wise shape, explained by the fact that this motif was built from six identical sites, and thus basically corresponds to a single word. The steps of the theoretical distribution correspond to the probability of observing from 0 to 7 matching residues by chance, which fits a binomial distribution. A similar effect is observed, to a lesser extent, with the yeast Ste12 p motif discovered by detecting over-represented words in ChIP-chip data (Supplementary Data). In this case, the motif of width 11 was built from 59 sites, but the strong conservation of the heptanucleotidic core (TGTTTCA) imposes a step-wise shape, which is only slightly smoothed by the contribution of the poorly informative flanking residues.

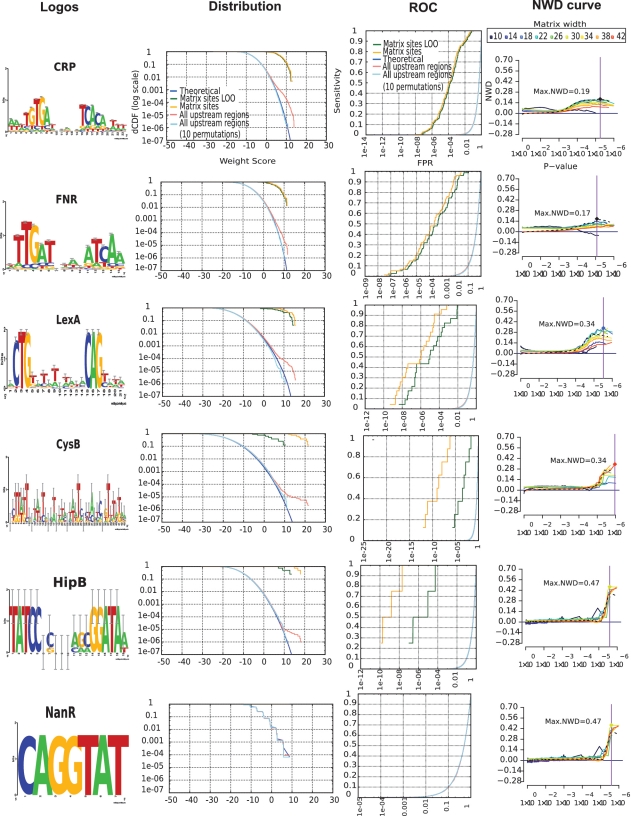
Figure 3.

Sequence logos and score distributions for a selection of representative TFs. Each row corresponds to one TF, indicated in the left column. (First column) Sequence logos. (Second column) Score distributions. (Third column) ROC curves displayed with a logarithmic scale on the abscissa (FPR). (Fourth column) Score difference curves to compare alternative matrices for the same TF. Each curve represents the score differences (abscissa) between positive and negative sets, for different P-values (ordinate).

Background models especially affect estimation of high-scoring sites

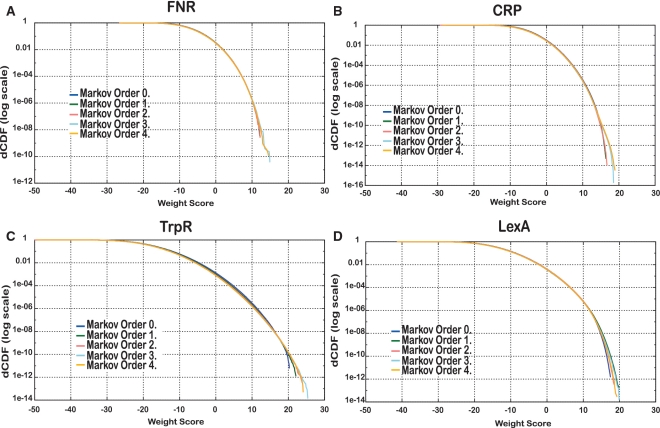
Figure 4 shows the impact of the background model on the theoretical score distributions. For most factors, the Markov order has a negligible effect on the lower weight values (corresponding to the non-coding genomic background), but it particularly affects the right tail of the weight distribution (the range of high W_S corresponding to true binding sites). Curiously, TrpR is the only TF that shows a difference between low and high order background models over the whole distribution (Figure 4C). This is likely due to the presence of the tetranucleotide CTAG in TrpR sites (Figure 1A), which is heavily under-represented in the E. coli K12 genome due to the so-called ‘very short patch repair system’ (22).

Figure 4.

Impact of the background model on the theoretical score distribution for four matrices annotated in RegulonDB. For each factor, the theoretical weight distribution was computed using Markov models of various orders (from 0 to 4) estimated from k-mer frequencies measured in all upstream regions of E. coli K12. (A) FNR. (B) CRP. (C) TrpR. (D) LexA.

In general, the theoretical distribution can be considered a convenient estimate of the FPR, but relies on the correctness of the background model. This assumption can be verified empirically, as shown in the following sections.

Empirical weight score distributions

An empirical score distribution is the collection of W_S measured using a PSSM at all possible positions of a given set of sequences. For each PSSM annotated in RegulonDB, we computed two empirical score distributions to assess the quality of a matrix: (i) the complete set of upstream non-coding sequences of E. coli K12, and (ii) the sequence set of binding sites used to build the matrix. Although these sequence sets are optional, we recommend using both of them to achieve a complete analysis. Additional sequence sets (e.g. sequence fragments pulled down by ChIP-chip or ChIP–seq, upstream sequences of co-expressed genes, etc.) can be added as input to ‘matrix-quality’ in order to compute their empirical distribution and measure their enrichment of putative binding sites.

Empirical W_S distribution in all upstream sequences

The W_S distribution was measured in the complete set of upstream non-coding sequences of E. coli K12 (Figure 2D, pink). This empirical distribution reasonably follows the theoretical distribution in the lower range (W_S ≤ 7). At higher weights the curves separate, revealing a small number of sites with a much higher score than expected by chance (W_S ≥ 9). These high-scoring sites supposedly correspond to experimentally reported TrpR-binding sites. The abrupt separation between the two curves results in a plateau-like shape, suggesting that, in the high score range, the TrpR matrix efficiently distinguishes functional binding sites from the background.

Permuted matrices as negative control

An ideal negative control would be a set of sequences to which the TF of interest does not bind. Unfortunately, experimental evidence of this type is generally not available. An alternative would be to select a random set of promoters, but this could accidentally include some real binding sites. Another possibility is to generate random sequences using some background model (e.g. Markov chain). However, nothing guarantees that Markov chains provide realistic models of biological sequences.

To circumvent these problems, ‘matrix-quality’ automatically performs a negative control by scanning input sequences with randomized matrices, obtained by permuting the columns of the original PSSM, as recommended in other studies (23,24). Column-permuted matrices (e.g. Figure 1 E) have the advantage of preserving important characteristics of the PSSM such as residue composition (sum of each row), number of sites (sum of any column), total information content (14), and complete theoretical score distribution (for Bernoulli models).

All upstream regions of E. coli K12 (579 kb) were scanned on both strands using ten randomized versions of the TrpR PSSM. The distribution of permuted matrices is thus estimated from a total of >10⁷ weight scores (579 kb × 2 strands × 10 matrices). The score distribution of all permuted matrices (Figure 2D, cyan curve) closely follows the theoretical distribution (blue curve) on its whole range, without showing any separation at high scores. This confirms that the plateau observed for the original TrpR PSSM (Figure 2D, pink curve) corresponds to sites specifically detected by this matrix in the genome.

The column-permuted distribution can be considered an ‘empirical estimate of the FPR’. This distribution is estimated from scanning a few megabases of sequence and hence its precision is limited. For example, the highest score observed for the negative control of TrpR had a frequency of ∼1 × 10⁻⁶. This empirical distribution would not allow us to estimate lower P-values, which are the most relevant for binding site evaluation. To combine the advantages of theoretical and empirical FPR curves, we propose the following strategy: (i) scan a representative set of biological sequences with column-permuted matrices; and (ii) if the results fit the theoretical distribution, use the latter to estimate the P-value of predicted sites.

Note that the column-permutation test fails for TFs showing low-complexity motifs (e.g. GGGCGG, TATATA). In such cases, the consensus residues of the permuted matrix will frequently match those of the original matrix, resulting in similar empirical distributions.

Estimation of sensitivity

The sensitivity of a PSSM is the fraction of correct sites detected above a score threshold, which is usually estimated by scoring the sites originally used to build the matrix (‘Materials and Methods’ section). As an example, scores for annotated TrpR sites range from 14.90 to 19.42 (Figure 2C, orange curve). However, this PSSM is probably over-fitted to these particular sites, since each of them is used in the alignment from which the matrix is derived (Figure 1). For an unbiased estimate of sensitivity, we would ideally need two separate collections of sites: one for building the PSSM, another for testing it. Unfortunately, for most TFs, very few binding sites are known. In order to ensure an independent assessment while minimizing the loss of information, the program ‘matrix-quality’ performs a LOO validation, iteratively discarding one annotated site, re-building the matrix, and scoring the left-out site with the new matrix. The program also discards multiple copies of identical sites, if those are not from independent sources, which would otherwise induce the same kind of bias. RegulonDB contains 10 TrpR sites (Figure 1A), with only five remaining after redundancy filtering. Not surprisingly, when applying the redundancy filter and the LOO procedure these sites have lower scores ranging from 9.62 to 15.78 (Figure 2C, green). The LOO score distribution thus corrects obvious biases in the estimation of the matrix sensitivity, and the difference with the matrix sites distribution (Figure 2C, orange curve) indicates the level of over-fitting to the training sites.

Strong differences between uncorrected and LOO curves reveal problematic matrices. For instance, the CysB matrix from RegulonDB covers 43 columns, which is unusually large for a TF-binding motif. Initially, the score distribution in all promoters follows the theoretical distribution for low score values (weight < 5), and shows a clear plateau for high scores (weight > 10), with a few sites scoring above 20, thus suggesting that the motif has good specificity. However, the LOO test (Figure 3, green curve) returns much lower scores than the uncorrected site distribution (Figure 3, orange curve), thereby revealing a strong effect of over-fitting. The CysB matrix is able to recognize the eight genomic sites used to build it, but fails to predict additional sites.

In contrast, matrices built from many sites (CRP, FNR) show almost no difference between LOO and uncorrected site distributions (Figure 3). For factors like LexA, over-fitting seems reasonably low, thanks to the sufficient number of annotated sites (23 sites).

ROC curves indicate the trade-off between sensitivity and FPR

The ROC curve (25) is a standard representation of the trade-off between FPR and sensitivity. However, the risk of false positives applies to every position of the scanned sequences. Even with an apparently low FPR, the actual number of FP can be very high when scanning a genome. For example, E. coli K12 upstream regions scanned on both strands represent more than 1 million scored positions, so that an FPR of 0.001 would return 1159 FPs. Consequently, regular ROC curves are of no use for estimating the discriminatory power of a matrix. For the same reason, the Area Under the Curve (AUC), classically used to assess the quality of ROC curves, is ineffective. Indeed, the AUC is obtained by integrating sensitivity over the full range of FPR from 0 to 1, yet genome-wide predictions performed with an FPR of 90%, 50%, 10% or even 1% are not useful at all. To emphasize the lower, more relevant, range of FPR, ROC curves are drawn with a logarithmic abscissa, and we use alternative statistics instead of the AUC.

For the TrpR PSSM, the LOO curve (Figure 2 E, green curve) shows that 60% sensitivity can be attained with a FPR of 6.8 × 10⁻⁷, or a cost of 1 FP every 1/(6.8 10⁻⁷)bp = 1.47 Mb. This estimation of sensitivity with LOO procedure is unbiased, but it is based only on five non-redundant sites, thus being of questionable robustness (this could change if new TrpR sites become available). For the LexA matrix, built from 23 binding sites, the ROC curve shows a gradual increase (Figure 3); at 50% sensitivity the expected FPR remains reasonably low (FPR_50% = 1.3 × 10⁻⁵), whereas 90% sensitivity includes almost 1FP per 100 bp (FPR_90% = 8.3 × 10⁻³). HipB is a typical case of TF with a very small number of characterized sites (four sites, all involved in the regulation of the hipBA operon). Since each site contributed 25% of the matrix frequencies, the matrix is over-fitted, as denoted by a 10 000-fold difference in FPR between the uncorrected (orange) and the LOO (green) site score distributions (Figure 3). It is thus essential to estimate the FPR on the LOO curves rather than on the simple distribution of scores in the annotated sites. We systematically analyzed the FPR_50%, FPR_90% and FPR_100% for all the PSSM annotated in RegulonDB (Table 1). The ratio between the FPR computed with the LOO approach and from the matrix sites (biased) shows wide variations (from 2 to 10¹⁰). High ratio values indicate an over-fitting of the matrix to the training sites, and can be used to detect poorly predictive matrices in a TF database.

Table 1.

Characterization of the 60 PSSM stored in RegulonDB

Nb	Factor	Width	Target genes	Matrix Consensus (IUPAC)	Total IC	IC per column	E-value	FPR50% (LOO)	FPR90% (LOO)	FPR100% (LOO)	FPR50% (matrix sites)	FPR90% (matrix sites)	FPR100% (matrix sites)	LOO/Matrix sites (FPR 50%)
1	AgaR	25	11	rmvdwbCrwtwtswttCGtwtkkyt	8.18	0.33	2.6 E-02	3.20 E-04	3.90 E-02	1.00 E-01	1.60 E-06	4.50 E-04	5.80 E-04	200
2	AraC	19	9	kayssrCyaawctkmtSyr	6.88	0.36	2.7 E-03	8.50 E-04	2.30 E-02	5.30 E-02	2.80 E-05	5.00 E-04	1.40 E-03	30
3	ArcA	62	153	hysksrykbvkksaswmkktwgwtwacmayhakttaamtmaymkkyracmwwcsbdbvsgbs	7.00	0.11	3.3 E-27	7.90 E-04	4.60 E-02	2.10 E-01	5.20 E-05	8.40 E-03	6.30 E-02	15
4	ArgP	14	5	tkrmCmayaaSCSr	6.18	0.44	1.8 E + 00	6.30 E-03	4.50 E-02	4.50 E-02	3.90 E-06	5.40 E-05	5.40 E-05	1615
5	ArgR	19	37	ymkwktSmmtawwaaysCa	7.97	0.42	9.1 E-20	3.50 E-05	4.70 E-03	7.50 E-03	5.10 E-06	4.60 E-04	7.70 E-04	7
6	CpxR	16	58	GTwamrykbsGtaamr	5.43	0.34	2.8 E-11	6.10 E-04	4.40 E-02	6.60 E-02	1.40 E-04	4.00 E-03	2.00 E-02	4
7	CRP	23	413	wwwtGtGatsyrsrtCaCrtwtt	6.42	0.28	7.5 E-249	1.80 E-04	1.50 E-02	6.80 E-02	1.30 E-04	8.90 E-03	5.10 E-02	1
8	CsgD	12	9	rYGGsTsabYya	6.34	0.53	1.1 E-02	4.50 E-05	8.60 E-02	8.60 E-02	4.20 E-07	9.30 E-05	9.30 E-05	107
9	CysB	43	24	mCkkaktsmtwtyrrmwcktmcwwatCrcymryCsGtytakav	12.38	0.29	2.0 E + 00	3.10 E-04	2.30 E-02	2.30 E-02	9.60 E-10	6.20 E-07	6.20 E-07	3.23 E + 05
10	CytR	41	12	ksksakbsvAwttykkraryvrktkysMykyghwGySrtrs	11.83	0.29	5.8 E-03	2.30 E-03	1.20 E-02	1.80 E-02	6.10 E-08	3.10 E-07	1.00 E-06	3.77 E + 04
11	DeoR	17	6	tGtkrsAAtgCyArMAw	7.49	0.44	8.7 E-03	6.00 E-04	4.70 E-02	4.70 E-02	4.20 E-06	1.00 E-04	1.00 E-04	143
12	DgsA	24	9	ttaTTtyRmwGYGCGaaatwaats	11.58	0.48	6.0 E-11	3.40 E-06	7.10 E-04	7.10 E-04	8.50 E-09	3.70 E-07	3.70 E-07	400
13	DnaA	10	10	TrTsSAYaar	6.11	0.61	7.5 E-07	1.40 E-04	1.80 E-02	1.80 E-02	3.50 E-05	1.40 E-03	1.40 E-03	4
14	FadR	18	11	rRCTGRTCsGAycwstwm	9.32	0.52	2.5 E-13	2.20 E-05	9.90 E-03	1.00 E-02	4.70 E-07	2.60 E-05	7.20 E-05	47
15	FhlA	41	30	tmktgmkkTkmrwmrmRwmradRvtGwcGAaaksayrtkTt	15.51	0.38	1.3 E-01	2.50 E-04	4.00 E-03	4.00 E-03	1.80 E-14	1.40 E-11	1.40 E-11	1.E + 10
16	Fis	22	168	ryyGsybrwwwwttvrsCrrwy	4.75	0.22	3.7 E-43	2.20 E-03	3.90 E-02	1.20 E-01	1.20 E-03	2.40 E-02	7.90 E-02	2
17	FlhDC	17	80	TtwwcSssckawrwarc	6.62	0.39	6.6 E-09	8.70 E-04	1.70 E-02	2.00 E-02	7.00 E-05	7.80 E-04	1.50 E-03	12
18	FNR	15	271	tttGatstaaatCaa	5.72	0.38	7.4 E-59	4.60 E-04	1.50 E-02	1.10 E-01	2.40 E-04	7.20 E-03	2.80 E-02	2
19	FruR	19	36	wsSTGAAtCGwTtCaGyas	10.62	0.56	3.6 E-24	3.70 E-06	1.30 E-04	3.80 E-04	1.20 E-07	2.30 E-06	4.00 E-06	31
20	Fur	16	82	atGakaaysrttmkCa	8.83	0.55	1.6 E-94	1.70 E-05	7.40 E-04	5.00 E-02	3.00 E-06	2.40 E-04	6.50 E-03	6
21	GadE	21	31	mYtaGGmkkttRYtAttkavA	8.78	0.42	8.5 E-02	1.00 E-03	4.50 E-03	4.50 E-03	2.70 E-07	8.20 E-07	8.20 E-07	3704
22	GalR	17	10	tGkaAvCGrTthCAytg	9.65	0.57	2.7 E-11	5.50 E-06	7.50 E-03	7.50 E-03	8.90 E-08	1.80 E-05	1.80 E-05	62
23	GalS	17	9	tGkaAvCGrTthCAytg	9.65	0.57	2.8 E-11	5.50 E-06	7.50 E-03	7.50 E-03	8.90 E-08	1.80 E-05	1.80 E-05	62
24	GcvA	30	5	mkCckktGysryratmwAttktCcsytScS	10.59	0.35	2.7 E + 01	4.30 E-03	9.50 E-03	9.50 E-03	6.70 E-10	3.00 E-09	3.00 E-09	6.42 E + 06
25	GlpR	21	9	wwwatGykCGwwwhSGmdCrt	7.89	0.38	1.3 E-13	4.80 E-04	1.30 E-02	4.00 E-02	1.80 E-05	1.00 E-03	1.20 E-03	27
26	GntR	21	12	tGTtrCsSrTAwCAgdwrvwr	9.78	0.47	2.7 E-12	4.10 E-05	4.80 E-03	4.00 E-02	1.60 E-07	1.50 E-05	2.90 E-04	256
27	H-NS	16	141	yvtGvmaTrkytSrck	4.31	0.27	2.8 E + 04	6.30 E-03	3.10 E-02	5.20 E-02	2.20 E-03	1.10 E-02	2.10 E-02	3
28	HipB	19	2	TATCCsSkmkmGCGGATAa	11.02	0.58	3.9 E-09	2.70 E-07	5.60 E-05	5.60 E-05	1.90 E-10	2.00 E-08	2.00 E-08	1421
29	IclR	8	4	ryytYYGm	4.41	0.55	4.4 E-02	4.60 E-03	3.20 E-02	3.70 E-02	4.60 E-04	3.80 E-03	5.10 E-03	10
30	IHF	14	218	watCarskvvttrm	3.80	0.27	2.0 E + 00	4.30 E-03	3.60 E-02	2.70 E-01	2.40 E-03	2.40 E-02	1.80 E-01	2
31	IscR	26	26	wAtAvCCvmyYrrwwTrStsGggtaw	9.73	0.37	1.4 E-03	1.20 E-04	1.10 E-02	1.10 E-02	8.00 E-08	1.20 E-05	1.20 E-05	1500
32	LexA	21	44	rCTGkayrtmhatmCAGyatw	10.40	0.50	8.0 E-48	9.80 E-06	8.10 E-03	8.70 E-03	1.10 E-06	2.90 E-05	6.20 E-04	9
33	Lrp	13	91	grawwwtabbCtk	3.51	0.27	8.6 E + 09	9.70 E-03	4.20 E-02	8.10 E-02	5.60 E-03	2.10 E-02	5.10 E-02	2
34	MalT	11	10	ycmkkGmTymT	4.67	0.42	4.7 E-01	6.80 E-04	2.90 E-02	1.60 E-01	1.30 E-05	5.50 E-03	2.30 E-02	52
35	MarA	22	24	kyrawmrRtrSsrymwkycwvw	6.36	0.29	2.1 E + 01	2.20 E-03	6.80 E-02	9.40 E-02	9.40 E-05	2.80 E-03	3.00 E-03	23
36	MelR	19	3	GaAramtCwGattTwCtGs	8.58	0.45	3.0 E-03	1.60 E-03	2.40 E-02	2.40 E-02	3.40 E-07	1.80 E-05	1.80 E-05	4706
37	MetJ	9	13	TrGAYGTCy	7.15	0.79	2.2 E-36	1.20 E-04	6.10 E-03	3.50 E-02	1.80 E-05	1.90 E-03	9.50 E-03	7
38	MetR	25	6	rayswkGarmrammyyCrykTCsss	9.88	0.40	9.6 E-01	1.10 E-03	1.30 E-03	1.30 E-03	2.40 E-09	5.10 E-08	5.10 E-08	4.58 E + 05
39	ModE	28	46	wktCGmtrtatacmrvMytayatwrCSw	10.89	0.39	4.6 E-04	1.90 E-03	2.40 E-02	2.40 E-02	3.40 E-07	2.00 E-06	2.00 E-06	5588
40	Nac	16	15	CaywwKCdtrtsmkww	5.71	0.36	7.1 E + 01	1.90 E-03	6.70 E-03	1.10 E-02	4.30 E-05	2.10 E-04	4.80 E-04	44
41	NagC	24	19	ywttycrYSayrMRAawwrtsykS	9.02	0.38	4.2 E-06	3.20 E-05	5.70 E-04	1.50 E-03	1.90 E-07	5.80 E-06	9.60 E-06	168
42	NanR	7	8	CaGGTaT	6.47	0.92	2.0 E-11	1.60 E-02	1.60 E-02	1.60 E-02	6.50 E-05	6.50 E-05	6.50 E-05	246
43	NarL	8	101	kTaCycmk	3.57	0.45	1.9 E-05	6.10 E-03	4.30 E-02	2.30 E-01	4.00 E-03	3.50 E-02	1.00 E-01	2
44	NarP	8	43	mTAMCcmt	5.22	0.65	3.1 E-09	1.70 E-03	1.80 E-02	1.80 E-02	3.70 E-04	1.90 E-03	1.90 E-03	5
45	NsrR	24	16	taaGatGCatttsarataCayCtt	12.24	0.51	3.2 E-07	9.90 E-08	1.70 E-06	1.70 E-06	7.80 E-12	1.50 E-10	1.50 E-10	1.27 E + 04
46	NtrC	18	44	wGCmCcAwawTGGtGCAw	9.30	0.52	7.6 E-29	2.20 E-05	5.20 E-03	7.90 E-03	1.90 E-06	2.40 E-04	2.60 E-04	12
47	OmpR	21	16	GtwaCmkmwystwaMaktktk	5.98	0.28	5.9 E-01	8.40 E-04	6.80 E-03	1.60 E-02	7.40 E-05	3.60 E-04	1.20 E-03	11
48	OxyR	46	19	bswdsswMgmwyttayCkatygyaymartsramvkrwymrvymvaa	12.85	0.28	3.5 E-01	9.10 E-04	9.50 E-03	9.50 E-03	3.30 E-09	8.30 E-08	8.30 E-08	2.76 E + 05
49	PhoB	21	38	cytktCayrmarctGtvaCmw	7.60	0.36	2.2 E-10	2.00 E-04	3.70 E-02	2.20 E-01	2.10 E-06	3.20 E-03	1.40 E-02	95
50	PhoP	18	31	yyrtttrksvwykGttkA	6.66	0.37	2.7 E-08	2.80 E-04	1.00 E-02	2.60 E-02	1.40 E-05	7.00 E-04	1.10 E-03	20
51	PurR	17	31	asGCAAACGtTTkCstt	10.98	0.65	7.1 E-44	6.60 E-07	4.70 E-04	4.90 E-02	1.00 E-07	3.60 E-05	1.00 E-03	7
52	RcsAB	15	22	CCTtaRKatamtyCb	7.19	0.48	1.3 E-02	2.30 E-04	6.30 E-04	6.30 E-04	9.40 E-07	5.00 E-06	5.00 E-06	245
53	RhaS	18	4	wyKmsrwGGKyGssArTd	8.06	0.45	1.2 E-01	4.30 E-04	2.90 E-03	2.90 E-03	7.10 E-08	2.30 E-07	2.30 E-07	6056
54	Rob	22	14	KwawwsGmsrSvdyKSatwrds	8.40	0.38	1.6 E + 00	2.30 E-03	1.60 E-02	1.60 E-02	5.90 E-07	3.30 E-06	3.30 E-06	3898
55	SoxS	19	26	ttrryvsrkwrtGsmwway	6.39	0.34	1.3 E-04	1.80 E-03	2.30 E-02	3.10 E-02	1.20 E-04	1.70 E-03	2.40 E-03	15
56	TorR	11	12	mKCkRttCAtA	6.01	0.55	3.1 E-03	7.40 E-05	2.90 E-02	2.90 E-02	1.50 E-06	7.50 E-04	7.50 E-04	49
57	TrpR	19	12	GwACTmGtkwrCtrGTrCr	14.27	0.75	3.4 E-42	5.90 E-08	3.60 E-06	3.60 E-06	3.60 E-10	1.10 E-08	3.80 E-08	164
58	TyrR	23	12	awgtGtaawkwaatcttkACrsm	8.56	0.37	2.8 E-14	3.20 E-04	1.10 E-02	2.60 E-02	9.10 E-06	1.90 E-04	4.50 E-04	35
59	UlaR	21	7	tCGyGtCrsrwtkamyYatva	8.73	0.42	5.0 E-01	4.50 E-05	1.10 E-02	1.10 E-02	2.40 E-09	4.10 E-07	4.10 E-07	1.88 E + 04
60	XylR	19	6	krysaawwwyYkyaaTyGh	7.66	0.40	5.1 E + 00	6.90 E-04	9.40 E-03	9.40 E-03	4.60 E-08	1.20 E-06	1.20 E-06	1.50 E + 04

IC: Information Content; FPR: False Positive Rate.

Normalized weight difference curves

Comparison between the theoretical score distribution (Figure 2C, blue curve) and the observed score distribution in upstream non-coding regions (Figure 2D, pink curve) indicates the discriminative power of a matrix. Differences between theoretical and empirical distributions indicate the presence of a higher number of sites with a P-value smaller than expected, suggesting that the PSSM is capable of recovering significant putative binding sites.

At each frequency value (y-axis of Figure 2D) we calculated the weight score difference (WD), defined as the difference between the observed W_S in all upstream non-coding regions and the expected W_S in the theoretical distribution of the PSSM for a given P-value. The WD can be visualized as the horizontal distance between the distribution curves (Figure 2D, blue and pink curves). As larger matrices allow higher scores, we divided the difference by the matrix width to obtain the normalized weight difference (NWD). The NWD curve (Figure 2 F) indicates the capability of a PSSM to distinguish putative sites from the non-coding genomic background.

Superimposition of NWD curves facilitates comparison between different PSSM for a given TF. In Figure 2 F, the NWD curve of the TrpR matrix, annotated in RegulonDB (dotted line), is shown super-imposed with alternative TrpR matrices built from the same sites, but varying the widths from 10 to 42. Clearly the smaller matrix (width = 10) fails to distinguish known sites from the background, as revealed by its negative NWD. In contrast, matrices of width 18 to 30 show a sharp increase in NWD above P-values of ∼1 × 10⁻⁵, indicating enrichment in putative binding sites.

In some cases, the Maximal NWD (MNWD) score gives good results for PSSM selection as can be seen for LexA matrices. The most conserved residues were a pair of trinucleotides separated by 10 less conserved positions (CTGn₁₀CAG). This core is encompassed by a matrix of width 16, yet the annotated matrix extends over 21 nt in order to include information about the conservation of the flanking residues. The PSSM with the highest MNWD had 18 columns (Figure 3, cyan NWD curve for LexA), followed by one of 22 (turquoise). However, NWD curves can be misleading in case of over-fitted matrices, as for HipB: this factor has target genes with multiple binding sites arranged in tandem. Consequently, large matrices encompass multiple sites, so that increasing the PSSM width leads to ever increasing score separations (Figure 3). However, these matrices are only getting better at predicting the sites from which they were constructed, while getting worse at predicting novel sites, as denoted by the LOO analysis of site score distributions.

NWD curves give a feeling about the enrichment in high-scoring binding sites observed in a reference sequence set (e.g. all upstream regions of the organism of interest) by comparison to the theoretical expectation. In Bacteria, an abrupt slope in the NWD curve reveals the presence of a handful of high-scoring binding sites for highly specific TFs (e.g. TrpR, LexA), whereas a progressive increase of the NWD slope is indicative of global factors, such as CRP, FNR (Figure 3), Fur, FruR, IHF and FIS (Supplementary Data). NWD curves can estimate matrix quality when individual binding sites can be distinguished from their background (the whole set of non-coding upstream sequences).

In metazoan genomes (drosophila, mammals), the NWD curves are generally flat for specific factors (unpublished data, JvH), because the number of high-scoring sites does not significantly exceed the theoretical expectation, due to the increase of gene number and upstream region sizes. In such genomes, transcriptional regulation is ensured by cis-regulatory modules, which combine multiple binding sites for one or several TFs. Also, individual binding sites generally show a wider range of variation, so that PSSMs are less discriminative than in microbial genomes.

Empirical score distributions distinguish global from specific TFs

The global TFs CRP and FNR have several hundred annotated functional binding sites. Their score distributions in all promoters do not show a plateau: rather, their empirical curves (Figure 3, pink curve) progressively separate from the theoretical distribution, starting from relatively low W_S (∼5), associated to high P-values (>1 × 10⁻³). This suggests that the high number of target genes of global TFs results from a spectrum of sites bound with a wide range of affinities. The progressive separation observed for global factors opens the question of whether their numerous binding sites result mostly from non-specific binding (reflected by a motif of low information content), which has been suggested previously (26), or from the presence of numerous specific binding sites in upstream regions of a large number of target genes. In the first scenario (poorly informative motifs) we would expect similar curves for the permuted and non-permuted matrices, since column permutations preserve the information content. This is however not the case. For all the global TFs (CRP, FNR, FIS and FUR), permuted matrices showed a tight fit to the theoretical distributions (see cyan curves on Figure 3 for CRP, FNR, and Supplementary Data for other factors). This suggests that there is room within the whole set of possible sequences, to have a large number of binding sites of lower affinity for TF binding enabling regulation of many target genes, and nonetheless different from those generated by permuted matrices.

However, the slow separation observed for global factors may be an artifact resulting from the fact that their matrices were built from a larger number of sites than specific TFs. In order to test this possibility, we built matrices by sampling random subsets of binding sites for CRP and FNR. We tested matrices built from 7 or 14 sites, respectively, and repeated the experiment three times (Supplementary Data). All the sub-sampled matrices showed the same characteristic distribution of global TFs: their empirical distribution slowly separates from the theoretical one above relatively low weight scores (w ≥ 5).

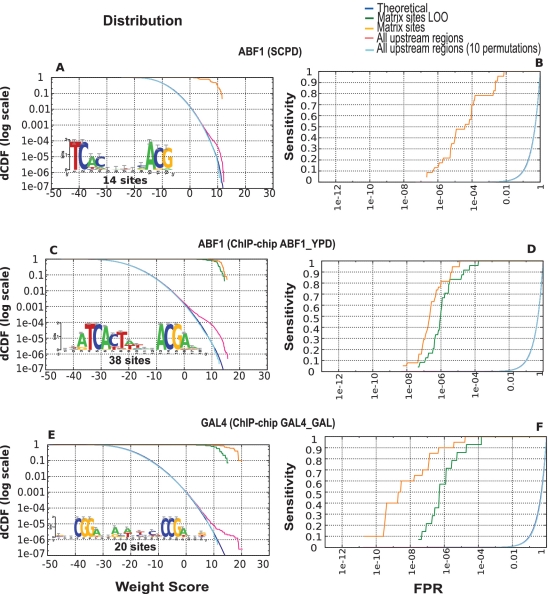
The distinction between global and specific factors can also be observed in yeast promoters: the Saccharomyces cerevisiae TF Abf1 p, described in SGD as a ‘multifunctional global regulator’, shows a progressive separation from the theoretical distribution above scores of 5 (Figure 7). The same behavior is observed for two other yeast global TFs, CBF1 and RAP1 (Supplementary Data). In contrast, for the GAL4 factor, which activates a handful of genes involved in galactose utilization, the empirical score distribution suddenly separates from the theoretical distribution at high scores (w ≥ 10), similar to specific TFs in E. coli.

Figure 7.

Matrices obtained from motif discovery in yeast promoters selected by ChIP-chip experiments. Score distribution and ROC curves for the ABF1 matrix annotated in SCPD (A and B), an ABF1 matrix discovered in promoters selected by ChIP-chip (C and D) and a GAL4 matrix discovered in promoters selected by ChIP-chip (E and F).

We further investigated the capability of ‘matrix-quality’ to distinguish global from specific TFs by evaluating the score distribution of the Bacillus subtilis FNR-binding motif. The B. subtilis FNR motif (TGTGA-N₆-TCACA) is highly similar to that of CRP in E. coli K12. However, in B. subtilis, the factor has been recruited for a specific function (adaptation to low oxygen tension) and regulates a much smaller regulon than CRP in E. coli. Consistently, the score distribution of B. subtilis FNR shows the typical shape of a specific TF: the empirical distribution follows the theoretical for low weight scores, and shows a neat separation above 10 (Supplementary Data). The distinction between the B. subtilis FNR and E. coli K12 CRP distributions nicely shows that the same motif (TGTGA-N₆-TCACA) can be bound by a generic factor in one genome, and a specific factor in another genome.

Multi-genome pattern discovery can compensate for a small number of annotated binding sites

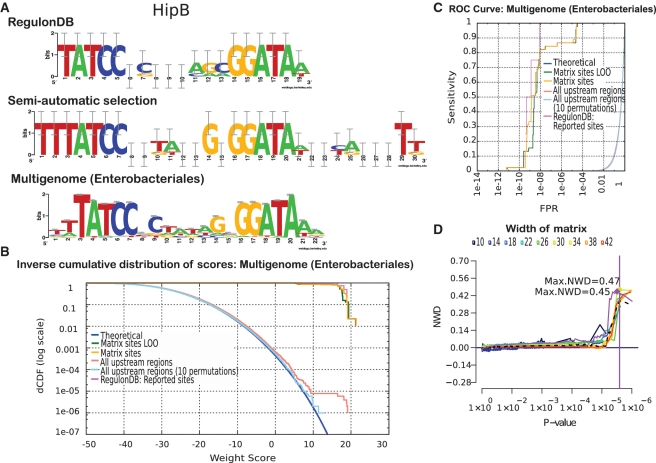
In some cases, the collection of annotated binding sites is insufficient to build a consistent matrix. The HipB PSSM in RegulonDB was built from four binding sites found in tandem in the hipB promoter (hipB is auto-regulated). Consequently, the collection of extended binding sites provided by RegulonDB shows redundancy, since each aligned site is flanked by one or two neighboring sites, and the motif has a poor predictive power, as discussed above. The paucity of annotated binding sites can however be compensated by a multi-genome approach. We ran the program ‘footprint-discovery’ (27) to discover conserved motifs in the promoters of 14 hipB orthologs found in Enterobacteriales. The resulting motif (Figure 5A) shows the same core as the annotated one, but the error bars are considerably smaller, because the matrix was built from a much larger collection of binding sites. The score distributions and the ROC curve (Figure 5B and C) show a neat improvement over the original annotated matrix (Figure 3): the difference between uncorrected matrix sites and LOO distribution becomes negligible, and the estimated FPR_70% improves from 1 × 10⁻⁵ to 1 × 10⁻⁸.

Figure 5.

Motif discovered by ‘footprint-discovery’ in the promoters of 14 hipB orthologs (Enterobacteriales). (A) Sequence logos from different matrices representing the binding motif for the TF HipB. (B) P-value distribution for the multi-genome matrix. (C) ROC curves for the multi-genome matrix. (D) Quality comparison of different matrices based on NWD distributions. Dotted curve: RegulonDB matrix. Light mauve: multi-genome matrix. Other curves: matrices of various widths built from the 4 HipB sites annotated in RegulonDB. Note the abrupt step in the light mauve curve, indicating the discriminant power of the multigenome matrix.

Enrichment of binding sites in promoters and peak regions selected by ChIP-chip and ChIP–seq experiments

Until recently, matrices stored in TF databases were built by assembling a restricted number of sites obtained from case-by-case experiments. ChIP-chip (18) and ChIP–seq (28) technologies now permit a genome-wise localization of the regions bound by a TF. However, these regions are not precisely defined, due to several technical difficulties: (i) during Chromatin Immuno-Precipitation (ChIP), the ultrasonication step cuts DNA into fragments of variable sizes; (ii) the DNA probes hybridized on ChIP-chip microarrays may contain regions of several tens, or even hundreds base pairs (this problem has been minimized with recent tiling arrays); and (iii) for ChIP–seq, the primary reads from the next generation sequencing machines correspond to the 5′ and 3′ extremities of the DNA fragments, which can be separated from the actual site by several tens of base pairs. The primary results (hybridized probes or genome-mapped sequence reads) are generally post-processed to detect the ‘peaks’, i.e. genomic regions most likely to contain one or more binding sites (29). Motifs can then be obtained by running pattern discovery algorithms in sequence sets resulting from those high-throughput methods.

In the next sections, we show that ‘matrix-quality’ can be used for two purposes during analysis of ChIP-chip and ChIP–seq results: (i) to evaluate the high-throughput sequence sets (e.g. a collection of peak regions) for enrichment of putative binding sites of a TF for which we already have a matrix; and (ii) to evaluate the quality of new motifs built from high-throughput data sets.

Enrichment of promoters selected by ChIP-chip in LexA-binding sites

Wade and co-workers (30) used high-density microarrays representing the entire E. coli genome to identify 49 high-confidence in vivo targets of the LexA repressor. Of these, 15 were already included in the 23 target genes annotated in RegulonDB.

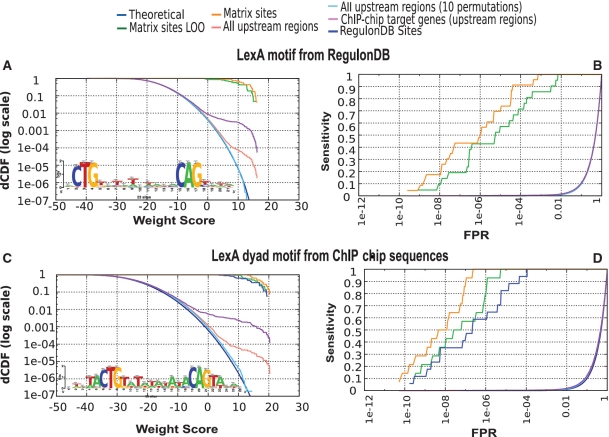
We first analyzed the enrichment in putative LexA-binding sites within the promoters of the high-scoring target genes identified by Wade and co-workers. Score distribution curves (Figure 6A) showed a significant enrichment of high-scoring sites in ChIP-selected promoters (purple curve) in comparison with the distribution in all promoters (salmon curve). This illustrates the use of ‘matrix-quality’ to compare collections of sequences obtained from various sources, and to estimate their respective enrichment in binding sites for a given TF-binding motif by comparing the entire W_S distributions.

Figure 6.

Analysis of LexA target genes detected by a ChIP-chip experiment. (A) Score distributions showing the enrichment of putative LexA-binding sites in the target promoters detected by ChIP–chip. Sites were predicted with the LexA matrix from RegulonDB. (B) ROC curve of the LexA matrix available in RegulonDB. (C) Score distributions of a LexA PSSM resulting from pattern discovery (‘dyad-analysis’) in the LexA target genes detected by ChIP–chip. (D) ROC curve of the matrix discovered with ‘dyad-analysis’.

Enrichment of ChIP–seq peaks shows interactions between mouse factors

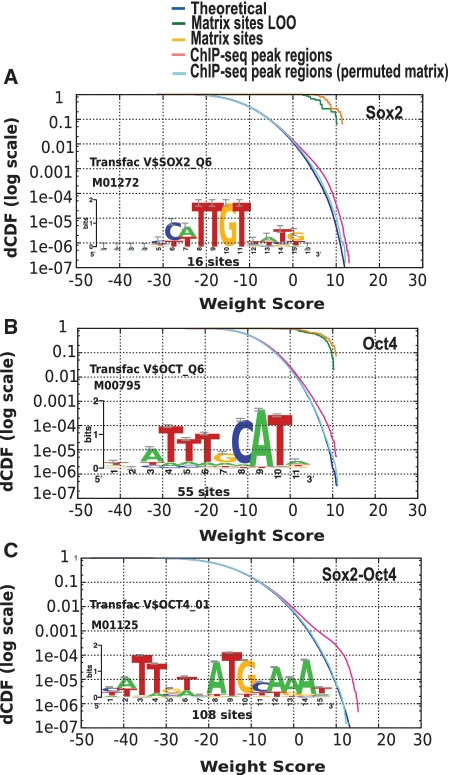
We used ‘matrix-quality’ to measure the enrichment of peak regions selected by ChIP–seq for 13 mouse TFs (19). Whenever available, we compared the motifs annotated in TRANSFAC with those built from the ChIP–seq peaks, taken either from JASPAR (31) or from a recent study by Bailey, et al. (32). Empirical score distributions show a clear enrichment of peak regions for some, but not all matrices (Supplementary Data). Beyond comparing the respective quality of alternative matrices, the distribution plots can in some cases highlight the interactions between two factors. For example, the mouse factors Sox2 and Oct4 can form a dimer that binds a spaced motif (the so-called ‘SOCT’ motif). Interestingly, Sox2 peak sequences are enriched not only for Sox2 (Figure 8A), but also for Oct4 (Figure 8B)-binding sites. However, the strongest enrichment is obtained with the Sox2-Oct4 hybrid motif (Figure 8C), thereby confirming the capability of the two factors to bind DNA in the dimeric form.

Figure 8.

Enrichment of putative binding sites for mouse TFs in peak sequences detected by ChIP–seq experiments. Score distributions in peak regions detected by a Sox2 ChIP–seq experiment, analyzing motifs for Sox2 (A), Oct4 (B) and Sox2-Oct4 (C).

Improving matrix qualities by running motif discovery in promoters pulled down by ChIP–chip

We used the pattern discovery program ‘dyad-analysis’ (33) to build a new matrix from the LexA-binding regions reported by Wade and co-workers, and analyzed its quality as described above. This matrix shows a plateau of high-scoring binding sites within the complete collection of E. coli K12 promoters (salmon curve), and a strong enrichment of such sites in the promoters of the target genes selected by ChIP-chip (Figure 6C). Interestingly, the ROC curve shows better performance for the new LexA motif than for the motif annotated in RegulonDB: the FPR_50% drops from 10⁻⁵ for the annotated motif (green curve on Figure 6B) to 10⁻⁷ for the new one (Figure 6D). The newly discovered motif also shows a good capability to recover the 23 binding sites annotated in RegulonDB, although only some of those sites were used to build it.

A similar improvement can be obtained by discovering motifs in yeast promoters selected by ChIP-chip experiments: for the yeast global factor Abf1 p, we analyzed three matrices annotated in TRANSFAC (34), one from SCPD (35), and a matrix built with ‘dyad-analysis’ (33) in Abf1p target promoters selected by ChIP-chip (18). The matrix obtained with ‘dyad-analysis’ (Figure 7C and D) shows a 100-fold lower FPR than the matrix annotated in SCPD (Figure 7A and B). We obtained similar improvements for several yeast TFs for which ChIP-chip data were available (Supplementary Data).

DISCUSSION

We described a method to characterize the ability of a PSSM to detect TF-binding sites in genome sequences. The method combines theoretical and empirical score distributions and is implemented in a program called ‘matrix-quality’, which is part of the RSAT (36).

We applied the method to a collection of 60 PSSMs from the RegulonDB database (2,17). We analyzed seven representative E. coli K12 PSSMs, and showed that matrices can be significantly improved by enlarging the set of sites using either data from high-throughput experiments (yeast ChIP–chip, mouse ChIP–seq) or from comparative genomics (‘footprint discovery’).

Our study shows that any single-criterion selection will fail to capture the multiple aspects required to assess the predictive power of a matrix. Consequently, our general strategy was to select matrices presenting a good trade-off between the multiple parameters discussed in the previous sections: (i) the discriminative power of the PSSM is first estimated by examining the separation between the theoretical and empirical distribution in all upstream sequences (MNWD); (ii) the fitting between the theoretical distribution and the empirical distribution of permuted matrices indicates the correctness of the background model; (iii) over-fitted matrices are revealed by a large distance between the biased and unbiased (LOO) distributions of W_S in annotated binding sites; and (iv) the ROC curves indicate the tradeoff between sensitivity and risk of false positives.

The distributions of scores and the ROC curves can give relevant information for researchers who are using matrices to predict putative binding sites in genome sequences. It is important to remark that this evaluation is context-specific: rather than evaluating intrinsic properties of the matrix (e.g. information content, E-value), we monitor its practical behavior in the context of a given genome. The method can thus provide realistic estimates of the expected sensitivity and FPR when scanning real genome sequences to predict TF-binding sites. In addition, we saw that the shape of the distribution observed in complete sets of promoters provides clues about the global versus specific nature of a TF. Since this interpretation does not require any prior knowledge of proven binding sites, it can also be used for evaluating matrices resulting from pattern discovery in various data types: promoters of co-expressed genes, promoters of orthologous genes, whole-genome analyses and collections of peak regions obtained from ChIP–seq or ChIP-chip experiments, among others.

Our method is also of pragmatic value for annotators of TF databases. The analysis of score distributions allowed us to detect problems related to the annotated binding sites (e.g. five redundant sites out of 10 for TrpR, six identical sites for NanR, over-fitted matrix for HipB), or to the matrices built from those sites (e.g. excessively large matrix for CysB).

The method can also help to guide annotators in the choice of optimal parameters to build matrices from collections of binding sites (e.g. matrix width, background model, exclusion of poorly scoring sites, etc.). As a systematic test, for each one of the seven study case factors (Figures 2 and 3), we collected their binding sites from RegulonDB and generated a series of PSSM using two alternative algorithms (MEME and consensus), two alternative background models (Bernoulli or Markov order 1) and motif length ranging from 8 to 42. By comparing all the ‘matrix-quality’ results, we selected, for each factor, the matrix providing the best tradeoff between sensitivity and FPR robustness (based on the LOO analysis). The parameters of the selected matrices are shown in Table 2, and are compared to those of the original RegulonDB matrices (Table 1). In addition, we are generating a collection of matrices enriched by multi-genome pattern discovery. This study is currently being extended to the whole RegulonDB collection, in preparation for the next database release.

Table 2.

Selection of PSSM on the basis of ‘matrix-quality’ results

Factor	Program	Markov order	Width	No. sites	Matrix Consensus (IUPAC)	Total IC	IC per column	E-value	FPR50% (LOO)	FPR90% (LOO)	FPR100% (LOO)	FPR50% (matrix sites)	FPR90% (matrix sites)	FPR100% (matrix sites)	LOO/Matrix sites (FPR 50%)
TrpR	meme	1	24	6	tyGtACtmGykaACtaGTaCratr	13.62	0.57	1.30 E-10	1.00 E-08	7.70 E-06	7.70 E-06	1.50 E-12	1.50 E-09	1.50 E-09	6.67 E + 03
CRP	meme	0	24	198	aaawwtgtGayryagaTCACawww	7.29	0.30	6.40 E-242	6.20 E-05	3.70 E-03	2.80 E-02	4.50 E-05	2.70 E-03	2.10 E-02	1.38 E + 00
CysB	meme	1	30	8	gGAavGrrrtaAyKrmwtrmcarakykmkt	10.67	0.36	1900	2.60 E-04	1.40 E-01	1.40 E-01	2.80 E-08	3.20 E-05	3.20 E-05	9.29 E + 03
NanR	meme	1	20	6	ktATAmMwGktataMmrGww	10.28	0.51	8.30 E-07	2.30 E-06	1.60 E-03	1.60 E-03	1.50 E-11	6.40 E-07	6.40 E-07	1.53 E + 05
LexA	meme	1	22	21	wwtrCTGtayatamammCAGya	11.65	0.53	2.60 E-46	2.00 E-08	4.60 E-04	3.10 E-03	1.50 E-09	1.50 E-05	1.50 E-04	1.33 E + 01
HipB	meme	1	18	4	ATCCsskagmGCGGATAA	10.95	0.61	0.00022	5.00 E-08	4.30 E-06	4.30 E-06	1.50 E-11	3.10 E-09	3.10 E-09	3.33 E + 03
FNR	consensus	0	20	72	tdywwwtTGaTwwmraTCaa	6.94	0.35	2.09 E-71	1.30 E-04	5.30 E-03	1.80 E-02	7.60 E-05	2.90 E-03	9.80 E-03	1.71 E + 00

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

A.M.-R. was supported during her PhD studies (Programa de Doctorado en Ciencias Biomédicas, Universidad Nacional Autónoma de México) by a fellowship from the Consejo Nacional de Ciencia y Tecnología (Mexico). The BiGRe laboratory is supported by the BioSapiens Network of Excellence funded under the sixth Framework program of the European Communities (LSHG-CT-2003-503265); Belgian Program on Interuniversity Attraction Poles, initiated by the Belgian Federal Science Policy Office, project P6/25 (BioMaGNet) and by the MICROME Collaborative Project funded by the European Commission within its FP7 Programme, under the thematic area ‘BIO-INFORMATICS—Microbial genomics and bio-informatics’, contract number 222886-2.’; Actions de Recherches Concertées de la Communauté Française de Belgique (ARC grant number 04/09-307), the Bureau des Relations Internationales et de Coopération (BRIC, Université Libre de Bruxelles) and UNAM for travel costs of A.M.-R.; National Institutes of Health, grant number R01 GM071962-05 (to J.C.-V.); Alexander von Humbold Stiftung (to M.T.C.). Funding for open access charge: Belgian Program on Interuniversity Attraction Poles, initiated by the Belgian Federal Science Policy Office, project P6/25 (BioMaGNet); Consejo Nacional de Ciencia y Tecnología (Mexico).

Conflict of interest statement. None declared.