Abstract
The efficacy of platelet adhesion in shear flow is known to be substantially modulated by the physical presence of red blood cells (RBCs). The mechanisms of this regulation remain obscure due to the complicated character of platelet interactions with RBCs and vascular walls. To investigate this problem, we have created a mathematical model that takes into account shear-induced transport of platelets across the flow, platelet expulsion by the RBCs from the near-wall layer of the flow onto the wall, and reversible capture of platelets by the wall and their firm adhesion to it. This model analysis allowed us to obtain, for the first time to our knowledge, an analytical determination of the platelet adhesion rate constant as a function of the wall shear rate, hematocrit, and average sizes of platelets and RBCs. This formula provided a quantitative description of the results of previous in vitro adhesion experiments in perfusion chambers. The results of the simulations suggest that under a wide range of shear rates and hematocrit values, the rate of platelet adhesion from the blood flow is mainly limited by the frequency of their near-wall rebounding collisions with RBCs. This finding reveals the mechanism by which erythrocytes physically control platelet hemostasis.
Introduction
Platelets are the principal components of the hemostatic plug formed to arrest bleeding after an injury to the vascular wall. Their adhesion to the site of damage and to the previously adsorbed platelets is a critical stage in the formation of both hemostatic plugs and pathological thrombi (1,2). Experiments have shown that the wall shear rate and hematocrit are two major independent parameters of blood flow that determine the rate of platelet adhesion to various surfaces (3–11). The mechanisms of this regulation are unclear due to complicated and poorly understood processes occurring in and around platelets during adhesion. In this work, a theoretical approach is used to bridge this gap; thus, it was necessary to update the existing models of platelet adhesion.
The delivery of platelets to the vascular wall is a process that combines their axial convection by the blood flow and shear-induced lateral diffusion resulting from continuous collisions between red blood cells (RBCs) (12–14). In addition to causing this lateral diffusion in bulk flow, the presence of RBCs greatly increases the probability that a platelet flowing near the wall will collide with it (14–16). Subsequent adhesion of platelets to an active, i.e., von Willebrand factor (vWf)-bearing, surface is a complicated multistage process closely resembling leukocyte adhesion. A platelet captured from the flow slowly moves along the wall, undergoes activation, and either firmly adheres to the surface or becomes detached from it if firm adhesion contact did not form (1,17–19). The large number of factors that collectively influence platelet transport and adhesion account for the variety of mathematical models that have been proposed in this field (8,10,12,13,20–24).
All of these models describe platelet adhesion using a direct analogy to that of molecules transported across the flow by Brownian diffusion and undergoing one-step irreversible adhesion. This analogy is an oversimplification that has frequently been the object of criticism (11,25–27) because it is in conflict with a wealth of data suggesting the following: 1), a strong dependence of the adhesion rate constant on the hematocrit level and shear rate (11,28,29); 2), systematic differences between platelet shear diffusion constants determined from adhesion experiments and those from adhesion-independent methods (25); and 3), the detachment of the majority of captured platelets by the flow (1). Therefore, this approach cannot be used to study the regulation of platelet adhesion and needs to be modified.
In this study, platelet adhesion is viewed as a multistage process beginning with inelastic collision of a near-wall platelet with an RBC followed by platelet reversible capture and arrest. Platelet flux toward the wall and the effective adhesion rate constant are calculated for the first time, to our knowledge. The proposed model agrees fairly well with experimental dependences of platelet adhesion rate on axial coordinate, wall shear rate, hematocrit level, and size of erythrocytes that were obtained in earlier in vitro studies. Comparison between predictions of the full model and of the reduced one, which takes into account only near-wall collisions of platelets with erythrocytes, shows that these collisions control platelet adhesion under a wide range of parameters.
Description of the processes
Conditions of platelet adhesion
We have modeled a blood flow carrying erythrocytes and platelets over an active, i.e., platelet-capturing surface. This model corresponds to the well-known and convenient perfusion chamber experimental model that has been extensively used to study platelet adhesion in vitro (3,4,8–11,30,31). In these experiments, whole or reconstituted blood is pumped over a physiologically appropriate activator (exposed subendothelium of an everted vascular segment or a collagen-coated substrate) under controlled conditions, and mean surface density of adsorbed platelets is measured as a function of time.
The result is used to calculate the initial adhesion rate and its dependence on the wall shear rate, hematocrit level, and axial coordinate. These dependences characterize the overall effects of platelet delivery and surface binding. The use of collagen, a strong platelet activator, and aspirin, a cyclooxygenase inhibitor, permits the experimenters to exclude, or at least significantly diminish, the influence of platelet-derived activators, ADP and TxA2, and thrombin production is suppressed by citrate. As a result, the platelets are activated by collagen alone, and adhere to it by forming a monolayer.
Stages of platelet adhesion
To our knowledge, what distinguishes our study from all previous continuous models of platelet adhesion is the consideration of this process as a multistage one constituted by the after successive events (Fig. 1 A):
I. Transport within the flow:
Convective transport of platelets in the direction of the blood flow with their simultaneous crosswise dispersive motion.
II. Near-wall and wall processes:
-
a.
Collision of a platelet traveling in the immediate vicinity of the wall with an erythrocyte or other blood cell resulting in platelet collision with the wall;
-
b.
Capture of the platelet at the wall surface;
-
c.
Deceleration of the captured platelet relative to the flow as it moves along the surface; and
-
d.
Detachment of the captured platelet by the flow or its stable arrest at the surface.
These stages are distinguished based on the results of experimental studies of platelet behavior in the flow and during adhesion. The lateral motion of platelets in the presence of erythrocytes has been thoroughly examined experimentally by Goldsmith and co-worker (14–16), who demonstrated that the physical presence of erythrocytes promotes transverse migration of platelets (Stage I) and increases the frequency of their collisions with the wall (Stage IIa) by several orders of magnitude.
Figure 1.
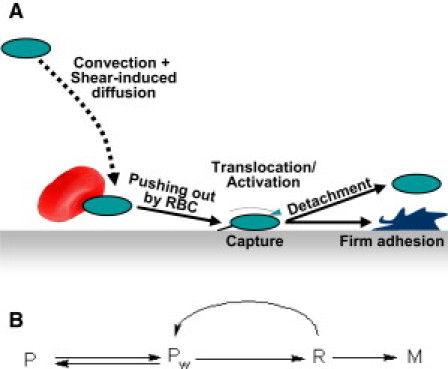
Platelet transport toward the wall, along the wall, and off the wall. (A) The successive stages of platelet adhesion. A platelet traveling within the flow is brought into its near-wall layer by shear-induced diffusion, expelled onto the surface after a new inelastic collision with a blood cell, e.g., an erythrocyte, and captured at the surface. Its subsequent deceleration and activation is followed by irreversible binding and arrest or, otherwise, detachment by the flow. (B) The relevant kinetic scheme. (P, free platelets transported with the flow far from the wall; Pw, the same platelets near the wall; R, captured platelets rolling or sliding along the wall and slowed by it; and M, firmly bound platelets.)
Recent studies have shown that a platelet coming in contact with a vWf-bearing wall does not immediately adhere to it but first tethers via the GPIbα-vWf bonds (Stage IIb), slows down (Stage IIc), and only then firmly adheres through integrin bonds or is detached by the flow (Stage IId) (1,17–19). To our knowledge, these mechanisms have never been considered in the framework of an integrated mathematical model.
Mathematical model
Equations of the model
Blood was assumed to flow from left to right in the x direction between two parallel planes with a constant parabolic velocity profile:
| (1) |
This profile corresponds to the linear shear rate distribution:
| (2) |
Here, defines the wall shear rate, and 2H is the channel width (0 ≤ y ≤ 2H). Platelet transport in the flow was described by the convection-diffusion equation (13,22)
| (3) |
where P (platelets/μm3) is the platelet concentration and is the diffusion flux. The platelet diffusion (dispersion) coefficient was taken to be equal to the sum of the coefficients corresponding to the motion of erythrocytes, platelets in the absence of erythrocytes, and the coefficient of platelet Brownian diffusion:
| (4) |
Here, dRBC and dP are the main erythrocyte and platelet diameters, respectively, ΦRBC and VPP are the erythrocyte and platelet volume fractions, respectively, VP is the platelet volume, and kZC = 0.15. The first two terms in this formula represent an approximation of the experimentally measured dispersion coefficient of RBCs and other deformable particles in the shear flow (32). The distribution of the RBC volume fraction in the flow was assumed to be uniform (see the Supporting Material). The platelet Brownian diffusion coefficient was assumed to be DBr = 0.158 μm2/s (33).
The boundary condition for Eq. 3 at the active boundary (y = 0) had the form (13,22)
| (5) |
where the right-hand side is the platelet adhesion rate. Boundary conditions at the upper (y = 2H) and outflow (x = L) boundaries had the form . The initial and entrance conditions corresponded to the uniform distribution of platelets across the flow
| (6) |
where P0 is the average platelet concentration.
The platelet adhesion rate was calculated based on the kinetic scheme presented in Fig. 1 B, which corresponds to the succession of adhesion stages shown in Fig. 1 A. Accordingly, the overall adhesion rate was determined by the rate of the last stage of the process
| (7) |
where R(x) is the surface concentration of captured platelets, and kbind is the binding rate constant, which equals the inverse activation time (Ta) of GPIIb-IIIa integrins of the captured platelet. R obeys the reaction-convection equation written down at the active boundary (y = 0),
| (8) |
where w is the translational velocity of a decelerating platelet, J(x) is the platelet flux toward the wall, Θ(x) is the surface availability function, α is the capture efficiency (the probability that a platelet that has collided with fully available wall will be captured by it), and kdet is the detachment rate constant of the captured platelet. The experimental value of w is a few μm/s (34–36); therefore, the platelet's deceleration distance was neglected because it is too small in comparison with the length of the adhesion surface. The characteristic time of platelet activation Ta ∼ 1–3 s (37–39)is sufficiently smaller than the duration of experiment (1–5 min), which permits us to assume the quasistationarity of R that gives
| (9) |
Platelet flux toward the wall was computed from the frequency of their near-wall inelastic collisions with erythrocytes and other platelets based on Smoluchowski's theory (see the Supporting Material),
| (10) |
where
| (11) |
Here,
(note that λ1=dP/dRBC) (see Eq. S14 in the Supporting Material) are hydrodynamic collision efficiencies (data for spherical platelets and their aggregates in a simple shear flow (40) were used in the absence of those for platelets and erythrocytes of real flattened shape near the wall), and
and
are coefficients of Smoluchowski's theory corrected by factors k1 and k2, which account for nonspherical particle shape and the wall proximity ignored in calculations of collision frequency and collision efficiency.
Capture efficiency α was assumed to be independent of in accord with experimental findings that binding efficiency for two colliding platelets (which bind via a GPIbα-vWf-GPIbα bridge) suddenly increases only at pathological shear rates above 5000 s−1 (41,42). The binding rate constant kbind was assumed to decrease with increasing because even slow motion of a platelet hinders its firm binding. The linear dependence was assumed for simplicity to be
| (12) |
where k0bind and β are constants. The detachment rate constant kdet was assumed to be proportional to the wall shear rate because the probability of platelet detachment by the flow is proportional to the wall shear stress (43,44):
| (13) |
The resulting expression for the platelet adhesion rate from Eq. 7 takes the form
| (14) |
with the effective rate constant
| (15) |
where
The surface availability was calculated as (13,22)
| (16) |
where M∞ = 4/πd2P (8) is the platelet monolayer density at 100% surface coverage. To obtain the percent surface coverage, computed values of M were normalized by M∞/100% and, except in the case when the dependence M(x) was of special interest, averaged over the entire active boundary. A zero initial condition for M(x) was employed.
Reduced adhesion model
The above full model was partly reduced to study the regulation of platelet adhesion rate by collisions of platelets with erythrocytes. The reduced model disregarded
-
1.
Changes in platelet concentration in the flow related to adhesion;
-
2.
Saturation of the surface with adhered platelets; and
-
3.
Platelet flux toward the wall resulting from their collisions with one another.
To this effect, it was assumed that P = P0 and Θ = 1 in Eq. 14, and the second term in Eq. 11 was omitted. The simplified analytical formulas for the adhesion rate and value had the form
| (17) |
| (18) |
where
| (19) |
In all calculations, parameter values in the full and reduced models were identical.
Fixed model parameters
Model parameters that matched platelet and erythrocyte size and calculated collision efficiencies are listed in Table S1 and Table S2 in the Supporting Material. In the description of experiments on platelet adhesion from rabbit blood (8–10), P0 and ΦRBC were assumed to be 3.74 × 10−4 platelets/μm3 and 0.38, respectively, and P0 was 5.96 × 10−4 platelets/μm3 in platelet-rich plasma (PRP) (9). In experiments on human platelet adhesion from reconstituted blood (3), PRP containing PB = 1.9 × 10−4 platelets/μm3 was mixed with washed RBCs to achieve the desired hematocrit; thus, P0 was assumed to be equal to (1 – ΦRBC) × PB in the corresponding calculations. The lengths of adhesion surfaces was 0.7 and 2 cm in Turitto and Baumgartner (8), 1.4–2 cm in Turitto and Baumgartner (10), and 2 cm in Aarts et al. (3) (indicated in Aarts et al. (4)). Thus, the length of the computational domain was L = 2 × 104 μm; its width was 2H = 1200 μm, matching the gap in the perfusion chamber.
Estimation of free model parameters
Three kinetic parameters, α, ka, and ξ, as well as the particle shape correction factors k1 and k2, were unknown. To estimate ka and ξ from the shear rate-dependence of the adhesion rate, Eq. 17 combined with Eq. 19 and Eq. S14 in the Supporting Material was expressed in the form
| (20) |
where
| (21) |
The factor converts the adhesion rate to % monolayer/min. The constants A, ka, and ξ varied independently to achieve good agreement with the experimental shear rate-dependence of the adhesion rate (see later in Fig. 3, A and B). To estimate the ratio k1:k2, Eqs. 18 and 19 were rewritten as
| (22) |
The platelet adhesion data plotted as a left-hand side of this equation versus dRBC were found to lie approximately on one line passing through the origin (see Fig. 4 A), indicating the near-zero value of k1. It denotes the minor role of platelet size in the near-wall collisions with erythrocytes. Thus, k1 was set to 0, whereas k2 was set to 1. The α-values in these two cases were roughly estimated as A divided by the bracketed expression in Eq. 21 and as a cube of the slope of a fitted line (Eq. 22), respectively. Finally, the α-values were slightly varied to achieve a reasonable agreement of the adhesion rates calculated by the full model with the experimental data in the entire range of (see Fig. 3 A), ΦRBC, and dRBC (see Fig. 4 B).
Figure 3.
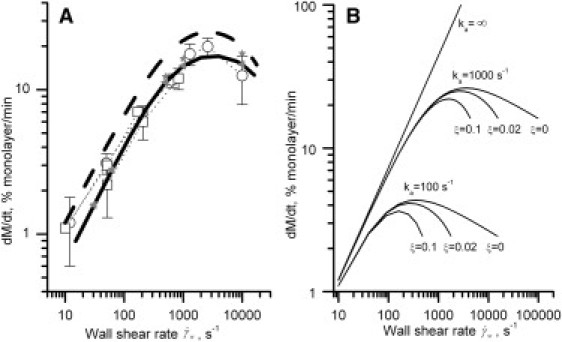
(A) The wall shear rate-dependence of the initial platelet adhesion rate calculated by the reduced (dashed line) and full (solid line) models at α = 0.12, ka = 1000 s−1, ξ = 0.02, k1 = 0, k2 = 1 and obtained in vitro (open markers). The reduced model was in the form of Eq. 20 with A = 0.2. Equations of the full model at varying shear rates were integrated over the time interval t = 0–3 min followed by division of computed M values by the factor of 3. The experimental data were borrowed from Turitto and Baumgartner (8) (squares, abscissas of points at 10 and 170 s−1 were corrected as described in Turitto and Baumgartner (10)) and from Turitto and Baumgartner (10) (circles). Dotted lines connect one set of data; errors are indicated if reported. (Solid markers) Calculations performed by the extended model directly accounting for the kinetics of R at k0bind = 1 s−1, δ = 10−3, β = 2 × 10−5 (triangles) and k0bind = 0.01 s−1, δ = 10−5, β = 2 × 10−7 (asterisks). (B) The platelet adhesion rate calculated by the reduced model at A = 0.2 and varying values of ka and ξ.
Figure 4.
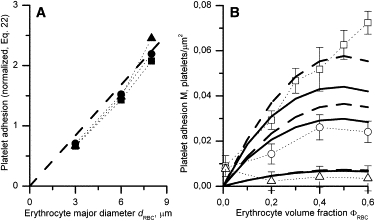
Platelet adhesion as a function of erythrocyte major diameter (A) and volume fraction (B) obtained experimentally in Aarts et al. (3) (markers) and calculated by the reduced (dashed lines) and full (solid lines) models at by the time t = 5 min. (A) Experimental data at ΦRBC = 0.2 (squares), 0.4 (circles), and 0.6 (triangles) were plotted against dRBC according to Eq. 22; the theoretical line slope was α1/3k2 = 0.28 providing α ≈ 0.022 at k2 = 1. (B) Platelet adhesion in the presence of human (squares), rabbit (circles), and goat (triangles) erythrocytes compared with simulation results (lines) at RBC sizes matching that of these species and α = 0.022, ka = 1000 s−1, ξ = 0.02, k1 = 0, and k2 = 1.
Numerical methods
Equations 3, 5, and 14 were solved numerically with the COMSOL 3.2a software package using the finite element method with second-order Lagrangian elements. Unstructured triangular mesh was refined close to the boundary y = 0: the maximum element size in the x direction over the entire computational domain was 1400 μm compared with 10 μm at the boundary y = 0 and 0.5 μm at the point (0,0). The characteristic y size of mesh elements was 10 times smaller than the x size because the mean platelet concentration gradient perpendicular to the flow (in the y direction) was significantly greater than the gradient parallel to the flow (in the x direction). Mesh independence was achieved.
Results
Platelet adhesion in the full and reduced models
To form a clear picture of platelet adhesion to an active surface, Fig. 2 shows the results of one typical simulation of this process. The free model parameters used were identical to those estimated in the following sections from the description of platelet adhesion at varying shear rates, erythrocyte sizes, and volume fractions. Fig. 2 A shows isolines of platelet concentration P(x,y) in the near-wall region of the flow (y = 0…60 μm) calculated by the full model at time t = 3 min. Evidently, the region of reduced platelet concentration develops along an active surface. Fig. 2 B shows the surface density of the adhered platelets M(x) at the same time point calculated by the full model (solid line), reduced model (dashed line), and determined experimentally (8) (markers). It was observed that surface coverage, both experimental and estimated from the full model, decreases insignificantly along the x axis.
Figure 2.
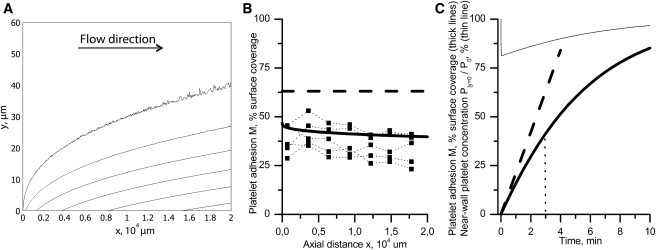
(A) The computed platelet distribution in a perfusion chamber at , t = 3 min. The free model parameters were α = 0.12, ka = 1000 s−1, ξ = 0.02, k1 = 0, and k2 = 1. The isolines correspond to concentrations 3.7, 3.6, 3.5, 3.4, 3.3, and 3.2 × 10−4 platelets/μm3 (from top to bottom). Note that the figure is stretched along the y axis for better resolution. (B) The surface coverage by adhered platelets M(x) in the full (solid line) and reduced (dashed line) models and in the experiment (8) (markers) at the same time point. (C) The time dependence of surface coverage averaged over the entire active surface in the full (thick solid line) and reduced (thick dashed line) models. The interval of usual calculation of the initial adhesion rate (t = 3 min) is indicated. (Thin line) Averaged near-wall platelet concentration in the flow normalized by P0/100%.
Thick lines in Fig. 2 C show the kinetics of M predicted by the full (solid line) and reduced (dashed line) models. These models predict similar initial adhesion rates. As in the reduced model, the initial growth of M in the full model is virtually linear. Then, its rate gradually decreases while surface coverage approaches 100%. Obviously, this decrease in the adhesion rate is due to a vanishing Θ, but not due to the removal of platelets from the near-wall region because this is insignificant and is rapidly compensated for by delivery of new platelets from the bulk flow (thin line).
The focus of this study is the regulation of platelet delivery to the place of adhesion (damaged vessel wall and primary clot), and a saturation effect is a specific feature of the experiments with inhibited platelet activation and aggregation (see Description of the Processes, above). Thus, further analysis is limited to the initial times of platelet adhesion.
The shear-rate dependence of platelet adhesion results from the collision mechanism of platelet delivery
The fact that both the wall shear rate and the physical presence of erythrocytes markedly enhance platelet adhesion has been well established, but the ruling mechanism underlying it was unknown. To test the hypothesis that this mechanism consists of erythrocytes pushing platelets from the near-wall layer to the wall, predictions of the reduced and full models were compared with data on platelet deposition from whole rabbit blood onto the subendothelium of a rabbit aorta determined at varying (8,10). Dashed and solid lines in Fig. 3 A show the initial adhesion rates calculated from these models at α = 0.12, ka = 1000 s−1, and ξ = 0.02 (k1 and k2 were set to 0 and 1 in accord with the dRBC-dependence of platelet adhesion described in the next section).
At all shear rates studied, both models were in general agreement with the experimental data (open markers). The difference between the two theoretical curves was insignificant and comparable with the experimental error, indicating the minor effect of the factors disregarded during model reduction. Exploration of the effect of changes in ka and ξ-values on the adhesion rate calculated by the reduced model is shown in Fig. 3 B. An increase in ka led to an increase of the maximal adhesion rate, whereas an increase in ξ reduced adhesion at high but not at low shear rates. An increase of the A value, and thus the α-value, shifted the whole curve upwards (not shown). This exploration demonstrates the unambiguous determination of free model parameters by fitting the experimental data with the reduced model.
To investigate in detail the effect of the assumption of quasistationarity of R, calculations by the extended model that disregarded this assumption were performed. To this effect, Eq. 14 was substituted for Eqs. 7 and 8, right-hand side of Eq. 5 was substituted by αJΘ − kdetR, and M in Eq. 16 was replaced by M + R. All parameters remained unaltered, and the values of k0bind, δ, and β were chosen such as to satisfy the ratios
and
Because the time of platelet activation is small and equals one to few seconds, the fast (k0bind = 1 s−1) and very slow (k0bind = 0.01 s−1) regimes were simulated. The solid markers in Fig. 3 A show the rate of M + R accumulation obtained in these two regimes. Evidently, the deviation from the model that assumed the quasistationarity of R (solid line) was insignificant supporting the validity of this assumption.
Thus, the shear rate-dependence of the adhesion rate obtained in the models and the experiment is completely governed by the shear-rate dependence of the effective rate constant keff. Below, we show that this result remains valid for the dependence of the adhesion rate on hematocrit and erythrocyte size.
The size and concentration of erythrocytes determine platelet adhesion rate
To further test the hypothesis that collision with RBC is the governing mechanism of platelet delivery to an active surface, values of human platelet adhesion to human artery subendothelium in the presence of human, rabbit, and goat erythrocytes (3) were plotted as a function of erythrocyte major diameter according to Eq. 22 (Fig. 4 A, markers). All of these values were found to lie approximately on one line. Because this line tended to pass through the origin, k1 and k2 were set to 0 and 1, respectively. The dashed line in Fig. 4 A was plotted as a right-hand-side of Eq. 22 with α1/3=0.28. The same adhesion data in coordinates of platelet adhesion-erythrocyte volume fraction are presented in Fig. 4 B (markers) along with calculations performed by the reduced (dashed lines) and full (solid lines) models. The ka and ξ-values were assumed to be 1000 s−1 and 0.02, respectively, in accordance with those determined in the preceding section.
In general, the predictions of both models were consistent with the experimental findings, and the differences between the two models were within the experimental error. Nevertheless, the calculated and experimental values disagreed in the boundary cases, such as zero hematocrit and high concentration of large erythrocytes. As discussed below, this discrepancy might arise from both experimental artifacts and imperfections in the theory.
Discussion
The main result of this study is the theoretical substantiation of the hypothesis that platelet adhesion from the blood flow is limited by their near-wall inelastic collisions with erythrocytes (Fig. 1 A). This statement was confirmed by the fact that the reduced model gives adhesion rates very similar to the full one and reproduces fairly well all parametric dependences ensuing from the full model and the experimental data.
Computation of the platelet flux toward the wall using the reduced model accounts only for collisions of near-wall platelets with erythrocytes. The limiting role of these collisions was suggested by the experimental data, but this is the first time, to our knowledge, that they were taken into account in a quantitative theory. Indeed, it has been shown that elevated hematocrit caused a significant rise in the platelet adhesion rate (3–5,7,9,11), which occurred due to the physical presence of erythrocytes themselves rather than by platelet activation under the effect of ADP contained in erythrocytes (9). This finding provided a basis for the postulation of an additional RBC-dependent mechanism influencing platelet binding to the surface (11). However, its nature has never been exactly specified. We speculated that this mechanism may consist of pushing the platelet against the wall as a result of its inelastic rebounding collision with an outrunning erythrocyte or other blood cell.
This suggestion logically ensues from the available theoretical and experimental data. Direct observations of platelet motion in a suspension of erythrocyte ghosts showed that, in their presence, platelets contacted the wall much more frequently than in erythrocyte-free plasma (15,16,33). In the absence of erythrocytes, the probability of a single platelet that is traveling close to the wall will collide with it is very low for two reasons.
First, the platelet can only very gradually leave its flow tube because its inertia and Brownian diffusion are small: at
the Reynolds and Peclet numbers of a platelet are approximately
and
where the plasma density and viscosity were assumed to be ρ = 1 g/sm3 and μ = 1 sP, respectively.
Second, the hydrodynamic inertial force that acts on a near-wall particle at such Rep is directed from the wall toward the midflow and thereby hinders their rapprochement (45). A recent experimental and theoretical study has demonstrated that a platelet must be forced into the wall to initiate its capture by an active (vWf-coated) surface (46). Therefore, the physical presence of erythrocytes is qualitatively necessary to ensure normal adhesion of platelets. However, the problem of quantitatively considering the effects of erythrocytes has thus far remained unresolved.
Therefore, an additional contribution of this work is a method for quantitative calculation of platelet flux toward the wall and the resulting adhesion rate. For the first time to our knowledge, the theoretical calculation of these quantities was performed resulting in a precise description of earlier experimentally determined dependences of platelet adhesion rate on the wall shear rate, hematocrit level, and erythrocyte size, i.e., on all the parameters influencing the frequency of cell-cell collisions in the shear flow (Figs. 3 A and 4 B). All of these dependences can be described fairly well using a single expression for the effective adhesion rate constant (Eq. 19).
In earlier studies, the value of this constant was estimated by fitting the adhesion rate values measured under varied conditions with the solution of the equations of a simpler mathematical model. In that model, platelet adhesion was assumed to occur in one step and to be irreversible. This approach necessitated the assumption of both an increase (29) and a decrease (11,28) of keff with increasing wall shear rate and suggested that diffusional control of adhesion at low-to-moderate shear rates passed to kinetic control at higher shear rates (8,10,11). The values of keff determined in the kinetic regime (implying finiteness of keff) at normal hematocrit and = 50–10,000 s−1 were in the range from 0.4 to 7.2 μm/s (7,11,13,20,28). These findings agree with calculations using Eq. 19, which gave the values of 0.6–3.3 μm/s for rabbit blood cells at α = 0.12, ka = 1000 s−1, ξ = 0.02, k1 = 0, and k2 = 1 within the same range of .
The comparison of the determined α-, ka-, and ξ-values with literature data is of special interest. Huang and Hellums (42) obtained the overall binding efficiency for two colliding human platelets at shear rates ranging from 3600 to 7650 s−1. They found this binding efficiency to be and at higher shear, it suddenly increased. The capture efficiency α can be extracted from their data by dividing the overall binding efficiency by the hydrodynamic collision efficiency ɛh calculated from Eq. S14 in the Supporting Material for λ = 1. At shear rates 3600–5000 s−1, ɛh (λ = 1) ≈ 0.15, resulting in an α-value of ∼0.005–0.01. This value is in reasonable agreement with the value of 0.022 estimated in this study for human platelets. For a more detailed comparison, the hydrodynamic collision efficiency should be measured or calculated by accounting for both the nonspherical platelet shape and the wall proximity. The sudden increase in capture efficiency for colliding platelets at high shear rates (42) correlates well with the sudden onset of thrombi formation on subendothelium (in addition to platelet adhesion) at shear rates above 1000 s−1 (10). The description of these events was out of the scope of this study.
Other available reports directly concerning the probability of platelet capture (47,48) are related to firm adhesion of activated platelets via integrin-fibrinogen bridges, and their results cannot be compared with the α-values determined here.
The value of ka = 1000 s−1 is consistent with data obtained in Kulkarni et al. (1). In that work, the probability of firm adhesion of a platelet captured to the vWf expressed on the immobilized platelets decreases from 70% to 30% as the wall shear rate increases from 150 to 1800 s−1. The calculation of this probability by the formula
| (23) |
gives 87% and 35% for the same shear rate values. This result suggests a good agreement between theoretical and experimental findings.
The cause of the discrepancies between predicted and observed values of human platelet adhesion in the case of zero hematocrit and high concentrations of large erythrocytes (Fig. 4 B) remains unclear. The point ΦRBC = 0 appears to lie much higher than the extrapolations of all the three experimental curves from the nonzero hematocrit region. According to these data, 40% hematocrit caused only a 5.8- (human RBCs) or 3.2-fold (rabbit RBCs) increase in platelet adhesion compared to PRP. Under similar conditions, but using whole rabbit blood, the effect of erythrocytes on platelet adhesion was investigated in Turitto and Baumgartner (9). At the wall shear rate of 840 s−1 and hematocrit 38%, erythrocytes were shown to increase the platelet adhesion rate by a factor of 57 compared with PRP. Calculations using the full model gave a 164-fold increase, suggesting some underestimation of the platelet-platelet collision frequency or efficiency. It is possible that this was caused by using k1 = 0 in the absence of its exact estimation (Fig. 4 A). However, at k1 = 0.5, this increase becomes 76-fold, in better agreement with Turitto and Baumgartner (9).
The predicted decrease of the adhesion rate and that apparent in the lower and middle experimental curves at a hematocrit level over 40% (Fig. 4 B) are attributable to the method of perfusate preparation in Aarts et al. (3) that consisted of mixing PRP containing a constant concentration of platelets with an erythrocyte suspension to achieve the desirable hematocrit. Using this method, platelet concentration in the perfusate linearly decreased with increasing hematocrit (see Fixed Model Parameters, above). Together with the linear proportionality between keff and ΦRBC (Eqs. 11, 15, and 19), the resulting dependence of the initial adhesion rate on hematocrit is expected to be in the form of ΦRBC × (1–ΦRBC). The maximum of this function occurs at ΦRBC = 0.5, which is shown by the curves in Fig. 4 B, excluding the upper experimental one.
The linear dependence on hematocrit depicted by this curve might be a manifestation of non-Newtonian properties intrinsic in both blood and dense RBC suspensions, such as flattening of the velocity profile and off-wall lateral migration of RBCs. They account for the hematocrit-dependent increase of the wall shear rate in narrow tubes compared with that calculated for the Poiseuille flow (33,49) and for the enrichment of the near-wall layer with platelets (50,51), respectively. In principle, these effects could explain the rise in platelet adhesion for the case of human erythrocytes at 50–60% hematocrit. However, it is unlikely that both effects could be realized in the experiments in which the above results were obtained because the effective thickness of the gap was 1200 μm. Therefore, there is no convincing explanation for this phenomenon thus far.
Conclusions
This theoretical study provides qualitative and quantitative evidence that the platelet adhesion rate from the blood flow is controlled by the frequency of their rebounding collisions with erythrocytes in the immediate vicinity of the wall. This finding is of importance for the understanding of biophysical mechanisms governing hemostasis and thrombosis; also, it provides an impetus for the further development of basic research in this field. Evidently, the role of erythrocytes should be taken into account in any theoretical consideration of mechanisms underlying the regulation of platelet behavior in the blood flow.
Recent work (52–54) has been devoted to the mechanical effects of erythrocytes on platelet transport within the flow, but these studies disregarded platelet adhesion. However, considerable progress has been achieved in simulation of leukocyte-wall interactions (55–57); it has lately been extended to platelets (58). The combination of these strategies is highly promising and may help validate the constants determined in this study. Alternatively, the application of a reduced model that is much simpler than the full one but yields similar results may substantially facilitate the construction of large-scale mathematical models of thrombosis. It is especially of great importance when the thrombus forms in a small region of a complex vascular network, and the main computational resources are used for solving the equation governing hydrodynamics of blood flow (59).
Acknowledgments
The authors thank Drs. E. Shnol and E. Ermakova for helpful discussions, Drs. I. Sirakov and V. Volpert for computational assistance, and Dr. M. Panteleev for help in the preparation of the manuscript.
This work is a part of joint French-Russian Programme International de Cooperation Scientifique “Mathematical Modeling of Blood Diseases”. It was supported in part by grant Nos. 09-04-92427, 09-02-00018, 09-04-00232, 09-04-00357, 10-01-91055, and 10-04-00035 from the Russian Foundation for Basic Research and by the RAS Presidium program “Basic Sciences—to Medicine” (“The Search for New High-Efficient Direct Low-Molecular Inhibitors of Thrombin”).
Supporting Material
References
- 1.Kulkarni S., Dopheide S.M., Jackson S.P. A revised model of platelet aggregation. J. Clin. Invest. 2000;105:783–791. doi: 10.1172/JCI7569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ruggeri Z.M., Mendolicchio G.L. Adhesion mechanisms in platelet function. Circ. Res. 2007;100:1673–1685. doi: 10.1161/01.RES.0000267878.97021.ab. [DOI] [PubMed] [Google Scholar]
- 3.Aarts P.A., Bolhuis P.A., Sixma J.J. Red blood cell size is important for adherence of blood platelets to artery subendothelium. Blood. 1983;62:214–217. [PubMed] [Google Scholar]
- 4.Aarts P.A., Steendijk P., Heethaar R.M. Fluid shear as a possible mechanism for platelet diffusivity in flowing blood. J. Biomech. 1986;19:799–805. doi: 10.1016/0021-9290(86)90130-2. [DOI] [PubMed] [Google Scholar]
- 5.Antonini G., Guiffant G., Dosne A.M. Estimation of platelet diffusivity in flowing blood. Biorheology. 1978;15:111–117. doi: 10.3233/bir-1978-15205. [DOI] [PubMed] [Google Scholar]
- 6.Cadroy Y., Hanson S.R. Effects of red blood cell concentration on hemostasis and thrombus formation in a primate model. Blood. 1990;75:2185–2193. [PubMed] [Google Scholar]
- 7.Feuerstein I.A., Brophy J.M., Brash J.L. Platelet transport and adhesion to reconstituted collagen and artificial surfaces. Trans. Am. Soc. Artif. Intern. Organs. 1975;21:427–435. [PubMed] [Google Scholar]
- 8.Turitto V.T., Baumgartner H.R. Platelet deposition on subendothelium exposed to flowing blood: mathematical analysis of physical parameters. Trans. Am. Soc. Artif. Intern. Organs. 1975;21:593–601. [PubMed] [Google Scholar]
- 9.Turitto V.T., Baumgartner H.R. Platelet interaction with subendothelium in a perfusion system: physical role of red blood cells. Microvasc. Res. 1975;9:335–344. doi: 10.1016/0026-2862(75)90070-9. [DOI] [PubMed] [Google Scholar]
- 10.Turitto V.T., Baumgartner H.R. Platelet interaction with subendothelium in flowing rabbit blood: effect of blood shear rate. Microvasc. Res. 1979;17:38–54. doi: 10.1016/0026-2862(79)90006-2. [DOI] [PubMed] [Google Scholar]
- 11.Turitto V.T., Weiss H.J. Platelet and red cell involvement in mural thrombogenesis. Ann. N. Y. Acad. Sci. 1983;416:363–376. doi: 10.1111/j.1749-6632.1983.tb35199.x. [DOI] [PubMed] [Google Scholar]
- 12.Leonard E.F., Grabowski E.F., Turitto V.T. The role of convection and diffusion on platelet adhesion and aggregation. Ann. N. Y. Acad. Sci. 1972;201:329–342. doi: 10.1111/j.1749-6632.1972.tb16309.x. [DOI] [PubMed] [Google Scholar]
- 13.Stubley G.D., Strong A.B., Absolom D.R. A review of mathematical models for the prediction of blood cell adhesion. PCH PhysicoChem. Hydrodyn. 1987;8:221–235. [Google Scholar]
- 14.Goldsmith H.L. The Microcirculatory Society Eugene M. Landis Award lecture. The microrheology of human blood. Microvasc. Res. 1986;31:121–142. doi: 10.1016/0026-2862(86)90029-4. [DOI] [PubMed] [Google Scholar]
- 15.Goldsmith H.L. Red cell motions and wall interactions in tube flow. Fed. Proc. 1971;30:1578–1590. [PubMed] [Google Scholar]
- 16.Goldsmith H.L., Marlow J.C. Flow behavior of erythrocytes. II. Particle motions in concentrated suspensions of ghost cells. J. Colloid Interface Sci. 1979;71:383–407. [Google Scholar]
- 17.Savage B., Almus-Jacobs F., Ruggeri Z.M. Specific synergy of multiple substrate-receptor interactions in platelet thrombus formation under flow. Cell. 1998;94:657–666. doi: 10.1016/s0092-8674(00)81607-4. [DOI] [PubMed] [Google Scholar]
- 18.Ruggeri Z.M. von Willebrand factor. J. Clin. Invest. 1997;99:559–564. doi: 10.1172/JCI119195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Konstantopoulos K., Kukreti S., McIntire L.V. Biomechanics of cell interactions in shear fields. Adv. Drug Deliv. Rev. 1998;33:141–164. doi: 10.1016/s0169-409x(98)00024-6. [DOI] [PubMed] [Google Scholar]
- 20.Grabowski E.F., Friedman L.I., Leonard E.F. Effects of shear rate on the diffusion and adhesion of blood platelets to a foreign surface. Ind. Eng. Chem. Fundam. 1972;11:224–232. [Google Scholar]
- 21.Sorensen E.N., Burgreen G.W., Antaki J.F. Computational simulation of platelet deposition and activation: II. Results for Poiseuille flow over collagen. Ann. Biomed. Eng. 1999;27:449–458. doi: 10.1114/1.201. [DOI] [PubMed] [Google Scholar]
- 22.Sorensen E.N., Burgreen G.W., Antaki J.F. Computational simulation of platelet deposition and activation: I. Model development and properties. Ann. Biomed. Eng. 1999;27:436–448. doi: 10.1114/1.200. [DOI] [PubMed] [Google Scholar]
- 23.Strong A.B., Stubley G.D., Absolom D.R. Theoretical and experimental analysis of cellular adhesion to polymer surfaces. J. Biomed. Mater. Res. 1987;21:1039–1055. doi: 10.1002/jbm.820210810. [DOI] [PubMed] [Google Scholar]
- 24.Wootton D.M., Markou C.P., Ku D.N. A mechanistic model of acute platelet accumulation in thrombogenic stenoses. Ann. Biomed. Eng. 2001;29:321–329. doi: 10.1114/1.1359449. [DOI] [PubMed] [Google Scholar]
- 25.Diller T.E. Comparison of red cell augmented diffusion and platelet transport. J. Biomech. Eng. 1988;110:161–163. doi: 10.1115/1.3108422. [DOI] [PubMed] [Google Scholar]
- 26.Eckstein E.C., Bilsker D.L., Tilles A.W. Transport of platelets in flowing blood. Ann. N. Y. Acad. Sci. 1987;516:442–452. doi: 10.1111/j.1749-6632.1987.tb33065.x. [DOI] [PubMed] [Google Scholar]
- 27.Turitto V.T., Hall C.L. Mechanical factors affecting hemostasis and thrombosis. Thromb. Res. 1998;92(Suppl2):S25–S31. doi: 10.1016/s0049-3848(98)00157-1. [DOI] [PubMed] [Google Scholar]
- 28.Turitto V.T., Weiss H.J., Baumgartner H.R. The effect of shear rate on platelet interaction with subendothelium exposed to citrated human blood. Microvasc. Res. 1980;19:352–365. doi: 10.1016/0026-2862(80)90054-0. [DOI] [PubMed] [Google Scholar]
- 29.David T., Thomas S., Walker P.G. Platelet deposition in stagnation point flow: an analytical and computational simulation. Med. Eng. Phys. 2001;23:299–312. doi: 10.1016/s1350-4533(01)00047-9. [DOI] [PubMed] [Google Scholar]
- 30.Baumgartner H.R. The role of blood flow in platelet adhesion, fibrin deposition, and formation of mural thrombi. Microvasc. Res. 1973;5:167–179. doi: 10.1016/0026-2862(73)90069-1. [DOI] [PubMed] [Google Scholar]
- 31.Sakariassen K.S., Hanson S.R., Cadroy Y. Methods and models to evaluate shear-dependent and surface reactivity-dependent antithrombotic efficacy. Thromb. Res. 2001;104:149–174. doi: 10.1016/s0049-3848(01)00344-9. [DOI] [PubMed] [Google Scholar]
- 32.Zydney A.L., Colton C.K. Augmented solute transport in the shear flow of a concentrated suspension. PCH PhysicoChem. Hydrodyn. 1988;10:77–96. [Google Scholar]
- 33.Goldsmith H.L., Turitto V.T. Rheological aspects of thrombosis and hemostasis: basic principles and applications. ICTH-Report—Subcommittee on Rheology of the International Committee on Thrombosis and Hemostasis. Thromb. Haemost. 1986;55:415–435. [PubMed] [Google Scholar]
- 34.Cranmer S.L., Ulsemer P., Jackson S.P. Glycoprotein (GP) Ib-IX-transfected cells roll on a von Willebrand factor matrix under flow. Importance of the GPib/actin-binding protein (ABP-280) interaction in maintaining adhesion under high shear. J. Biol. Chem. 1999;274:6097–6106. doi: 10.1074/jbc.274.10.6097. [DOI] [PubMed] [Google Scholar]
- 35.Doggett T.A., Girdhar G., Diacovo T.G. Selectin-like kinetics and biomechanics promote rapid platelet adhesion in flow: the GPIb(α)-vWF tether bond. Biophys. J. 2002;83:194–205. doi: 10.1016/S0006-3495(02)75161-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Savage B., Saldívar E., Ruggeri Z.M. Initiation of platelet adhesion by arrest onto fibrinogen or translocation on von Willebrand factor. Cell. 1996;84:289–297. doi: 10.1016/s0092-8674(00)80983-6. [DOI] [PubMed] [Google Scholar]
- 37.Hantgan R.R. A study of the kinetics of ADP-triggered platelet shape change. Blood. 1984;64:896–906. [PubMed] [Google Scholar]
- 38.Frojmovic M., Wong T., van de Ven T. Dynamic measurements of the platelet membrane glycoprotein IIb-IIIa receptor for fibrinogen by flow cytometry. I. Methodology, theory and results for two distinct activators. Biophys. J. 1991;59:815–827. doi: 10.1016/S0006-3495(91)82294-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Frojmovic M.M., Mooney R.F., Wong T. Dynamics of platelet glycoprotein IIb-IIIa receptor expression and fibrinogen binding. I. Quantal activation of platelet subpopulations varies with adenosine diphosphate concentration. Biophys. J. 1994;67:2060–2068. doi: 10.1016/S0006-3495(94)80689-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tandon P., Diamond S.L. Hydrodynamic effects and receptor interactions of platelets and their aggregates in linear shear flow. Biophys. J. 1997;73:2819–2835. doi: 10.1016/S0006-3495(97)78311-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mody N.A., King M.R. Platelet adhesive dynamics. Part I. Characterization of platelet hydrodynamic collisions and wall effects. Biophys. J. 2008;95:2539–2555. doi: 10.1529/biophysj.107.127670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Huang P.Y., Hellums J.D. Aggregation and disaggregation kinetics of human blood platelets. Part II. Shear-induced platelet aggregation. Biophys. J. 1993;65:344–353. doi: 10.1016/S0006-3495(93)81079-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wu Y.P., de Groot P.G., Sixma J.J. Shear-stress-induced detachment of blood platelets from various surfaces. Arterioscler. Thromb. Vasc. Biol. 1997;17:3202–3207. doi: 10.1161/01.atv.17.11.3202. [DOI] [PubMed] [Google Scholar]
- 44.Goodman P.D., Barlow E.T., Solen K.A. Computational model of device-induced thrombosis and thromboembolism. Ann. Biomed. Eng. 2005;33:780–797. doi: 10.1007/s10439-005-2951-z. [DOI] [PubMed] [Google Scholar]
- 45.Longest P.W., Kleinstreuer C., Buchanan J.R. Efficient computation of micro-particle dynamics including wall effects. Comput. Fluids. 2004;33:577–601. [Google Scholar]
- 46.Mody N.A., Lomakin O., King M.R. Mechanics of transient platelet adhesion to von Willebrand factor under flow. Biophys. J. 2005;88:1432–1443. doi: 10.1529/biophysj.104.047001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Xia Z., Frojmovic M.M. Aggregation efficiency of activated normal or fixed platelets in a simple shear field: effect of shear and fibrinogen occupancy. Biophys. J. 1994;66:2190–2201. doi: 10.1016/S0006-3495(94)81015-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Guy R.D., Fogelson A.L. Probabilistic modeling of platelet aggregation: effects of activation time and receptor occupancy. J. Theor. Biol. 2002;219:33–53. [PubMed] [Google Scholar]
- 49.Goldsmith H.L., Skalak R. Hemodynamics. Annu. Rev. Fluid Mech. 1975;7:213–247. [Google Scholar]
- 50.Eckstein E.C., Koleski J.F., Waters C.M. Concentration profiles of 1 and 2.5 microns beads during blood flow. Hematocrit effects. ASAIO Trans. 1989;35:188–190. [PubMed] [Google Scholar]
- 51.Yeh C., Eckstein E.C. Transient lateral transport of platelet-sized particles in flowing blood suspensions. Biophys. J. 1994;66:1706–1716. doi: 10.1016/S0006-3495(94)80962-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Munn L.L., Dupin M.M. Blood cell interactions and segregation in flow. Ann. Biomed. Eng. 2008;36:534–544. doi: 10.1007/s10439-007-9429-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Al-Momani T., Udaykumar H.S., Chandran K.B. Micro-scale dynamic simulation of erythrocyte-platelet interaction in blood flow. Ann. Biomed. Eng. 2008;36:905–920. doi: 10.1007/s10439-008-9478-z. [DOI] [PubMed] [Google Scholar]
- 54.Crowl L.M., Fogelson A.L. Computational model of whole blood exhibiting lateral platelet motion induced by red blood cells. Int. J. Numer. Meth. Biomed. Eng. 2009;26:471–487. doi: 10.1002/cnm.1274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Jadhav S., Eggleton C.D., Konstantopoulos K. A 3-D computational model predicts that cell deformation affects selectin-mediated leukocyte rolling. Biophys. J. 2005;88:96–104. doi: 10.1529/biophysj.104.051029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Caputo K.E., Lee D., Hammer D.A. Adhesive dynamics simulations of the shear threshold effect for leukocytes. Biophys. J. 2007;92:787–797. doi: 10.1529/biophysj.106.082321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Verdier C., Couzon C., Singh P. Modeling cell interactions under flow. J. Math. Biol. 2009;58:235–259. doi: 10.1007/s00285-008-0164-4. [DOI] [PubMed] [Google Scholar]
- 58.Blyth M.G., Pozrikidis C. Adhesion of a blood platelet to injured tissue. Eng. Anal. Bound. Elem. 2009;33:695–703. [Google Scholar]
- 59.Quarteroni A., Tuveri M., Veneziani A. Computational vascular fluid dynamics: problems, models and methods. Comput. Visualiz. Sci. 2000;2:163–197. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


