Nonadditivity in Conformational Entropy upon Molecular Rigidification Reveals a Universal Mechanism Affecting Folding Cooperativity

Abstract

Previously, we employed a Maxwell counting distance constraint model (McDCM) to describe α-helix formation in polypeptides. Unlike classical helix-coil transition theories, the folding mechanism derives from nonadditivity in conformational entropy caused by rigidification of molecular structure as intramolecular cross-linking interactions form along the backbone. For example, when a hydrogen bond forms within a flexible region, both energy and conformational entropy decrease. However, no conformational entropy is lost when the region is already rigid because atomic motions are not constrained further. Unlike classical zipper models, the same mechanism also describes a coil-to-β-hairpin transition. Special topological features of the helix and hairpin structures allow the McDCM to be solved exactly. Taking full advantage of the fact that Maxwell constraint counting is a mean field approximation applied to the distribution of cross-linking interactions, we present an exact transfer matrix method that does not require any special topological feature. Upon application of the model to proteins, cooperativity within the folding transition is yet again appropriately described. Notwithstanding other contributing factors such as the hydrophobic effect, this simple model identifies a universal mechanism for cooperativity within polypeptide and protein-folding transitions, and it elucidates scaling laws describing hydrogen-bond patterns observed in secondary structure. In particular, the native state should have roughly twice as many constraints as there are degrees of freedom in the coil state to ensure high fidelity in two-state folding cooperativity, which is empirically observed.

Introduction

The past decade has seen an explosion in experimental (1–5) and computational (6,7) studies on protein dynamics and thermodynamic populations for better understanding of functional mechanisms. From these studies, it is clear entropy plays a key mechanistic role for cooperative structural transitions in proteins regarding allosteric events (8). Moreover, entropy can also modulate cooperativity in ligand binding by shifting the thermodynamic stability of a complex through the accessible conformational ensemble (9). It is known that changes in entropy and rigidification of a protein are both modulated by osmolytes and other solvation effects (10). Unfortunately, fundamental relationships among entropy, thermodynamic stability, molecular rigidity, and cooperativity remain poorly understood (11–14). In this report, the thermodynamic nature of folding cooperativity is addressed quantitatively.

Identification of the relevant degrees of freedom (DOF) and constraints within a polypeptide chain is fundamental to a complete understanding of the origin of cooperativity. A completely unfolded chain constrained only by quenched covalent bonding defines a flexible coil state. The number of DOF decreases as the chain folds into a compact structure because new constraints form due to cross-linking hydrogen bonds (H-bonds) and packing. Levinthal's paradox explains why folding cooperativity is necessary for proteins to fold on observed timescales, rather than timescales that would span longer than the age of the universe in its absence (15). Folding cooperativity implies the progress of a chain segment to fold into specific native structure depends on the folding progress of other segments.

Specific microscopic mechanisms are commonly invoked to model the folding process under native state conditions. The process of a polypeptide to transition from a coil to helix is modeled as a coupling between neighboring amino acids that bias the conformation toward the α-helix state through a nucleation/propagation process (16,17). To fold proteins that are soluble in aqueous solution requires a hydrophobic collapse (18,19), and this mechanism is commonly thought to be the primary thermodynamic driving force. However, the hydrophobic effect also applies to the stability of the nonspecific molten globule collapsed state, meaning it cannot be the sole driving force. Folding processes require specific arrangement of atomic interactions. Consequently, additional mechanisms must be invoked to describe the self-organization of structure, such as diffusion-collision (20,21) or posit of a hierarchical sequence of events starting from coil to the onset of secondary structure to tertiary structure (22–24).

A fundamental question is whether different microscopic processes for self-organization share an underlying mechanism that serves as the origin of folding cooperativity. Manifested as different folding processes that could dramatically affect kinetics (25), we present a simple model that suggests the origin of folding cooperativity is a thermodynamic driving force caused by the link between nonadditivity in conformational entropy and flexibility/rigidity within molecular structure. By employing an all-atom-based distance constraint model (DCM) within a mean field approximation, the essential features of structural phase transitions observed in proteins and polypeptides are captured.

Based on profound insight of Maxwell (26), mechanical stability of a network with uniformly distributed constraints can be characterized by constraint counting, requiring no detailed knowledge of the network. In modern terms, Maxwell constraint counting is a mean field approximation that treats the density of constraints within a network as uniform, where local constraint density fluctuations are ignored. Applied to proteins, Maxwell counting qualitatively describes the unfolding process as rigidity is lost (27,28).

Although the connection between the rigidity transition and two-state behavior was previously made using an athermal model (28), the McDCM differs fundamentally because the quantitative link between independent constraints and conformational entropy (29) allows a statistical mechanics treatment for the calculation of thermodynamic stability and thermodynamic response functions, such as heat capacity. Recently (27), we demonstrated that the Maxwell counting DCM (McDCM) well describes cooperativity within the α-helix/coil transition, thus indicating that this approximation is not too severe to capture essential features of two-state folding.

Because atomic interactions form within the molecular structure, this corresponds to constraints being added to a network. Under the Maxwell counting approximation, constraints added anywhere to the network remove DOF associated with a drop in conformational entropy until the network becomes rigid. Thereafter, additional constraints are redundant and pay no entropic price. As a result, Fig. 1 shows the expected competition between two free energy basins that emerge at intermediate temperatures corresponding to the folded and unfolded states. An important aspect of Fig. 1 is that it directly relates the microscopic interactions that form within a protein to its thermodynamic properties. In this report, we demonstrate that the McDCM appropriately describes cooperativity within both polypeptide and protein-folding transitions. Moreover, our results uncover scaling laws that maintain the universal applicability of the approach.

Figure 1.

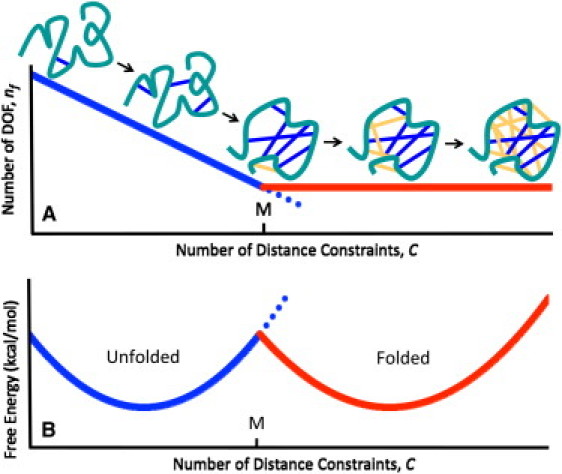
(A) Using Maxwell constraint counting, the number of internal degrees of freedom of a protein decreases linearly as the backbone is cross-linked by distance constraints (dark coloring) until the Maxwell level, M, is reached. Beyond M, all additional distance constraints are redundant (light coloring). (B) For T ≈ T_m, two basins in the free energy landscape yield two-state behavior.

Distance Constraint Model

Based on a free energy decomposition scheme combined with constraint theory (29), a distance constraint model (DCM) is a statistical mechanical model that explicitly accounts for nonadditivity in conformational entropy by modeling atomic interactions as a network of distance constraints. Fluctuating interactions are each associated with a component energy and entropy. Although total energy of a given network is the sum of constituent energy components, the conformational entropy is nonadditive (30,31) due to correlated motions.

Additive models neglect correlations in atomic motion that extend throughout the protein and therefore overestimate conformational entropy. In response, the DCM relates nonadditivity of conformational entropy to rigid and flexible regions within molecular structure depending on the numbers and types of interactions that form. For example, cross-linking disulfide bonds and H-bonds critically affect the formation of flexible and rigid regions. Of particular importance are interactions that break and form due to thermodynamic fluctuations. A reduction in conformational entropy does not occur when atomic interactions form within rigid regions because atomic motions are not further restricted. The DCM provides a fast estimate for the total conformational entropy of the macromolecule (described below) without recourse to computationally expensive simulations that sample the available phase space.

Because atomic interactions form and break due to thermal fluctuations, an ensemble of mechanical frameworks must be considered. Each framework, F, is composed of A atoms and C distance constraints. In the simplest case, an energy of formation, ɛ_k, and maximal entropy cost, Rγ_k, are assigned to the k^th distance constraint (for 1 ≤ k ≤ C). Here, R is the universal gas constant and γ_k is a dimensionless pure entropy. The energy of a framework, E(F), is obtained by summing over all C energy contributions. The entropy of a framework is given by

$$S\left(F\right)=S_o-S_c\left(F\right),$$

where S_o is the reference entropy of a polypeptide chain in the coil state, and S_c(F) is the entropic cost of adding constraints. The conformational entropy that the chain loses is S_c(F) = ln (Ω_c), where Ω_c is the excluded phase space because of constraints placed on atomic motions. In the case of one constraint per interaction, it is convenient to define η_k(F) = 1 or 0 when the k^th constraint is present or not, respectively. Whenever a constraint is present, it can be independent, ν_k(F) = 1, or redundant, ν_k(F) = 0. Thus, (0,0), (1,0), and (1,1) are valid combinations for (η_k, ν_k). Quenched constraints that model covalent bonds are critical to the properties of rigidity, but their energy and entropy contributions are constant across all terms in the partition function, and therefore factor out. Consequently, the free energy

$$G\left(F\right)=\left[E\left(F\right)-TS\left(F\right)\right]-G_o$$

for framework F relative to the coil state is of interest, and it is expressed in terms of fluctuating distance constraints only, given by

$$G\left(F\right)=\sum _{k=1}^{C\left(F\right)}\left[{\varepsilon }_k{\eta }_k\left(F\right)+RT{\gamma }_k{\nu }_k\left(F\right)\right]\text{.}$$ (1)

The first term in Eq. 1 is linear over all distance constraints. The second term in Eq. 1 is nonlinear because the k^th distance constraint does not reduce conformational entropy when it is placed in a rigid region (i.e., ν_k(F) = 0). The formation of a rigid region will depend upon all other distance constraints within the network through a nonlocal collective effect. The details regarding size, shape, and location of rigid and flexible regions depend on the number of constraints, C(F), and how they are distributed within framework F.

All possible arrangements of constraints define the ensemble of mechanical frameworks. Independent and redundant constraints are identified within a given framework using graph-rigidity algorithms (32,33). Summing over the entropy contributions from independent distance constraints (i.e., only for the terms with ν_k(F) = 1) yields an upper bound estimate for S(F). However, in graph-rigidity algorithms, the order that constraints are placed in the network affects which constraint is identified as independent or redundant. As such, many different upper-bound estimates can be obtained. The best estimate that can be made is to determine the lowest possible upper-bound estimate.

The DCM obtains the lowest possible upper-bound estimate for conformational entropy by first sort-ordering the constraints in terms of their maximal entropy cost, γ_k, from greatest to smallest. Second, in the graph-rigidity algorithm, distance constraints are placed one at a time in the network with the preferential ordering that γ_k ≥ γ_k+1. Details can be found in Jacobs et al. (29). Note that although the mathematical process of preferentially placing constraints in the network is required to estimate a thermodynamic quantity, the kinetics of constraints forming is irrelevant. Because conformational entropy is a thermodynamic state function, all that matters is which constraints are present. The complex issue of accounting for nonadditivity in conformational entropy, S(F), is rendered to a sorting process involving all constraints within the network, and summing only over the greatest entropy loss contributions from C_i independent constraints (C_i ≤ C). From constraint theory (34), the number of internal DOF, J, in a system of A atoms in d dimensions with C constraints, of which C_r constraints are redundant, is given by

$$J=dA-d\left(d+1\right)/2-C+C_r\text{.}$$ (2)

Note that C_i = C – C_r. Graph-rigidity algorithms calculate C_i based on recursively adding constraints to a network one at a time (32,33), which conveniently couples to the presorting process. Consequently, S(F) decreases as the number of DOF decreases.

Using standard formulas from statistical mechanics, the probability for framework F is tied to its Boltzmann weight normalized by the partition function, Q, given by

$$P\left(F\right)=\exp \left(-\sum _{k=1}^{C\left(F\right)}{\nu }_k\left(F\right){\gamma }_k\right)\exp \left(-\beta \sum _{k=1}^{C\left(F\right)}{\eta }_k\left(F\right){\varepsilon }_k\right)\frac{1}{Q},$$ (3)

where β = 1/RT. Calculating Q is a formidable task due to the astronomical number of graph-rigidity calculations on all accessible mechanical frameworks. Nevertheless, the most probable state (or competitive states across a first-order transition) dominates the total contribution of the sum. Hence, only a tiny fraction of frameworks have appreciable contribution to the partition function, and characterize physical observables. For this reason, a template structure is used to define fluctuating interactions, N_f, that are allowed to break and form independently to create a subensemble of 2^N_f accessible frameworks. The native structure is appropriate to use as a template for describing protein stability and the folding/unfolding process (25). Using this native state ensemble, efficient computational methods were developed to calculate Q accurately (29,35). With phenomenological parameters, the DCM robustly reproduces excess heat capacity curves for protein folding (36). In addition, myriad applications involving studies of protein stability, flexibility, and their relationships lead to successful comparison with experiments (37–42).

Despite demonstrated utility of the DCM, an important question is whether the lowest upper-bound estimate for conformational entropy provides sufficient accuracy to predict protein stability. This concern is warranted because the model requires fitting parameters, similar to how the Lifson and Roig model (16) is applied to the helix-coil transition. However, this concern is mitigated by the robustness of the fitting parameters across a diverse set of systems. Moreover, by comparing to an exact geometry-based rigidity calculation (43) , it was shown that the key approximation involving the lowest upper bound estimate for conformational entropy involves systematic errors that are compensated by transferable parameters. In short, the DCM captures essential mechanisms of cooperativity, and it is not simply a matter of curve fitting.

Maxwell Counting

In previous works the approach described above was shown to be quantitatively robust in modeling folding cooperativity across a variety of polypeptide and protein length scales, including: the α-helix/coil transition (27,29,44), the β-turn/coil transition (45), and folding in globular protein structures (35,36). However, due to varying scope, these investigations decomposed molecular structure into mechanical frameworks differently, and used different methods to calculate the partition function. For example, a transfer matrix method was developed for the α-helix/coil transition due to its one-dimensional character (29), whereas a hybrid method combining mean-field theory with Monte Carlo sampling was developed for three-dimensional protein structures (35).

The process of characterizing network rigidity is greatly simplified within the McDCM because its mean-field character allows J to be determined by Maxwell counting (26) by replacing Eq. 2 with the formula

$$J=\min \left(3A-6-C,0\right),$$ (4)

where d = 3 reflects three-dimensional space. The meaning of Eq. 4 is that all constraints are assumed to be independent until the entire molecular structure is globally rigid, at which point all further constraints are redundant. Consequently, the number of independent DOF within the network is a decreasing linear function in the number of constraints, C, present in the network until the number of internal DOF is zero, as shown in Fig. 1 A. We define the Maxwell level, M, as the minimum value of C that rigidifies the network corresponding to when J = 0 and C_r = 0. The network is flexible when C < M, just rigid at C = M, and overconstrained when C > M. When the network is overconstrained, the number of redundant constraints is given as C_r = C – M. All the constraints that are recursively added one at a time to the network before the Maxwell level is reached are independent, whereas the constraints added thereafter are redundant.

Ignoring local constraint density fluctuations, Maxwell counting approximates the structure as globally flexible or globally rigid, rendering the graph-rigidity calculation into a counting exercise. Combining the preferential rank ordering of entropies, and the Maxwell level as a global criterion for when constraints are independent (flexible state) or redundant (rigid state), the concept of an entropy spectrum defined by accessible {γ_k}, where the indexing is such that γ_k ≥ γ_k+1 for all interactions proves convenient (27). The McDCM is translated into a process that fills entropy levels within a spectrum from bottom to top as constraints are added. With the entropy spectrum and constraint filling procedure, a transfer matrix method to calculate Q for arbitrary molecular geometries becomes possible.

Transfer Matrix Method

The partition function for a molecular system with N_f number of fluctuating interactions can be calculated exactly using a transfer matrix method within the McDCM. To this end, we define the statistical weights, B_k, for independent constraints, and b_k, for redundant constraints, based on the Boltzmann factors given by

$$B_k=\exp \left(-\beta {\varepsilon }_k-{\gamma }_k\right)\mathrm{and}{b}_k=\exp \left(-\beta {\varepsilon }_k\right),$$ (5)

where redundant constraints do not have an entropic penalty. We also introduce the generating function

$$f_{gen}=\prod _{k=1}^{N_f}\left(1+B_k\right),$$ (6)

where 1 represents no constraint. For one distance constraint per interaction, f_gen expands into 2^N_f terms, each of which is a product of C statistical weights where 0 ≤ C ≤ N_f. For a network with N_f ≤ M, all constraints are independent, and Q = f_gen. For an overconstrained network with N_f > M, any term with C > M will contain redundant constraints, causing Q ≠ f_gen.

To obtain Q, nonadditivity in entropy is accounted for by replacing B_k → b_k for all the constraints added beyond the Maxwell level. Fig. 2 illustrates the procedure for a network with three fluctuating interactions (i.e., N_f = 3), and thus Q will consist of eight terms. The number of B_k → b_k substitutions in f_gen increases exponentially as a function of C_r. The transfer matrix method facilitates exact summation over all terms in the partition function in ∼(N_f)² operations (vs. ∼ 2^N_f).

Figure 2.

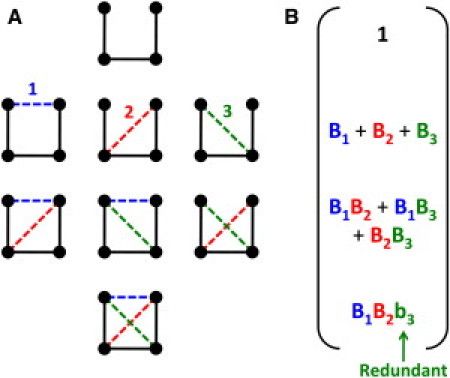
Schematic calculation of the partition function for a two-dimensional four-atom system. (A) The system includes three quenched (solid lines) and N_f = 3 fluctuating (dashed lines) constraints with entropies γ₁ > γ₂ > γ₃. Labels for the fluctuating constraints are provided. All 2³ frameworks are accessible microstates. (B) Statistical weights defining the eight terms in Q are grouped into four rows indicating 0, 1, 2, or 3 fluctuating constraints are present. Summing over all components in the macrostate vector gives Q. As indicated, the maximally interacting microstate has one redundant constraint, whereas in this example all other constraints are independent.

Three possible cases can occur when the k^th constraint is considered; the constraint is 1), not present, or when the constraint is present, then it is 2), independent or it is 3), redundant. To generate all three cases, a transfer matrix, T_k, is constructed as

$${\mathbf{T}}_k=1+{\mathbf{W}}_k,$$ (7)

where 1 is the unit matrix. The matrix, W_k, is sparse with nonzero statistical weights that are offset below the diagonal. It is useful to work within a subspace defined by fluctuating constraints of dimension D_f. For one distance constraint per interaction, the dimension of the subspace is D_f = N_f + 1. In the example shown in Fig. 2, D_f = 4, M = 2, and the macrostate vector is generated using the matrices

$$1=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\text{and}{\mathbf{W}}_k=\left(\begin{array}{cccc}0& 0& 0& 0\\ B_k& 0& 0& 0\\ 0& B_k& 0& 0\\ 0& 0& b_k& 0\end{array}\right),$$ (8)

where k = 1, 2, 3 labels the constraints with γ₁ > γ₂ > γ₃. The B_k weights defined in Eq. 5 appear along the offset diagonal in W_k until M is reached; thereafter the constraints are redundant with b_k weights. Subsequently, the partition function for the example in Fig. 2 is given as

$$Q=\left(1,1,1,1\right){\mathbf{T}}_3{\mathbf{T}}_2{\mathbf{T}}_1\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right),$$ (9)

where the multiplication order of the transfer matrix for k^th constraint inherits its entropy-rank ordering. When a distance constraint is added to a network with C constraints, the new partition function, Q(C + 1), is related to the current partition function, Q(C), through matrix multiplication that accounts for all possible ways that C can increment by 1.

In general, an interaction may consist of more than one distance constraint. In this case, the transfer matrix represents an interaction rather than a single distance constraint. Then, when the i^th interaction forms, associated with c_i distance constraints, the transfer matrix, T_i, is employed to relate the partition function Q(C + c_i) relative to the current partition function Q(C). For a general molecular structure with N_f fluctuating interactions, the partition function is given as

$$Q=\langle l|\prod _{i=1}^{N_f}{\mathbf{T}}_i|r\rangle ,$$ (10)

where all entries in the left row vector, 〈l|, are one, and for the right column vector, |r〉, all entries are zero, except the first entry is one. The i^th interaction has a formation energy, ɛ_i, and each independent distance constraint contributes the same maximal entropy loss, γ_i. The product of N_f number of T_i transfer matrices are ordered such that γ_i > γ_i+1. To fill the appropriate levels of the entropy spectrum by constraint filling, the matrix elements of W_i are given as

$$\langle j|{\mathbf{W}}_i|k\rangle ={\delta }_{j-c_i,k}\exp \left(-\beta {\varepsilon }_i\right)\exp \left(-\left[\min \left(\max \left(M-k,0\right),c_i\right)\right]{\gamma }_i\right),$$ (11)

where δ_{k′, k} is the Krönecker delta. Again W_i is sparse, where all matrix elements are zero except those that increase the number of constraints in the system by c_i when the interaction forms. If C ≤ M − c_i, then all the distance constraints are independent. When the number of constraints within the network is within c_i constraints from the Maxwell level, it can happen that one or more of these constraints will be redundant. The second exponential term in Eq. 11. accounts for all the possible ways the total number of distance constraints can exceed the Maxwell level. The dimension of the state space (length of the macrostate vector) is given by

$$D_f=1+{\sum }_i{c}_i\text{.}$$

The calculation of Q for a 1000-residue protein (i.e., D_F ∼ 10⁴) takes just a fraction of a second.

Results and Discussion

Here, the McDCM uses effective parameters to keep it identical to the model employed in Vorov et al. (27) so that transferability of parameters between polypeptides and proteins can be assessed. Namely, 1), native torsions and 2), H-bonds are modeled. In the McDCM, H-bonds include salt bridges. Packing is indirectly modeled through the locking of torsion angles into a native conformation that reduces the available phase space. Native torsions are modeled as one distance constraint with degenerate parameters (ɛ_nt, γ_nt). H-bonds are modeled as three distance constraints with degenerate parameters (ɛ_hb, γ_hb). The physical regime corresponds to γ_hb > γ_nt. These four effective parameters, {ɛ_nt, γ_nt, ɛ_hb, γ_hb}, represent the smallest number of fitting parameters that are found to robustly fit to excess heat capacity curves. The coupling between these two modes of competing interactions suggest there may be a scaling law that controls their relative numbers in structural motifs as a function of number of residues.

Scaling laws

The free chain reference state has the maximum number of DOF. Formation of native torsions or H-bonds will lower energy, and reduce conformational entropy as the number of DOF decrease. Assuming all native torsion interactions are present, but no H-bonds are formed, the structure will be marginally rigid. Adding native H-bonds to this state will overconstrain the network. The balance between the number of constraints and DOF determines, respectively, the parameters D_f and M. For polypeptides, the number of native (backbone) H-bonds is related to the number of residues, N_r, by N_hb = N_r − 4, and the number of backbone ϕ and ψ torsions is given by N_nt = 2N_r. This gives D_f ≈ 5N_r and M ≈ 0.40 D_f. For the α-helix geometry, side-chain interactions are not included because they do not substantially participate in cross-linking interactions with limited side-chain packing.

Conversely, side-chain interactions must be considered in proteins due to the native structure's tight atomic packing. From sequence alone, M is readily determined as the number of free dihedral angles assuming no cross-linking, M = N_nt, which now includes side-chain dihedrals. It is found that N_nt ∼ 4.8 N_r for each of the four proteins analyzed here, and generally across globular proteins. This scaling estimate is then used as input to the McDCM. Similarly, the number of H-bonds within the native state scales as N_hb ≈ 1/3 M, where the proportionality constant of 1/3 appears in globular protein structures. These relationships lead to D_f ≈ 9 N_r and M ≈ 0.53 D_f. That is, the Maxwell level, compared to the total number of possible native distance constraints, is approximately half-filling in both proteins and polypeptides.

McDCM parameters

The McDCM incorporates the scaling relations found above to set the subspace dimension and the Maxwell level. The only information about the protein that determines the transfer matrix is the number of residues, and the specific type of structural motif (i.e., α-helix or globular protein). The McDCM is applied to four single-domain proteins. Model parameters are determined by fitting to differential scanning calorimetry C_p data (46–50) shown in Fig. 3 A. The McDCM reproduces the C_p curves markedly well only when the fitting parameters have physically realistic values, although the parameters are not expected to be transferable. Nevertheless, parameter values are consistent across the four considered proteins (compare to Table 1 and Fig. S1 in the Supporting Material). Including our prior results on four polypeptides that undergo the α-helix to coil transition (27), the three parameters {ɛ_nt, γ_nt, γ_hb} are seen to be qualitatively conserved.

Figure 3.

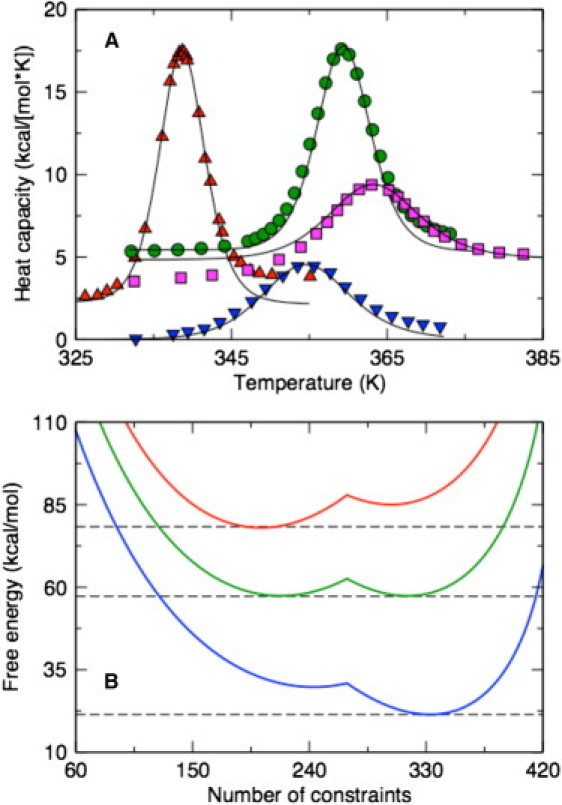
(A) The McDCM (solid lines) reproduce experimental C_p curves across a diverse set of proteins (up-triangles, lysozyme; circles, thioredoxin; squares, ubiquitin; and down-triangles, Protein G). (B) The free energy landscapes for protein G (top to bottom) at T = 310, 355, and 391 K. At T_m = 355 K, the native and disordered state basins are competitive, whereas at T¹T_m, one state is clearly more probable than the other. Dashed lines are provided to guide the eye.

Table 1.

Summary data for the four considered proteins

Protein	Nres	Nhb	Nnt	ɛhb	ɛnt	γhb	γnt
Protein G	56	269	90	2.10	0.70	1.15	0.59
Ubiquitin	76	365	122	2.30	0.78	1.05	0.49
Thioredoxin	108	518	173	2.15	0.42	1.20	0.42
Lysozyme	130	624	208	2.17	0.56	1.25	0.40
Percent deviation				3.9	25.8	7.3	18.1

Energy parameters have units of kcal/mol, and entropy parameters are dimensionless. The last row gives the percent deviation in the model parameters.

As expected, the least transferable parameter is ɛ_hb, because it reflects an overall increase in residue solvent accessibility in a helical polypeptide compared to a protein. This effective H-bond energy simultaneously accounts for the stability gained upon formation of an intramolecular H-bond, ɛ_i, and the cost of breaking competing interactions with solvent, u. As such, the net H-bond energy is given by ɛ_hb = ɛ_i − u. The decrease in ɛ_hb between polypeptides and proteins is explained by differences within u. In polypeptides and protein positions near the solvent interface, the stability gained from an intramolecular H-bond is similar to the energetic cost of breaking solvent H-bonds (51), meaning ɛ_i ∼ u. However, within the core, compensating H-bonds to solvent are unlikely to occur. Consequently, the average solvent H-bond energy is larger in protein structures, u_prot > u_poly, as the double-sided arrow in Fig. S1 shows.

Two-state behavior from nonadditivity

Although the fit to experimental C_p curves parameterize the model (compare to Fig. 3 A), this result is not a demonstration of folding cooperativity. Rather, two-state behavior in the free energy landscape is required to show coexistence of the folded and unfolded states near the melting temperature, T_m. As an exemplar case, the free energy of protein G is shown in Fig. 3 B as a function of number of constraints formed, where G(C) = −RT ln [Q(C)] and Q(C) is an entry in the macrostate vector component as Fig. 2 B depicts. At low temperature, the folded state is stabilized by an increase in the number of constraints by lowering energy. At high temperature, the entropy cost of forming interactions surpasses the energetic loss, leading to an unfolded conformational state. One caveat is that if the cross links are too weak they will not reduce atomic motions appreciably, and folding cooperativity can be substantially reduced or eliminated. Thus, the strength of an atomic interaction is important, where (ɛ_i, γ_i) represents (depth, width) of a potential energy well. Due to the narrow range of physically realistic parameter values, the most interesting aspects of folding cooperativity derive from properties of constraint networks.

Nonadditivity in conformational entropy occurs because of two options in constraint topology. Either the network is globally flexible with all independent constraints, or it is globally rigid when the number of constraints exceeds the Maxwell level. As previously shown, the McDCM cannot exhibit two-state behavior when there is an insufficient number of cross links for a rigidity transition to take place (27). The empirical scaling laws described above ensure a sufficient number of constraints to facilitate a rigidity transition from a globally floppy to rigid network. In particular, the ratio $M/N_f\approx 0.5$ indicates that proteins and polypeptides are well balanced in the number of native distance constraints for cooperative behavior. As a mathematical result, assuming M is fixed, with N_nt and N_hb as independent variables, the transfer matrix yields maximum cooperativity at $M/N_f=1/2$, and as shown previously for the helix-coil transition (27), folding cooperativity is lost under the extreme conditions where $M/N_f\to 1$ or $M/N_f\to 0$. Therefore, the degree of nonadditivity is linked to the relationship between M and N_f. However, M and N_f cannot be independently varied, because the number of fluctuating constraints, N_f, depends on the size of the polypeptide or protein. Recall that

$$N_f=N_{nt}+3N_{hb},$$

where N_nt is fixed based on the size of the protein, and M ≡ N_nt. Adjusting $M/N_f$ can be achieved by changing the number of native H-bonds. Because a native structure supports more H-bonds, the ratio $M/N_f$ will decrease. However, even in the limit that $M/N_f\to 0$, not all constraints will be redundant, because at least M number of constraints will always be independent.

Interestingly, $M/N_f\approx 0.40$ for the α-helix and $M/N_f\approx 0.53$ for globular proteins are markedly close to 0.5 for maximum cooperativity. As $M/N_f$ deviates away from empirically observed values, McDCM cannot reproduce C_p with physically realistic parameters, if at all. These results suggest that the nature of H-bond patterns within proteins and polypeptides have evolved to favor a high-degree of cooperativity through structural characteristics that support an optimal balance between constraints and DOF.

For the same size protein (fixed M), it is interesting to consider what happens when the number of H-bonds in the native structure deviates from the observed scaling law. As discussed above, the ratio $M/N_f$ will depend on the number of native H-bonds. Using the fixed parameters in Table 1, Fig. 4 demonstrates that the free energy barrier between the native and unfolded basins decreases as $M/N_f$ increases (lower number of H-bonds), and eventually the two basins gradually merge together until no transition occurs. Of course, the C_p curves do not match experiment when we deviate from the empirically determined ratio. Conversely, as more native H-bonds are added ($M/N_f\to 0$), the free energy barrier increases as the two basins are separated further. At some point, an intermediate state forms (compare to insets in Fig. 4), where multiphasic behavior can appear by reducing the ratio $M/N_f$ by as little as 15%. However, upon initial onset of the intermediate state, the barrier flattens and the transition quantitatively responds as a two-state folding process. This result is consistent with observation that single domain globular proteins are typically two-state folders.

Figure 4.

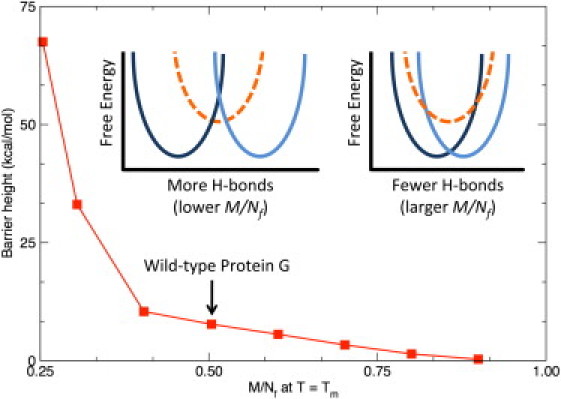
Using Protein G as an example, the straddling barrier height is plotted versus $M/N_f$ at the respective T_m for each. (Insets) Adding H-bonds (smaller values of $M/N_f$) separates the basins, thus increasing the barrier height. In addition to the native and unfolded basins, additional states (dashed) are possible, but their probabilities are generally zero; yet they do emerge when the barrier height is increased as $M/N_f\to 0$. Conversely, the barrier height is suppressed as $M/N_f\to 1$ because the basins share greater overlap, transforming into a continuous transition, and then eventually no transition without any H-bonds. (Highlighted) The wild-type value ($M/N_f=0.502$) for Protein G.

There are other important features in the free energy landscapes. Unfolded proteins are not predicted to be random coils, meaning C ≠ 0 within the unfolded basin. For example, protein G in the unfolded state at T_m has ∼220 less DOF than the reference coil state. Similarly, proteins are predicted to have many native interactions broken in the folded state. Both ΔG and ΔG^‡ values that occur at intermediate temperatures are appropriately small compared to the overall scale. These results underscore the importance of fluctuations in the number of constraints, and suggest that nonadditivity in conformational entropy upon molecular rigidification is a universal mechanism affecting folding cooperativity. Although solvation effects contribute to the folding process (i.e., hydrophobic collapse), it is a mechanism that does not depend on the formation of specific intramolecular interactions characteristic of atomic structure. Conversely, molecular rigidification explains two-state behavior in both polypeptide and protein systems related to the dramatic loss in conformational entropy.

The McDCM in perspective

The McDCM captures the essential physics of folding cooperativity, and due to its simplicity, it takes less than a second of CPU-time for a 1000-residue protein. Improvements can be made by using energy/entropy parameters that depend on local environments in the template structure, use more than one template structure, and/or generalize the transfer matrix to couple constraint density to solvent exposure. In related published works (35–42), the more accurate minimal DCM (mDCM) that employs graph-rigidity algorithms has been extensively used. Before closing, results from the McDCM are compared to those from mDCM, and the need for an extended DCM is discussed.

The most severe approximation in the McDCM is that distance constraints are uniformly distributed within molecular structure. For this discussion, assume favorable interactions readily lower energy and conformational entropy. At low constraint density, the drop in energy from favorable interactions cannot overcome the concomitant drop in conformational entropy. At high constraint density, a large decrease in energy occurs without a concomitant drop in conformational entropy due to redundancy. This means that nucleation of a rigid structure occurs when there is sufficient number of redundant constraints. Separation of regions of low and high constraint density promotes folding cooperativity as an emergent property caused by enthalpy-entropy compensation among molecular interactions that are coupled through network rigidity. In proteins, secondary structure is rich in constraints whereas loops will have lower than average constraint density. The same enthalpy-entropy compensation mechanism applies in the heterogeneously distributed regions that are flexible or rigid, leading to altered properties of the transition state (36). What significance does variation in atomic-interaction effectiveness and fluctuations in spatial constraint density play?

The McDCM predicts the rigidity transition defined by the Maxwell level, M, to coincide with the thermodynamic transition state, and G_TS = −RT ln [Q(M)] is at the cusp that separates two free energy wells, as shown in Fig. 3 B for protein. Rader et al. (28) suggested that globular proteins exhibit this coincidence. The McDCM reveals that this coincidence occurs whenever there is nearly perfect two-state folding cooperativity. More generally, the rigidity transition and transition state do not coincide as we reported previously (35,36,40) because the size, shape, and locations of rigid clusters fluctuate within a protein as atomic interactions break and form due to thermal fluctuations. Fluctuations in rigid cluster size reach a maximum at the rigidity transition, similar to the peak in heat capacity that is used to define the melting temperature. The mDCM shows that heterogeneity in the effectiveness of atomic interactions and spatial variation in rigid and flexible regions affects the transition state barrier's height and location. In the mDCM, the rigidity transition can take place before or after the transition state as more distance constraints are added. Interestingly, the folded basin can occur before the rigidity transition (40), indicating that the mDCM allows a protein in its native state to have a flexible folding core. This latter effect has been observed experimentally (12).

A drawback of the McDCM is that detailed information about the rigid cluster decomposition and identification of regions of correlated motion is lost due to the mean field approximation. Nevertheless, it demonstrates that a critical aspect of modeling folding cooperativity is to account for nonadditivity in conformational entropy that links to flexibility and rigidity properties within molecular structure. Whereas the hydrophobic effect (52) in aqueous solution thermodynamically drives globular compaction, rigidification of molecular structure is a universal mechanism that thermodynamically drives self-organization in the folding process. Consequently, modeling only solvation effects yields an incomplete picture of folding cooperativity because it does not discriminate between specific and nonspecific (molten globule) collapse (53).

Due to elective simplifications, the McDCM and mDCM are also incomplete models because they implicitly model solvation effects using nontransferable phenomenological parameters. Although McDCM is an oversimplified version of mDCM, it is important because it highlights an essential mechanical mechanism generally ignored in free energy decomposition schemes. Going forward, network rigidity will be coupled with explicit solvation effects using a more sophisticated DCM that explicitly accounts for solvation, pH, hydrophobic effects, and rigidity (unpublished).

Conclusions

A transfer matrix method was developed to calculate the partition function of a DCM within a mean field approximation where molecular structure is described by uniform flexibility or rigidity characteristics. This approximation replaces the graph-rigidity algorithm by Maxwell constraint counting. Based on this simplification, an entropy spectrum is defined by the native state where entropy levels are occupied or unoccupied because distance constraints representing native interactions are present or not, respectively. This Maxwell counting DCM, referred to as McDCM, underscores the link between nonadditivity in conformational entropy to flexibility and rigidity in molecular structure. Moreover, this effect is unique in its ability to appropriately model cooperativity across length and complexity scales, as illustrated by the helix-coil and protein folding transitions, thus suggesting an important physical significance. For example, scaling laws are found that connect H-bond patterns observed in secondary structure to folding cooperativity. A ratio near 1:2 for the DOF in a coil state to maximum distance constraints in the native state will have a high fidelity two-state folding cooperativity. We suggest maintaining this balance is an evolutionary constraint that leads to the ubiquity of cooperativity.