Application of an extended equalization-cancellation model to speech intelligibility with spatially distributed maskers

Abstract

An extended version of the equalization-cancellation (EC) model of binaural processing is described and applied to speech intelligibility tasks in the presence of multiple maskers. The model incorporates time-varying jitters, both in time and amplitude, and implements the equalization and cancellation operations in each frequency band independently. The model is consistent with the original EC model in predicting tone-detection performance for a large set of configurations. When the model is applied to speech, the speech intelligibility index is used to predict speech intelligibility performance in a variety of conditions. Specific conditions addressed include different types of maskers, different numbers of maskers, and different spatial locations of maskers. Model predictions are compared with empirical measurements reported by Hawley et al. [J. Acoust. Soc. Am. 115, 833–843 (2004)] and by Marrone et al. [J. Acoust. Soc. Am. 124, 1146–1158 (2008)]. The model succeeds in predicting speech intelligibility performance when maskers are speech-shaped noise or broadband-modulated speech-shaped noise but fails when the maskers are speech or reversed speech.

INTRODUCTION

In everyday life, processing with two ears provides an improved analysis of the sound environment relative to either ear alone. This binaural advantage appears in a large number of circumstances, including the well-known binaural detection advantage for cases in which the target and masker have different interaural relationships. More generally, significant binaural advantages are observed when there are multiple sources, which are referred to as the “cocktail party effect” (Cherry, 1953). In such an environment, people can focus on an individual conversation with some effort while other conversations are going on simultaneously. The work presented in this paper aims to model human performance in a subset of these speech intelligibility tasks and investigate (1) how much binaural advantage can be predicted by an extended version of the equalization-cancellation (EC) model, and (2) what components of the model need to be further developed to improve the modeling of human speech perception.

In order to understand the binaural advantage, many experiments have been performed for a variety of listening tasks and numerous data sets have been collected (cf. review chapters by Durlach and Colburn, 1978; Bronkhorst, 2000; Stern and Trahiotis, 1996). These experiments include simple tone-detection tasks (e.g., Blodgett et al., 1962; Jeffress et al., 1962; Colburn and Durlach, 1965; Green, 1966; Rabiner et al., 1966) and more complicated speech-intelligibility tasks in various environments (e.g., Cherry, 1953; Hawley et al., 2004; Marrone et al., 2008). Several theoretical descriptions of binaural processing have been developed over the past half century in connection with this empirical work (cf. reviews by Colburn and Durlach, 1978; Colburn, 1995; Stern and Trahiotis, 1996). In a series of papers particularly relevant to the current study, Durlach developed the EC model (Durlach, 1963, 1972). With a relatively simple structure, the EC model predicts a large set of binaural masking level differences (BMLDs), where the BMLD is defined as the difference in the detection threshold between diotic and dichotic conditions.

Following the success of modeling efforts in simple tone-detection tasks, the models have been extended to interpret experimental data in speech intelligibility tasks. For example, Zurek (1992) used equations for the dependence of binaural thresholds from the modeling of Colburn (1977) together with the Articulation Index (ANSI, 1969) to predict the improvement in intelligibility when a speech signal is masked by a single noise masker in anechoic space. In particular, Zurek predicted the dependence of the intelligibility threshold on the angle of the masking noise (relative to the angle of the speech source) and found that predicted behavior matched available threshold measurements. Culling et al. (2004) used the EC model to interpret intelligibility performance in two experiments in a simulated anechoic environment involving multiple speech-shaped noise (SSN) maskers. In the first experiment, they measured binaural speech reception thresholds (SRTs) for target speech located straight ahead and masked by three noise maskers at different locations in a simulated anechoic environment. In the second experiment, they created diotic noise maskers and attenuated the noise spectrum level at each frequency in proportion to the observed binaural advantages in tonal masking data in the same environment. They found that the diotic performance in the second experiment was approximately the same as the dichotic performance in the first experiment. Even though there were no binaural advantages in the second experiment (since the straight-ahead speech source generated diotic target speech and the noise was diotic), the masker attenuation expected from the binaural advantages resulted in equivalent performance. This led to the conclusion that binaural speech-intelligibility benefits are predictable from narrowband detection benefits, even with multiple maskers. More recently, Beutelmann and Brand (2006) applied an extended EC model to predict performance in speech intelligibility tasks in several environments, ranging from anechoic space to a cafeteria hall, for both normal-hearing and hearing-impaired subjects. Their task involved a single noise masker presented at different azimuths with a speech target presented in front. Their model consisted of a gammatone filterbank, an independent EC process in each frequency band, a broadband signal resynthesis process, and the ANSI standard speech intelligibility index (SII) calculator. Internal noise was applied to parallel processing units so that each unit provided an SRT prediction. The final SRT prediction was then obtained by averaging the SRTs across all the units. Their model predicted human performance reasonably well for the conditions considered in their study, with an overall correlation coefficient of 0.95 between the empirical measurements and the predictions. Beutelmann et al. (2010) further extended this study to incorporate short-time strategies to predict the cases involving nonstationary interferers. Taken together, these previous studies have demonstrated that the BMLD data for tonal targets are fundamental and capture a great deal of the advantage that the binaural system affords in both detection tasks and speech-intelligibility tasks.

The present work describes an EC-based model with time-varying jitters and applied to a wide range of experiments. We consider speech intelligibility in situations where there are multiple interfering sounds (maskers) at different locations, as well as different types of interfering sounds. We compare the predictions of our model to the speech intelligibility data of Hawley et al. (2004) and Marrone et al. (2008).

This work differs from previous work both in the details of the model developed and the data to which the model is applied. One notable example is that this model uses time-varying jitters, which have not been proposed in any previous modeling work. Further discussion of these differences appears in later sections of this paper after the details of our model and the applications of our model have been presented.

The remainder of this paper is organized into three sections. Section 2 specifies in detail the assumptions for the EC model used in this paper. Section 3 applies the model to certain speech intelligibility data, after checking that its predictions for tone detection data are adequate. Finally, Sec. 4 presents a general discussion of the model, including suggestions for future work.

MODEL SPECIFICATION

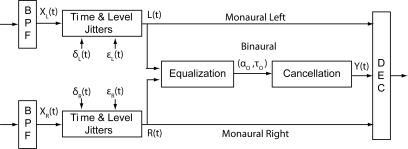
A block diagram of the EC model as used in this paper is shown in Fig. 1. The input signals on the left side of the figure are the acoustic inputs; bandpass peripheral filtering is applied to these inputs for each frequency band (the outputs of only one band are shown); time-varying jitters in both time delay and level are applied independently to each filter output; EC processing is applied in parallel with the monaural channels; and a final decision device (DEC) selects, for each frequency band, the signal with the best signal-to-noise ratio (SNR) (from the binaural and monaural pathways)1 and combines information across frequency bands.

Figure 1.

System diagram of the EC model used in this paper. Note that the processing of a single frequency band is shown, and that the subscript i, used in the text to distinguish individual bands, is omitted from the notation in this figure for ease of reading. As described in the text, the equalization parameters are chosen independently for each frequency band and held constant throughout the duration of the waveform. The time argument t for the jitter parameters indicates that the time and level jitters are time-varying (chosen independently for each frequency band and for each time sample).

Peripheral processing

The peripheral processing of the auditory system is simulated by a set of bandpass filters followed by random jitters. Since our primary intent is to model speech intelligibility performance, we followed the idea of Zurek (1992) to use the SII to make our predictions and choose the peripheral filters to be compatible with the ANSI standard. Specifically, the filterbank includes 18, one-third-octave eighth-order Butterworth filters, with the center frequencies ranging from 160 Hz to 8 kHz spaced uniformly on a logarithmic scale. In order to explore the sensitivity of the modeling to the choice of peripheral filters, the predicted thresholds for tones were calculated using two sets of filterbanks, the Butterworth filterbank and the gammatone filterbank implemented using the matlab Auditory Toolbox (Slaney, 1998). After comparing model performance in tone detection using both types of filterbank, we believe gammatone filters are a better choice, especially for frequencies below 300 Hz; however, one-third octave Butterworth filters are adequate substitutes for gammatone filters, especially within the frequency range of interest for speech.2

After the filterbank, the output of every frequency band is jittered independently on the left and right sides. The jitter is assumed to be independent for every frequency band. Specifically, the outputs of the ith filter pair, X_Li(t) and X_Ri(t), are jittered in both time and level, with jitter values denoted as δ_Li(t) and ε_Li(t) for the left ear and δ_Ri(t) and ε_Ri(t) for the right ear, so that the jittered waveforms are given by

$$\begin{array}{l}{L}_i(t)=(1+{ò}_{Li}(t))X_{Li}(t-{\delta }_{Li}(t)),\text{and}\\ R_i(t)=(1+{ò}_{Ri}(t))X_{Ri}(t-{\delta }_{Ri}(t)).\end{array}$$ (1)

The jitter is chosen independently for every time sample of the waveform.3 As in the original EC model, the time and amplitude jitters are characterized as zero-mean, Gaussian random variables with standard deviations that are independent of frequency. The values of these standard deviations (for all times, all frequency bands, and all conditions) were assumed to be the same as those chosen by Durlach (1963, 1972). In particular, the standard deviation σ_δ of the zero-mean time jitter is equal to 105 μs,4 and the standard deviation σ_ε of the zero-mean amplitude jitter is equal to 0.25. Note that the jittered outputs, L_i(t) and R_i(t), are used for both the binaural and monaural pathways, as assumed previously (e.g., Green, 1966). For each frequency band, the jittered signals for the monaural pathways are sent directly to the DEC whereas the jittered signals for the binaural pathway are further processed through the equalization and cancellation system.

Binaural processing: Equalization and cancellation operations

In the computation of the binaural (EC) output, it is assumed that the processor in every frequency band uses a pair of equalization parameters, τ_oi and α_oi, to minimize the residual energy of the masker after cancellation in that band, where τ_oi is the optimal interaural time equalization parameter and α_oi is the optimal interaural amplitude equalization parameter in the ith frequency band. Both parameters are chosen independently for each frequency band and assumed to be constant throughout the duration of the waveform. These assumptions are generally consistent with the modified EC-models of Culling and Summerfield (1995) and of Beutelmann and Brand (2006) and are consistent with the experimental results of Akeroyd (2004).

It is assumed that the listeners implicitly know the best choice of the equalization parameters, either from a priori information about the noise or by searching all possible equalization parameters and choosing the best, consistent with Durlach (1972). For example, a priori information may be obtained if, at the beginning of the experiment, the experimenter chooses to present the listeners with the noise alone. When a priori information of the interaural parameters of the noise is not available, listeners may determine these parameters by scanning across all choices and determining which choice leads to the perception of a tone (when the target is present in the stimulus) or silence (when the target is not present), consistent with the conclusion of Bernstein and Trahiotis (1997). The strategy that listeners use in the tone detection or speech intelligibility tasks is still an open question. The predictions here assume an optimal choice of equalization parameters for each band without specifying how they are chosen.

With respect to the interaural time equalization, it is assumed here, consistent with assumptions in Durlach (1972), that the repertoire of equalization transformations is limited to a fixed range of interaural time delays. More specifically, it is assumed that the available interaural time delays in each frequency band are limited to values less than or equal to a half cycle of the center frequency of the band.

With respect to the interaural amplitude equalization, the assumption that α_o is adjustable is different than the assumption in the model described in Durlach (1972), where it was assumed that interaural amplitude is not equalized. As discussed further below, both of these assumptions are oversimplifications and are contradicted by some of the available data; however, the simplicity of these assumptions is advantageous for understanding the tradeoffs and alternatives.

Combining all these assumptions, one can write the residual noise energy of the masker in each band after cancellation by τ and α as follows (with the subscript i omitted for simplicity):

$$\begin{array}{c}{E}_{NY}(\tau ,\alpha )={\int }_0^T{[{\alpha }^{-\frac{1}{2}}{n}_L(t+\frac{\tau }{2})-{\alpha }^{\frac{1}{2}}{n}_R(t-\frac{\tau }{2})]}^2\mathrm{d}t\\ ={\alpha }^{-1}{\int }_0^T{n}_L^2(t+\frac{\tau }{2})\mathrm{d}t+\alpha {\int }_0^T{n}_R^2(t-\frac{\tau }{2})\mathrm{d}t-2{\int }_0^T{n}_L(t+\frac{\tau }{2})n_R(t-\frac{\tau }{2})\mathrm{d}t\\ ={\alpha }^{-1}{E}_{NL}+\alpha E_{NR}-2\rho (\tau )\sqrt{E_{NL}{E}_{NR}}.\end{array}$$ (2)

In these equations, the variables n_L and n_R represent the jittered masker for the left ear and right ear, respectively; E_NL, E_NR, and E_NY represent the energies of n_L, n_R and the residual masker over a burst of duration T, respectively; and ρ(τ) represents the normalized cross-correlation function of the jittered masker for the left ear and right ear

$$\rho (\tau )=\frac{{\int }_0^T{n}_L(t)n_R(t-\tau )\mathrm{d}t}{\sqrt{{\int }_0^T{n}_L^2(t)\mathrm{d}t}\sqrt{{\int }_0^T{n}_R^2(t)\mathrm{d}t}}=\frac{{\int }_0^T{n}_L(t)n_R(t-\tau )\mathrm{d}t}{\sqrt{E_{NL}{E}_{NR}}}.$$ (3)

Note that ρ(τ) always has a magnitude less than unity, i.e., |ρ(τ)| ≤ 1.

With a_N defined by

$$a_N=\sqrt{\frac{E_{NL}}{E_{NR}}},$$ (4)

the residual noise energy E_NY of the EC output can be written as

$$E_{NY}(\tau ,\alpha )=[\frac{a_N^2}{\alpha }+\alpha -2\rho (\tau )a_N]E_{NR}.$$ (5)

To determine the optimal values of the internal parameters, τ_o and α_o, i.e., the values that minimize the residual noise energy, it is easy to verify that the optimal internal parameter τ_o should be the value of τ that maximizes ρ(τ),

$${\tau }_o=\underset{\tau }{\text{argmax}}\{\rho (\tau )\},\left|\tau \right|<\frac{\pi }{{\omega }_0},$$ (6)

and the optimal internal parameter α_o is the value of α that minimizes $(a_N^2∕\alpha )+\alpha$, i.e.,

$${\alpha }_o=a_N.$$ (7)

With these optimal values, the minimum output noise energy is given by

$$\underset{\tau ,\alpha }{\min \hspace{0.17em}}\}{E}_{NY}(\tau ,\alpha )\}=E_{NY}({\tau }_o,a_N)=2(1-\rho ({\tau }_o))a_N{E}_{NR}=2(1-\rho {\int }_{\max }^{})\sqrt{E_{NL}{E}_{NR}},$$ (8)

where ρ_max denotes the maximum of ρ(τ).

Note that the effects of the internal noise are only implicit in these equations. The time-varying internal jitters cannot be fully compensated for by the equalization parameters because the equalization parameters are assumed to be constant throughout the duration of the waveform. The jitter has a significant impact on the value of ρ(τ), so that ρ(τ) is reduced from unity even when the input noise is diotic and requires no equalization transformation. Similarly, the jitter also influences the values of E_NL and E_NR.

In the cancellation step, the output of the ith band, Y_i(t), is generated by subtracting the signals equalized using the optimal internal parameters, resulting in the equation

$$Y_i(t)={\alpha }_o^{-\frac{1}{2}}{L}_i(t+\frac{{\tau }_o}{2})-{\alpha }_o^{\frac{1}{2}}{R}_i(t-\frac{{\tau }_o}{2}),$$ (9)

where τ_o and α_o also vary from band to band. Note that the processing is structured so that signals from both ears are transformed symmetrically in order to achieve left-right symmetry, i.e., if the left ear and right ear inputs are switched, the cancellation output remains the same.

Decision device operation

The DEC in the model receives all the waveforms from both the monaural and binaural pathways as inputs. It selects the input that provides the best SNR in each frequency band, and then further processes the resulting cross-frequency array, in a manner depending on the task, to provide the final decision.

For tone detection tasks, the DEC only operates on the frequency band of the target tone, and the model output leads directly to the BMLD prediction. Consistent with Durlach (1963), the BMLD is calculated by taking the difference of the SNR (in decibels) between the binaural pathway and the better-ear monaural pathway. If the SNR on the binaural pathway is lower than that in one of the monaural pathways, i.e., if binaural performance is worse than monaural performance, the BMLD is predicted to be 0 dB.

For speech intelligibility tasks, the DEC combines information from all the frequency bands. The SRT, defined as the level corresponding to 50% correct, is calculated using SII-based procedures. Specifically, the SII value is calculated using a linear weighted combination of the SNRs between −15 and +15 dB from all the frequency bands, with the weights given by ANSI S3.5 (1997). The final SRT output is calculated from the SII value, as specified in the next section.

Computational methods

The processing outlined above, including the time-varying jitters in each frequency band and the EC operation, was implemented in matlab. The temporal sequences of values for the time and amplitude jitters were chosen for each trial, and multiple trials were used to generate threshold values, from which means and standard deviations were computed. All waveforms, including tones, noise maskers, and speech sentences, were sampled at 20 kHz. The tone waveforms were generated digitally with a length of 2.5 s, and the speech waveforms were randomly chosen from the Harvard IEEE sentences (Rothauser et al., 1969), consistent with Hawley et al. (2004), or from the coordinate response matrix (CRM) corpus (Bolia et al., 2000), consistent with Marrone et al. (2008). Time and amplitude jitters were generated by a Gaussian random generator and applied to each sample of the waveform in each frequency band independently. More specifically, each sample of the jittered waveform was determined by taking a sample of the unjittered waveform in its neighborhood according to the time jitter, and then scaling it by the amplitude jitter, as described in Eq. 1. The time jitters were rounded to the nearest integer multiple of the sampling period (50 μs) to avoid interpolation. After jittering, optimal equalization parameters were calculated from the noise-alone waveforms, according to Eqs. 6, 7, separately for each frequency band on that trial. The optimal time equalization parameter, τ_o, was found by searching for the delay τ that gave the maximum of the normalized cross-correlation, ρ(τ), within a cycle in that band; the optimal amplitude equalization parameter, α_o, was calculated by taking the square root of the energy ratio for the jittered maskers. The optimal equalization parameters were kept constant over the whole duration of the waveform, so they could not fully compensate for the time-varying internal jitters. After the equalization step, the cancellation step was implemented according to Eq. 9 using the optimal equalization parameters found previously. Finally, both the cancellation output from the binaural pathway and the jittered waveforms from the monaural pathways were sent to the DEC.

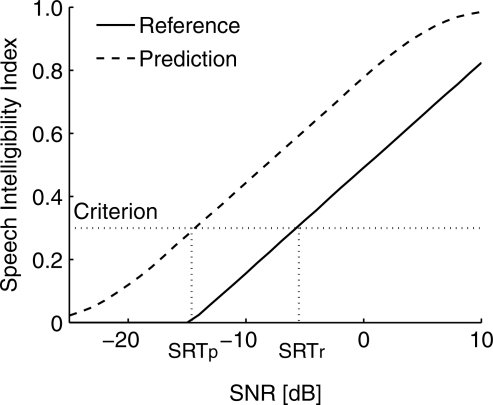
When the model was applied to speech intelligibility tasks, with maskers in different spatial locations relative to the straight-ahead target, the criterion value for the SII was chosen for a specific type and number of maskers to match the reference condition and used to predict all other spatial conditions with the same type and number of maskers presented at different locations. The reference condition was taken by default to be the condition in which the target and masker(s) were co-located in front. For example, Fig. 2 shows two SNR-SII curves calculated from the model, one for the reference condition and one for a test condition. The criterion was chosen such that the SRT of the reference condition matched the empirical data, and this criterion value was used to find the SRT of the prediction condition. With this approach, the SII criterion is the only free parameter, and, as is well known, its value depends on speech materials, environments, and the difficulty of the speech task (Kryter, 1962). The underlying assumption is that, for a specific set of target speech materials, a specific type of masker, and a specific experimental protocol, the same SII value gives the same performance.

Figure 2.

Example SII-SNR calculations. The solid line shows SII as a function of SNR for the reference condition, and the dashed line shows the SII for another condition. Since the SRT of the reference condition, denoted as SRT_r, is specified by the data, the criterion is determined and can be used to predict the SRT for the other condition, denoted as SRT_p.

PREDICTIONS FOR PSYCHOACOUSTIC DATA

In this section, the predictions of the model outlined in Sec. 2 are presented for speech intelligibility tasks. We consider tasks in which the number of maskers may be greater than one, the masking sources may be located at various azimuths relative to the listener’s head, and the maskers may be various types of noises or speech. In addition, in order to test our methods for deriving predictions, results for some classic tone-in-noise detection cases are considered prior to consideration of the speech-intelligibility cases.

Detection of a tonal target in a background consisting of a single noise source

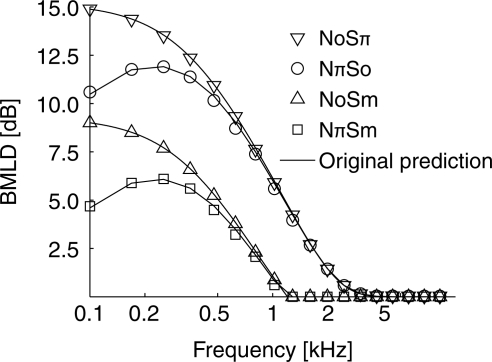
In Fig. 3, predictions from the current model (calculated using the computational methods described above) are compared with Durlach’s theoretical predictions (Durlach, 1972) for the four basic configurations N_oS_π, N_πS_o, N_oS_m, and N_πS_m. (Consistent with traditional notation, the symbols N and S denote the noise masker and the tonal-signal target, respectively; the subscript o or π denote the interaural phase, and the subscript m stands for the monaural presentation to one ear only.) Each point shown in the figure is the mean of 100 repetitions of the computation with different samples of white Gaussian noise waveforms and different samples of time-varying jitters. Only the mean is provided in the figure because the standard error estimated from the 100 repetitions is less than 0.2 dB. This figure illustrates the consistency of our model predictions (symbols) with Durlach’s predictions (lines) for these basic configurations, and therefore, because Durlach’s predictions were found to be consistent with the data (e.g., see Durlach, 1972), with the data themselves.

Figure 3.

Model predictions for tone detection in white Gaussian noise for the cases N_oS_π, N_πS_o, N_oS_m, and N_πS_m, where N and S denote the noise masker and the tonal-signal target, respectively, the subscript o and π denote the interaural phase, and the subscript m stands for the monaural presentation to one ear only. The curves are the theoretical predictions made by Durlach (1972). Although model predictions (symbols) are mean values of simulations with random jitter, the standard errors are so small (about 0.2 dB) that the predicted values are essentially deterministic.

As indicated above, the purpose of the comparison shown in Fig. 3 is to increase confidence in the computational methods used to derive the predictions of speech intelligibility in complex environments described in Sec. 3B1. Note, however, that for the relatively simple case of detecting a tone in the background of a single white Gaussian noise masker, an analytic expression (approximation) of the BMLD predictions of our extended EC model, denoted B([a_S, τ_S] | [a_N, τ_N]), can be derived without the use of simulations. The derivation and comparisons to the predictions of Durlach (1972) for the tone-detection case are provided in a supplemental document.5

It should also be noted that the current model gives consistent predictions with the “Revised Model” of Durlach (1972) only when the level of the binaural masker is the same in both ears (i.e., a_N = 1), as in all of the cases considered in Fig. 3. When the masker level is not equal interaurally (a_N ≠ 1), the current model gives different predictions from the original predictions given by Durlach. This difference is caused by the assumption of level equalization in the current model. In the original model (Durlach, 1972), no such equalization was allowed. In general, neither of these approaches is adequate for predicting the observed dependence of the BMLD on the interaural level difference.6

Intelligibility of a speech source in multiple maskers

Model predictions for data from Hawley et al. (2004)

Hawley et al. (2004) measured the SRTs in a simulated anechoic space for a sentence masked by one, two, or three interferers at different locations for four types of interferers. The types of interferers included SSN, broadband-modulated speech-shaped noise (modulated SSN), speech, and reversed speech. Both the target speech and maskers were from the same male talker, and the measurements included SRTs for both binaural listening and monaural listening. We created the same experimental scenarios virtually. We convolved head-related impulse responses from the CIPIC database (Algazi et al., 2001) with different types of interferers and with speech sentences from the Harvard IEEE corpus, consistent with what Hawley and colleagues did in their experiments. These virtual stimuli were used as the input waveforms to the EC model simulations described above.

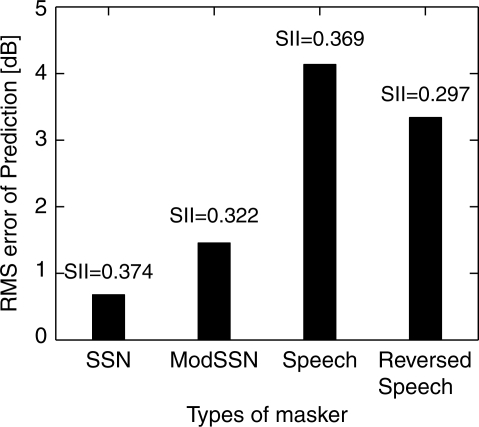
We used a single SII criterion parameter to fit the model prediction to the empirical measurements in Hawley et al. (2004) for all the cases, including binaural and monaural modes, different types of maskers, and different spatial locations. The best fit SII criterion for all cases is 0.331, and the RMS (root-mean-square) error for this overall prediction is 3.6 dB. The best fits and associated rms-errors for each type of masker are shown below in Fig. 4.

Figure 4.

The best fit SII value and associated rms-error for each type of masker.

As seen in this figure, the model can best interpret the data for the SSN and modulated SSN cases. When the maskers are speech or reversed speech, the performance of the model is substantially degraded. This trend in model performance is not too surprising because it is generally agreed that the perception of a speech target in speech-like maskers involves more than just simple energetic masking (Freyman et al., 2001; Durlach et al., 2003). In particular, different types of maskers probably cause different kinds and∕or amounts of cognitive confusion. Moreover, the interaction between different spatial attributes and different masker types may cause the cognitive load to diversify even more. For example, when the maskers are co-located in front with the target, speech maskers may cause much more cognitive load than SSN maskers do. In order to investigate the model performance in each condition carefully, we fitted different SII criteria separately for different numbers of maskers.

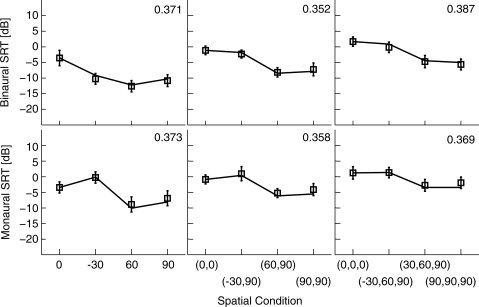
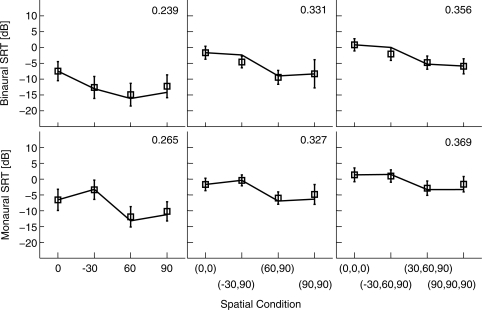
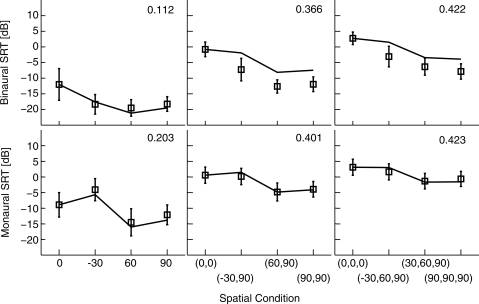
The model predictions are shown in Figs. 5678 along with the empirical measurements, with one figure for each of the four types of maskers considered (SSN, modulated SSN, speech, and reversed speech). Each of the four figures includes both binaural and monaural conditions (top row and bottom row, respectively), as well as conditions with different numbers of maskers (so that the three columns correspond to one, two, and three maskers, respectively). An SII criterion was fitted to each panel separately, as shown on the top right corner of the panel. The monaural conditions show the performances and predictions for the left ear; predictions are obtained by jittering the left ear waveforms on the monaural pathway and using them in the SII calculation with no binaural processing. In all conditions, the target speech was presented from the front (0°), and the maskers were presented from various locations, as indicated on the abscissa of each panel. For the one-interferer case (left column), the interferer was presented at 0°, −30°, 60°, or 90°; for the two-interferers case (middle column), the interferers were presented at (0°,0°), (−30°,90°), ( 60°,90°), or (90°,90°); for the three-interferers case (right column), the interferers were presented at (0°,0°,0°), (−30°,60°,90°), (30°,60°,90°), or (90°,90°,90°). Positive azimuths are to the listener’s right side, and negative azimuths are to the listener’s left side. Each prediction plotted is the mean of 100 repetitions (with different target and masker samples), and the standard error across repetitions, not shown here, is less than 0.1 dB.

Figure 5.

Simulated and measured SRTs for SSN masker cases in a simulated anechoic environment. Symbols are the measurements from Hawley et al. (2004), and the error bar is one standard error. The curves are the predictions of our model. No error bars are shown for the predictions because the standard errors are too small (less than 1 dB). The number in the upper right corner of each panel gives the value of the SII criterion used for that panel (chosen to match prediction and data for the reference case in that panel).

Figure 6.

As in Fig. 5, but for broadband modulated, SSN maskers.

Figure 7.

As in Figs. 5 and 6, but for speech maskers.

Figure 8.

As in Figs. 567, but for reversed-speech maskers.

In each panel, the SII criterion is chosen to match the prediction with the empirical data for the co-located case (plotted as the left-most point in each graph). Although matching to the co-located case is not necessarily the best in the least-mean-square-error sense, this criterion value gives us a quantitative measure of the difficulty of the task under co-located conditions and a better clue to what kind of difficulty listeners might be experiencing in these cases. The values of the matching SII criteria are discussed below for each case.

For the monaural listening conditions, the model predictions match fairly well to the measured thresholds. The predictions account for 95.7% of the variance in the empirical data for the monaural conditions (with an rms-error of about 1.0 dB). In Figs. 678, the fitted values of the SII criterion for the single-masker conditions (left columns) are smaller than those for the multiple-masker conditions, presumably reflecting listeners’ abilities to “listen in the gaps” when the masker is modulated, as discussed further below. The SII criterion values increase as the number of maskers increases, consistent with the filling in of the gaps when multiple independent maskers are combined.

For the binaural conditions, the model predictions again give reasonable fits to the empirical data when the maskers are SSN (an rms-error of 0.7 dB) or modulated SSN (an rms-error of 1.3 dB), as illustrated in Figs. 5 and 6. In these cases, the SII criterion for the modulated-SSN case is lower than that for the SSN case, as one would expect with “gap listening” possible in the modulated case. In contrast to the SSN cases, the model does not give good predictions for the binaural conditions when the maskers are speech (an rms-error of 3.8 dB) or reversed-speech (an rms-error of 3.6 dB), as illustrated in Figs. 7 and 8. In these cases, an obvious problem is that, for the multiple masker cases, the predicted thresholds for masker locations that are not co-located are consistently too high relative to the co-located thresholds to which the SII criterion was fit. In other words, the advantage of spatial separation is not captured by the model when the maskers are speech or reversed speech. This is consistent with the hypothesis that the spatial release is due to not only energetic unmasking but also informational unmasking (Freyman et al., 2001).

In the following paragraphs, these results are discussed at a more refined level. The discussion is divided into three sections to focus separately on three distinct factors. First, the effects of the spatial filtering [as captured by the head-related transfer functions (HRTFs)] and the benefits of the EC processing are evaluated by considering the SSN masking case as represented by the results in Fig. 5. Second, the additional effects of masker modulation are evaluated by considering the modulated-SSN case as represented by the results in Fig. 6. Finally, the additional effects of speech-like maskers, including cognitive confusions or informational masking, are evaluated by considering the results for the speech and reversed-speech maskers shown in Figs. 7 and 8.

Effective SNRs.

As described by articulation theory and the SII, speech intelligibility in noisy environments depends on the effective SNRs for individual frequency bands. In the SSN cases in Fig. 5, the effective SNRs are determined by the physical acoustics as captured by the HRTFs in the virtual environments and by the binaural processing when maskers have different locations than the target. These cases have relatively small fluctuations in the short-term energy of the maskers, and share little cognitive similarity with target speech; thus, they are expected to test the EC model and the SII performance measure relatively directly.

As seen in Fig. 5, there is an excellent prediction of the forms of the dependence on the position(s) of the masker sources for both monaural and binaural listening. This good match between model predictions and empirical data indicates that (1) the SII evaluation component is capable of predicting speech intelligibility performance caused by the SNR, and (2) the extended EC model, which combines HRTFs and EC processing, is capable of predicting the SNRs for multiple maskers in different locations. Furthermore, the SII criterion values are approximately constant in all the cases in Fig. 5, supporting the hypothesis that the difficulty in these speech intelligibility tasks arises almost purely from SNR effects. The small changes in the SII criterion over the number and locations of maskers, approximately 0.035, correspond to an SRT change of only about 1 dB. Note that the cases compared include different numbers of maskers and multiple locations of maskers.

Listening in the gaps.

When the envelopes of the maskers include substantial temporal fluctuations, the SNRs created are not only a function of frequency band but also a function of time. Furthermore, evidence (e.g., Festen and Plomp, 1990; George et al., 2008) indicates that human listeners have the ability to exploit intervals during which the SNR is high even for a short time. The fluctuating noise cases in Fig. 6 show directly the benefits of this ability. In these cases, the effects of SNR are still important, but the advantages of listening in the gaps are also apparent. Comparing the model performance between Figs. 5 and 6 provides a clue to how much benefit listeners get from gap listening. The value of the SII criterion implicitly indicates the difficulty of the task. The SII criterion, as noted above, is clearly lower (better performance) in the single-masker cases with modulation than those cases without modulation, and the best-fit SII criterion increases as the number of maskers increases. For example, in binaural conditions, the SII criterion gradually increases from 0.239 to 0.356 as the number of maskers increases from one to three, indicating that the difficulty of the intelligibility task increases by about 3.5 dB. This increased difficulty, which is not related to locations, presumably reflects the filling-in of gaps by the independent maskers. Consistent with this idea, as the number of maskers increases, the SII criterion approaches that of the unmodulated SSN. All of these trends in SII criterion can be explained by the diminished benefit of gap-listening when the number of modulated maskers increases. The temporal gaps available for listening to the target speech decrease, eventually approaching the situation that occurs with SSN maskers. The success of the model predictions of the spatial dependence for SSN and modulated-SSN cases with only criterion changes suggests that the effects of listening-in-gaps are almost independent of spatial effects and can be accounted for by an overall SII shift.

The only points in Fig. 6 for which the SRT dependence on location shows a consistent deviation between data and predictions are cases when modulated maskers occur on both sides, i.e., (−30°,90°) and (−30°,60°,90°). In these cases, the SRT predictions are consistently 2 or 3 dB higher than the data. This discrepancy could be due to the fact that the model is unable to change the cancellation parameters dynamically over time. Peissig and Kollmeier (1997) suggested that the binaural system is capable of canceling two interferers dynamically, using the pauses in one interferer to suppress the other interferer. When dealing with stationary maskers, such as SSN, the optimal cancellation parameters remain stable over time, so that the current model with a single cancellation parameter value throughout the interval will generally be the optimum choice. But when the maskers are independently amplitude modulated, as in the experiments that generate the results in Fig. 6, the model’s constraint of calculating cancellation parameters over the whole duration of the waveform is not optimal, causing the predictions to require a higher SNR. This effect is more prominent when the maskers are located on both sides of a listener’s head. When the modulated maskers are located on the same side of a listener’s head, the model still captures the data reasonably well, indicating that the spatial separation on the same side does not help much in the intelligibility tasks.

Cognitive confusion with speech-like maskers.

As shown in Fig. 7, when both the target and the maskers are speech, additional factors come into play. Factors like the effective SNR and gap-listening still affect the perception of the target speech, but, in addition, cognitive confusions may occur due to the similarity between target and masker. For example, listeners may hear both target words and masker words and still be uncertain about which word is the target. Some researchers refer to such confusions as “informational masking” (e.g., see Durlach et al., 2003). Factors that can affect the amount of such masking include differences among sources in pitch, spatial location, etc.

These cognitive factors are discussed for the monaural listening conditions first. As shown in Fig. 7, the model predictions for the dependence on spatial condition (the positions of the maskers) are very good for the monaural conditions, although the SII criteria are much higher for multiple-masker cases than that for single-masker cases. This trend is similar to that seen with modulated SSN, although performance with the single speech masker is marginally better than with modulated SSN (with the SII criterion of 0.244 compared to 0.265, less than 1 dB of SNR), whereas the performance with the multiple speech maskers is significantly worse (with SIIs of approximately 0.5 compared to 0.37, about 4 dB of SNR). This increase of the SII criterion with more maskers is presumably a combination of filling in the gaps (as discussed above), as well as increasing the cognitive confusion with an increasing number of maskers. The ability of the model to predict the spatial dependence of the SRT indicates that the cognitive confusion factor is roughly independent of spatial location, consistent with the hypothesis that there are almost no spatial perception factors involved in these monaural conditions.

For binaural listening conditions with speech maskers, the model predictions and the data show different patterns of spatial dependence between single-masker cases and multiple-masker cases. In multiple-masker cases, there is a consistent difference between the data and the predictions for non-co-located cases (with an rms-error of about 4.6 dB) when the criterion is matched to the co-located cases (as plotted in Fig. 7). In this case, when the co-located conditions are used to set the SII criterion, this criterion is comparable in binaural and monaural conditions, indicating that the binaural system is not providing any benefit over monaural conditions when the maskers are co-located with the target in front (as would be expected since in this case there is no extra information available to the binaural system). But when the maskers are spatially separated from the target, human performance is consistently better than the model prediction by approximately 5 dB. This difference is consistent across all spatial configurations in the binaural listening condition, indicating that the binaural system not only provides energetic unmasking and improves the effective SNRs but also provides release from informational masking by creating spatial cues for separating the target from the masker. When the SII criterion is matched to one of the non-co-located cases, it becomes clear that performance is slightly better than predicted for cases with maskers on both sides of the head, namely the (−30°,90°) and (−30°,60°,90°) cases, presumably, as discussed above, because listeners can dynamically adapt their processing according to the fluctuating levels of the sources on opposite sides of the straight-ahead target.

For the single-masker binaural case, the model matched to the co-located thresholds gives good predictions for all SRTs (with an rms-error of about 1.2 dB), which suggests that human performance in single-masker cases is different than in multiple-masker cases. Since the SRT for the co-located configuration is much lower in single-masker cases than those in multiple-masker cases, it appears that human subjects are not experiencing much target-masker confusion for the single-masker cases even though the target and masker speech sentences are co-located. This result is consistent with the summaries of Kidd et al. (2007), and the performance is probably achieved by using memory and divided attention. Note that, in the Hawley et al. (2004) experiments analyzed in this section, listeners were provided with the text of the masker sentences before the stimulus was presented, so that it would be relatively easy to identify the target if both target and masker were perceived. With multiple maskers, however, the memory load becomes increasingly significant.

As shown in Fig. 8, when the masker is reversed speech, both the data and the predictions show similar patterns to those seen in Fig. 7 for the speech maskers (an rms-error of 1.3 dB for single-masker case and an rms-error of 4.4 dB for multiple-masker cases). One difference is that the SII criterion for each panel is consistently lower for the reversed-speech masker than for the speech masker, consistent with better performance with reversed speech for the same SNR. Considering the three factors discussed above, one might expect the predictions of the model to be consistent with those in the modulated-SSN cases, since both of these maskers can give temporal modulation benefits without direct competition of speech words; however, the similarity in the results for speech-masker cases and reversed-speech-masker cases suggest that significant interference comes from the similarity of time-frequency patterns in the target and masker waveforms for the speech-like reversed-speech maskers.

Model predictions for data from Marrone et al. (2008)

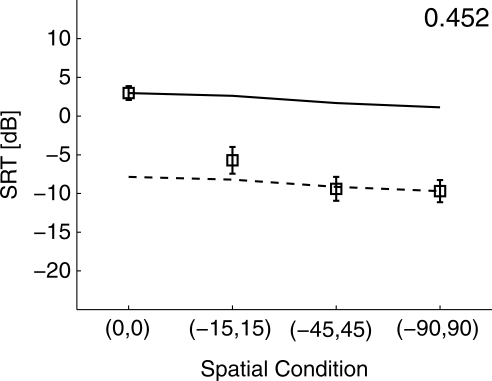
Marrone et al. (2008) performed a set of speech intelligibility tests in both low and high reverberant conditions. In low reverberant conditions, they measured (1) the binaural SRTs for a target speech sentence masked by two speech maskers that were symmetrically located around the frontal (0°) speech target [masker pairs were located at (0°,0°), (−15°,15°), (−45°,45°), and (−90°,90°)]; (2) the binaural spatial release for two symmetrically located reversed-speech maskers located at (−90°,90°); and (3) the monaural spatial release for two symmetrically located speech maskers located at (−90°,90°). The experiments were conducted using loudspeakers in a large sound booth (12′4″ × 13′ × 7′6″) with very low reverberation (reverberation time of 0.06 s and direct-to-reverberant ratio of 6.3 dB). Both target and masker sentences were chosen from the CRM corpus spoken by three different talkers. They also measured SRTs in a highly reverberant environment, which are not modeled in this paper. We created a similar experimental scenario virtually by using the same speech corpus and following the same experimental paradigm, except that we used head-related impulse responses from the CIPIC database to simulate virtually the free-field anechoic space. All other methods used to calculate the SII and the SRT are the same as those described above in connection with the Hawley et al. (2004) data. Note that Hawley et al. (2004) provided a priori information about the maskers before each trial, whereas Marrone et al. (2008) did not provide this information.

Figure 9 shows both the measured and predicted binaural SRTs. As in previous cases, each prediction is the mean of 100 repetitions with different target and masker samples. The standard error (not shown here) is less than 0.05 dB. The behavior of the model is similar to that applied to Hawley et al. (2004), as shown in the top middle panel of Fig. 7. When the co-located case is chosen as the reference, all of the spatially separated measurements are substantially lower than the predictions (solid line). Instead, if the (−90°,90°) case is chosen as the reference, the model predictions (dashed line) substantially underestimate the reception threshold for the co-located case by about 10 dB. This mismatch can be at least partly attributed to the spatial release from “informational masking” as described in Sec. 3B1c. Furthermore, the difference between the data and the prediction is smaller for the (−15°,15°) case than for the other two cases in Marrone et al. (2008). In Hawley et al. (2004), these differences between model predictions and the measurements are almost constant when maskers are spatially separated from the target. This result for the Marrone et al. (2008) data suggests that the binaural informational unmasking resulting from spatial factors depends on the degree of spatial separation, at least when the separation is small. One might expect that when the maskers are so close to the target that the target is not easily perceived as a separate object, the size of the informational unmasking is relatively small. The release from masking would be expected to increase with larger spatial separations, but then to saturate so that further spatial separation would not contribute much to the informational unmasking. Finally, the difference between the data and the prediction is also due to the fact that the model cannot dynamically change the cancellation parameters, as described in Sec. 3B1b.

Figure 9.

Simulated and measured binaural SRTs for speech masker cases in a pseudo-anechoic environment. Symbols are the measurements from Marrone et al. (2008), and the error bar is one standard error. The solid curve is the model prediction using the (0°,0°) case as reference, and the dashed curve is the prediction using the (−90°,90°) case as reference.

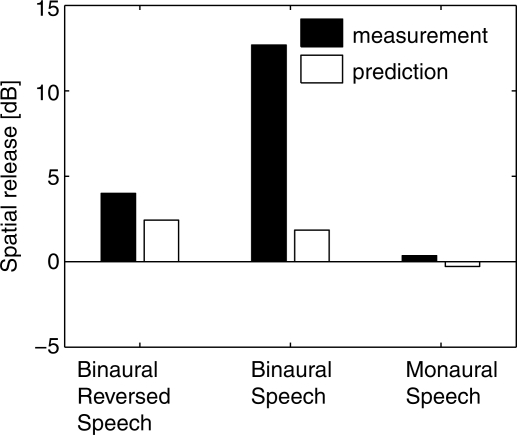
Figure 10 shows measurements and predictions of spatial release from masking for all anechoic cases measured by Marrone et al. (2008). Spatial release is defined as the threshold difference between the co-located (0°,0°) case and the (−90°,90°) case. The negligible spatial release predicted for the monaural case is consistent with the data, but the model under-predicts the binaural spatial release for both the speech-masker case and the reversed-speech-masker case. For the speech-masker case, the prediction strongly deviates from the data by about 10 dB, indicating that the cognitive components combined with the spatial separation play an important role in this speech intelligibility task. However, when the maskers are reversed speech, the model underestimates the spatial release by only 2 dB. This large difference between the results for the speech masker and the reversed speech masker is different in Hawley et al. (2004) where the results for these two cases are very similar.

Figure 10.

Spatial release for speech perception in an anechoic space. Measurements are from Marrone et al. (2008). Predictions are provided by the model for a simulated anechoic environment.

This large empirical difference emphasizes the complexity of the speech intelligibility task and the importance of many factors in determining performance in these cases. Although researchers have generally referred to many of these factors under the general heading “informational masking” (Durlach et al., 2003), these factors may affect intelligibility performance in different ways, to different extents, and in opposite directions. For example, the differences between the data of Hawley et al. (2004) and that of Marrone et al. (2008) may come from the fact that the Hawley study used the same talker for each source, whereas the Marrone study used different talkers for each source, including both target and maskers. Using the same talker for all the sources can add informational masking for the listener because there are reduced voice cues (e.g., pitch) available for the auditory system to segregate the different sources. On the other hand, the difference may also come from the fact that the Hawley study gave additional prior information about the masker compared to the Marrone study, thus reducing the amount of informational masking. Additionally, one can reasonably assume that the effects of informational masking also depend on the speech material. For example, Hawley et al. (2004) used the IEEE corpus, which is open-set, whereas Marrone et al. (2008) used the CRM corpus, which is closed-set. Finally, in considering the symmetrical masker cases in Marrone et al. (2008), it should be noted that they are the cases most affected by the assumption that the EC processing in the current model is not permitted to change dynamically during the stimulus interval.

DISCUSSION

This paper presents the application of an extended version of the EC model of Durlach (1972) to predict speech intelligibility performance in complex environments, including conditions with multiple interfering sources. As an extension of the original EC model, the current model has several distinctive aspects: (1) time-varying jitters are introduced, both in interaural time delay and interaural amplitude ratio; (2) speech stimuli are processed by equalizing the masker in each frequency band separately and combining information across bands using the SII; and (3) full equalization of interaural level is allowed. With these modified assumptions, the extended model is able to predict speech intelligibility performance in a number of interference situations and also remains compatible with tone-in-noise detection conditions. The interferer conditions include multiple maskers in variable spatial locations and different types of maskers (SSN, modulated SSN, speech, and reversed speech).

As described in Sec. 1, previous studies have applied results from tone detection to predict speech intelligibility performance. First, Zurek (1992) used the SII with the predicted BMLD in each frequency band to predict speech intelligibility performance as a function of masker direction for a single SSN masker in anechoic space. The current study is a direct extension of Zurek’s approach except that we have implemented an explicit internal noise process in contrast to the use of a formula for SNR improvement, which is limited to simpler cases. Second, Culling et al. (2004) used the measured BMLD in each frequency band to predict speech intelligibility performance for cases involving multiple SSN maskers in anechoic space. The approach presented in this paper follows these previous studies and explicitly combines an extended EC model with objective speech intelligibility evaluation (the SII) to predict speech intelligibility performance in anechoic space involving multiple maskers. In addition to the application of the model to SSN maskers, we have investigated model performance for other types of maskers.

Among the studies that combine binaural models with speech intelligibility performance, Beutelmann and Brand (2006) developed an EC-based model to predict speech intelligibility performance. This model differs from our model in their assumptions about the internal noise. Durlach (1963, 1972) assumed time and amplitude jitters (i.e., variability in time delays and amplitudes of the filtered inputs) that were fixed during the duration of the stimulus, primarily to allow ease of computations. Beutelmann and Brand followed this idea and used parallel units with distributions of time-invariant jitter values and then averaged the SRT outputs over all the units. In contrast to their model, the model presented here assumes that every time sample of the filtered stimulus waveform is independently jittered and that jitters are applied independently in each frequency channel. The parameters that describe the statistics of the jitter (the mean and variance of the Gaussian distributions) are the same for all channels and are equal to the values chosen by Durlach. This assumption is more realistic than a single sample of jitter in each trial and also avoids the statistical averaging over the whole set of jitters for each trial presentation as used in Beutelmann and Brand (2006). Their recent revision and extension of the model (Beutelmann et al., 2010) make it analytical, applicable to nonstationary interferers, and more similar to the present study. In the Beutelmann et al. (2010) paper, the effects of reverberation and the effects of hearing loss on speech intelligibility performance were investigated with a single noise masker. The present study used multiple maskers and included speech as well as reversed-speech maskers but was limited to anechoic environments and listeners with normal hearing. It would be interesting and helpful to compare the performance of these two models over a wider range of conditions.

Overall, this study has demonstrated that relatively direct extensions of current binaural models can help us understand available data and separate out the contributions of different factors. More specifically, for the SSN and modulated-SSN cases, the application of an extended version of the EC model combined with the SII predicts most of the spatial dependence of the SRT. For the speech and reversed-speech cases, the large spatial release that is seen in the empirical data is underestimated, presumably because the cognitive confusions (or aspects of informational masking) that are important in these cases have not been included in the modeling. These results also demonstrated that several factors are important for speech intelligibility in the presence of multiple, spatially distributed interferers. Specifically, these factors include SNR of the stimuli in different frequency bands, effective SNR improvements from binaural processing, strategies for listening in the gaps, and spatial release from informational masking. Although the current model obviously cannot account for all the factors in speech intelligibility tasks, some insight has been gained by looking at the changes of the SII criterion in different conditions. For example, the SII criterion for the unmodulated SSN cases is relatively consistent across conditions with different numbers of maskers. This indicates that the current model is capable of interpreting the effects of SNR. The increasing trend of the SII criterion in modulated SSN or speech-like masker cases indicates that the current model cannot explicitly interpret the effects of gap-listening or cognitive confusion involved in speech intelligibility tasks.

There are three areas in which further modeling work is needed. The first, and most straightforward, improvement would be to allow the cancellation parameters to vary with time during the stimulus. The dynamics of this process would be an important part of the modeling, since rapid EC operation would eliminate the internal noise. The goal of this modification would be to make the predictions compatible with the measurements for cases in which the maskers are non-stationary, such as modulated noise or speech with multiple sources in different locations, and listeners could benefit from responding to short-term changes in the direction of the dominant interference. Obviously, these cases are frequently encountered in daily life. The second area needing improvement concerns the assumption about available interaural-level equalization. A better understanding of the differences among free level equalization, constrained level equalization, and even no level equalization is needed. Modifications could improve predictions for tone-in-noise detection as well as for complex speech-intelligibility tasks. Finally, the third area for improvement, which is the most challenging, is to extend the model to include informational masking and other cognitive effects, not only because such effects are frequently encountered in daily life, but also because such improvement is needed for understanding both binaural listening and monaural listening.