Abstract
Hypotheses regarding patterns of stress, strain and deformation in the craniofacial skeleton are central to adaptive explanations for the evolution of primate craniofacial form. The complexity of craniofacial skeletal morphology makes it difficult to evaluate these hypotheses with in vivo bone strain data. In this paper, new in vivo bone strain data from the intraorbital surfaces of the supraorbital torus, postorbital bar and postorbital septum, the anterior surface of the postorbital bar, and the anterior root of the zygoma are combined with published data from the supraorbital region and zygomatic arch to evaluate the validity of a finite-element model (FEM) of a macaque cranium during mastication. The behavior of this model is then used to test hypotheses regarding the overall deformation regime in the craniofacial haft of macaques. This FEM constitutes a hypothesis regarding deformation of the facial skeleton during mastication. A simplified verbal description of the deformation regime in the macaque FEM is as follows. Inferior bending and twisting of the zygomatic arches about a rostrocaudal axis exerts inferolaterally directed tensile forces on the lateral orbital wall, bending the wall and the supraorbital torus in frontal planes and bending and shearing the infraorbital region and anterior zygoma root in frontal planes. Similar deformation regimes also characterize the crania of Homo and Gorilla under in vitro loading conditions and may be shared among extant catarrhines. Relatively high strain magnitudes in the anterior root of the zygoma suggest that the morphology of this region may be important for resisting forces generated during feeding.
Keywords: biomechanics, facial buttresses, feeding, hominins, mastication
Introduction
Primates exhibit a diverse range of morphology in the craniofacial haft – the structures joining the rostrum to the braincase. The functional significance of this morphological diversity is important for our understanding of primate craniofacial evolution because many of the features defining primate higher taxa are part of the craniofacial haft. The postorbital bar is a synapomorphy of Primates, the postorbital septum a synapomorphy of Haplorhini (tarsiers and anthropoids), extreme orbital convergence and frontation are synapomorphies of anthropoids, and the close approximation of the orbits below the olfactory tract in haplorhines distinguishes them from most strepsirrhines (Cartmill, 1970, 1975, 1980; Ravosa, 1988, 1991; Ross & Ravosa, 1993; Ross, 1995; Ross & Hylander, 1996b). Evidence for the functional significance of these features in the craniofacial haft, where many functional systems overlap, requires innovative experimental and modeling approaches. For example, the highly frontated (vertically orientated) orbits of anthropoids and some strepsirrhines might be effects of increased frontal lobe size or retraction of the palate, or adaptations for visual inspection of manually acquired food (Cartmill, 1970). In any case, increased orbital verticality increases resistance of the face to dorsoventral shearing and bending forces (Ross, 2001).
Describing the in vivo deformation regimes during feeding is the first step in determining whether the shape of the circumorbital region reflects selection for its ability to resist those deformation regimes. Estimates of the relative bone strain magnitudes in the circumorbital region during feeding provide insight into the probable importance of bone size and shape for resisting feeding forces (Hylander et al. 1991). The research reported here presents new strain data from the intraorbital surface of the supraorbital torus, postorbital bar and postorbital septum, the anterior surface of the postorbital bar and the anterior root of the zygoma in macaques during mastication. These data are combined with published data on deformation regimes in the supraorbital region and zygomatic arch (Hylander et al. 1991; Hylander & Johnson, 1997b) to evaluate the validity of a finite-element model (FEM) of a macaque cranium during simulated mastication. The behavior of this model is then used to test hypotheses regarding the overall deformation regime in the craniofacial haft of macaques. The macaque FEM is then compared with in vivo bone strain data collected from Chlorocebus and published data on in vitro deformation regimes of dry crania of Homo and Gorilla. These comparisons suggest hypotheses about the degree to which deformation regimes in the circumorbital regions are shared among extant catarrhines.
In what follows, the term loading regime refers to the combination of external forces acting on the skull in vivo or in silico (i.e. in the FEM); the term deformation regime refers to the pattern of deformation of the skull produced by that loading regime; and the terms stress or strain regime refer to the associated patterns of internal forces or strains acting within the skull or FEM.
Hypotheses
Axial compression of facial pillars
Several workers have modeled the primate face as a rigid frame composed of straight elements, often referred to as facial ‘buttresses’ (Görke, 1904; Richter, 1920; Benninghoff, 1925; Bluntschli, 1926; Sicher & Tandler, 1928; Endo, 1966b; Roberts & Tattersall, 1974; Couly, 1976; Rak, 1983). The concept of facial ‘buttresses’ persists in the clinical literature on craniofacial skeleton deficiencies due to fractures and tumor removal (Manson et al. 1980; Gruss & Mackinnon, 1986; Yamamoto et al. 1998; Nagasao et al. 2005; Andrades et al. 2008; Rodriguez et al. 2008). The simplest of these framework models posit that the bones of the craniofacial haft are axially compressed during mastication and incision and transmit these stresses from the molar region up to the frontal bone via the interorbital ‘pillar’ medially, the postorbital bar laterally, and the pterygoid processes of the sphenoid posteriorly (Görke, 1904; Benninghoff, 1925; Roberts & Tattersall, 1974). Roberts and Tattersall's model is presented as an example in Fig. 1(A). The ‘axial compression’ hypotheses are general statements regarding dissipation of stresses in the face, and do not make precise predictions regarding patterns of deformation. However, simple axial compression models are unlikely to predict deformation regimes in the primate lateral orbital wall because in most primates this structure is not a straight member, but a curved, irregularly shaped structure. This shape makes it difficult to predict how the lateral orbital wall will be deformed by superiorly directed force components during biting. However, the medial position of the toothrow relative to the lateral orbital wall does mean that bite forces will bend the lateral orbital wall, rather than axially compress it. Similarly, the force vectors of the masticatory musculature are almost certainly off axis, suggesting that the lateral orbital wall is probably bent, twisted and/or sheared by these muscle forces as well. The relative orientations of muscle force vectors are taken into account by Endo, Rak and Hylander's recent models of circumorbital function in primates.
Fig. 1.
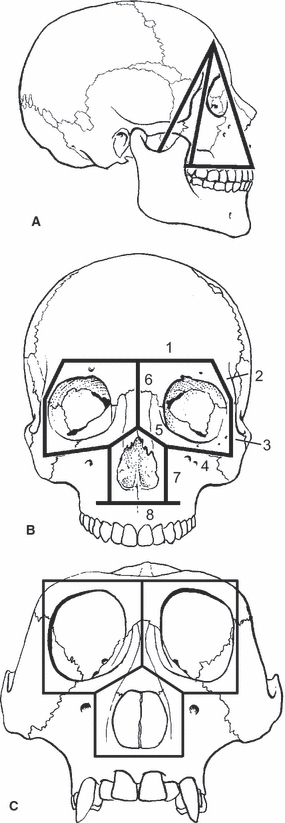
(A) Facial pillars modeled by Roberts & Tattersall (1974) as transmitting compressive forces from the toothrow to the braincase. (B) Endo's fundamental framework of the human face, consisting of (1) transversely oriented frontal member, (2) oblique superior zygomaticofrontal member, (3) vertically oriented inferior zygomaticofrontal member, (4) oblique maxillozygomatic member, (5) lower nasal member, (6) midline upper nasal member, (7) maxillary member, and (8) transversely oriented alveolar member. (C) Endo's fundamental framework of the gorilla face. This framework differs from the human frame in having a single zygomaticofrontal member, a horizontally oriented maxillozygomatic member, and an alveolar member that does not extend lateral to the maxillary member. The methods for deriving these models are not presented by Endo, so the reasons for these differences are not discussed.
Endo's in vitro analyses
Endo's (1966a,b, 1970, 1973) rigid frame models of the human and gorilla faces (Fig. 1B,C) have influenced many investigations of primate craniofacial biomechanics (Picq & Hylander, 1989). These models comprise straight members of uniform cross-section loaded by external forces simulating in vitro occlusal and muscle loadings. Endo used frame analysis to estimate bending moments and stresses in these facial frames in frontal, lateral and oblique perspectives, and then qualitatively compared the magnitudes of these stresses with the distribution of bone around the frames. The bending moments acting on the facial framework of the human skull are illustrated in Fig. 2(A,C). Bending moments are illustrated here because Endo argued that they were the most important deformation regimes acting on the facial skeleton. It should be noted that these members are subjected to varying degrees of compression, tension and shear, which Endo also calculated. Schemata of the stresses acting on the members of the model are diagrammed in Fig. 2(B,D). Figure 2(E,G) illustrates strains perpendicular to selected cross-sections during right molar and incisor loading, respectively. Figure 2(F,H) illustrates strains along the margins of the orbits and piriform aperture during these deformation regimes.
Fig. 2.
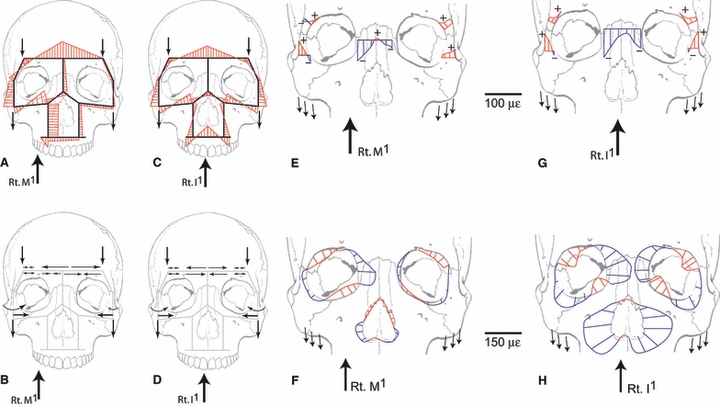
Endo's rigid frame model of the human face in anterior perspective (derived from Fig. 4.1 of Endo, 1966a,b;). (A) Diagram of bending moments calculated from molar loading. Figure is redrawn from Fig. 4.3A, top, in Endo (1966a,b);. Bending moments in red are indicated on the tensile side of the members. (B) Schema of the stresses acting on the members of the rigid frame during right molar loading (derived from Figs 4.3 and 6.1 in Endo, 1966a,b;). Converging arrow pairs indicate compression; diverging arrow pairs indicate tension; single arrows indicate external forces; curved arrows indicate bending moments. (C) Diagram of bending moments calculated from incisor loading. Figure is redrawn from Fig. 4.3A, bottom, in Endo (1966a,b);. Bending moments in red are indicated on the tensile side of the members. (D) Schema of the stresses acting on the members of the rigid frame during incisor loading (derived from Figs 4.3 and 6.1 in Endo, 1966a,b;). Converging arrow pairs indicate compression; diverging arrow pairs indicate tension; single arrows indicate external forces; curved arrows indicate bending moments. (E) Fiber strains along selected cross-sections during right first molar loading. Red denotes tensile strain, blue compressive strain. Lateral orbital margins are primarily tensile units, although bending moments do generate compressive strains in the bar cross-sections on the working side, and slightly on both sides during incisor loading. The nasal cross-section experiences primarily compressive strain. Redrawn from Endo (1966a,b; Fig. 3.11). (F) Strain distributions around rims of orbits and pyriform aperture during right first molar loading. Lengths of lines perpendicular to the orbital margin are proportional to the magnitude of strains along the margin at that point. Blue is compressive strain, red is tensile. Redrawn from Endo (1966a,b; Fig. 3.8). (G) Strains along selected cross-sections during incisor loading. Red denotes tensile strain, blue compressive strain. Lateral orbital margin strains are primarily tensile, although bending moments do generate compressive strains in the bar cross-sections on the working side, and slightly on both sides during incisor loading. The nasal cross-section experiences primarily compressive strain. Redrawn from Endo (1966a,b; Fig. 3.11). (H) Strain distributions around the rims of the orbits and pyriform aperture during right first incisor loading. Lengths of lines perpendicular to orbital margin are proportional to the magnitude or strains along the margin at that point. Blue is compressive strain, red is tensile. Redrawn from Endo (1966a,b; Fig. 3.8).
The overall deformation regime under incisor loading (Fig. 2D) is bending in the frontal plane. The lateral ends of the frontal member are pulled inferiorly by the temporalis muscle forces, as well as by masseter forces transmitted to the frontal member by the zygomaticofrontal members. The lower lateral corners of the orbits are similarly pulled inferiorly by masseter muscle forces, inducing bending moments, especially in the lower zygomaticofrontal member and the zygomaticomaxillary members (Fig. 2C). These inferiorly directed forces cause the orbit to deform, such that the upper lateral inside corner bends to open out, or ‘unbends’, whereas the lower lateral corner bends to close up (Fig. 2H). The inferiorly directed components of masseter muscle force acting on the lateral edges of the model and the superiorly directed bite forces acting on the alveolar member are both resisted by the zygomaticomaxillary members, which are sheared (not shown) and bent as a result. Under this deformation regime, sections through the postorbital bar are primarily under tension, except for the medial end of the lower section (Fig. 2G), predicting tensile strains oriented along the long axis of the postorbital bar.
Under unilateral molar loading (Fig. 2A,B) the working side orbit is deformed in a very similar manner to the orbits in the incisor loading model (cf. Fig. 2F,H). Compared to the incisor loading regime, the magnitude of the bending moments in the medial end of the zygomaticomaxillary member is higher, due to the transmission of greater amounts of force through the working side maxillary member. Also, the lateral orbital wall experiences greater bending moments (Fig. 2A), and a greater degree of compressive strain at the medial end of the lower cross-section through the postorbital bar (Fig. 2E).
Although there is some variation in the magnitudes of the internal forces associated with different bite points, the deformation of the lateral orbital wall inferred by Endo is similar, regardless of whether the toothrow is loaded on the incisors, the premolars, or the molars, whether the simulated forces from the temporalis and masseter act alone or together, and whether the species involved is Gorilla or Homo. When the temporalis force and bite force are applied without the masseter, axial compressive forces within the lateral orbital wall increase, and when the masseter force and bite force are applied without the temporalis, axial tensile forces within the lateral orbital wall increase. Regardless of where the toothrow is loaded, Endo's model posits that the inferiorly directed forces of the masseter and temporalis acting on the lateral orbital wall subject the wall to internal bending moments. These bending moments are one component of an overall deformation regime in the craniofacial haft that can be simply described as bending in a frontal or coronal plane. In general, the medially located members in the model experience high axial forces (predominantly compressive) and the lateral members experience high bending moments and shearing forces (Fig. 2E,G).
To test his frame models, Endo performed in vitro strain gage analyses of skulls of Homo and Gorilla (Endo (1966a,b, 1970, 1973)). Figure 3 illustrates the patterns of bone strain found in the faces of Gorilla and Homo during loading of the upper first molar and simulated loading at the attachment sites of temporalis and masseter (Fig. 2 from Endo, 1973 and Fig 3 and 9 from Endo, 1966a,b;). The patterns of stress predicted by the mathematical model are similar to patterns of bone strain recorded under in vitro loading (but see Picq & Hylander, 1989).
Fig. 3.
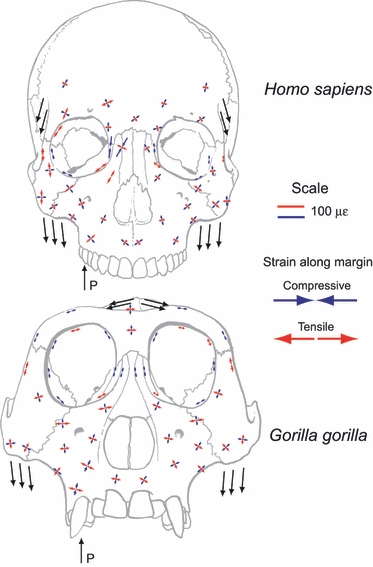
Bone strain data measured during in vitro studies of skulls of Homo and Gorilla by Endo (1966a,b);.
Fig. 9.

Strain vector plots of strain data collected from the intraorbital surface of the frontal portion of the postorbital septum. Septum data were collected from the right side of the skull in experiment 32, but the working side data are reflected onto the left side to facilitate comparison with the FEM data. The top two figures show the orientations of the in vivo tensile and compressive strain vectors recorded during experiment 32. The black arrows on the in vivo plots represent the extremes of the ranges of the mean ε1 orientations from the in silico‘gage sites’. The bottom two figures illustrate in silico data from corresponding ‘gage sites’ on the model. For the in silico data, each line is a vector representing the mean orientation and magnitude of maximum (ε1) (red to yellow) and minimum (ε2) (blue to green) principal strains from all the elements at the gage site. Note that the variance among the vectors from the in silico gage sites is due to variation in bite point, and the variance among vectors from in vivo gage sites is due to variation in magnitude and location of bite force, joint reaction forces and muscle forces. In vivo strain orientations are presented in Table 3 and in this figure as angles relative to a line following the anterior surface of the postorbital bar in the plane of the orbital aperture.
Rak (1983) invoked Endo's hypotheses regarding frameworks and their deformation regimes in Homo and Gorilla to reconstruct frameworks and posit their deformation regimes in the faces of ‘australopithecine’ hominins. Rak argued that the frames of the upper faces of australopithecines resemble the frameworks of Homo and Gorilla, but that their lower frames differed in having a zygomaticoalveolar member, corresponding in position to the zygomaticoalveolar crest (Fig. 4) (Figs 37A and 4B of Rak, 1983: p. 94). This additional member ‘serves as a supporting column between the heavily loaded occlusal surfaces of the upper teeth, on the one hand, and the site of origin of the powerful masseter, on the other’ (Rak, 1983: p. 94). Rak hypothesized that the lateral orbital walls of the australopithecines, like those of Homo and Gorilla, are principally tensile elements subjected to external forces from temporalis and masseter. In Paranthropous boisei, rostral displacement of the masseter origin relative to the lateral orbital wall removes the tensile support of the lateral orbital wall from the anterior zygoma root, necessitating evolution of the visor-like appearance of the boisei infraorbital region to compensate.
Fig. 4.
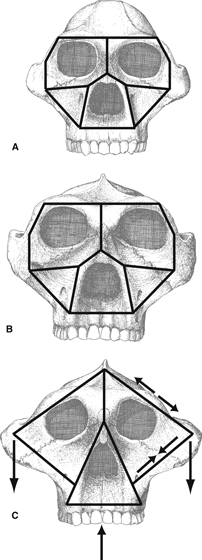
Fundamental rigid frameworks of faces of (A) Australopithecus africanus, (B) Paranthropous robustus, and (C) Paranthropus boisei hypothesized by Rak (1983). Skull drawings are from Rak (1983: with permission). Rigid frames are constructed from interpretation of the text and from Figs 37 and 44 in Rak (1983). Rak states that the upper facial parts of the frames of A. africanus and P. robustus resemble the generalized condition, and that these taxa resemble P. boisei in having a zygomaticoalveolar member extending from the lower end of the inferior zygomaticofrontal member to the alveolar member. In (C) converging arrows represent compression of the zygomaticoalveolar member and diverging arrows represent tension of the single zygomaticofrontal member.
Hylander et al. (1991) used in vivo bone strain data to evaluate hypotheses regarding deformation regimes of the supraorbital torus in macaques and baboons during feeding. The results supported Endos (1966a,b); hypothesis that during incision and mastication the supraorbital regions of macaques and baboons are bent in a frontal plane by inferiorly directed components of masseter and temporalis muscle forces. However, they noted that ‘it is clear that because of its morphological complexity, the browridge cannot be accurately modeled, even for a first-approximation analysis, as a slightly curved or straight beam’ (Endo 1966a,b: p. 33, emphasis in original). One reason for their caution is the observation that strain orientations in the dorsal orbital gage site, above the center of each orbit, did not match the predictions of the frontal bending hypothesis. In this study we present data from the inferior, or intraorbital, surface of the supraorbital torus, which we refer to as the orbital roof. These data, in conjunction with data from the lateral orbital wall, allow hypotheses regarding deformation regimes in the circumorbital region to be evaluated.
Ross & Hylander (1996a,b); reported strain data from the medial (intraorbital) and lateral surfaces of the postorbital septum in the owl monkey, Aotus. They reported primarily superoinferiorly oriented tensile strains on the lateral surface of the working side septum and superoinferiorly oriented compressive strains on the medial surface. They hypothesized that both working and balancing septa are primarily bent in frontal planes and that the balancing side septum is under some torsion due to posteroinferiorly oriented force from masseter contraction (Ross & Hylander, 1996a).
Finite-element modeling of the macaque facial skeleton
These hypotheses regarding deformation regimes in the primate craniofacial haft have used simple structures, such as beams, plates and cylinders, to interpret patterns of strain and infer deformation regimes. However, these models are limited in their accuracy and precision by the geometric and material complexity of primate facial form, and by the complexity of the external forces acting on the facial skeleton during feeding (Hylander et al. 1991; Ross & Hylander, 1996a; Ravosa et al. 2000a; Ross, 2001; Ross & Metzger, 2004; Metzger et al. 2005). To address these problems, our hypothesis regarding deformation regimes in the macaque face is a finite-element model (FEM) of the macaque face subjected to external forces modeled on muscle and bite forces, as described in this paper and elsewhere (Strait et al. 2002, 2005, 2008, 2009; Ross et al. 2005; Wang et al. 2008; Chalk et al. 2010). Predictions of this hypothesis, in the form of strain orientation and relative magnitude data, are evaluated in this paper using in vivo bone strain data from the facial bones of macaques. These predictions are presented in Figs 6–14, where they are compared with the in vivo strain data.
Fig. 6.

Strain vector plots of in vivo strain data collected from the anterior surface of the postorbital bar on the right and left sides of the skull. In experiment 38, data were collected from the left side of the skull but are reflected onto the right about a vertical axis to facilitate comparisons. The gage in experiment 48 was positioned lower (approximately 1/3 of the orbit height) than one half orbit height (lower bar site); in the remaining experiments the gages were positioned at approximately mid-orbit height (upper gage site). The reference line is a horizontal line superimposed on the images. The black arrows represent the extremes of the ranges of the mean ε1 orientations from the in silico‘gage sites’ in Fig. 7.
Table 6.
Descriptive circular statistics for in vivo bone strain orientations recorded from anterior root of the zygoma.
| Experiment | 8 | 8 | 8 | 9 | 9 |
|---|---|---|---|---|---|
| Side | Incision | Working | Balancing | Working | Balancing |
| n | 35 | 169 | 136 | 23 | 216 |
| Mean vector (μ) | 19.144 | 13.636 | 13.239 | 13.207 | 16.467 |
| Length of mean vector (r) | 0.989 | 0.994 | 0.999 | 0.997 | 0.985 |
| Median | 19.123 | 13.535 | 13.261 | 13.617 | 16.133 |
| Concentration | 44.813 | 81.566 | 400.448 | 180.554 | 33.038 |
| Circular variance | 0.006 | 0.003 | 6.25E-04 | 0.001 | 0.008 |
| Circular SD | 4.304 | 3.182 | 1.432 | 2.135 | 5.023 |
| 95% confidence interval (±) for μ | 17.718 | 13.156 | 12.998 | 12.334 | 15.797 |
| 20.57 | 14.115 | 13.48 | 14.079 | 17.136 | |
| 99% confidence interval (±) for μ | 17.27 | 13.005 | 12.922 | 12.06 | 15.586 |
| 21.018 | 14.266 | 13.555 | 14.354 | 17.347 | |
| Rayleigh test (Z) | 34.219 | 166.928 | 135.66 | 22.873 | 209.461 |
| Rayleigh test (P) | < 0.0001 | < 0.0001 | < 0.0001 | < 0.0001 | < 0.0001 |
| Watson's U2 test (von Mises, U2) | 0.048 | 0.079 | 0.041 | 0.267 | 0.38 |
| Watson's U2 test (P) | > 0.5 | 0.25 > P > 0.15 | > 0.5 | < 0.005 | < 0.005 |
| Test for working/balancing differences | |||||
| W | F = 65.202 | F = 1.809 | 9.551 | ||
| P | < 0.0001 | ns | 0.002 | ||
Strain gradients in the facial skeleton
Hylander et al. (1991) noted that the in vivo bone strain data reveal significant strain gradients in macaque and baboon faces. They found very low strains in the supraorbital region, including dorsal interorbital, dorsal orbital and rostral interorbital gage sites, data that replicated the results reported by Endo from his in vitro strain recordings from skulls of Homo and Gorilla (Picq & Hylander, 1989). Hylander et al. concluded that the function of the supraorbital torus in catarrhines is unlikely to be dissipation of masticatory stresses. Instead they posited that the anterior displacement of the orbits relative to the neurocranium necessitates the presence of bone above the orbits to resist high strain magnitude traumatic loads associated with infrequent blows to the head (Hylander et al. 1991; Hylander & Johnson, 1992, 1997a,b; Hylander & Ravosa, 1992). Subsequent work has shown that strain gradients are widespread in the craniofacial skeleton of primates and other vertebrates, leading Ross and Metzger to argue that there are various reasons why bone strain magnitudes might vary from one region to another (Ross, 2001; Ross & Metzger, 2004). Low strained bony sheets around the orbit have been hypothesized to function to support the brain (orbital roof), provide attachment for chewing muscles (postorbital septum), provide attachment for the nasal epithelium and support the eyeball (orbital floor) (Ross, 2001). These hypotheses are evaluated here with in vivo bone strain data collected from the intraorbital surfaces in macaques.
Materials and methods
Subjects
Three adult females and one adult male rhesus macaques (Macaca mulatta) served as subjects. All of these animals had previously been unilaterally enucleated (i.e. had the orbital contents removed) on the right side for reasons unrelated to our research. This enabled placement of strain gages on the intraorbital surface of the lateral orbital wall and on the orbital roof. Enucleation occurred several years before our research on the adult animals and no skeletal asymmetries were evident.
Strain-gage placement
During 10 different experiments, delta (SA-06-030WY-120; Micromeasurements, Raleigh, NC, USA) (wired in a three-wire quarter-bridge circuit) or rectangular (FRA 1-11-1L; Texas Measurements) rosette strain gages were placed in various combinations along: (i) the medial or intraorbital surface of the lateral orbital wall (septum); (ii) on the anterior surface of the frontal process of the zygomatic bone at midorbital height (bar); (iii) on the intraorbital surface of the supraorbital torus (roof); (iv) on the anterior surface of the anterior root of the zygomatic arch (arz); (v) on the frontal bone immediately adjacent to the temporal line and behind the supraorbital torus (temp); (vi) on the lateral surface of the zygomatic arch (arch); and (vii) on the lateral surface of the mandibular corpus below the M1 or P4 (corpus) (Fig. 5, Table 1).
Fig. 5.
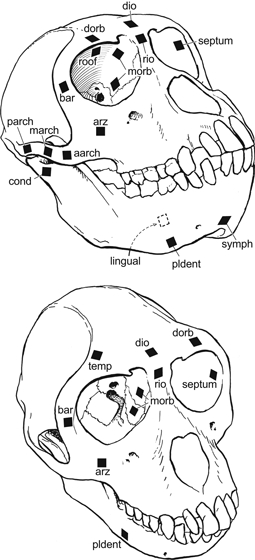
Diagram of skull of Macaca illustrating gauge locations. Abbreviations and region groups: Orbital region: dio, dorsal interorbital; rio, rostral interorbital; dorb, dorsal orbital; roof, orbital roof; bar, postorbital bar (anterior surface). Septum: postorbital septum (intraorbital surface of zygomatic bone); morb, medial orbital wall. Zygomatic: Arch, aarch, anterior 1/3 of zygomatic arch; March, middle 1/3 zygomatic arch, on zygomatic/jugal bone, immediately anterior to zygomatico-temporal suture; parch, posterior arch on zygomatic process of squamous part of temporal bone; arz, anterior root of zygoma; cond, condylar neck; Mandible, symph, symphysis; lingual, lingual aspect of mandibular corpus.
Table 1.
List of experiments from which data are derived.
| Experiments | Individual | Gage number and type | Gage locations reported here |
|---|---|---|---|
| 8 | Macaca mulatta 2 (F) | Rectangular rosettes | Medial orbital wall and anterior root of zygoma (R) |
| 9 | Macaca mulatta 1 (M) | Rectangular rosettes | Medial orbital wall and anterior root of zygoma (R) |
| 10 | Macaca mulatta 1 (F) | Rectangular rosette | Intraorbital, postorbital septum (R) |
| 13 | Macaca mulatta 1 (F) | Rectangular rosette | Orbital roof (R) |
| 32 | Macaca mulatta 2 (F) | 4 delta stacked rosettes | Intraorbital, postorbital septum, frontal bone (R) |
| 38 | Macaca mulatta 2 (F) | 4 delta stacked rosettes | Postorbital bar; zygomatic arch; mandibular corpus (L) |
| 42 | Macaca mulatta 5 (F) | 2 delta stacked rosettes | Postorbital bar; postorbital septum (R) |
| 46 | Macaca mulatta 5 (F) | 4 delta stacked rosettes | Postorbital bar (R) |
| 47 | Macaca mulatta 4 (F) | 4 delta stacked rosettes | Dorsal orbital; orbital roof; postorbital bar; postorbital septum (R) |
| 48 | Macaca mulatta 4 (F) | 4 delta stacked rosettes | Postorbital bar (L) |
| 57 | Chlorocebus aethiops | 3 delta stacked rosettes | Bar (R), corpus (R), dorsal orbital (R) |
The animals were food-deprived for 24 h before each experiment. The animals were then either heavily sedated using an intramuscular injection of ketamine and acepromazine or anesthetized using inhalant isofluorane. To eliminate discomfort to the animals and to abet hemostasis, a local anesthetic (2% lidocaine HCl with epinephrine) was infiltrated subcutaneously over the area where the strain gage was to be bonded. About 5 min after infiltration, a small incision was made in the skin overlying the gage site and the periosteum elevated to expose the bone. A small area of the cortical bone was degreased with clinical grade chloroform and neutralized [M-Prep Neutralizer 5A (Ammonia water); Measurement Group Inc., Raleigh, NC, USA], then the rosette was bonded to it with a cyanoacrylate adhesive. To prevent movements of the lead wires from causing strain in the gage, the lead wires were bonded to the bone for 3–4 mm using the same adhesive. Following bonding of the strain gage and wires, the incision was sutured closed with the lead wires of the strain gage passing out through the incision. The lead wires were secured to the skin in areas where skin movement is minimal. Dorsoventral, lateral and anteroposterior radiographs were taken to document strain gage position and orientation.
The macaques were placed in a commercially available restraint (XPL-517-CM; Plas Labs, Lansing, MI, USA) that restrained an animal's arms while enabling the head and neck to move freely. The animals were allowed to recover for at least 1 h after isofluorane anesthesia and up to 2 h after ketamine sedation before data collection.
Each of the three elements of the rosettes was connected to form one arm of a Wheatstone Bridge. Bridge excitation was 2 V. Voltage changes were conditioned and amplified on a Vishay 2100 system, and then recorded on a PC at between 2.7 and 10 kHz (Table 1). Data acquisition to the PCs was controlled using lab-view software (National Instruments, Austin, TX, USA) running in Windows 3.1 NT.
The animals were presented hard apricots, hard prunes with pits, gelatin candies (‘gummi bears’, ‘jelly beans’), nuts (almonds or Brazil nuts), apples, taffy (chewy candy), and tootsie rolls (chewy candy). Strains were recorded while the animals incised and chewed these foods. Chewing side was recorded.
After each recording session (or Experiment) the animal was again anesthetized and radiographs were taken to document strain gage position and orientation. The gages were then removed, the wound cleaned and closed with sutures, analgesics and antibiotics were administered, and the animal was returned to its cage.
Strain analysis
The data were analyzed in igor pro 4.0 (WaveMetrics, Inc., Lake Oswego, OR, USA) using custom written software. The strain data were sampled at a rate of 1000 Hz then converted to microstrain (με) using calibration files made during the recording sessions. The strain tracings were examined along with simultaneous electromyograms (EMGs) and the video tapes of the experiments were examined to identify movement artifacts and chewing side. Sequences were selected for analysis on the basis of length, the clarity of chewing side, and the lack of food manipulation other than incision and mastication. Early power strokes in a sequence were excluded if the animal was manipulating food, and late power strokes were excluded if the magnitudes of the strains decreased so as to be unreliably distinguishable from noise (which ranged from 5 to 10 mV in each channel).
Strain (ε), a dimensionless unit equaling the change in length of an object divided by its original length, is measured in microstrain (με) units which are equal to 1 × 10−6 inches per inch, or mm mm−1. Tensile strain is registered as a positive value and compressive strain as a negative value. The maximum principal strain (ε1) is usually the largest tensile strain value, whereas the minimum principal strain is usually the largest compressive strain value (ε2). ε1 minus ε2 is equal to the maximum shear strain, or γ-max. For selected sequences, the direction of the maximum principal strain relative to the A-element of the gage, the magnitude of the shear strains, and the ratio of maximum to minimum strains (ε1/| ε2|) were calculated with standard equations (Dally & Riley, 1965). The magnitude and timing of the peak shear strain were calculated for each power stroke, and then the direction of the maximum principal strain and the ratio of maximum to minimum strains at the same point in time were calculated.
In vivo data analyses
Previous reports have illustrated the mean of the peak ε1 orientation during left and right chews and incisions (e.g. Hylander et al. 1991; Ross & Hylander, 1996a,b; Ross, 2001). In this study, figures illustrate the peak ε1 and ε2 orientation and magnitude recorded during every power stroke analyzed, with the results presented as plots of strain vectors overlaid on diagrams of macaque skulls. These illustrations allow intuitive estimation of relative magnitudes of peak tensile and compressive strains, an appreciation of the range of strain orientations recorded, as well as relationships between strain orientations and strain magnitudes. The strain vector plots were created in igor pro using custom software that converts strain orientations (in degrees) and magnitudes (in microstrain) to polar coordinates. Skull images were output from the FEM of the macaque skull and oriented so that the surface of the gage site was approximately parallel with the plane of the illustration. The orientations of the vectors relative to the skull images were determined from notes and radiographs taken during the surgeries, as explained in the figure captions. Maximum principal (tensile) strains, or ε1, are in red; minimum principal (compressive) strains, or ε2, are in blue.
Quantitative analyses of the data were performed using oriana 2.02e (Kovach Computing Services, http://www.kovcomp.com). Circular statistics were calculated for the orientations of ε1 at each gage site, with chew cycles grouped according to whether the animal chewed ipsilateral or contralateral to the gage site, yielding ‘working-side’ and ‘balancing-side’ chews, respectively. Strain orientations recorded from the same area during different experiments were converted to a common reference frame to enable comparisons between experiments and between the in vivo and FEM data. The strain orientations from the postorbital septum, orbital roof and dorsal orbital region were calculated relative to the plane of the orbital opening; the data from the postorbital bar were oriented relative to a horizontal line through the orbits. The statistics presented are: the angle (μ) of the mean vector relative to the A-element of the strain gage; the length of the mean vector (r), ranging from 0 to 1, with a larger r value indicating the observations are clustered more closely around the mean than a lower r; the concentration (κ), the maximum likelihood estimate of the population concentration (Fisher, 1993; Mardia & Jupp, 2000), a parameter specific to the von Mises distribution that measures the departure of the distribution from a uniform distribution; the circular variance V, calculated as V=1 − r; the circular standard deviation S =[−2 ln(r)]½ (in radians); the standard error of the mean (formula 4.42 in Fisher, 1993); and the 95% and 99% confidence intervals derived from the standard error. (Note that the length of the mean vector is not an estimate of the mean magnitude of ε1, but instead an estimate of the degree to which the strain orientations cluster.) In addition, results of Rayleigh's test of uniformity are presented, along with Watson's U2 test to determine whether the data are derived from a von Mises distribution. To determine whether working and balancing side deformation regimes differ, mean ε1 orientations recorded during chewing on left and right sides were compared using a nonparametric Mardia–Watson–Wheeler test when the data did not match a von Mises distribution, and a Watson–Williams F-test when they did. To determine whether strain orientation changed as the magnitude of loading increased, circular-linear correlation coefficients were calculated between ε1 orientation and magnitude following Zar (1999) with tests of significance using the approximation of the F distribution presented by Mardia & Jupp (2000). There is no sign to these correlations; however, after examination of bivariate plots of orientation vs. magnitude, signs were added to the results table to indicate whether the angle became oriented more clockwise (a negative sign) or more counterclockwise (positive sign) with increasing strain magnitude.
Three-way anova (general linear model in spss for Windows 8.0) was used to investigate the effects of experiment, food and chewing side (i.e. working or balancing) on shear strain magnitudes at all sites. Post hoc tests of differences in means were performed using a Games–Howell pairwise comparison test (which does not assume homogeneity of variances).
Strain gradients were documented using pairwise t-tests of mean differences in shear strain recorded simultaneously at each site. Pairwise comparisons between working and balancing sides were not possible because in each experiment, strain gages were only placed on one side of the face. t-Tests of independent samples were used to compare strain magnitudes recorded at the same site when it was on working and balancing sides.
Finite-element modeling
Finite-element analysis (FEA) or modeling (FEM) is an engineering technique used to examine how structures of complex design respond to external loads (Huiskes & Chao, 1983; Cook et al. 2002). The structure of interest (e.g. a skull) is modeled as a mesh of simple bricks and tetrahedra (finite elements) joined at nodes. The elements are assigned material properties and certain nodes are constrained against motion, forces are applied, and displacements, stresses and strains at each node and within each element are calculated. Recent advances in computer software and imaging technology have made it possible to capture and digitally reconstruct skeletal geometry with great precision, thereby facilitating the generation of detailed FEMs of bony structures, including non-human vertebrate crania (Rayfield et al. 2001; Strait et al. 2002, 2005, 2007, 2008, 2009; Rayfield, 2004, 2005a,b, 2007; Dumont et al. 2005; Richmond et al. 2005; Kupczik et al. 2007; McHenry et al. 2007; Moazen et al. 2007, 2008a,b, 2009; Moreno et al. 2007, 2008; Bourke et al. 2008; Pierce et al. 2008; Rayfield & Milner, 2008). However, the incorporation of realistic muscle forces, bone material properties, modeling constraints, and experimental bone strain data are equally important components of FEA that are necessary to ensure biologically meaningful results (Richmond et al. 2005; Ross et al. 2005; Strait et al. 2005; Rayfield, 2007).
The finite-element model of the skull of Macaca used to derive our predictions regarding deformation regimes in the macaque facial skeleton has been described previously (Ross et al. 2005; Strait et al. 2005). Briefly, it was built by digitizing 61 CT scans 2-mm-thick of a Macaca fascicularis skull (housed at the National Museum of Natural History, Smithsonian Institution) in CAD Software (Dassault Systems Solidworks Corp., Concord, MA, USA). A mesh of 311 047 brick and tetrahedral elements was created in algor fem pro (Autodesk Inc., Pittsburgh, PA, USA) (Fig. 3A). The model was assigned material properties based on data derived from macaque skulls (Wang & Dechow, 2006). The FEM was converted to nastran format and imported into strand 7.4. The data presented here were extracted from the model as solved by strand 7.4.
The model was loaded in a manner designed to approximate in vivo loading during mastication at unknown bite points along the left postcanine toothrow. External forces generated by four muscles on each side of the head were modeled (superficial and deep masseter, medial pterygoid and anterior temporalis) for a total of eight muscle loads. Relative muscle force magnitudes were calculated using electromyographic data (Ross et al. 2005) and data on physiological cross-sectional area collected according to Antón (1993). One node on the working side articular eminence was fixed against translation along Y and Z directions, one node on the balancing side eminence was fixed against translation in X, Y and Z directions, and the model was ‘solved’ six different times, all with the same external muscle forces and temporomandibular joint (TMJ) constraints, but each with a different bite point constraint condition. In each of these bite point conditions, the medial cusps on left upper postcanine tooth/teeth were constrained against translation in X, Y and Z. The constraint conditions were: left M3 constrained; left M2 constrained; left M1 constrained; left P4 constrained; left P3 constrained; and all of the left side postcanine teeth constrained together. In this way we sought to estimate, at all in silico gage sites, variance in strain regimes associated with variation in bite point. Bite point is unknown in vivo, so this method provides a reasonable and conservative estimate of model variance to compare with the in vivo situation.
In silico data extraction and analyses
To compare the surface strains recorded in vivo with the strains on the surface of the macaque model the strain orientations on the surfaces of the FEM need to be calculated at in silico‘gage sites’. The centroid locations and the strain tensors for the external surface bricks of the model were exported from strand and imported into matlab®. Custom-written code (Iriarte-Diaz & Ross, 2010; see Supporting Information Data S1) was used to calculate the orientation and magnitude of maximum and minimum principal strain on bricks in the macaque FEM that corresponded to the bone surfaces from which in vivo strain data were collected. The software first allows the user to interactively define a ‘gage site’ on the FEM surface, including defining the local coordinate system of the gage; then it transforms the strain tensors of the bricks in the gage site into the coordinate system of the gages according to the equations presented in Appendix 1. One of us (C.F.R.) selected the areas on the model surface that most closely approximated the position of the gages in the in vivo experiments. The vectors representing the orientation and magnitude of the principal strains on the gage sites were exported from matlab® and were used to create vector plots that were exported to adobe illustrator® where they were oriented into the coordinate system of the in vivo strain data. These data are presented for comparison in the figures. In each figure the mean vector recorded at an in silico gage site under one bite point constraint condition is represented by a colored line.
Results
Postorbital bar
In vivo strain orientations
Vectors representing the maximum principal strains recorded from the anterior surface of the postorbital bar in vivo are presented in Fig. 6. Strain data are reported from the left postorbital bar in two experiments (38 and 48) and from the right postorbital bar in three experiments (42, 46, 47). The images in Fig. 6 present all the working side data on the left postorbital bar and all balancing side data on the right postorbital bar, regardless of the side from which the data were actually collected. No usable strain data were recorded from the balancing side during experiment 48.
In three of the five experiments for which working side data are available (42, 46, 48), ε1 orientations are primarily inferolateral, oriented between 45 and 67° counterclockwise of the horizontal. In experiments 38 and 47, ε1 orientations are horizontal on the working side, deviating from the horizontal by only 1–2°. In three of the four experiments for which balancing side data are available, mean ε1 orientations are primarily inferolateral, ranging from ca. 50–67° counterclockwise of the horizontal. The exceptions are the data from the balancing side in experiment 38, which are oriented almost directly laterally (ranging from 2.7 to 6° clockwise of the horizontal). In all experiments, strain orientations recorded during chews ipsilateral to the gage are significantly different from those recorded contralateral to the gage (Table 2). In all cases, the working side ε1 orientations are directed more laterally, while those on the balancing side are oriented slightly more inferiorly. In all experiments except for experiment 47, strain orientation on the anterior surface of the postorbital bar is correlated with strain magnitude, i.e. the deformation regime in the bar changes with increasing strain magnitude (Table 2). In all but one case, ε1 orientations become more inferiorly directed as ε1 increases. During balancing side chews in experiment 42, ε1 orientations rotate clockwise as ε1 increases, but only slightly (Fig. 6).
Table 2.
Descriptive circular statistics for in vivo bone strain orientations recorded from anterior surface of postorbital bar.
| Experiment | 38 | 38 | 42 | 42 | 46 | 46 | 47 | 47 | 48 |
|---|---|---|---|---|---|---|---|---|---|
| Side | Balancing | Working | Balancing | Working | Balancing | Working | Balancing | Working | Working |
| n | 421 | 458 | 183 | 117 | 194 | 128 | 21 | 50 | 179 |
| Mean vector (μ) | −4.373 | 1.316 | 53.386 | 54.524 | 66.968 | 50.119 | 50.596 | 2.307 | −75.133 |
| Length of mean vector (r) | 0.904 | 0.97 | 0.998 | 0.997 | 0.974 | 0.945 | 0.999 | 0.974 | 0.835 |
| Median | 0.338 | 2.968 | 53.195 | 54.303 | 68.717 | 47.402 | 50.56 | 3.656 | −71.58 |
| Concentration | 5.513 | 16.8 | 266.484 | 148.075 | 19.844 | 9.335 | 568.908 | 19.422 | 3.362 |
| Circular variance | 0.048 | 0.015 | 9.39E-04 | 0.002 | 0.013 | 0.028 | 4.40E-04 | 0.013 | 0.083 |
| Circular SD | 12.85 | 7.099 | 1.757 | 2.358 | 6.515 | 9.651 | 1.202 | 6.588 | 17.219 |
| 95% confidence interval (±) for μ | −3.147 | 1.967 | 53.132 | 54.097 | 66.051 | 48.447 | 50.082 | 0.481 | −72.628 |
| −5.599 | 0.666 | 53.641 | 54.952 | 67.885 | 51.79 | 51.11 | 4.133 | −77.639 | |
| 99% confidence interval (±) for μ | −2.762 | 2.171 | 53.052 | 53.963 | 65.763 | 47.922 | 49.921 | −0.093 | −71.841 |
| −5.984 | 0.462 | 53.721 | 55.086 | 68.173 | 52.315 | 51.272 | 4.707 | −78.426 | |
| Rayleigh test (Z) | 344.271 | 430.725 | 182.313 | 116.21 | 184.22 | 114.267 | 20.963 | 47.425 | 124.725 |
| Rayleigh test (P) | < 1E-12 | < 1E-12 | < 1E-12 | < 1E-12 | < 1E-12 | < 1E-12 | 3.85E-09 | < 1E-12 | < 1E-12 |
| Watson's U2 test (von Mises, U2) | 3.948 | 1.718 | 0.061 | 0.191 | 2.525 | 1.014 | 0.035 | 0.052 | 0.752 |
| Watson's U2 test (P) | < 0.005 | < 0.005 | 0.5 > P > 0.25 | < 0.005 | < 0.005 | < 0.005 | > 0.5 | 0.5 > P > 0.25 | < 0.005 |
| Test for working/balancing differences | |||||||||
| W | 29.019 | 7.226 | 135.436 | 44.363 | |||||
| P | < 0.0001 | 0.027 | < 0.0001 | < 0.0001 | |||||
FEM orientations
Strain orientations on the anterior surface of the postorbital bar vary with location, as shown by the FEM strain fields shown in Fig. 7 (top). The in vivo strain gage recordings were taken from the anterior surface of the bar at mid-orbit height (upper bar, experiments 38, 42, 46, 47) (Fig. 7, middle) or at approximately one-third of orbit height (lower bar, experiment 48) (Fig. 7, bottom). One upper and one lower postorbital bar gage site were sampled on both working and balancing sides in silico. Each of the colored vectors in Fig. 7 represents the mean strain orientations for all bricks underlying the in silico‘gages’ under a different in silico‘bite point’ constraint condition. The ranges of these mean ε1 vectors are represented by black arrows that were then added to the vector plots of the in vivo strains in Fig. 6.
Fig. 7.

Strain orientations on the anterior surface of the postorbital bar on the right (balancing) and left (working) sides of the FEM of the macaque cranium. Each line is a vector representing the mean orientation and magnitude of maximum (ε1) (red to yellow) and minimum (ε2) (blue to green) principal strains from all the elements at the gage site. Note that the variance among the vectors from the in silico gage sites is due to variation in bite point, and the variance among vectors from in vivo gage sites is due to variation in magnitude and location of bite force, joint reaction forces and muscle forces. The top figures show the strain field of maximum principal strain orientations at the centroid of each element. Note that the strain field vectors values were not transformed into the coordinate system of the model surface, which the strain gages sample, whereas the bite point means were appropriately transformed. The second row of figures shows the orientations of the mean tensile and compressive in silico strain vectors at the lower gage site. The third row of figures shows the orientations of the mean tensile and compressive in silico strain vectors at the upper gage site. The ranges of the maximum (ε1) principal strains in silico were transferred to Fig. 6 for comparison with the in vivo strain vectors using the reference line indicated.
On both working and balancing sides and at both upper and lower bar sites, ε1 orientations are oriented supero-inferiorly along the lateral edge of the bar's anterior surface (Fig. 7). At the upper bar site, ε1 is oriented obliquely inferolaterally on both working and balancing sides, with the working side strains being slightly more horizontal than the balancing (Fig. 7). At the lower bar site, working ε1 orientations are similar to those at the upper bar site. At the balancing side lower bar site, ε1 orientations are predominantly laterally directed.
The in vivo experiments exhibited sufficient variation between individuals that it would have been impossible for the in silico data to match the data from all of them (i.e. when two experiments exhibit non-overlapping ranges in strain orientation, the single, average in silico vector obviously cannot fall within the ranges of both). At the lower bar gage site, the in vivo ε1 orientations from experiment 48 include the entire range of orientations sampled in silico. At the upper bar site, the range of orientations sampled in silico broadly overlapped those recorded on the working and balancing sides in experiment 46 and on the working side in experiment 42, and are only ca. 10 degrees different from the balancing side data collected during experiment 42. In contrast, the in silico data are not overlapped by the very horizontally directed ε1 orientations recorded during experiments 38 and 47. In sum, the range of in silico mean vectors recorded from the bar gage sites were well matched by in vivo data from two experiments (38 and 46), and were matched or closely approximated by the data from one other (experiment 42).
Postorbital septum
In vivo strain orientations
Strain vectors recorded from the intraorbital surface of the postorbital septum are illustrated in Fig 8 and 9. Strain orientations are presented in Table 3 as angles relative to the plane of the orbital aperture, represented in Fig 8 and 9 by a line following the anterior surface of the postorbital bar. Strain was recorded from the zygomatic portion of the septum, at mid-orbit height, in three experiments (10, 42, 47) (Fig. 8) and from the frontal portion at the top of the septum in experiment 32 (Fig. 9). In two of the three experiments on the zygomatic portion of the septum, ε1 orientations on the working side are anteroinferiorly directed at 121 and 134° relative to the orbital plane. In experiment 47, ε1 orientations on the working side are more superiorly directed at only 65° to the orbital plane. Strains on the balancing side are much more variable than those on the working side in experiments 10 and 42. Comparison of the concentration statistics (κ) also reveals that at the zygomatic sites (experiments 10, 42, 47) strain orientations recorded on the working side are more concentrated than those recorded on the balancing side. However, despite this variability, all balancing side ε1 orientations average an anteroinferior orientation ranging from 132 to 167° relative to the orbital plane. In all experiments, strain orientations recorded during chews ipsilateral to the gage are significantly different from those recorded contralateral to the gage (Table 3). In all cases the working side ε1 orientations are rotated clockwise relative to the balancing side ε1 orientations (Fig. 8).
Fig. 8.
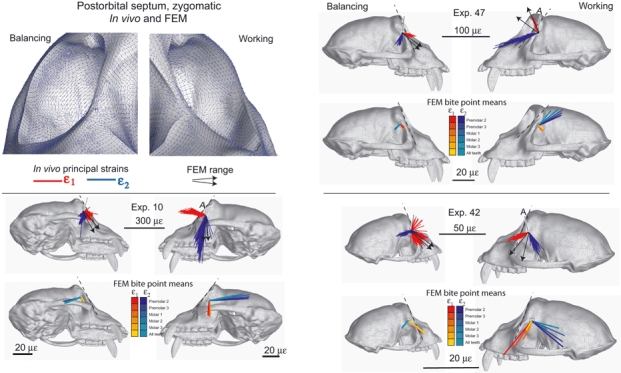
Strain vector plots of strain data collected from the intraorbital surface of the zygomatic portion of the postorbital septum. Septum data were collected from the right side of the skull, but the working side data are reflected onto the left side to facilitate comparison with the FEM data. The figures in the top left panel show the strain field of maximum principal strain orientations at the centroid of each element. Note that the strain field vectors values were not transformed into the coordinate system of the model surface, which the strain gages sample, whereas the bite point means were appropriately transformed. The remainder of the panels pair figures showing the orientations of the in vivo tensile and compressive strain vectors recorded during experiments 10, 47 and 42 with the in silico data from corresponding ‘gage sites’ on the model. For the in silico data, each line is a vector representing the mean orientation and magnitude of maximum (ε1) (red to yellow) and minimum (ε2) (blue to green) principal strains from all the elements at the gage site. Note that the variance among the vectors from the in silico gage sites is due to variation in bite point, and the variance among vectors from in vivo gage sites is due to variation in magnitude and location of bite force, joint reaction forces and muscle forces. The black arrows on the in vivo plots represent the extremes of the ranges of the mean ε1 orientations from the in silico‘gage sites’. All strain data are presented as seen through the bone of the septum. In vivo strain orientations are presented in Table 2 and in this figure as angles relative to a line following the anterior surface of the postorbital bar in the plane of the orbital aperture.
Table 3.
Descriptive circular statistics for in vivo bone strain orientations recorded from intraorbital surface of postorbital septum.
| Experiment | 10 | 10 | 32 | 32 | 42 | 42 | 47 | 47 |
|---|---|---|---|---|---|---|---|---|
| Side | Balancing | Working | Balancing | Working | Balancing | Working | Balancing | Working |
| n | 268 | 240 | 148 | 37 | 183 | 117 | 181 | 107 |
| Mean vector (μ) | 132.565 | 121.25 | 36.287 | 14.932 | 167.207 | 134.695 | 141.971 | 65.667 |
| Length of mean vector (r) | 0.782 | 0.931 | 0.969 | 0.904 | 0.799 | 0.972 | 0.98 | 0.994 |
| Median | 130.328 | 121.378 | 38.827 | 13.765 | 169.729 | 135.729 | 141.687 | 65.788 |
| Concentration | 2.655 | 7.549 | 16.646 | 5.501 | 2.852 | 17.96 | 24.828 | 79.962 |
| Circular variance | 0.109 | 0.034 | 0.015 | 0.048 | 0.1 | 0.014 | 0.01 | 0.003 |
| Circular SD | 20.111 | 10.814 | 7.132 | 12.867 | 19.182 | 6.858 | 5.809 | 3.214 |
| 95% confidence interval (±) for μ | 130.184 | 119.883 | 35.138 | 10.791 | 164.457 | 133.452 | 141.125 | 65.058 |
| 134.947 | 122.617 | 37.436 | 19.072 | 169.957 | 135.938 | 142.818 | 66.276 | |
| 99% confidence interval (±) for μ | 129.436 | 119.453 | 34.777 | 9.491 | 163.593 | 133.062 | 140.859 | 64.867 |
| 135.695 | 123.047 | 37.797 | 20.372 | 170.821 | 136.328 | 143.083 | 66.468 | |
| Rayleigh test (Z) | 163.72 | 208.128 | 139.105 | 30.241 | 116.879 | 110.483 | 173.708 | 105.662 |
| Rayleigh test (P) | < 1E-12 | < 1E-12 | < 1E-12 | < 1E-12 | < 1E-12 | < 1E-12 | < 1E-12 | < 1E-12 |
| Watson's U2 test (von Mises, U2) | 1.041 | 0.306 | 2.581 | 0.095 | 1 | 0.11 | 0.051 | 0.274 |
| Watson's U2 test (P) | < 0.005 | < 0.005 | < 0.005 | 0.1 > P > 0.05 | < 0.005 | 0.1 > P > 0.05 | 0.5 > P > 0.25 | < 0.005 |
| Test for working/balancing differences | ||||||||
| W | 68.318 | 57.146 | 172.777 | 115.667 | ||||
| P | < 1E-12 | < 1E-12 | < 1E-12 | < 1E-12 | ||||
Strain orientations at the frontal bone site recorded during experiment 32 are differently oriented relative to the orbital plane than the strains recorded at the lower, zygomatic site. ε1 orientations on the working side closely approximate the plane of the orbital margin, whereas those on the balancing side are rotated about 36º clockwise of the orbital margin (Fig. 9).
Calculations of circular–linear correlation coefficients between orientation and magnitude revealed significant relationships in all but one case, the exception being the balancing side of experiment 47. However, after examination of the bivariate plots of orientation vs. magnitude, and the vector diagrams, it was not obvious that there was a consistent trend for higher strains to be rotated more clockwise or more counterclockwise than lower strains in any case. Rather, as strain magnitudes increase, strains converge on a preferred orientation.
FEM orientations
Strain orientations and magnitudes vary across the intra-orbital surface of the postorbital septum in silico. On both working and balancing sides ε1 orientations on the upper half of the septum (frontal and part of zygomatic bone) are parallel with or slightly oblique to the plane of the orbital rim, whereas more inferiorly they are close to orthogonal to the orbital plane (Fig 8 and 9). In comparison with the in vivo data recorded during experiment 32, average in silico ε1 orientations recorded from the frontal portion of the FEM septum fall within the range of the values recorded on the working side, but not within the range of the values recorded on the balancing side (Fig. 9). The range of ε1 orientations recorded from the zygomatic portion of the septum in silico is within the range of values recorded on the balancing side during experiments 10 and 42, but outside the range of values recorded during experiment 47. The working side in silico strains broadly overlap the working side strains recorded during experiment 47, but not during experiments 10 and 42.
Supraorbital torus
In vivo strain orientations
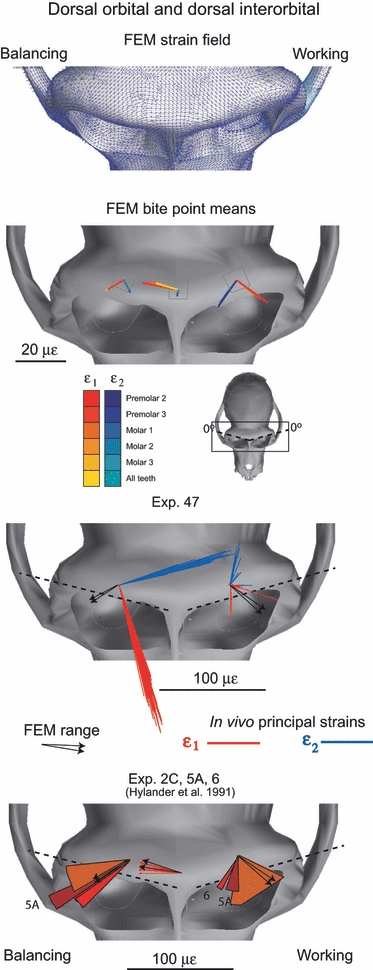
In Fig. 10 the ε1 strain orientations from our FEM are compared with those recorded at the dorsal orbital site during experiment 47 and with those reported from the dorsal orbital and dorsal interorbital sites by Hylander et al. (1991). In Fig. 11, ε1 strain orientations from our FEM are compared with those recorded from the orbital roof (i.e. the intraorbital surface of the torus) during experiments 47 and 13. The strain vectors for these intraorbital sites are viewed in Fig. 11through the supraorbital torus, i.e. the strain vectors were reflected about the A-element of the strain gage so as to be viewed from the bone out to the gage, rather than from the gage down towards the bone. In Fig. 12 the ε1 strain orientations from our FEM are compared with those reported from the rostral interorbital site by Hylander et al. (1991). In all figures, the working side data are presented in the left orbit and all balancing side data are presented in the right orbit.
Fig. 10.
Strain vector plots of strain data collected from dorsal orbital surfaces of the supra-orbital torus. The top figure shows the strain field of maximum principal strain orientations at the centroid of each element. Note that the strain field vectors values were not transformed into the coordinate system of the model surface, which the strain gages sample, whereas the bite point means were appropriately transformed. The second figure illustrates in silico data from corresponding ‘gage sites’ on the model. For the in silico data, each line is a vector representing the mean orientation and magnitude of maximum (ε1) (red to yellow) and minimum (ε2) (blue to green) principal strains from all the elements at the gage site. Note that the variance among the vectors from the in silico gage sites is due to variation in bite point, and the variance among vectors from in vivo gage sites is due to variation in magnitude and location of bite force, joint reaction forces and muscle forces. The in vivo strain vectors for experiment 47 are shown in the third figure. In vivo strain orientations are presented in Table 4 as angles relative to the plane of the orbital aperture. Also shown is the range of ε1 vectors recorded from the dorsal orbital site during three experiments reported by Hylander et al. (1991). Strain data for the balancing side shown in the skull's left orbit were actually recorded from within the right orbit: they are illustrated on the left side after reflecting them about the mid-sagittal plane. The black arrows on the in vivo plots represent the extremes of the ranges of the mean ε1 orientations from the in silico‘gage sites’.
Fig. 11.

Strain vector plots of strain data collected from the intra-orbital surfaces of the supraorbital torus. The top figure shows the strain field of maximum principal strain orientations at the centroid of each element. Note that the strain field vectors values were not transformed into the coordinate system of the model surface, which the strain gages sample, whereas the bite point means were appropriately transformed. The second figure illustrates in silico data from corresponding ‘gage sites’ on the model. For the in silico data, each line is a vector representing the mean orientation and magnitude of maximum (ε1) (red to yellow) and minimum (ε2) (blue to green) principal strains from all the elements at the gage site. Note that the variance among the vectors from the in silico gage sites is due to variation in bite point, and the variance among vectors from in vivo gage sites is due to variation in magnitude and location of bite force, joint reaction forces and muscle forces. The in vivo strain vectors for experiments 47 and 13 are shown in the bottom two figures. The black arrows on the in vivo plots represent the extremes of the ranges of the mean ε1 orientations from the in silico‘gage sites’. In vivo strain orientations are presented in Table 4 as angles relative to the plane of the orbital aperture. The strain vectors for the intraorbital sites are viewed through the supraorbital torus. To illustrate their orientation, the strain vectors were reflected about the A-element of the strain gage. In addition, it should be noted that the strain data for the working side shown in the skull's left orbit were actually recorded from within the right orbit: they are illustrated on the left side after reflecting them about the mid-sagittal plane.
Fig. 12.
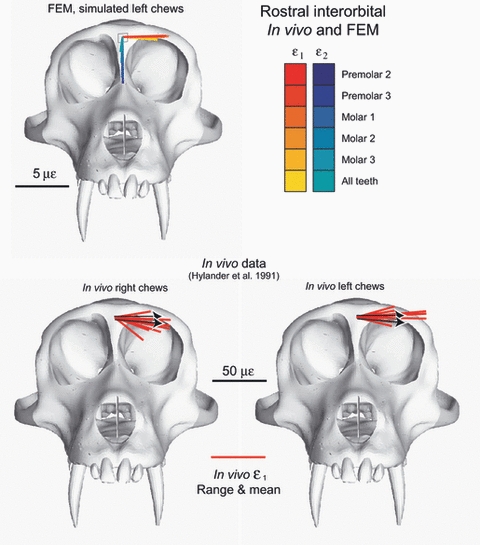
Strain vector plots of strain data collected from the rostral interorbital gage site in vivo and from the FEM. The top figure illustrates in silico data from the rostral interorbital ‘gage site’ on the model. Each line is a vector representing the mean orientation and magnitude of maximum (ε1) (red to yellow) and minimum (ε2) (blue to green) principal strains from all the elements at the gage site. Note that the variance among the vectors from the in silico gage sites is due to variation in bite point, and the variance among vectors from in vivo gage sites is due to variation in magnitude and location of bite force, joint reaction forces and muscle forces. The in vivo strain vectors for the data presented by Hylander et al. (1991) are shown in the bottom two figures. The red lines indicate the means and ranges of the data. The black arrows on the in vivo plots represent the extremes of the ranges of the mean ε1 orientations from the in silico‘gage’ sites.
In experiment 47, the working side in vivo ε1 orientations at the dorsal orbital site ranged widely from anteromedial to posterolateral, whereas on the balancing side they were oriented anterolaterally. During the three experiments reported by Hylander et al. (1991), the strain orientations on the balancing side were more laterally directed than those recorded in the one experiment (47) reported here. Strain orientations from the intraorbital, orbital roof site are predominantly laterally directed on both working and balancing sides in both experiments 47 and 13. Strain orientations do not deviate from the line of the upper orbital margin by more than 10° on both working and balancing sides (Table 4). During experiment 47 on the balancing side, strain data were successfully recorded simultaneously from both the superior and inferior surfaces of the supraorbital torus: these strains are orthogonal to each other. On the working side, good quality simultaneous strain data are less common, but the laterally directed strains recorded from the inferior surface in experiments 13 and 47 are roughly orthogonal to those recorded from the superior surface by Hylander et al. (1991). Mardia–Watson–Wheeler and Wheeler–Williams tests reveal that strain orientations from working and balancing orbital roofs are significantly different. Linear–circular correlations reveal significant relationships between ε1 orientations and magnitudes in both experiments on the orbital roof. As illustrated in Fig 10 and 11, ε1 orientations rotate counterclockwise on the working side and clockwise on the balancing side as strain magnitudes increase, making the ε1 orientations more transversely oriented.
Table 4.
Descriptive circular statistics for in vivo bone strain orientations recorded from dorsal and intraorbital surfaces of supraorbital torus.
| Experiment (site) | 13 | 13 | 47 (roof) | 47 (roof) | 47 (dors orb) | 47 (dors orb) |
|---|---|---|---|---|---|---|
| Side | Balancing | Working | Balancing | Working | Balancing | Working |
| n | 50 | 52 | 127 | 153 | 153 | 107 |
| Mean vector (μ) | 1.159 | 5.073 | 9.088 | −2.177 | 34.917 | 72.449 |
| Length of mean vector (r) | 0.988 | 0.993 | 0.992 | 0.977 | 0.796 | 0.891 |
| Median | 1.12 | 4.812 | 8.682 | −3.275 | 36.639 | 75.062 |
| Concentration | 43.419 | 75.606 | 60.173 | 21.726 | 2.816 | 4.868 |
| Circular variance | 0.006 | 0.003 | 0.004 | 0.012 | 0.102 | 0.055 |
| Circular SD | 4.373 | 3.306 | 3.709 | 6.22 | 19.342 | 13.787 |
| 95% confidence interval (±) for μ | −0.053 | 4.175 | 8.443 | −3.162 | 31.885 | 69.841 |
| 2.372 | 5.972 | 9.733 | −1.191 | 37.949 | 75.056 | |
| 99% Confidence interval (±) for μ | −0.434 | 3.893 | 8.24 | −3.472 | 30.933 | 69.022 |
| 2.752 | 6.254 | 9.936 | −0.882 | 38.902 | 75.875 | |
| Rayleigh test (Z) | 48.848 | 51.312 | 124.889 | 145.956 | 96.987 | 84.879 |
| Rayleigh test (P) | < 0.0001 | < 0.0001 | < 0.0001 | < 0.0001 | < 0.0001 | < 0.0001 |
| Watson's U2 test (von Mises, U2) | 0.085 | 0.045 | 0.505 | 0.297 | 0.098 | 0.244 |
| Watson's U2 test (P) | 0.15 > P > 0.1 | > 0.5 | < 0.005 | < 0.005 | 0.1 > P > 0.05 | < 0.005 |
| Test for working/balancing differences | ||||||
| W | F = 25.671 | 162.578 | 121.238 | |||
| P | < 0.0001 | < 0.0001 | < 0.0001 | |||
FEM orientations
The ε1 strain field across the superior surface of the supraorbital torus during a left M1 bite is shown at the top of Fig. 10. ε1 orientations vary across the supraorbital region, with anterolaterally directed orientations on both sides. A line of reversal in strain orientation runs obliquely across the mid-line from the medial corner of the balancing side (right) orbit. Average strain orientations at the dorsal orbital and dorsal interorbital gage sites are reproduced, along with ε2 orientations, in the second row of Fig. 10. The dorsal interorbital strains recorded in silico agree well with those reported by Hylander et al. (1991), falling within the range of values reported by them. Similarly, the in silico ε1 orientations recorded from the balancing side dorsal orbital site match those reported from multiple experiments by Hylander et al. (1991), but they do not match those recorded in our experiment 47 (Fig. 10). The in silico ε1 orientations recorded from the working side dorsal orbital site fall within the range of values reported by Hylander et al. (1991: Table 7) and our data from experiment 47.
The ranges of in silico ε1 orientations recorded from the orbital roof sites overlap those recorded in experiments 13 and 47, with the exception of the working side in experiment 13 (Fig. 11). The in silico data are rotated clockwise by approximately 15º relative to the working side in vivo strains in Experiment 13. The ranges of in silico ε1 orientations recorded from the rostral interorbital site fall within the range of values reported by Hylander et al. (1991) (Fig. 12).
Anterior root of the zygoma
In vivo strain orientations
Maximum and minimum principal strains recorded from the anterior root of the zygoma during experiments 8 and 9 are illustrated in Fig. 13 along with the principal strains sampled from homologous sites on the FEM. Strain orientations in Table 4 are calculated relative to a horizontal plane passing through the tops of the zygomatic arches. In experiment 8, ε1 orientations are almost directly lateral during incision and mastication, with the orientations recorded during mastication being slightly clockwise of those recorded during incision. ε1 orientations on both working and balancing sides are, on average, rotated 13° counterclockwise of the horizontal plane. In experiment 8, strain orientations recorded during left chews are not significantly different from those recorded during right chews. In experiment 9, ε1 orientations are almost directly lateral during mastication. Strain orientations recorded during experiment 9 are significantly different during left and right chews, but the means differ by only 3°. ε1 orientations are, on average, rotated 13° counterclockwise of the horizontal plane on the working side and 16° on the balancing side. Although there are significant relationships between ε1 orientations and magnitudes in both experiments, the differences are small.
Fig. 13.
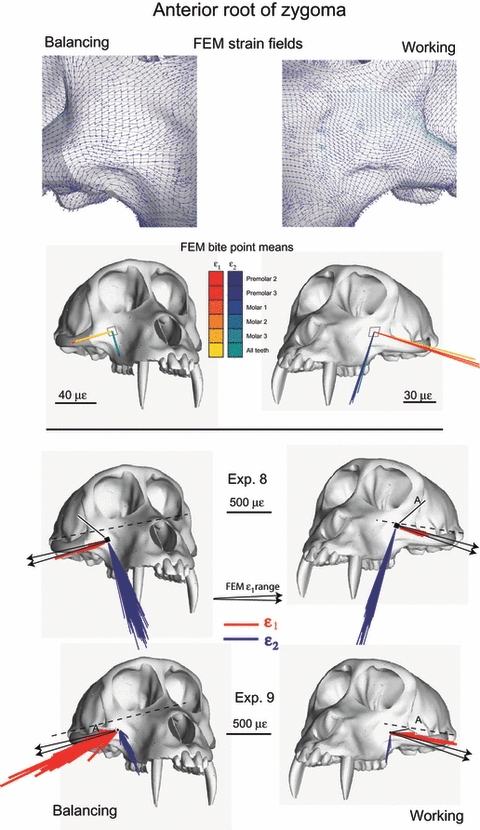
Strain vector plots of in vivo and FEM strain data collected from the anterior root of the zygoma. The top figure shows the strain field of maximum principal strain orientations at the centroid of each element. The second figure illustrates in silico data from corresponding ‘gage sites’ on the model. For the in silico data, each line is a vector representing the mean orientation and magnitude of maximum (ε1) (red to yellow) and minimum (ε2) (blue to green) principal strains from all the elements at the gage site. Note that the variance among the vectors from the in silico gage sites is due to variation in bite point, and the variance among vectors from in vivo gage sites is due to variation in magnitude and location of bite force, joint reaction forces and muscle forces. The third and fourth rows of figures show the in vivo principal strain vectors from experiments 8 and 9. The black arrows on the in vivo plots represent the extremes of the ranges of the mean ε1 orientations from the in silico‘gage sites’. Strain orientations in Table 6 are calculated relative to a horizontal plane passing through the zygomatic arches.
FEM strain data
The ε1 strain fields across the anterior root of the zygoma on the working and balancing sides are shown at the top of Fig. 13. The orientations and magnitudes of maximum and minimum principal strains at the FEM locations corresponding to the gage sites on the working and balancing anterior zygoma roots are indicated. The range of ε1 orientations recorded from the balancing side FEM, illustrated with black arrows, is oriented slightly clockwise of the orientation on the working side. The mean ε1 orientations from the anterior zygoma root in silico lie within the range of strain orientations recorded in vivo during experiments 8 and 9, except for the balancing side during experiment 9, which is slightly more horizontal than those recorded in silico (Fig. 13).
Zygomatic arches
In vivo strain orientations and FEM data
Hylander & Johnson (1997a,b); reported strain orientations and magnitudes recorded from three sites along the zygomatic arches of five M. fascicularis. The vectors of ε1 are reproduced in Fig. 14 and are oriented relative to the line along the bottom of the arch, which is parallel with the reference line of Hylander & Johnson (1997a,b);. Figure 14 also presents the range of mean ε1 strain vectors recorded from these sites on the FEM on the working and balancing sides. The range of ε1 vectors recorded in silico overlap the ranges of the values reported in vivo at the anterior and posterior sites. At the middle zygomatic arch site, in silico strain orientations on the working side fall well outside the in vivo range; on the balancing side, the in silico strain orientations are rotated slightly clockwise of the in vivo data. Close examination of the strain field in the middle of the arch reveals wide variation in strain orientations in this area. Moreover, a slightly more anterior gage position in the model yields strain orientations that overlap those seen in vivo.
Fig. 14.
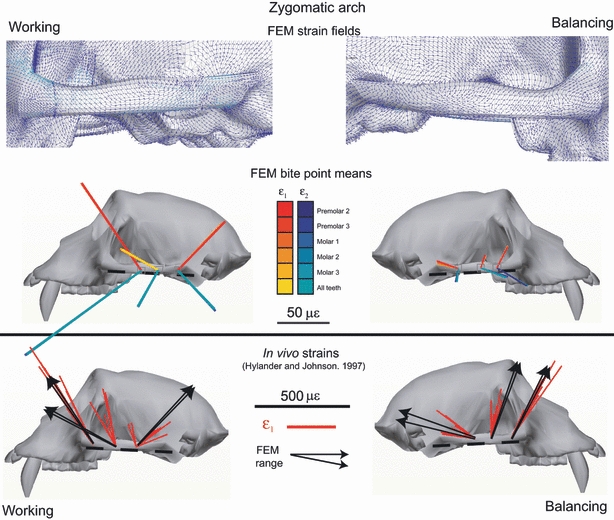
Strain vector plots of in vivo and FEM strain data collected from the zygomatic arch. The in vivo data are from Hylander & Johnson (1997a,b).; The top figure shows the strain field of maximum principal strain orientations at the centroid of each element. The second figure illustrates in silico data from corresponding ‘gage sites’ on the model. For the in silico data, each line is a vector representing the mean orientation and magnitude of maximum (ε1) (red to yellow) and minimum (ε2) (blue to green) principal strains from all the elements at the gage site. Note that the variance among the vectors from the in silico gage sites is due to variation in bite point, and the variance among vectors from in vivo gage sites is due to variation in magnitude and location of bite force, joint reaction forces and muscle forces. The third row illustrates strain vector plots of in vivo strain data from the zygomatic arch reported in Tables 1 and 4 of Hylander & Johnson (1997a,b);. These strain orientations are calculated relative to a horizontal plane passing through the zygomatic arches. The black arrows on the in vivo plots represent the extremes of the ranges of the mean ε1 orientations from the in silico‘gage sites’.
Strain magnitude analyses
Three-way anova revealed significant effects of experiment and food type on shear strain magnitudes at all sites. Post hoc comparisons revealed that mean shear strain magnitudes at the corpus site were not significantly different across experiments 46 and 48, and at the bar site were not significantly different during experiments 38, 46 and 48, but all other sites showed significantly different magnitudes across experiments. Post hoc comparisons revealed that mean shear strain magnitudes did not always differ between foods. For example, strain magnitudes elicited during chewing on apricots, almonds and grapes did not differ from one another, nor did those elicited during feeding on jawbreakers and taffy, and isometric biting on a plastic syringe. The only site where all foods elicited significantly different strain magnitudes was the postorbital septum.
Three-way anovas also revealed that chewing side (i.e. working or balancing) was a highly significant factor (P < 0.0001) in shear strain magnitudes at the dorsal orbital, orbital roof, and postorbital septum sites, but was a less significant factor (P = 0.03) at the corpus site, and was not a significant factor on shear strain magnitudes at the postorbital bar and zygomatic arch sites.
Strain gradients
Pairwise t-tests of mean differences in shear strain recorded simultaneously across the working or balancing sides of the face were possible in 15 cases. On the working side, the rank order of mean shear strains from highest to lowest was separated by significant mean differences in με: arch (389), corpus (318), bar (69), temporal line (20), septum (17), and dorsal orbital + orbital roof. On the balancing side, the rank order of mean shear strains was separated from highest to lowest by significant mean differences in με: arch (390), corpus (400), bar (343), dorsal orbital (103) and orbital roof (26).
Independent sample t-tests of strain magnitudes found shear strains to be significantly different and higher at the bar, arch, corpus and dorsal orbital sites when they were on the balancing side. The postorbital septum showed higher strains on the working than the balancing sides, and the orbital roof evinced no significant difference.
Figure 15 compares the shear strain (γmax) magnitudes recorded in vivo with those recorded from the FEM at 20 sites. At six sites the raw FEM data fall below the range of the in vivo data. This may be because the skull modeled is larger and/or stiffer than that of the animals from which data were gathered. To account for this possibility, the data were standardized by dividing all the strain magnitudes by the strains at the site with the highest strain magnitude (anterior arch). When this was done, most of the FEM values fall within the in vivo range, with the exception of the left septum sites, and the right postorbital bar and dorsal orbital sites. Notable rank order differences between the datasets are the low values on the balancing side (right) zygomatic arch, balancing side (right) postorbital bar and dorsal interorbital region of the FEM, and high values on the working side (left) septum.
Fig. 15.
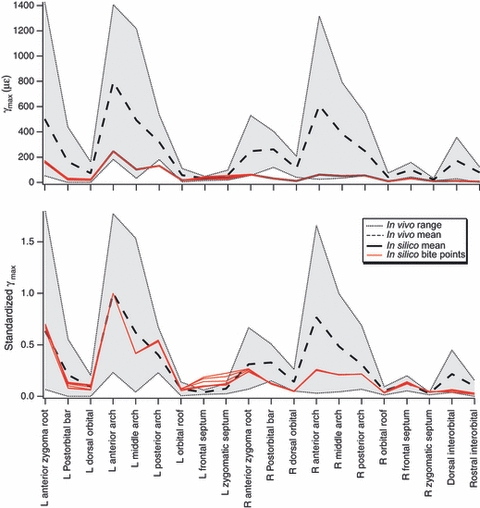
Plots comparing in vivo and FEM γmax values at 20 sites. L = left side = biting side, R = right = balancing side. Top figure presents absolute values of γmax; bottom figure shows γmax standardized by dividing the in vivo data by the average value recorded at the anterior zygomatic arch site and the in silico data by the largest value recorded at the same site. The in vivo mean is the average across all data recorded at that site; the in vivo range was estimated as the largest and smallest values across all experiments of the mean ± 2 SD. In vivo data are from apple chewing data collected in this study and published in the literature (Hylander et al., 1991; Hylander & Johnson, 1997a,b; Strait et al., 2005).
Discussion
This paper presents new bone strain data from the intraorbital (inferior) surface of the supraorbital torus, the intraorbital surface of the postorbital bar and septum, the anterior surface of the postorbital bar, and the anterior surface of the anterior root of the zygoma of macaques during mastication. These data, in combination with published bone strain data from the supraorbital region and zygomatic arch (Hylander et al. 1991; Hylander & Johnson, 1997a,b;), are used to evaluate the accuracy of our finite-element model of the facial skeleton of Macaca, and this model is in turn used to test hypotheses regarding deformation regimes in the craniofacial skeleton of macaques during mastication (Endo, 1966a,b; Rak, 1983; Hylander et al. 1991).
Finite-element models can be ‘validated’ by comparing model output with some variables measured experimentally, such as bite force, in vitro strain gage measurements or, as in this case, in vivo bone strain data (Richmond et al. 2005). The research reported here sought to determine how well bone strain on the surface of our finite-element model matches bone strain data recorded in vivo from chewing macaques. Various uncontrolled factors might produce differences between the FEM and in vivo data that are independent of model accuracy. First, our FEM was built from CT scans of a wild-shot male Macaca fascicularis from a museum collection, whereas the in vivo data come from living, male and female, adult and subadult M. fascicularis and M. mulatta obtained from biological supply companies. Moreover, the bone material properties data incorporated into the model came from a different set of animals, as did the estimates of muscle physiologic cross-sectional area used to load the model. The effects of these variables on comparisons between strain patterns on the surface of the model and those collected in vivo cannot be predicted at present. Secondly, although all care was taken to carefully document the position and orientation of the strain gages in vivo, these cannot be determined as precisely as can in silico‘gage sites’. Therefore, homology of in vivo and in silico gage sites cannot be guaranteed. Thirdly, the in vivo strain data were collected while the animals chewed on food of varying material properties and at various undocumented positions along the toothrow.
Despite these factors, there is a fairly good match between in vivo and in silico surface strains. Strait et al. (2005) summarized the strain magnitude data: this paper focuses on the strain orientation results, summarized in Table 5. The range of ε1 orientations at the two in silico‘gage sites’ on the anterior surface of the working side postorbital bar fell within the range of three of five in vivo experiments. All of the in vivo ε1 orientations on the anterior surface of the working side postorbital bar could be found somewhere on the anterior surface of the FEM postorbital bar, albeit in small patches. The ε1 orientations recorded in silico from the balancing side postorbital bar replicated one of the in vivo experiments and were very close to two others. The average in silico ε1 orientations recorded from the working side zygomatic septum fell within the range of in vivo values recorded during one experiment and the average in silico ε1 orientations recorded from the balancing side zygomatic septum are within the range of values recorded during two in vivo experiments and very close to the third. The average in silico ε1 orientations from the dorsal interorbital and working and balancing side dorsal orbital sites fall within the ranges reported by Hylander et al. (1991). The in silico ε1 orientations on the orbital roof overlap with the in vivo ranges. The in silico ε1 orientations on the anterior root of the zygoma and from the anterior and posterior gage sites on both the working and balancing side zygomatic arches all fall within the ranges of our in vivo results and those published previously (Hylander et al. 1991). The in silico data do not overlap with those gathered in vivo from the frontal septum site. It should be noted that at all of the sites where there was poor or variable correspondence between the FEM and the in vivo data, there is a lot of variation in ε1 orientation around the putative gage sites. This is best seen at the zygomatic septum and postorbital bar sites, but is also true at the middle zygomatic arch site.
Table 5.
Summary of agreement between in vivo and in silico strain orientations.
| Gage site | In silico range overlaps range measured in #/# in vivo experiments |
|---|---|
| Rostral interorbital | 3/3 |
| Dorsal interorbital | 8/8 |
| Dorsal orbital (working) | 2/4 |
| Dorsal orbital (balancing) | 2/4 |
| Orbital roof (working) | 1/2 |
| Orbital roof (balancing) | 2/2 |
| Postorbital bar (working) | 3/5 |
| Postorbital bar (balancing) | 1/4 |
| Postorbital septum, frontal bone (working) | 1/1 |
| Postorbital septum, frontal bone (balancing) | 0/1 |
| Postorbital septum, zygomatic (working) | 1/3 |
| Postorbital septum, zygomatic (balancing) | 2/3 |
| Anterior root of zygoma (working) | 1/2 |
| Anterior root of zygoma (balancing) | 2/2 |
| Zygomatic arch, anterior (working) | 3/3 |
| Zygomatic arch, anterior (balancing) | 3/3 |
| Zygomatic arch, middle (working) | 0/3 |
| Zygomatic arch, middle (balancing) | 0/3 |
| Zygomatic arch, posterior (working) | 1/3 |
| Zygomatic arch, posterior (balancing) | 2/3 |
Considering the range of factors that might have influenced these comparisons (interindividual or interspecific variation in bone material properties, geometry and deformation regimes, interexperiment variation in gage position and orientation, and/or errors in estimation of gage orientation and position), the similarities between the in vivo and in silico strain patterns documented above suggest that the stress, strain and deformation regimes in our macaque FEM constitute a plausible working hypothesis regarding in vivo behavior of the macaque craniofacial skeleton during mastication. Some reviewers of this paper have questioned the usefulness of our FEM, given that there is not perfect correspondence between the FEM strain orientations and those recorded in vivo. Supporting this argument it was noted that at some sites there was no overlap between the in vivo strain data and that reported from the model. We acknowledge that our model is not a perfect representation of all macaque skulls during chewing. However, just as a few relatively large residuals from a regression line do not necessarily invalidate conclusions regarding the slope and elevation of that line, similarly, poor correspondence between in vivo strain orientations and FEM strains at three sites out of 20 does not, in our opinion, invalidate our FEM. Moreover, it is worth noting that the lateral orbital wall is characterized by high variance in strain orientations across its anterior (postorbital bar) and medial (intraorbital) surfaces, probably because of its complex morphology and/or loading regimes. It is therefore hardly surprising that in vivo strains also show high variance between experiments, and less than perfect correspondence with the FEM. Similarly, the strain orientations recorded in vivo at the middle zygomatic arch site can be readily recovered from a slightly more anterior position on the FEM arch than we originally hypothesized corresponded to the gage site. In conclusion, we believe that this model constitutes a better hypothesis (more accurate, more precise and more testable) than other hypotheses regarding cranial deformation that refer to simple geometries and loading regimes (e.g. the skull functions like a cylinder that is twisted) (Görke, 1904; Richter, 1920; Benninghoff, 1925; Bluntschli, 1926; Sicher & Tandler, 1928; Endo, 1966a,b, 1970, 1973; Roberts & Tattersall, 1974; Couly, 1976; Rak, 1983; Greaves, 1985). We look forward to future improvements to the model.
Deformation regimes in the circumorbital region
A dynamic view of the deformation of our FEM, available online (Supporting Information Video S1), provides the clearest picture of the deformation regime that we hypothesize occurs during mastication in Macaca. The finite-element model, including its specific geometry and material properties, and the resulting loading, stress and deformation regimes, is our hypothesis (Chalk et al. 2010). Nevertheless, the following descriptors provide rough approximations as to the deformation of the skull of Macaca during mastication.
Masseter muscle forces bend the zygomatic arches inferiorly and twist them about an anteroposteriorly oriented axis passing through the anterior and posterior roots, as suggested by Hylander & Johnson (1997a,b);. Downward bending of the zygomatic arches subjects the infraorbital region and anterior root of the zygoma to shear in coronal planes. Twisting of the zygomatic arch about its long axis is associated with inferolaterally directed tension acting on the lateral orbital wall, the infraorbital plate, and the anterior root of the zygoma. On the working side this deformation twists the working side mid-facial skeleton about the bite point, pulling the lateral orbital margin inferolaterally. These inferolaterally directed forces do generate tensile stresses in the lateral orbital wall but, because the wall is curved, the principal effect of these forces is bending, or rather ‘unbending’ (cf. Ross & Hylander, 1996a,b);, in the sense that the postorbital bar bends in such a way as to become less curved. This ‘unbending’ of the lateral orbital wall on the working side contributes to deformation of the orbital aperture, characterized by increase in diameter along a superomedially–inferolaterally directed axis accompanied by decrease in diameter along an inferomedially–superolaterally directed axis. Figure 16 illustrates the patterns of variation in tensile and compressive strain magnitudes (top figures) associated with this deformation, as well as a static illustration of the deformation of the model (bottom). The lengthening of the orbit along an inferolaterally oriented axis is associated with concentrations of tensile strain along the edges parallel with this vector, i.e. the inferomedial and superolateral corners of the orbit. Similarly, compression of the orbit along a superolaterally directed axis is associated with compressive strain concentrations in the inferolateral and superomedial corners.
Fig. 16.
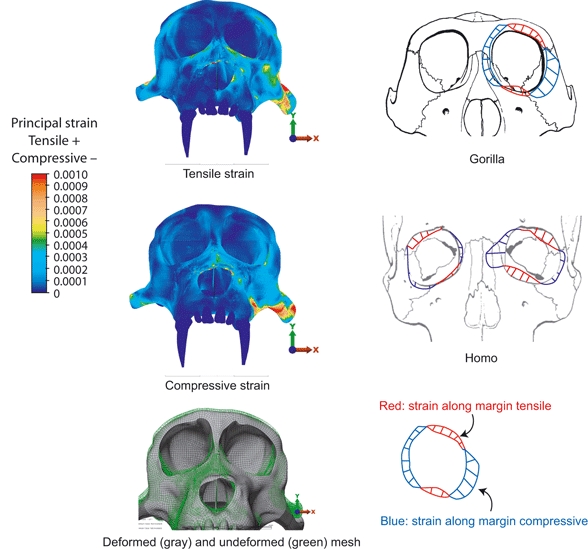
Summary of circumorbital deformation regimes in Macaca, Homo and Gorilla. The magnitudes of maximum (tensile) and minimum (compressive) strain in and around the working side orbits of Macaca are shown in the anterior views of the FEM. The bottom left figure illustrates the deformation of the model deformed at a scale of 5% of model size. The figures on the right show strain distributions around the rims of the orbits during molar loading in Homo and Gorilla (cf. Fig. 2F). Lengths of lines perpendicular to orbital margin are proportional to magnitude or strains along the margin at that point. Blue is compressive strain, red is tensile. Figures on right redrawn from Endo (1973; Fig. 3).
Inferiorly directed components of deformation of the lateral orbital walls acting on the lateral ends of the supraorbital torus bend the supraorbital region in the frontal plane, resulting in large lateral components to the tensile strain orientations in the dorsal interorbital region (Fig. 10) (Hylander et al. 1991). However, as noted by Hylander et al., the deformation regime in the supraorbital torus is not a simple one. If the supraorbital torus were a simple beam bent in frontal planes, the inferior surface would experience anteriorly directed tensile strains and the superior surface laterally directed tensile strains. The latter is only true in the dorsal interorbital region and the former is not true in the orbital roof. As Fig. 10 illustrates, maximum principal strain orientations in the dorsal orbital region vary with location, but with significant anteriorly directed components, whereas tensile strains on the inferior surface of the supraorbital torus (i.e. the roof of the orbit) are laterally directed.
The dynamic view of the macaque FEM provides insight into the deformation regime producing these strains. The inferolaterally directed deformation of the lateral orbital wall associated with the deformation of the orbital aperture described above produces a region of tensile strain in the superolateral corner of the orbit. As reported elsewhere (Ross, 2001), the medial wall of the orbit experiences very low strain magnitudes during chewing with variable strain orientations; however, principal tensile strains are oriented predominantly anteriorly. This orientation of the tensile strains suggests that the medial orbital wall is subjected to compressive strains in the plane of the orbital aperture, as predicted by Fig. 16.
The high strain magnitudes evident in the zygomatic arch and its anterior root, in conjunction with the high level of interspecific variation in the morphology of this region, suggest that the biomechanics and morphology of this region deserve attention (Fig. 16). An obliquely oriented field of tensile strain is evident in the upper lateral region of the anterior root of the zygoma, at the junction of the root with the lateral orbital wall, and elevated compression characterizes the inferiorly directed edge of the anterior zygoma root as it converges on the alveolar process of the maxilla. At the junction of the inferomedial border of the anterior root of the zygoma with the snout is a concentration of both high tensile and high compressive strains, indicating the presence of high shear strains. We hypothesize that this shear strain concentration is due to the presence of superiorly directed components of bite force acting medial to this site and inferiorly directed components of masseter muscle force acting lateral to it. The high strain magnitudes apparent in this region suggest that the morphology of this region of the cranium may reflect selection for feeding performance.
In the Introduction, it was argued that the geometry of the lateral orbital wall and interorbital pillar, in conjunction with the orientation of the external forces, makes it implausible that these structures experience pure axial compression during chewing (Görke, 1904; Richter, 1920; Bluntschli, 1926; Sicher & Tandler, 1928; Roberts & Tattersall, 1974; Couly, 1976). Rather, hypotheses of bending and twisting of the bony elements of the face (Endo, 1966a,b; Rak, 1983; Hylander et al. 1991; Hylander & Johnson, 1997a,b;), in conjunction with some axial compression and shear, are more plausible a priori. The stress, strain and deformation regimes in the macaque FEM confirm these predictions: the lateral orbital margins are primarily bent, not purely compressed.
Other catarrhines
Chlorocebus aethiops
In vivo bone strain data are only available from the circumorbital region of one other catarrhine species (C. aethiops); these data are in agreement with those observed in Macaca (Fig. 17). Data from one experiment on C. aethiops performed by us (experiment 57) recorded inferolaterally directed ε1 orientations from the anterior surface of the working side postorbital bar during mastication. Oyen and Tsay (1991) also recorded bone strain from the anterior surface of the postorbital bar while the animals bit on a bite force transducer. Their working side strain orientations are extremely vertical, approximating those recorded by us. The strain orientations reported by them from their balancing side gages are highly variable. In addition to data from the postorbital bar, we also recorded bone strain from the dorsal interorbital gage site in C. aethiops during experiment 57. Maximum principal strain orientations at this site are directed slightly anterior of directly lateral, closely resembling those reported by Hylander for Macaca and Papio, and resembling the in silico data from our FEM. Thus, the working strain orientations recorded by us and reported by Oyen and Tsay from the anterior surface of the working side postorbital bar of C. aethiops closely resemble the strain orientations reported for Macaca and can be found at sites on the anterior surface of the postorbital bar in our Macaca FEM. This suggests that a hypothesis of a similar deformation regime in the lateral orbital wall of Chlorocebus and Macaca cannot be ruled out.
Fig. 17.
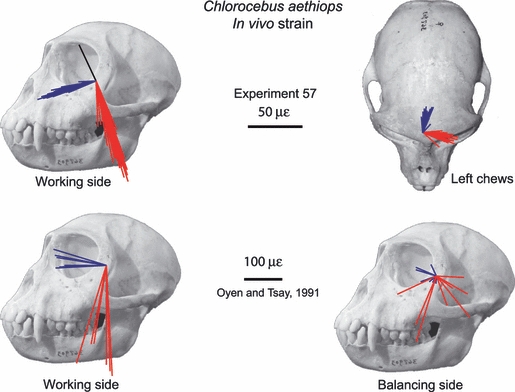
Strain vector plots of in vivo bone strain data collected by us from the dorsal interorbital site and from the anterior surface of the postorbital bar during chewing ipsilateral to the bar (Experiment 57), along with data from the postorbital bar reported by Oyen & Tsay (1991). Data from Oyen and Tsay were collected from their Figs 3–11. All data are shown as if the gages were placed on the left side postorbital bar and working side = left.
Homo sapiens and Gorilla gorilla
These two species are discussed together because both were the subjects of an in vitro strain gage study by Endo (1966a,b, 1970, 1973) (Fig. 3). Comparison of the surface strains presented by Endo with those in our FEM is difficult without clear criteria for establishing homologies of strain gage sites. Therefore our discussion instead focuses on comparison of the overall deformation regimes of the circumorbital regions in these three taxa. Figure 16 illustrates the pattern of deformation (bottom left) along with the distribution of tensile and compressive strain magnitudes in our FEM of Macaca during a left bite. For comparison, Endo's data on tensile and compressive strains around the orbital rims in Homo and Gorilla are summarized on the right in Fig. 16. Comparisons of these images reveal some basic similarities. In all three species, tensile strain magnitudes are highest in the superolateral and inferomedial corners of the orbits, whereas compressive strain magnitudes are highest in the inferolateral and inferomedial corners. The pattern of deformation of the orbit suggested by Endo matches that hypothesized by our FEM: during mastication the working side orbit is elongated along an inferolaterally directed axis by torsion of the zygomatic arch, outward rotation of the anterior root of the zygoma and bending of the postorbital bar in the frontal plane. Notably, the same distribution of tensile and compressive strain peaks is also manifest in the orbits of Australopithecus africanus during simulated premolar biting (Strait et al. 2009; Fig. 2). The widespread presence of this pattern of deformation in the catarrhine lateral orbital margin suggests that Rak's (1983) hypothesis (summarized below) regarding patterns of stress and strain in this part of the P. boisei facial skeleton are essentially correct. We note that similar distributions of maximum tensile strains were reported by Curtis et al. (2008: Fig. 6) from a different FEM of a macaque loaded with external forces designed to replicate in vivo biting on the molars (Curtis et al. 2008). The similarity of their strain patterns to ours provides some independent corroboration of our results.
Strain magnitudes
Significant variation in strain magnitudes was documented at most sites across most experiments, even accounting for food and chewing side. The origins of this variation lie in differences in gage position, interindividual variation, and other factors that vary from one experimental session to another. This variation demonstrates the need for the use of multiple experimental subjects in the study of in vivo bone strain during feeding, and cautions against definitive statements based on small datasets. Care should be exercised in interpreting relative bone strain magnitudes not recorded simultaneously from different sites (Hylander et al. 1991). Note also that our strain magnitudes recorded from the corpus are higher on the balancing than on the working side. This difference runs counter to observations across a large number of animals by Hylander et al. (1991), suggesting that the animals in the present study might have chewed harder when the food was contralateral as compared to ipsilateral to the gages. With these caveats, several observations can be made.
First, there were no significant differences between in vivo working and balancing strain magnitudes at the postorbital bar and zygomatic arch sites. This suggests that bite forces may not directly affect strain magnitudes in the postorbital bar and anterior root of the zygoma, and that the external force(s) acting on these structures during mastication are primarily produced by muscles of mastication. It is notable that strain orientations at the anterior root of the zygoma changed only very slightly with changes in chewing side (Fig. 13), as did strain orientations in the postorbital bar during most experiments (Fig. 6). Moreover, strain orientations on orbital roof sites (experiments 13 and 47) show little variance with chewing side.
Secondly, on both working and balancing sides, strains in the zygomatic arch and mandibular corpus are higher than those in the circumorbital region, and the postorbital bar exhibits the highest strains among the circumorbital sites. On the working side the postorbital septum exhibits higher strains compared with the supraorbital region. The reverse is true on the balancing side, but both of these areas experience low strains compared with the mandibular corpus, zygomatic arch and anterior root of the zygoma (Fig. 15). These results, mirrored by FEA of Pan troglodytes (Wroe et al. 2007), confirm the conclusion that, if optimality is defined as maximum strength with minimum material, the postorbital septum and supraorbital regions of the catarrhine facial skeleton are not optimized for resisting and transmitting external forces experienced during mastication (Hylander et al. 1991). While highly strained areas of the facial skeleton might be more closely optimized for feeding, other hypotheses must be invoked to explain the presence of browridges and plates of circumorbital bone in macaques (Ravosa, 1991; Ravosa et al. 2000b; Ross, 2001; Ross & Metzger, 2004).
The lateral orbital wall of robust australopithecines
Rak (1983) argued that differences between the P. boisei facial frame (Fig. 4) and that of other hominins [elevated glabella, inferolaterally sloping frontal member (representing the supraorbital tori) contacting a single zygomaticoalveolar member at the wide flaring ‘visor-like’ anterior zygoma root] (Fig. 44 from Rak, 1983) functioned to decrease bending moments acting on the circumorbital region, thereby improving the ability of the facial skeleton to resist powerful external forces. Rak argued that the facial framework of P. boisei needed these modifications because it was subjected to unusually large masseter muscle forces that acted relatively far rostral and lateral relative to the lateral orbital wall. Rak hypothesized that, as a result, P. boisei's lateral orbital wall was subjected to powerful inferolaterally directed forces that would generate bending stresses at the junctions between the frontozygomatic members, between the superior frontozygomatic member and supraorbital torus, and between the supraorbital torus and glabella (Rak, 1983: Fig. 41). He argued that, by straightening out the junction between the frontozygomatic member (lateral orbital wall) and the supraorbital torus, creating the characteristic inferolaterally sloping supraorbital torus and ‘sad eyes’ appearance of the P. boisei skull, and by creating the ‘visor-like’ anterior zygoma root, these bending stresses are minimized and tensile stresses predominate in the lateral orbital wall.
The data presented here suggest that in catarrhines the circumorbital region, including the lateral orbital wall, is indeed subjected to bending in the frontal plane. Moreover, similarities across hominids, including P. boisei, in the position and orientation of masseter muscle forces relative to the lateral orbital wall suggest that the circumorbital regions of all hominids, including P. boisei, are and were subjected to high bending moments in the frontal plane. However, the low in vivo and in silico strain magnitudes in the lateral orbital wall of Macaca and the low in silico strain magnitudes predicted for this region of extant hominids (Wroe et al. 2007) suggest that the size and shape of the lateral orbital wall is not optimized for resisting these bending moments. Whether the morphology of the P. boisei lateral orbital wall reflects selection for decreased bending moments in the lateral orbital wall must await detailed FEM of the P. boisei cranium: the data presented here suggest this hypothesis is probably not correct.
In contrast with the lateral orbital wall, the high in vivo and in silico strain magnitudes in the lateral infraorbital region/anterior zygoma root of Macaca reported here and elsewhere (Hylander & Johnson, 1992, 1997a) and the high in silico strains hypothesized for the anterior zygoma root of extant (Wroe et al. 2007) and fossil (Strait et al. 2009) hominids suggest that the biomechanics of this region, including the zygomatico-alveolar crest, the zygomatic prominence of A. africanus, the flaring, visor-like zygoma of P. boisei, the transverse buttress of the intra-orbital region and the zygomatic arch (Rak, 1983; Kimbel et al. 2004), should be addressed.
Conclusions
In conjunction with the in vivo bone strain data presented and summarized here, our FEM constitutes the best hypothesis to date regarding stress, strain and deformation regimes in the cranial skeleton of Macaca during mastication. Although the model only represents behavior during unilateral biting/mastication, it serves as the foundation for future work on variation in deformation regimes associated with bite point, food material properties and muscle recruitment patterns. Although we would prefer to avoid simplified descriptors of this deformation regime, referring instead to the model in its entirety as our hypothesis of deformation, it is reasonable to describe the global deformation of the macaque facial skeleton during mastication as ‘bending in a frontal plane’ caused in larger part by torsion of the zygomatic arch about its long axis and bending of the arch in sagittal planes. The similarity of this deformation regime to those observed in our FEM A. africanus (Strait et al. 2009) and to those in Endo's in vitro analyses of the crania of Homo and Gorilla suggests this may be a common pattern of deformation in all catarrhine crania. The extent to which changes in skeletal geometry reflect changes in the nature or magnitude of this deformation regime remains to be evaluated.
Acknowledgments
The staff at DLAR, Stony Brook, housed and cared for the animals. Technical assistance was provided by Brigitte Demes, Susan Larson, Jack Stern, Hylton Gordon and Mark Bookbinder. Dr. Clint Rubin generously loaned the bridges used in several of the experiments. The following students trained animals and assisted with data collection and analysis: R. Asher, C. Heesy, M. Irwin and K. Metzger. L. Betti-Nash and R. Markley assisted with the illustrations. We thank Ian Grosse and Betsy Dumont for advice and assistance and Sam Cobb and the reviewers for their comments. This research was funded by Stony Brook University and NSF Physical Anthropology (BCS 9706676; BCS 0240865; BCS 0725126).
Appendix 1
Strain coordinate transformation
To compare in vivo strain orientations and magnitudes recorded from bone surfaces with strain values from comparable areas in the FEM, it was necessary to transform the 3-D finite-element strains from the global coordinate system of the model into the local coordinate system of the surfaces of the model where strain gage data were sampled in vivo. Strain is a tensor, not a vector, so it is not possible to simply project the orientation of a 3-D strain vector such as maximum principal strain. Rather, the values of the strain tensor must be recalculated in the new coordinate system of the bone surface plane (P′). This was achieved in the following way:
1. The 3-D coordinates of three nodes (a,b,c) representing P’ were selected.
2. Two vectors representing P’ were calculated as A= a − b and B= a − c.
3. The normalized cross-product A× B = Z′, representing the normal to P’, was used to represent the orientation of P’.
4. The cross-product of Z′ and the normal to the horizontal plane of the global coordinate system yields X′, the unit vector in the horizontal plane that is orthogonal to Z′.
5. The cross-product Z′ × X′ gives Y′, the vector orthogonal to Z′ and X′.
6. The components of these three unit vectors, X′, Y′, Z′, in the global model coordinate system serve as direction cosines for the rotation matrix [T] defined below.
7. {ε′}, the strain tensor in the coordinate system X′, Y′, Z′ is calculated by premultiplying {ε}, the strain tensor in the global coordinate system of the model, by the rotation matrix [Tτ] given below; i.e.
{ε′} = [Tτ] {ε}
where the 3-D strain tensor
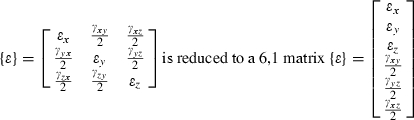 |
and premultiplied by
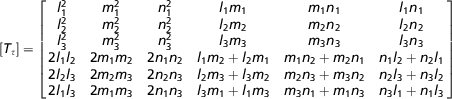 |
where l1, l2, l3 are the cosines of the angles between X and the X′, Y′ and Z′ axis, respectively, m1, m2, m are the cosines of the angles between the Y and the X′, Y′ and Z′ axis, respectively, and n1, n2, n3 are the cosines of the angles between Z and the X′, Y′ and Z′ axis, respectively.
8. {ε} was output from the fem software; [Tτ] and {ε′} were calculated in matlab® using steps 2–6 described above.
Author contributions
All authors conceived of and designed the research; C.F.R. collected and analyzed the in vivo data; C.F.R., M.B., M.S., L.P., B.R., P.D. and D.S. built, loaded and interpreted the FEM; J.I.D. and C.F.R. wrote the matlab code for processing data from the FEM; J.I.D. extracted surface strain data from the model; C.F.R. drafted the manuscript. All authors read and commented on the manuscript.
Supporting information
Data S1. Surface strain transformation and visualization software v2.0.
Video S1. Model deformations amplified 500×.
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.
References
- Andrades P, Rosenthal EL, Carroll WR, et al. Zygomaticomaxillary buttress reconstruction of midface defects with the osteocutaneous radial forearm free flap. Head Neck J Sci Spec Head Neck. 2008;30:1295–1302. doi: 10.1002/hed.20874. [DOI] [PubMed] [Google Scholar]
- Antón SC. Internal masticatory muscle architecture in the Japanese macaque and its influence on bony morphology. Am J Phys Anthropol Suppl. 1993;16:50. [Google Scholar]
- Benninghoff A. Spaltlinien am Knochen, eine Methode zur Ermittelung der Architektur platter Knochen. Verh Anat Ges. 1925;34:189–206. [Google Scholar]
- Bluntschli H. Rückwirkuneg des Kieferapparatus auf den Gesamyschädel. Z Zahnärtzte Orthop. 1926;18:71–85. [Google Scholar]
- Bourke J, Wroe S, Moreno K, et al. Effects of gape and tooth position on bite force and skull stress in the dingo (Canis lupus dingo) using a 3-dimensional finite element approach. PLoS ONE. 2008;3(5):e2200. doi: 10.1371/journal.pone.0002200. doi:10.1371/journal.pone.0002200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cartmill M. The Orbits of Arboreal Mammals: A Reassessment of the Arboreal Theory of Primate Evolution. Chicago: University of Chicago; 1970. [Google Scholar]
- Cartmill M. Primate Origins. Minneapolis: Burgess; 1975. [Google Scholar]
- Cartmill M. Morphology, function and evolution of the anthropoid postorbital septum. In: Ciochon RL, Chiarelli AB, editors. Evolutionary Biology of the New World Monkeys and Continental Drift. New York: Plenum; 1980. pp. 243–274. [Google Scholar]
- Chalk J, Richmond BG, Ross CF, et al. A finite element analysis of masticatory stress hypotheses. Am J Phys Anthropol. 2010 doi: 10.1002/ajpa.21416. doi: 10.1002/ajpa.21416. [DOI] [PubMed] [Google Scholar]
- Cook RD, Malkus DS, Plesha ME. Concepts and Applications of Finite Element Analysis. New York: Wiley; 2002. [Google Scholar]
- Couly G. La statique osseuse de la face. Rev Belge Stomatol. 1976;77:420–426. [PubMed] [Google Scholar]
- Curtis N, Kupczik K, O’Higgins P, et al. Predicting skull loading: applying multibody dynamics analysis to a macaque skull. Anat Rec Adv Integr Anat Evol Biol. 2008;291:491–501. doi: 10.1002/ar.20689. [DOI] [PubMed] [Google Scholar]
- Dally JW, Riley WF. Experimental Stress Analysis. New York: McGraw Hill; 1965. [Google Scholar]
- Dumont ER, Piccirillo J, Grosse IR. Finite-element analysis of biting behavior and bone stress in the facial skeletons of bats. Anat Rec A Discov Mol Cell Evol Biol. 2005;283A:319–330. doi: 10.1002/ar.a.20165. [DOI] [PubMed] [Google Scholar]
- Endo B. A biomechanical study of the human facial skeleton by means of strain-sensitive lacquer. Okajimas Folia Anat Jpn. 1966a;42:205–217. doi: 10.2535/ofaj1936.42.4_205. [DOI] [PubMed] [Google Scholar]
- Endo B. Experimental studies on the mechanical significance of the form of the human facial skeleton. J Fac Sci, Univ Tokyo, Section V. 1966b;III:1–106. [Google Scholar]
- Endo B. Analysis of stresses around the orbit due to masseter and temporalis muscles respectively. J Anthropol Soc Nippon. 1970;78:251–266. [Google Scholar]
- Endo B. Stress analysis on the facial skeleton of gorilla by means of the wire strain gauge method. Primates. 1973;14:37–45. [Google Scholar]
- Fisher NI. Statistical Analysis of Circular Data. New York: Cambridge University Press; 1993. [Google Scholar]
- Görke O. Beitrag zur fuktionellen Gestaltung des Schädels bei den Anthropomorphen und Menschen durch Untersuchung mit Rontgenstrahlen. Arch Anthropol. 1904;1:91–108. [Google Scholar]
- Greaves WS. The mammalian postorbital bar as a torsion-resisting helical strut. J Zool (Lond) 1985;207:125–136. [Google Scholar]
- Gruss JS, Mackinnon SE. Complex maxillary fractures: role of buttress reconstruction and immediate bone grafts. Plast Reconstr Surg. 1986;78:9. [PubMed] [Google Scholar]
- Huiskes R, Chao EYS. A survey of finite element analysis in orthopaedic biomechanics: the first decade. J Biomech. 1983;16:385–409. doi: 10.1016/0021-9290(83)90072-6. [DOI] [PubMed] [Google Scholar]
- Hylander WL, Johnson KR. Strain gradients in the craniofacial region of primates. In: Davidovich Z, editor. The Biological Mechanisms of Tooth Movement and Craniofacial Adaptation. Columbus, OH: The Ohio State University; 1992. pp. 559–569. [Google Scholar]
- Hylander WL, Johnson KR. In vivo bone strain patterns in the craniofacial region of primates. In: McNeill C, editor. Science and Practice of Occlusion. Chicago: Quintessence Publishing Co; 1997a. pp. 165–178. [Google Scholar]
- Hylander WL, Johnson KR. In vivo bone strain patterns in the zygomatic arch of macaques and the significance of these patterns for functional interpretations of craniofacial form. Am J Phys Anthropol. 1997b;102:203–232. doi: 10.1002/(SICI)1096-8644(199702)102:2<203::AID-AJPA5>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- Hylander WL, Ravosa MJ. An analysis of the supraorbital region of primates: a morphometric and experimental approach. In: Smith P, Tchernov E, editors. Structure, Function and Evolution of Teeth. London: Freund Publishing House Ltd; 1992. pp. 223–255. [Google Scholar]
- Hylander WL, Picq PG, Johnson KR. Masticatory-stress hypotheses and the supraorbital region of primates. Am J Phys Anthropol. 1991;86:1–36. doi: 10.1002/ajpa.1330860102. [DOI] [PubMed] [Google Scholar]
- Iriarte-Diaz J, Ross CF. Surface Strain Transformation and Visualization Software 2.0. Chicago: 2010. [Google Scholar]
- Kimbel WH, Johanson D, Rak Y. The Skull of Australopithecus afarensis. Oxford: Oxford University Press; 2004. [Google Scholar]
- Kupczik K, Dobson CA, Fagan MJ, et al. Assessing mechanical function of the zygomatic region in macaques: validation and sensitivity testing of finite element models. J Anat. 2007;210:41–53. doi: 10.1111/j.1469-7580.2006.00662.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manson PN, Hoopes JE, Su CT. Structural pillars of the facial skeleton: an approach to the management of LeFort fractures. Plast Reconstr Surg. 1980;66:54. doi: 10.1097/00006534-198007000-00010. [DOI] [PubMed] [Google Scholar]
- Mardia KV, Jupp PE. Directional Statistics. Chichester: Wiley; 2000. [Google Scholar]
- McHenry CR, Wroe S, Clausen PD, et al. Supermodeled sabercat, predatory behavior in Smilodon fatalis revealed by high-resolution 3D computer simulation. Proc Natl Acad Sci U S A. 2007;104:16010–16015. doi: 10.1073/pnas.0706086104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzger KA, Daniel WJ, Ross CF. Comparison of beam theory and finite-element analysis with in vivo bone strain data from the alligator cranium. Anat Rec A Discov Mol Cell Evol Biol. 2005;283A:331–348. doi: 10.1002/ar.a.20167. [DOI] [PubMed] [Google Scholar]
- Moazen M, Curtis N, O’Higgins P, et al. Musculoskeletal modelling and finite element analysis of lizard skulls. J Morphol. 2007;268:1108. [Google Scholar]
- Moazen M, Curtis N, Evans SE, et al. Combined finite element and multibody dynamics analysis of biting in a Uromastyx hardwickii lizard skull. J Anat. 2008a;213:499–508. doi: 10.1111/j.1469-7580.2008.00980.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moazen M, Curtis N, Evans SE, et al. Rigid-body analysis of a lizard skull: modelling the skull of Uromastyx hardwickii. J Biomech. 2008b;41:1274–1280. doi: 10.1016/j.jbiomech.2008.01.012. [DOI] [PubMed] [Google Scholar]
- Moazen M, Curtis N, O’Higgins P, et al. Assessment of the role of sutures in a lizard skull: a computer modelling study. Proc R Soc Lond B Biol Sci. 2009;276:39–46. doi: 10.1098/rspb.2008.0863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno K, Wroe S, McHenry C, et al. Komodo dragon cranial mechanics and kinesis as revealed by high-resolution finite element analysis. J Vertebr Paleontol. 2007;27 [Google Scholar]
- Moreno K, Wroe S, Clausen P, et al. Cranial performance in the Komodo dragon (Varanus komodoensis) as revealed by high-resolution 3-D finite element analysis. J Anat. 2008;212:736–746. doi: 10.1111/j.1469-7580.2008.00899.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagasao T, Nakajima T, Kimura A, et al. The dynamic role of buttress reconstruction after maxillectomy. Plast Reconstr Surg. 2005;115:1328–1340. doi: 10.1097/01.prs.0000156978.16358.1e. [DOI] [PubMed] [Google Scholar]
- Oyen OJ, Tsay TP. A biomechanical analysis of craniofacial form and bite force. Am J Dentofacial Orthop. 1991;99:298–309. doi: 10.1016/0889-5406(91)70012-L. [DOI] [PubMed] [Google Scholar]
- Picq PG, Hylander WL. Endo's stress analysis of the primate skull and the functional significance of the supraorbital region. Am J Phys Anthropol. 1989;79:393–398. doi: 10.1002/ajpa.1330790315. [DOI] [PubMed] [Google Scholar]
- Pierce SE, Angielczyk KD, Rayfield EJ. Patterns of morphospace occupation and mechanical performance in extant crocodilian skulls: a combined geometric morphometric and finite element modelling approach. J Morphol. 2008;269:840–864. doi: 10.1002/jmor.10627. [DOI] [PubMed] [Google Scholar]
- Rak Y. The Australopithecine Face. New York: Academic Press; 1983. [Google Scholar]
- Ravosa MJ. Browridge development in Cercopithecidae: a test of two models. Am J Phys Anthropol. 1988;76:535–555. [Google Scholar]
- Ravosa MJ. Interspecific perspective on mechanical and nonmechanical models of primate circumorbital morphology. Am J Phys Anthropol. 1991;86:369–396. doi: 10.1002/ajpa.1330860305. [DOI] [PubMed] [Google Scholar]
- Ravosa MJ, Johnson KR, Hylander WL. Strain in the galago facial skull. J Morphol. 2000a;245:51–66. doi: 10.1002/1097-4687(200007)245:1<51::AID-JMOR4>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- Ravosa MJ, Vinyard CJ, Hylander WL. Stressed out: masticatory forces and primate circumorbital form. Anat Rec. 2000b;261:173–175. doi: 10.1002/1097-0185(20001015)261:5<173::AID-AR6>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- Rayfield EJ. Cranial mechanics and feeding in Tyrannosaurus rex. Proc R Soc Lond B Biol Sci. 2004;271:1451–1459. doi: 10.1098/rspb.2004.2755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rayfield EJ. Aspects of comparative cranial mechanics in the theropod dinosaurs Coelophysis, Allosaurus and Tyrannosaurus. Zool J Linn Soc. 2005a;144:309–316. [Google Scholar]
- Rayfield EJ. Using finite-element analysis to investigate suture morphology: a case study using large carnivorous dinosaurs. Anat Rec A Discov Mol Cell Evol Biol. 2005b;283A:349–365. doi: 10.1002/ar.a.20168. [DOI] [PubMed] [Google Scholar]
- Rayfield EJ. Finite element analysis and understanding the biomechanics and evolution of living and fossil organisms. Annu Rev Earth Planet Sci. 2007;35:541–576. [Google Scholar]
- Rayfield EJ, Milner AC. Establishing a framework for archosaur cranial mechanics. Paleobiology. 2008;34:494–515. [Google Scholar]
- Rayfield EJ, Norman DB, Horner CC, et al. Cranial design and function in a large theropod dinosaur. Nature. 2001;409:1033–1037. doi: 10.1038/35059070. [DOI] [PubMed] [Google Scholar]
- Richmond BG, Wright B, Grosse I, et al. Finite element analysis in functional morphology. Anat Rec A. 2005;283A:259–274. doi: 10.1002/ar.a.20169. [DOI] [PubMed] [Google Scholar]
- Richter W. Der Obergesichtschädel des Menschen als Gebissturm, ein statische Kunstwerk. Dtsch Monatsschr Zahnheilkd. 1920;38:49–68. [Google Scholar]
- Roberts D, Tattersall I. Skull form and the mechanics of mandibular elevation in mammals. Am Mus Novit. 1974;2536:1–9. [Google Scholar]
- Rodriguez ED, Bluebond-Langner R, Park JE, et al. Preservation of contour in periorbital and midfacial craniofacial microsurgery: reconstruction of the soft-tissue elements and skeletal buttresses. Plast Reconstr Surg. 2008;121:1738–1747. doi: 10.1097/PRS.0b013e31816b13e1. [DOI] [PubMed] [Google Scholar]
- Ross CF. Muscular and osseous anatomy of the primate anterior temporal fossa and the functions of the postorbital septum. Am J Phys Anthropol. 1995;98:275–306. doi: 10.1002/ajpa.1330980304. [DOI] [PubMed] [Google Scholar]
- Ross CF. In vivo function of the craniofacial haft: the interorbital ‘pillar’. Am J Phys Anthropol. 2001;116:108–139. doi: 10.1002/ajpa.1106. [DOI] [PubMed] [Google Scholar]
- Ross C, Hylander WL. In vivo and in vitro bone strain in owl monkey circumorbital region and the function of the postorbital septum. Am J Phys Anthropol. 1996a;101:183–215. doi: 10.1002/(SICI)1096-8644(199610)101:2<183::AID-AJPA6>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- Ross CF, Hylander WL. In vivo and in vitro bone strain in the owl monkey circumorbital region and the function of the postorbital septum. Am J Phys Anthropol. 1996b;101:183–215. doi: 10.1002/(SICI)1096-8644(199610)101:2<183::AID-AJPA6>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- Ross CF, Metzger KA. Bone strain gradients and optimization in tetrapod skulls. Ann Anat. 2004;186:387–396. doi: 10.1016/S0940-9602(04)80070-0. [DOI] [PubMed] [Google Scholar]
- Ross CF, Ravosa MJ. Basicranial flexion, relative brain size and facial kyphosis in nonhuman primates. Am J Phys Anthropol. 1993;91:305–324. doi: 10.1002/ajpa.1330910306. [DOI] [PubMed] [Google Scholar]
- Ross CF, Patel BA, Slice DE, et al. Modeling masticatory muscle force in finite-element analysis: sensitivity analysis using principal coordinates analysis. Anat Rec A. 2005;283:288–299. doi: 10.1002/ar.a.20170. [DOI] [PubMed] [Google Scholar]
- Sicher H, Tandler J. Anatomie für Zahnärtzte. Berlin: Springer; 1928. [Google Scholar]
- Strait D, Richmond B, Ross C, et al. Finite element analysis of a macaque skull: applications for functional morphology. Am J Phys Anthropol. 2002;Supplement 34:149. [Google Scholar]
- Strait D, Wang Q, Dechow PC, et al. Modeling elastic properties in finite element analysis: how much precision is needed to produce an accurate model? Anat Rec. 2005;283A:275–287. doi: 10.1002/ar.a.20172. [DOI] [PubMed] [Google Scholar]
- Strait D, Richmond BG, Spencer M, et al. Something to chew on: masticatory biomechanics and its relevance to early hominid phylogeny. J Hum Evol. 2007;52:585–599. doi: 10.1016/j.jhevol.2006.11.019. [DOI] [PubMed] [Google Scholar]
- Strait DS, Wright B, Richmond BG, et al. Craniofacial strain patterns during premolar loading: implications for human evolution. In: Vinyard CJ, Ravosa MJ, Wall CE, editors. Primate Craniofacial Function and Biology. New York: Springer; 2008. pp. 149–172. [Google Scholar]
- Strait DS, Weber GW, Neubauer S, et al. The feeding biomechanics and dietary ecology of Australopithecus africanus. Proc Natl Acad Sci U S A. 2009;106:2124–2129. doi: 10.1073/pnas.0808730106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, Dechow PC. Elastic properties of external cortical bone in the craniofacial skeleton of the rhesus monkey. Am J Phys Anthropol. 2006;131:402–415. doi: 10.1002/ajpa.20438. [DOI] [PubMed] [Google Scholar]
- Wang Q, Dechow PC, Wright BW, et al. Surface strain on bone and sutures in a monkey facial skeleton: an in vitro method and its relevance to finite element analysis. In: Vinyard CJ, Ravosa MJ, Wall CE, editors. Primate Craniofacial Function and Biology. New York: Springer; 2008. pp. 173–198. [Google Scholar]
- Wroe S, Moreno K, Clausen P, et al. High-resolution three-dimensional computer simulation of hominid cranial mechanics. Anat Rec Adv Integr Anat Evol Biol. 2007;290:1248–1255. doi: 10.1002/ar.20594. [DOI] [PubMed] [Google Scholar]
- Yamamoto Y, Minakawa H, Kawashima K, et al. Role of buttress reconstruction in zygomaticomaxillary skeletal defects. Plast Reconstr Surg. 1998;101:943–950. doi: 10.1097/00006534-199804040-00009. [DOI] [PubMed] [Google Scholar]
- Zar JH. Biostatistical Analysis. Upper Saddle River, NJ: Prentice Hall; 1999. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


