RosettaEPR: An Integrated Tool for Protein Structure Determination from Sparse EPR Data

Abstract

Site-directed spin labeling electron paramagnetic resonance (SDSL-EPR) is often used for the structural characterization of proteins that elude other techniques, such as X-ray crystallography and nuclear magnetic resonance (NMR). However, high-resolution structures are difficult to obtain due to uncertainty in the spin label location and sparseness of experimental data. Here, we introduce RosettaEPR, which has been designed to improve de novo high-resolution protein structure prediction using sparse SDSL-EPR distance data. The “motion-on-a-cone” spin label model is converted into a knowledge-based potential, which was implemented as a scoring term in Rosetta. RosettaEPR increased the fractions of correctly folded models (RMSD_Cα < 7.5Å) and models accurate at medium resolution (RMSD_Cα < 3.5Å) by 25%. The correlation of score and model quality increased from 0.42 when using no restraints to 0.51 when using bounded restraints and again to 0.62 when using RosettaEPR. This allowed for the selection of accurate models by score. After full-atom refinement, RosettaEPR yielded a 1.7Å model of T4-lysozyme, thus indicating that atomic detail models can be achieved by combining sparse EPR data with Rosetta. While these results indicate RosettaEPR’s potential utility in high-resolution protein structure prediction, they are based on a single example. In order to affirm the method’s general performance, it must be tested on a larger and more versatile dataset of proteins.

Introduction

Protein modeling with Rosetta can serve as an alternative means of structure elucidation

The vast majority of proteins in the Protein Data Bank (PDB) have been determined by X-ray crystallography or nuclear magnetic resonance (NMR) [1]. However, a large number of biomedically relevant proteins continue to evade structural elucidation by these techniques due to membrane environment [2], high flexibility [3], and size [4]. Alternative techniques, such as computational structure prediction methods, can be employed in order to define the structure of such proteins. The usual experimental bottlenecks, such as obtaining highly pure, concentrated samples of protein, are thereby avoided. Rosetta routinely folds soluble proteins of less than 150 amino acids correctly [5]. It is generally among the top performers in the Critical Assessment of protein Structure Prediction (CASP) experiments [6-10]. In addition, Rosetta’s ability to obtain the correct fold of membrane proteins of various sizes and topologies has been demonstrated [11-13]. More recently, Das et al introduced RosettaFOLD-AND-DOCK, which allows for the de novo structure prediction of homomeric proteins [14].

Rosetta’s sampling and scoring capabilities for protein folding have been reviewed extensively elsewhere [15-18]. Briefly, the Rosetta de novo protein structure prediction algorithm is divided into two steps: low-resolution protein folding to obtain the overall topology and high-resolution refinement of the backbone and sidechains. Metropolis Monte Carlo peptide fragment insertion is driven by a variety of knowledge-based potentials to rapidly predict protein folds. In high-resolution refinement, the protein backbone ϕ and ψ angles are perturbed while the overall fold is maintained. Sidechain conformations are predicted via a Metropolis Monte Carlo search of rotamer space, and all torsional degrees of freedom are subjected to gradient-based minimization.

Sparse NMR restraints can be combined with Rosetta to obtain atomic detail structures

While the algorithm described above performs well in the de novo prediction of relatively small, soluble proteins, effectively sampling protein conformational space remains the limiting factor in the accurate prediction of more complex proteins. To this end, distance and orientational restraints, such as those obtained by NMR, have been incorporated into the Rosetta protein folding protocol [19]. Chemical shifts are converted into backbone torsional angle restraints, which are used in the generation of the peptide fragment libraries. Distance restraints from nuclear Overhauser effects (NOEs) are also employed in this process. Additionally, distance and orientaitonal restraints (NOEs and residual dipolar couplings, or RDCs, respectively) have been incorporated into the scoring function and are evaluated during protein folding. Bowers et al demonstrated that Rosetta, combined with a sparse set of NOEs (approximately one restraint per residue) and backbone chemical shifts, can produce models with atomic detail accuracy [20]. Similarly, a combination of sparse RDCs and chemical shifts was used to produce correctly folded models [16]. Shen et al have made significant progress in improving the robustness and accuracy of CS-Rosetta with incomplete chemical shift datasets, obtaining atomic detail models based on much data that would otherwise be considered unsuitable for high-resolution structure determination [21-23].

SDSL-EPR offers an advantage over traditional structure determination techniques

Despite such advances, some proteins remain un-amenable to structure determination by these methods. Site-directed spin labeling electron paramagnetic resonance spectroscopy (SDSL-EPR) allows for structural studies of membrane proteins and large macromolecular assemblies in native or native-like environments [24-31]. SDSL involves mutating residues of interest to cysteines, which can be reacted with a paramagnetic spin label, such as methanethiosulfonate (MTS). A sensitive structural probe at a known sequence position is created, forgoing the need to “assign” signals in the spectrum as is necessary in NMR spectroscopy. Additionally, resolution of SDSL-EPR is not limited by the size of the system. Similar to fluorescence and NMR spectroscopy, however, SDSL-EPR generates information concerning both the local environment of the spin label and the overall global fold of the protein. SDSL-EPR has been used to characterize conformational changes, such as those seen in MsbA [28,29], rhodopsin [32-34], and KcsA [27,35,36]. More recently, it has been demonstrated that the fold of a protein can be determined by structural restraints derived from SDSL-EPR data alone [37].

Atomic detail protein structure determination by SDSL-EPR is difficult and computationally demanding

Challenges in using SDSL-EPR structural data arise from the possible perturbation of the system by introduction of the spin label, sparseness of datasets resulting from the need to construct a dedicated mutant for every data point collected, and uncertainty in the position and dynamics of the spin label relative to the protein backbone. In the past, proteins have displayed a surprising robustness with respect to the introduction of spin labels [38-42]. Molecular dynamics simulations [43] and crystallography [39,44] have been employed to explicitly model the spin label in order to help interpret SDSL-EPR structural data. However, these calculations are relatively slow and computationally demanding. In addition, most studies of this nature are designed to examine a specific protein and are not easily expanded to other systems. For the purpose of protein structure determination, a faster, broadly applicable approach to relate the spin label position to the protein backbone is needed. As an exhaustive experimental mapping of intra-protein distances is infeasible given time and the labor intensiveness of the SDSL-EPR method, a limited dataset that unambiguously defines the fold of the protein needs to be defined (see Kazmier et al, accompanying article in this issue).

RosettaEPR is designed specifically to work with sparse SDSL-EPR data

In 2008, Alexander et al introduced the implicit “motion-on-a-cone” model, or cone model (Figure 2B), which is based on the structure of the MTS spin label (Figure 2A) [37]. This model was used to convert an observed spin label distance, d_SL, into an “allowed” range for the distance of the Cβ atoms, d_Cβ ∈ [d_SL–12.5Å, d_SL+2.5Å] (Figure 2C). The authors demonstrate that these distance restraints are sufficient to determine the structure of T4-lysozyme to atomic detail accuracy from 25 SDSL-EPR restraints The present study introduces RosettaEPR, which replaces the soft interpretation of the distance constraints used in the previous study with a knowledge-based restraint potential optimized for SDSL-EPR distance data. Alexander et al utilized RosettaNMR, with the consequence that all d_Cβ distances falling within the allowed range were considered equally favorable during de novo folding. All other distances were disfavored using a quadratic penalty function (Figure S1). However, while the distance difference, d_SL–d_Cβ, falls within a wide range, values between 0Å and 5Å are more likely than values outside this range. We used the cone model, in combination with the PDB, to derive a probability function for d_SL–d_Cβ, which was then converted into a scoring function using the Boltzmann relation. We demonstrate that treatment of SDSL-EPR distance restraints with this scoring function is superior. Following the benchmarking presented in this paper, RosettaEPR will be made available to the scientific community.

Figure 2.

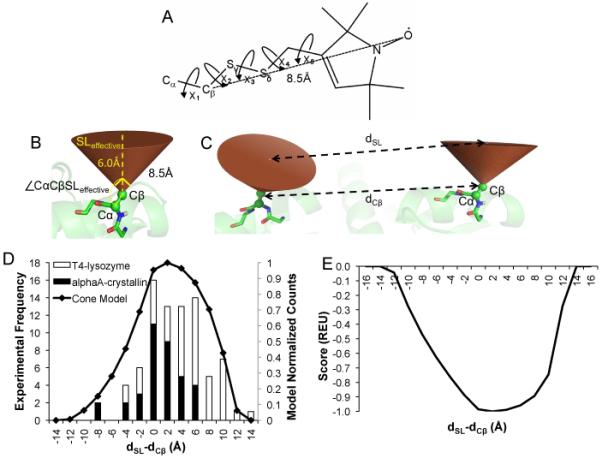
The “motion-on-a-cone” model. A) Methanethiosulfonate (MTS) spin label. The Cβ-SL distance is approximately 8.5Å. B) In the cone model, the Cβ-SL distance (SL_effective) is assumed to be 6Å, and the cone has an opening angle of 90°. The Cα-Cβ-SL_effective angle is restrained to angles 135° ≤ (∠CαCβSL_effective) ≤ 180°. C) The cone model is used to calculate d_SL-d_Cβ values. D) The normalized frequency of d_SL-d_Cβ values for a database of proteins (black line, right y-axis) compared to experimentally observed values for T4-lysozyme and αA-crystallin (open and filled bars, respectively, left y-axis. E) The propensity of d_SL-d_Cβ values can be converted into a knowledge-based potential according to the Boltzmann relation. The resulting energies were normalized such that the most favored d_SL-d_Cβ value correlates with an energy of −1.0 Rosetta Energy Unit (REU), and the least favored d_SL-d_Cβ value correlates with a Rosetta energy of 0.0 REU.

Materials and Methods

The protocol described in the present work is outlined in Figure 1. It is divided into two subsections corresponding to the implementation and development of RosettaEPR and the prediction of the T4-lysozyme structure to atomic detail.

Figure 1.

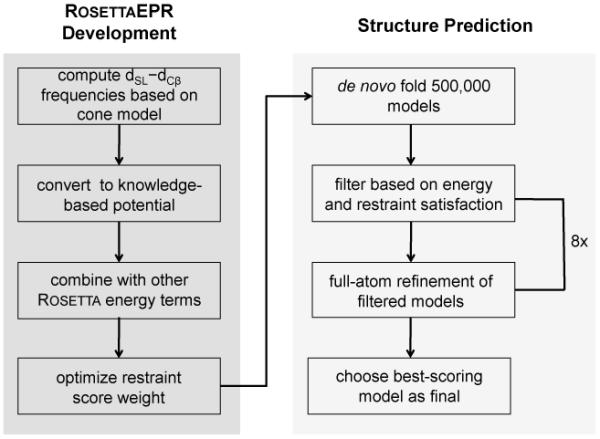
Flowchart outlining the currently described protocol.

Conversion of the motion-on-a-cone model into a knowledge-based potential

The d_SL–d_Cβ histogram (Figure 2D) was generated by placing a cone model-based simulated spin label at every exposed amino acid position in 3,584 proteins from a non-redundant protein database [45] . That is, the simulated spin label was placed at residue positions that had a neighbor count [46] of less than ten, resulting in over 140 million measured distances. For every pairwise distance within each protein, the protein’s d_Cβ was subtracted from the simulated d_SL and stored in 0.5Å-wide bins. Because the highest frequency of d_SL–d_Cβ values was on the order of 10⁶, a pseudocount of 10⁶ was added to the total counts computed so that less commonly observed values are also considered.

The potential (Figure 2E) was calculated by taking the negative logarithm (−ln) of the propensity of each d_SL–d_Cβ value, where the propensity is defined as:

$$\mathit{\text{propensity}}=\frac{\left(\frac{\mathit{\text{frequency}}+\mathit{\text{PseudoCounts}}}{\mathit{\text{TotalCounts}}}\right)}{\left(\frac{1}{\#\mathit{\text{bins}}}\right)}$$

PseudoCount equals 10⁶, and # bins equals 64. The resulting values were normalized and shifted such that they were all negative. This relationship is based on the Boltzmann relationship, which is used to correlate a population of a species to an associated energy. The potential was re-scaled to give a maximum bonus of −1.0 for d_SL–d_Cβ values between −12.0 and 12.0 (observed by the cone model) and a 0.0 penalty for values outside this range.

Model quality was assessed according to RMSD_Cα relative to the 2LZM crystal structure

In order to best assess the ability of RosettaEPR to recover native-like folds, only the α-helical core domain of T4-lysozyme (residues 58-164) was modeled, as experimental restraints for other regions of this protein were not available. The experimentally determined distances used as restraints are reported in Table S1 and are mapped onto the T4-lysozyme crystal structure in Figure S2. Models of the protein were generated a) without restraints, b) with restraints using RosettaEPR’s knowledge-based potential, and c) with restraints defined by the same boundaries as those used by Alexander et al. Model quality was assessed by computing the RMSD_Cα relative to the X-ray crystal structure of T4-lysozyme (PDBID: 2LZM [47]). Only core residues 70-155, excluding loops, were considered in computing the RMSD_Cα (see Table S2).

Weight optimization for the knowledge-based SDSL-EPR restraint potential

To optimize the factor by which the RosettaEPR scoring function should be applied, 10,000 models of the α-helical region of T4-lysozyme were constructed for a wide variety of weights (Table S3). The fraction of models with RMSD_Cα values below 7.5Å was taken as measure for the correct fold. The fraction of models with RMSD_Cα values below 3.5Å was employed to identify candidate models for successful atomic detail refinement; models generated with this level of accuracy are considered to be “native-like.” The knowledge-based potential was implemented as a spline approximation in the Rosetta AtomPairConstraint score. The bounded restraint uses the AtomPairConstraint score as computed according to a bounded quadratic equation (Figure S1).

Rosetta was used to de novo fold and refine T4-lysozyme

Secondary structure prediction of the 107 C-terminal residues of T4-lysozyme was performed using Jufo [48], Psipred [49], and Sam [50]. Peptide fragments to be used in de novo structure prediction were generated as previously described, and fragments based on homologous proteins were excluded during folding. Rosetta’s low-resolution de novo protein folding algorithm was used to generate 10,000 models of T4-lysozyme guided by experimental restraints (Table S1) [37] weighted to various extents, resulting in models containing structural information of the protein backbone only. During de novo folding, residues are represented as superatoms, or “centroids” [15]. After determining that the RosettaEPR knowledge-based potential optimally predicts the fold of T4-lysoyzme when multiplied by a factor of 4.0, this weight was used in the generation of 500,000 models of the protein.

The 500,000 models were filtered according to their overall Rosetta energy and the extent to which they satisfied the experimental restraints. Only the top 1% of models by total score that had a restraint score of at least 85% of the optimum value was included in the filtered ensemble. These 1,388 models were then refined to atomic detail, in which the centroids were replaced with sidechain rotamers based on a backbone-dependent rotamer library [51]. During refinement, Rosetta’s full-atom scoring potentials are used to guide refinement through an iterative cycle of sidechain repacking and gradient-based minimization [17,52]. Each round of refinement yielded ten times the initial number of models. That is, one round of refinement resulted in 13,880 new, refined models. All de novo folding and full-atom refinement computations were performed using Rosetta trunk revision 34586.

Structure determination with RosettaEPR is computationally feasible

All models were generated by independent simulations using Vanderbilt University’s Center for Structural Biology computing cluster and the university’s Advanced Computing Center for Research and Education (ACCRE). Computations were performed on a combination of AMD Opteron and Intel Nehalem processor nodes. The average time needed to fold one model of the 107 C-terminal residues of T4-lysozyme was approximately 240 seconds. The same time is required for a single round of high-resolution refinement for one model.

Results

Knowledge-based potential reflects likelihood of model in light of observed SDSL-EPR distance

Cone model-based statistics were collected over a database of non-redundant proteins (see Meterials and Methods) and compared to d_SL–d_Cβ values determined experimentally for T4-lysozyme and αA-crystallin (Figure 2D). The set of cone model statistics recovers several features of the experimental data, including the range of d_SL–d_Cβ values and a shift towards d_SL–d_Cβ values greater than 0Å. The shift towards positive d_SL–d_Cβ values indicates that spin labels are more likely to point away from each other. This is expected for soluble proteins, where mutations of surface residues are not expected to destabilize the protein.

For conversion into a knowledge-based potential, the negative logarithm (−ln) of the propensity of each d_SL–d_Cβ value was computed such that less frequently seen d_SL–d_Cβ values are considered less favorable than one that is more often observed (Figure 2E).. In result, a restraint that is fulfilled in the most likely area of the distribution improves the total score by one point, and a restraint that is violated is not counted towards the total score. This knowledge-based potential was then incorporated into Rosetta’s low-resolution scoring function where it is affiliated with a dedicated weight (see Knowledge-based potential section below). The current model is an improvement upon the original implementation of the cone model, in that a) protein structures, not ellipsoids, were used to generate the statistics, and b) the knowledge-based potential considers the likelihood of d_SL–d_Cβ values instead of a simple binary classification.

Knowledge-based potential achieves up to 55% correctly folded T4-lysozyme models

Ten thousand T4-lysozyme models were folded de novo in the presence of the same restraints used previously (Table S1 and Figure S2) [37]. Restraints were incorporated with various weights, and the results were compared to the bounded potential used by Alexander et al (Table S3). The usage of restraint scoring functions results in more native-like folds than when folding with no restraints at all (Figure 3 and Table 1). This reaffirms that experimental data increases sampling of more native-like structures. RosettaEPR recovers the native topology of the T4-lysozyme α-helical region in up to 55% of the models. This compares to 7% if no restraints are used and 42% when using bounded restraints. Furthermore, folding with bounded restraints consistently resulted in approximately 1.0-1.5% of all built models having native-like conformations, compared to 2.1% when using the EPR knowledge-based potential with an optimal weight of 4.0. This improvement is significant, as additional starting structures for high-resolution refinement increase the chance of successfully obtaining atomic detail models (see Ten-fold enrichment of low-RMSD models). Further, conversion to a knowledge-based potential enabled fine-tuning of the weight of the SDSL-EPR potential for optimal performance, while the bounded potential provided constant suboptimal performance over wide ranges of the weight.

Figure 3.

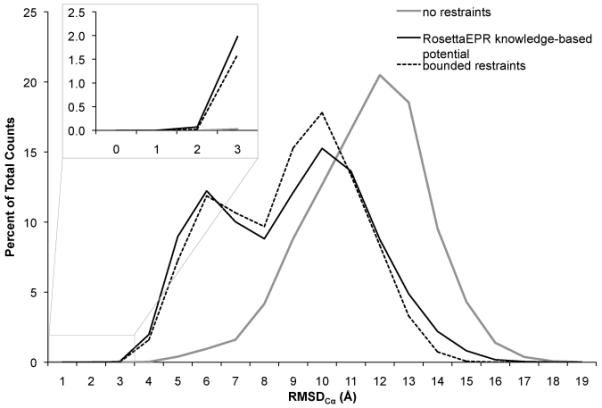
] Comparison of the RosettaEPR knowledge-based potential to the bounded potential. T4-lysozyme was folded de novo in Rosetta guided by 25 experimental restraints. Restraint violations were scored according to either a bounded potential or the EPR knowledge-based potential. The RMSD_Cα distributions of the resulting models when folded with optimally weighted restraint energies are compared to folding without restraints.

Table 1.

Summary of benchmarking results of T4-Lysozyme using no restraints, 25 restraints scored according to the optimally weighted RosettaEPR knowledge-based potential, and 25 bounded restraints with a weight of 4.0^a

Restraint Type	% Models with RMSDCα < 3.5Å	% Models with RMSDCα < 7.5Å	Enrichmentb
none	0.03	7.17	--c
knowledge-based potential (weight = 4.0)	2.05	42.08	7.0
bounded restraints (weight = 4.0)	1.62	41.09	5.3

^aResults for all tested weights reported in Table S3

^bEnrichment = (fraction of low-RMSD models in filtered ensemble) ÷ (fraction of low-RMSD models of all models generated); filtered ensemble = within the top 1% of models by total score, the top 35% of models according to restraint score

^cEnrichment could not be computed as with the other data sets due to lack of restraint score

Knowledge-based function improves correlation of score and model quality

The correlation of the scoring function with model quality is key to selection of native-like models when the structure is not known. The correlation coefficient improves from 0.42 in the absence of restraints to 0.51 when using the bounded function and further to 0.62 when using RosettaEPR (Figure 4). To quantify the value of the score for filtering native-like models, the enrichment for each optimized scenario was also computed (see Table 1). For the knowledge-based potential weighted by a factor of 4.0, the benchmark resulted in an enrichment of 7.0. The same analysis was performed on the models folded with the equally weighted bounded restraint potential, resulting in an enrichment of 5.3. The ensemble of models generated with no restraints contained only three native-like models, all of which were among the 10% best-scoring models, but this method was unable to produce enough native-like models to justify any high-resolution refinement.

Figure 4.

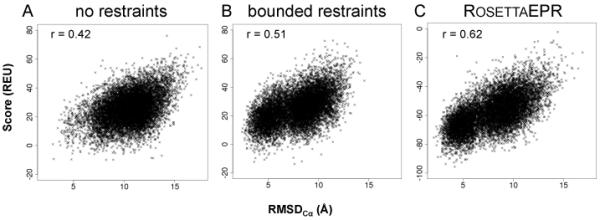
Correlation between total Rosetta energy and RMSD_Cα of de novo folded models. Score vs. RMSD_Cα for 10,000 models de novo folded A) with no restraints, B) with 25 bounded restraints, and C) with 25 restraints guided by the RosettaEPR knowledge-based potential.

Ten-fold enrichment of low-RMSD models through knowledge-based SDSL-EPR score for high-resolution refinement

500,000 models of T4-lysozyme were de novo folded in Rosetta guided by 25 EPR distance restraints (weight equals 4.0). From the 1% best-scoring models, models achieving at least 85% of the optimal knowledge-based restraint score were selected for high-resolution refinement. The enrichment of native-like models in the filtered pool was 10.6, while the enrichment of correctly folded models was 2.3, where enrichment was defined as the fraction of native-like or correctly folded models in the filtered pool divided by the fraction of native-like or correctly folded models in the entire ensemble. Filtering decreases the number of models considered for high-resolution refinement to a more manageable ensemble and enriches the fraction of low-RMSD models such that more native-like folds are refined to full-atom detail.

High-resolution refinement of T4-lysozyme yields structural model that is accurate at atomic detail

The resulting 1,388 models of T4-lysozyme were refined to high-resolution using Rosetta’s full-atom potentials, which include knowledge-based van der Waals attraction, repulsion, hydrogen bonding, solvation, and electrostatic terms [17]. Each input model was refined ten times without experimental restraints, resulting in 13,880 models. Ideally, low-RMSD models would be considered energetically favored according to Rosetta’s scoring function. Therefore, the models were then filtered such that only the top 10% by total score were carried on to the next round of refinement. This process was repeated through eight iterations, at which point the score of the refined models converged. The total score of each model was plotted against its RMSD_Cα (Figures 5A). The correlation between energetically favorable and low-RMSD models improves after each round of refinement until it converges after the eighth iteration. The lowest energy model produced with this strategy had an RMSD_Cα of 1.76Å relative to the native (Figure 6), and the lowest RMSD_Cα observed was 1.73Å. The previously reported model was determined to have an RMSD_Cα of 1.66Å.

Figure 5.

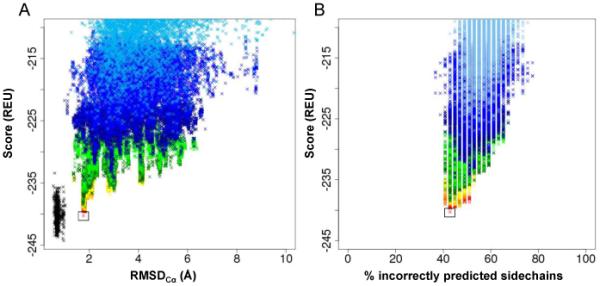
Correlation between Rosetta energy and RMSD_Cα of refined models. A) Score vs. RMSD_Cα plot of T4-lysozyme models for eight cycles of full-atom refinement. Each cycle of refinement resulted in ten times the number of input models. After each cycle, the refined models were filtered by total Rosetta energy, and the top 10% were refined again. Color key: refined crystal structure – black; round 1 = sky blue; round 2 = bright blue; round 3 = dark blue; round 4 = light green; round 5 = dark green; round 6 = yellow; round 7 = orange; round 8 = red. B) Percent of incorrectly predicted sidechains of core residues (see Table S2) as a function of total Rosetta score. The same coloring scheme in Figure 5A was used.

Figure 6.

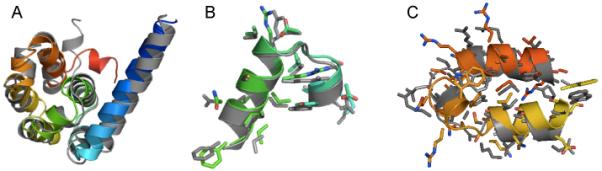
Atomic detail model of T4-lysozyme de novo folded with RosettaEPR. A) Superimposition of the lowest-scoring model of T4-lysozyme (rainbow) with the 2LZM crystal structure (gray). The RMSD_Cα for the lowest-scoring model to the native is 1.76Å. Sidechains are displayed as sticks. B) Residues 86-104. C) Residues 126-154.

The ability of Rosetta to recover native-like sidechain conformations was tested by comparing sidechain rotamer agreement of refined models of T4-lysozyme with the X-ray crystal structure. A rotamer of a given amino acid residue is defined by its χ_1-4 angles. Sidechain conformations are classified by assigning them to the closest rotamer in terms of χ_1-4 angle deviation [51,53]. The total Rosetta energy is plotted as a function of the percentage of incorrectly predicted sidechain rotamers (Figure 5B). In general, the Rosetta energy correlates well with rotamer agreement, with the percent of correct rotamers predicted increasing after each round of refinement.

Discussion

The RosettaEPR knowledge-based potential proves to be superior to the bounded potential during de novo folding

We have demonstrated the advantages of using a knowledge-based potential to convert EPR distance data into structural restraints. The potential is derived from the cone model [37] and has been shown to perform better than a simple bounded potential. From a conceptual standpoint alone, the energetic bonus correlates with the likelihood of observing d_SL–d_Cβ values. As a result, the knowledge-based potential inherently uses the structural information from SDSL-EPR data more completely compared to the bounded scoring function used by Alexander et al. Furthermore, the knowledge-based potential, in combination with Rosetta’s low-resolution scoring function and de novo folding algorithm, proves more robust in obtaining low-RMSD models of T4-lysozyme, from which atomic detail structures can be generated through full-atom refinement.

The correlation between score and RMSD improves through multiple rounds of refinements

The Rosetta full-atom scoring function allows the most native-like model to be identified unambiguously by its overall score, if model accuracy is better than 2.0Å. This model should have the lowest overall Rosetta energy and therefore exhibit not only the correct topology, but also native-like sidechain and backbone conformations. Similarly, less favorable conformations should have higher computed energies; these models will also have higher computed RMSDs relative to the native structure. One therefore expects to observe an energy “funnel” after several rounds of full-atom refinement, where both the score and RMSD of the models converge to the native structure. The overall scores of the predicted models of T4-lysozyme are plotted against their RMSD_Cα relative to the crystal structure in Figure 5. The correlation improves after each round of filtering and refinement, resulting in several atomic detail models with Rosetta energies comparable to the 2LZM crystal structure, which was refined using the same potentials as the predicted models.

RosettaEPR will be developed continuously as more data become available

Although a larger benchmarking set would be ideal, there are a limited number of systems for which both experimentally determined three-dimensional structures and EPR data can be obtained. However, the resulting atomic detail models of T4-lysozyme generally satisfy the experimental EPR data, and benchmarking will be expanded to more diverse systems as more data become available. In the mean time, a larger benchmark on a variety of proteins of known structure using simulated data will be performed to assess the general performance of the method. The current work serves as a proof of principle. It will be interesting to test whether the similar results will be obtained for other proteins. It has already been shown that NMR restraints greatly aid Rosetta’s ability to recover native-like models [16,19,20,54,55], a method which is widely applicable to other biological systems, including the fumarate sensor DcuS [56] and a chordin-like cysteine-rich (CR) repeat from procollagen IIA [57]. It is believed that the same will be true with RosettaEPR after further testing and refinement.

Sparse SDSL-EPR distance data alone are not able to yield atomic detail models

SDSL-EPR affords several advantages over other structure determination techniques, such as X-ray crystallography and NMR. No crystallization is required, there are few size constraints, proteins, and membrane proteins in particular, can be studied in a native-like environment, and there is no need to assign resonance signals. Thereby, SDSL-EPR overcomes some experimental limitations in the high-resolution structure determination of proteins that are large, highly flexible, or natively reside in lipid bilayers.

However, while quantitative in nature, the structural information obtained by SDSL-EPR is limited due to the flexibility of the spin label, which adds large uncertainties to the distances determined. Introduction of spin labels into proteins requires removal of native cysteine residues without affecting the protein structure and assumes that the spin label does not perturb the structure. Datasets obtained by SDSL-EPR remain sparse due to the requirement to create a dedicated double-mutant for each distance to be measured. Therefore, SDSL-EPR a) will be applied to systems where crystallography and NMR spectroscopy are not applicable and b) will be combined with crystallography and other techniques to study structural dynamics of proteins.

The current work and the results presented by Alexander et al [37] provide the first indication that sparse (approximately 0.25 restraints per residue) SDSL-EPR distance data can be combined with Rosetta for de novo protein structure elucidation with atomic detail accuracy. While RosettaEPR can be applied to soluble proteins, it is expected that the need and applicability of RosettaEPR will be highest for the structure determination of membrane proteins, the majority of which continue to evade more traditional techniques. A benchmark of RosettaEPR involving more proteins and membrane proteins in particular will be executed as suitable datasets become available

RosettaEPR will be accessible to the scientific community

Other researchers will have access to RosettaEPR via software licenses granted by the RosettaCOMMONS (www.rosettacommons.org). These licenses are free for academic and non-profit institutions. To encourage usage of RosettaEPR, web tutorials will be made available.

Conclusions

RosettaEPR is the first tool designed to generate high-resolution protein structures from sparse EPR data. It can also be used in combination with an optimized restraint-selecting algorithm (see Kazmier et al, accompanying article in this issue) to assist experimentalists in determining protein structures to high-resolution. In the future, RosettaEPR will be modified such that it can be used to effectively determine the structures of membrane proteins, an EPR accessibility knowledge-based potential will be implemented, and high-resolution modeling of the MTS spin label will be included. The ultimate goal of this research is to optimize the structural information that can be achieved through EPR spectroscopy. RosettaEPR will enable the high-resolution structure elucidation of a plethora of proteins for which structures have, until now, not yet been determined.

Abbreviations

EPR

electron paramagnetic resonance

NMR

nuclear magnetic resonance

PDB

Protein Data Bank

SL

spin label

SDSL

site-directed spin labeling

MTS

methanethisulfonate

Cα

α-carbon on the protein backbone

Cβ

β-carbon on the amino acid sidechain

d_Cβ

distance between two β-carbons on the protein in angstroms (Å)

d_SL

distance between two MTS spin labels on the protein in angstroms (Å)

RMSD

root mean square distance in angstroms (Å)