Abstract
Adequate control of serum glucose in critically ill patients is a complex problem requiring continuous monitoring and intervention, which have a direct effect on clinical outcomes. Understanding temporal relationships can help to improve our knowledge of complex disease processes and their response to treatment. We discuss a Dynamic Bayesian Network (DBN) model that we created using the open-source Projeny toolkit to represent various clinical variables and the temporal and atemporal relationships underlying insulin and glucose homeostasis. We evaluated this model by comparing the DBN model’s insulin dose predictions against those of a rule-based protocol (eProtocol-insulin) currently used in the ICU. The results suggest that the DBN model’s predictions are as effective as or better than those of the rule-based protocol. The limitations of our methods are discussed, with a brief note on their generalizability.
1. INTRODUCTION
Several studies have shown that critically ill patients often become hyperglycemic even if they are not diabetic, due to various stress response mechanisms and the administered drugs1. Increased glucose levels further worsen the patient’s condition and outcomes, whereas active control of the patients’ blood glucose levels may improve the outcomes1 and reduce mortality by up to 15%2. Rule-based protocols used to control serum glucose include the ones from Yale University and Intermountain Healthcare 3, 4.
Temporal reasoning deals with the understanding of relationships between different variables over time. It can contribute to models that explain the past and predict the future based on available data. The ability to explain the past can provide an understanding of a patient’s disease processes and response to treatment. Predicting future events is a natural continuation of the temporal reasoning process, and can help in estimating prognosis, planning treatment, and avoiding complications. Various techniques have been explored in temporal reasoning such as autoregressive moving average, support vector machines, neural networks, and first-order logic-based methods5, 6. Probabilistic methods have various advantages over these methods, with the flexibility to infer any variable in the model instead of fixed input and output variables, and an ability to explain the inferences using causal relationships7.
We present a novel approach to predict the future serum glucose levels of patients in the ICU and to recommend appropriate insulin drip rates to maintain the patients’ serum glucose within the normal range. We used Dynamic Bayesian Networks, a temporal probabilistic method, and we built, trained and tested the model using the Projeny toolkit that we developed for this research8.
2. BACKGROUND AND CHALLENGES
Several computerized models to represent clinical or pathophysiological processes have been described by other authors. These include systems that calculate insulin dosage in diabetic patients using lab results, physiological parameters, or clinical observations that are mostly numerical and often fully available9, 10.
2.1. Dynamic Bayesian Networks (DBN)
A Dynamic Bayesian Network (DBN), also known as a Temporal Bayesian Network, allows complex causal relationships within and across time instances to be represented as a directed acyclic graph (DAG) with Bayesian probabilities. A DBN may be considered as a Hidden Markov Model (HMM) in which the probabilistic relationships are represented using complex interactions and dependencies between many variables as a Bayesian Network11.
2.2. Clinical Problem Description
Several clinical studies have shown that insulin resistance and hyperglycemia are common in critically ill patients, including those without a history of diabetes mellitus. The older treatment in such cases is to administer insulin when the serum glucose is greater than 215 mg/dl. A relatively newer intensive insulin therapy aims to maintain the patients’ serum glucose between 80 and 110 mg/dl by actively adjusting the intravenous glucose drip and intravenous insulin dosage with periodic monitoring and adjustment once every two hours or less. In clinical trials involving critically ill patients, those who had intensive insulin therapy demonstrated reduced mortality and morbidity compared with patients who had conventional insulin therapy1, 12–14. However, a few studies have suggested that patients undergoing intensive insulin therapy may have slightly increased mortality. Large scale clinical trials are underway to study this area further. The general consensus in the medical community at present is that intensive insulin therapy is likely to reduce the mortality and morbidity among critically ill patients.
3. MATERIALS AND METHODS
3.1. Data Selection
Anonymized data of adult patients who were treated in the Shock Trauma Respiratory ICU at LDS Hospital in Salt Lake City, Utah between January 2004 and December 2005 was used for this research. The final dataset included the data of 796 patients whose serum glucose was actively controlled using a computerized, rule-based protocol developed at LDS Hospital (eProtocol-insulin)4, which provided a gold standard for comparison. The data was measured once every two hours on average in our dataset, which became our models’ timeslice width.
3.2. Model Structure
Several models were tested, but only the final model is described in this paper. Temporal structure learning tools do not support hidden nodes since known data is required to learn relationships between various nodes, and hence were not usable for our models. The hidden and observed variables (nodes), and the relationships (edges) were described manually by the first author through a review of clinical literature. The model was then refined through a review by the last author and three other physicians at the University of Utah.
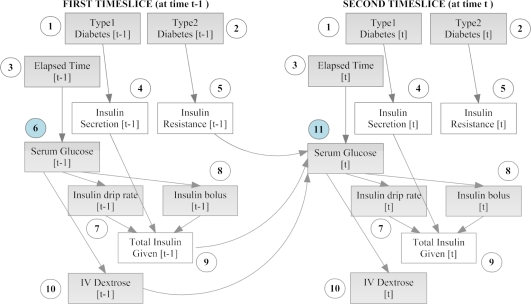
The model had endogenous insulin secretion and insulin resistance as hidden nodes, since they cannot be measured directly. The observable nodes included the diabetes status of the patient (type I, type II or neither), serum glucose (mg/dL), intravenous (IV) insulin dose (both bolus and drip, U/hr), IV dextrose dose, and the time elapsed between consecutive measurements. The relationships between these variables were modeled as a two time-slice DBN (2TBN) as shown in fig. 1. All the variables in the model were discrete due to a limitation of our algorithms. Various manual and automated discretization techniques were tested to discretize the continuous variables, and will be described in a separate paper. The experiment described in this paper used a k-means clustering algorithm for discretization15, which produced more accurate predictions than manual discretization.
Figure 1.
DBN model for serum glucose control and insulin dosing in the ICU. Two timeslices are shown here – the model is automatically expanded (unrolled) by Projeny for as many timeslices present in each patient’s data. Observed nodes are shaded, hidden nodes are clear. Numbers within circles denote equivalence classes obtained through parameter tying (see section 3.5).
3.3. Challenges in using DBN models in medicine and our solutions
Scenarios involving entirely numerical values that are fully available are very limited in the clinical setting, and techniques to deal with descriptive and missing data are highly desirable. Clinical decision making is often performed with incomplete data under uncertainty. We used an expectation-maximization algorithm to impute the missing data. This approach tends to be robust under less-than-ideal circumstances.
Clinical data also has several peculiarities that require special techniques. Different clinical variables have different orders – some are first-order Markov processes, whereas others may be of higher order11. Our current toolkits only support first-order DBNs16. Hence, we modeled all temporal relationships as first-order. Another issue with modeling clinical processes using DBNs involves defining the hidden variables and their states. The hidden variables and their states are not always directly obtainable from medical literature. Hidden variables and their states were defined through a review of medical literature by the first author, and were refined through review by the last author and three other physicians at the University of Utah.
3.4. Toolkits
The tools used include the open-source Projeny toolkit running as the front-end and interfaced using JMatLink to the backend comprising of Bayes Net Toolbox (BNT) running inside Matlab. Projeny has been developed by the first author and is based on Bayesian Network tools in Java (BNJ)8.
Projeny allows the user to create first order DBNs as two time-slice models using a graphical front end, and to define nodes, their states, and their status as observed or hidden. Projeny also allows graphical authoring of intra- and inter-slice edges. During training and testing, Projeny automatically unrolls (expands) the model for as many timeslices as is present in each patient’s data8.
Projeny connects to a database to allow queries of training or testing data. It then sends the model and the data to BNT for parameter learning (training) or for inference (testing) as desired. It saves the results in a relational database and makes them available for analysis8.
3.5. Parameter Tying and Equivalence Classes
An important feature of Projeny is the automatic detection of equivalence classes. Equivalence classes are groups of variables that have the same set of ancestors and have the same parameters (conditional probability tables or CPTs), i.e. their parameters are ‘tied’11. Parameter tying is a benefit derived from the Markov property. This reduces the computational complexity of the model by a factor of t, the number of time slices. For example, let us unroll the model above to fit the data of a patient who is treated in the ICU for five days with measurements being made once every two hours (60 measurements in total). The number of variables per time slice (slice size) n is 10, and the number of time slices t is 60. Without parameter tying, nt = 600 parameters (CPTs) will be required to describe this model. With parameter tying, we will only need a maximum of 2n = 20 parameters (CPTs) to describe this model. In our model described above, we only need 11 parameters since it has only 11 equivalence classes, which are denoted by the numbers within the circles.
3.6. Training (Parameter Learning)
The training dataset had 508 patients and the test dataset had 287 patients, assigned randomly. Training was done through an Expectation Maximization (EM) variant of the junction tree algorithm to accommodate missing data. The EM algorithm converged after 19 iterations, and took about 5 hours on a computer with a quad-core Intel Xeon 3GHz processor and 8GB of memory.
3.7. Testing (Inference)
Testing was done later using a junction-tree-based exact inference algorithm. The evaluation method was based on a technique described by Anthony Wong et al17., and the test dataset was created accordingly. We artificially divided the data of patients in the test dataset into samples of four continuous timeslices each using a sliding window of four timeslices, since most patients had a much larger number of timeslices. We created 7,543 testcases from the data of 287 patients.
In each 4-timeslice testcase, we preserved the values of serum glucose in the first three timeslices (G1, G2, G3), and set the value of serum glucose in the fourth timeslice (G4) to 95 mg/dL, the midpoint of our desired normal glucose range of 80 to 110 mg/dL. We preserved the insulin drip rates in the first two timeslices (I1 and I2), but removed it from the last two timeslices (I3 and I4).
We then performed the inference where the DBN model was made to predict the value of insulin drip rate I3 in the third timeslice to achieve a target serum glucose G4 of 95 mg/dL in the fourth timeslice. This simulates the clinical scenario where at time T3, the physician or the eProtocol predicts I3 based on the past few measurements to achieve a normal value for glucose (G4 of 95mg/dL) at a future time T4.
4. EVALUATION
The DBN model was evaluated by comparing its I3 (DBN-I3) recommendations against those of eProtocol (eProt-I3) for the same patients at the same timeslices, in context of the actual values of G4 (eProt-G4) in the medical record. The real-world glucose level (eProt-G4) measured at time T4 while the patient was treated using eProtocol helped to determine the better protocol for a given test case.
If the patient encountered hypoglycemia (G4 < 80 mg/dL) at time T4, the protocol that recommended a lower insulin dose I3 is the better (and safer) protocol. If the patient encountered hyperglycemia (G4 > 110 mg/dL) at time T4, then the protocol that recommended a higher insulin dose I3 is the better (and effective) protocol in this case. Both eProtocol and DBN model had a target G4 of 95 mg/dL. Hence, 95mg/dL was used as the target to compare DBN-I3 and eProt-I3 to determine the winning protocol.
The results were tabulated and stratified by the serum glucose value G4 into several hypoglycemic, normoglycemic and hyperglycemic ranges. The number of cases where DBN-I3’s suggested dose exceeded eProt-I3’s and vice-versa are shown graphically in figure 3. In the extremely hypoglycemic ranges (G4 < 70 mg/dL), we can see that DBN recommended less insulin (DBN-I3) than eProtocol (eProt-I3) in a large number or cases, and is hence the safer protocol. However, eProtocol recommended a lower insulin dose than DBN in the mildly hypoglycemic cases (G4 between 70 and 90 mg/dL) and was better in these ranges. In normoglycemic cases, DBN recommended a higher insulin dose most of the time, and in the mildly to moderately hyperglycemic cases, where G4 was between 110 and 200 mg/dL DBN also recommended more insulin. If the three categories (<40, 400 – 500 and >500) with a total of less than 10 testcases are excluded, it can be seen from figure 1 that DBN recommended a preferable insulin dose in 6 categories (4,176 cases), and eProtocol recommended a better insulin dose in 4 categories (3,365 cases), showing that the DBN provided good insulin drip rate predictions compared to the gold standard.
Figure 3.
Number of test-cases where the insulin dose suggested by DBN-I3 exceeded that of eProt-I3 and vice-versa.
5. DISCUSSION
We also performed statistical analyses on the results: we calculated the Pearson and Spearman correlation co-efficients which showed very high correlation between the serum glucose and insulin drip rates calculated by the DBN model, which will be described separately. It must be noted that the patients’ feeding (enteral and parenteral) data was not available at the time of this experiment to be included in the DBN model, whereas this data was available to the eProtocol. The probabilistic DBN model shows comparable accuracy to that of a rule-based model. We hypothesize that the accuracy of the DBN model can be improved with availability of the patients’ feeding data which influences the patients’ serum glucose. The addition of severity of illness data (APACHE II and Multiple Organ Failure scores), which indirectly affect serum glucose levels by affecting the insulin resistance, may also be useful.
This experiment has several limitations. The temporal relationships were modeled as first-order Markov due to the limitations of our toolkits. Furthermore, the evaluation technique could only determine if the DBN could have produced less hypoglycemia or hyperglycemia compared to gold standard. It could not determine if the patient’s glucose would have overshot the normal range with the DBN. For example, in cases where G4 was above normal (hyperglycemia) and DBN-I3 was greater than eProt-I3, DBN could have produced hypoglycemia (G4 < 80, an adverse event due to overdose) instead of normoglycemia. Our evaluation technique could not identify such cases.
6. CONCLUSION
This study is among the first to use DBN for glucose control with real clinical data, and it uses a much larger sample size composed of a more diverse patient group than previous studies9. This experiment shows good temporal prediction of biomedical variables of interest in spite of various limitations. Further testing with a more extensive dataset is required before this technique can be applied in the real world. The methods were also used in early detection of sepsis in the emergency department with very high accuracy. This suggests a degree of generalizability for these methods, and will be described separately.
Figure 2.
Comparison method for insulin doses recommended by DBN versus eProtocol-insulin. (Nodes of interest shown here. Model’s full structure is as in fig 1.)
Acknowledgments
The authors thank Dr. Kathy Sward at the University of Utah and the eProtocol group at Intermountain Healthcare for the eProtocol dataset.
References
- 1.Van den Berghe G. Beyond diabetes: saving lives with insulin in the ICU. Int J Obes Relat Metab Disord. 2002;26(Suppl 3):S3–8. doi: 10.1038/sj.ijo.0802171. [DOI] [PubMed] [Google Scholar]
- 2.Pittas AG, Siegel RD, Lau J. Insulin therapy and inhospital mortality in critically ill patients: systematic review and meta-analysis of randomized controlled trials. JPEN J Parenter Enteral Nutr. 2006;30(2):164–72. doi: 10.1177/0148607106030002164. [DOI] [PubMed] [Google Scholar]
- 3.Goldberg PA, Siegel MD, Sherwin RS, Halickman JI, Lee M, Bailey VA, et al. Implementation of a safe and effective insulin infusion protocol in a medical intensive care unit. Diabetes Care. 2004;27(2):461–7. doi: 10.2337/diacare.27.2.461. [DOI] [PubMed] [Google Scholar]
- 4.Morris AH, Orme J, Jr, Truwit JD, Steingrub J, Grissom C, Lee KH, et al. A replicable method for blood glucose control in critically Ill patients. Crit Care Med. 2008;36(6):1787–95. doi: 10.1097/CCM.0b013e3181743a5a. [DOI] [PubMed] [Google Scholar]
- 5.Combi C, Shahar Y. Temporal reasoning and temporal data maintenance in medicine: issues and challenges. Comput Biol Med. 1997;27(5):353. doi: 10.1016/s0010-4825(96)00010-8. [DOI] [PubMed] [Google Scholar]
- 6.Keravnou ET. Temporal reasoning in medicine. Artificial Intelligence in Medicine. 1996;8(3):187. doi: 10.1016/0933-3657(95)00032-1. [DOI] [PubMed] [Google Scholar]
- 7.Hart A, Wyatt J. Evaluating black-boxes as medical decision aids: issues arising from a study of neural networks. 1990;15(3):229. doi: 10.3109/14639239009025270. [DOI] [PubMed] [Google Scholar]
- 8.Nachimuthu SK. p. 2009. Projeny: An Open Source Toolkit for Probabilistic Temporal Reasoning. In: AMIA Annu Symp Proc; 2009.
- 9.Cavan DA, Hejlesen OK, Hovorka R, Evans JA, Metcalfe JA, Cavan ML, et al. Preliminary experience of the DIAS computer model in providing insulin dose advice to patients with insulin dependent diabetes. Comput Methods Programs Biomed. 1998;56(2):157–64. doi: 10.1016/s0169-2607(98)00022-4. [DOI] [PubMed] [Google Scholar]
- 10.Andreassen S, Hovorka R, Benn J, Olesen KG, Carson ER. Third Conference on Artificial Intelligence in Medicine. Springer-Verlag; 1991. 1991. A Model-based Approach to Insulin Adjustment; pp. 239–248. [Google Scholar]
- 11.Murphy KP. 2002. Dynamic bayesian networks: representation, inference and learning. PhD thesis: U.C.Berkeley;
- 12.Dossett LA, Cao H, Mowery NT, Dortch MJ, Morris JM, Jr, May AK. Blood glucose variability is associated with mortality in the surgical intensive care unit. Am Surg. 2008;74(8):679–85. doi: 10.1177/000313480807400802. discussion 685. [DOI] [PubMed] [Google Scholar]
- 13.Finney SJ, Zekveld C, Elia A, Evans TW. Glucose control and mortality in critically ill patients. Jama. 2003;290(15):2041–7. doi: 10.1001/jama.290.15.2041. [DOI] [PubMed] [Google Scholar]
- 14.Krinsley JS. Effect of an intensive glucose management protocol on the mortality of critically ill adult patients. Mayo Clin Proc. 2004;79(8):992–1000. doi: 10.4065/79.8.992. [DOI] [PubMed] [Google Scholar]
- 15.Lloyd SP. Least squares quantization in PCM. 1982;28(2):129. [Google Scholar]
- 16.Murphy KP. Bayes Net Toolbox. [cited 2010/03/10]; Available from: http://bnt.googlecode.com/
- 17.Wong A, Al-sheikh YT, Warner HR, Haug PJ, Sward KA, Morris AH. Evaluation and comparison of IV insulin-treatment protocols using data from critically ill patients in the ICU. AMIA Annu Symp Proc. 2008:1178. [PubMed] [Google Scholar]