Statistical Mechanics of Integral Membrane Protein Assembly

Abstract

During the synthesis of integral membrane proteins (IMPs), the hydrophobic amino acids of the polypeptide sequence are partitioned mostly into the membrane interior and hydrophilic amino acids mostly into the aqueous exterior. Using a many-body statistical mechanics model, we analyze the minimum free energy state of polypeptide sequences partitioned into α-helical transmembrane (TM) segments and the role of thermal fluctuations. Results suggest that IMP TM segment partitioning shares important features with general theories of protein folding. For random polypeptide sequences, the minimum free energy state at room temperature is characterized by fluctuations in the number of TM segments with very long relaxation times. Moreover, simple assembly scenarios do not produce a unique number of TM segments due to jamming phenomena. On the other hand, for polypeptide sequences corresponding to actual IMPs, the minimum free energy structure with the wild-type number of segments is free of number fluctuations due to an anomalously large gap in the energy spectrum. Now, simple assembly scenarios do reproduce the minimum free energy state without jamming. Finally, we find a threshold number of random point mutations where the size of the anomalous gap is reduced to the point that the wild-type ground state is destabilized and number fluctuations reappear.

Introduction

Anfinsen (1) established in a landmark study that the three-dimensional structure of globular proteins is determined by their primary amino-acid sequences and he identified this structure as the minimum free energy state. Integral membrane proteins (IMPs) such as ion channels, ion pumps, porins, and receptor proteins, do not easily lend themselves to Anfinsen's method (2) and whether assembled IMPs represent global free energy minima still has not been established. The focus of this article is on one of the most common IMP structures: bundles of, typically, 7–12 transmembrane (TM) α-helices (Fig. 1, inset). The helices consist of ∼20–25 mostly apolar amino-acid residues linked outside the membrane by short, disordered polypeptide sequences of mostly hydrophilic amino acids. The TM segments can exist as stable entities inside the membrane in the absence of any bundle structure because the characteristic energy scale of tertiary structure formation is significantly lower than the formation free energy of the α-helices (3). This separation in energy scales, which allows for separate determinations of the secondary and tertiary structures, provides important simplifications. For example, the identification of prospective α-helical TM segments of a polypeptide sequence is an easier task than the prediction of the secondary structure of globular proteins, which do not have this separation in energy scales. One procedure for determining the TM segment structure starts from a hydropathy plot—a plot of the free energy gained by transferring a certain number of successive amino acids of the primary sequence from aqueous environment into the membrane interior in the form of an α-helix, as a function of the start site of the segment (see Fig. 1). TM segment insertion free energies are assigned based on an empirical hydrophobicity scale for the different amino acids (4). Locations along the plot where the free energy gain for segment formation exceeds a certain threshold are possible start sites for TM segments. The hydrophobicity δ of individual amino acids in earlier hydropathy plots was obtained from solubility studies of amino acids in organic solvents, with considerable variation between different scales. In a commonly used scale (5), the variation of δ-values was ∼15 kcal/mole and the hydropathy plot values varied roughly between –40 and +30 kcal/mole. Segment placement for IMP sequences based on hydropathy plots is relatively straightforward and reproduces reasonably well the locations of α-helical segments of IMPs as obtained from x-ray structural studies (6). More elaborate hidden Markov models, trained on known IMP structures, produce quite accurate structures ((7), and references therein). Yet other, Hamiltonian-based, approaches employ mean-field alignment techniques to optimize for the correct fold of a sequence while avoiding local minima trappings (8,9).

Figure 1.

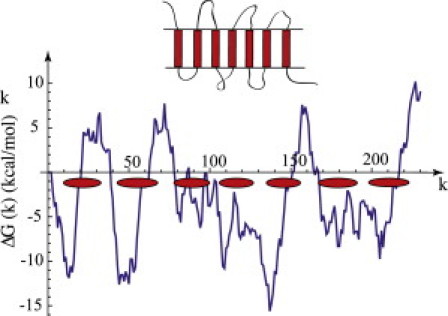
Insertion free energy ΔG(k) of a transmembrane α-helical segment (Eq. 1 with μ = 0.7 kcal/mol and L_α = 26) for different values of the location k of the first amino acid. The insertion free energy was computed using the hydrophobicity scale of Hessa et al. (11) for the membrane protein bacteriorhodopsin (bR). (Ellipses) Ground state of the seven-segment wild-type structure. (Inset) Seven ordered α-helical segments connected by disordered linker sections are shown schematically.

Implicit in the hydrophobicity construction is the assumption that fluctuations of the number of TM segments—which obviously would interfere with IMP functionality—can be neglected. In other words, the thermal energy k_BT should be small compared to the free energy difference δE between structures with different numbers of segments obtained by the construction, but is this true? Assume that the hydrophobicities of residues j = 1,…,N adopt the values δ S(j), where S(j) = ±1 with equal probability 1/2. A TM segment of size L starting at site k has an insertion energy

$$\Delta G\left(k\right)\sim \delta M\left(k\right)-L\mu ,$$

with

$$M\left(k\right)={\sum }_{j=k}^{k+L-1}S\left(j\right)$$

being the sum of L random variables (the mean hydrophobicity is absorbed in μ). According to the central limit theorem, for L >> 1, M is a Gaussian random variable of zero mean and variance 〈M²〉 equal to L. A chain of length N composed of N/L segments corresponds to N/L independent tries of this random variable. The average spacing δE between different tries in the distribution of outcomes is then of the order of

$$\delta E\sim \delta {\langle M^2\rangle }^{1/2}/\left(N/L\right)\sim \delta L^{3/2}/N.$$

According to that crude statistical argument, the typical δE of a long, generic (i.e., randomly picked) polypeptide sequence should be of the order of

$$\delta E\sim {\langle {\delta }^2\rangle }^{1/2}{L}^{3/2}/N,$$

with 〈δ²〉^1/2 the root-mean-square variation of the hydrophobicity scale for the residues of the sequence, L the mean TM segment length, and N the chain length. It follows that in the limit of large N, thermal segment number fluctuations are unavoidable. For reasonable values such as N∼200, 〈δ²〉^1/2 ∼8 kcal/mole, and L∼20, δE would be in the range of 3.6 kcal/mole. It is not obvious whether, for k_BT ∼0.59 kcal/mole (room temperature), thermal number fluctuations can be neglected.

Thermal fluctuations are actually believed to play a key role during the assembly process. Synthesis of IMPs by ribosomes takes place on the surface of the endoplasmic reticulum where active clusters of proteins—translocons—thread unfolded, nascent polypeptide sequences through a transmembrane channel (10). The translocon sequentially recognizes hydrophobic sections along the primary sequence and partitions them into the membrane. A remarkable study by Hessa et al. (11) showed that the translocon partitioning probabilities of different amino-acid repeat sequences appear to follow equilibrium Boltzmann statistics. This appears to suggest that, like globular proteins, IMPs may adopt minimum free energy structures. From their measured probabilities, Hessa et al. (11) also established a new hydrophobicity scale appropriate for translocon partitioning. This scale shows a relatively small range of hydrophobicity values, roughly from –0.6 to +3.5 kcal/mole, depending also on the location of the amino acid within the segment (12), while insertion free energies of IMP TM segments are in the range of –5 to +4 kcal/mole. If the insertion energies of 7–12 segments are uniformly distributed over this range, then—using our earlier estimate—δE should be roughly equal to the thermal energy for a generic sequence. This means that, using the Hessa scale, strong segment thermal number fluctuations should be expected for generic sequences, notwithstanding the fact that IMP functionality requires a well-defined number of TM segments. The obvious inference is that IMPs somehow must encode in their polypeptide sequence suppression of thermal segment number fluctuations.

This article applies methods of statistical mechanics to examine, for a simple model system, the segment-number fluctuations of polypeptide sequences inserted into a membrane for a minimum free energy state. We also will examine the conditions under which sequentially assembled structures (as in the translocon scenario) that have segment number fluctuations suppressed by large kinetic barriers still can be expected to produce the proper segment positions. We will show that, for this model system, the problem of placing variably-sized, nonoverlapping TM segments at finite temperature along a polypeptide sequence, with an insertion energy obtained from a hydrophobicity scale, reduces to a particular many-body problem of one-dimensional statistical mechanics whose minimum free energy state can be computed exactly. When this method is applied to purely random polypeptide sequences of the same length as IMPs, one finds that the minimum free energy state at room temperature is characterized by strong thermal segment number fluctuations, as expected from the crude estimate we gave earlier. The free energy barrier that has to be overcome to change the number of TM segments is, unlike δE, still large compared to the thermal energy (even on the Hessa scale). It follows that, for laboratory timescales, the secondary structure of a generic polypeptide sequence should be described as a glassy state with a structure determined by assembly history. For polypeptide sequences corresponding to actual IMPs, we find, however, a surprisingly large gap in the excitation energy spectrum of the minimum free energy state when the number of inserted segments P exactly corresponds to the wild-type number of segments P_w. Because of this gap, IMPs are, in a state of minimum free energy, practically free of segment number fluctuations at room temperature. When P exceeds P_w, number fluctuations in general play an important role in the minimum free energy state even for IMPs. It is known that for a representative sample of IMPs, the distribution of segmental hydrophobicities is bimodal with underlying TM and non-TM distributions overlapping to an extent (20). In the context of our statistical-mechanical model, the energy gap also can be seen as a consequence of this distribution. States for which P = P_w can be constructed by sampling from the lower energy, TM part of the distribution. A state with P > P_w implies sampling from the higher energy, non-TM part of the distribution, while P < P_w implies excluding sampling from the lower energy, TM part of the distribution.

We investigated the accessibility of this minimum free energy state for simple assembly scenarios. For the specific polypeptide sequences associated with IMPs, sequential assembly does reproduce the correct number of segments of the ground state but only as long as the number of segments P is ≤P_w . For P > P_w, jamming-type phenomena cause sequential assembly to produce nonunique segment placements. Only the structures produced by sequential assembly with P = P_w reproduce, at room temperature, the minimum free energy state. For generic sequences, jamming phenomena appear for P values << P_w. In the presence of point mutations, the stabilizing anomalous energy gap shrinks as the number of random point mutations increases until a threshold is reached marked by rapid growth of thermal number fluctuations.

This contrast between the wild-type and random sequences in terms of thermodynamics and assembly kinetics is rather similar to that between the glassy molten globule state of collapsed generic polypeptide sequences in bulk solutions and the designed folded state of globular proteins at the lowest point of the folding funnel (13,14). This folded state is usually free of large-scale, destabilizing thermal fluctuations, and is accessible from the unfolded state by rapid assembly kinetics. This suggests that in terms of the energy spectrum, IMPs and globular proteins can be described by a common phenomenology.

The Model System

Assume a polypeptide sequence composed of N hydrophilic and hydrophobic residues. Let the start site of a particular TM segment be denoted by the integer index k and the number of TM residues by L_α with α indexing the set of observed different TM sizes. The model assigns a segment insertion free energy

$$\Delta G_{\alpha }\left(k\right)=\sum _{j=k}^{k+L_{\alpha }-1}\left(\delta \left(j\right)-\mu \right),$$ (1)

with δ(j) the hydrophobicity of residue j, for which we use the Hessa scale. Thermodynamic changes of the environment that shift the zero of the hydrophobicity scale are included by the parameter μ. Physically, ΔG_α(k) can be viewed as the external potential energy of a TM segment of length L_α sliding along the primary sequence. Fig. 1 shows ΔG_α(k) with μ = 0.7 kcal/mole and L_α = 26 residues for the case of the well-studied integral membrane protein bacteriorhodopsin (bR), a 7-TM segment protein found in the outer membrane of Halobacterium salinarium.

We will assume an excluded-volume repulsion between the TM segments, i.e., segments are not allowed to overlap while the end site of one TM segment can be adjacent within two residues to the start site of the next TM segment with no free energy penalty. Specifically, for a rod of species α starting at site j followed by another rod (of any species) starting at site k > j, the interaction potential is assumed to be

$$V_{\alpha }\left(k-j\right)=\{\begin{array}{l}0k-j\ge L_{\alpha }+2\\ \mathrm{\infty }k-j<L_{\alpha }+2\end{array}.$$ (2)

This interaction does not include the interhelix attractive interactions that determine the tertiary structure of IMPs. The justification for neglecting helix-helix attraction is that it operates on an energy scale significantly lower than that of the segment insertion energy and thus does not have a strong effect on the distribution of segment number, size, and location. This energy-scale separation—known as the two-stage model (15)—was already noted in the Introduction. Other low-energy correlations between segments, such as variations in the effective hydrophobicity of a residue due to correlations with neighboring residues and linker-mediated interactions between adjacent segments, are neglected for the same reason.

Recursion relations

Next, we want to determine the statistical likelihood for an arbitrary sequence of TM segments of variable length and location placed in a hydrophobic environment, connected by disordered linker segments of residues placed in aqueous environment, in a state of thermodynamic equilibrium. The Boltzmann statistical weight for the formation of a single TM segment of species α starting at site k is defined as $e^{-\beta \Delta G_{\alpha }\left(k\right)}$ with β = 1/k_BT. The Boltzmann statistical weight ρ_α(k) for the site k to be the start of a TM segment of length L_α as part of an ensemble of other segments is expressed as

$${\rho }_{\alpha }\left(k\right)=e^{-\beta \Delta G_{\alpha }\left(k\right)}{\Xi }_{\alpha }^F\left(k\right){\Xi }_{\alpha }^B\left(k\right)/\Xi .$$ (3)

The term ${\Xi }_{\alpha }^F\left(k\right)$ represents the forward Boltzmann statistical weight of all possible TM segment distributions located anywhere between sites 1 and k given that that there is a TM segment of size L_α that starts at site k. Similarly ${\Xi }_{\alpha }^B\left(k\right)$ represents the backward weight, while Ξ is the overall normalization. Once ρ_α(k) has been determined, the mean number of TM segments

$${\rho }_{TM}={\sum }_{\alpha }{\sum }_k{\rho }_{\alpha }\left(k\right)$$

can be obtained as a function of μ. The slope

$$\chi =\frac{d{\rho }_{TM}\left(\mu \right)}{d\mu }$$

at the values of μ where ρ_TM(μ) is equal to an integer P plays the role of the susceptibility of a P-segment structure to thermal number fluctuations (note that in the grand canonical ensemble, it corresponds to the second derivative of the thermodynamic potential with respect to the chemical potential). For a segment of length L, thermal number fluctuations become important when χ is of the order of L/k_BT or larger. Of interest also is the occupancy

$$\sigma \left(k\right)={\sum }_{\alpha }{\sum }_{j=k-L_{\alpha }+1}^k{\rho }_{\alpha }\left(j\right),$$

defined as the probability that a residue k is part of a TM segment of any allowed size. A plot of σ(k) shows the most probable locations of the TM segments.

Mathematically, the problem of computing TM placement probabilities is the computation of the grand canonical partition function Ξ and the site-specific, one-sided partition functions ${\Xi }_{\alpha }^F\left(k\right)$ and ${\Xi }_{\alpha }^B\left(k\right)$ of a one-dimensional, multispecies liquid of variable-sized hard rods subject to an external potential. This computation can be carried out exactly using the recursion relation method discussed in the Supporting Material. The recursion relation method is closely related to hidden Markov models (7) while for the special case that all segments have the same size, it reduces to the analytically soluble Percus model (16) of hard rods in an external potential. In this method, one first breaks up ${\Xi }_{\alpha }^F\left(k\right)$ as a sum over the different possible values of the distance k–j (in residues) between a segment of size L_α starting at k and a neighboring segment starting at site j with 1 ≤ j < k:

$${\Xi }_{\alpha }^F\left(k\right)=e^{\beta \Delta G_{\alpha }\left(k\right)}\sum _{\gamma }\sum _{j=1}^{k-1}{\Xi }_{\gamma }^F\left(j\right)W_{\alpha ,\gamma }\left(k-j\right).$$ (4)

The term

$$W_{\alpha ,\gamma }\left(k-j\right)=\exp \left(-\beta V_{\gamma }\left(k-j\right)\right)$$

takes into account the excluded volume interaction between two neighboring TM segments of length L_α and L_γ starting at sites k and j, respectively. If the linker length obeys k − j − L_γ < 2, then $W=0$ while $W=1$ otherwise. Note that in Eq. 4 one takes an annealed average over allowed TM segment sizes. Starting from the initial condition ${\Xi }_{\alpha }^F\left(1\right)=1$, the values of ${\Xi }_{\alpha }^F\left(k\right)$ for k > 1 can be computed by forward iteration. A similar relation holds for the backward weights,

$${\Xi }_{\alpha }^B\left(k\right)=e^{\beta \Delta G_{\alpha }\left(k\right)}\sum _{\gamma }\sum _{j=k+1}^N{\Xi }_{\gamma }^B\left(j\right)W_{\alpha ,\gamma }\left(j-k\right),$$ (5)

which is reconstructed starting from ${\Xi }_{\alpha }^B\left(N\right)=1$. Using these recursion relations it is possible to numerically reconstruct ρ(k) under conditions of thermodynamic equilibrium for any given amino-acid sequence.

Results

Ground-state stability and thermal fluctuations

Fig. 1 shows the bR ground state structure, computed for the case that thermal fluctuations were turned off (i.e., the limit of large β), μ = 0.7 kcal/mol and L_α = 21–26 as compared with a hydropathy plot computed for L_α = 26. Segment start sites correspond reasonably to the local minima of the plot and the computed number, size, and locations of the TM segments are in reasonable agreement with the reported structure (see Fig. S1 in the Supporting Material). Fig. 2 shows the mean segment number ρ_TM(μ) as a function of μ for three different temperatures. For very weak thermal fluctuations (Fig. 2 A), ρ_TM(μ) has a discontinuous, staircase-like shape with steps at the integer values of ρ_TM. A vertical step of the staircase represents the insertion of another TM segment, say to a state with P segments. The subsequent horizontal width Δμ(P) measures the free energy change per amino acid required to add yet one more segment to the P-segment state and hence measures the thermodynamic stability of the P-segment state against changes in the number of segments. The Δμ(P) values for P equal to two, three, four, and five are less than 0.1 kcal/mole. When k_BT is increased to 0.2 kcal/mole (∼100°K, Fig. 2 B), these steps are nearly completely washed out, and when k_BT is increased to room temperature (Fig. 2 C), steps with P equal to one and six are smeared out as well. Note that ρ_TM(μ) now is a smoothly continuous function with a typical susceptibility χ—given by the slope—in the range of L/k_BT. The exception is the seventh step, which has survived as a section with a slope that is practically zero at the center. Thermal number fluctuations can be neglected only in this μ-interval. The room temperature occupancy plot of this state shows well-defined locations of the seven segments closely corresponding to the ground state, apart from some fluctuations in location and size of the sixth segment (Fig. S2). As a control, we repeated the calculation for random (i.e., randomly shuffled) bR sequences. At room temperature, the susceptibility χ is now consistently of the order of L/k_BT over the whole the range of μ-values where the actual bR sequence had its plateau (Fig. S3), while the occupancy pattern of the random bR sequence shows an ill-defined placement pattern with occupation probabilities adopting a wide range of values (Fig. S2).

Figure 2.

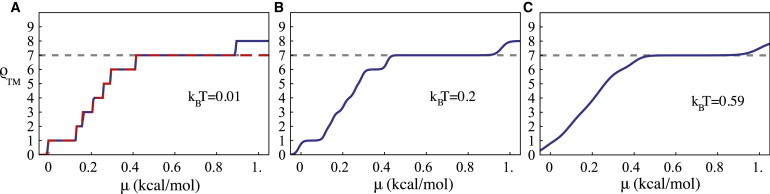
Mean number ρ_TM of TM segments of bR as a function of the average insertion free energy gain μ per amino acid for different temperatures. (A) k_BT = 0.01 kcal/mole. (Dashed line) Mean number ρ_SA of TM segments placed by sequential adsorption. For μ < ∼0.85 kcal/mole, the two plots coincide, but for μ > 0.85 kcal/mole, ρ_SA no longer increases. (B) k_BT = 0.2 kcal/mole. Only the 1-TM, 6-TM, and 7-TM segment structures have zero slopes at the respective center of the sections. (C) Room temperature (k_BT = 0.59 kcal/mole). Only the seven-segment structure has a zero slope.

Occupancy profiles can be used to assess the effect of thermal fluctuations by overlaying them on the hydropathy plot, as is done in Fig. 3 for the random bR sequence. The thermal energy k_BT was set to 0.1 kcal/mole and μ to 0.57 kcal/mole. This occupancy pattern is the superposition of occupancy patterns corresponding to four and five segments, respectively. In the five-segment state (bottom of Fig. 3), the last two segments occupy the two minima of the hydropathy plot indicated by circles. In the four-segment state (top of Fig. 3) one TM segment is placed with starting site either on the first circle or on the square, two nearly degenerate minima of the hydropathy plot. The energy differences between these three states are comparable to 0.1 kcal/mole so that all three states contribute at that temperature to the statistical ensemble and the occupancy plot is the superposition of the three states. There are thus both segment number fluctuations as well as large-scale positional fluctuations in this frustrated state.

Figure 3.

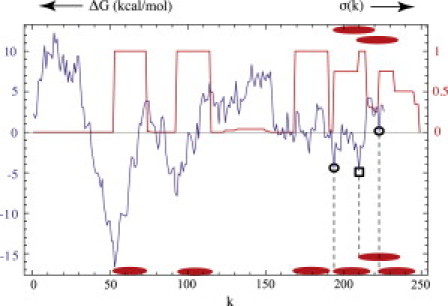
Occupancy plot for the randomly shuffled bR sequence at μ = 0.57 kcal/mol overlaid on the hydropathy plot for k_BT set at 0.1 kcal/mol. (Bottom row of ellipses) Structure of the 5-TM segment ground state. (Circles) Locations of the last two segments. The minimum at k = 210 (square) is blocked in this structure. (Top) Two alternative placements of the last segment in the two competing 4-TM segment states. The occupancy plot is the superposition of these three nearly degenerate states.

To check whether these results were specific for bR, we repeated the analysis for five 7-TM segment proteins and five 12-TM segment proteins (Table S1, column 3). In all cases, Δμ(P_w) was anomalously large and only the wild-type ground state configuration survived at room temperature (typical cases of 3-TM and 12-TM segment IMPs, i.e., diacylglycerol kinase and cytochrome c oxidase, respectively, are shown in Fig. S4).

Assembly robustness

To transform the five-segment state of Fig. 3 into one of the two four-segment states, the fifth segment must be pulled out of the membrane. The mean free energy barrier for pull-out can be estimated as μL, which is ∼15 kcal/mole for μ equal to 0.6 kcal/mole. An Arrhenius estimate of the rate of segment pull-out by thermal fluctuations leads to macroscopic timescales (note that for an Arrhenius rate with an attempt frequency k_BT/η_md³, with d the membrane thickness of 50 Ångstroms and η_m a membrane viscosity of 0.1 in SI units, the timescale for removing the last segment by thermal fluctuations would be in the range of 10 s, assuming a 15 kcal/mole activation barrier). On laboratory timescales, structures whose (equilibrium) number susceptibility χ approaches L/k_BT need not be in a state of thermodynamic equilibrium. In this section we will examine TM segment states that are not in full thermodynamic equilibrium—as was the case in the previous section—in the sense that segment number fluctuations are forbidden but size and location thermal fluctuations are still allowed. The number of TM segments will be determined by the initial assembly. We will inquire for two simple sequential assembly scenarios, under which conditions the assembled state still would be close to the actual minimum free energy state.

In a linear assembly scenario, the first scenario starts at one end of the polypeptide sequence and sweeps through the sequence, placing a new TM segment on the first available low-energy binding site not covered by the previous segment, demanding only that the binding energy exceeds a certain threshold. By carefully tuning this threshold, placement of the TM segments can be made to agree for the bR sequence both with the measured structure and the computed ground state (Fig. S1). In the sequential adsorption scenario, one places the first TM segments at the minimum of ΔG_α(k) with respect to k and α, then searches for the next lowest value of ΔG_α(k) that is not blocked by the first segment, repeating this procedure as long as sites with negative ΔG_α(k) can be located for the given μ. All four rows place the segments in approximately the same locations. For bR, sequential adsorption also nearly reproduces the ground state (Fig. S1). Fig. 2 A includes a plot of the mean segment number ρ_SA(μ) obtained by sequential adsorption for the bR sequence as a dashed line. Sequential adsorption exactly reproduces ρ_TM(μ) up to and including P = 7, but sequential adsorption then halts while ρ_TM(μ) continues to increase. This jamming phenomenon is a familiar feature of studies of sequential adsorption in other systems (17). For sequential adsorption of the randomized bR chain of Fig. 3, discrepancies between ρ_SA(μ) and ρ_TM(μ) appear already at P = 4, as expected from Fig. 3 (Fig. S3). We repeated this analysis for other proteins and always found that sequential adsorption reproduces the ground state up to the wild-type number of TM segments, while random sequences encounter placement discrepancy for lower values of μ .

Recall that we found that the room temperature susceptibility χ for number fluctuations was negligible for P = P_w at the center of the wild-type stability interval, so number fluctuations were not required for thermal equilibration. We conclude that simple assembly scenarios effectively can produce the unique minimum free energy state of IMPs with P = P_w. Structures with lower μ-values, where sequential assembly also produced the correct ground state, but now with P less than P_w, did require segment number fluctuations for thermal equilibration. The earlier conclusion thus only holds for P = P_w. For shuffled IMP sequences with μ in the same range, different sequential assembly scenarios are not consistent with each other and their final states could not reach thermodynamic equilibrium without slow number fluctuations. This result suggests that random mutations could interfere with IMP assembly, which we will now investigate.

Mutational robustness

The structure of many globular proteins is known to be robust with respect to random point mutations (18). In addition to the obvious advantage of preserving functionality in the presence of mutations, mutational robustness also increases the number of sequences that map to the same folding structure, thereby promoting diversification and evolvability (19).

Is the large energy gap that protects the ground state of IMPs against destructive segment number fluctuations related to robustness against mutations?

We computed the number of randomly chosen single point mutations (SPMs) required to produce a change in the ground state number of TM segments, both for IMP sequences and their random analogs. The value of μ was fixed at the center of the stability gap Δμ(P_w) for the wild-type structure. We repeated this procedure a hundred times and computed the average number of SPMs (normalized by sequence length) to produce a change in the number of segments as well as the standard deviation. We then repeated this procedure for each protein with an ensemble of a hundred realizations of randomly shuffled sequences. For the random sequences, one-to-five point mutations per hundred residues typically were sufficient to change the number of TM segments in the ground state. For bR, and other 7-TM segment IMPs, the SPM threshold was approximately five times higher, but for certain 12-TM segment IMPs, like lactose permease of Escherichia coli, the SPM threshold enhancement was only a factor-of-two larger (see Table S1). There is some correlation between the thresholds of the wild-type and shuffled sequences and also some correlation between the thermodynamic stability interval Δμ(P_w) and the mutation threshold for most IMPs but there were also are striking exceptions. An example is the bacterial protein glycerol-3 phosphate transporter (E. coli) that has the largest energy gap yet only modest mutational robustness. We conclude that the ground state of wild-type IMPs are, in most cases, significantly more stable against point mutations than their shuffled control sequences, but thermodynamic and mutational robustness clearly are, in general, separate properties of an IMP.

Is there perhaps a relation between the mutational threshold and the susceptibility to segment number fluctuations?

Fig. 4 shows the average susceptibility for number fluctuations of bR at the center of the seven-segment interval as a function of the number of mutations. The mutation threshold is indicated as a vertical line with the dashed lines indicating the error bars. The mutation threshold is seen to be the locus of a rapid rise of the susceptibility for number fluctuations. The mutation threshold thus marks both a change in the ground state structure and an increased susceptibility against segment number fluctuations.

Figure 4.

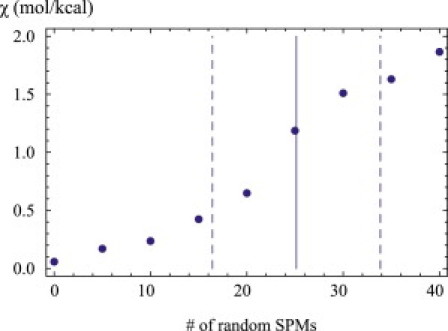
Susceptibility χ = dρ_TM/dμ for thermal segment number fluctuations of bR as a function of the number of randomly chosen single point mutations (SPMs) of the sequence. Each point is an average over 100 trials. (Solid vertical line) Threshold where the ground state structure is destabilized by mutations, and corresponds to the mean given in Table S1. (Dashed vertical lines) Error bars.

Conclusions

According to the model presented in this article, polypeptide sequences associated with actual IMPs can be assembled into minimum free energy structures by simple sequential assembly scenarios, though this is not true for generic sequences. Assembly robustness is achieved by

• 1.An anomalously large gap in the energy excitation spectrum that prevents thermal number fluctuations.
• 2.By the absence of jamming-type phenomena for segment numbers equal to or less than the wild-type.

Generic sequences of the same length and the same amino-acid abundance as an IMP sequence are in a glassy state with a structure that depends on the details of the assembly history.

Is there evidence for thermal number fluctuations in IMPs? If segment number fluctuations are frozen on laboratory timescales then this could show as statistical uncertainty in the number of TM segment after IMP assembly. The TM helix formation of the GABA_A receptor α1 subunit is destabilized by a particular point mutation, the A322D mutation, which causes a form of myoclonic epilepsy (21). The wild-type GABA_A receptor subunit is a 4-TM segment structure, and for the A322D mutant, the third segment fails to insert into the lipid bilayer ∼33% of the time. Fig. 5 A shows ρ_TM(μ) computed for both the wild-type and the A322D mutant in the absence of thermal fluctuations. Note that the stability interval of the 4-TM segment structure of the mutant is noticeably shorter compared to the wild-type. Fig. 5 B shows ρ_TM(μ) of the wild-type and the A322D mutant at room temperature, with the occupancy plot inset. For μ near the value where the mean number of segments is ∼3.5 (indicated by the arrow in Fig. 5 B), the susceptibility approaches L/k_BT. The A322D mutant is thus predicted by the model to be characterized by strong segment number variations, consistent with the experimental results.

Figure 5.

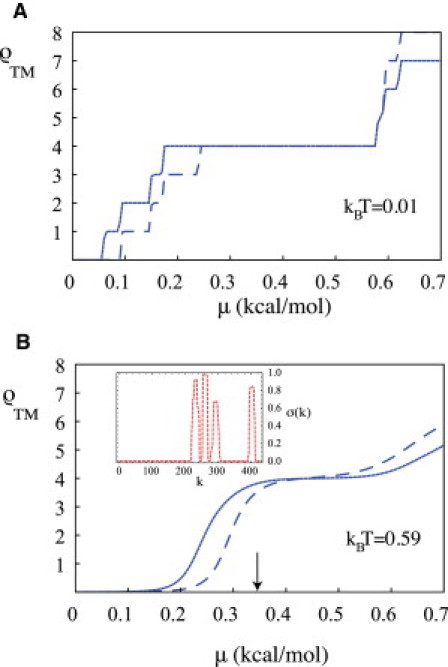
Effect of the A322D mutation on the GABA_A receptor α1 subunit. (A) ρ_TM at k_BT set at 0.01 kcal/mole. (Dashed line) Mutant. (B) ρ_TM at room temperature. (Dashed line) Mutant. (Inset) Occupancy of the mutant at the value of μ = 0.34 kcal/mol (arrow). The mutation occurs in the third TM segment.

We close by noting that a model similar to the one discussed in this article has been applied to the problem of the placement of nucleosomes along genomic DNA molecules. By comparing measured structures with the minimum free energy state computed for the model, it was established that the assembly of DNA-nucleosome fibers does generate a state of near-minimum free energy (22), despite very large free energy barriers between structures with different numbers of nucleosomes. Because of the much greater length of the genome sequence, assembly frustration of the form shown in Fig. 3 was unavoidable. The competing states appear to act as biological switches (23). It would be interesting if artificial IMPs could be synthesized that—like the GABA_A subunit—can exist in two alternative switch forms with different numbers of segments. One method for doing that would be to alter the amino-acid sequence of an IMP, explicitly introducing assembly frustration of the form shown in Fig. 3, and testing which of the competing structures is assembled by the translocon.