Assessing the performance of the MM/PBSA and MM/GBSA methods: II. The accuracy of ranking poses generated from docking

Abstract

In molecular docking, it is challenging to develop a scoring function which is accurate to conduct high throughput screenings (HTS). Most scoring functions implemented in popular docking software packages were developed with many approximations for computational efficiency, which sacrifices the accuracy of prediction. With advanced technology and powerful computational hardware nowadays, it is feasible to use rigorous scoring functions, such as Molecular Mechanics/Poisson Boltzmann Surface Area (MM/PBSA) and Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) in molecular docking studies. Here we systematically investigated the performance of MM/PBSA and MM/GBSA to identify the correct binding conformations and predict the binding free energies for 98 protein/ligand complexes. Comparison studies showed that MM/GBSA (69.4%) outperformed MM/PBSA (45.5%) and many popular scoring functions to identify the correct binding conformations. Moreover, we found that molecular dynamics (MD) simulations are necessary for some systems to identify the correct binding conformations. Based on our results, we proposed the guideline for MM/GBSA to predict the binding conformations. We then tested the performance of MM/GBSA and MM/PBSA to reproduce the binding free energies of the 98 protein-ligand complexes. The best prediction of MM/GBSA model with internal dielectric 2.0, produced a Spearman correlation coefficient of 0.66, which is better than MM/PBSA (0.49) and almost all scoring functions used in molecular docking. In summary, MM/GBSA performs well for both binding pose predictions and binding free energy estimations and is efficient to re-score the top-hit poses produced by other less accurate scoring functions.

Introduction

Molecular docking is one of the most important techniques for receptor-based drug design (RBDD).¹ It can be used to propose the structural hypotheses of how ligands interact with the targets and screen compound libraries to identify potential drug candidates against the targets prior to experimental high throughput screenings (HTS).² Despite of the significant successes, molecular docking still faces a lot of challenges, especially for efficiently exploring the conformational space of target proteins and ligands and developing scoring functions to estimate the free energies of protein-ligand binding. Scoring function is critical for molecular docking to identify the correct binding poses as well as to rank different ligands with respect to calculated binding free energies. However, it is not practical to utilize the most accurate and also computationally expensive scoring functions in docking studies, in which a great number of docking poses and molecules needs to be evaluated. In consideration of computational efficiency, approximations were introduced in most docking scoring functions, which often affect the accuracy of predictions.

The available scoring functions for molecular docking can be roughly divided into three categories: force-field-based, empirical and knowledge-based approaches. Force-field-based approach estimates the binding affinities by calculating the non-bonded interactions based on traditional force fields, such as the scoring functions used by DOCK³ and Autodock.⁴ The empirical approach (e.g. Ludi,⁵ FlexX,⁶ ChemScore,⁷ Xscore⁸ and Glide⁹) incoraporates some empirically weighted interaction terms such as van der Waals, electrostatic and solvation energies with adjustable parameters for scoring. These parameters are fitted from the experimental binding free energies of a set of crystal complexes. The knowledge-based (mean force) scoring function (e.g. SMoG,¹⁰ PMF¹¹ and DrugScore¹²) was developed from statistical analysis of the distances between pairs of atom types found in protein-ligand structures. In spite of the continuous efforts to improve the scoring functions,^13–15 their accuracy to rank the binding poses and to predict the binding free energies still remains unsatisfactory.

In many molecular docking approaches, one scoring function is used for two tasks: identifying the correct binding pose of a ligand and ranking ligands using the predicted binding affinities. Alternatively, one can use a computationally efficient scoring function to predict the binding poses and then use a more rigorous scoring function to recalculate the binding energies of the top-hit poses. Such an approach may make a good balance between computational efficiency and accuracy.

Since the end of the last century, combining molecular mechanics energy and implicit solvation models, such as Molecular Mechanics/Poisson Boltzmann Surface Area (MM/PBSA) and Molecular Mechanics/Generalized Born Surface Area (MM/GBSA), became popular in free energy calculations and molecular docking studies.^16–18 MM/PBSA and MM/GBSA are more rigorous than most empirical or knowledge-based scoring functions. In addition, molecular dynamics (MD) simulations MM/PBSA or MM/GBSA can effectively deal with the conformational change upon ligand binding. Moreover, both of MM/PBSA and MM/GBSA allow for rigorous free energy decomposition into contributions originating from different groups of atoms or types of interaction.^19–21

Previous studies have shown that MM/PBSA or MM/GBSA are efficient to identify the correct binding poses and rank the inhibitors for specific targets.^22–27 However, there is no systematic and large-scale evaluation of the performance of MM/PBSA or MM/GBSA to identify the correct docking poses and rank the affinities of ligands for a diverse set of binding sites. Here we conducted a systematic investigation of MM/PBSA and MM/GBSA for 98 protein/ligand complexes. Our results showed that MM/PBSA and MM/GBSA outperformed 11 scoring functions widely used in molecular docking. To our best knowledge, this work represents one of the most extensive studies of MM/PBSA or MM/GBSA for molecular docking. We found that MM/GBSA is computationally more efficient than MM/PBSA and also achieved a comparable or even better accuracy, although MM/PBSA is theoretically more rigorous.

Materials and Methods

1. Preparation of protein-ligand complexes

The dataset used in this study is from Wang and coworkers.¹⁵ In the original applications, this data set, which contains 100 protein/ligand complexes was used to compare the performance of 11 popular scoring functions. For each complex, 100 docked conformations were generated by the Autodock program (version 3.0). These docked conformations were assumed to cover the entire binding pocket and its vicinity area. The total number of the docking poses of each ligand is 101, including 100 docked conformations and the bound conformation of the ligand defined by experiment. We found that the data for the complex 1tet reported by Wang et al. is not correct. In their study, a citric acid was taken to be the ligand. In fact, Cholera toxin peptide 3 (CTP3) was in complex with the protein TE33, the Fab fragment of a monoclonal antibody. The original binding data was also reported for the CTP3/TE33 interactions. Therefore, we took out 1tet from the Wang et al.'s data set. In addition, we also removed 1tha since the GB parameters for iodine were not available in AMBER9.0. Finally, we have 98 protein/ligand complexes in the data set.

All ligands were optimized using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) technique. We then used the semi-empirical quantum method implemented in the divcon program²⁸ in AMBER9²⁹ to derive AM1-BCC partial charges for all ligand atoms. We used the same protonation states of the ligands as Wang and coworkers.¹⁵ The AM1-BCC charges calculation is much faster than the HF/6-31G* RESP charges.³⁰ And previous studies showed that MM/PBSA using AM1-BCC and RESP charges gave compatible binding free energies.³¹

In our calculations, all Asp and Glu residues were negatively charged, and all Lys and Arg residues were positively charged. In the MM minimizations and MD simulations, we used AMBER03 force field for proteins,³² and the general AMBER force field (gaff) for ligands.³³ Counter-ions of Cl- or Na+ were placed at grids with the largest positive or negative Coulombic potentials around the receptors to neutralize the charge of the systems.

2. Optimization of protein/ligand complexes

For each complex, the conformations of the 100 docking poses and the experimentally-determined binding pose were optimized in the active site of the target. Considering the large number of binding poses in our study, we studied the solvent effect by using a 16 Å water cap instead of a water box with Periodic Boundary Conditions (PBC). We placed the water cap in the center of mass of the ligand, which encapsulated the whole ligand. The maximum number of minimization steps was set to 4000 and the convergence criterion was set to be 0.05 kcal/mol/Å of the root-mean-square (rms) of the Cartesian energy gradient. The first 500 minimization steps were performed with the steepest descent algorithm and the rest with the conjugate gradient algorithm. During the minimizations, only the ligand, the protein residues and the water molecules within 9 Å of the ligand were allowed to move and other atoms were fixed.

3. Rescoring with MM/PBSA

For each minimized ligand pose/protein complex, the binding free energy of MM/PBSA was estimated as in Equation 1^16,17,34:

$$\begin{array}{cc}\hfill \Delta G_{\mathit{bind}}& =G_{\mathit{complex}}-G_{\mathit{protein}}-G_{\mathit{ligand}}\hfill \\ \hfill & =\Delta E_{MM}+\Delta G_{PB}+\Delta G_{\mathit{nonpolar}}-T\Delta S\hfill \end{array}$$ (1)

where ΔE_MM is the gas-phase interaction energy between protein and ligand, including the electrostatic and the van der Waals energies; ΔG_PB and ΔG_nonplar are the polar and non-polar components of the desolvation free energy, respectively; −TΔS is the change of conformational entropy upon ligand binding, which was not considered here due to the expensive computational cost. The ΔG_PB term was calculated by Delphi II³⁵ to solve the finite-difference Possion-Boltzmann equation. In Delphi calculations, the grid spacing was set to 0.5 Å, and the grid size was determined to have the longest linear dimension extended 20% outside the protein. The Parse radii were employed for all atoms.³⁶ Because the radii of F and Br were absent from the Parse set, the Pauling van der Waal radii of F and Br (1.35 and 1.95 Å)³⁷ were adopted for Delphi calculations. The value of the exterior dielectric constant was set to 80, and the solute dielectric constant was set to three different values: 1, 2 and 4. The non-polar contribution was determined based on solvent-accessible surface area (SASA) with the LCPO method:³⁸ ΔG_SA=0.0072×ΔSASA.

4. Rescoring with MM/GBSA

In MM/GBSA calculations, the gas-phase interaction energy (ΔE_MM) and the non-polar (ΔG_SA) part of the solvation energy were calculated in the same way as MM/PBSA calculations. The electrostatic solvation energy (ΔG_GB) was calculated by using the GB models. Again we use 80 for the exterior dielectric constant, and three different values of 1, 2 and 4 for the solute dielectric constant. We used three GB models implemented in AMBER9.0, namely, the pairwise GB model developed by Hawkins and coworkers (termed as GB^HCT),^39,40 with parameters developed by Tsui and Case,⁴¹ and two modified GB models developed by Onufriev and coworkers (referred as GB^OBC1 and GB^OBC2).⁴² It should be noted that in AMBER, the GB^OBC1 and GB^OBC2 model were parameterized for Bondi radii.⁴²

5. Molecular Dynamics (MD) Simulations and rescoring with MM/GBSA

We carried out MD simulations to further optimize the protein-ligand interaction for the top 3 poses of 13 protein/ligand complexes, where the correct binding conformations were not ranked as the best conformations according to the MM/GBSA free energies. The binding free energies were then recalculated using the MD trajectories. The PDB entries for the 13 complexes were 1apw, 1bhf, 1cbx, 1d3d, 1dr1, 1exw, 1mnc, 1pph, 1rgl, 1tmn, 2csc, 2pk4, and 7tln.

To perform MD simulations, each protein/ligand complex was immersed in a rectangular box of TIP3P water molecules. The water box was extended 10 Å away from any solute atom. The particle mesh Ewald (PME) was employed to calculate the long-range electrostatic interactions.⁴³ The complexes were first relaxed using 2,000 cycles of minimization procedure (500 cycles of steepest descent and 1500 cycles of conjugate gradient minimization). The system was then gradually heated in the NVT ensemble from 10 K to 300 K over 20 ps.⁴⁴ Initial velocities were assigned from Maxwellian distribution at the starting temperature. Then 300 ps MD simulations were preformed in the NPT ensemble with target temperature at 300 K and target pressure at 1 atm. The SHAKE procedure was employed to constrain all hydrogen atoms, and the time step was set to 2.0 fs. MD snapshots were saved every 4 ps after the systems were well equilibrated. The MM optimization and MD simulations were accomplished with the sander program in AMBER9.0.²⁹ Finally, the binding free energies were calculated using the MM/GBSA method averaged over 60 snapshots that were evenly extracted from the single trajectory of complex between 60 to 300 ps MD simulations.

Results and Discussion

1. The predictions of binding poses of MM/GBSA or MM/PBSA rescoring

(a). The prediction accuracy of the MM/GBSA rescoring

We first applied the MM/GBSA technique to rescore the docking decoys of 98 protein–ligand complexes compiled by Wang et al.¹⁵ The rescoring was only based on the single minimized structures. In the GB calculations, the modified GB model developed by Onufriev and Case (igb=2 in AMBER9.0 and termed as GB^OBC1) was used and the solute dielectric constant was 1.⁴² We used the RMSD as the criterion for the success of the prediction. If RMSD (root-mean-square deviation) of the best scored pose was less than or equal to 2.0 Å from the experimentally observed conformation, we considered it was a successful prediction. As shown in Table 1, we observed that MM/GBSA successfully recognizes the native-like poses for 61 of the entire 98 complexes, i.e. the success rate was 62.2%. Then we calculated the success rate considering the best two to five best scored poses of each ligand (Table 1), in which the success rate was improved significantly. For example, if the top three and five conformations were considered, the success rate was improved from 62.2% to 84.7% and 88.8%, respectively. For some target proteins, the experimentally determined pose was in the very top scored conformations even though it was not recognized as the best by MM/GBSA.

Table 1.

Success rates of MM/PBSA and MM/GBSA considering one to five best scored conformations

	Success rate (%)
Scoring functions	Best 1	Best two	Best three	Best four	Best five
MM/GBSA (igb=1, εin=1)	64.3(63/98)	78.6(77/98)	85.7(84/98)	85.8(84/98)	88.8(87/98)
MM/GBSA (igb=1, εin=2)	67.3(66/98)	76.5(75/98)	82.7(81/98)	84.7(83/98)	85.7(84/98)
MM/GBSA (igb=1, εin=4)	54.1(53/98)	69.4(68/98)	71.4(70/98)	76.5(75/98)	77.6(76/98)
MM/GBSA (igb=2, εin=1)	62.2(61/98)	77.6(76/98)	84.7(83/98)	86.7(85/98)	88.8(87/98)
MM/GBSA (igb=2, εin=2)	69.4(68/98)	76.5(75/98)	82.7(81/98)	83.7(82/98)	85.7(84/98)
MM/GBSA (igb=2, εin=4)	58.2(57/98)	71.4(70/98)	73.5(72/98)	75.5(74/98)	77.6(76/98)
MM/GBSA (igb=5, εin=1)	31.6(31/98)	49.0(48/98)	56.1(55/98)	60.2(59/98)	65.3(64/98)
MM/GBSA (igb=5, εin=2)	39.8(39/98)	55.1(54/98)	59.2(58/98)	66.3(65/98)	69.4(68/98)
MM/GBSA (igb=5, εin=4)	43.9(43/98)	55.1(54/98)	63.3(62/98)	68.4(67/98)	75.5(74/98)
MM/PBSA (εin=1)	38.8(38/98)	43.9(43/98)	50.0(49/98)	50.0(50/98)	53.1(52/98)
MM/PBSA (εin=2)	56.1(55/98)	56.1(55/98)	60.2(59/98)	66.3(65/98)	68.4(67/98)
MM/PBSA (εin=4)	50.0(49/98)	63.3(62/98)	69.7(69/99	75.5(74/98)	79.6(78/98)

In MM/GBSA or MM/PBSA, the solute dielectric constant (ε_in) is a key parameter. For each system, another two solute dielectric constants, 2.0 and 4.0, were also tested for calculating the solvation free energies (Table 1). If we considered only the best scored conformation, the success rate of ε_in=1 (62.2%) was apparently worse than that of ε_in=2 (69.4%), but better than that of ε_in=4 (58.2%). However, when top three scored conformations were considered, the success rate of ε_in=1 (84.7%) was the best, which was slightly better than that of ε_in=2 (82.7%) and much better than that of ε_in=4 (73.5%). Therefore, for most cases, 1 or 2 was a good choice for the solute dielectric constant.

Three GB models, namely, the pairwise GB model developed by Hawkins and coworkers (GB^HCT, referred as igb=1)^39,40 and two modified GB models developed by Onufriev and coworkers (GB^OBC1 and GB^OBC2, referred as igb=2 and 5, respectively),⁴² were implemented in AMBER9.0. The 101 decoys of each of the 98 protein-ligand complexes were rescored again by the MM/GBSA method using the three GB models. For each model, three different solute dielectric constants (ε_in =1, 2 and 4) were tested. According to the success rates listed in Table 1, for all of three solute dielectric constants, the performance of GB^OBC2 was worse than that of GB^HCT and GB^OBC1, while the performance of GB^HCT and GB^OBC1 was quite similar. It is not clear what is the reason behind the different performance of GB^OBC1 and GB^OBC2, since they have the same theoretic framework. Interestingly, our previous studies of the MM/PBSA or MM/GBSA calculations on six protein/ligand systems also showed that GB^OBC1 performed much better than GB^OBC2 for predicting the binding free energies.⁴⁵

(b) The prediction accuracy of the MM/PBSA rescoring

Numerical solution of the Poisson–Boltzmann (PB) equation is more theoretically rigorous than the GB model and is believed to be more accurate but more computationally demanding. The performance of the MM/PBSA method on the docking pose rescoring was also evaluated. The success rates for the MM/PBSA calculations are listed in Table 1. If we only consider the best scored conformations, the success rates of MM/PBSA were 31.3% for ε_in=1, 45.5% for ε_in=2 and 42.4 % for ε_in=4. The success rates were increased to 41.4%, 53.5% and 60.6%, respectively, when the best three conformations were considered. In comparison to the three GB models, the performance of MM/PBSA was only marginally better than that of GB^OBC2, but much worse than that of the MM/GBSA schemes based on GB^HCT and GB^OBC1. This result is consistent with our previous observations,⁴⁵ in which the MM/GBSA based on GB^OBC1 scheme performed better than MM/PBSA to rank the binding affinities of ligands for protein systems without metals in the binding sites. Recently, Thompson and coworkers applied MM/PBSA to discriminate correct and incorrect docking poses. They found that the solvation energy calculated by PB cannot improve the prediction accuracy significantly in the absence of X-ray structures of complexes.⁴⁶ Our analysis indicates that the solvation free energy is very important and it is critical to choose an appropriate solvation model and solute dielectric constant.

(c) Comparison with other scoring functions

Wang et al. compared the performance of 11 popular scoring functions for molecular docking on the 98 complexes.¹⁵ The success rates of these scoring functions vary from 26% (DSCORE) to 76% (PLP). Our results showed that the MM/GBSA based on the GB^OBC1 model achieved a success rate of 69.4% using a solute dielectric constant of 2.0 if we only considered the best scored conformation. This success rate was higher than those of seven scoring functions (D-Score, G-Score, AutoDock, ChemScore, X-Score, LUDI and PMF), but lower than those of four other scoring functions (PLP, F-Score, LigScore and DrugScore).¹⁵ If the three best conformations were considered, the success rate given by MM/GBSA was higher than those of nine scoring functions, but lower than those of PLP and F-Score. When the top five conformations were considered, the performance of MM/GBSA was only worse than F-Score, but better than the other ten scoring functions (See Table S1 in the Supporting Materials).

In general, for the 11 scoring functions studied by Wang et al, the force field-based scoring functions (Autodock, GScore and DScore), without explicit desolvation energy, achieved lower success rates than the other types of scoring functions. The higher success rate of MM/GBSA implies that the desovlation term is critical to identify the correct binding poses. For the other eight empirical and knowledge-based scoring functions, a caveat is that they were developed by fitting the experimentally determined structural and binding data for a large training set with various sets of protein-ligand complexes. Indeed, many proteins in Wang et al.'s data set were used in the training sets to parameterize these scoring functions. For example, all 100 experimentally determined complexes in the dataset used by Wang et al. were also used as the training set for training the X-Score scoring function. Therefore, the success rate of such scoring functions may only reflect how well the parameterization is done. In contrary, the parameterization of MM/GBSA does not include any information of the interaction between the ligands and the proteins in the studied complexes.

(d) The energy landscape for protein-ligand binding

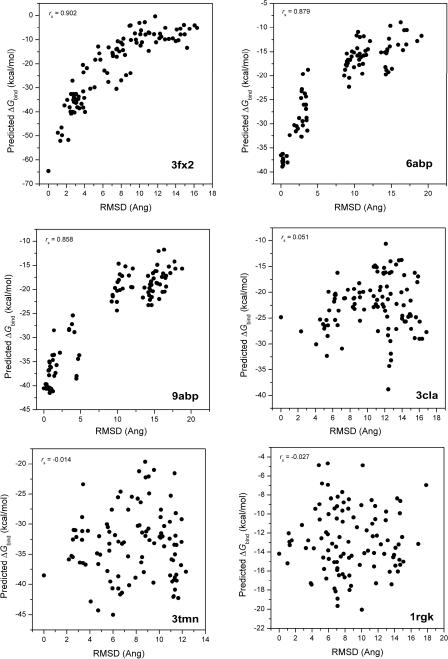
The protein-ligand complexation is speculated to have a funnel-shaped energy surface,¹⁵ originally used in protein folding studies. Similar to the work reported by Wang and coworkers,¹⁵ we studied the energy landscape of ligand binding by using RMSD as the reaction coordinate. It is expected that a lower RMSD is associated with a stronger binding value and vice versa. We analyzed the correlations between the RMSD and the binding free energies calculated using MM/PBSA or MM/GBSA models listed in Table 1. The Spearman correlation coefficients (r_s) are listed in Table 2. We also provided cumulative occurrences of r_s values for comparison. As shown in Table 2, MM/GBSA gave better correlations than MM/PBSA while the GB^OBC1 and GB^HCT models performed better than GB^OBC2. More specifically, the GB^OBC1 model using a solute dielectric constant of 2 gave the best correlation, and its r_s values were better than or equal to 0.60 for 60% of the 98 proteins. Six examples with the best and worst correlations are shown in Figure 1.

Table 2.

Correlations between the calculated binding free energies and RMSD given by the MM/PBSA and MM/GBSA calculations

	Cumulative occurrence of Spearman correlation coefficient (rs)
Scoring functions	≥0.00	≥0.20	≥0.40	≥0.60	≥0.80
MM/GBSA (igb=1, εin=1)	96	92	77	47	11
MM/GBSA (igb=1, εin=2)	96	91	76	57	13
MM/GBSA (igb=1, εin=4)	91	85	72	49	3
MM/GBSA (igb=2, εin=1)	96	93	74	46	7
MM/GBSA (igb=2, εin=2)	96	91	77	60	13
MM/GBSA (igb=2, εin=4)	95	90	77	55	6
MM/GBSA (igb=4, εin=1)	81	70	59	31	2
MM/GBSA (igb=4, εin=2)	86	78	62	39	6
MM/GBSA (igb=4, εin=4)	95	87	68	44	5
MM/PBSA (εin=1)	55	28	19	2	0
MM/PBSA (εin=2)	75	60	38	17	1
MM/PBSA (εin=4)	85	73	58	27	0

Figure 1.

The correlations between the predicted binding free energies of MM/GBSA and the RMSD values for three complexes with the best correlations and three complexes with the worst correlations.

The good performance of MM/GBSA seems more impressive if we compare it with the results of 11 scoring functions compared by Wang and coworkers.¹⁵ In the data reported by Wang and coworkers, the cumulative occurrences of r_s ≥ 0.6 for 11 scoring functions vary from 16% to 53% for the 100 proteins, which is obviously worse than that of MM/GBSA. In summary, the MM/GBSA scoring gives a better funnel-shaped energy landscape than all scoring functions compared by Wang et al.

2. The importance of MD sampling for recognizing the correct binding poses

In the practice of virtual screening, we usually keep the best conformation predicted by molecular docking for further analysis. As shown in Table 1, the best MM/GBSA model, GB^OBC1 using a solute dielectric constant of 2, ranked the correct binding conformation as the best scored conformation from the 101 docking decoys for 68 complexes. For the other 30 protein complexes, 13 had their correct binding conformations ranked in the top three, and 3 in top five but not in top three, and 14 beyond top five. Because only a single minimized conformation was used for MM/GBSA calculations, it is possible that insufficient sampling of conformational space may harm the performance of MM/GBSA. Here we studied whether conformational sampling could improve the prediction accuracy.

For the 13 complexes whose binding conformations were ranked in the top three but not the best one, we conducted MD simulations for the best three scored docking poses The PDB entries for these 13 complexes are 1apw, 1bhf, 1cbx, 1d3d, 1dr1, 1exw, 1mnc, 1pph, 1rgl, 1tmn, 2csc, 2pk4, and 7tln. The binding free energy for each docking pose was calculated by averaging 60 snapshots evenly taken from 60 to 300 ps MD simulations (Table 3 and Table S1 in the Supporting Materials). As shown in Table 3, with solute dielectric constant 2, the conformations in 9 complexes with the most favorable binding free energies were very close to the experimentally observed binding poses (RMSD less or equal to 2.0 Å). For 2csc, the best conformation was not far from the correct binding pose either (RMSD = 2.49 Å). The correct binding poses could not be identified as the best scored conformations in three complexes, 1mnc, 1pph and 1rgl. In summary, MD simulation improved the prediction accuracy by conformational sampling.

Table 3.

The predicted binding free energies and the individual energy terms for the best three scored poses of 13 complexes based on the single minimized structures using the MM/GBSA technique based on the GB^OBC1 model and the solute dielectric constant of 2

PDB	Rank	ΔEele	ΔEvdw	ΔGPB	ΔGSA	−TΔS	ΔHcal.	ΔGcal.	RMSD1a	RMSD2b
1apw	8	−21.79	−55.37	30.05	−7.86	−27.73	−54.98	−27.25	3.84	4.53
	101	−30.06	−55.09	35.94	−7.98	−23.91	−57.19	−33.28	0.00	1.38
	7	−8.71	−50.65	19.43	−6.98	−23.50	−46.91	−23.41	3.30	4.29
1bhf	20	−276.04	−39.14	258.20	−6.88	−28.54	−63.86	−35.32	4.77	5.31
	8	−293.42	−34.40	273.86	−6.54	−31.80	−60.51	−28.71	5.92	5.92
	101	−271.16	−37.93	251.62	−7.23	−27.61	−64.70	−37.09	0.00	1.77
1cbx	10	−71.98	−23.67	72.81	−3.87	−16.83	−26.72	−9.89	3.56	4.13
	9	−64.70	−18.89	58.78	−4.05	−15.39	−28.86	−13.47	3.01	1.16
	101	−81.05	−22.03	74.70	−3.86	−18.22	−32.24	−14.02	0.00	1.08
1d3d	10	−9.98	−56.55	18.30	−7.83	−19.85	−56.08	−36.23	2.29	2.81
	5	−10.14	−58.94	19.83	−7.73	−20.08	−56.98	−36.90	1.77	1.35
	6	−8.70	−58.94	20.49	−7.98	−27.19	−55.15	−27.96	3.37	4.51
1dr1	22	−23.50	−33.67	26.36	−4.23	−16.64	−35.04	−18.40	2.92	1.79
	1	−22.65	−33.43	26.52	−4.16	−18.75	−33.73	−14.98	1.05	1.20
	101	−23.19	−34.68	26.60	−4.14	−18.88	−35.40	−16.52	0.00	1.55
1exw	12	32.10	−40.57	−25.94	−6.25	−17.63	−40.65	−23.02	2.45	3.05
	1	11.13	−39.62	−9.48	−6.15	−21.93	−44.12	−22.19	1.24	1.45
	13	21.56	−39.24	−21.00	−5.96	−20.88	−44.65	−23.77	2.24	1.55
1mnc	3	−18.25	−46.15	22.62	−6.01	−22.55	−47.78	−25.23	8.58	7.45
	45	−16.44	−49.06	25.03	−6.36	−22.97	−46.83	−23.86	8.47	10.10
	11	−36.29	−38.60	33.78	−5.71	−24.26	−46.81	−22.55	1.31	1.41
1pph	29	−4.90	−34.74	2.87	−4.72	−20.27	−41.50	−21.23	4.27	4.96
	17	12.16	−43.45	−10.82	−5.44	−21.06	−47.55	−26.49	7.25	7.58
	101	−17.16	−37.36	13.62	−4.66	−23.14	−45.56	−22.42	0.00	1.20
1rgl	42	70.88	−21.97	−60.82	−3.37	−16.91	−15.27	1.64	7.44	12.16
	30	110.25	−23.05	−94.95	−3.52	−21.60	−11.27	10.33	0.99	1.79
	13	88.01	−25.58	−82.29	−3.94	−21.33	−23.80	−2.47	3.89	4.23
1tmn	9	124.74	−42.19	−111.51	−6.24	−24.33	−35.19	−10.86	6.82	8.01
	1	106.37	−41.73	−96.71	−6.41	−19.69	−38.40	−18.71	2.28	2.38
	101	97.74	−43.21	−89.42	−6.22	−16.88	−41.11	−24.23	0.00	1.52
2csc	18	−193.72	−8.87	168.62	−2.41	−15.73	−36.39	−20.66	3.16	2.49
	16	−174.91	−8.50	159.30	−2.54	−14.11	−26.66	−12.55	3.04	1.75
	13	−137.80	−8.74	124.05	−2.44	−12.62	−24.93	−12.31	1.75	2.06
2pk4	6	−75.08	−10.43	66.53	−2.74	−17.74	−21.72	−3.98	2.92	1.39
	101	−20.47	−15.44	22.02	−2.65	−15.03	−16.50	−1.47	0.00	2.63
	1	−26.30	−14.60	27.11	−2.70	−15.52	−16.49	−0.97	0.90	1.87
7tln	16	−19.61	−20.91	19.60	−3.91	−12.87	−24.84	−11.97	4.39	4.56
	10	−7.43	−24.82	11.94	−4.01	−11.65	−24.31	−12.66	1.50	1.84
	5	−8.10	−25.97	13.46	−4.20	−14.22	−24.81	−10.59	2.01	2.65

^aRMSD for pose before MD simulations

^bRMSD between the averaged structure of the MD simulations and the crystal structure

Next, we investigated the effect of conformational entropy. We first predicted the binding poses only using enthalpy (ΔH_cal). For eight systems, the correct binding poses can be successfully identified by using ΔH_cal. The inclusion of entropy can only improve the prediction for one system, i.e. 7tln. For 7tln, the binding enthalpies for three poses are quite similar. After considering entropy, the binding free energy of the correct pose is marginally better than those of the other two poses. Therefore, the inclusion of the entropies did not significantly improve the results for the protein systems studied here.

Interestingly, for most of the 13 protein systems, the van der Waals energies of the best three binding conformations did not differ significantly, which means the ligand has similar van der Waals or hydrophobic contacts with the receptor although the orientations of the three docking poses are different. However, with regard to the electrostatic energies (ΔE_ele and ΔG_GB), the three docking poses are significantly different. Therefore, for most cases the accurate predictions of the electrostatic terms are essential for the successful predictions of the binding poses.

We then tested another solute dielectric constant (ε_in=1) for the MM/GBSA calculations (Table S2 in the Supporting Materials). The comparison between Table 3 and Table S2 shows that the absolute binding free energies calculated by using two different solute dielectric constants are quite different but the performance of ranking binding poses is similar. MM/GBSA based on ε_in=1 also give correct predictions for nine systems. For two systems, 1rgl and 2csc, the MM/GBSA cannot give the correct answers for both dielectric constants. For 1pph, the correct docking pose is correctly predicted by using MM/GBSA with ε_in=1, but not with ε_in=2. For 7tln, MM/GBSA with ε_in=2 gives the correct answer but not for ε_in=1. Therefore, the performance of ε_in=1 and 2 is not different for predicting the binding poses.

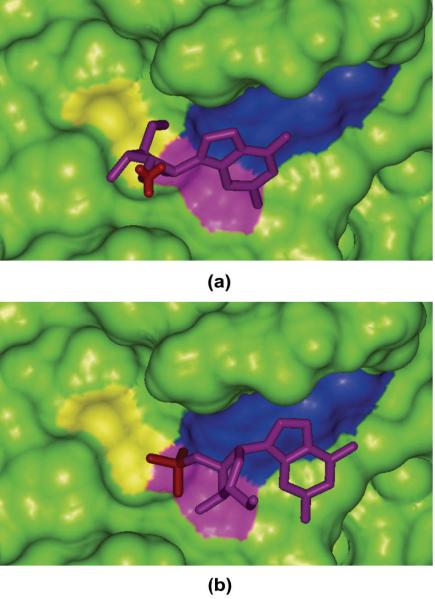
For the 13 complexes listed in Table 3, the correct binding poses for 1rgl and 2csc, cannot be successfully identified as the best scored conformations with MM/GBSA based on either ε_in=2 or ε_in=1. For 2csc, the prediction is not bad because the best scored conformation is not far from the correct binding pose (RMSD = 2.49 Å). Compared with 2csc, 1rgl is obviously a more difficult system. For 1rgl, the binding free energy (−2.47 kcal/mol) of the best scored pose (conformation 13) is much more favorable than that (10.33 kcal/mol) of the experimentally determined pose (conformation 30). According to the analysis of the binding interface of 1rgl (Figure 2a), three charged residues can be found in the binding site of 1rgl, including Glu58, Arg77, and His92. More importantly, the ligand in 1rgl has a highly negatively charged phosphate group (net charge is −2), which can form strong ion-ion interactions with Arg77 and His92. While for conformation 13, as shown in Figure 2b, the phosphate group is exposed to the solvent and no longer forms ion-ion interactions with the charged residues in the binding pocket. Therefore, conformations 13 and 30 form different binding interfaces, and it is possible that we need to apply different solute dielectric constant to characterize the different electrostatic properties of the binding interfaces. Another possible reason is that the PB or GB models usually cannot give good predictions for the solvation of ions,⁴⁷ probably because the errors of force fields and reaction field calculation cannot be effectively cancelled out when ion-ion interactions dominate the binding free energies.

Figure 2.

The interaction between Rnase T1 Mutant Glu46Gln and (a) conformation 13 and (b) conformation 30 of ligand 2'GMP. The charged phosphate groups are shown in red stick; the Connolly surfaces for Glu50, Arg77 and His92 are colored in yellow, violet and blue, respectively.

In conclusion, in most cases, short MD simulation can help MM/GBSA to identify the experimentally determined binding conformations. Previous results reported by Kuhn et al. concluded that applying the MM-PBSA energy function to a single optimized complex structure is an adequate and sometimes more accurate approach than the standard free energy averaging over MD snapshots.²⁴ Our calculations here clearly show that applying MM/GBSA scoring to a single relaxed structure may not be enough to predict the binding poses correctly. The ultimate reason why MM/GBSA based on a single structure is not successful for some systems is that a single structure cannot characterize the conformational fluctuations in different local minima. Therefore, for these systems, MD simulations are necessary to improve the predictions.

3. Why some systems could not be correctly predict by MM/GBSA

There are 11 complexes in our test set for which MM/GBSA based on either ε_in=1 or 2 cannot pick the correct binding conformation within an RMSD threshold of 2.0 Å in the top five conformations, which are 1cla, 1d3p, 1etr, 1rgk, 1tlp, 2sns, 3cla, 3tmn, 4cla, 4tln and 8xia (Table S3 in the Supporting Materials).

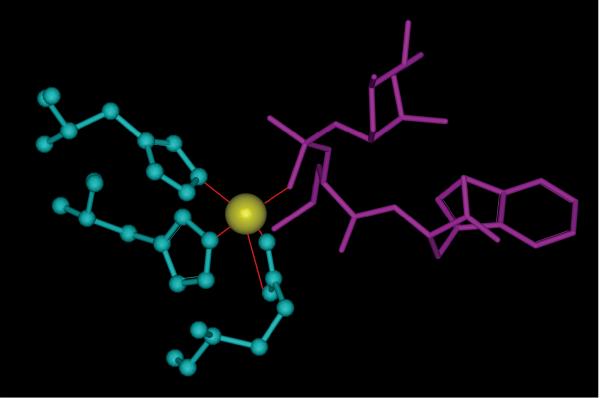
In 1tlp, the inhibitor N-phosphoryl-L-leucinamide (P-Leu-NH2) complexed to thermolysin, and one phosphoramidate oxygen atom, one glutamin and two histidine residues interact with the zinc to form a pentacoordinate (see Figure 3). Unfortunately, this zinc ion was removed from the protein when generating the decoys by molecular docking. We believe that removal of this zinc will underestimate the interactions between the correct binding conformation and thermolysin. The failures in other three cases, 2sns, 4tln and 8xia are also due to the similar reasons. It is clear that the currently available scoring functions still need to be improved for systems with ions which form coordinate bonds with ligands.

Figure 3.

The coordinate bonds formed by the zinc ion with one phosphoramidate oxygen atom, one glutamin and two histidine residues. The zinc ion is colored in yellow, protein residues colored in blue, and ligand colored in violet.

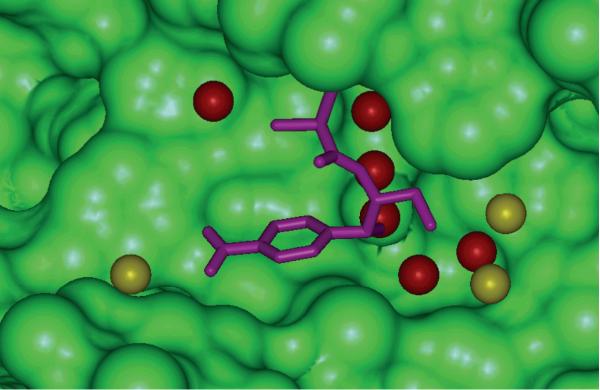
The complexes 1cla, 3cla and 4cla are type II chloramphenicol acetyltransferases in complex with chloramphenicol (3cla is the wild type of chloramphenicol acetyltransferase; 1cla is a S148A mutant; and 4cla is a L160F mutant). According to our predictions, for these three complexes the best five scored conformations are far from the correct ones. For 3cla, according to our predictions, the binding free energies for the best five scored conformation are −38.32, −34.30, −33.18, −32.33, and −31.91 kcal/mol, respectively, while the binding free energy for the correct binding conformation is −24.84 kcal/mol. For these three complexes, the experimentally determined binding poses cannot even be found in the best ten scored conformations. Analysis of the 3cla crystal structure shows that many water molecules mediate the protein-ligand interactions (see Figure 4). According to Wang et al.'s report,¹⁵ when generating the decoys by Autodock, the crystal water molecules were removed. The correct binding conformation of the ligand in 3cla is not energetically favorable when the important bridging water molecules are not considered. Another point is that even though the crystal structure is explicitly added to the decoys, the predictions of the binding free energies for these three systems are still difficult. It remains challenging for MM/GBSA or MM/PBSA to handle bridging crystal water molecules and define the appropriate solute dielectric constant with many water molecules. Moreover, according to Wang et al.'s study,¹⁵ none of the 11 scoring functions is able to pick the correct conformation for these two complexes. The unsuccessful predictions for other systems may also be explained by the neglect of the important bridging water molecules, such as in the cases of 1d3p and 1etr. In 1etr three water molecules are important for the interactions between the ligand and the protein, and in 1d3p there is one such important water molecule. Correctly considering the effects of the essential bridging water molecules is thus an important task for developing scoring functions. Explicitly including some water molecules, especially the crystal waters, in MM/PBSA and MM/GBSA calculations may be an efficient way to tackle the challenging problem.

Figure 4.

The interaction between chloramphenicol and chloramphenicol acetyltransferase in complex with 3cla. Ligand is colored in violet. The water molecules within 5 Å of ligand are shown as the CPK model, and the water molecule which can mediate the interactions between ligand and proteins are colored in red.

The complex 1rgk, i.e. Rnase T1 mutant Glu46Gln is in complex with inhibitor 2'gmp. As noted above, for 1rgl the correct binding pose cannot be identified even after a short MD simulation. The protein in 1rgl is also Rnase T1 mutant Glu46Gln but the ligand is 2'amp, which is similar to that in 1rgk. Therefore, it is straightforward to understand why the prediction for 1rgk is not successful: the electrostatic terms cannot be accurately predicted.

The reason for the poor predictions on the system 3tmn is not obvious. For 1d3p, the predictions are not very bad. In the best scored conformations, three of them are not far from the correct binding poses (RMSD < 3.0 Å).

4. The prediction of MM/PBSA or MM/GBSA to rank the binding affinities for various protein-ligand complex systems

Prediction of binding poses is the first step of molecular docking. Another important task is to rank compounds using the predicted binding free energies. Therefore, the accuracy of the binding free energy prediction is also critical for evaluating a scoring function.

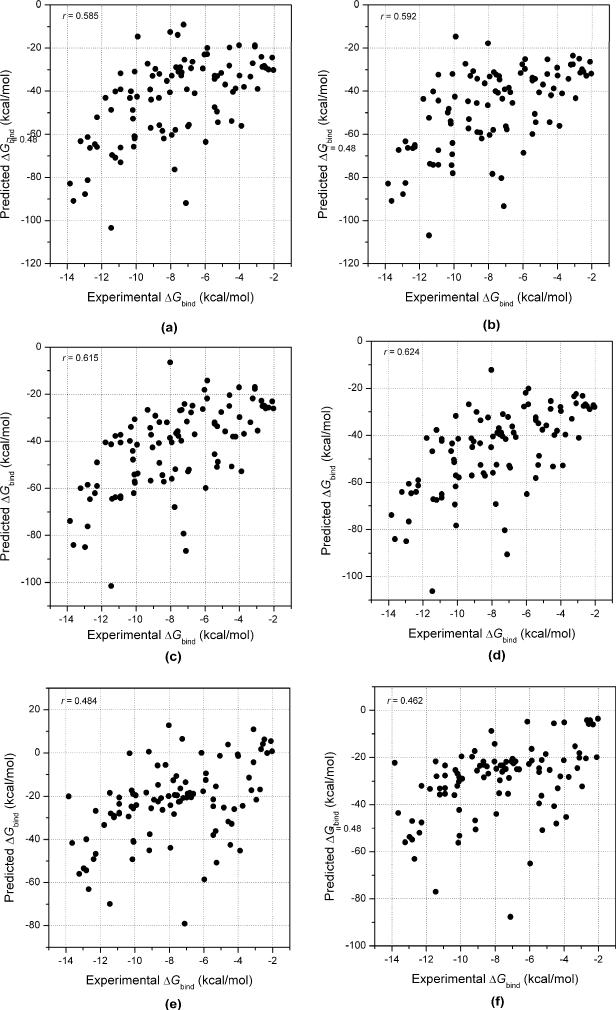
We first examined the performance of MM/GBSA for the 98 protein-ligand complexes. The linear correlation coefficients (r) and the Spearman rank correlation coefficients (r_s) between the predicted and the experimental binding free energies are summarized in Table 4. The Spearman correlation coefficients may be a better choice to evaluate a scoring function for ranking the binding affinities. For each case, both of the binding free energies for the experimentally observed conformations and those of the best scored conformations were used for the correlation analysis. Overall, the Spearman correlation coefficients using the experimentally observed conformations are better than those using the best scored conformations, but the differences are not significant. For the two GB models compared here, the MM/GBSA scores with ε_in=2 perform better than those with ε_in=1. Using ε_in=1, GB^OBC1 and GB^HCT perform comparatively to predict the binding free energies, while using ε_in=2 GB^OBC1 performs significantly better than GB^HCT. Among all these models, the MM/GBSA scores based on GB^OBC1 with ε_in=2 give the best ranks for all complexes studied here, which has a Spearman coefficient of 0.66 using the experimentally observed conformations and 0.63 using the best scored conformations.

Table 4.

The linear correlation coefficients (r) and the Spearman correlation coefficients (r_s) between the predicted binding free energies and the experimental values based on the experimentally observed conformations and the best scored conformations

Scoring functions	r		rs
	Experimentally observed conformations	Best scored conformations	Experimentally observed conformations	Best scored conformations
MM/GBSA (igb=1, εin=1)	0.497	0.484	0.548	0.526
MM/GBSA (igb=1, εin=2)	0.585	0.592	0.596	0.597
MM/GBSA (igb=1, εin=4)	0.602	0.628	0.609	0.568
MM/GBSA (igb=2, εin=1)	0.451	0.482	0.541	0.529
MM/GBSA (igb=2, εin=2)	0.615	0.624	0.655	0.625
MM/GBSA (igb=2, εin=4)	0.633	0.652	0.645	0.628
MM/PBSA (εin=1)	0.214	0.157	0.207	0.193
MM/PBSA (εin=2)	0.484	0.462	0.493	0.487
MM/PBSA (εin=4)	0.246	0.242	0.474	0.482

As shown in Table 4 and Figure 5, the correlation between the predicted binding free energies by MM/PBSA and the experimental values are 0.48. That means that MM/PBSA performs much worse than MM/GBSA. This observation is also consistent with our previous report.⁴⁵ Here the Parse parameter set was used to define the dielectric boundary. However, studies have shown that Parse parameter set cannot give good predictions of solvation free energies for amino acid side chain analogs and some relatively complicated functional groups for all three solute dielectric constants (ε_in = 1, 2, or 4).¹⁶

Figure 5.

The linear correlations coefficients between the experimental binding free energies and the predicted values given by (a) MM/GBSA using the GB^HCT model and the solute dielectric constant of 2 based on the experimentally observed conformations, (b) MM/GBSA using the GB^HCT model and the solute dielectric constant of 2 based on the best scored conformations, (c) MM/GBSA using the GB^OBC1 model and the solute dielectric constant of 2 based on the experimentally observed conformations, (d) MM/GBSA using the GB^OBC1 model and the solute dielectric constant of 2 based on the best scored conformations, (f) MM/PBSA using the solute dielectric constant of 2 based on the experimentally observed conformations, (g) MM/PBSA using the solute dielectric constant of 2 based on the best scored conformations.

Finally we compared the performance of the MM/GBSA with those of the 11 scoring functions reported by Wang et al.¹⁵ The Spearman correlation coefficients reported by Wang and coworkers cover the range from 0.14 to 0.66 for the experimentally observed conformations and 0.37 to 0.70 for the best scored conformations. According to the results reported by Wang et al. and our predictions, MM/GBSA is only marginally worse than X-Score, but better than the other ten scoring functions. It should be stressed that all 100 complexes used by Wang and coworkers have been included in the training set to train the X-Score scoring function. It is thus expected that the X-Score performs better on this set of complexes than the other scoring functions. For MM/GBSA, no binding affinity data are needed for parameter training and therefore it does not rely on any particular protein data sets for training, while most docking scoring functions do. Since MM/GBSA does not need training for specific protein systems, it has a capacity to study a wide range of targets and ligands. We have also demonstrated that MM/GBSA achieves a satisfactory performance in identifying the experimentally determined conformations from docking decoys as well as in predicting the binding free energies. One thing we need to mention is that MM/PBSA or MM/GBSA is certainly time-consuming than most scoring functions (usually less than 5 s for each system) used in molecular docking. For example, for 1a46, the whole running time of MM/PBSA or MM/GBSA for each pose is ~520 (2.55 s for charge calculations, 396 s for 5000 steps of GB-based minimization and 120 s for MM/PBSA) and ~410 s (2.55 s for charge calculations, 396 s for 5000 steps of GB-based minimization and 8 s for MM/PBSA), respectively. If we need to perform MM minimization and MM/GBSA calculations for 1000 systems, the total running time is ~285 days one CPU-time; however, if the calculations can be distribute to a cluster with 100 nodes, the total running time is less than 3 days.

Discussion

We studied MM/PBSA or MM/GBSA for identifying the correct binding conformations and predicting the binding free energies. First, we studied 98 protein-ligand complexes with MM/PBSA or MM/GBSA method to discriminate correct docking poses from the incorrect ones. The MM/GBSA can successfully identify the correct binding conformations for most systems, indicated by a success rate about 69% if only considering the best scored conformation or a success rate about 85% if considering the top three conformations. Comparison studies show that MM/GBSA performs much better than MM/PBSA and most scoring functions used in molecular docking to recognize the correct binding conformations.

We then studied 13 complexes whose correct binding conformations could not be identified as the best scored conformation but as the second or the third best scored conformation. For these 13 complexes, the binding free energies for the best three scored conformations were re-evaluated by MM/GBSA based on short MD simulations. The results show that the conformational sampling by MD can significantly improve the predictions for these 13 complexes. For the most promising candidates (less than 100) in virtual screenings, MD simulations followed by MM/GBSA analysis is a good protocol to achieve good predictions of protein-ligand interactions. Here, for three conformations of 1apw, 300 ps MD simulations consumed about 48 (16×3) CPU hours. For 100 molecules, it takes roughly 6.2 days with a 32-CPU Linux cluster, which is becoming commonly available.

Finally, we evaluated the performance of MM/GBSA and MM/PBSA to rank the binding free energies of the 98 protein-ligand complexes. The best MM/GBSA predictions yield Spearman correlation coefficients of 0.63 for the experimentally determined conformations and 0.66 for the best scored conformations, which are much better than MM/PBSA and also almost all the scoring functions used in molecular docking. Compared with most scoring functions in molecular docking, the MM/GBSA can achieve a better balance between identifying the binding poses and predicting the binding free energies. Therefore, using a rapid scoring scheme followed by the MM/GBSA rescoring is an efficient protocol to improve the predictions of molecular docking. According to our predictions it is obvious that predicting the docking poses is usually an easier task than predicting the binding free energies for different molecules. When predicting the binding poses for a small molecule, the systematical errors caused by the predictions may be considered as a constant. But when we predict the binding free energies for a set of different molecules the systematic errors for different ligands cannot be considered as a constant. This is the reason why MM/PBSA or MM/GBSA usually cannot give good performance for dissimilar ligands.¹⁶