Atomistic folding simulations of the five helix bundle protein λ_6–85

Abstract

Protein folding is a classic grand challenge that is relevant to numerous human diseases, such as protein misfolding diseases like Alzheimer’s. Solving the folding problem will ultimately require a combination of theory, simulation, and experiment; with theory and simulation providing an atomically-detailed picture of both the thermodynamics and kinetics of folding and experimental tests grounding these models in reality. However, theory and simulation generally fall orders of magnitude short of biologically relevant timescales. Here we report significant progress towards closing this gap: an atomistic model of the folding of an 80-residue fragment of the λ repressor protein with explicit solvent that captures dynamics on 10 millisecond timescales. In addition, we provide a number of predictions that warrant further experimental investigation. For example, our model’s native state is a kinetic hub and biexponential kinetics arise from the presence of many free energy basins separated by barriers of different heights rather than a single low barrier along one reaction coordinate (the previously proposed incipient downhill scenario).

Understanding protein folding is a long-standing problem with important medical applications, such as elucidating the role of protein misfolding in diseases like Alzheimer’s. Solving the folding problem will ultimately require a combination of theory, simulation, and experiment; with theory and simulation providing an atomically-detailed picture of both the thermodynamics and kinetics of folding and experimental tests grounding these models in reality. However, modeling long timescale dynamics (e.g. microseconds, milliseconds, and beyond) with sufficient statistical accuracy and chemical detail to make a quantitative connection with experiments is extremely challenging. Much progress has been made with small, fast-folding proteins (less than 40 residues and one millisecond folding timescales¹) but can the methods used scale to larger, slower systems? Here we report significant progress in this direction: an atomistic model of the folding of an 80-residue fragment of the λ repressor protein (λ_6–85) with explicit solvent that captures dynamics on a 10 millisecond timescale.

This advance builds on a growing body of work on describing molecular kinetics with network models called Markov state models (MSMs). MSMs are discrete time master equation models that essentially serve as maps of a molecule’s conformational space.^1–3 The states in an MSM come from kinetic clustering of atomistic simulations (i.e. conformations that can interconvert rapidly are grouped together into what is called a metastable state). Thus, these models are an important advance over previous approaches, like diffusion-collision models,^4,5 as an MSM’s states are derived from dynamics in detailed simulations rather than human intuition. One can exploit the kinetic definition of states in an MSM to perform simulations efficiently^6–8 and make a direct connection to experiments.^9–11 For example, we have successfully used MSMs for all-atom, ab initio structure prediction of small systems, like the villin headpiece (35 residues, microsecond folding time).⁹ Noe et al. have predicted the relaxation kinetics of a PinWW domain (34 residues, microsecond folding time)¹⁰ and Voelz et al. have done the same for NTL9 (39 residues, millisecond folding time).¹¹

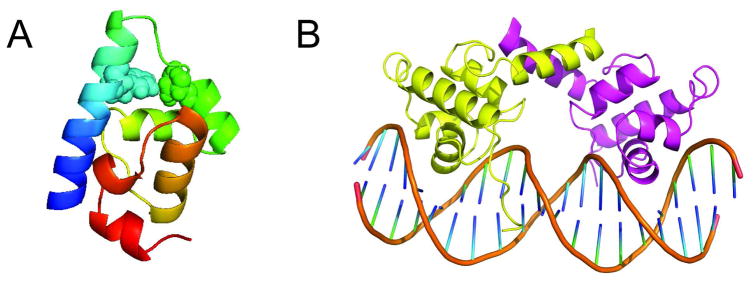
To test whether the MSM approach can scale to larger systems, we have built MSMs for the D14A mutant of λ_6–85 (Figure 1A).¹² D14A has the following mutations: D14A, Y22W, Q33Y, G46A, and G48A. This system was chosen because it is twice as large as the small model systems that have been studied with MSMs to date yet, surprisingly, is still reported to fold on a 10 microsecond timescale.¹² Since molecular dynamics (MD) simulations can now reach 10s of microsecond timescales on a routine basis, it should be feasible to run many folding simulations for this system. Future comparison with other large, slower folding proteins could also help us to understand what properties of D14A allow it to fold as quickly as ultra-fast folding proteins less than half its size.

Figure 1.

(A) A model of λ_6–85 taken from (B) with the Trp22-Tyr33 pair monitored in T-jump experiments space-filled. (B) The crystal structure of the λ_1–92 dimer bound to DNA (PDB code 1LMB).

MSMs for D14A

We have built atomically-detailed network models (MSMs) for D14A from 3,265 MD simulations with explicit solvent. Each trajectory is up to 1 μs in length, for an aggregate of 1.3 milliseconds of simulation—an enormous dataset given that most simulation studies are based on only nanoseconds to microseconds of data. These simulations were started from six initial configurations drawn from replica exchange simulations in implicit solvent.¹³ One is native-like, three are partially unfolded, and two have β-sheets. A more detailed description of our simulations is given in the Supporting Information (SI).

The highest resolution MSM we created for D14A has 30,000 microstates and is appropriate for making quantitative connections with experiments due to its great structural and temporal detail. A low-resolution model with 5,000 macrostates was created from the high-resolution MSM to facilitate interpretation of the model. More details on our use of the MSMBuilder package¹⁴ to construct these models are given in the SI. While no single trajectory visits every state, these MSMs are able to capture long timescale dynamics by exploiting overlap between our simulations to stitch them together in a physically and statistically meaningful way (see Figure S1 for a 1 second long trajectory). Examination of the implied timescales of the microstate MSM shows that a 5 ns lag time yields Markovian behavior (Figure S2–S4).

The native state

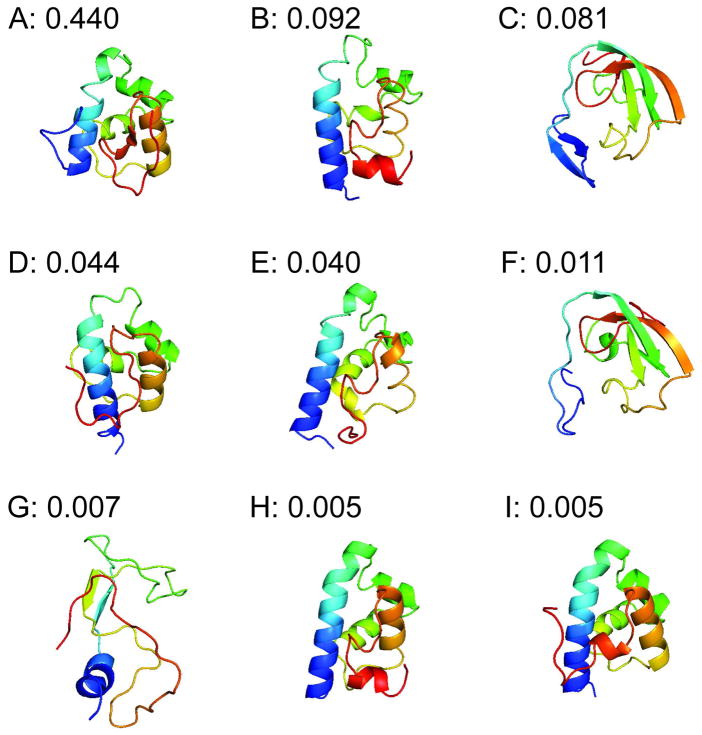
One of the first observations from our coarse-grained MSM is that our model’s native state (Figure 2A) differs from the crystal structure (Figure 1A) in helix five. The crystal structure is a highly metastable state (Figure 2H), which we refer to as the crystallographic state. However, in the native state of our model, helix five is unraveled and packed against the side of the remainder of the protein (Figure 2A). Figure 2 also shows that helix five is unstructured in many of the other highly populated states of our model.

Figure 2.

The nine most populated states from our coarse-grained MSM with their equilibrium probabilities.

While this difference could be due to force field errors, we argue that helix five is actually likely to be unstructured in solution given the origins of this model system for folding. Full length λ repressor is a 236-residue transcription factor that binds to DNA as a dimer, maintaining the λ phage in the lysogenic state. Figure 1B shows the crystal structure of a 92-residue fragment that can still dimerize and bind to DNA.^15,16 Based on this structure, Huang and Oas selected an 80-residue fragment (λ_6–85) that favors the monomeric state (Figure 1A), making it appropriate for folding studies.¹⁷ In the 92-residue fragment, helix five is extended by seven residues and forms important packing interactions between the two members of the dimer. These extra interactions likely stabilize helix five. Truncating the sequence to favor the monomer could destabilize the fifth helix, leading to a lack of structure and a strong propensity either to fill in the hydrophobic cavity normally occupied by the corresponding helix of the other member of the dimer or to adopt one of a number of the other well-populated, unstructured conformations shown in Figure 2.

There is also a reasonable amount of experimental data corroborating our hypothesis that helix five is unstructured in solution. First, the stability of this system seems to be insensitive to mutations in helix five.¹³ A crystal structure for λ_6–85 also has high B-factors in helix five.¹⁸ Therefore, it is plausible that helix five is stabilized by packing interactions in this crystal but is still intrinsically unstable and likely to be more unstructured in solution.

Further support for our hypothesis comes from theoretical studies. For example, helix five has negligible helical propensity according to Agadir¹⁹ (Figure S5). Similar results were also found in a G3 model study, where helix five tended to un-dock from the rest of the protein.²⁰ However, these models do not include non-native interactions, so helix five was not found to unravel or pack against the protein in that work.

β-sheet states

Figure 2 also shows that a number of the most populated states in our model have significant β-sheet content. The prediction of β-sheet states in the unfolded ensemble is somewhat surprising for a helical protein; however, experiments have shown that the unfolded and denatured states of many systems can have significant populations of compact, β-sheet structures yet still display the random coil statistics characteristic of expanded conformations.^21,22 Thus, our prediction of compact, β-sheet structures is not unreasonable.

Folding kinetics

While the experimentally reported folding time for D14A is ten microseconds, analysis of our high-resolution MSM reveals the presence of microscopic transitions on timescales up to 10 milliseconds. These timescales are preserved in subsamples of the dataset and an independent dataset run at a lower temperature (Figures S3 and S4), indicating that they are a robust feature of the simulated system.

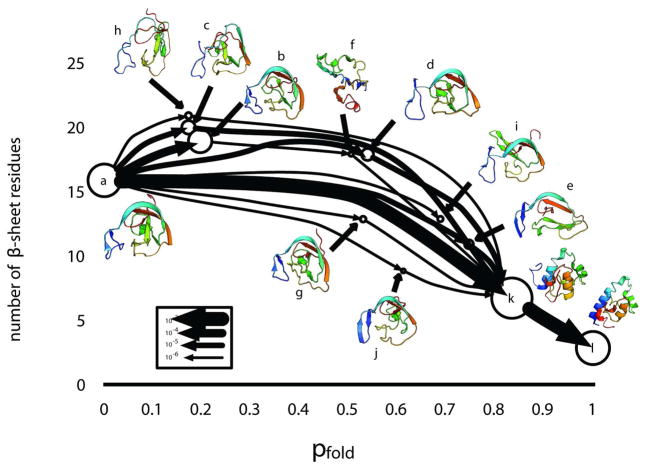
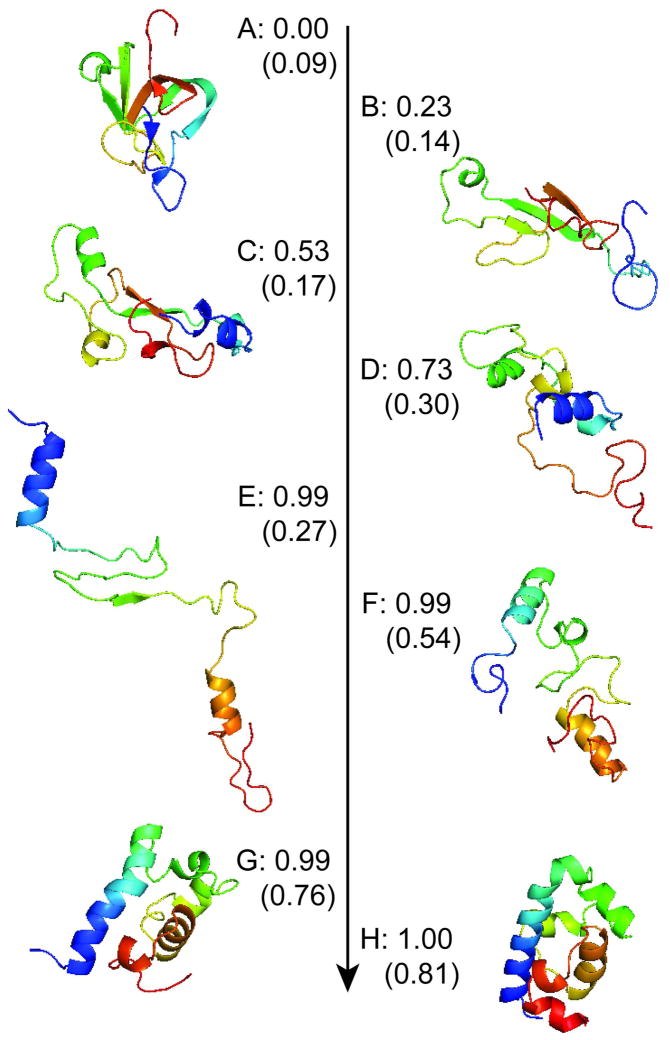
Analysis of our coarse-grained MSM reveals that this slow timescale corresponds to exchange between the compact β-sheet structures in the unfolded ensemble and the crystallographic state through multiple parallel pathways (Figure 3 and S6). A more detailed view of one of these pathways, and portions thereof, are shown in Figures 4 and S7. In this particular pathway, the compact β-sheet structure first expands (A–E), breaking apart the β-sheets. Then helices 1 and 4 begin to form, followed by collapse into a native-like topology (F–G). Finally, the remaining helices form (G–H). The ability to extract these detailed pathways highlights one of the advantages of MSMs over conventional analysis techniques like projections of free energy surface, which tend to over-simplify folding and paint different pictures depending on the order parameters chosen (Figures S8 and S9 and Ref 20). However, one must take care in interpreting these pathway diagrams because they show the net flux from one state to another, leaving out the backwards steps and excursions that molecules in solution will make as they stochastically explore conformational space.

Figure 3.

A coarse-grained view of the 10 millisecond timescale transition with state sizes proportional to the log of the state’s equilibrium probability and arrow widths proportional to the log of the flux along the edge (see key in figure). The states are laid out in terms of the average number of β-sheet residues (calculated from 100 random conformations from each state) and the p_fold (probability of reaching state in L before state A).

Figure 4.

A representative high-resolution pathway that occurs on a 10 millisecond timescale with p_fold values (probabilities of reaching state H before A). The proportion of native contacts is also given in parentheses as an estimate of how native-like the topology is. Relative contact orders for each state are given in Table S1.

One possible explanation for the difference between our simulation results and experiment is that the experimental probe used to monitor folding is not sensitive to the slow transition from compact β-sheet structures to the crystallographic state. To test this hypothesis, we used our MSM to calculate the macroscopic rate measured in experiment by modeling the relaxation of a surrogate for the Trp22-Tyr33 quenching interaction measured in T-jump experiments (Figure S10). We also calculated the relaxation of the C_α RMSD to the crystal structure to test whether a more global metric could capture slower timescales than the experimental probe, which could just capture local relaxations (Figure S10). Both have biexponential relaxation—a characteristic of D14A that has been used to argue that it is a downhill folder—and similar timescales but their slow phase is about two orders of magnitude slower than in experiment (1 millisecond versus 10 μs).

This result suggests that this slow transition is not present in solution because the experimental probe would capture it if it were. Further support comes from the fact that ignoring simulations started from β-sheet structures yields better agreement between simulation and experiment (Figure S11). First, the Trp22-Tyr33 surrogate has a 1 μs fast phase and a 4.3 μs slow phase, in reasonable agreement with the experimental values of 2 and 10 μs.¹² Secondly, the RMSD now relaxes on different timescales, consistent with observed probe dependent kinetics.^23,24

While it is natural to consider the potential flaws in a force field when confronted with a discrepancy between simulation and experiment, we suggest that there are alternative possibilities as well. The folding rate of λ_6–85 is known to be highly sensitive to solvent viscosity.^25,26 For example, one variant of λ_6–85 folds on a 210 μs timescale in the absence of denaturant but folds on a 5 millisecond timescale in the presence of only 0.5 GuHCL.²⁶ Force field errors are known to destabilize proteins, so it is possible that our simulated system is more like D14A in mild denaturant than it is like D14A in aqueous solution. It is also still possible that future experiments will reveal the presence of a 10 millisecond timescale for D14A. Indeed, one might expect D14A, with its sizeable hydrophobic core, to fold on slower timescales given that the wild-type villin headpiece (which is less than half the size of D14A and barely has a hydrophobic core) is also reported to fold in just under 10 μs.²⁷

Fully resolving this issue will likely require more experiments and simulations to yield more points of comparison between simulation and experiment. Regardless of the outcome, our work shows that MSMs built from atomistic simulations can now sample 10 millisecond timescales, qualitative phenomena like biexponential relaxation, and possibly even quantitative agreement with experiment. Moreover, the ability to make such direct comparisons on long timescales opens the door to further improvements of atomistic models used in MD simulation.

A native hub

The biexponential relaxation of D14A and other variants of λ_6–85 have previously been attributed to incipient downhill folding. The incipient downhill folding model is similar to the more conventional two-state model often used to describe folding but has a lower barrier (on the order of 1 kT) separating the folded and unfolded states (Figure S12A). As a result, there is believed to be a moderate population of proteins on top of the barrier that can slide downhill into the native state, giving rise to a fast phase, in addition to an unfolded population that must cross the barrier before folding, giving rise to the slow phase.

Projections of the free energy onto a kinetically meaningful order parameter (p_fold, the probability of folding before unfolding²⁸) are consistent with incipient downhill folding. When the full dataset is used such projections appear to be two-state but once simulations started from the compact β-sheet conformations are removed—thereby yielding better agreement with experiment—the barrier between the folded and unfolded states is greatly reduced, consistent with incipient downhill folding (Figure S13).

Further analysis of our MSM, however, indicates that the biexponential relaxation of D14A may be due to metastability and a hub-like native state rather than incipient downhill folding. When a single non-native state is chosen as the starting point for p_fold calculations then other non-native states actually appear to have p_folds near one (i.e. they appear on the native side of the projection), indicating folding is more complex than the incipient downhill folding scenario. The MSM reveals that there are many metastable states separated by barriers of different heights (e.g. there is reasonable variability in the transition times between states) and the convolution of these dynamics gives rise to biexponential relaxation and fast folding. These states are arranged such that the native state acts as a kinetic hub, as has been observed for a number of smaller systems.²⁹

A first hint that D14A may also have a native hub comes from the large number of connections to our native state (Figure S12). The native state in our model makes direct connections to 98% of the non-native states while non-native states only connect to 0.1% of the other states on average. Moreover, the MFPTs to the native state are typically ~10 times faster than the MFPTs between non-native states, as shown in Figure S14, and this holds regardless of whether the β-sheet simulations are included in the analysis. Therefore, molecules in non-native states can generally fold faster than they can transition to other non-native states. The fastest way to transition between two randomly selected non-native states is then to fold and unfold. The large number of folding pathways that result from this topology is hidden by projections of the free energy onto p_fold.

Conclusions

The combination of simulations and MSMs can now access ~10 millisecond timescales for moderately large (~80 residue) systems with explicit solvent, greatly increasing the common ground between simulation and experiment (the previous state of the art was 1 millisecond timescales for ~40 residue proteins in implicit solvent). The ability of our MSMs to capture biexponential kinetics also indicates that proteins previously designated as incipient downhill folders actually have many barriers of differing heights. In addition, our model leads to a number of predictions for D14A: 1) helix five unfolds and fills a hydrophobic pocket in the native state and lacks structure in other well populated states, 2) there is significant β-sheet structure in the unfolded ensemble, 3) there are structural rearrangements on 10 millisecond timescales that were not detected in past experiments or, alternatively, the simulated system reflects dynamics in mild denaturant, and 4) the native state acts as a kinetic hub. Our ability to reconcile these observations with existing experiments suggests that more experimental data will be necessary to provide a detailed description of how D14A and other variants of λ_6–85 fold. We suggest that MSMs could be used to help design such experiments and lead to important new insights into folding or, at the very least, provide more data for refining existing force fields and improving the agreement between simulation and experiment.