Silk Fiber Mechanics from Multiscale Force Distribution Analysis

Abstract

Here we decipher the molecular determinants for the extreme toughness of spider silk fibers. Our bottom-up computational approach incorporates molecular dynamics and finite element simulations. Therefore, the approach allows the analysis of the internal strain distribution and load-carrying motifs in silk fibers on scales of both molecular and continuum mechanics. We thereby dissect the contributions from the nanoscale building blocks, the soft amorphous and the strong crystalline subunits, to silk fiber mechanics. We identify the amorphous subunits not only to give rise to high elasticity, but to also ensure efficient stress homogenization through the friction between entangled chains, which also allows the crystals to withstand stresses as high as 2 GPa in the context of the amorphous matrix. We show that the maximal toughness of silk is achieved at 10–40% crystallinity depending on the distribution of crystals in the fiber. We also determined a serial arrangement of the crystalline and amorphous subunits in lamellae to outperform a random or a parallel arrangement, putting forward what we believe to be a new structural model for silk and other semicrystalline materials. The multiscale approach, not requiring any empirical parameters, is applicable to other partially ordered polymeric systems. Hence, it is an efficient tool for the design of artificial silk fibers.

Introduction

Silk fibers constitute an intriguing class of natural materials. Through a flawless assembly of strong and soft building blocks, they exhibit astonishing mechanical properties. Silk fibers may have an ultimate strength comparable to steel, toughness greater than that of Kevlar (DuPont, Wilmington, DE), and a density lower than that of cotton or nylon (1). Furthermore, many natural silk fibers exhibit high rupture strain (∼30%), which is one of the major reasons for their energy-absorbent behavior upon impact (1,2). Even today, natural silk fibers outperform their artificial counterparts in terms of mechanical performance. Therefore, many experimental (1,3–8) and theoretical studies (4–6,9–11) have tried to understand the process of silk fiber formation and the origins of the mechanical characteristics of silk fibers.

Natural silk fibers share a common structural architecture consisting of two major types of components, namely, the crystalline and amorphous subunits (Fig. 1) (12–14). Crystalline subunits of spider silk involve short peptides of 6–10 amino acids containing alanine or glycine-alanine residues. These short peptides organize themselves into mechanically strong crystal blocks measuring 2–5 nm on a side (15). They are made of parallel or antiparallel layers of β-strands (16) interacting via hydrogen bonds and via noncovalent bonds between amino-acid side chains (9). Crystalline subunits constitute 10–25% of the fiber volume in spider silk (1,17). They are axially oriented along the fiber and reinforce the soft amorphous subunits by acting as comparably stiff cross-linking sites (3). The amorphous subunit of a silk fiber is composed of longer, glycine-rich peptide sequences (1,3,5). Even though the amorphous subunit may include some semiordered peptide chains with partial secondary structure (11,17–19), it is predominantly disordered (7,20,21), rendering itself as a soft matrix in stretching experiments (1,3,4,6).

Figure 1.

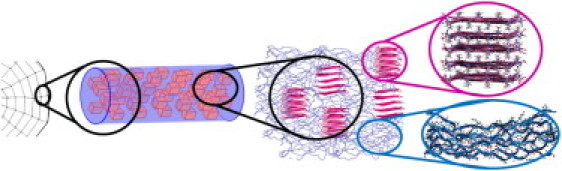
Schematic of the spider silk architecture from macro- to nanoscales. Spider silk fibers are composed of crystalline subunits that are made of β-sheets (pink), and semiextended disordered peptide chains (blue).

Assessing the determinants of the mechanics of natural silk fibers is challenging not only due to the possible variety in the peptide chemistry, but also due to the influence of the fiber assembly conditions, such as the shear rate and ion concentration, on the fiber mechanics (8,22). The macroscopic mechanical characteristics of silk fibers originate from the nanoscale morphology, in particular from the interactions within and between the fiber subunits, which are experimentally not easily accessible. Computational studies on the atomistic scale have so far considered only the crystalline subunits and, therefore, were limited in the understanding of silk fiber mechanics (9,11,23). An approximate yet elegant nanoscale mean field approach by Vollrath, Porter, and co-workers (4,24) successfully predicted some features of macroscopic fiber mechanics and its dependence of order.

In this study, our aim was to understand the mechanical properties of spider silk fibers using a bottom-up computational approach that starts at the atomistic scale and incorporates both the crystalline and amorphous subunits. Our approach bridges two discrete methods and scales: atomistic molecular dynamics (MD) simulations for individual and coupled subunits, and finite element (FE) simulations for a comprehensive fiber model on the continuum scale—a combination pioneered by Cleri et al. (25) and Serebrinsky et al. (26) for other nonbiological materials like inorganic or metallic crystals. The contributions from the subunits to the mechanical properties of spider silk were investigated. Different structural architectures regarding fiber subunits were tested for optimal mechanical performance. The calculated values for the elastic moduli, rupture stress and strain, and toughness were in good agreement with experimental values. Our results make testable suggestions for a synthetic silk-mimicking polymer. Because our approach is applicable to similar polymeric systems, it is a useful tool for the design of artificial silk fibers.

Materials and Methods

Molecular dynamics simulations

We modeled the crystalline and amorphous subunits of the spider silk fiber from the major ampullate gland of Araneus diadematus (1), namely, a β-sheet stack from 5×5 (Ala)₈ peptides (9) and 24-residue peptides of the disordered region

$$\text{GPGGYGPGSQGPSGPGGYGP}\text{GGPG},$$

respectively. All MD simulations of these all-atom models and combinations thereof were performed with the GROMACS package (27) using the OPLS-AA force field (28), TIP4P water (29), and an NpT ensemble (300 K, 1 bar) with periodic boundary conditions. Please see Methods in the Supporting Material for further details.

Finite element simulations

We constructed a three-dimensional skeleton model of the crystalline subunit, consisting of peptide backbones and side-chain elements with linear elasticity and hydrogen bonds with nonlinear elasticity. Crystalline subunits were coupled with amorphous chains to build a skeleton model of a composite unit. All finite element (FE) simulations were performed with the COMSOL Multiphysics package. For convenience, we modeled the structural members as purely elastic, thereby neglecting rate-dependent viscous and dissipative plastic effects. The starting geometries of the structures, the nominal lengths of the members and their elastic (Young's) moduli, E, were obtained from the all-atom models.

Linear elastic members of the skeleton model were assumed to be Hookean solids with isotropic mechanical properties. Nominal values of stress and strain were used in the calculations. For the nonlinear elastic members the elastic modulus, E, was considered as strain-dependent, i.e., as a function of the actual member length (e.g., the weakening hydrogen bonds or the stiffening amorphous chains with increasing length). Basically, such members behaved like neo-Hookean solids under finite deformations. We next built a comprehensive fiber model with transversely isotropic crystalline subunits embedded into a matrix of isotropic amorphous subunits, both of which were treated as linear elastic solids mainly subjected to tensile load. Elastic moduli of the subunits were calculated from all-atom MD simulations. Please see the Supporting Material for further details.

Results and Discussion

Mechanical characteristics of individual subunits

Silk mechanics on a macroscale originates from the molecular characteristics of the crystalline and amorphous subunits on a nanoscale. Therefore, the first step of our approach was to model the individual subunits with simplified skeleton models and validate them by comparing to their all-atom models. We developed a three-dimensional skeleton model for the crystalline subunits formed by five layers of five-stranded antiparallel β-sheets, in which the side-chain interactions link the two-dimensional skeleton layers, which were previously developed (9). The stress-strain curve and the resulting pull-out resistance of the skeleton model obtained from FE simulations (54.1 GPa; see Fig. S1 and Methods in the Supporting Material) compared well to that obtained from the more accurate all-atom model in MD simulations (66.3 GPa).

In addition, the skeleton model was able to reproduce the force distribution pattern as observed in the all-atom model, namely, a steady decay of the load along the pulled strand and in lateral and vertical directions perpendicular to the plane of pulling (Fig. S2). We concluded that the skeleton model for FE simulations, being parameterized on the basis of the all-atom description, captures the features of the crystalline subunit mechanics.

We straightforwardly modeled the second constituent of the spider silk fibers, the disordered peptide chains of the amorphous subunit, by inputting the force-extension data obtained from long-timescale all-atom MD simulations. The nonlinear elastic response, approximately following a wormlike chain behavior up to intermediate extensions, was the basis for the nonlinear elastic modulus of the amorphous subunits (Fig. S3).

Mechanical characteristics of the composite unit

We next serially coupled the crystalline and amorphous subunits to dissect their relative contributions to the strength and toughness of spider silk fibers. The connectivity between the disordered chains in the amorphous subunit and the β-sheet crystal in a silk fiber is unknown, but is likely to show a high variation within the fiber. We here chose a symmetric connectivity, details of which are given in the Methods in the Supporting Material. The composite unit comprised 300,000 atoms (including solvent) in the all-atom model, which served as a reference, and 3000 members in the simplified skeleton model. Fig. 2 a shows the force-elongation curves for the skeleton and all-models of the composite unit. In both models, the strength of the composite unit increased with higher elongation. The skeleton model showed a force-elongation relationship that one would expect if the subunits, most importantly the individual disordered peptide chains, behaved additively.

Figure 2.

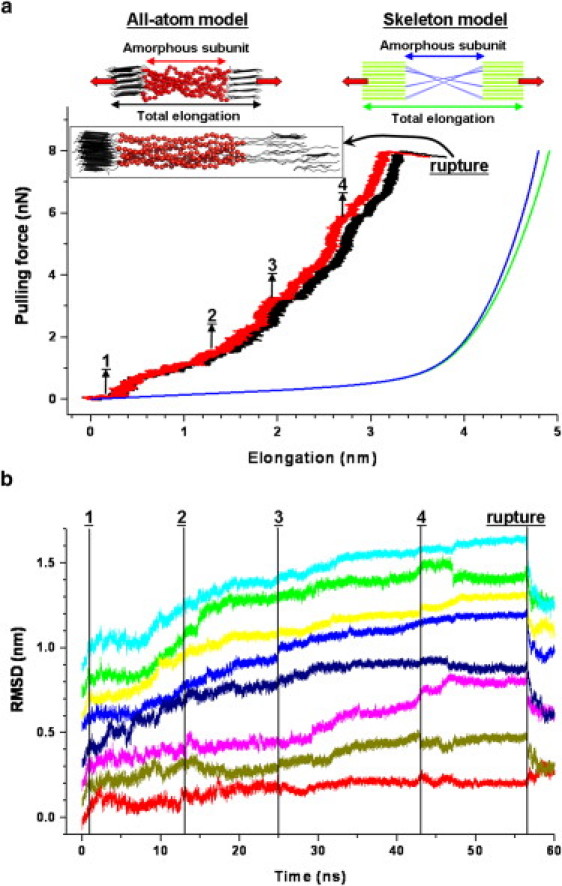
Mechanical response of the composite unit. (a) Force-elongation curves from the skeleton (green, whole unit; blue, amorphous subunit) and all-atom models (black, whole unit; red, amorphous subunit). (Insets at the top) Schematics for the composite unit from all-atom (left) and skeleton models (right). (Inset next to the rupture point) Representative structure of the all-atom model right after the rupture event, at which peptide chains partially disengage from the crystal. Numbers 1–4 in panels a and b indicate the events at which peptide chains rearrange themselves. (b) Root mean-square displacement (RMSD) of the peptide chains in the all-atom model during force-probe MD simulations. Individual traces are vertically shifted for clarity.

More specifically, the nonlinear elasticity of the chains in the amorphous subunit dominated the overall mechanical response, and the crystalline subunits were strained only at high stresses. The force-elongation behavior of the all-atom model shares the main features with the one from the skeleton model. However, the all-atom model yielded a significantly lower elasticity for the disordered chains, resulting in a smaller strain at rupture. Apparently, the more realistic all-atom description of the amorphous subunit took internal friction into account that led to higher energy absorption than what was expected from the mere sum of the individual chains.

Indeed, there were horizontal jumps in the force-elongation curve of the all-atom model (Fig. 2 a) correlating with the structural rearrangements of individual disordered chains relative to each other (Fig. 2 b). Such short-range diffusional motion is characteristic for rubbery-elastic mechanics of amorphous polymers (30). We interpret the difference between the force-elongation curves of the all-atom and skeleton models as the additional mechanical work taken up by the entangled chains within the amorphous subunit. The skeleton model failed to take this effect into account because interchain interactions were neglected. We suggest that this nonadditive behavior of the chains in the amorphous subunit crucially enhances the toughness of spider silk fibers.

The all-atom model of the composite unit ruptured at a stress of ∼2.0 GPa with 33% strain (black curve in Fig. 2 a). Gosline et al. (1) reported an experimental rupture stress of 1.1 GPa with 27% strain for the same spider silk type. Experiments by Liu et al. (31) resulted in a rupture stress of 1.7 GPa with 24% strain. Considering the simplicity and the limited size of the all-atom system, our values are in good agreement with the experimental results in literature. In fact, given the high crystallinity of our composite model (∼65% as opposed to ∼25% for natural spider silk), and the high loading rate applied to induce rupture, the overestimation of the rupture stress in the all-atom model was expected.

Varying the loading rate by one order of magnitude resulted in a change in rupture stress of smaller than 10% and in toughness of only ∼3%, due to the high extension of the amorphous chains at the rupture point. Complementary MD simulations with a bare amorphous subunit showed that in the absence of the crystalline subunits the peptide chains would slide from each other, i.e., give rise to yielding, and rupture at a low stress of ∼0.4 GPa (Fig. S4). Therefore, the crystalline subunits are the determinant factors in the rupture of the composite unit, in agreement with the previous notion of crystalline subunits acting as cross-links in silk fibers (3,10,17). For further validation, we also estimated the toughness of the all-atom model and obtained 147 MJ/m³. Previous experimental studies reported values between 141 and 225 MJ/m³ (1,31–33). The agreement is striking regarding the tremendous difference between the length scales.

The distribution of the pulling force within the composite unit gives additional insight into the molecular contributions to the toughness of silk fibers. As a general finding, the axial force was high in disordered peptide chains but decayed within the crystalline subunits due to an efficient distribution of the pulling force along and across β-strands (Fig. 3, a and b). This was in particular the case in the skeleton model, where the peptide chains in the amorphous subunit acted as individual strings and thus, carried axial loads of very high and strongly varying magnitude (up to 400 pN) depending on their linkage to the crystalline subunit (Fig. 3 a). As a consequence, the distribution of the pulling force within the crystalline subunit was heterogeneous (Fig. 3 c). In contrast, the amorphous chains in the all-atom model carried forces only slightly higher than the ones in the crystalline subunit.

Figure 3.

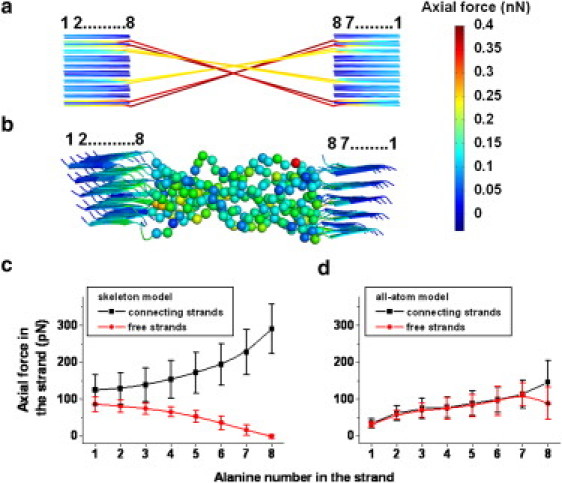
Distribution of the external pulling force (∼2.5 nN) within the composite unit. (a and b) The force distribution pattern in the skeleton (a) and all-atom models (b) of the composite unit. (c and d) Average axial force along the poly(Ala) strands in the crystalline subunits in the skeleton (c) and all-atom (d) models. The order of alanines are indicated in panels a and b. The term “connecting strands” in panels c and d refers to the poly(Ala) strands bonded to the disordered chains in the amorphous subunits. Error bars represent the standard deviation for 34 free strands and 16 connecting strands in a 5×5 crystalline subunit. Smooth lines in panels c and d are spline fits for the data points.

More importantly, these forces (∼200 pN) were independent of the linkage and entanglement of the chains (Fig. 3 b). The distribution of the pulling force in the crystalline subunit was also more homogeneous (Fig. 3 d). Overall, the skeleton model overestimated the absolute and relative axial loads in the composite unit because of the heterogeneous distribution of the pulling force across amorphous subunits. The force distribution analysis corroborates our earlier finding that the interchain interactions enable efficient stress propagation and homogenization, as an important contribution to the fiber toughness. Overall, the pronounced differences between the all-atom MD simulations and the FE calculations of the skeleton model helped us to dissect the contributions of the structure to mechanical resilience. Improving the skeleton model further by incorporating interchain interactions might be the subject of further investigations, but was not of interest here, as the further upscaling was based on only the all-atom simulations.

Elastic moduli of the crystalline (E_c) and amorphous (E_a) subunits in the all-atom model were calculated as 80.0 GPa and 2.7 GPa, respectively. The elastic modulus of the poly(Ala) spider silk crystals is currently unknown, but Krasnov et al. (6) reported the E_c for silkworm silk poly(Gly-Ala) crystals as 26.5 GPa. In these experiments, the stress in the crystalline subunits in a full fiber was inferred by assuming a homogeneous stress distribution. However, we below show that in the range of experimental crystallinity values (10–25%), crystalline subunits carry stresses 2–3 times larger than the macroscopic fiber stress (see the comprehensive fiber model).

Based on this information, the corrected experimental E_c is ∼50.0–80.0 GPa, thus close to our calculated E_c value. Regarding the amorphous subunits, Krasnov et al. (6) reported an E_a value of 6.3 GPa as an indirect estimation based on their experiments with silkworm silk. In Termonia's computational study (10), the disordered chains in the amorphous subunits were assumed to be entropic springs, with E_a calculated as 70.0 MPa. Apparently, similar to our skeleton model of the individual peptide chains, Termonia's study underestimated the stiffness of the amorphous subunit by two orders of magnitude because it overlooked the effects of interchain force distribution, which our study suggests to be a hallmark of rubbery behavior.

Mechanical characteristics of the comprehensive fiber model

The skeleton and all-atom models of the composite unit, albeit representing minimal models of a spider silk fiber, proved useful in assessing the silk fiber mechanics. The important question arises how the relative amount and arrangement of the two subunits influence the macroscopic mechanical properties. We built a comprehensive fiber model with crystals embedded into an amorphous matrix and parameterized their elastic properties from the all-atom simulations. The comprehensive fiber model enables us to reach higher length scales with a smaller computational cost (1–5 CPU hours as compared to ∼1 M CPU hours for a several million atom system and microsecond timescales).

Fig. 4 a shows the dependence of the fiber elastic modulus, E_f, on the fiber crystallinity. We considered three possible distributions of the crystalline subunits in the fiber:

• 1.A serial (lamellarlike) arrangement of the crystalline and amorphous subunits.
• 2.A parallel (longitudinal) arrangement.
• 3.A random arrangement between these two extremes.

As shown in Fig. 4 a, for any given crystallinity, a serial assembly resulted in the lowest fiber elastic modulus E_f dominated by the mechanical characteristics of the amorphous subunits. On the other hand, a parallel assembly, being reinforced by the crystalline subunits throughout the fiber axis, resulted in the highest values of E_f. Unsurprisingly, these two extremes follow the behavior of simple two-phase isotropic models (blue and red curves in Fig. 4 a), validating our FE simulations. A random distribution of the crystalline subunits in the fiber yielded intermediate E_f values, as expected. At natural crystallinity (i.e., 25%) a fiber with randomly arranged crystals, as suggested by Gosline et al. (1), has an E_f value of 6.4 GPa. This value is in excellent agreement with the reported experimental data ranging between 4.0 and 10.0 GPa (1,31–33), despite the approximations in our model such as a two-phase system with linear elastic components.

Figure 4.

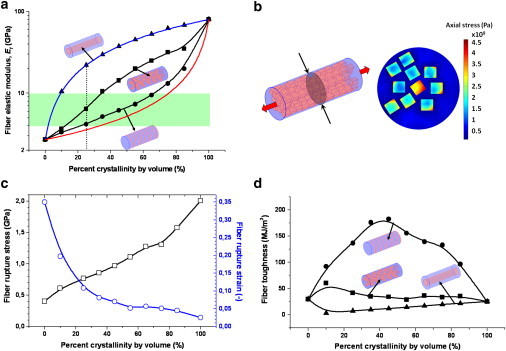
Variation of the mechanical properties with respect to the silk fiber crystallinity. (a) The effects on the fiber elastic modulus, E_f, are shown. Results for three different crystalline subunit distributions are shown as indicated by the schematics. The parallel (triangles) and serial (circles) distributions obey simple two-phase isotropic models, namely, the Voigt composite model (blue line) for the parallel distribution: E_f = E_cu_c + E_au_a and the Reuss composite model (red line) for the serial distribution: 1/E_f = u_c/E_c + u_a/E_a, where E_c, u_c, and E_a, u_a are the elastic moduli and volume percentage of the crystalline and amorphous subunits, respectively. The small discrepancy with the Reuss model is due to the geometric effects arising from nonzero Poisson's ratios used in three-dimensional FE simulations. The random distribution (squares) yields intermediate values for E_f. (Dashed line) Percent crystallinity of dry spider silk in nature. Green band spans the interval of experimental values from literature (1,31–33). (b) Schematic of the comprehensive fiber model with random distribution of crystals (left) and the stress distribution at an arbitrary cross section of a 25% crystalline fiber with an external stress of 0.8 GPa (right). (c) Variation of the rupture stress (squares) and rupture strain (circles) with respect to the fiber crystallinity, again for a fiber with random distribution of crystals. Values for 0% crystallinity were calculated with the all-atom model. (d) Variation of the toughness with respect to the silk fiber crystallinity. Results for the parallel (triangles), serial (circles), and random (squares) distribution states of the crystalline subunits are shown as indicated by the schematics. Smooth lines in panels a, c, and d are spline fits for the data points.

While the serial arrangement at 25% crystallinity (E_f = 4.2 GPa) is another feasible model for natural spider silk, the parallel arrangement (E_f = 22.1 GPa) can be excluded on the basis of our calculations. We note that our comprehensive fiber model neglects the details of connectivity between the two phases and of the entanglement within the amorphous matrix. Interestingly, given that the experimental results can be reproduced, the amorphous and crystalline phases apparently act largely as a continuum, presumably due to the stress homogenization described above, and render this approximation feasible.

Apart from high elasticity, spider silk was presumably also optimized for high rupture strength. The comprehensive fiber model, being based on conventional FE calculations, is not capable of showing the fiber rupture. However, the rupture can be indirectly inferred from the average tensile stress in the crystalline subunits, as they failed at a tensile stress of ∼2.0 GPa in the all-atom model (Fig. 2 a). The stress distribution across the fiber cross section showed that the crystalline subunits carried higher stresses (by a factor of ∼3 at 25% crystallinity with random distribution) compared to the amorphous subunit (Fig. 4 b).

In other words, the tensile stress was concentrated in the crystalline subunits. However, the distribution of tensile stress became more homogeneous within the fiber with increasing crystallinity and it approached the upper limit of 2.0 GPa, the rupture strength of the crystalline subunits (Fig. 4 c). Our comprehensive model predicted a fiber with 25% crystallinity and random arrangement of subunits to rupture at 0.8 GPa, which is close in magnitude to the experimental value of 1.1 GPa reported by Gosline et al (1). The corresponding rupture strain was calculated as 11%, a clear underestimation of the experimental value of 27% (1).

Our model reached 27% rupture strain only with mechanically weak fibers having ∼5% crystallinity. A major reason for this discrepancy lies in the neglect of any plastic deformation, as constant elastic moduli (i.e., E_a and E_c) were employed for the fiber model. In contrast, in silk-stretching experiments and for many semicrystalline polymers, the linear elastic regime is followed by yielding that leads to a further increase in the strain before rupture (1,24). Despite these discrepancies, Fig. 4 c reveals interesting insight into the structural constraints of natural spider silk fibers. As expected, a fiber purely composed of amorphous subunits would be highly elastic, but also very weak, while a 100% crystalline fiber would be brittle. Thus, the crystalline and amorphous subunits improve the fiber strength and elasticity, respectively, while resulting in a balanced tradeoff between the two.

The question arises whether this trade-off results in a maximal toughness, as another consequence of the structural architecture in spider silk fibers. Fig. 4 d shows that the parallel distribution of the crystalline subunits resulted in the lowest toughness, while the random distribution state yielded slightly higher values. Fibers with the serial distribution largely outperformed the other two alternatives in terms of toughness. An optimal toughness of silk fibers is achieved in the range of 10% (random distribution) and 40% (serial distribution), which overlaps with the spider silk's natural crystallinity level of 10–25%. Naturally, the calculated toughness (41 MJ/m³ at 25% crystallinity for the random distribution) underestimates the experimental results (141–225 MJ/m³) (1,31–33) because of neglecting the plastic deformations before rupture in this linear elastic model. Furthermore, a certain degree of serial arrangement in the fiber might further increase the toughness, as suggested by our model. Overall, the qualitative comparison between the possible geometries clearly reveals that the serial distribution is superior over other alternatives when taking fiber toughness into account.

Conclusions

Our bottom-up computational approach incorporated both the crystalline and amorphous subunits in the fiber and provided a deeper understanding for the mechanical nature of spider silk fibers. Mechanical properties such as strength, elasticity, rupture, and toughness were investigated and we provided their calculated values (Table 1). We compared the capabilities of the skeleton and all-atom models of spider silk components. The skeleton models were in qualitative agreement with the all-atom models, and the quantitative discrepancies between them allowed us to identify the important determinants of spider silk mechanics—in particular, the friction between the entangled chains causing higher stiffness and energy absorbance, and allowing an efficient homogenization of stress.

Table 1.

Comparison of the calculated mechanical properties with the experimental data in literature

	Calculation (method)	Experiment
Pull-out resistance (crystalline subunit only)	66.3 GPa (all-atom)	N/A
	54.1 GPa (skeleton)
Rupture stress
Crystalline subunit	2.0 GPa (all-atom)	N/A
Amorphous subunit	0.4 GPa (all-atom)	N/A
Fiber	2.0 GPa (all-atom)	1.1–1.7 GPa‡¶
	0.8 GPa (FE)∗†
Rupture strain
Crystalline subunit	25% (all-atom)	N/A
Amorphous subunit	35% (all-atom)	N/A
Fiber	33% (all-atom)	24–27%‡¶
	11% (FE)∗†
Elastic modulus
Crystalline subunit	80.0 GPa (all-atom)	26.5 GPa§‖ →50.0–80.0 GPa
Amorphous subunit	2.7 GPa (all-atom)	6.3 GPa§∗∗
Fiber	4.2–6.4 GPa (FE)∗†††	4.0–10.0 GPa‡¶‡‡¶¶
Toughness (fiber)	147 MJ/m3 (all-atom)	141–225 MJ/m3‡¶‡‡¶¶
	41–137 MJ/m3 (FE)∗†††

^∗The term FE stands for finite element calculations regarding the comprehensive fiber model.

^†The result was obtained for 25% fiber crystallinity with transversely isotropic crystalline members.

^‡From Gosline et al. (1).

^¶From Liu et al. (31).

^§From Krasnov et al. (6).

^‖The result was reported for poly(Gly-Ala) crystals. The corrected value we propose takes the higher stress in crystals into account (see text).

^∗∗The result was reported for silkworm silk and it is an indirect estimation from the overall fiber elastic modulus.

^††The results were obtained for serial and random distribution of the crystalline subunits.

^‡‡From Swanson et al. (32).

^¶¶From Koehler and Vollrath (33).

We show that the crystalline and amorphous subunits are the sources of strength and elasticity, respectively. In particular, the crystalline subunits are crucial elements as they act as cross-linking sites at which the stress is higher compared to the amorphous subunits in the fiber. The rupture in spider silk fibers originates from the failure of the crystalline subunits.

We showed that Nature makes a balanced trade-off among elasticity, strength, and toughness in spider silk fibers by choosing a moderate crystallinity level of 10–25%. Different possibilities for the distribution of crystalline subunits provide advantages in specific mechanical characteristics. We find that 10% crystallinity with random distribution yields a moderate elastic modulus, rupture strength, and rupture strain. Interestingly, a significantly higher toughness can be achieved in fibers with lamellar structures at 40% crystallinity. While being directly inferable from simple composite models, to our knowledge this has not yet been suggested for silk, and the current picture for silk fibers is the one with randomly distributed crystals. However, a certain tendency of silk proteins to assemble into lamellae is plausible, as

• 1.We find that the mechanical properties of the lamellar structures fall into the experimental range.
• 2.Multimerization domains in silk might enhance the alignment of the poly(Ala) repeats to form lamellae (34).
• 3.Similar structures have been observed for synthetic polymer blends (see, e.g., the study of Basire and Ivanov (35)).

In conclusion, to reach the toughness of natural silk fibers with synthetic analogs, our simulations emphasize the importance of well-defined segment lengths in crystalline-amorphous copolymers to form lamellae (36) and strongly interacting, yet highly disordered polymer types for the amorphous subunit.

Using a bottom-up computational approach, our conclusions are not based on empirical parameters. A major limitation, however, lies in the need of high loading rates in the MD simulations, which entail an overestimation of the predicted rupture forces and toughness, as discussed above. Together with the restricted system size of all-atom models, here for the composite model several 100,000 atoms, moving to the continuum scale for the full fiber, could relieve these limitations. The assumption of a simple two-phase fiber with isotropic (amorphous) and transversely isotropic (crystalline) subunits is a drastic, but apparently a reasonable approximation in the elastic deformation regime, as we could validate our model by a number of quantitative comparisons to the experiments.

The incorporation of viscous and plastic behavior will help to further improve the accuracy of the model. The explicit treatment of water at the nanoscale allows us to address the pivotal role of wetting in silk mechanics (37), which will be the subject of future investigations. Our computational approach is a helpful tool in artificial fiber design, inasmuch as it does not require any empirical parameters and therefore is straightforwardly applicable to other partially or highly-ordered polymeric and composite systems.