MHC-I prediction using a combination of T cell epitopes and MHC-I binding peptides

Abstract

We propose a novel learning method that combines multiple experimental modalities to improve the MHC Class-I binding prediction. Multiple experimental modalities are often accessible in the context of a binding problem. Such modalities can provide different labels of data, such as binary classifications, affinity measurements, or direct estimations of the binding profile. Current machine learning algorithms usually focus on a given label type. We here present a novel Multi-Label Vector Optimization (MLVO) formalism to produce classifiers based on the simultaneous optimization of multiple labels. Within this methodology, all label types are combined into a single constrained quadratic dual optimization problem.

We apply the MLVO to MHC class-I epitope prediction. We combine affinity measurements (IC50/EC50), binary classifications of epitopes as T cell activators and existing algorithms. The multi-label vector optimization algorithms produce classifiers significantly better than the ones resulting from any of its components. These matrix based classifier are better or equivalent to the existing state of the art MHC-I epitope prediction tools in the studied alleles.

Introduction

CD8+ T cells are stimulated by epitopes presented in the context of Type I Major Histocompatibility Complex (MHC-I) molecules. These epitopes, are preprocessed by the cellular machinery, and eventually bind MHC-I molecules [1]. Not all peptides generated from endogenous or exogenous proteins can bind MHC-I molecules. The MHC-I molecule has a limited binding cleft that allows only 8-10mers peptides to bind, with the vast majority of epitopes being 9mers [2]. Within all 8-10 amino acid long peptides, only those with a high enough affinity (as defined by the peptide half-life on the MHC-I molecule) can serve as epitopes. MHC molecules are extremely polymorphic [3] yielding a wide range of binding potentials and a diverse T cell epitope repertoire. Each MHC-I molecule has different binding properties, and thus requires a separate binding prediction algorithm.

The identification of MHC-I binding epitopes has many applications in T cell activation and in vaccine development. The accumulation of experimental epitope data and in silico computational methods led to the development of a large number to MHC-I binding prediction algorithms (see for example among many others: [4]).

Various assay types have been used to detect CD8+ T cell epitopes and measure their properties. Most of these measurements were combined through generic ontologies into large scale databases, such as the IEDB (Immune Epitope Database) [5] and the SYFPEITHI [6] databases. The determination of a peptide as an epitope can be divided into two label types: binary definitions (epitopes vs. non-epitopes or MHC-binding vs. non binding peptides) and quantitative measurements, such as off-rate or affinity estimates. Beyond the explicitly published epitope affinities, a posteriori estimations of the binding properties can be extracted from existing binding prediction algorithms. Some of the prediction algorithms are based on published data (e.g. IEDB [7] and NetMHC [8]), and are thus redundant with the same published data. Other algorithms only provide estimate of the binding affinity/off-rate, but not the experimental data used to generate them (e.g. BIMAS [9]). In such cases, the existing algorithm itself can be considered as an indirect third data label type.

We here introduce a supervised learning algorithm combining both binary and continuous experimental observations as well as a priori estimate of the optimal solution. The combined optimization problem is translated into a quadratic programming problem. We apply this new methodology to MHC-I epitope prediction and show that it performs better than existing algorithms. We call this algorithm Multi-Label Vector Optimization (MLVO).

Multiple labels can increase the classifier precision in two ways. In alleles with a large learning set, the combination of labels can introduce different qualitative aspects of the sampled data. In alleles where the total amount of samples per label is limited, a combination of alleles can be used to increase the size of the learning sets. Previous attempts to define the binding properties of alleles with limited data were mainly based on sharing similar label data among neighboring alleles (i.e. alleles with similar biding properties or super-alleles) [10]. We here propose a larger formalism that can merge an a priori guess based on neighboring alleles with all the data available in a given allele.

Machine learning Model

The multi-label vector optimization problem can be posed as follows: Assume a learning set with points: x_i ∈ Rⁿ,i = 1…m that have two possible label types y_i and s_i. y_i is a binary classification, and s_i is a continuous observation that is monotonically related to the binary classification y_i. Each sampled point can have either one of the two label types or both. Beyond the explicit measurements on x_i, an a priori estimate of w(w₀) can be given. The a priori estimate can be based on previous algorithms, structural insight, or results obtained in similar systems (e.g. similar alleles/molecules). We are looking for a score w and a constant b that would properly separate a set of test points x_j ∈ Rⁿ, j = 1…k, so that y_j(w^Tx_j + b) is positive for the maximal number of samples in the positive and negative test sets. In the presence of only binary classifications y_i in the learning set, this problem converges to a binary Support Vector Machine (SVM) algorithm (with a linear Kernel, although any other kernel could be used). If only continuous measurements s_i are given, a logistic regression over the s_i would be a possible solution. If only w₀ is given, then w₀ is the optimal solution. However, given the three components, we may be able to better predict the test classification combining all three data label types. These three label types can be combined into a single constrained optimization problem, with the following weighted objective function:

$$\underset{w,b,\xi ,\alpha ,\beta }{\min }c1\cdot E_1(w,b,\xi )+E_2\left(w\right)+c3\cdot E_3(w,\alpha ,\beta )$$

where we set the weight of E₂ to 1.

The first element (E₁) is the term for the optimal separation between the data points based on the binary classifications (we follow the classical SVM formalism [11]):

$$\begin{array}{cc}\hfill & E_1=\frac{1}{2}{\Vert w\Vert }_2^2+c2\sum _{i=1}^m{\xi }_i\hfill \\ \hfill & s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i,{\xi }_i\ge 0\hfill \end{array}$$

The sum and the constraints are over all the learning set points x_i with a binary classification. As in the SVM formalism, a linear classifier is defined as a hyper-plane (w^T x + b = 0), such that y_i(w^T x_i + b) ≥ 1−ξ_i. In the absence of the ξ_i term, this expression implies that all points classified as y_i = 1 are at a distance of at least $\frac{1}{\Vert w\Vert }$ to the right of the hyper-plane and all points classified as y_i = −1 are at a distance of at least $\frac{1}{\Vert w\Vert }$ to the left of the hyper-plane. The minimization term $\frac{1}{2}\Vert w{\Vert }_2^2$ is introduced to obtain the widest margin in the learning set between points classified as 1 and −1. The variables ξ_i allow for violations of the constraint. c2 controls the tradeoff between the penalty for mistakes and the margin width.

The second element (E₂) is based on an apriori guess (w₀): $E_2=\frac{1}{2}\Vert w_0-w{\Vert }_2^2$. Given an existing linear classification algorithm based on samples not included in the learning or test sets, one can hope to improve the classification of the validation set by choosing a solution not too far from w₀.

The last element (E₃) is a linear regression based on the samples for which a continuous measurement s_i is given:

$$E_3=\frac{1}{2}{\Vert Pw-(\alpha s+\beta )\Vert }_2^2$$

s is a column vectors with all the values s_i. P_m×n is a matrix with all the sample points x_i having a continuous score s_i, α and β are the regression coefficients of s on Pw. Note that the units of the continuous scores s_i may differ from the units of the a priori guess w₀, or the optimal separating hyper-plane of the binary data. E₃ . We simultaneously make a regression of s on Pw and of the optimal hyper-plane w on a linear transformation of the values of s. In a pure regression problem, we can set α = 1, and adapt the values of w appropriately. However, in the MLVO formalism, the other terms induce limits on w, and the two regression elements are required. Assume for example that ${w_0}^t{x}_i$ is the a priori estimate of the off-rate and s_i is a measurement of the log of the affinity. In order to improve the off-rate estimate, we correlate it to the affinity, but either the affinity or the off-rate has to be properly linearly transformed to fit one each other: $\stackrel{‒}{s}=1_{1\times m}\alpha +s\cdot \beta$. We compute the appropriate regression coefficients (α, β) using a least squares algorithm. The combined optimization problem is a quadratic problem with linear constrains. The resulting solution is affected by the weight given to each component: c1, c2 and c3.

Results

We here apply the MLVO to predict MHC binders using three sources: A) the affinity of MHC-binding epitopes in the proper HLA allele, B) T cell epitopes again on the proper allele, and C) published predictors obtained from regression on MHC-binding peptides off-rates [9]. The off-rates of peptides were not used as direct measurements in order to avoid information leaks between the learning and test sets. In each classifying task, 20% of the data was kept as an external test set, and the MLVO was applied to the remaining 80% of the data. The weights of the MLVO were determined to optimize the learning set accuracy. The negative learning and test sets were composed of 8,000 random peptides each with amino acid composition similar to the positive learning set. We have not used true negative peptides, since their quantity was limited in most alleles. Moreover, the goal of the classifiers was to maximize the precision, not the specificity. Thus, we wanted to be sure that when applying the scores to a large amount of sequences, most predicted positive values would indeed be positive. Only ninemers were used, as these are the vast majority of peptides presented to T Cells. The affinity data was separated by the measured units (e.g. IC50, EC50). Duplicated epitopes and epitopes overlapping between the different sets were removed.

The classifiers were built as a position weight matrices (PWM), assigning each amino acid at each position in the ninemer a weight [9]. The vectors w were 9*20 matrices reshaped into a 180*1 vector. The peptides were described as a 9*20 occupancy matrix, with a value of 1 for the relevant amino acid at each position and values of 0 for all other amino acids. This matrix was then reshaped into a 180*1 vector x. Thus the score assigned to a vector is w^T x + b, where b is the offset of the PWM.

The MLVO prediction was tested using a Leave One Out (LOO) method. The accuracy of the vast majority of alleles increased in the MLVO to over 0.95 (with AUC of over 0.98) compared with accuracies of 0.8-0.9 for the vast majority of alleles in the other learning methods (Table 1). For some alleles, very large learning sets were available. Increasing the size of the learning sets did not increase the accuracy of the MLVO predictors. Similarly, enlarging the negative data set did not improve the prediction (data not shown). The precision obtained in these binding predictions may thus be approaching the maximal precision of PWM.

Table 1.

False positive and False negative rates for the binary classification, regression and MLVO in test set. The MLVO has systematically lower FP and FN values. When using the same data as the MLVO in combination with a cutoff to classify, the results are worse than Using an SVM.

	BIMAS		SVM		MLVO		SVM +cutoff
	Sens.	Spec.	Sens.	Spec.	Sens.	Spec.	Sens.	Spec.
A*0101	0.7692	0.8385	0.8462	0.9142	1	0.9736
A*0201	0.8499	0.872	0.7949	0.8298	0.935	0.9116
A*0301	0.6765	0.8744	0.8824	0.8367	1	0.9292	0.792	0.844
A*1101	0.3929	0.9439	0.878	0.8788	0.9767	0.9304	0.781	0.828
A*2402	0.8837	0.7615	0.907	0.8796	0.9821	0.916	0.866	0.932
A*3101	0.5556	0.9197	0.8889	0.8912	1	0.9348	0.782	0.83
A*6801	1	0.8166	0.963	0.8995	1	0.9376	0.903	0.95
B*0702	0.8095	0.9129	0.925	0.8853	0.9048	0.9536
B*0801	0.7297	0.9298	0.8108	0.8454	0.8919	0.954
B*1501	0.9531	0.817	0.8906	0.9176	1	0.9464	0.79	0.84
B*2702	1	0.9109	1	0.939	1	0.9712
B*2705	1	0.6215	0.9922	0.9566	1	0.9634
B*3501	0.902	0.7996	0.902	0.8812	0.9804	0.9568
B*3701	0.92	0.7156	0.84	0.8601	0.96	0.9562
B*3901	1	0.818	0.9726	0.9423	1	0.9672
B*40	1	0.8016	1	0.9304	1	0.963
B*4001	1	0.9028	1	0.9375	1	0.974
B*4403	1	0.8548	0.9048	0.9072	1	0.9536	0.928	0.847
B*5101	0.9697	0.8312	0.9394	0.9154	1	0.9602	0.853	0.871
Cw*0401	0.9273	0.8353	0.9636	0.9489	0.9818	0.9838

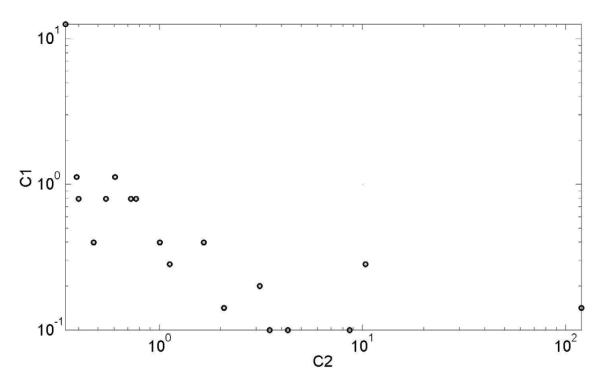
The optimization formalism used incorporates multiple elements. The contribution of each element to the optimization is determined by its weight. The optimal values were almost always obtained for intermediate values (Figure 1), showing that the combination of multiple labels does decrease the total error function. The improved performance occurs even if the a priori guess is far from optimal. Interestingly, a negative correlation can be seen between the values of c1 and c2. In other words, as we increase the importance we give to the a priori guess vs. the size of the SVM margin, we must allow a higher error rate in the binary classification.

Figure 1.

The optimal c1 and c2 values for the partial MLVO. The optimal values where almost always obtained for intermediate values 10 > c_i > 0.1 showing that the combination of multiple labels does help decreasing the total error function. A positive correlation can be seen in the values of c1 and c2.

Instead of using the MLVO, one could propose to combine the data by thresholding the continuous data and transforming it into a binary data. For example in the case of the MHC-I, we used the standard 50 NM threshold for the EC50 or IC50 data and replaced each affinity measure by a binary classification and then applied an SVM to the binary data. We have here tested such a method for the MHC-I binding prediction algorithm, and the results are not better than the standard SVM (Table 1).

The LOO results may be biased, since the sensitivity and specificity are computed for the optimal parameter set. In order to test that the LOO results are credible, a double validation was performed for alleles with enough samples. The data was divided into learning and validation sets. At the first stage, a LOO methodology was applied to the learning set, and the optimal constants for the MLVO were selected. At the second stage, we used these constants and applied the MLVO on the full learning set. We then used the resulting score and tested the external validation set. We applied this external validation to four alleles for which enough samples are available (HLA A*0201, A*2402, A*1101 and B*2705). For all alleles tested, no significant difference was found between the LOO results and the two stage validation results (Table 2). Given this good fit, we believe that the precision level of the LOO results obtained for the other alleles are also correct.

Table 2.

Comparison between LOO and external validation set for alleles with enough data samples. The difference between the LOO and the external validation are very small.

	LOO		External Validation
	Sens.	Spec.	Sens.	Spec.
A*1101	0.98	0.93	1	0.91
A*2402	0.98	0.92	1	0.93
B*2705	1	0.97	1	0.96
B*1501	1	0.95	1	0.95

Discussion

We have developed a novel optimization algorithm using different modalities, called multi label vector optimization. This formalism can be treated as the combination of a SVM, a linear regression and an initial guess. In the current analysis we have used the MLVO to produce MHC-I binding matrices. We used the BIMAS matrices as an initial guess, and focused on 20 MHC-I alleles, having at least another modality (classification data) sufficient for training sets.

Even the two-label combination of the a priori guess and SVM performed better than each of them separately, giving less than 5 % FP and FN each. The combination of all three elements further improved the precision for most alleles. In the context of MHC-I, this methodology can be expanded to use the prediction matrix of similar allele as an a priori guess. Using such a methodology, if the differences between alleles are small, a small number of samples for the new allele can be used to translate the existing matrix to a new allele.

The MHC-I binding prediction is only one example of applications of the MLVO. It can actually be used as a general supervised learning method when multiple types of data are available. Such a situation often emerges in biological interactions, such as transcription factor binding or protein-protein interactions. In such cases, observations can either be binary (the presence or absence of an interaction) or continuous (the affinity).

The mathematical interpretation of the MLVO is straight-forward. Given a classifier based on a linear hyper-plane, the normal vector of the plain is perpendicular to it. The a priori estimate provides a second vector, and the regression line of all the continuous samples provides a third vector. The MLVO is a method to optimally combine these three vectors into a single optimization problem.