Intramembrane cavitation as a unifying mechanism for ultrasound-induced bioeffects

Abstract

The purpose of this study was to develop a unified model capable of explaining the mechanisms of interaction of ultrasound and biological tissue at both the diagnostic nonthermal, noncavitational (<100 mW·cm⁻²) and therapeutic, potentially cavitational (>100 mW·cm⁻²) spatial peak temporal average intensity levels. The cellular-level model (termed “bilayer sonophore”) combines the physics of bubble dynamics with cell biomechanics to determine the dynamic behavior of the two lipid bilayer membrane leaflets. The existence of such a unified model could potentially pave the way to a number of controlled ultrasound-assisted applications, including CNS modulation and blood–brain barrier permeabilization. The model predicts that the cellular membrane is intrinsically capable of absorbing mechanical energy from the ultrasound field and transforming it into expansions and contractions of the intramembrane space. It further predicts that the maximum area strain is proportional to the acoustic pressure amplitude and inversely proportional to the square root of the frequency (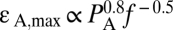) and is intensified by proximity to free surfaces, the presence of nearby microbubbles in free medium, and the flexibility of the surrounding tissue. Model predictions were experimentally supported using transmission electron microscopy (TEM) of multilayered live-cell goldfish epidermis exposed in vivo to continuous wave (CW) ultrasound at cavitational (1 MHz) and noncavitational (3 MHz) conditions. Our results support the hypothesis that ultrasonically induced bilayer membrane motion, which does not require preexistence of air voids in the tissue, may account for a variety of bioeffects and could elucidate mechanisms of ultrasound interaction with biological tissue that are currently not fully understood.

A central hypothesis regarding nonthermal interactions of ultrasound (US) energy and biological tissue is that they are primarily mediated by cavitation, that is, the activity in the US field of gas bubbles generated from submicron-sized gas pockets known as cavitation nuclei: their steady pulsations (stable cavitation) or rapid collapse (inertial cavitation) (1) and their interaction with cells, tissue, and organs (2–4). Nevertheless, this hypothesis has major limitations because low-intensity noncavitational US exposures of <100 mW·cm⁻², spatial peak temporal average (SPTA), have also been shown to induce bioeffects in cells and tissues without evidence of inertial or stable cavitation being present (3–5). On the other hand, whereas the source of in vivo cavitation is not clear, the bilayer membrane seems to be associated with many of the cellular bioeffects at a wide range of US intensities: from excitation of neuronal circuits [3 W·cm⁻² spatial peak temporal peak (SPTP), 0.44 MHz] (6) to increased transfection rates in smooth muscle cells (400 mW·cm⁻² SPTP, 1 MHz) (7). Our objective here is to introduce a unique hypothesis of direct interaction between the oscillating acoustic pressure and the cellular bilayer membranes that could potentially explain both cavitational and noncavitational US-induced bioeffects. We hypothesize that the intramembrane hydrophobic space between the two lipid monolayer leaflets inflates and deflates periodically when exposed to ultrasound: The two leaflets are pulled apart when the acoustic negative pressure overcomes the molecular attractive forces between the two leaflets (pushing away the surrounding tissue) and pushed back together by the positive pressure. We propose the term “bilayer sonophore” (BLS) to emphasize that the bilayer membrane is capable (under appropriate conditions) of transforming the (millimeter wavelength) oscillating acoustic pressure wave into (nanometric and micrometric) intracellular deformations. This cyclic expansion and contraction of the BLS could stimulate cycles of stretch and release in the cell membranes and in the cytoskeleton, which could activate mechano-sensitive proteins and/or increase membrane permeability.

What pressures are involved in the BLS's response to US? Delicate alterations in cells and tissues have been induced by US at pressure amplitudes lower than one atmosphere or 0.1 MPa (∼300 mW·cm⁻² SPTP intensity for a propagating wave where 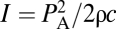, P_A is the pressure amplitude, ρ the density, and c the speed of sound). Pressure amplitudes as low as 0.04 MPa (50 mW·cm⁻² SPTP, 2 MHz) have also been shown to induce angiogenesis in ischemic muscle in vivo (8), and angiogenic-related effects were observed in vitro with pressure amplitudes of 0.03 MPa (30 mW·cm⁻² SPTP, 1 MHz) in endothelial cells (9). In contradistinction for cell rupture in vivo, much greater P_A had to be applied, as first demonstrated by hemorrhage and the damage induced in the capillary walls in the lungs of mice when exposed to P_A = 2 MPa (∼130 W·cm⁻² SPTP, 1 MHz) (10). The BLS model potentially offers a plausible framework that ties together these different observations by noting that modest negative pressures, <0.1 MPa, are expected to overcome the molecular attraction forces between the bilayer leaflets, on the basis of modeling (11) and experimental measurements (12). Clearly, an understanding of the interaction between ultrasound and the bilayer membrane at its most basic level could facilitate the development of ultrasound-based therapeutic applications such as blood–brain barrier (BBB) permeabilization, excitable tissue modulation, controlled and targeted release of drugs from circulating carriers, gene transfection, and the induction of angiogenesis. These applications would involve targeted and noninvasive US exposures for mechanical manipulation applied at the subcellular and cellular levels, as well as in whole tissues and organs.

To explore the dynamic response of the BLS in a living cell to US exposure we constructed physical models that incorporate molecular forces, bubble dynamics, and gas diffusion in and around a membrane bilayer. Using such models we evaluated the BLS dynamical response to US for multiple parameters, including the size of the free membrane when the BLS is surrounded by water (model I) and the combined effect of acoustic pressure amplitude and frequency for a more realistic BLS bounded by a thin layer of tissue on the order of a size of a cell (model II). Next, we explored the dependence of the BLS response to US in the presence of exogenous gas microbubbles. Studies have shown that when encapsulated microbubbles (ultrasound contrast agents, UCAs) are introduced into veins and exposed to high-intensity US (9 MPa peak negative pressure, 2,700 W·cm⁻² SPTP, 1.13 MHz), the damage to the veins intensifies, in comparison with the induced effects in the absence of the UCAs (13). Furthermore, in vitro studies have shown that the response of cells in culture to US [2 W·cm⁻² at 1 MHz (14) and 0.675 MPa at 1.8 MHz (15)] could be amplified by introducing UCAs in proximity to the cells. Examples such as these represent a common notion that cavitation bioeffects are induced in the US field by microbubbles in the liquid medium external to a cell surface—whether they are in the medium above the cell culture or in the lumen of a blood vessel near the endothelium—and that the microbubbles apply mechanical stress on the surface (see, e.g., refs. 16–18). The amplification of the pressure amplitude by a nearby microbubble is studied in a third model (model III) for a bubble in proximity to a solid boundary. The modeling results and predictions are finally compared with experimental observations of ultrastructural effects produced in vivo by US exposures.

Model I: The BLS Model of a Bilayer Membrane Surrounded by Water

We first studied the dynamic response of a BLS to continuous wave (CW) US using a model membrane (model I) where a flat and round BLS (Fig. 1A) is composed of two parallel monolayer leaflets bound by a circular ring of transmembrane proteins. The acoustic pressure, which is the driving force, is applied at the hydrophilic sides of the BLS at a frequency (f) of 1 MHz (see SI Text and Table S1 for detailed parameters). This pressure oscillates between “positive” (compression) pressure, i.e., greater than atmospheric pressure, where it pushes water molecules closer to each other, and “negative” (rarefaction) values when the water molecules are pulled away from each other against cohesion forces. At negative pressure, the leaflets are pulled apart by the acoustic pressure, overcoming the molecular attraction forces between the leaflets, the tension that develops in a curved leaflet, the inertial forces of the surrounding water, and viscous forces. This process is reversed during positive acoustic pressure, and the entire cyclic motion of the leaflets is determined by a dynamics force (pressure) balance equation, on the basis of the Rayleigh–Plesset (RP) equation for bubble dynamics (19) and a diffusion equation determining the rate of transport of dissolved gas into and out of the BLS from the surrounding water. Regarding the gas content of the water, it is assumed to be saturated (i.e., it contains 0.693 mol·m⁻³ of dissolved air). Symmetry of the BLS structure and the equal acoustic pressures on both sides of the BLS allow one to simplify by assuming that one leaflet is fixed while the other (free) leaflet acquires a dome shape (Fig. 1A).

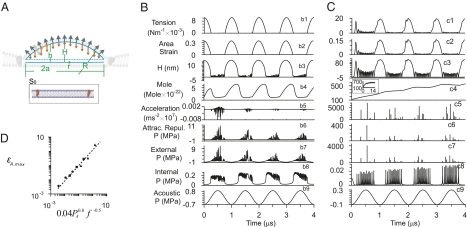
Fig. 1.

Dynamics of model membranes exposed to ultrasound (model I). (A) Schematics of a model bilayer sonophore (BLS) forming under a dome-shaped leaflet, initially (S₀) a round flat membrane. The dynamics during the first four cycles are shown of a round membrane exposed to ultrasound with f = 1 MHz, when (B) 2a = 50 nm, P_A = 0.8 MPa, and k_s = 0.03 N·m⁻¹ and when (C) 2a = 500 nm, P_A = 0.2 MPa, and k_s = 0.12 N·m⁻¹ (∼30k_BT J·nm⁻²). Illustrated in the moving leaflet are the tension (T′, N/m) (labeled by b1 and c1, respectively), the area strain (b2 and c2), the deviation (H, nm) of the dome apex (b3 and c3), the mole content of gas (mol·10⁻²²) in the BLS cavity between the leaflets (b4 and c4), the acceleration (ms⁻²) of the water just above the moving leaflet (b5 and c5), the average attraction/repulsion force per area (P_ar, MPa) between the two leaflets (b6 and c6), the external pressure (MPa) in the water just above the moving leaflet (b7 and c7), the internal gas pressure (P_i, MPa) in the BLS cavity between the leaflets (b8 and c8), and the acoustic pressure (P_A, MPa) far away from the leaflets (b9 and c9). (D) The maximum areal strain of a leaflet coupled to a 10-μm-thick piece of tissue (model II) for frequency of 0.1 MHz (▲), 1 MHz (■), and 10 MHz (●) at acoustic pressure amplitudes of 0.2, 2, and 20 MPa, for a circular membrane of diameter 500 nm.

As shown in Fig. 1A, the US exposure creates an intramembrane space, bound between a moving dome-shaped leaflet (with diameter 2a and areal compression modulus k_s) and a fixed and flat leaflet, where h(r) is the local distance between the leaflets, H is the distance at the dome apex, and R is the radius of curvature of the moving leaflet. Additional forces that act on the moving leaflet include molecular attraction/repulsion forces (described also as force per leaflet area, i.e., attraction/repulsion pressure, P_ar) between the leaflets, gas pressure from the hydrophobic side of the leaflet (P_in), tension (T′) in the leaflet, and inertial forces needed to accelerate the surrounding water. Simulations were also carried out in two BLS models that differed in the size, areal stiffness, and the applied pressure amplitude: (i) 2a = 50 nm, P_A = 0.8 MPa, and k_s = 0.03 N·m⁻¹ (Fig. 1B) and (ii) 2a = 500 nm, P_A = 0.2 MPa, and k_s = 0.12 N·m⁻¹ (Fig. 1C). Simulation results for model I for the BLS dynamics during the first four cycles demonstrate that once exposed to ultrasound, the BLS becomes a mechanical oscillator and a source of cavitation activity (Fig. 1 B and C). Similarly to a gas bubble under ultrasound exposure, the BLS is capable of transforming acoustic pressure into relatively large periodic displacements, on the order of the diameter of the BLS itself, and amplifying the oscillating pressure in the liquid surrounding it.

From the first cycle, immediately after the ultrasound exposure commences, the leaflets are detached and a dome-shaped BLS is generated, where the deviation of the dome apex from the base reaches a maximum of ∼15 nm (Fig. 1B) and 100 nm (Fig. 1C), respectively. At the same time, large areal strains reaching a maximum value of ∼0.15 and 0.3 develop in the pulsating leaflet, and the leaflet tension rises substantially to maximum levels of 0.010 N·m⁻¹ (Fig. 1B) and 0.016 N·m⁻¹ (Fig. 1C), respectively [areal strain, 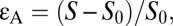where S is the surface area; leaflet tension, 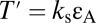]. These values appear to be larger than the tension capable of causing polyunsaturated lipid bilayers to rupture (0.003–0.01 N·m⁻¹) (20). They are also close to 0.038 N·m⁻¹, being the theoretical tension required to generate hydrophilic pores in a bilayer membrane, on the basis of molecular dynamics simulations (21). The response of the BLS is instantaneous, and in addition to the deviation of the dome-shaped apex, tension in the leaflet and areal strain also oscillates according to the frequency of the variations of the acoustic pressure, where all these parameters reach maximum amplitude from the first cycle after the onset of US. In contrast, the cyclic variations in internal gas pressure and gas content amplitude require multiple cycles (2 in Fig. 1B and ∼12 in Fig. 1C) to reach a stable level. This time required for the gas to accumulate, however, does not prevent the BLS from reaching its maximal size during the first cycle. Gas transport does not appear to be the limiting factor in BLS expansion. Instead, the deviation of the apex is limited primarily by the opposing tension force in the stretched leaflet. Degassing the surrounding water (reducing the gas content from 0.693 to 0.1 mol·m⁻³) did not affect the maximal deviation of the leaflet or the maximal areal strain relative to the saturated water. Under degassed conditions, however, air did not accumulate in the BLS, and the internal air pressure in the BLS did not rise, in contrast to the BLS in saturated water (Fig. 1C).

As the moving leaflet approaches the other, stationary leaflet (pushed by the positive acoustic pressure), the water just outside the BLS is brought to an abrupt halt. In the water adjacent to the moving leaflet high-amplitude (“external”) pressure pulses are generated on the order of 10³ MPa [such high pressures are also predicted to develop for inertial cavitation during the collapse of a spherical bubble (1)] with high frequencies that can be roughly estimated at ∼25 MHz (Fig. 1C; ∼6 MPa pressure and ∼100 MHz frequency for the 50-nm model in Fig. 1B). At the same time, high-acceleration pulses on the order of 5 × 10⁴ m·s⁻² are generated in the water, as well as large peaks of repulsive pressures on the order of 100 MPa between the almost touching leaflets (Fig. 1C). The generation of natural frequencies, one and two orders of magnitude higher than the ultrasound frequency of 1 MHz used in the simulations (Fig. 1 B and C), suggests that resonance conditions can be achieved for properly chosen US frequencies. Interesting to note is that when two leaflets are forced to approach each other at a speed of 25,600 m·s⁻¹ by a compression shock wave, molecular dynamics simulations predicted that passages open up in the damaged lipid bilayer and that water subsequently penetrates through the leaflets into the hydrophobic region (22).

Model II: The BLS Model Embedded in a Cellular Tissue

When progressing to more complex conditions for the model, the first obvious question that can be asked is the following: What effect does the surrounding tissue have on the BLS dynamics and its level of stretching (e.g., its maximal area strain ε_A,max)? The basic model portrays a BLS on a free surface, as, for instance, in the membrane of an endothelial cell closest to the lumen of a blood vessel (neglecting the contribution of the thin coating layer of the glycocalyx and extracellular receptors). In such a case the water exterior to the membrane is not bound and water inertia is the main external force resisting BLS expansion. Nevertheless, when the membrane is within the cell or between cells, the periodic expansion of the moving leaflet in the BLS is associated with pushing and stretching of nearby subcellular structures. The effect of the complex structures of the surrounding tissue corresponding to an attenuation of ε_A,max is incorporated into model I as an additional “tissue membrane,” made of a linear viscoelastic isotropic continuum, connected in parallel to the BLS moving leaflet. Thus, a modified model is developed (model II) where areal expansion modulus 2Gd (23) is added to k_s of the leaflet. Here, G is the dynamic shear modulus of a cell and d is the apparent tissue thickness (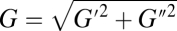, where G′ and G′′ are the elastic and the loss modulus, respectively). For f = 1 MHz, G is predicted (24) to increase above 1 MPa and the extra BLS tissue membrane is usually much stiffer compared with the leaflet; i.e., 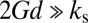and substantially limits BLS expansion. Even for a thin tissue layer d = 0.6 μm thick, for example, the value of ε_A,max for the case shown in Fig. 1B is reduced ninefold. This result may explain why disruption of blood capillaries was the first evidence of damage observed in a study of mouse lungs exposed to relatively high-intensity US of ∼130 W·cm⁻² SPTP (2 MPa, 1 MHz) (10), because the BLS of the endothelial cells at the free surface of the capillary lumen is freer to expand compared with BLS in cells deep inside the tissue. Moreover, critical values of ε_A,max could potentially be used to dictate cavitation safety limits beyond which stretching of the BLS leaflet will result in irreversible damage. We find that at ultrasound frequencies (24) 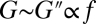and model II predicts 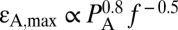(Fig. 1D) and 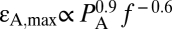for a layer of tissue 10 and 1 μm thick, respectively, attached to the moving leaflet. Interestingly, current standards for ultrasound safety associated with mechanical effects [thermal effects and safety associated with heating are determined by the thermal index (TI) (25)] are based on the mechanical index (25, 26) (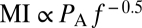), with an MI = 1.9 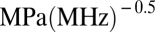being the cavitation threshold safety limit determined by the Food and Drug Administration (FDA) for the human body (25). Above this cavitation threshold, the first sign of tissue damage appears as hemorrhage in the form of endothelial cell rupture. However, our model predicts that BLSs will start forming in the membranes of endothelial cells below this threshold. These results suggest that a more detailed understanding is warranted of the effects that occur in endothelial and other cell types in vivo at MIs below the FDA safety limits and their clinical impact. (We must note, however, that, to the best of our knowledge, no harmful effects relevant to clinical conditions were found in diagnostic ultrasound in >40 y).

Model III: Pressure Amplification by a Bubble near a Wall

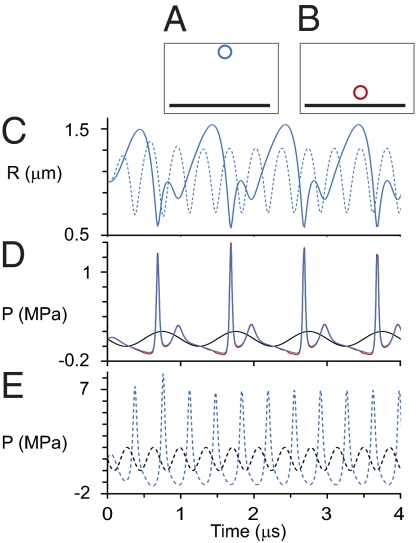
To elucidate the effects induced on the BLS by an extracellular gas bubble in an ultrasound field, we constructed a third model (model III) for a spherical gas bubble pulsating steadily near a flat solid boundary. The dimensions were chosen to roughly simulate a UCA gas bubble (without the encapsulating shell), located, e.g., near the outer cell membrane at the endothelium in capillaries and other blood vessels of the microcirculation. To simplify, we designated the bubble as spherically symmetrical and surrounded by an incompressible and nonviscous fluid (see SI Text for more details). The pressure at the solid boundary induced by a 3-μm diameter gas bubble exposed to US field was calculated for a bubble center located 2.35 and 12 μm away from the solid boundary. The simulation results demonstrate that the pulsating bubble effectively acts as a local amplifier of the pressure pulse peaks (Fig. 2). For example, an US field with pressure amplitude of 0.1 MPa and 1 MHz frequency induces pressure amplitude of ∼0.65 MPa (Fig. 2D) on the wall, just below the bubble. This value is 6.5-fold greater than the ultrasonic pressure amplitude, calculated as half the difference between maximum pressure and minimum pressure over a cycle. This amplification increases as the US frequency approaches conditions of the bubble's natural resonance (∼2.79 MHz for a 3-μm diameter free bubble in water). When using an ultrasound frequency of 2.79 MHz in model III (12 μm away from the wall), the pressure amplitude at the wall increases to ∼5.5 MPa, ∼55-fold greater than the ultrasonic pressure amplitude at infinity (Fig. 2E). One can argue on the basis of these predictions that any BLS that inflates and deflates periodically in the US field may itself amplify the acoustic pressure pulse at nearby “walls” in the same way a gas bubble does. More generally, the BLSs of multiple cells held in suspension could cross-interact with each other as “bubble amplifiers,” generating a complex pressure amplification pattern. This result may offer a simple explanation to the perplexing observation that ultrasound-induced hemolysis of whole blood requires lower acoustic pressures than that of diluted blood (27).

Fig. 2.

Dynamics of a model microbubble near a rigid wall (model III). (A and B) A free bubble with equilibrium diameter of 3 μm that pulsates in an ultrasound field with two frequencies 1 MHz and 2.79 MHz (the resonance frequency for 3 μm diameter) and P_A = 0.1 MPa at (A) a distance of 12 μm (in blue) and (B) 2.35 μm (in red) between the bubble center and the wall. (C) Prediction of the bubble radius (R) variations in time for 1 MHz (solid blue line) and for 2.79 MHz (dashed blue line). (D) Pressure pulse at infinity (black line) and at the wall just below the pulsating bubble for distance of 2.35 μm (red line) and 12 μm (blue line) between the bubble center and the wall. (E) pressure pulse at infinity (dashed black line) and 12 μm (dashed blue line) between the bubble center and the wall.

Experimental Results

Experimental validation for the model's predictions comes from carefully reexamining in vivo experiments with a multilayered epithelium model that was previously used by us for studying ultrasound induced bioeffects (28–30). The epidermis of fish is located exterior to their scales and lacks the stratum corneum of terrestrial vertebrates. It closely resembles their mucous membranes, being similarly composed of multiple layers of all live cells. The experimental procedure was composed of treating fish with continuous ultrasound exposures at 1 or 3 MHz, or to both frequencies given in succession, at spatial-averaged, temporal-averaged intensities of up to 2.2 W·cm⁻² (∼0.25 MPa) and for durations of up to 360 s (see SI Text for more details). The exposures were carried out as previously described (28–30). In short, anesthetized goldfish (4 g) were placed individually in a tank filled with tap water (at room temperature) and given exposures with a standard physical therapy device (Sonicator 720; Mettler Electronics). Exposures were carried out at 1 and 3 MHz, using a planar transducer (surface areas of 10 and 5 cm², respectively) positioned over the top. The distance between the transducer and the exposed region in the fish was set to ∼15 cm, being in the far field. The intensities of the exposures were calibrated using the force-balance technique, and the detection of cavitation was carried out using an imaging ultrasound scanner; both these procedures were carried out in the experimental treatment tank. Samples of sham and treated skin were taken immediately after the exposures and prepared for observations using transmission electron microscopy. Micrographs were captured at magnifications ranging from 2,000× to 50,000×.

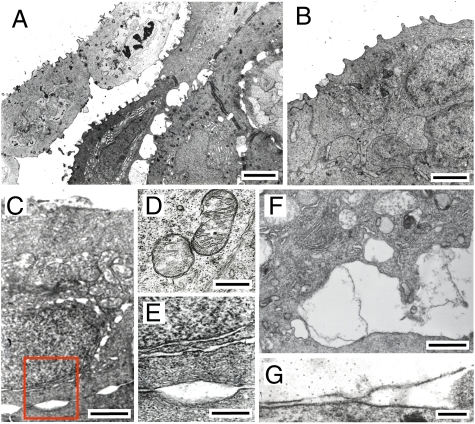
What typifies the epithelium's response to the ultrasound exposures (Fig. 3) is the generation of cavities over a range of shapes (from round and elliptical to parallel or undulated slits) and sizes (from narrow cavities <50 nm wide between two neighboring desmosomes to a few micrometers in width). Cavities around the outer membranes and between the cells were the most common. Cavities around nuclei were, however, less frequently observed. In some cases two narrow undulated slits were observed on the perimeter of nuclei, which may have originated from the two membranes that enclose the nucleus. In general, observations were made in many cases where the normally organized arrangement of membranes making up the different structural units within the cellular organelles, such as the mitochondria and the endoplasmic reticulum (ER), was disrupted. Similar patterns of cavity formation were observed in additional experiments where the treated skin was fixed in situ over the last portion of the treatments before terminating the exposures. These effects were not observed in the untreated controls, excluding the possibility that the observed effects were due to artifacts created by the sampling and fixing process of the treated tissue (e.g., dehydration or physical manipulation) (30). At 3 MHz, we observed that cavities formed predominantly between the first (i.e., outermost) and second cell layers; whereas at 1 MHz cell rupture and the generation of cavities occurred as deep as the fifth and sixth cell layers.

Fig. 3.

Membrane-localized cavitation following in vivo ultrasound exposure. The images show transmission electron micrographs of ultrasound-exposed fish skin. (A) Outer three layers of skin 2 h after receiving a 1-MHz (1 W·cm⁻², 30 s) and then 3-MHz (2.2 W·cm⁻², 360 s) exposure. Pocket-shaped gaps are observed between the second and the third layer of cells and to a lesser extent between the third and fourth layers, all of which are still viable (the outer layers are necrosed, evident by compromised apical membrane and reduced electron density). In the cell on the left in the second layer, intracellular gaps are also observed in the endoplasmic reticulum. Larger gaps are also observed where desmosomes are absent. (Scale bar, 4 μm.) (B) Outer layers of control skin. Outer cells possess microridges on their apical surfaces. (Scale bar, 2 μm.) (C) Outer cell immediately after receiving a 3-MHz (1.7 W·cm⁻², 90 s) exposure. Gaps are observed within the intercellular space between the surface cell and the cell immediately beneath it. Gaps are also visible at the nuclear membrane, being larger closer to the apical (upper) side of the cell. (Scale bar, 1 μm.) (D) Enlargement of box in C. Widening of the two nuclear membranes is shown at the upper part above the pocket-like gap between cells. (Scale bar, 0.5 μm.) (E) Mitochondria in a second-layer cell immediately after receiving a 3-MHz (2.2 W·cm⁻², 90 s) exposure. Disruption of the outer membrane is observed in the mitochondrion on the right, as well as some disruption of the cristae. The cristae in the mitochondrion on the left appear to be completely disrupted. (Scale bar, 0.5 μm.) (F) Gap between first- and second-layer cells immediately after receiving a 3-MHz (2.2 W·cm⁻², 90 s) exposure, where membrane sheets, some intact and some not, bridge between the two cells. Some mitochondria in the outer cell appear to be completely disrupted. (Scale bar, 1 μm.) (G) Widening of the apical membrane, with some ruptures, of a second-layer cell immediately after receiving a 1-MHz (1.0 W·cm⁻², 60 s) exposure. The outer-layer cell has already sloughed off during the exposure. (Scale bar, 0.2 μm.) [Reprinted from Victor Frenkel, Eitan Kimmel, Yoni Iger (2000) Ultrasound-induced intercellular space widening in fish epidermis. Ultrasound Med Biol 26:473–480, Copyright (2000), with permission from Elsevier.]

Discussion

The localized cavity formation and cell rupture observed in these experiments are consistent with an intracellular cavitation mechanism, originating in BLSs and possibly leading to irreversible alterations in the cells through membrane tears or fatigue/damage by high-frequency/large displacement cyclic loading. All cavities appeared to have developed around membranes and were more pronounced in size and in abundance in the first few cell layers, consistent with model II's predictions that the thinner the layer of surrounding tissue attached to the leaflet is, the greater the BLS inflation. Finally, the categorical difference between the tissue's response at 3 MHz (superficial) and at 1 MHz (deep layers) could be explained by the predicted augmentation of the acoustic pressure amplitude experienced by the BLSs by extracellular bubbles created at 1 MHz (model III). Even the highest intensity of 2.2 W·cm⁻² used at 3 MHz was below the free-field cavitation threshold for this frequency (30). Extracellular cavitation could also account for the gradual temporal increase in the depth of observed damage, as the contents of cells are gradually replaced by water rich with cavitation nuclei that surround the fish and are in immediate contact with the fish epithelia (28).

The observed cavities were not limited to the outer membrane and were also seen within intracellular membranes (that are inaccessible to extracellular cavitation), in agreement with the model's prediction and with observations in related studies. Disruption of the mitochondrial cristae was observed by transmission electron microscopy (TEM) in frog muscle fibers exposed to US at a low pressure amplitude of 12.5 kPa (85 kHz) for 1–30 min (31); whereas increasing the US intensity a few fold in this study induced the presence of spherically shaped bodies. Morphologically similar observations were reported in the epidermis of tadpoles (32) when TEM was used to observe the effects of US exposures (1 MHz, 11 W·cm⁻², ∼0.6 MPa, 5 min). Especially interesting in their results was the fact that the ER was irregular and disordered only in regions farthest from the nucleus and in proximity to the free cytoplasm. This phenomenon also supports the predictions of the BLS model, where more pronounced effects occur closer to a free surface. Also observed in the treated tissues of our study were detached pieces of membranes that appeared in some cavities, possibly suggesting that membranes might be involved in cavity formation in response to the ultrasound exposures. Another study, using high-intensity focused ultrasound (HIFU) (intensity not specified) for ablating the liver in rabbits, also observed their treated tissues with TEM. In this study, in cells that were not completely disrupted by the exposures, the mitochondria and ER were both found to be distended where the latter appeared as large circular vacuoles (33). On the basis of the results of the present study, where substantially lower intensities were used, it is not unreasonable to assume that these more robust structural changes could have occurred due to the higher-intensity exposures. We note that although the fish provides an effective model for studying various US-induced bioeffects in vivo, these phenomena are not expected to appear in most clinical applications of US except for perhaps in the mucosal linings of cavities, in the alveoli of the lungs, and adjacent to the lumen of the bladder. Another phenomenon that might involve the response of biological tissue to acoustic exposures is the appearance of gas-filled cavities—a few millimeters in diameter—in the livers of dead whales (34). This study raised the question of whether those cavities, as well as the sudden death of whales and other marine mammals, are the result of exposure to low-frequency (∼1 kHz) acoustic waves to military sonar with acoustic pressure amplitudes that are on the order of 1 MPa near the sonar source and reduced with distance (34–36). Effects of exposing marine mammals to sonar are expected, according to the BLS model, to first manifest themselves in the membranes of tissue that offer relatively low resistance of the surrounding tissue against BLS expansion, such as the semisoft parenchyma of the liver.

To conclude, many of the different bioeffects induced by ultrasound could thus potentially be interpreted in light of the BLS model as progressive stages along a graded scale of induced phenomena that differ in ε_A,max due to different ultrasound exposure parameters (Table S1), mechanical tissue properties, proximity to a free surface, or the presence of extracellular gas bubbles, such as UCAs that were administered systemically. With increasing ε_A,max we can expect to encounter (Fig. 4) (i) delicate and reversible bioeffects induced by leaflet stretching or bending in excitable cells (6) or cells that have mechano-sensitive membrane proteins (3, 4, 9, 37); (ii) damage to membrane proteins (38) and/or cytoskeletal fibers (37) as they become dislodged, denatured, or fragmented; (iii) membrane perforation, pore formation (39), and rupture, potentially facilitating the uptake of drugs and genes (even through the blood–brain barrier), inducing sonophoresis and enhancement of tissue permeability; and iv) complete membrane disruption and irreversible cellular damage, e.g., capillary hemorrhage, which is generally attributed to the rupture of endothelial cells (3, 4). All and all, we showed in this study that the bilayer membrane is capable of directly transforming acoustic energy into mechanical stresses and strains at the subcellular and cellular level, which do not require a prior existence of air voids in the tissue, and that overall, the model provides a unified foundation that could be used for understanding a wide range of bio-acoustic phenomena that are currently not fully understood.

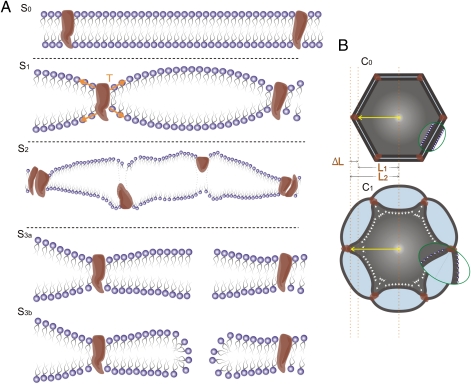
Fig. 4.

Different stages in the interaction of a BLS and an ultrasound field can induce different bioeffects on the cell membrane and the cytoskeleton. (A) As tension increases gradually in the leaflets around a pulsating BLS, from the reference stage (S₀), the slightly stretched leaflets might at first activate mechano-sensitive proteins (S₁); growing tension in the leaflets might damage membrane proteins (S₂) and then might induce pore formation (S_3a, S_3b) or cause membrane rupture at high levels of stretching. (B) Pulsations of the BLSs that surround a cell initially (at C₀) might induce from reversible mild stretching of cytoskeleton fibers to irreversible rupture (C₁).