Feedback regulation of proliferation vs. differentiation rates explains the dependence of CD4 T-cell expansion on precursor number

Abstract

The mechanisms regulating clonal expansion and contraction of T cells in response to immunization remain to be identified. A recent study established that there was a log-linear relation between CD4 T-cell precursor number (PN) and factor of expansion (FE), with a slope of ∼−0.5 over a range of 3–30,000 precursors per mouse. The results suggested inhibition of precursor expansion either by competition for specific antigen-presenting cells or by the action of other antigen-specific cells in the same microenvironment as the most likely explanation. Several molecular mechanisms potentially accounting for such inhibition were examined and rejected. Here we adopt a previously proposed concept, “feedback-regulated balance of growth and differentiation,” and show that it can explain the observed findings. We assume that the most differentiated effectors (or memory cells) limit the growth of less differentiated effectors, locally, by increasing the rate of differentiation of the latter cells in a dose-dependent manner. Consequently, expansion is blocked and reversed after a delay that depends on initial PN, accounting for the dependence of the peak of the response on that number. We present a parsimonious mathematical model capable of reproducing immunization response kinetics. Model definition is achieved in part by requiring consistency with available BrdU-labeling and carboxyfluorescein diacetate succinimidyl ester (CFSE)-dilution data. The calibrated model correctly predicts FE as a function of PN. We conclude that feedback-regulated balance of growth and differentiation, although awaiting definite experimental characterization of the hypothetical cells and molecules involved in regulation, can explain the kinetics of CD4 T-cell responses to antigenic stimulation.

In response to cognate antigens, specific T-cell numbers rapidly increase and then steeply decline, approaching relatively stable frequencies higher than those in the naive cell population (1–4). What determines the magnitude of the response? Several conceptual frameworks have been proposed: predator–prey-like interaction between lymphocytes and antigen (5–8), cell-autonomous expansion and contraction following a brief priming (9–14), and cell population-level feedback control (15–18).

The first concept inspired the development of a broad range of mathematical cell-population models to describe the dynamics of the response to viruses and bacteria with the view of antigen (the prey) as the sole, positive regulator of the proliferation, differentiation, and death of lymphocytes (the predator). Criticism of this approach can be found in ref. 19. The second concept, antigen-initiated, but not antigen-driven, expansion and contraction, does not appear to apply to CD4 T cells, which require the continued presence of antigen to proliferate (20, 21). Note that such a requirement for antigen does not necessarily imply antigen-mediated control of the duration and size of the immune response; these parameters could still be determined by a cell-autonomous “program” or by feedback, via extracellular factors other than antigen. In particular, lymphocyte proliferation and/or viability may be limited by competition for cytokines or by the action of specialized suppressor cells such as regulatory T cells (Treg). Indeed, even in the case of CD8 T-cell–mediated responses, the data suggested that a program does not mean a fixed number of divisions but that the number of divisions depends on the extent of antigenic stimulation and/or on other external factors (12). Hybrid models, incorporating a phase of strictly programmed cell division followed by a feedback-controlled phase, have also been proposed (17).

The number of divisions executed by each antigen-specific naive CD4 T-cell upon activation strongly depends on the number of cells present before immunization (3, 4, 22). Defining the factor of expansion (FE) as the ratio between the number of antigen-specific cells at 7 d after immunization and the number of precursors (PN), it has been reported very recently that, over four orders of magnitude of PN, the relation between the change in FE in response to immunization and the change in PN was log-linear. Log(FE) fell by slightly less than half a log for each log increase in PN, with an r² of 0.79 (23). This result means that when PN increased n-fold in this range, the fold decrease in FE was approximately sqrt(n). Remarkably, this relationship existed already in the physiologic range of very small PN, e.g., when the number of TCR-transgenic CD4 T cells that homed to lymph nodes after being transferred to mice increased from 3 to 30, representing an increase in the frequency from ∼1/3,300,000 to 1/330,000 (assuming 10 million lymph node CD4 T cells). A similar decrease in FE was observed in experiments comparing 30 and 300 precursors and those comparing 300 and 30,000 precursors (23).

This phenomenon was antigen specific: The FE of small numbers of precursors of a given specificity was minimally affected by concomitant responses of large numbers of precursors of a different specificity despite the fact that small and large numbers of precursors of the same specificity had a very different FE. There was robust proliferation at both low and high PN, but at low PN the proportion of cells in S phase between 3.5 and 7.5 d after immunization was sufficiently greater than that of cells at high PN to account for most of the differences in FE (23).

Together, these observations suggested that the control that PN has on the magnitude of expansion is a delayed effect, occurring when the number of responding cells has increased substantially, and that, given the antigen specificity of this effect, it likely occurs in localized microenvironments (“cell clusters”) defined by the presence and activity of cells that effectively present the cognate antigen used for immunization. Accordingly, cell proliferation is progressively inhibited as the number of specific CD4 T cells clustering about individual antigen presenting cells (APCs) increases. If APCs are limiting, immunization at small PN would require responding cells to divide more times, compared with large PN, before reaching the density at which within-cluster inhibition becomes significant, explaining at least in part the difference in FE. Indeed, increasing dendritic cell (DC) number, which presumably increased the number of effective APCs, resulted in larger FEs. Interestingly, this increase did not change the degree of advantage that precursors at low frequency displayed over precursors at high frequency, suggesting that the DC number “is limiting for the expansion of precursors but that it is equally limiting for cells at high and low precursor frequency” (23). This observation of a similar dependence of FE on PN at small and large DC numbers further suggests that in both cases all effective APCs are eventually engaged, so that cell clusters become essentially replicas of each other and the limitations on FE that are imposed within each cluster are simply mirrored by the whole system.

At the single-cell level, possible mechanisms underlying within-cluster inhibition at high cell densities include competition for antigen or for locally secreted growth factors, as well as direct inhibitory effects mediated during cell–cell interactions by inhibitory cytokines and cell-surface molecules or by Tregs. Increasing the amount of antigen had a very limited effect on FE (23). Increasing antigen amount or exogenous IL-2, IL-7, or IL-15 did not significantly affect FE nor did FE depend on Fas, TNFRα, CTLA4, IL-2, or IFN-γ. Small numbers of Foxp3-deficient TCR transgenic cells expanded to a greater extent than did large numbers, implying that inhibition is not mediated by Tregs (23). Despite these negative results, signals exchanged during TCR-mediated interactions other than those tested might be involved, and differences in the strength of these signals resulting from differences in PN could then explain the differences in FE. Such an explanation would depend on assumptions regarding the nature of the mechanisms that control the magnitude and duration of the response.

First, consider a strictly cell-autonomous expansion model with a fixed expansion time. In the absence of cell-crowding effects, each activated cell would have given rise to a number of progeny that are independent of the presence of other responding cells (i.e., there would be no dependence of FE on PN) and the total number of responding cells at the end of the expansion phase would be proportional to the initial number of precursors. Because cell crowding does exist, proliferation of responding cells arising from a larger number of precursors would be subject to a stronger inhibition during the fixed (preprogrammed) expansion phase, resulting in less proliferation and smaller FE. We would assume that the majority of cells that have come to the end of their proliferation phase are programmed also to differentiate into tissue-seeking cells and/or undergo activation-associated cell death, accounting for the contraction phase of the response.

In fact, smaller numbers of precursors do require more time to reach the peak of their response (figure 2B in ref. 23), suggesting that the responding cells “measure” their population size to determine the length of their expansion phase. This observation may be incorporated by assuming a more flexible (and physiologically more plausible) cell-intrinsic setting of response duration that depends on the strength of some external stimuli, antigenic and other, during priming or at some later critical phase. Cell crowding would affect the “time-counting” program of activated cells and not just their proliferation by reducing the strength of these stimuli; in turn, cell crowding depends on PN in this model, as discussed, linking both the duration of the response and FE to PN. Such generalization of the programmed-expansion model is in line with suggestions made earlier by others aiming to bring models into closer agreement with experiments involving CD8 T-cell responses and the manifestations of immunodominance in such responses (12, 24).

An alternative view is that feedback-control mechanisms, rather than programming, determine both the magnitude and the duration of the response. Cell crowding per se, or any other “direct” feedback control, is unlikely to be the major determinant of the response duration and magnitude. If it were, we would expect the peak number of responding cells to be independent of initial PN, assuming that all APCs presenting the relevant antigen become engaged. Expansion would cease when a certain density of cells surrounding individual APCs was reached, at which point cell proliferation and migration/death would balance. However, in fact, the peak increased with increasing PN, although not proportionally.

The objective of this study is to investigate whether feedback-regulated balance of growth and differentiation (18, 25) can be used to accurately reproduce our relatively comprehensive results on immunization-induced T-cell response in mice (23), including cell population kinetics, BrdU labeling, and carboxyfluorescein diacetate succinimidyl ester (CFSE) dilution, and, if it does, whether it predicts the quantitative relationship found between FE and PN. To this end, the concept was translated into a family of related mathematical models applicable to the description of various aspects of the data. These models, their application to the data, and analysis of the results are presented in the following section. Methods are described in SI Methods. In the Discussion we include comments on the state of the art.

Model

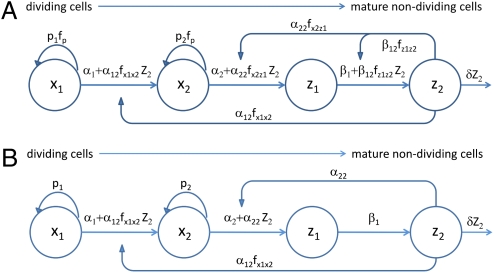
To address the feedback regulation of T-cell expansion, we formulated a general mathematical model for the local dynamics of responding antigen-induced T cells over the short term (<2 wk; this restriction is further addressed in the Discussion). As reasoned earlier, a single localized cell population (a single cell cluster) is probably representative of the entire population of responding cells for our purposes. We assumed that during antigen-driven responses, monoclonal antigen-specific T cells exhibit a heterogeneous structure in which some effector cells continue their cell division and other, more differentiated effectors and memory cells are no longer proliferating. Cell proliferation and differentiation were considered to be intracluster regulated processes. It was further assumed that antigen availability was not a limiting factor in the experiments described. The biological scheme underlying the equations of the mathematical model is shown schematically in Fig. 1A. For parameter definition see Table S1. The dividing cell compartment consists of two subsets X₁ and X₂, where X₁ is less mature than X₂. This difference in maturation state is manifested by their relative rates of cell cycle progression, so that the net proliferation rates obey the ranking p₁ < p₂. The differentiated cells Z₁ and Z₂ are no longer dividing; Z₂ controls the balance of proliferation and differentiation of X₁ and X₂ via positive feedback on differentiation, thus negatively affecting proliferation. Biologically, such a positive effect on differentiation rate could involve different alternative mechanisms. In particular, the differentiated cells might either act directly on their precursors, inducing their differentiation or increasing its probability by inhibiting proliferation, or modify the function of APC. The subdivision of the proliferating and nonproliferating populations into two subsets each was done, on biological grounds, to capture the heterogeneity of the system of activated cells (18). Mathematically, it facilitates emergence in the model of a sufficiently prolonged, variable time delay between the activation of naive cells and the accumulation of substantial numbers of feedback differentiation-inducing mature cells. Such a delay is essential for reproducing the FE–PN effect. Note that Foxp3-expressing Tregs would have been natural candidates for Z₂ (18), but a significant contribution of Tregs to inhibiting proliferation was excluded here (23). The population dynamics of the above four subsets of T cells were modeled using a system of ordinary differential equations (Section S1).

Fig. 1.

Biological schemes of the feedback regulation models. (A) Conceptual model for T lymphocyte growth and differentiation following antigenic stimulation. There is a sequence of functionally distinct stages in cell development. Cell proliferation and differentiation rates are assumed to be regulated in a feedback fashion; i.e., they depend on the number of differentiated cells. (B) Simplified model: Interaction scheme corresponding to the reduced version of the model, which provides a consistent description of the experimental data sets.

The core mathematical model was used for data assimilation either directly (data on the kinetics of clonal expansion and contraction) or in two extended forms in which the cell subsets were further subdivided into unlabeled and labeled compartments, to describe the BrdU-labeling data (Fig. S1A) and CFSE dilution data (Fig. S1B) (Sections S2 and S3, respectively). The parameters are listed and described in Section S1, along with their best-fit estimates (Tables S1 and S2).

The data sets used for parameter estimation include (i) kinetics of clonal expansion–contraction of CD4 T cells over 10 d after immunization starting from PNs of 3 × 10² and 3 × 10⁴ cells (Fig. S2A and Table S3), (ii) percentage of BrdU-positive CD4 T cells after a 6-h BrdU “pulse” given at various times between 3.5 and 7.5 d after immunization (Fig. S2B and Table S4), (iii) dilution of CFSE at days 5 and 7 postimmunization (Fig. S2C and Table S5), and (iv) the peak size at day 7 for PNs of 3 and 30 and the FE for a broader range of PNs (Fig. S2D and Table S6). A brief technical account of a more detailed characterization of these data sets, required for their use in estimating the model's parameters, and of the procedures of “data assimilation” implemented in the estimation process, is presented in Sections S4 and S5.

Results

Sensitivity Analysis, Model Reduction, and Parsimony.

The number of reliably identifiable parameters in mathematical models is limited by the amount and quality of the available datasets and, more fundamentally, also by the fact that the model structure usually has no a priori proof of validity. We applied a sensitivity analysis to rank the model parameters (listed in Section S1) with respect to their impact on the model solution (26, 27) as described in Section S6. The results (Table S7), in conjunction with the uncertainty intervals around the best-fit parameter estimates (Tables S1 and S2), suggested that some model parameters have a relatively small impact on the magnitude of clonal expansion. We found that setting 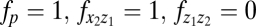(Fig. 1A) still allows a consistent match of the datasets used for parameter estimation of the complete model. The simplified model reads

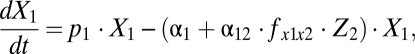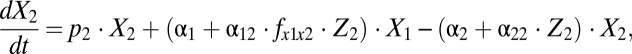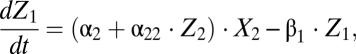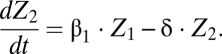The model is shown schematically in Fig. 1B. The number of parameters in the reduced model is 10 (compared with 15 in the complete version, Section S1). The corresponding versions for BrdU and CFSE labeling reduce accordingly. The best-fit parameter estimates are presented in Table S2. By information-theoretic criteria, the more parsimonious version ranks higher (Section S7). The results presented below and in the figures are based on the simplified model.

Clonal Kinetics.

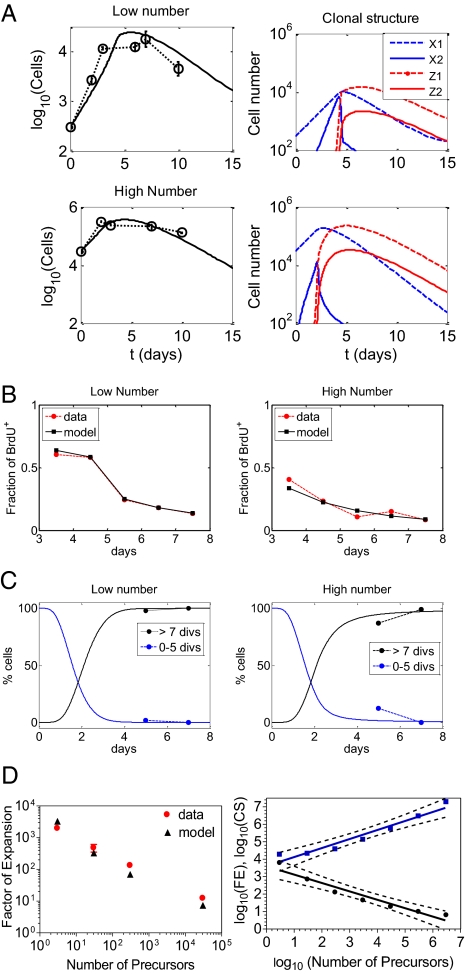
Fig. 2A (Left) shows a comparison of the experimental and model-simulated kinetics of expansion and contraction of transgenic 5C.C7 CD4 T cells adoptively transferred into B10.A mice (either 5,000 or 500,000 cells) followed by immunization with 100 μg of pigeon cytochrome C (PCC)/25 μg of LPS. Initial experiments indicated that the numbers of cells homing to lymph nodes (LNs) were ∼300 (the low number case) and 30,000 (the high number case) (23). These estimates were used in simulations as the starting values for precursor cells, X₁(t₀), t₀ = 0 with the other subsets set to zero. This initial condition implies that all of the naive precursor cells transit to X₁ upon activation. This is actually a simplification, because there is essentially no proliferation in the 24 h after stimulation. This delay, however, is taken into account indirectly in our parameter estimates given that the proliferation rates in the model are average quantities. The model simulations show a good fit to the time-series data. When PN is smaller, clonal growth is more vigorous and lasts longer, so that the number of responding cells reaches a maximum between days 6 and 7 after introduction of antigen. In the high PN case, the fold increase is smaller and clonal size reaches its maximum value before day 5. Therefore, measuring cell numbers at day 7 postimmunization, and thereby calculating FE according to its definition (23), provides only approximate estimates of the “true” factor of expansion corresponding to the actual peak of the response. The kinetics of the subsets comprising T-cell clones are shown in Fig. 2A (Right).

Fig. 2.

Data assimilation and parameter estimation. (A) Clonal dynamics: The kinetics of clonal expansion and contraction for different initial numbers (5,000 cells vs. 5 × 10⁵ cells) of transferred antigen-specific CD4 T cells. The time evolution of the total number of cells (Left) and evolution of the clonal structure (Right) are shown. (B) BrdU incorporation: Comparison of experimental and model-simulated data. Left, 300 antigen-specific precursor CD4 T cells in the LNs at the time of immunization; Right, 3 × 10⁴ antigen-specific precursor CD4 T cells at immunization. (C) CFSE dilution: Comparison of experimental and model-simulated data by days 5 and 7. Left, 300 antigen-specific precursor CD4 T cells in the LNs at the time of immunization; Right, 3 × 10⁴ antigen-specific precursor CD4 T cells at immunization. (D) Factor of expansion for various precursor numbers. Left, comparison of experimental data and model predictions of the factor of expansion as a function of the number of antigen-specific precursor CD4 T cells in the LNs ranging from 3 to 3 × 10⁴ cells; Right, log-linear regression (solid lines) of the model-predicted dependence of the clonal size and FE on PN ranging from 3 to 3 × 10⁶ cells (symbols). Peak-response estimates are shown. Dashed lines indicate the 95% confidence band of the regression line.

BrdU Incorporation.

The observed BrdU uptake at different time points indicates higher proliferation rates when PN is 3 × 10² cells than when PN is 3 × 10⁴ cells. The evolution of the fraction of BrdU-labeled T cells in time is very well reproduced by the simplified model shown in Fig. 2B, both at low (Fig. 2B, Left) and high (Fig. 2B, Right) PN. The best-fit estimates of p₁ and p₂ (Table S2) suggest that the mean net doubling times of the less and more mature cell populations are ∼21 and 8.3 h, respectively. However, the genuine proliferation rates p₁ + d and p₂ + d (where d is the per-capita death-rate constant), which effectively determine the percentage of BrdU-labeled cells during the 6-h pulse labeling (Section S2), have larger values corresponding to mean cell-doubling times of 9.3 and 5.6 h, respectively.

CFSE Dilution.

To validate the identified mathematical model we considered the experimental data on CFSE dilution. TCR transgenic cells were labeled with CFSE before they were transferred to syngeneic recipients that were immunized with the cognate antigen and LPS. Every cell division reduces the CFSE content of daughter cells by half. The CFSE dilution data show that by day 7 virtually all transferred 5C.C7 CD4 T cells in the groups of recipients with either 3 × 10² or 3 × 10⁴ PNs completed more than seven divisions (Table S5). Simulations of the version of the model adapted to explicitly describe the CFSE-labeling dilution kinetics (Section S3) were performed and proved to be consistent with the data shown in Fig. 2C.

FE Dependence on PN.

As the data on the dependence of the FE on initial clonal size were only minimally used for model calibration, we used the experimental results to validate the identified model. The simplified model equations were solved numerically for different PNs (3, 30, 3 × 10², and 3 × 10⁴ cells) and FE evaluated from day 7 numbers. The predicted day 7 FE closely approximates the experimental data (Fig. 2D, Left), providing additional support for the potential validity of the proposed regulatory scheme.

Using the identified simplified model, we analyzed the quantitative dependence of both FE and clonal size (CS) on PN. Day 7 expansion was calculated for PN ranging from 3 to 3 × 10⁶ cells. Regression analysis of log(FE) on log(PN) suggests the following quantitative relationships: FE = (PN)^−0.54 × 2,512 and CS = (PN)^0.46 × 2,512 (cells) for FE and CS, respectively.

Finally, the calibrated simplified model was further used to estimate the dependency of the “genuine” FE and CS at the estimated peak of the response, which is reached at different times after immunization (Fig. 2D, Right). A similar regression analysis predicts that FE and CS dependence on PN is closer to the “square-root law”: FE = (PN)^−0.48 × 3,981 and CS = (PN)^0.52 × 3,981.

Discussion

As quantitative data characterizing the antigen-induced immune response under different conditions and at different levels of resolution become increasingly available, mathematical models based upon sound concepts of immune regulation are required to systematically integrate various features of the process.

A new feature that has recently been added is a strikingly uniform dependence of the magnitude of expansion of antigen-activated CD4 T cells on the initial number of naive precursors (PN), starting within the physiological range of antigen-specific cell frequencies. When precursor frequency in secondary lymphoid tissues was increased n-fold, the number of responding cells at day 7 postimmunization increased as well but only by a factor of (n)^0.46, implying a reduction in the FE by (n)^0.54. The proportion of cells in S phase at low precursor frequency over the period between 3.5 and 7.5 d was sufficiently greater than that of cells at high precursor frequency to account for most of the differences in FE (figure 3 in ref. 23).

As discussed in Model above, the PN–FE relation could be explained as a consequence of a differential inhibitory effect of cell crowding for different PNs on the net proliferation of responding cells toward the end of the expansion phase, due to competition for access to stimulatory molecules and growth factors or by the action of responding cells to actively inhibit each other's growth. Such explanations require a model in which the duration of the expansion phase is largely a cell-autonomous characteristic. Indeed, in such a model the level of crowding during the (fixed) expansion phase would be directly related to the initial number of precursors, with more crowding resulting in less efficient proliferation and smaller FE. Instead, if we assume that the feedback inhibitory effect of increasing cell crowding is the primary determinant of the duration and magnitude of expansion, we should expect the expansion phase to end once a certain number of cells is reached, independently of the initial number of precursors, contrary to observation. FE at the peak of the response (approximated by the day 7 number) would be inversely proportional to PN, also inconsistent with the observed relationship.

In this communication, we did not further investigate the cell-autonomous regulation model, with cell crowding as a secondary effect, a) because of the fact that smaller numbers of precursors do require more time to reach the peak of their response, suggesting that the responding cells “measure” their population size to determine the length of their expansion phase (gearing the cellular time-setting machinery to stimulation strength could resolve this apparent discrepancy, but such a model, which is no longer really cell-autonomous, would have too many degrees of freedom in the absence of experimental constraints); b) because no evidence has been found in support of the notion that different levels, at high and low PN, of competition for antigen or several known stimulatory molecules, or of a differential expression of one or more of several inhibitory cytokines and surface molecules, can explain the difference in FE and in the magnitude of the peak of expansion; and c) because we wanted to investigate whether an alternative model, which combines the basic simplicity of the feedback-regulation concept with additional theoretically attractive features (18, 25, 28, 29), could assimilate the empirical observations in a consistent and unifying way.

On the basis of the previously formulated theory of feedback-regulated balance of growth and differentiation (15, 18), a “conceptual” mathematical model of the clonal dynamics of CD4 T lymphocytes considering the proliferation, differentiation, and death of T cells in mice after immunization was formulated. The model describes the differentiation of recently activated naive T cells (“effectors”) from a proliferative into a nonproliferative stage (two compartments at each stage) with feedback interactions regulating the balance between division and differentiation. The model does not incorporate mechanisms thought to be involved in the transformation of a certain portion of the effector-cell population into “resting,” long-lived memory cells, e.g., temporally patterned interactions with dendritic cells (30) and the “tuning” of cellular properties associated with transient induction of a refractory state (18, 31), and therefore it is not supposed to adequately describe the kinetics of the contraction phase far beyond the peak of the response. We did not relate here to the possibility, discussed in qualitative terms elsewhere (18), that a delayed onset of tuning, occurring stochastically, or initiated by Treg cells and/or resulting from a preceding T-cell density-dependent suppression of APCs, may actually participate in the feedback that determines the duration and peak of the response and not only in determination of the fate of effector cells. Therefore, our model should be considered as a “minimal model.” The model was readily adapted for the analysis of BrdU-labeled cell kinetics and CFSE-dilution data. We estimated the parameters of the basic model using our own data on the expansion of adoptively transferred transgenic 5C.C7 CD4 T cells (23).

The four compartments of the basic model do not specifically reflect biologically characterized cell populations, because such particular classification of effector T cells does not exist biologically and is likely to be an oversimplification. Note, for example, that the small constitutive-differentiation parameters, α₁ and α₂, are average quantities, and in reality they might be equal to zero initially but assume larger values as cells continue to proliferate, but our simple model is not aimed to capture such details. Nevertheless, the essential features of the experimental data on the dynamics of T lymphocytes are consistently reproduced by the model. In particular, the calibrated model with the specified feedback regulation predicts FE as a function of the initial PN in a quantitatively consistent way.

To explain how this was accomplished, we highlight the inherent “overshooting” property of the model (and indeed of the immune response). In the model, differentiation exceeds proliferation once a certain number of differentiated CD4 T cells of the appropriate phenotype have accumulated, that is, when mitotic cells, on average, are more likely to undergo differentiation than to divide again. However, given the built-in delay in the multicompartmental differentiation process and the fact that responding cells proliferate rapidly during this delay period, the number of differentiated cells at the peak of the response greatly exceeds (overshoots) the number defining an exact balance between proliferation and differentiation, so that overdifferentiation into short-lived and/or tissue-seeking differentiated cells occurs in the lymph nodes/spleen and a rapid decline follows. The transition from growth to decline is relatively fast, due to the autocatalytic nature of differentiation in this model; as the number of differentiated cells increases, they are more rapidly recruited from proliferating cells. Together, these characteristics of the proposed regulatory process give the kinetics of the immune response its typical burst-like quality.

It is not difficult to see that the degree of overshooting, as defined above, and hence the number of responding cells at the peak of the response (or at day 7), must be smaller with a smaller PN. Consider responses initiated by activation of two different precursor numbers, PN₁ and PN₂, respectively, such that PN₁ < PN₂. When the total number of responding cells in the first case reaches the PN₂ level, this responding cell population already includes, in addition to X₁, cells belonging to the more differentiated subsets X₂, Z₁, and Z₂, whereas essentially all of the cells that initiate the second response, also PN₂ in number, belong to the X₁ subset. From that time point onward, this already-skewed profile toward more differentiated cells in the PN₁ case results in the responding cells requiring less time to reach the critical number of fully differentiated cells, Z₂, compared with the time required in the larger-PN case. By then, smaller numbers of cells populate the less-differentiated compartments in the smaller-PN case and consequently the subsequent feedback-induced differentiation of these cells results in a smaller peak. We note that the overall length of the expansion phase is nevertheless longer in the smaller PN case, because of the additional time required to reach the PN₂ level; the FE is larger, because of the additional cell-division cycles performed by each precursor cell during this initial phase of expansion from PN₁ to PN₂.

Obviously, the overshooting characteristic was not introduced into the model in the first place to account for the PN–FE relation. Rather, this characteristic was regarded from the outset as a fundamental aspect of the immune response to pathogens (15, 28, 29, 32, 33). Indeed, we have reasoned that overshooting may be instrumental in facilitating complete elimination of many pathogens. Considering that in real life (as distinguished from the experimental conditions pertinent to this study) antigen is a positive regulator of the immune response, although not the sole regulator, and that antigen is cleared by the very effector cells it induces to proliferate, the delay in the development of large numbers of effector cells from proliferating cells following infection may be necessary to prevent the stimulus from diminishing too early and the size of the response from being too tightly geared to the amount of antigen, which could readily result in a predator–prey-like coexistence of effectors and pathogen and in a chronic, only partially controlled, disease. The delayed emergence of effectors, controlled in a feedback fashion by a factor or factors other than the effect of these effectors on antigen availability, allows for the generation of an excessive number of effectors sufficient to eliminate the pathogens down to the last one. The capacity for an overshooting response is expected to be considerably reduced when the initial stimulus is weak and/or increases slowly on the scale of effector-cell differentiation times. This kinetic effect has been proposed as an explanation for certain “sneaking through” phenomena in which cancer cells or slowly replicating pathogens evade the immune response and establish a chronic state in tissues (29, 32) and even, along with tuning, as a basis for self–nonself discrimination (15, 28, 33).

We showed that for the considered datasets the model parameters can be identified using a simpler version of the complete model. Using a criterion that estimates the relative distance to the unknown true model and statistical hypothesis testing, we found that the reduced model is a parsimonious description of the considered datasets. However, one needs to distinguish between the model of the data and the model of the system. The data available to us do not allow, for example, rejection of nonsimplistic models incorporating programmed proliferation and differentiation. More generally, the dependence of T-cell recruitment and proliferation on the presence and/or strength of antigenic stimulation during development of the immune response, which was the focus of other studies pertaining to the primary CD8 response (12, 24), was deliberately largely eliminated in the present study's experimental design (23), where antigen is nonlimiting, and therefore has not been explicitly incorporated in our model. Even as we acquire better and more sophisticated tools for data analysis, the rules that govern regulation of the real system remain tentative. An ideal approach (although not always practical) to achieving a better fundamental understanding of the system, which could be translated into a better correspondence between the system's structure and the interactions among its elements on the one hand and a model's variables and parameters on the other, would be an iterative process of hypothesis-driven experimentation, reformulation of the hypothesis, and more experimentation. As suggested by this report, and by the work of others, mathematical analysis can help in the process of data assimilation and hypothesis testing and modification.

Methods

Our data analysis methods are described in more detail in the SI Methods. In SI Methods, we explicitly present the different mathematical models leading to or derived from the simplified parsimonious model featuring in the text, as well as several tables and figures, referenced from the text in the order they appear, summarizing different aspects of the data and estimated parameter values of the models. Also described are the techniques used to identify the parameters, to compare the models, and to calculate the sensitivity of the simulated results to variation in parameter values (sensitivity analysis). This calculation, summarized in Table S7 in the form of partial rank correlation coefficients between the parameters and FE, in conjunction with the uncertainty ranges around the best-fit parameter estimates (Tables S1 and S2), allows simplification of the model.