Investigating the Impact of Selection Bias in Dose-Response Analyses of Preventive Interventions

Abstract

This paper focuses on the impact of selection bias in the context of extended, community-based prevention trials that attempt to “unpack” intervention effects and analyze mechanisms of change. Relying on dose-response analyses as the most general form of such efforts, this study provides two examples of how selection bias can affect the estimation of treatment effects. In Example 1, we describe an actual intervention in which selection bias was believed to influence the dose-response relation of an adaptive component in a preventive intervention for young children with severe behavior problems. In Example 2, we conduct a series of Monte Carlo simulations to illustrate just how severely selection bias can affect estimates in a dose-response analysis when the factors that affect dose are not recorded. We also assess the extent to which selection bias is ameliorated by the use of pretreatment covariates. We examine the implications of these examples and review trial design, data collection, and data analysis factors that can reduce selection bias in efforts to understand how preventive interventions have the effects they do.

As preventive interventions become larger and more complex, researchers are increasingly likely to examine the outcomes of randomized control designs as well as investigate possible mechanisms of change. These implementation studies focus on how differences in factors such as intervention dose, therapeutic process, or fidelity might account for differences in participant outcomes. However, these efforts to “unpack” intervention effects are vulnerable to selection biases (Winship & Mare, 1992), which occur when either known or unknown compositional differences among subgroups of participants – rather than factors related to the intervention itself – account for final observed differences (Rosenbaum, 2002). For example, the conscientiousness and competence that compel a teacher to administer an intervention as intended might affect other ways in which she or he teaches, so that children in that classroom would do well, almost regardless of the study condition to which they were assigned. Unfortunately, such selection biases are rarely acknowledged and adequately addressed (see studies included in the review of implementation research by Durlak & DuPre, 2008).

Selection Bias and Dose-Response Analyses

Problems with selection bias are not new and apply to most studies of intervention implementation. The threat selection bias poses to internal validity as well as to external validity has been discussed at length elsewhere (e.g., Shadish et al., 2002). The key feature of selection bias is that there is some systematic difference between those participants who partake in some aspect of treatment and those participants who do not. Researchers commonly think of selection bias that results from pretreatment differences, but selection bias also can result from known or unknown differences that arise during the study period as the result of variation in treatment adherence, quality of implementation, and attrition. This threat to validity is known as unreliability of treatment implementation or selection by treatment interactions (Shadish et al., 2002); it can be especially problematic whenever investigators seek to understand what happened within the treatment condition of a preventive intervention trial.

In those cases when selection bias occurs after the start of an intervention, features of study design, like random assignment, will be insufficient to control the bias. Likewise, unless the confounder is a stable trait that is known and measureable and exerts all its influence prior to the beginning of the intervention, the use of pretreatment covariates will be insufficient to control the bias. In those cases when the confounder varies over time, only more sophisticated statistical analyses can be used to reduce its influence (e.g., Rosenbaum, 1984a, 1984b; Rosenbaum & Rubin, 1983; Winship & Mare, 1992).

Although problems with selection bias apply to most studies of intervention processes, these problems are most apparent in dose-response analyses. Such analyses examine the fundamental logic model underlying preventive interventions – that participants must receive services to improve (Cicchetti & Hinshaw, 2002; Domitrovich & Greenberg, 2000). In such analyses, dose does not represent the hypothesized mechanisms of change, like the factors studied in mediation analyses; rather dose is a coarse indicator of how much treatment was received in which to acquire those mechanisms of change.

The strongest design for a planned dose-response analysis would be to randomize different levels of dose among participants, as randomization limits the possibility that there are compositional differences between the subgroups assigned to different doses. Whenever dose is not randomized, or when the randomized dose is not adhered to, variables that affect selection of the dose received produce compositional differences between the subgroups. If these variables also affect the outcome, the observed dose-response relation confounds the effects of these compositional differences with the true dose-response relation. For example, motivation is a confounder if more motivated participants adhere more closely to the recommended dose and exhibit better outcomes than less motivated participants, or family disorganization is a confounder if children who are frequently absent receive fewer sessions of a school-based curriculum and exhibit worse outcomes than children who attend regularly. In both cases, better outcomes are associated with higher dose; the selection bias is positive and the observed dose-response relation appears stronger than the true relation. However, if a counselor decides to schedule an extra session of treatment for a family in crisis or extra tutoring is provided to those children who are failing a class, then worse outcomes would be associated with a higher dose; the selection bias would be negative and the observed dose-response relation would appear weaker than the true relation.

The Present Research

This paper focuses on the impact of selection bias in the context of extended, community-based preventive intervention trials. It demonstrates how selection bias can affect estimation of treatment effects when confounders are unknown or incompletely recorded and therefore cannot be controlled via analysis. In particular, this paper offers two detailed examples in which confounding makes treatment appear less effective than it might be or even iatrogenic. In Example 1, we describe an actual intervention in which selection bias was believed to play havoc in estimates of the dose-response analysis of a preventive intervention for young children with severe behavior problems. In Example 2, a series of Monte Carlo simulations illustrate how severely selection bias can affect estimates in a dose-response analysis when dose is tailored to participants’ need but when the reasons for tailoring dose are unrecorded. In the final section of the paper, we examine the implications of these examples and review trial design, data collection, and data analysis factors that can reduce selection bias in implementation studies, such as dose-response analyses, of preventive interventions.

Example 1

The purpose of Example 1 is to illustrate with real data how purported selection bias can make it very difficult to interpret dose-response relations in an adaptive intervention. Increasingly, preventive interventions are using adaptive designs, in which the amount or type of an intervention component is adapted to participant need (Collins et al., 2004). The rationale is that researchers can achieve more efficient and cost-effective interventions than standard one-size-fits-all programs by providing more intensive treatment only when it is warranted (Jacobson et al., 1989; Kreuter et al., 2000; Lavori et al., 2000). In the present example, however, on-going decisions regarding the need for additional treatment most likely results in selection bias as well. Depending on how we attempt to control for this selection bias, we come to dramatically different conclusions about dose-response relations.

This example relies on data from Fast Track (Conduct Problems Prevention Research Group [CPPRG], 1992), a multi-site, multi-year, randomized trial evaluating a six-component intervention designed to prevent the development of severe conduct problems among children exhibiting high rates of aggression at school entry. Evaluations of Fast Track intervention effects have been published elsewhere (CPPRG, 1999; 2002). Intent-to-treat analyses, comparing the randomized intervention and control groups, revealed a pattern of positive intervention effects on various measures of social competence at the end of first grade (CPPRG, 1999).

Because many treatment effects were small in magnitude and because some components of the intervention required more resources to deliver, we were interested in conducting dose-Selection response analyses to determine how well the various intervention components were working. The peer pairing component was of particular interest for this study. Peer pairing sought to enhance the impact of the social-skills training children received in the universal classroom curriculum and small therapeutic groups by helping them generalize the use of those new skills to individual peer interactions (Bierman et al., l996). Peer pairing consisted of structured dyadic play sessions involving the intervention child and a rotating, same-sex classmate who did not have behavior problems. In first grade, all children in the intervention condition were offered one session of peer pairing per week for a total of 22 sessions. After one year of intervention, some children were exhibiting normal levels of social competence and aggression and were not experiencing peer rejection. Therefore, in second grade, peer pairing was offered only to those children who still appeared to need it.

Continued need for peer pairing was based on objective criteria, measured at the end of first grade. If children received a t-score of 65 or higher on the aggressive behavior or attention problems syndrome of the Teacher’s Report Form (Achenbach, 1991), they were considered to have clinically significant behavior problems that could undermine peer relations and thus were supposed to receive peer pairing throughout second grade. T-scores between 60 and 65 were considered borderline. If children received patterns of sociometric nominations for “like most” and “like least” indicating they were rejected by their classmates (Coie & Dodge, 1988), they also were considered in need of an additional year of peer pairing. Children whose sociometric nominations suggested they were controversial or neglected were considered borderline. If children were “borderline” in terms of teacher ratings or sociometric nominations, Fast Track allowed staff members to use their best clinical judgment, based on their own observations and discussions with teachers, to decide whether the child should receive peer pairing in second grade. When project guidelines specified peer pairing or staff members determined that a child should receive peer pairing, that child was supposed to receive peer pairing throughout the fall and spring of second grade. However, Fast Track also allowed staff members to initiate peer pairing sessions at any point during second grade if they noticed worrisome declines in children’s social functioning. In addition, staff members could deliver extra peer pairing sessions if they believed the sessions would be helpful. The number of peer pairing sessions children received ranged from 0 to 43.

Measures

For this study, dose is the total number of peer pairing sessions that each child received during second grade, based on weekly records kept by clinical staff members. Response is the child’s social competence, as rated by teachers at the end of second grade. Social competence was measured using the Social Health Profile, a questionnaire developed for Fast Track, which consisted of nine items, such as “Friendly” and “Controls temper when there is a disagreement.” Each item was rated on a 6-point Likert scale, with response options ranging from “almost never” to “almost always” (Cronbach a > .80). Pre-second grade covariates included social competence (using the Social Health Profile) measured at the end of first grade, as well as study cohort, study site, child race, and child sex.

Analyses

Regression analyses of intervention-control group differences among children who were promoted to second grade and entered the adaptive phase of peer pairing intervention (n = 410 and 403 in the intervention and control groups, respectively) revealed a small and marginally significant effect of being in Fast Track on growth in social competence during second grade, after controlling for end-of-first-grade social competence scores, cohort, site, race, and sex: Standardized β (for treatment) = 0.06, p = 0.06 (unstandardized parameter estimate = 0.12, F [n = 745, df = 9 and 735] = 15.07, p < 0.001, R² = 0.16).¹ Relations like this – suggesting that children in the intervention condition were doing better than children in the control condition but that the adjusted mean difference was less than one-tenth of one standard deviation – often motivate efforts to examine intervention effects in greater depth to understand exactly what might be happening.

Dose-response analysis 1: All intervention children who were promoted to second grade

Our first implementation analyses relied on data from the children in the intervention group only to examine whether the dose of peer pairing in second grade affected their growth in social competence. Controlling for end-of-first-grade social competence scores, cohort, site, race, and sex, a linear regression equation revealed a marginally significant negative association between the peer pairing dose and the social competence outcome: β (for dose of peer pairing) = −0.09, p = 0.07 (unstandardized parameter estimate = −0.01, F [n = 383, df = 9 and 373] = 8.94, p < 0.001, R² = 0.18).

In hindsight, the emergence of this negative effect is not surprising: By design, the children who were displaying the most problems and the least social competence were provided the highest doses of peer pairing. From a theoretical and clinical standpoint, it seems highly unlikely that peer pairing actually had a negative effect on children’s growth in social competence. The overall positive effect of the Fast Track intervention on social competence also argues against this interpretation. Thus, it is plausible that the negative estimated effect of peer pairing is being driven by systematic differences between those children receiving more peer pairing and those receiving less – in other words, by selection bias.

There are many analytic methods available for dealing with such bias, and we employed several as a follow-up to the above dose-response analysis. When pretreatment characteristics affect the quantity of dose (i.e., when selection bias is the result of pretreatment differences between those children receiving different doses), it is common to adjust for the relevant pretreatment covariates in the regression model. Indeed, we conducted additional analyses adjusting for up to 15 relevant covariates assessed at the beginning and end of first grade, and a negative association between peer paring dose and the social competence response still emerged. This suggests that controlling for both distal pre-first grade covariates and more proximal end-of-first grade covariates was not enough to ameliorate the confounding.

Again, in hindsight this is not surprising: The dose of peer pairing was adapted to each child not only at the beginning of second grade but also during second grade, based on the child’s functioning. Unfortunately, variables that may have factored into the use of clinical judgment to adapt and re-adapt the dose of peer pairing during second grade were not recorded. Because these time-varying confounders were not recorded, the use of methods for dealing with them was precluded.

Dose-response analysis 2: Intervention children who were promoted to second grade, were determined to need peer pairing, and actually received it

Another way of controlling for confounding is to focus only on the dose-response relation within a subgroup of participants who are subject to a reduced level of selection bias. For example, in the Fast Track intervention, one potential source of selection bias was the aforementioned use of clinical judgment which was used to supplement and modify assessments of child functioning to determine a child’s need for peer pairing. According to Fast Track guidelines regarding teacher behavior ratings and sociometric nominations at the end of first grade, 240 children were supposed to receive peer pairing throughout second grade. Of these children, however, only 159 actually received peer pairing in both spring and fall; the other 81 did not, primarily because of moves out of core schools, feasibility issues, or staff members’ idiosyncratic decisions that peer pairing was no longer needed. Because we believed that selection bias due to clinical judgment would be least at work among this subsample of 159 children for whom staff members’ judgment did not override project guidelines, we conducted a second dose-response analysis which focused only on them.

In this regression equation we again controlled for end-of-first-grade social competence scores, cohort, site, race, and sex. Interestingly, the dose-response relation within this subsample of children – for whom we expected selection bias due to clinical judgment to have the least impact – was positive: β (for dose of peer pairing) = 0.18, p = 0.02 (unstandardized parameter estimate = 0.03, F [n = 157, df = 9 and 147] = 2.93, p < 0.003, R² = 0.15). In this subsample only, children who received more peer pairing appeared to show greater gains in social competence during second grade.

Discussion of Example 1

Did peer pairing in second grade reduce or improve children’s social competence in Fast Track? In the end, this question really cannot be addressed by our analyses. Individual researchers might put different emphasis on the credibility of the two dose-response analyses and come to different conclusions. The first dose-response analysis suggests that the gains in social competence that emerged when comparing the randomized intervention and control groups might have been the result of some other components of the Fast Track intervention, not peer Selection Bias in Dose-Response Analyses 12 pairing. In fact, peer pairing might have even worked against those broad gains that resulted from the other components of the intervention. The second dose-response analysis, however, suggests that peer pairing might have improved social competence, at least for those children who were in need of the intervention component and actually received it as planned. It is important to remember, however, that in each analysis we cannot be sure of our ability to control for the selection bias that exists or to avoid introducing new bias by stratifying on post-randomization variables to choose a sub-group for analysis.

Selection bias in dose-response analyses exists for a variety of reasons. Recall that selection bias occurs when there are common factors for why a child received treatment and the child’s outcome, and these factors are unknown, improperly measured, or not controlled in the analysis. In Fast Track these factors are likely due to both the use of clinical judgment in the adaptation and re-adaptation of peer pairing, and to feasibility issues in the delivery of services.

Clinical judgment, presumably based on more proximal, but unrecorded, assessments of child functioning, contributed to selection bias in Fast Track because it affected whether children did or did not receive peer pairing in a large proportion of cases. Clinical judgment was supposed to be used in recommending whether those children who were “borderline” in terms of objective indicators of need received peer pairing in second grade. However, staff members also were allowed to initiate peer pairing during second grade if they observed new problems. Some staff members also provided extra peer pairing (up to 43 sessions) when they thought it was especially helpful for a particular child. And, in some instances staff members made the unsanctioned decision to withhold peer pairing when they thought it was unnecessary or might be stigmatizing for a particular child.

Feasibility issues also might have contributed to selection bias in Fast Track. Like many community-based preventive interventions targeting early-starting conduct problems (e.g., Rohrbach et al., l993), we encountered real-world obstacles in implementation. Over 29% of intervention children transferred schools by the end of second grade, and many children were absent on the days they were supposed to receive peer pairing.² In our case, feasibility issues could have resulted in positive selection bias if unknown factors positively related to children’s social competence, such as child cooperativeness, affected the ease with which staff members could deliver peer pairing. On the other hand, feasibility issues could have resulted in negative selection bias if staff members strove harder to overcome logistical barriers when they were especially concerned about a particular child or when they believed that peer pairing was an especially important component of intervention for a particular child.

Thus, Example 1 highlights, with real-world data, how selection bias affects our ability to unpack intervention effects in prevention programs. Depending on our success in reducing selection bias – and our success in not introducing additional bias in the process, a feat we rarely can be certain of – our conclusions about dose effectiveness can change dramatically.

Example 2

In Example 2, a series of Monte Carlo simulations illustrate the degree to which confounding can impair the interpretation of intervention effects when conducting implementation studies of preventive interventions. We wanted to determine whether we could reproduce a similar pattern of results to what we observed in Example 1. Because real data were used in Example 1, we could not know with certainty what the true effect of peer pairing dose was. Through simulations, however, we could generate data with specific dose-response relations and assess our ability to detect them. In Example 2, we demonstrate the frequency with which confounding might contribute to an incorrect assessment of the dose-response relation, illustrate the extent to which the duration of the preventive intervention affects the degree of selection bias, and examine the conditions under which including pretreatment covariate controls might attenuate selection bias.

The simulated data mimic aspects of the Fast Track example. The maximal dose was set at one session per week for 22 weeks, but the receipt of treatment was variable from week to week, thereby modeling actual variation in child attendance and participation. We simulate data with a time-varying confounder that positively affects the received dose and negatively affects child outcome. This variable represents factors such as time-varying clinical judgment that might operate to increase the participation of higher risk children in the intervention and decrease the participation of lower risk children. To mimic that aspect of Fast Track in which the time-varying confounder was unrecorded, we used a time-varying confounder to generate our simulated datasets, and then we deleted that variable before conducting any analyses.

Data Generation

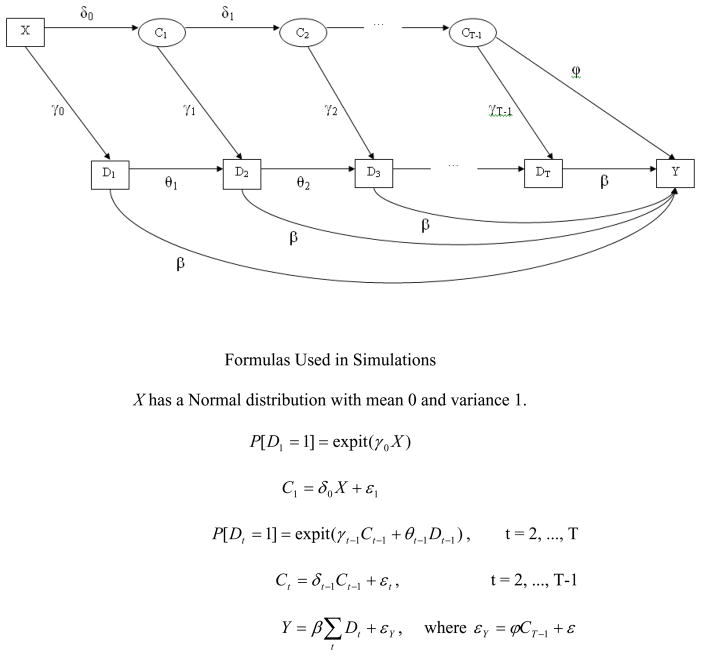
Figure 1 provides a pictorial representation as well as the generative models used to create each of the variables for these simulations. (Programming code for these simulations is available at http://www.stat.lsa.umich.edu/~samurphy/papers/McGowanSimCode.txt.) We generated each participant’s data by first drawing a variable (X) that represents a recorded pretreatment variable. Next, we drew an indicator of receipt of the first intervention dose (D₁), which could be affected by this pretreatment variable. For each of the remaining time points (t = 2,…,22), we drew a time-varying confounder (C_t) prior to each intervention session, which represents an unrecorded covariate that affects both the dose and the outcome. An indicator that dose was either received at session t (D_t = 1) or not (D_t = 0) was then generated. Finally, after 22 sessions the outcome (Y) was generated. The continuous variables (X, C_t, and Y) were standardized to have a mean of 0 and a standard deviation of 1.

Figure 1.

Relations Modeled in Simulations

Note: $\text{expit}(\text{x})=\frac{exp(\text{x})}{1+exp(\text{x})}$ Note: ε₁, …, ε_T−1, ε are independent Normally distributed random variables each with mean 0 and variance 1, and ${\epsilon }_Y=\varphi \left({\displaystyle \prod _{t=0}^{T-2}}{\delta }_t\right)X+{\displaystyle \sum _{s=1}^{T-2}}\varphi \left({\displaystyle \prod _{t=s}^{T-2}}{\delta }_t\right){\epsilon }_s+\varphi {\epsilon }_{T-1}+\epsilon$ is a Normally distributed random variable with mean zero and variance: $\mathit{Var}({\epsilon }_Y)={\varphi }^2{\left({\displaystyle \prod _{t=0}^{T-2}}{\delta }_t\right)}^2+{\displaystyle \sum _{s=1}^{T-2}}{\varphi }^2{\left({\displaystyle \prod _{t=s}^{T-2}}{\delta }_t\right)}^2+{\varphi }^2+1$

As seen in Figure 1, the effect of cumulative dose ( ${\displaystyle \sum _t}{D}_t$) on the outcome (Y) is given by β. Also seen in Figure 1, the strength of the confounding was represented by the product of the relation between the confounder and dose (γ_t) and the relation between the confounder and the response (ϕ). The direction of these relations was set so that the selection bias was negative: Those participants with higher values of C_t received a higher dose of treatment (γ_t > 0) but had worse outcomes (ϕ< 0). In an adaptive intervention, negative selection bias like this occurs when higher doses are provided for participants with more serious problems, as was the case with Fast Track in Example 1. The magnitude of the relation between the confounder and dose (γ_t) was set to .14 or .39, and the magnitude of the relation between the confounder and the outcome (ϕ) was set to −.14 or −.39, so that the product of standardized versions of these two parameters (γ_t * ϕ) was equal to one of two negative values, −0.02 or −0.15 (i.e., .14 * −.14 = −.02 and .39 * −.39 = −.15). These values indicate that the confounding would account for less than one-half of 1% of the variance in the outcome or for about 2% of the variance in the outcome, respectively.³ According to Cohen (1988), even our larger value would only correspond to a conventional small effect, for the conversion of an R² statistic in a multiple regression equation. We purposefully chose levels of confounding that most prevention researchers would consider negligible to illustrate the degree of selection bias that can affect the dose-response relation.

Simulation Design

Three simulations, A, B, and C, each of 1,000 data sets with 400 participants, were generated. The sample size for each simulated data set was selected to be similar to the size of the intervention group from Fast Track.

For simplicity, in Simulations A and B, data were generated so that all participants were homogenous prior to treatment (e.g., there was no effect of the pretreatment covariate X, γ₀ = d₀ = 0). Simulation A was designed so there was no effect of cumulative dose (β = 0) to determine whether a null treatment effect could be overpowered by selection bias, resulting in a negative estimated treatment coefficient. In Simulation B there was a true positive effect of cumulative dose (β > 0). The purpose was to examine whether even a true positive effect could be overpowered by selection bias, resulting in an estimated negative effect of cumulative dose, as we suspected was happening in Fast Track. In both simulations, we analyzed the data by a simple linear regression of Y on the cumulative treatment dose ${\displaystyle \sum _t}{D}_t$. The slope in this regression equation will be our estimator of β. (Recall that C_t has been discarded from the analyzed data so as to mimic Example 1, and that we did not need to include the pretreatment covariate [X] in these analyses because the data were generated so that X had no effect on Y.)

In Simulation C, data were generated so that a pretreatment covariate (X) explains some of the confounding (γ₀ > 0, d₀ > 0), and there was no effect of treatment (β = 0). This simulation was designed to assess the extent to which adjusting for pretreatment covariates in the estimated regression model can reduce selection bias. To analyze the data in Simulation C, we again used linear regression, but this time we regressed Y on both the cumulative treatment dose ( ${\displaystyle \sum _t}{D}_t$) and the pretreatment covariate X. In this model, the regression coefficient of cumulative treatment dose represents the effect of cumulative dose controlling for X.⁴

Findings from the Simulations

Table 1 lists the results for all of the simulations. The left and right columns under each simulation provide results for when the strength of the confounding was very small (γ_t * ϕ = − 0.02) or small (γ_t * ϕ= −0.15).

Table 1.

Simulation Results

Simulation A
Effect of Unrecorded Confounding	Very Smallb	Smallb
Mean Estimated Standardized βa	−0.04	−0.23
Type I Error Rate	0.12	0.995
Standardized Parameters (t=1,…,22)	β=0, γt=0.14, f= −0.14, dt=θt=1, γ0=d0=0	β=0, γt=0.39, f= −0.39, dt=θt=1, γ0=d0=0
Simulation B
Effect of Unrecorded Confounding	Very Smallb	Smallb
Mean Estimated Standardized βa	0.11	−0.08
Power	0.69	0
Standardized Parameters (t=1,…,22)	β=0.15, γt=0.14, f= −0.14, dt=θt=1, γ0=d0=0	β=0.15, γt=0.39, f= −0.39, dt=θt=1, γ0=d0=0
Simulation C
Effect of Unrecorded Confounding	Very Smallb	Smallb
Mean Estimated Standardized βa	−0.008	−0.07
Type I Error Rate	0.051	0.24
Standardized Parameters (t=1,…,22)	β=0, γ0= γt=0.14, f= −0.14, d0=dt=θt=1	β=0, γ0= γt=0.39, f= −0.39, d0=dt=θt=1

^aBecause the simulation size is large, e.g. 1000, the mean of the estimated standardized β is significantly different at the 0.05 level from the true value.

^bA very small (or small) amount of confounding is operationalized as the product f *γ_t = −0.02 (f *γ_t = −0.15).

Simulation A

In Simulation A, when there was no effect of cumulative dose (β= 0) and the strength of the confounding (γ_t * ϕ) was −0.02, the average standardized estimate of β was −0.04. In the absence of a true treatment effect, with no selection bias, and using a 0.05 significance level for a two-sided test of the null hypothesis, we would expect to make a Type I error and estimate a non-zero treatment effect in only 5% of the simulations. However, a test for zero treatment effect was rejected in 12% of the simulated data sets. This means that, even with an almost trivial amount of confounding, the selection bias is not insubstantial: We were more than twice as likely to make a Type I error. The situation was much worse when the level of confounding (γ_t * ϕ) was −0.15. Here, the average standardized estimate of β was −0.23, and the Type I error rate escalated to over 99%. Thus, even a small amount of confounding virtually guarantees that, in the absence of a true treatment effect, a statistically significant estimate of a false negative treatment effect will emerge.

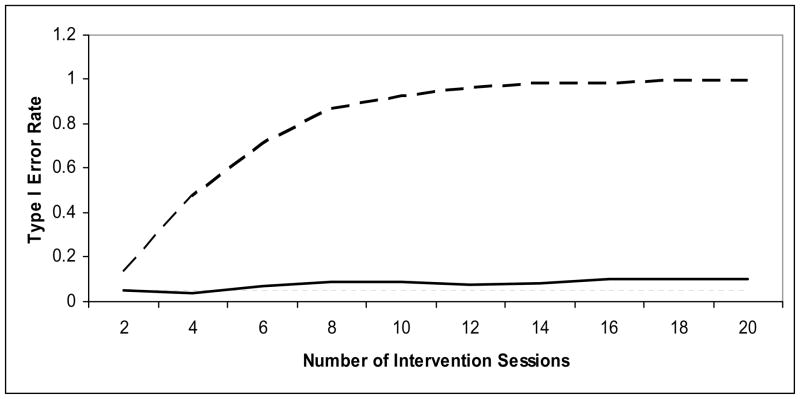
To determine the extent to which the level of selection bias depends on the number of intervention sessions, Simulation A was re-run specifying fewer intervention sessions, ranging from 2 to 20. The relations among the Type I error rate, the number of intervention sessions, and the different levels of confounding are depicted in Figure 2. It appears that the impact of selection bias shows modest growth over time when the strength of the confounding (γ_t * ϕ) is −0.02, as represented by the solid line. The Type I error rate doubles by the time there are 16 intervention sessions. The impact of selection bias was much more striking, however, when the strength of confounding was −0.15, as represented by the dashed line. The Type I error rate more than doubles after only 2 intervention sessions and reaches 90% by 10 intervention sessions.

Figure 2.

Effects of Selection Bias Over Multiple Sessions

Note: The dashed line represents the effects of selection bias when the strength of the confounding is −0.15. The solid line represents the effects of selection bias when the strength of the confounding is −0.02. The thin, dotted line represents the expected 5% Type I Error rate when a 0.05 significance level is used.

Simulation B

Table 1 also lists the results for Simulation B, in which there was a true positive effect of cumulative dose (β > 0). For both the left and right columns of Table 1, the true standardized β was set at 0.15, corresponding to a conventional small effect for an F-test in a multiple regression equation (Cohen, 1988), and representative of the size of the intervention effects in many preventive interventions. The power of the test H₀: β = 0 versus H_A: β > 0 represents the proportion of simulated data sets in which the positive effect of the treatment was detected. With no confounding (γ_t* ϕ= 0), the power of this test is greater than 0.80 (not shown in Table 1). When the strength of the confounding was −0.02, the average standardized estimate of β was 0.11, and the power of the test was only 0.69. When the strength of the confounding was −0.15, the average standardized estimate of β was −0.08, far from what we knew the true value to be, and the power of the test was 0.00. It appears as though a small amount of confounding can completely overwhelm a small true effect of cumulative dose.

To see what would happen if our true effect of cumulative dose were larger, we also ran Simulation B with a true standardized β of 0.36, which would correspond to a medium effect size (Cohen, 1988). These results are not shown in Table 1. With no confounding (γ_t * ϕ = 0), the power of this test is 1.00. When the strength of the confounding was −0.02, the average standardized estimate of β was 0.32 and the power of the test was still 1.00. However, when the strength of the confounding was −0.15, the average standardized estimate of β was 0.13 – less than half of what we know the true dose effect to be – and the power of the test was 0.82. Thus, even when the true dose effect was medium in size, a small amount of confounding appears to result in a severe underestimation of that dose effect.

Simulation C

Simulation C was similar in design to Example 1 in that there was a pretreatment covariate (X) that most likely was correlated with an unrecorded confounder (C_t). However, for Simulation C, there was no true effect of dose (β = 0). The pretreatment covariate (X) influenced the unrecorded confounder through the value of d₀. In our simulation, this relation was perfect (d₀ = 1), indicating that the covariate accounted for all of the confounding prior to the beginning of treatment. The covariate influenced dose at the first session through the value of γ₀, as shown in Figure 1. The overall effect of this covariate was reflected by the product of the standardized values of these two parameters (d₀ * γ₀).

When the strength of the confounding (γ_t * ϕ) was set at −0.02, and there was no effect of the pretreatment covariate (specifically, there was no relation between the pretreatment covariate and the confounder [d₀ = 0]), the average standardized estimate of β was −0.04, and the Type I error rate was 13.6% (not shown in Table 1). However, as presented in the left column of Simulation C in Table 1, when the effect of the pretreatment covariate (d₀ * γ₀) was set to 0.14, the average standardized estimate of β was −0.008 and the Type I error rate was an acceptable 5.1%. In this case of very small confounding, adjusting for the pretreatment covariate appears successful in removing the selection bias.

When the strength of the confounding (γ_t * ϕ) was set to −0.15, and there was no effect of the pretreatment covariate (d₀ = 0), the average standardized estimate of β was −0.23, and the Type I error rate was 99.3% (not shown in Table 1). But, as presented in the right column of Simulation C in Table 1, when the effect of the pretreatment covariate (d₀ * γ₀) was set to 0.39, the average standardized estimate of the treatment effect was −0.07 and the corresponding Type I error rate was 24%. Thus, even when the strength of the confounding was small, the use of the distal pretreatment covariate could not ameliorate the selection bias completely.

In Simulation C, the effect of the pretreatment covariate (X) on the outcome (Y) had to operate indirectly through the confounder and dose. When we allowed a medium or large direct relation between the pretreatment covariate and the outcome – as most investigators would expect when they have a pre- and post-intervention assessment of the same construct – the results of Simulation C were virtually identical.

Discussion of Example 2

These simulations highlight the potential impact of selection bias. Simulation A demonstrates that selection bias could lead a researcher to believe that there was a negative treatment effect when there was, in fact, no treatment effect. The remaining simulations illustrate just how bad the selection bias can be, overshadowing true treatment effects, as in Simulation B, and persisting even with the use of a pretreatment covariate, as in Simulation C.

The impact of selection bias depends heavily upon the strength of the confounding. When a very small amount of selection bias (accounting for less than one-half of 1% of the variance in the outcome) was introduced in the absence of a treatment effect, Type I error rates increased two-fold. When a small amount of selection bias (accounting for 2% of the variance in the outcome) was introduced in the absence of a treatment effect, false positive treatment effects were almost certain, occurring in over 99% of the simulations.

Somewhat surprisingly, a small amount of confounding can cause bias in the estimated dose-response relation, even in the presence of a true positive effect of dose. (This might have been what we observed with Fast Track in Example 1.) With a true small treatment effect, a small amount of confounding can lead to a severe underestimation of the treatment effect and a reduction in power. With a true medium treatment effect, a small amount of confounding still can lead to severe underestimation of the treatment effect.

The length of the intervention program also affects the impact of confounding on conclusions. When the confounding is very small and there is no true treatment effect, the Type I error rate climbs in a linear fashion with each successive intervention session. With a small amount of confounding and no true treatment effect, the Type I error rate doubled after only two intervention sessions and reached 90% by 10 sessions.

In some cases, pretreatment covariates may successfully reduce the effects of selection bias. In our simulation, this occurred when the effect of the confounder was very small and the pretreatment covariate was related to the confounder. When the confounding was stronger, or when there was no relation between the pretreatment covariate and the unrecorded confounder, the use of the pretreatment covariate did not offer this protection.

Thus, the results of Example 2 illustrate how studies seeking to unpack intervention effects using a dose-response analysis are highly susceptible to inaccurate interpretations when the reasons for assigning dose at each time point are unrecorded (i.e., when selection bias exists due to unmeasured time-varying confounders). Even when the strength of the confounding is very small, the impact of selection bias is such that researchers cannot have confidence in estimates of significant relations – or lack thereof – in most dose-response analyses.

Summary and Recommendations

To make optimal progress in the prevention and treatment of mental health or behavior problems, we must determine not only which intervention programs are effective but also how they work (Silverman, 2006). Implementation studies, such as dose-response analyses and examinations of fidelity, are invaluable in this regard. They have been used to assess the theory of change and determine whether exposure to the experimental manipulation of the intervention is related to degree of improvement (Hill et al., 2003; Lyons-Ruth & Melnick, 2004). In addition, they have been recommended when investigators are trying to determine whether null or weak treatment effects reflect implementation difficulties, such that few participants got the intervention as intended (Rohrbach et al., l993). As with other descriptive or correlational studies, however, efforts to peer inside the “black box” of preventive interventions can be susceptible to selection biases (Shadish et al., 2002). Even if the preventive intervention itself is experimental, implementation studies, such as dose-response analyses, typically are not.

This paper highlights the significant risk of confounding when conducting dose-response analyses, particularly when the reasons why dose is adapted – or why assigned dose is not adhered to – are unrecorded. The “real-life” example of the Fast Track peer pairing component, along with the simulation studies, demonstrate that even minimal confounding cannot be ignored, as it increases the chance of falsely detecting a treatment effect when there is none or failing to detect a treatment effect when one exists. Fortunately, these examples suggest a number of methodological features that might guard against confounding and foster the capacity to use implementation studies to learn more about mechanisms of change.

Controlling Selection Bias Through Design

Obviously, the best solution to the threat of confounding is through experimental design. This is the only certain means to address problems associated with unknown and unmeasured confounders. If researchers are specifically interested in using dose-response relations to discern potential thresholds of participation necessary to achieve specific outcomes, an ideal study design would involve the random assignment of dose, and the analysis of “assigned dose” levels, rather than dose levels actually received (Feinstein, 1991).

The relation between dose and response also can be assessed through some natural experiments. For example, in a study of the effects of a special program for adolescent mothers (Seitz et al., 1991), dose was determined by the month of delivery, a factor that, although not random, was unlikely to be related to pertinent confounders.

If researchers are interested in the impact of one part of a multi-component intervention – like peer pairing within the larger Fast Track project – they might consider factorial designs, which can be more powerful and more efficient than typical two-group designs (Shadish et al., 2002; Trochim, 2006; Box et. al., 1978). Similarly, there are dismantling studies in which a specific component is isolated and tested against the effects of a more comprehensive intervention (e.g., Dimidjian et al., 2006; Dobson et al., 2008). The Multiphase Optimization Strategy (Collins et al., 2005; Collins et al., 2007) provides explicit instruction on how to use experimental design to systematically investigate which combinations of intervention components might be most effective in bringing about change.

Controlling Selection Bias Through the Use of Covariates

Most implementation studies are undertaken in a post-hoc fashion to examine mechanisms of change operating within a randomized control trial. It is rarely adequate, however, to simply assess dose or some other aspect of implementation quality and examine relations to outcomes (Pocock & Abdalla, 1998). Instead, researchers must rely on the careful selection, collection, and use of relevant covariates to control for selection biases.

Careful selection of relevant covariates at the point of program design might allow researchers to identify and determine appropriate measures of potentially important time-varying confounding variables so they may be utilized during analysis. Researchers should pay special attention to those variables that have been related to motivation, participation in intervention, or adherence to intervention protocols in previous studies, as well as variables that were predictive of response to treatment. In the case of adaptive interventions, researchers also should consider those variables that would be expected to influence staff members’ clinical judgment regarding need for services (Collins et al., 2004), such as a global assessment of functioning (Hall, 1995) or some indicator of a primary outcome, like social competence and aggression in Fast Track. To assist in the identification of important potential confounding variables, it would be beneficial for prevention researchers to report the strongest predictors of dose received, project guidelines regarding how and when dose was adjusted, and characteristics of those participants most likely to respond to services.

Just as with any construct, it is critical to assess covariates with psychometrically-sound measures. Ideally, these would rely on objective informants or methods that are independent of participants’ or staff members’ decisions to adjust dose.

Careful collection of relevant covariates requires assessment each time a decision to change dose is made. When participants in the intervention make those decisions on their own – by choosing to attend or miss an intervention session – it will be difficult to conduct perfectly-timed assessments. In that case, it might make sense to conduct brief, frequent assessments throughout the intervention. In adaptive interventions, it is best to time assessments so they coincide with staff members’ decisions to alter dose. In Fast Track, it was not useful to have covariates at the end of kindergarten or even first grade because decisions to adjust the dose of peer pairing were made throughout second grade. It would have been preferable if staff members had completed brief ratings of social competence and aggression on every child in their caseload at the end of each week in second grade; staff members also could have checked in with teachers more systematically and recorded their impressions. Regardless of who makes the decision to change dose, it is critical to conduct assessments on all participants in the intervention, regardless of whether a particular participant’s dose was changed or not.

When investigators collect measures prior to the start and throughout the duration of the intervention, they will be in a much better position to evaluate and control for the impact of selection bias (Wilkinson & the Task Force on Statistical Inference, 1999). There exist a number of well-documented analytic techniques that can reduce the effects of selection bias due to pretreatment confounders, such as inclusion of pretreatment covariates in the regression model, use of propensity scores techniques (e.g., Rosenbaum & Rubin, 1983; Rubin, 1997), or use of the Heckman estimator (Heckman, 1976). The goal of any of these analytic techniques is the same: To compare subjects with similar characteristics across the range of covariates who differ only with respect to dose received. It has been shown that, if treatment assignment is independent of the response after accounting for the covariates (i.e., if treatment assignment is strongly ignorable, in the language of causal inference), then unbiased estimates of the treatment effect can be found (Rosenbaum & Rubin, 1983). Like any analytic technique, however, each of these statistical models depends on certain assumptions and will only be successful in controlling selection bias to the extent that the assumptions are satisfied.

When dose is adapted and readapted at multiple time points, either informally as indicated by participants’ variable attendance or by formal design according to participants’ assessed need, pretreatment covariates are unlikely to be sufficient predictors of dose. Additional mid-intervention assessments of outcomes and individual characteristics that function as time-varying confounders are required to adequately predict which participants will receive more intervention services.

In the epidemiology literature, the propensity score method has been adapted for use with time-varying confounders and is known as the marginal structural model (e.g., Robins et al., 2000; Hernán et al., 2000; Bodnar et al., 2004). In the first step of such analyses a regression equation, referred to as the treatment model, is estimated to predict the receipt of intervention at time point t. The independent variables in this logistic regression equation would include indicators of the receipt of intervention for every session prior to time point t and measures of time-varying confounders, such as child behavior problems, assessed at regular intervals throughout the intervention. The results of this logistic regression equation yield a predicted probability of the receipt of intervention for each participant at time point t conditioned on the confounders and treatment history up to that time. For example, participants who had attended all prior sessions of the intervention would have a high predicted probability of the receipt of that final session, whether they actually attended that final session or not. (A modeling note: When dose at each time point is recorded as a binary [1/0] variable according to whether a participant did or did not receive treatment at that time, care must be taken to model the receipt of intervention [1] rather than its absence [0]. For example, in SAS proc logistic, it is necessary to specify the ‘descending’ option in the model statement.)

The predicted probabilities from the treatment model are then used to calculate sample weights (for details on how to construct these weights, see Barber et al., 2004; Cole & Hernán, 2008; Mortimer et al., 2005). The weights are based on the inverse of the predicted probabilities so that more weight is given to participants who are less represented in the observed data than they would have been if assignment to intervention had been randomized (Mortimer et al., 2005). This serves to decouple the relation between the history of attendance and the history of time-varying confounders from the receipt of intervention at time point t. In other words, the weights can mimic what would have happened if participants with similar histories of attendance and similar histories of time-varying confounders had been randomly assigned to receive intervention at time point t, balancing participants with different histories of attendance and different histories of the time-varying confounders across different doses of intervention.

In the final step of a marginal structural model, the weighted data are used in a typical regression equation to assess the dose-response relation. The most important assumption guaranteeing that the coefficient for dose provides an unbiased estimate of the treatment effect is that there is no unmeasured confounding; this is sometimes referred to as the sequential randomization assumption and implies that all important time-varying confounders have been accounted for in the treatment model (Cole & Hernán, 2008; Mortimer et al., 2005). Research has shown, however, that with a marginal structural model selection bias is reduced, though not eliminated, even if every important time-varying confounder is not included (Barber et al., 2004; Bray et al., 2006).

In applying a marginal structural model, it is critical to remember that bias is only reduced to the extent that the treatment model is correctly specified. It is usually unwise to simply “dump” all measured time-varying confounders into the treatment model; careful fitting is necessary to determine the best form and complexity (Cole & Hernán, 2008; Mortimer et al., 2005; for examples of how to determine the most appropriate treatment model and calculate probability weights, see Barber et al., 2004; Cole & Hernán, 2008; Mortimer et al., 2005). It also is critical to remember that all time-varying confounders must be assessed for all children and families assigned to the intervention at every time point the decision to change dose for any individual is considered. Otherwise, it will be impossible to compare participants with similar characteristics who differ with respect to dose received.

Final Thoughts

It is important to remember that the validity of a dose-response analysis hinges on variation in dose that is unrelated to participants’ need or to reasons why they might respond to a particular intervention. Otherwise, dose-response analyses are likely affected by selection bias, as illustrated in this paper.

Randomization of dose is the optimal strategy for assessing dose effects, as it avoids selection bias, and can be extended to studies in which treatment is time-varying (Murphy et al., 2006). Without randomization of dose, researchers can never be certain of their ability to completely remove confounding; they can only use sensitivity analysis and bounding methods to assess the likely magnitude of any residual bias (Robins, 1999). As with any analysis of observational data, causal claims of treatment effectiveness must be tempered with appropriate caution about the possibility of residual confounding.

When randomization is not possible, or when adherence to randomized dose is low, prevention researchers can control for systematic differences between those participants receiving different doses through the careful selection, measurement, collection, and use of both pretreatment and time-varying confounding variables. In these post-hoc analyses, it is only by removing systematic differences through the proper use of relevant covariates – for example, by using a marginal structural model – that investigators can hope to gain a less biased understanding of what is happening inside the “black box” of preventive interventions.