A Bayesian Semi-parametric Survival Model with Longitudinal Markers

Abstract

We consider inference for data from a clinical trial of treatments for metastatic prostate cancer. Patients joined the trial with diverse prior treatment histories. The resulting heterogenuous patient population gives rise to challenging statistical inference problems when trying to predict time to progression on different treatment arms. Inference is further complicated by the need to include a longitudinal marker as a covariate. To address these challenges, we develop a semi-parametric model for joint inference of longitudinal data and an event time. The proposed approach includes the possibility of cure for some patients. The event time distribution is based on a non-parametric Pólya tree prior. For the longitudinal data we assume a mixed effects model. Incorporating a regression on covariates in a non-parametric event time model in general, and for a Póolya tree model in particular, is a challenging problem. We exploit the fact that the covariate itself is a random variable. We achieve an implementation of the desired regression by factoring the joint model for the event time and the longitudinal outcome into a marginal model for the event time and a regression of the longitudinal outcomes on the event time, i.e., we implicitly model the desired regression by modeling the reverse conditional distribution.

1 Introduction

We discuss inference for data from a phase III clinical trial on treatments of metastatic prostate cancer. The challenges include patient heterogeneity due to prior treatment history and the need to include a regression on prostate specific antigen (PSA) as a longitudinal marker. We constuct a semi-parametric Bayesian model to address these challenges. It implements joint inference on event time and longitudinal observations, with the possibility that some patients are cured.

Let T be the event time and Y be the longitudinal covariate. Most existing approaches are based on factoring the joint model as P(T, Y) = P(Y)P(T | Y). The first factor is the longitudinal submodel P(Y), typically assumed to be a mixed model. The second factor is the survival submodel P(T | Y). In the following discussion, we use the terms event time, survival time, time to progression and failure time exchangably. There is an extensive literature on the joint modeling of longtitudinal and event time data without a cured fraction (De Gruttola and Tu, 1994; Tsiatis et al., 1995; Lavalley and De Gruttola, 1996; Wulfsohn and Tsiatis, 1997; Dafni and Tsiatis, 1998; Henderson et al., 2000; Xu and Zeger, 2001; Lin et al., 2002; Ibrahim et al., 2004). A review can be found in Tsiatis and Davidian (2004). Less work has been published on the joint modeling of longitudinal and event time data with cure. Law et al. (2002) proposed a model with the longitudinal process described by an exponential-decay-exponential-growth model and a mixture model to accomodate cure. The imputed values of the longitudinal measurements are covariates in a proportional hazard model. Brown and Ibrahim (2003) and Chen et al. (2004) assume event times to arise from the development of an unobserved number of metastatis-competent tumer (MCT) cells, modeled by a Poisson distribution. Subjects with zero MCT cells constitute the cure group. Yu et al. (2004) provide a recent review of joint longitudinal-survival-cure models.

Specific to modeling PSA, Pauler and Finkelstein (2002) propose a joint analysis using a change-point regression model for PSA trajectory, and a Cox model for cancer recurrence time with time-dependent covariates including functions of longitudinal parameters and imputed PSA mean function. Lin et al. (2002) considered a latent class model to uncover subpopulation structure for both PSA trajectories and a survival outcome. Given latent class membership, the longitudinal marker and outcome are assumed independent. The model assumes class-specific baseline hazard functions and accommodates possibly time-dependent covariates. Yu et al. (2008) investigated individual prediction in prostate cancer studies using a joint longitudinal-survival-cure model. A logistic model is specified for the probability of an individual being in the susceptible group and separate nonlinar mixed effect models are assumed for the cure and susceptible groups. The event-time process is modeled by a proportional hazard model with time-dependent covariates including the current slope and current value of the PSA trajectory.

In the joint analysis of longitudinal and event time data, most researchers assume parametric or semi-parametric models for P(T | Y). However, it is difficult to implement non-parametric models for P(T | Y) because most non-parametric models do not allow straightforward incorporation of a regression on covariates. We propose to use the alternative factorization, P(T, Y) = P(T)P(Y | T). We proceed under the Bayesian paradigm. Choosing a non-parametric model for P(T) is the traditional problem of non-parametric inference for an event time. The model P(Y | T) is part of a convenient factorization of the joint model. It should not be interpreted as a predicting model of Y by future outcome T. We propose a mixed effect model for P(Y | T), with T conveniently included as a univariate covariate. The opposite, including a high-dimensional covariate Y in a non-parametric model for T, would pose challenging technical problems (This is distinct from the related problem of non-parametrically modeling a mean function E(T | Y), e.g., kernel smoothers). Both factorizations lead to a joint model, P(T, Y), describing the dependence between T and Y. It is this joint model that ultimately allows improved prediction of the event time given repeated measurements of the marker. Under the factorization P(T) P(Y | T) the desired regression P(T | Y) is not explicitly parametrized, but implied by Bayes theorem. In a parametric model and using maximum likelihood estimation the same factorization is used in Pawitan and Self (1993) to model longitudinal markers for AIDS patients. They assume Weibull models for the infection time and disease occurrence and a generalized linear model for the longitudinal measurements of T4 counts and T4/T8 ratio, with the intercept and slope being functions of the event times.

We use a Polya tree (PT) prior to model the event time distribution. The reasons for this modeling choice are the possibility to model multimodal distributions reflecting the diversity of the patient population, the computational simplicity, and the easy a priori centering at a parametric model. A PT prior can be constructed to give probability one to the set of continuous or absolutely continuous probability measures (Lavine, 1992).

Muliere and Walker (1997) implemented PT models in a survival analysis. Walker and Mallick (1997; 1999) applied PT priors in hierarchical generalized linear models, frailty models, and accelerated failure time models. Hanson and Johnson (2002) developed a general approach to modeling residual distributions with a mixture of PT. Neath (2003) used PT to model censored data. Paddock et al. (2003) developed randomized PT models, which uses random partitions to smooth out the effect of partitions on posterior inference. Hanson et al. (2007) used mixtures of PTs to construct a joint model for time-dependent covariates and survival time. They introduced flexible PT priors for the baseline distributions in the Cox model, the proportional odds model, and an accelerated failure time model accommodating time-dependent covariates. Their approach uses the factorization P(T, Y) = P(Y)P(T | Y). See Hanson (2006) for a review of recent development in finite PT models.

2 A Clinical Study

Androgen ablation (AA) is the preferred treatment for metastatic prostate cancer. AA therapy alters the natural history of the disease by disrupting the growth promoting effects mediated by androgen receptor signaling, which is usually accomplished by medical suppression of testicular endocrine function. Unfortunately, most patients with clinically detectable metastatic disease when the AA therapy started will eventually progress to androgen independent prostate cancer (AIPC). AIPC is a relentlessly progressive disease state, and is the cause of death for the vast majority of men in whom it develops. By this mechanism, prostate cancer leads to an annual death toll of more than 27,000 men in the United States.

To date, no treatment has been found to be curative for AIPC, and it is only fairly recently that some therapies are shown to alter the natural history of the disease. A chemotherapy demonstrated a survival advantage over historical results in a phase II trial conducted at M.D. Anderson Cancer Center (Ellerhorst et al., 1997). This therapy, dubbed KA/VE, treats patients with ketoconazole and doxorubicin alternating with vinblastine and estramustine.

In this paper we analyze data from a phase III trial at M.D. Anderson Cancer Center that comapred conventional AA therapy versus AA therapy plus three 8-week cycles of KA/VE. The aim of this trial was to investigate whether better clinical benefit can be achieved by applying the chemotherapy “early”, i.e., before the metastatic prostate cancer develops into the far-advanced AIPC. The two treatment arms are denoted by AA and CH, respectively. The patient population includes metastatic prostate cancer patients whose high risk of developing AIPC justifies long-term, sustained, androgen ablation. The primary endpoint is the time to progression (TTP) to AIPC, which is diagnosed by the following criteria: 1) Symptoms attributed by the treating physician to reflect progressive cancer; 2) Radiographic progression; 3) Rising PSA, with value greater than 1 and doubling time < 9 months; 4) Treatment with chemotherapy. The first 3 also require demonstration of testosterone < 50 and withdrawal of antiandrogens. More details about the clinical trial can be found in Millikan et al. (2008).

Besides TTP, we also observed the longitudinal measurements of PSA level from each patient. Carter et al. (2006) demonstrated that PSA velocity is associated with prostate cancer death even 10–15 years before diagnosis. To further improve the understanding of this important marker we propose to build a joint model of TTP and PSA.

To statisticians, a challenge posed by this clinical trial is the considerable heterogeneity among patients. Before coming to M.D. Anderson Cancer Center these patients had been treated by different physicians with different therapies at different institutions. These differences might have a long-term impact on the development of prostate cancer. Second, there is no completely satisfactory way to define “early” in the natural history of metastatic prostate cancer. As a practical solution, the clock start of the trial is defined as the initiation of the AA therapy. Thus at the beginning of the trial, the true stage of cancer might not be exactly the same for each patient.

3 Notation and Model

We use v = 1, 2 to denote the two treatment arms (1 for CH and 2 for AA). Let n_v be the number of subjects in each arm. For the i-th subject on arm v, we use y_vi = {y_vij, j = 1, ⋯ , m_vi} to denote the longitudinal PSA measurements, where m_vi is the number of repeat measurements. We define T_vi to be the TTP, which is the time between the start of the CH/AA treatment and the progression to AIPC. We use t_vi to denote the censoring time for censored observations, and the actual TTP for non-censored observations. We introduce a failure indicator d_vi with d_vi = 1 if T_vi = t_vi and d_vi = 0 if T_vi > t_vi. The number of observed and unobserved TTP in each arm are denoted by n_v1 and n_v0, respectively. In summary, the observed data from each subject is (y_vi, t_vi, d_vi). We use [X] and [X | Y] to generically indicate the probability model for a random variable X and the conditional distribution of X given Y.

3.1 The Likelihood

We define the sampling model for the observed data (y_vi, t_vi, d_vi) from each patient. If d_vi = 1, the progression time T_vi is observed. Therefore all subjects with d_vi = 1 belong to the susceptible group. On the other hand, we only observe T_vi > t_vi when d_vi = 0. In this case the subject could be either in the susceptible group or in the cure group. We define a variable ω_vi = 0/1 indicating membership in the susceptible/cure group. For d_vi = 1, we have ω_vi ≡ 0 by definition, and T_vi = t_vi. The following discussion simplifies greatly by introducing latent variables T_vi and ω_vi for subjects with censored TTP, d_vi = 0.

If ω_vi = 0, the subject is at risk of developing AIPC. We assume T_vi to be a random sample from distribution G_v, i.e., [T_vi | ω_vi = 0,G_v] = g_v(T_vi). Here g_v(·) is the density function of G_v. If ω_vi = 1, the subject is a long-term survivor. We assume T_vi = t_c, where t_c is an extremely long TTP that could not be observed in the clinical trial. Thus the model for TTP is [T_vi | ω_vi,G_v] = {δ(t_c)}^ω_vi{g_v(T_vi)}^1−ω_vi, where δ(t_c) denotes a point mass at t_c. We assume ${\omega }_{\mathit{\text{vi}}}|p_v\stackrel{\mathit{\text{iid}}}{\sim }$ Bernoulli(p_v) with p_v being the probability of cure under treatment v. In summary, we assume that T_vi arises from the mixture of a point mass and a continuous distribution. The prior distribution of TTP is G_v for all susceptible subjects under treatment v. The posterior distribution of TTP given PSA, however, may be very different across subjects.

Given T_vi, the longitudinal measurements y_vi are modeled by a mixed effects model [y_vi | T_vi, Ψ], indexed by parameters Ψ. We include T_vi in [y_vi | T_vi, Ψ] via a regression on u(T_vi), as a subject-specific covariate. Here u(·) is a certain function of T_vi. With different specifications of u(T_vi) and [y_vi | T_vi, Ψ], we can model various mechanisms between T_vi and y_vi. In summary, the likelihood factors corresponding to (y_vi, t_vi, d_vi) are

$$\begin{array}{ccc}{L}_{\mathit{\text{vi}}1}\hfill & =[{\mathit{y}}_{\mathit{\text{vi}}}|T_{\mathit{\text{vi}}},\mathbf{\Psi }][T_{\mathit{\text{vi}}}=t_{\mathit{\text{vi}}}|{\omega }_{\mathit{\text{vi}}}=0,G_v][{\omega }_{\mathit{\text{vi}}}=0|p_v],\hfill & \text{for}{d}_{\mathit{\text{vi}}}=1,\hfill \\ L_{\mathit{\text{vi}}0}\hfill & =[{\mathit{y}}_{\mathit{\text{vi}}}|T_{\mathit{\text{vi}}},\mathbf{\Psi }]I(T_{\mathit{\text{vi}}}>t_{\mathit{\text{vi}}})[T_{\mathit{\text{vi}}}|{\omega }_{\mathit{\text{vi}}},G_v][{\omega }_{\mathit{\text{vi}}}|p_v],\hfill & \text{for}{d}_{\mathit{\text{vi}}}=0.\hfill \end{array}$$ (1)

Note that L_vi0 is an augmented likelihood with latent variable T_vi and ω_vi.

For L_vi0, the two values taken by ω_vi lead to two models of different dimensions. If ω_vi = 0, T_vi is a random parameter with prior G_v. In contrast, T_vi is fixed at T_vi = t_c if ω_vi = 1. Such a change in dimension complicates posterior simulation (Green, 1995). We use the pseudo prior approach by Carlin and Chib (1995) to avoid this complication. In words, we augment the smaller probability model under ω_vi = 1 by defining a prior probability model for a hypothetical T_vi (but keep t_c in the regression for y_vi). The new variable T_vi has no meaningful interpretation under ω_vi = 1. It is only introduced to match the model dimensions. The pseudo prior mechanism serves the same purpose as reversible jump (Green, 1995), but avoids the changing dimension of the parameter vector (Dellaportas et al., 2002). See Web Appendix A for implementation details.

3.2 The Prior Probability Model

We assume prior independence, $[\mathbf{\Psi },p_v,G_v,v=1,2]=[\mathbf{\Psi }]·{\displaystyle {\prod }_{v=1}^2[p_v]·[G_v]}$. The prior specification [Ψ] and posterior inference for mixed models of repeated measurements have been discussed extensively. See, for example, Ibrahim et al. (2004). For priors [p_v], v = 1, 2, we assume p_v ~ Beta(a_p, b_p) with a_p and b_p being fixed hyperparameters.

For the unknown survival distribution G_v, we consider two choices. The first choice is a parametric model assuming G_v to be indexed by a finite-dimensional parameter vector. In this case the prior specification involves assigning priors to these parameters. Recall that G_v is the therapy-specific prior TTP distribution for susceptible subjects, who might be different in many important aspects. A parametric model may not suffice to characterize the complexity of G_v. This difficulty motivates the second choice, a non-parametric method. A Bayesian non-parametric prior defines G_v as a random probability measure, i.e., a prior for the unknown distribution G_v, denoted by PT(Π_v,𝒜_v).

A PT prior is indexed by two hyper-parameters: a nested sequence of partitions Π = {B₀, B₁, B₀₀, B₀₁, …, B_ε0,B_ε1, …} of the sample space S, with S = B₀ ∪ B₁ and B_ε = B_ε0 ∪ B_ε1; and parameters 𝒜 = {α₀, α₁, α₀₀, α₀₁, …, α_ε0, α_ε1, …}. Here ε = ε₁ ⋯ ε_m denotes a binary sequence of length m. We can center the PT prior around a given distribution G̃, by setting α_ε0 = α_ε1 and defining B_ε at level m to coincide with quantiles G̃⁻¹(k/2^m), k = 0, 1, ⋯ , 2^m. The parameter 𝒜 has a similar role as the precision parameter in a Dirichlet process prior. Berger and Guglielmi (2001) considered a family of the form α_{ε1, ⋯, εm} = c·ρ(m), where ρ(m) = m², m³, 2^m, 4^m or 8^m, and c > 0 is a constant. In general, any ρ(m) such that ${\displaystyle {\sum }_{m=1}^{\mathrm{\infty }}{\rho (m)}^{-1}<\mathrm{\infty }}$ guarantees the PT to be absolutely continuous. See Hanson (2006) for a recent review. More details are presented in Web Appendix B.

3.3 Posterior Inference and Model Validation

To facilitate discussion, we define the following notation. The set of observed and unobserved TTPs under treatment v are denoted by ${\mathit{t}}_v^1=\{t_{\mathit{\text{vi}}}:d_{\mathit{\text{vi}}}=1\}\text{and}{\mathit{T}}_v^0=\{T_{\mathit{\text{vi}}}:d_{\mathit{\text{vi}}}=0\}$, respectively. We also define ${\mathit{\omega }}_v^0=\{{\omega }_{\mathit{\text{vi}}}:d_{\mathit{\text{vi}}}=0\}$ to be the set of unknown indicators of cure. Without loss of generality, we assume that d_vi = 0 for i = 1, ⋯ , n_v0, and d_vi = 1 for i = n_v0+1, ⋯ , n_v. Let Λ denote the collection of model parameters, including $\mathbf{\Psi },G_v,{\mathit{T}}_v^0,{\mathit{\omega }}_v^0\text{and}{p}_v$. We have the full posterior distribution:

$$[\mathbf{\Lambda }|\mathit{Y},\mathit{t},\mathit{d}]\mathrm{\propto }{\displaystyle \prod _{v=1}^2\left\{\right({\displaystyle \prod _{i=1}^{n_{v0}}{L}_{\mathit{\text{vi}}0}}{\displaystyle \prod _{i=n_{v0}+1}^{n_v}{L}_{\mathit{\text{vi}}1}})[p_v][G_v]\}[\mathbf{\Psi }],}$$ (2)

where (Y, t, d) = {(y_vi, t_vi, d_vi) : v = 1, 2; i = 1, ⋯, n_v}. We implement posterior inference by Markov Chain Monte Carlo (MCMC) posterior simulation.

Before proceeding with posterior MCMC, we analytically marginalize (2) with respect to G_v. Recall that each subject with ω_vi = 0 is assumed to have a TTP arising from G_v. Define ${\mathit{T}}_v^s={\mathit{t}}_v^1\cup \{T_{\mathit{\text{vi}}};d_{\mathit{\text{vi}}}={\omega }_{\mathit{\text{vi}}}=0\}$ to be the set of observed and unobserved TTP in the susceptible group. The size of ${\mathit{T}}_v^s\text{is}{n}_{\mathit{\text{vs}}}=n_v-{\displaystyle {\sum }_{i=1}^{n_v}{\omega }_{\mathit{\text{vi}}}}$. Finally, let $T_{\mathit{\text{vj}}}^s$ denote the j-th element in ${\mathit{T}}_v^s$, with the index j assigned arbitrarily. The joint probability model of ${\mathit{T}}_v^s$ and G_v is $[{\mathit{T}}_v^s,G_v]={\displaystyle {\prod }_{j=1}^{n_{\mathit{\text{vs}}}}[T_{\mathit{\text{vj}}}^s|G_v]·[G_v]}$. We marginalize G_v by replacing $[{\mathit{T}}_v^s,G_v]\text{with}[{\mathit{T}}_v^s]={\displaystyle {\prod }_{j=2}^{n_{\mathit{\text{vs}}}}[T_{\mathit{\text{vj}}}^s|T_{v1}^s,\dots ,T_{v,j-1}^s]·{\tilde{G}}_v(T_{v1}^s)}$. Here $[T_{\mathit{\text{vj}}}^s|T_{v1}^s,\cdots ,T_{v,j-1}^s]$ is the (posterior) predictive distribution under a PT model, defined in Web Appendix B. The marginalization is important. Instead of working with the infinite dimensional random distributions G_v, it allows us to manipulate only the (finite dimensional) set of event times ${\mathit{T}}_v^s$. Details of the MCMC transition probabilities are presented in Web Appendix C.

We compare the proposed model with four natural alternatives. Details of the competing models and results are described later, in Section 5. We use the conditional predictive ordinates (CPO) proposed by Gelfand et al. (1992) to compare different models. The CPO for subject i in group v (henceforth subject (v, i)) is defined as the posterior predictive distribution evaluated for the observation from subject (v, i), conditional on all the data minus the response from subject (v, i). Formally, letting (Y_(−vi), t_(−vi), d_(−vi)) = (Y, t, d) \ (y_vi, t_vi, d_vi), we define CPO_vi = [y_vi, t_vi | Y_(−vi), t_(−vi)], where d_vi is assumed given. Then we compute a summary statistic called the logarithm of the pseudomarginal likelihood (LPML), $\mathit{\text{LPML}}={\displaystyle {\sum }_{v=1}^2{\displaystyle {\sum }_{i=1}^{n_v}\text{log}({\text{CPO}}_{\mathit{\text{vi}}})}}$. A small value of LPML suggests disagreement between the observations and the model. Gelfand et al. (1992) show how the CPO for each subject, in our case v = 1, 2 and i = 1, …, n_v, can be evaluated through an importance sampling scheme. We describe the computation of CPO in Web Appendix D.

4 A Phase III Study of Prostate Cancer

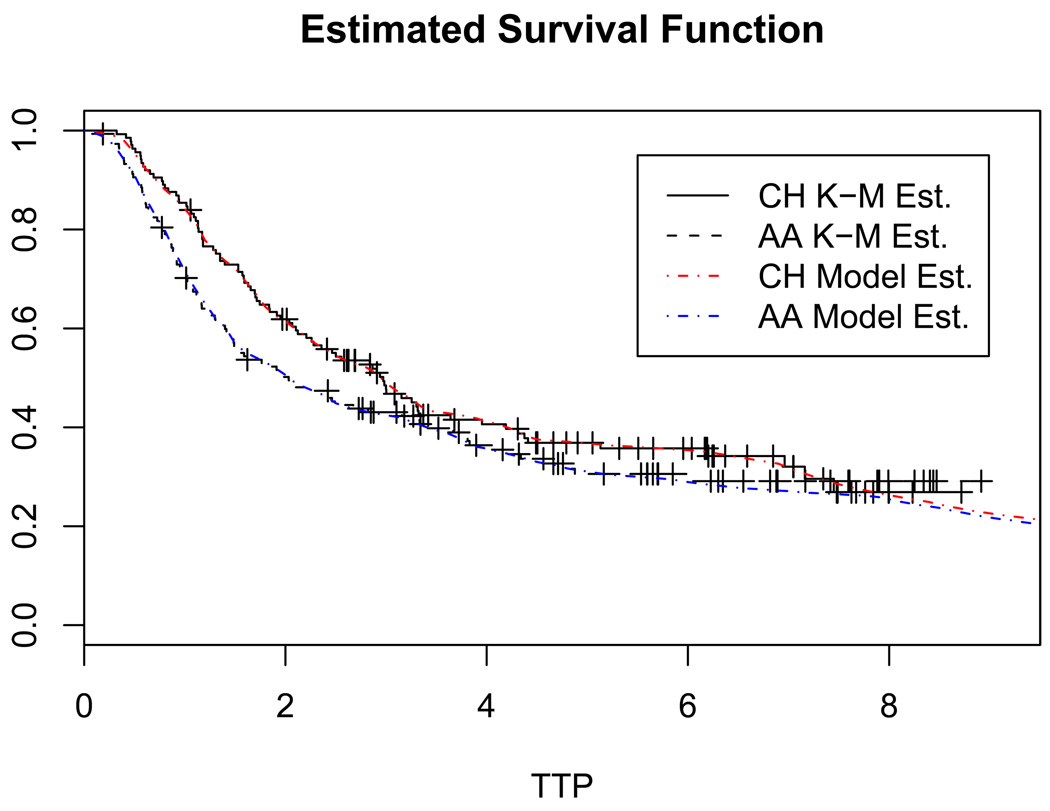
We return to the clinical trial from Section 2. The phase III trial for advanced prostate cancer had a total enrollment of 286 patients, with n₁ = 137 in the CH arm and n₂ = 149 in the AA arm. Starting from the diagnosis of prostate cancer, the PSA level of each patient was monitored for up to 10 years. On average, about 30 PSA measurements were collected from each patient. We use y_vij (j = 1, ⋯ ,m_vi) to denote the log-transformed longitudinal PSA measurement, y_vij = log(1 + PSA). The age at which y_vij was recorded is denoted by s_vij. As reference points, the age at diagnosis of prostate cancer is denoted by u_vi0, and the age at the initiation of the CH/AA treatment is denoted by u_vi1. The number of observed TTP events in the two treatment arms are n₁₁ = 87 and n₂₁ = 98, respectively. Figure 1 shows the Kaplan-Meier estimates of the survival function under the two treatments. There are plateaus at the end of the curves. This observation suggests that a significant portion of subjects have an excessively long event time and a cure model is appropriate.

Figure 1.

The horizontal axis indicates years after treatment. The censoring times are marked by +. “K-M Est.” denotes Kaplan-Meier estimates. “Model Est.” denotes estimates based on model M₁, where TTP are assumed to arise from the mixture of a point mass at t_c and an unknown distribution G_v. For T < 6 the Kaplan-Meier estimates and the model based estimates of the survival curves are virtually indistinguishable.

PSA level normally increases as the prostate enlarges with age. When prostate cancer develops, however, it increases much faster. The typical effect of a treatment on PSA level is a sharp drop in PSA level immediately after the treatment. Then gradually, the body adjusts to offset the treatment effect, and the PSA level bounces back. The speed of rebound depends on the progress of cancer. Web Figure 1 plots the longitudinal profiles of four randomly selected patients. Note the variability among the profiles. Exploratory analysis indicates a negative correlation between the PSA slope and TTP. Based on these considerations, the longitudinal submodel [y_vi | T_vi, Ψ] is specified as y_vij = f_vi(s_vij) + e_vij with

$$f_{\mathit{\text{vij}}}(s_{\mathit{\text{vij}}})={\theta }_{0\mathit{\text{vi}}}+{\theta }_{1\mathit{\text{vi}}}{s}_{\mathit{\text{vij}}}+{\gamma }_{2\mathit{\text{vi}}}(e^{-{\phi }_{0\mathit{\text{vi}}}{(s_{\mathit{\text{vij}}}-u_{\mathit{\text{vi}}0})}^{+}}-1)+{\eta }_v(e^{-{\phi }_{1v}{(s_{\mathit{\text{vij}}}-u_{\mathit{\text{vi}}1})}^{+}}-1)+{\gamma }_{1v}{(s_{\mathit{\text{vij}}}-u_{\mathit{\text{vi}}1})}^{+}+({\theta }_{1\mathit{\text{vi}}}+{\gamma }_{1v})(e^{-{\xi }_v{T}_{\mathit{\text{vi}}}}-1){(s_{\mathit{\text{vij}}}-u_{\mathit{\text{vi}}1})}^{+},$$ (3)

where (x)⁺ = x if x > 0, and (x)⁺ = 0 otherwise. We assume independent normal residuals, $e_{\mathit{\text{vij}}}\stackrel{\mathit{\text{iid}}}{\sim }N(0,{\sigma }^2)$. The first two terms define a line with intercept θ_0vi and slope θ_1vi, describing the baseline linear trend of PSA over age. The coefficients are subject-specific. Parameters η_v and φ_1v model the size and the slope of the drop after the intervention with CH or AA. As age s_vij moves beyond u_vi1, η_v{exp[−φ_1v(s_vij − u_vi1)⁺] − 1} drops from 0 and eventually levels off at −η_v, i.e., η_v controls the depth and φ_1v controls the slope of the drop. A smaller value of φ_1v indicates that the treatment effect persists longer. Similarly, parameters γ_2vi and φ_0vi model the size and the slope of the drop due to the initial therapy right after the diagnosis of prostate cancer. We assume γ_2vi and φ_0vi to vary individually since information about the initial therapy is unavailable. We use γ_1v to model the average change of slope in the baseline trend, induced by treatment v. Finally, model (3) reflects our belief that subjects with flatter longitudinal profiles take longer to progress. To see this, first we observe that in (3) the slope after treatment, i.e., the coefficient of (s_vij − u_vi1)⁺, is θ_1vi + γ_1v + (θ_1vi + γ_1v)[exp(−ξ_vT_vi) − 1]. Here ξ_v is constrained to be positive. With T_vi changing between 0 and +∞, the slope changes from θ_1vi + γ_1v to 0. We substitute a realistic upper bound for the limiting T_vi → ∞ using t_c = 18 years. Matching with the earlier notation [y_vi | T_vi, Ψ] used in (2), we have Ψ = (θ₀, θ₁, γ₁, γ₂, η, φ₀, φ₁, ξ, σ²). Here θ₀ = {θ_0vi, v = 1, 2; i = 1, ⋯, n_v}, η = {η_v, v = 1, 2}, and θ₁, γ₂, φ₀, φ₁, ξ are defined in the same fashion. In (3) we use u(T_vi) = exp(−ξ_vT_vi) − 1. In summary, besides TTP, the covariates considered include age, treatment, and time under treatment.

As for the PT priors, G_v ~ PT(Π_v,𝒜_v), we use Π₁ = Π₂ = Π and 𝒜₁ = 𝒜₂ =𝒜. Thus E(G_v) = G̃ for v = 1, 2. That is, the two PTs are centered around the same distribution a priori. The matching hyperprior parameters for the two PT priors ensures that posterior inference about the differences between two treatment groups reflects the evidence from data. For the centering measure G̃, we assume a Weibull distribution, G̃(t) = Weibull(t; τ, β). Here β and τ are, respectively, the shape and scale parameter. The partition Π is specified by the dyadic quantile sets of G̃. The elements of 𝒜 at the mth level are specified to be c·m², with c being a constant.

The mixture probability p_v is assumed to be Unif(0, 1), i.e., a_p = b_p = 1. The prior of Ψ and other hyperprior parameters are specified as follows. We assume (θ_0vi, θ_1vi, γ_2vi)′ | µ, Σ ~ N₃(µ,Σ), γ_1v ~ N(0, 100), η_v ~ N(0, 100), ξ_v ~ Ga(a, b), φ_0vi ~ Ga(a, b), φ_1v ~ Ga(a, b), and 1/σ² ~ Ga(a, b), all with a = b = 0.01. Here Ga(a, b) denotes a Gamma prior with mean a/b. We further assume µ ~ N₃(0, 100I) and Σ ~ IW(3, 0.01I₃). Here IW(ν, A) indicates an inverse Wishart prior with ν degree of freedom and matrix parameter A. The specification of hyper-parameter (τ, β) for G̃ is based on estimation of the Weibull model M₂, described in Section 5. We set τ = 4.52 and β = 1.23, which are the posterior means of Weibull parameters from the CH group.

5 Results

Model Selection

To validate the proposed model we consider comparisons with four alternative models. Let M₁ denote the proposed model (2). The second model, M₂, is also based on the factorization P(T, Y) = P(T)P(Y | T), with P(Y | T) as in (3), but P(T) being fully parametric. We assume a Weibull regression model for (T_vi | ω_vi = 0) with an indicator of treatment as the covariate. The third model, M₃, assumes no cure group. It is obtained from model (2) by setting ω_vi = 0 for all patients. The last two models, M₄ and M₅, are constructed under the factorization P(T, Y) = P(Y)P(T | Y), where the longitudinal submodel P(Y) is specified as y_vij = f_vi(s_vij) + e_vij with

$$f_{\mathit{\text{vi}}}(s_{\mathit{\text{vij}}})={\theta }_{0\mathit{\text{vi}}}+{\theta }_{1\mathit{\text{vi}}}{s}_{\mathit{\text{vij}}}+{\gamma }_{2\mathit{\text{vi}}}\{e^{-{\phi }_{0\mathit{\text{vi}}}{(s_{\mathit{\text{vij}}}-u_{\mathit{\text{vi}}0})}^{+}}-1\}+{\eta }_v\{e^{-{\phi }_{1v}{(s_{\mathit{\text{vij}}}-u_{\mathit{\text{vi}}1})}^{+}-1}\}+{\gamma }_{1\mathit{\text{vi}}}{(s_{\mathit{\text{vij}}}-u_{\mathit{\text{vi}}1})}^{+}$$

and e_vij ~ N(0, σ²). The survival submodel P(T | Y) is assumed to be a proportional hazard model with a cure fraction p_v. The mean longitudinal process, f_vi(s_vij), together with the PSA slope, $f_{\mathit{\text{vi}}}^{\prime }(s_{\mathit{\text{vi}}})=\partial f_{\mathit{\text{vi}}}(s_{\mathit{\text{vi}}})/\partial s_{\mathit{\text{vi}}}$, are included as time-dependent covariates (Yu et al., 2004). We assume the following hazard function,

$$h_{\mathit{\text{vi}}}(t)=h_{v0}(t)\text{exp}[{\zeta }_{1v}{f}_{\mathit{\text{vi}}}(u_{\mathit{\text{vi}}1}+t)+{\zeta }_{2v}{f}_{\mathit{\text{vi}}}^{\prime }(u_{\mathit{\text{vi}}1}+t)],$$ (4)

where h_v0(t) is the baseline hazard and (ζ_1v, ζ_2v) are scaling parameters. Under M₄, we model h_v0(t) as a piecewise constant function of J = 8 steps. For 0 < q₁ < q₂ < ⋯ < q_J−1 < ∞, we assume h_v0(t) = κ_v1 if t ≤ q₁, h_v0(t) = κ_v2 if q₁ < t ≤ q₂, ⋯, and h_v0(t) = κ_vJ if t > q_J−1. Gamma priors are assumed for κ_vj. More details can be found in Ibrahim et al. (2004). Under M₅, we model h_v0(t) by a Weibull hazard, with Gamma priors for the scale and shape parameters. The priors of the other parameters are specified as in M₁.

The estimated LPML under M₁ through M₅ are 4833.6, 5115.2, 5007.9, 4889.1, and 5155.0, respectively. Clearly M₁ achieves the best performance. The nonparametric PT model allows the density function to deviate from the form imposed by the Weibull assumption. Assuming a cure group further improves the model fit. Model M₄ has the second best performance, which indicates that the PSA trajectory does play an important role in prostate cancer progression. The inferior performance of M₅ suggests that the Weibull hazard assumption might be too restrictive for our data. We further validate the survival and cure aspect of the model based on subject specific martingale residuals (Barlow and Prentice, 1988; Therneau et al., 1990; Lin et al., 2002). The residuals are scattered horizontally over age (with three outliers), suggesting no evidence against the proposed model. The residual plot is shown in Web Figure 2.

The posterior distribution of TTP

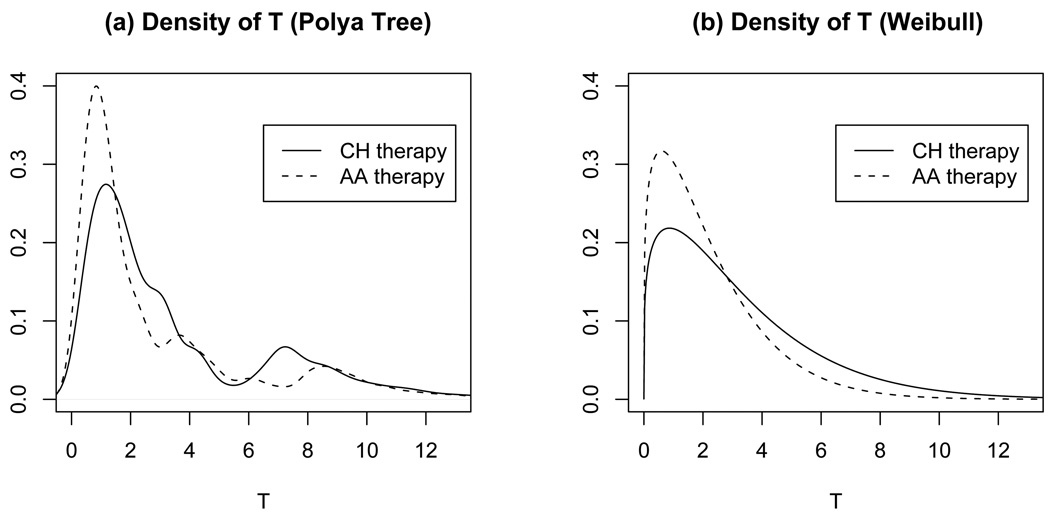
The estimated cure probabilities p_v (v = 1, 2) for the CH and AA treatments are 0.167 and 0.154, respectively. For advanced prostate cancer patients, here “cure” means that those patients take a very long time to progress to AIPC. Figure 2a shows the estimated densities of TTP in the susceptible group, E(G_v | Y, t, d), under the two treatments. The horizontal axis is in years after the treatments. For comparison, Figure 2b plots the posterior estimate of Weibull densities under M₂. Figure 2 clearly shows deviation from the parametric Weibull distribution. For example, there is a small bump in the CH density curve around 7.5, which is also visible in the Kaplan-Meier estimates in Figure 1. This feature can not be captured by M₂. In Figure 1 we also plot the posterior estimate of the survival function under model M₁, where TTP are assumed to arise from the mixture of a point mass at t_c and an unknown distribution G_v. Because a PT prior with a fixed partition has discontinuities at the partition points, we used additional kernel smoothing for the densities shown in Figure 2. Finally, we can assess the posterior uncertainty on G_v by plotting multiple random samples from its posterior distribution (Web Figure 3).

Figure 2.

Posterior estimated E(G_v | Y, t, d) under M₁ and M₂. The horizontal axis shows years after treatment.

The dependence of event times on longitudinal profiles

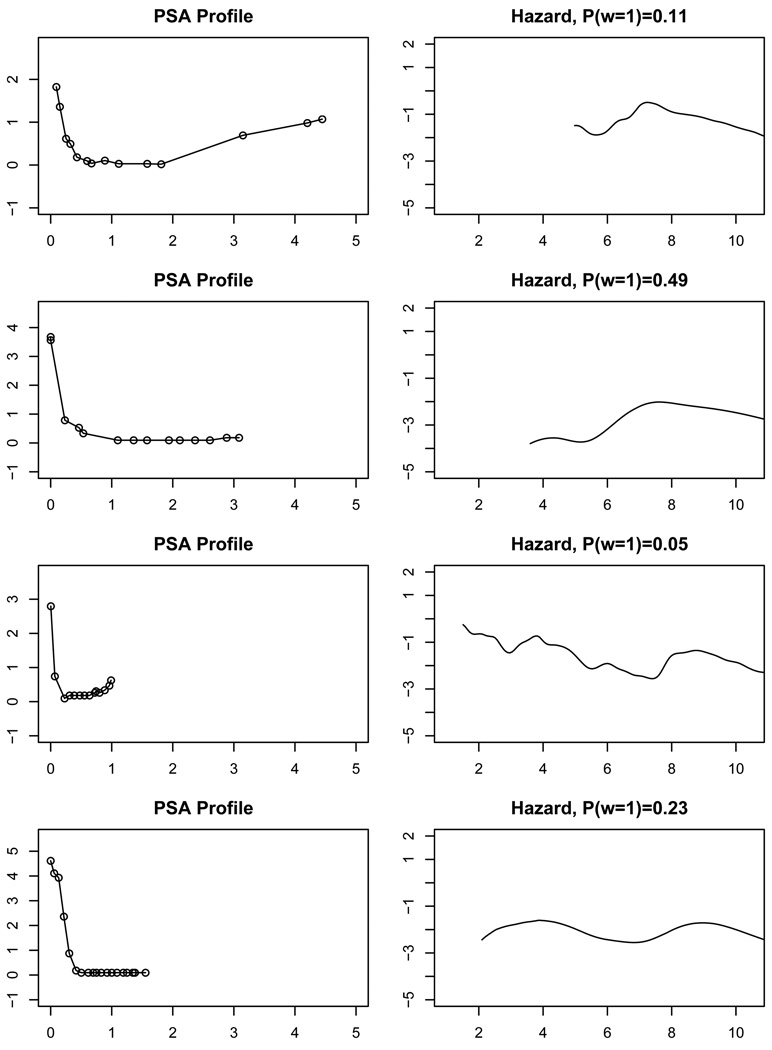
Under model M₁, different PSA profiles lead to different posterior distributions of T_vi. In Figure 3 we compare for four patients with censored TTP the PSA profiles (1st column) and the estimated posterior probability of “cure” P(ω_vi = 1) and the conditional hazard curve of T_vi given ω_vi = 0 (2nd column). Each row corresponds to one patient, with the first two under treatment CH, and the last two under AA. We plot the PSA profiles after initiation of the therapies. Figure 3 demonstrates the flexibility of M₁. Each patient has a hazard curve of a different shape.

Figure 3.

Posterior prediction of TTP (hazard given ω = 0 and P(ω = 1)) for four censored patients. The horizontal axis is time in years from the start of the AA/CH therapy.

The longitudinal model parameters

Web Figure 1 plots the longitudinal PSA profiles of four patients together with fitted values. Table 1 lists the posterior means and standard deviations of some parameters in M₁. The posterior estimates of ξ_v (v = 1, 2) are practically identical, implying that the impact of TTP on the trajectory of PSA profiles are similar across the two treatments. The estimates of γ_1v indicate that the PSA profiles of patients in the AA arm on average have an increased slope after treatment. The level and slope of the drop in PSA after the CH/AA treatment are modeled by l_v(t) = η_v[exp(−φ_1vt) −1], where t ≥ 0 is the time from the start of treatment v. The patients under CH therapy experience a deeper and longer drop in PSA. We plot l_v(t) in Web Figure 4.

Table 1.

Parameter Estimates in M₁

	Posterior Mean	Standard deviation
σ2	0.209	0.005
μθ0	−23.310	1.382
${\sigma }_{{\theta }_0}^2$	13.903	2.681
μθ1	0.483	0.023
${\sigma }_{{\theta }_1}^2$	0.004	0.001
γ11	0.447	0.122
γ12	0.689	0.139
μγ2	3.654	0.211
${\sigma }_{{\gamma }_2}^2$	0.131	0.016
φ11	11.077	0.864
φ12	9.471	0.585
η1	1.447	0.046
η2	1.948	0.047
ξ1	0.325	0.034
ξ2	0.326	0.034

Continuously reassessing the risk of progression

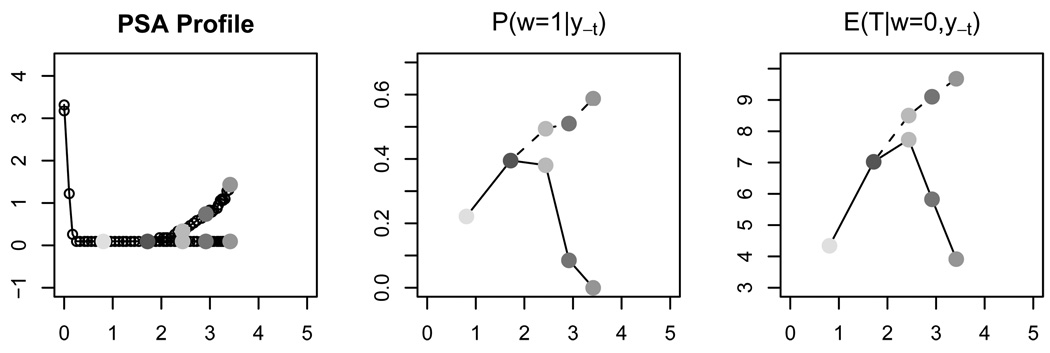
Given a currently observed PSA profile, we can use the proposed method to obtain the predictive distribution of TTP, which provides a good assessment of progression risk. This predictive distribution can be continuously updated with additional PSA measurements. We demonstrate this learning process in Figure 4. The left panel plots the PSA profiles of two hypothetical patients from the AA arm. Each point denotes a PSA measurement. The two patients have their PSA level measured at the same time points. Within the first two years the two PSA profiles are identical, and then they deviate: the first patient’s PSA level stays low, while the second gradually rises. The center panel shows the continuously updated posterior estimates of P(ω = 1 | y_−t), with y_−t being the accumulated PSA measurements up to the time of assessment. We interpret P(ω = 1 | y_−t) as the individual probability of long term survival. The right panel shows the continuously updated posterior estimates of E(T | ω = 0, y_−t).

Figure 4.

The left panel plots the PSA profiles of two hypothetical patients from the AA arm. The horizontal axis is time in years from the initiation of treatment. Each point denotes a PSA measurement. The center panel shows the continuously updated posterior estimates of P(ω = 1 | y_−t), where y_−t denotes the PSA measurements up to the point marked by the corresponding grey shades in the left panel. The dotted(solid) line denotes the first(second) patient. The third panel shows the continuously updated posterior estimates of E(T | ω = 0, y_−t).

Sensitivity analysis

We conducted a sensitivity analysis to explore the impact of t_c and c on posterior inference. We tried two values for c, (0.1, 1), and three values for t_c, (15, 18, 20). The posterior means of p_v and LPML are listed in Table 2. The estimated cure rate slightly increases with larger c, which implies stronger shrinkage of G_v to the parametric centering measure G̃. The parametric Weibull model G̃ can not represent the secondary mode that we see in the data and in the non-parametric inference for G_v. Compensating the missing secondary mode by an increased cure fraction could explain the change in the posterior means of p_v. The estimated LPML indicates the sensitivity of model fitting to t_c and c. This issue can be resolved by expanding the model with hyperpriors on c and t_c. We set them fixed to keep the discussion focused.

Table 2.

Sensitivity Analysis

	c=0.1	c = 1
tc = 15	(0.169, 0.153), −4930.50	(0.188, 0.159), −4889.98
tc = 18	(0.167, 0.154), −4833.62	(0.182, 0.160), −4936.39
tc = 20	(0.164, 0.154), −4979.03	(0.181, 0.160), −4845.34

In each cell we list the posterior estimations of (p₁, p₂) and LPML.

6 Discussion

The proposed model allows researchers to relax parametric assumptions on the survival submodel imposed by existing methods. An important limitation is that P(T, Y) = P(T)P(Y | T) does not explicitly state how T is affected by Y. Given a particular longitudinal profile, we need to carry out posterior simulation to learn about the posterior survival distribution given Y. The proposed approach can readily be generalized to problems with more than two treatments. The longitudinal data model (3) is appropriate for the discussed application to the prostate cancer trial. In general, any well specified model with a regression on the event time could be used.