Abstract
Hypothesis testing with multiple outcomes requires adjustments to control Type I error inflation, which reduces power to detect significant differences. Maintaining the prechosen Type I error level is challenging when outcomes are correlated. This problem concerns many research areas, including neuropsychological research in which multiple, interrelated assessment measures are common. Standard p value adjustment methods include Bonferroni-, Sidak-, and resampling-class methods. In this report, the authors aimed to develop a multiple hypothesis testing strategy to maximize power while controlling Type I error. The authors conducted a sensitivity analysis, using a neuropsychological dataset, to offer a relative comparison of the methods and a simulation study to compare the robustness of the methods with respect to varying patterns and magnitudes of correlation between outcomes. The results lead them to recommend the Hochberg and Hommel methods (step-up modifications of the Bonferroni method) for mildly correlated outcomes and the step-down minP method (a resampling-based method) for highly correlated outcomes. The authors note caveats regarding the implementation of these methods using available software.
Keywords: multiple hypothesis testing, correlated outcomes, familywise error rate, p value adjustment, neuropsychological test performance data
Neuropsychological datasets typically consist of multiple, partially overlapping measures, henceforth termed outcomes. A given neuropsychological domain—for example, executive function—is composed of multiple interrelated subfunctions, and frequently all subfunction outcomes of interest are subject to hypothesis testing. At a given α (critical threshold), the risk of incorrectly rejecting a null hypothesis, a Type I error, increases as more hypotheses are tested. This applies to all types of hypotheses, including a set of two-group comparisons across multiple outcomes (e.g., differences between two groups across several cognitive measures) or multiple-group comparisons within an analysis of variance framework (e.g., cognitive performance differences between several treatment groups and a control group). Collectively, we define these issues as the multiplicity problem (Pocock, 1997).
Controlling Type I error at a desired level is a statistical challenge, further complicated by the correlated outcomes prevalent in neuropsychological data. By making adjustments to control Type I error, we increase the risk of incorrectly accepting a null hypothesis, a Type II error. In other words, we reduce power. Failure to control Type I error when examining multiple outcomes may yield false inferences, which may slow or sidetrack research progress. Researchers need strategies that maximize power while ensuring an acceptable Type I error rate.
Many methods exist to manage the multiplicity problem. Several methods are based on the Bonferroni and Sidak inequalities (Sidak, 1967; Simes, 1986). These methods adjust α values or p values using simple functions of the number of tested hypotheses (Sankoh, Huque, & Dubey, 1997; Westfall & Young, 1993). Holm (1979), Hochberg (1988), and Hommel (1988) developed Bonferroni derivatives incorporating stepwise components. Using rank-ordered p values, stepwise methods alter the magnitude of change as a function of p value order. Mathematical proofs order these methods, from least to most power, as Bonferroni, Holm, Hochberg, and Hommel (Hochberg, 1988; Hommel, 1989; Sankoh et al., 1997). The Tukey-Ciminera-Heyse (TCH), Dubey/Armitage-Parmar (D/AP), and R2-adjustment (RSA) methods are single-step Sidak derivatives (Sankoh et al., 1997). Another class of methods uses resampling methodology. The bootstrap (single-step) minP and step-down minP methods adjust p values using the nonparametrically estimated null distribution of the minimum p value (Westfall & Young, 1993).
The Bonferroni-class methods and the Sidak method are theoretically valid with independent, uncorrelated outcomes only (Hochberg, 1988; Holm, 1979; Hommel, 1988; Westfall & Young, 1993). The D/AP and RSA methods incorporate measures of correlation (Sankoh et al., 1997), and the resampling-class methods incorporate correlational characteristics via bootstrapping procedures (Westfall & Young, 1993). However, it is unclear which methods perform better when analyzing correlated outcomes. Theoretical and empirical comparisons of these p value adjustment methods have been limited in the breadth of methods compared and correlation structures explored (Hochberg & Benjamini, 1990; Hommel, 1988, 1989; Sankoh, D'Agostino, & Huque, 2003; Sankoh et al., 1997; Simes, 1986). We aimed to identify the optimal method(s) for multiple hypothesis testing in neuropsychological research.
We organized this article into several sections. First, we provide definitions and illustrations of 10 p value adjustment methods. Next, we describe a sensitivity analysis, defined as using statistical techniques in parallel to compare estimates, hypothesis inferences, and relative plausibility of the inferences (Saltelli, Chan, & Scott, 2000; Verbeke & Molenberghs, 2001). Using a neuropsychological dataset, we compare the p value adjustment methods by the adjusted p value and inferences patterns. After the sensitivity analysis, we detail a simulation study, which, by definition, permits the examination of measures of interest under controlled conditions. We examined the Type I error and power rates of the p value adjustment methods under a systematic series of correlation and null hypothesis conditions. This allows us to compare the methods’ performance relative to simulation conditions, that is, when the truth is known. Last, we offer guidelines for using these methods when analyzing multiple correlated outcomes.
p Value Adjustment Method
Multiple testing adjustment methods may be formulated as either p value adjustment (with higher adjusted p values) or α-value adjustment (with lower adjusted α values). We focus on p value adjustment method formulas because adjusted p values allow direct interpretation against a chosen α value and eliminate the need for lookup tables or knowledge of complex hypothesis rejection rules (Westfall & Young, 1993; Wright, 1992). Furthermore, adjusted α values are not supported by statistical software.
We describe the methods assuming a neuropsychological dataset with N participants, belonging to one of two groups, with M outcomes observed for each participant. The objective is to determine which outcomes are different between groups using two-sample t tests. For the jth outcome, where j = {1, 2,…, M}, there exists a null hypothesis and an observed p value resulting from testing the null hypothesis, denoted V(j), H0j, and pj, respectively. The observed p values are arranged such that p1 ≥…≥ pj ≥…≥ pM. For each outcome, we test the null hypothesis of no difference between the groups, that is, the groups come from the same population. For any method, we calculate a sequence of adjusted p values in which we denote paj as the adjusted p value corresponding to pj.
Bonferroni-Class Method
The parametric Bonferroni-class methods consist of the Bonferroni method and its derivatives. The Bonferroni method, defined as paj = min{Mpj, 1}, increases each p value by a factor of M to a maximum value of 1. Holm (1979) and Hochberg (1988) enhanced this single-step approach with stepwise adjustments that adjust p values sequentially and maintain the observed p value order. Holm’s step-down approach begins by adjusting the smallest p value pM as paM = min{MpM, 1}. For each subsequent pj, with j = {M − 1, M − 2,…, 1}, paj is defined as min{jpj, 1} if min{jpj, 1} is greater than or equal to all previously adjusted p values, paM through pa (j + 1). Otherwise, it is the maximum of these previously adjusted p values. Therefore, we define Holm p values as paj = min{1, max[jpj, (j + 1)pj + 1, …, MpM]}, all of which are between 0 and 1. Hochberg’s method uses a step-up approach, such that paj = min{1p1, 2p2, …, jpj}. Converse to Holm’s method, adjustment begins with the largest p value, pa1 = 1p1, and steps up to more significant p values, where each subsequent paj is the minimum of jpj and the previously adjusted p values, pa1 through pa(j − 1).
Hommel’s (1988) method is a derivative of Simes’s (1986) global test, which is derived from the Bonferroni method. For a subset of S null hypotheses, 1 ≤ S ≤ M, we define pSimes = min{(S/S)p1, …, (S/[S − i + 1])pi, …, (S/1)pS}, for i = {1, 2, …, S}, where the pis are the ordered p values corresponding to the S hypotheses within the subset. Hommel extended this method, permitting individual adjusted p values, defining paj as the maximum pSimes calculated for all subsets of hypotheses containing the jth null hypothesis, H0j. Consider a simple case of M = 2 hypotheses, H01 and H02. We calculate pa1 as the maximum of the Simes p values for the subsets {H01} and {H01, H02}, such that pa1 = max[(1/1)p1, min{(2/2)p1, (2/1)p2}]. We calculate pa2 similarly with subsets {H02} and {H01, H02}. Wright (1992) provided an illustrative example and an efficient algorithm for Hommel p value calculations.
Sidak-Class Method
The Sidak method and its derivatives make up the parametric Sidak-class methods. The Sidak method defines paj = 1 − (1 − pj)M, which is approximately equal to Mpj for small values of pj, resembling the Bonferroni method (Westfall & Young, 1993). Like the Bonferroni method, the Sidak method reduces Type I error in the presence of M hypothesis tests with independent outcomes. The Sidak derivatives have the general adjusted p value form, paj = 1 − (1 − pj)g(j), where g(j) is some function defined per each method with 1 ≤ g(j) ≤ M. Some Sidak derivatives define g(j) to depend on measures of correlation between outcomes, where g(j) would range between M, for completely uncorrelated outcomes, and 1, for completely correlated outcomes. In turn, the magnitude of p value adjustment would range from the maximum adjustment (Sidak level) to no adjustment at all.
The TCH method defines g(j) = √M (Sankoh et al., 1997). The D/AP and the RSA methods incorporate measures of correlation between outcomes (Sankoh et al., 1997). The jth adjusted D/AP p value is calculated using the mean correlation between the jth outcome and the remaining M − 1 outcomes, denoted mean.ρ(j), such that g(j) = M1 − mean.ρ(j). The jth adjusted RSA p value uses the value of R2 from an intercept-free linear regression with the jth variable as the outcome and the remaining M − 1 variables as the predictors, denoted R2(j), such that g(j) = M1 − R2(j).
Resampling-Class Methods
Resampling-class methods use a nonparametric approach to adjusting p values. We examined the bootstrap variants of the minP and step-down minP (sd.minP) methods proposed by Westfall and Young (1993). The minP method defines paj = P[X ≤ pj | X ~ minP(1, …, M)], the probability of observing a random variable X as extreme as pj, where X follows the empirical null distribution of the minimum p value. This is similar to the calculation of a p value using a z value statistic against the standard normal distribution, except that the distribution of X is derived through resampling. We generate the distribution of X by the following algorithm. Assume the original dataset has M outcomes for each of the N participants. We transform the original dataset by centering all observations by the group- and outcome-specific means. Next, we generate a bootstrap sample with N observations by sampling observation vectors with replacement from this mean-centered dataset. We then calculate p values by conducting hypothesis tests on each bootstrap sample. These M p values are considered an observation vector of a matrix consisting of outcomes B(1) through B(M), where B(j) are p values corresponding to outcome V(j) of the bootstrap dataset. Unlike the p values calculated from the original dataset, these p values are not reordered by rank. A total of Nboot bootstrap datasets are generated, creating Nboot observations in each B(j). The minimum p value from each observation vector defines the Nboot values of empirical minP null distribution for the minP method, from which the adjusted p values are calculated.
The sd.minP method alters this general algorithm by using different empirical distributions for each pj. The matrix with outcomes B(1) through B(j) are calculated as before. For pj, we form an empirical minP null distribution from the minimum p values, not from the entire observation vectors with outcomes B(1) through B(M), but the subset corresponding to outcomes B(1) through B(j), and determine the values of P[X ≤ pj | X ~ minP(1, …, j)]. The last step of the sd.minP method is a stepwise procedure that ensures the observed p value order as in the Holm method. That is, paj is the maximum of the value P[X ≤ pj | X ~ minP(1, …, j)] and the values P[X ≤ pj + 1 | X ~ minP(1,…, j + 1)] through P[X ≤ pM | X ~ minP(1, …, M)] .
Illustrative Example
We demonstrate these methods with an illustrative example, with values summarized in Table 1. In practice, we would calculate most of these adjusted p values via efficient computer algorithms available in several statistical packages, including R (R Development Core Team, 2006) and SAS/STAT software (SAS Institute Inc., 2002–2006). Suppose we conduct two-sample t tests with M = 4 outcomes and observe ordered p values p1 = 0.3587, p2 = 0.1663, p3 = 0.1365, and p4 = 0.0117. Using the Bonferroni method, these unadjusted p values are each multiplied by 4, producing the values 1.4348, 0.6653, 0.5462, and 0.0470, respectively. By the minimum function, pa1 is set to 1 rather than 1.4348, ensuring adjusted p values between 0 and 1.
Table 1.
Illustrative Example: Observed p Values and Adjusted p Values by Class and Method
| Bonferroni | Sidak | Resampling | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Observed | Bonferroni | Holm | Hochberg | Hommel | Sidak | TCH | D/AP | RSA | minP | sd.minP |
| 0.3587 | 1.0000 | 0.4096 | 0.3587 | 0.3587 | 0.8309 | 0.5887 | 0.6622 | 0.7362 | 0.7980 | 0.3616 |
| 0.1663 | 0.6653 | 0.4096 | 0.3326 | 0.3326 | 0.5169 | 0.3050 | 0.3448 | 0.3919 | 0.4749 | 0.3328 |
| 0.1365 | 0.5462 | 0.4096 | 0.3326 | 0.2731 | 0.4441 | 0.2544 | 0.3017 | 0.3486 | 0.4055 | 0.3328 |
| 0.0117 | 0.0470 | 0.0470 | 0.0470 | 0.0470 | 0.0462 | 0.0234 | 0.0274 | 0.0323 | 0.0434 | 0.0434 |
Note. TCH = Tukey-Ciminera-Heyse; D/AP = Dubey/Armitage-Parmar; RSA = R2 adjustment.
The Holm (1979) and Hochberg (1988) methods begin by computing the values where jpj, which are 0.3587, 0.3326, 0.4096, and 0.0470. These are potential adjusted p values, determined ultimately by the stepwise procedures. Per the Holm method, we note 0.3326 < 0.4096. Because the method requires that pa2 ≥ pa3, we set pa2 = 0.4096, not the initial potential value 0.3326. Similarly, with the requirement pa1 ≥ pa2, we set pa1 = 0.4096, resulting in the Holm p values of 0.4096, 0.4096, 0.4096, and 0.0470. Per the Hochberg method, we again note that 0.3326 < 0.4096 and that the requirement pa2 ≥ pa3 exists. Under the Hochberg method, we set pa3 = 0.3326 rather than to the initial potential value 0.4096, resulting in the Hochberg p values 0.3587, 0.3326, 0.3326, and 0.0470.
The Hommel (1988) method requires the calculation of Simes (1986) p values for subsets of hypotheses for each adjusted p value. For example, pa3 requires the calculation of Simes p values for the following four hypothesis subsets: {H01, H02, H03, H04}, {H01, H02, H03}, {H01, H03}, and {H03}. The Simes p values for these subsets are 0.0470, 0.2495, 0.2731, and 0.1365, respectively, where pa3 is the maximum of these values, 0.2731. The Hommel p values are 0.3587, 0.3326, 0.2731, and 0.0470, respectively.
The Sidak-class methods have the same general form, paj = 1 − (1 − pj)g(j). Using g(j) = M = 4, the Sidak p values are 0.8309, 0.5169, 0.4441, and 0.0462, respectively, for the four hypothesis subsets. Using g(j) = √M = 2, the TCH p values are 0.5887, 0.3050, 0.2544, and 0.0234, respectively. The D/AP and RSA methods require correlation information. Suppose the values of mean.ρ(j), the mean correlation for the jth outcome with all other outcomes, are 0.3558, 0.3915, 0.3546, and 0.3841 for outcomes V(1)– V(4), respectively. Using the D/AP formula, the adjusted p values are 0.6622, 0.3448, 0.3017, and 0.0274, respectively. Similarly, with R2(j) values of 0.2077, 0.2744, 0.2271, and 0.2618, the RSA p values are 0.7362, 0.3919, 0.3486, and 0.0323, respectively.
The resampling-class methods rely on the empirical minP null distributions. We generated the distributions on the basis of Nboot = 100,000 resamples. By the minP method, paj is the probability of observing a value X ≤ pj, where X follows the empirical minP null distribution derived using all four outcomes. In a graphical representation, this corresponds to the area under the empirical distribution plot to the left of the value of pj. The minP p values based on our generated distribution are 0.7980, 0.4748, 0.4055, and 0.0434. Per the sd.minP method, we compare only p4, the smallest p value, against this distribution. Recall that each pj is compared with the distribution derived from using only outcomes B(1)–B(j). Thus, pa3 is calculated using the distribution based only on B(1)–B(3), and so forth. On the basis of these distributions, the potential value for each paj is the area to the left of pj and below the appropriate distribution curve. These potential values are 0.3616, 0.2925, 0.3328, and 0.0434. Similar to the Holm (1979) method, we note 0.2925 < 0.3328 and thus adjust pa2 upward to the value of pa3, resulting in sd.minP p values of 0.3616, 0.3328, 0.3328, and 0.0434. We provide a graphical representation in Figure S1 of the supplemental materials.
Sensitivity Analysis
Data
We used a dataset from a study of neuropsychological performance conducted through the University of Pittsburgh’s Advanced Center for Interventions and Services Research for Late-Life Mood Disorders, Western Psychiatric Institute and Clinic in Pittsburgh, PA (Butters et al., 2004). The study used a group of 140 participants (100 depressed participants and 40 nondepressed comparison participants), ages 60 and older, group matched in terms of age and education. We conducted our sensitivity analysis with respect to 17 interrelated neuropsychological test (i.e., outcome measures) from this dataset, with tests detailed and cited in Butters et al. These outcome measures were grouped into five theoretical domains. The outcome correlation matrix is shown in Table 2.
Table 2.
Neuropsychological Outcome Correlation Matrix
| ID and outcome | 1.1 | 1.2 | 1.3 | 2.1 | 2.2 | 2.3 | 3.1 | 3.2 | 3.3 | 3.4 | 4.1 | 4.2 | 4.3 | 5.1 | 5.2 | 5.3 | 5.4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.1. Grooved pegboard | — | ||||||||||||||||
| 1.2. Digit Symbol | .61 | — | |||||||||||||||
| 1.3. Trails Making Test–A (Trails A) | .63 | .62 | — | ||||||||||||||
| 2.1. Block design | .48 | .53 | .43 | — | |||||||||||||
| 2.2. Simple drawings | .55 | .46 | .41 | .54 | — | ||||||||||||
| 2.3. Clock drawing | .40 | .38 | .39 | .49 | .51 | — | |||||||||||
| 3.1. Trails Making Test–B (Trails B) | .62 | .61 | .69 | .49 | .52 | .40 | — | ||||||||||
| 3.2. Wisconsin Card Sorting Test | .43 | .48 | .40 | .47 | .35 | .42 | .44 | — | |||||||||
| 3.3. Executive Interview | .47 | .42 | .36 | .48 | .35 | .23 | .40 | .36 | — | ||||||||
| 3.4. Stroop | .60 | .40 | .50 | .32 | .32 | .32 | .60 | .36 | .23 | — | |||||||
| 4.1. California Verbal Learning Test | .42 | .49 | .39 | .38 | .30 | .38 | .40 | .38 | .43 | .36 | — | ||||||
| 4.2. Modified Rey-Osterrieth Figure | .47 | .32 | .40 | .49 | .38 | .25 | .37 | .22 | .35 | .29 | .38 | — | |||||
| 4.3. Logical Memory | .28 | .33 | .24 | .38 | .34 | .22 | .32 | .14 | .33 | .09 | .41 | .44 | — | ||||
| 5.1. Boston Naming Test | .54 | .40 | .36 | .38 | .48 | .30 | .36 | .33 | .38 | .22 | .34 | .47 | .33 | — | |||
| 5.2. Animal Fluency | .38 | .48 | .27 | .36 | .33 | .22 | .39 | .25 | .27 | .11 | .35 | .38 | .37 | .46 | — | ||
| 5.3. Letter Fluency | .34 | .47 | .30 | .22 | .35 | .22 | .37 | .24 | .44 | .12 | .36 | .23 | .27 | .41 | .50 | — | |
| 5.4. Spot-the-Word | .06 | .17 | .09 | .24 | .28 | .14 | .12 | .09 | .23 | .08 | .18 | .17 | .19 | .40 | .16 | .31 | — |
Note. For ID, x.y indicates the yth outcome of domain x. Domain 1 = information-processing speed; Domain 2 = visuospatial; Domain 3 = executive; Domain 4 = memory; Domain 5 = language.
Analysis
We compared the sensitivity analysis to compare the 10 adjustment methods, described in the p-Value Adjustment Methods section, with respect to patterns of hypothesis rejection and inference. We conducted two-sample t tests to test the null hypothesis of no difference between the depressed and comparison groups for each of the 17 outcome measures. The p value adjustment methods were applied using the multtest procedure, available in the SAS/STAT software (SAS Institute Inc., 2002–2006). This procedure allowed for the computation of adjusted p values for the Bonferroni- and resampling-class methods, as well as the Sidak method. For the resampling methods, we used 100,000 bootstrap samples in the calculations. The Sidak derivatives (TCH, D/AP, and RSA) were programmed in a SAS macro (available on request).
Results
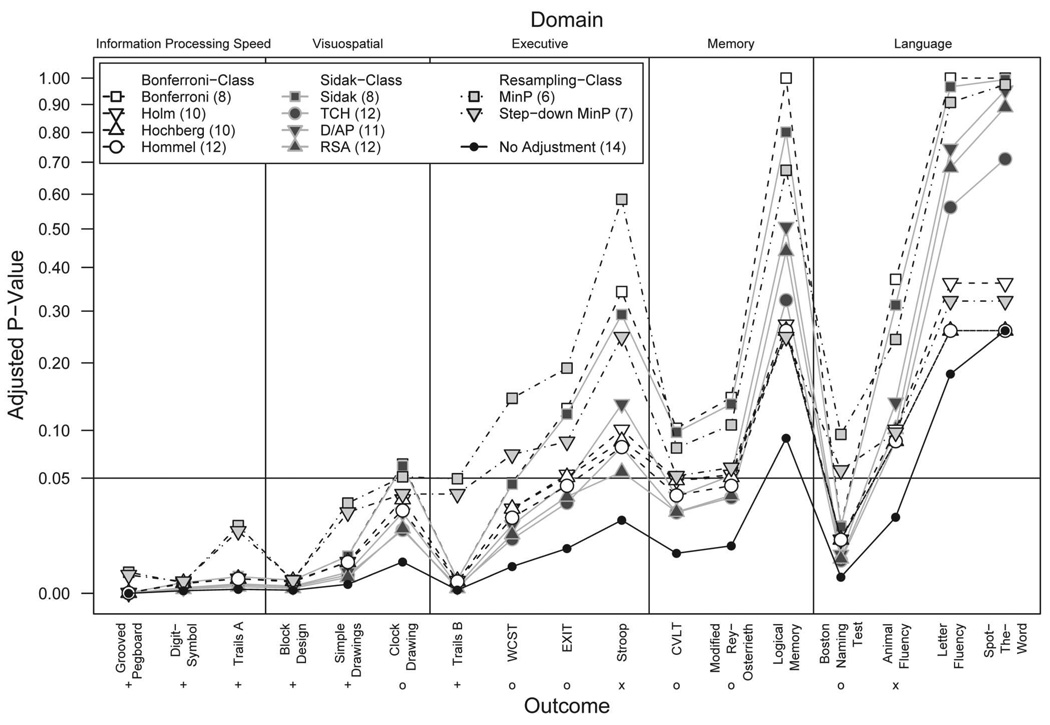
Figure 1 compares the adjusted p values for each method across all outcomes. The legend indicates the total number of rejected hypotheses per method. We used a square-root scale for the y-axis to reduce the quantity of overlapping points. Adjusted p values based on the smaller unadjusted p values, primarily in the information-processing speed and visuospatial ability domains, remained difficult to distinguish; the numerical values are shown in Table S1 in the supplemental materials. Among Bonferroni-class methods, the Bonferroni method had the largest p values and thus was the most conservative of the methods, followed by the Holm (1979), Hochberg (1988), and Hommel (1988) methods, which were the least conservative. The Sidak method produced similar results to the Bonferroni method. The Sidak derivatives were more liberal, all producing results similar to the Hochberg and Hommel methods; D/AP was most conservative of the three. Generally, TCH was the least conservative, although RSA produced some smaller p values, mostly when the observed p value was also quite small.
Figure 1.
Adjusted p values by method across neuropsychological outcomes. There are 17 observed p values for a set of 17 neuropsychological measures and adjusted p values per each method. A square-root scale is used to reduce overlapping points. Numbers in parentheses in the legend indicate the number of rejected hypotheses for that method. Symbols for outcomes with a null hypothesis rejected without adjustment indicate the following: + = null hypothesis rejected using each adjustment method; x = null hypothesis not rejected using any adjustment method; o = null hypothesis rejected by some adjustment methods. A full color version of this figure is included in the supplemental materials online.
The resampling methods produced relatively conservative results, with overall inferences similar to the Bonferroni and Sidak methods. The sd.minP method rejected the null hypothesis for the Clock Drawing Test, which was not rejected by the Bonferroni or Sidak methods. Whereas the order relations of the Bonferroni- and Sidak-class adjusted p values were highly consistent, this failed to hold for the resampling-class methods. The adjusted resampling-class p values were smaller than the Hommel counterpart for some outcomes and larger than the Bonferroni counterpart for others. Compared against each other, the sd.minP p values were smaller than the minP p values.
The importance of multiple hypothesis testing is highlighted by these results. Of the 17 outcomes and corresponding null hypotheses, we rejected 14 null hypotheses without adjustment. Of these 14, only 6 null hypotheses were rejected using each p value adjustment method. The null hypotheses regarding Animal Fluency and Stroop were not rejected using any method. Therefore, of the 14 null hypotheses rejected without adjustment, we can say confidently that 2 hypothesis decisions were Type I errors, 6 null hypotheses were rejected correctly, and 6 hypothesis decisions remain unclear. Without knowing the true differences (or lack thereof) between the populations regarding these seven outcomes, we gain confidence in our hypothesis rejection criteria by evaluating the Type I error and power of the p value adjustment methods.
Simulation Study
Method
The premise of the simulation study, conducted using the R statistical package (R Development Core Team, 2006), was to assess adjustment method performance across two series of trials. Performance included both Type I error protection and power to detect true effects. We defined each trial by a combination of hypothesis set and correlation structure conditions, defined below and summarized in Table 3. In a given trial, we generated 10,000 random datasets, termed replicates, with two groups of size N = 100 observations each. We chose to generate M = 4 outcome variables, termed V1 through V4, to represent an average neuropsychological domain. Outcomes were generated to follow multivariate normal distribution using the mvrnorm function (Venables & Ripley, 2002). Type I error and power estimates were calculated using the method-specific adjusted p values, based on two-sample, equal-variance, two-sided t test p values from each replicate. The number of resampled datasets, Nboot, nontrivially affects computation time but has less impact on performance estimation accuracy compared with the number of replicates (Westfall & Young, 1993). We set Nboot = 500 for efficiency.
Table 3.
Compound–Symmetry Simulation Series Parameters
| Outcome types | ||||
|---|---|---|---|---|
| Hypothesis sets | V1 | V2 | V3 | V4 |
| Uniform–true | TN | TN | TN | TN |
| Uniform–false | FN | FN | FN | FN |
| Split (split–uniform) | TN | TN | FN | FN |
| Correlation structure | ||||
| Correlation structure | V1 | V2 | V3 | V4 |
| V1 | 1 | ρ | ρ | ρ |
| V2 | ρ | 1 | ρ | ρ |
| V3 | ρ | ρ | 1 | ρ |
| V4 | ρ | ρ | ρ | 1 |
Note. Outcomes types: TN = true null; FN = false null; V1–V4 = ?.
Compound symmetry: ρ = {0.0, 0.1, …, 0.9}.
We defined a true null (TN) as a simulated outcome with no difference between groups. The null hypothesis is actually true, and the p value for the hypothesis test should be nonsignificant. True null outcomes were simulated with an effect size of 0.0 between the two groups and were used for Type I error estimation. We defined a false null (FN) as a simulated outcome with a significant difference between the groups, or, alternatively, the null hypothesis is false. False null outcomes were simulated with an effect size of 0.5 between groups and were used for power estimation. Varying combinations of TNs and FNs, termed hypothesis sets, defined the outcomes V1–V4. The uniform hypothesis sets defined all four outcomes to be the same type, either all true nulls or all false nulls, allowing only Type I error or power estimation, respectively. The split hypothesis set defined two outcomes as TNs and the other two as FNs and allows both Type I error and power estimation using the relevant simulated outcomes. These hypothesis sets defined the truth in a given trial, allowing for absolute comparisons of the p value adjustment methods against the truth instead of only the relative comparisons afforded by the sensitivity analysis.
For all trials, we defined the significance threshold for all p values at α = .05. We used several performance measures detailed by Dudoit, Shaffer, and Boldrick (2003) with adapted nomenclature. Using TN outcomes, we defined Type I error as the familywise error rate, meaning the probability of rejecting at least one TN hypothesis. We defined minimal power as the probability of rejecting at least one FN. We defined maximal power as the probability of rejecting all FNs. These performance measures were calculated as the proportion of replicates satisfying the respective conditions. We defined average power as the average probability of rejecting the FNs across outcomes. This measure was calculated as the mean proportion of rejected FNs across outcomes.
To examine the effect of correlation between outcomes on p value adjustment method performance, we varied the correlation levels in the two simulation series systematically. The first simulation series, the compound-symmetry (CS) series, used a CS correlation structure in which all outcomes were equicorrelated with each other. We varied the correlation parameter ρ from 0.0 to 0.9 with an interval of 0.1 for 10 possible values. With three specified hypothesis sets (uniform–true, uniform–false, and split) and 10 CS structures, 30 trials were conducted in this series, summarized in Table 3.
The second simulation series, block symmetry (BS), defined the outcomes V1–V2 and V3–V4 as constituting Blocks 1 and 2. Outcomes were equicorrelated within and between blocks, but with different levels. Within- and between-block correlation parameters W and B were varied among the values 0.0, 0.2, 0.5, and 0.8 (no, low, moderate, and high correlation), where within-block correlation was held strictly greater than between-block correlation, that is, W > B. The correlation structure of the sensitivity analysis data indicated higher correlation magnitude between outcomes within a block (domain) than between outcomes from different blocks. The BS correlation structure allows for the variation of these magnitudes in a simpler, four-outcome, two-block setting. In addition, the split–split hypothesis set was used, which defined a mix of outcome types overall and within blocks. This differed from the split, or split–uniform, hypothesis set in which block-specific hypothesis subsets were uniform. With four hypothesis sets and six correlation structures, 24 trials were conducted in this series. Table S2 in the supplemental materials summarizes the BS series parameters.
These structures represent correlation patterns observed between outcomes within and across several domains in the sensitivity analysis data. The CS structure is relevant to studies that focus on a single domain, for example, visuospatial ability, with multiple outcomes, for example, block design, simple drawings, and clock drawing. Although less intuitive compared with the CS structure, the BS structure is relevant for studies with multiple domains, for example, visuospatial ability and memory. Although correlation structures of real data are more complicated, these structures provided a relevant and convenient basis for evaluating the p value adjustment methods.
Results
For brevity, we report the simulation results for the CS series in full. BS series results exhibited similar patterns, and thus we provide BS series performance results in Figures S2, S3, and S4 in the supplemental materials. We also note that the primary purpose of the p value adjustment methods is to control Type I error, that is, they maintain Type I error near or below α =.05. When viewing the power plots, take note of Type I error as well, as methods with power greater than others but with insufficient Type I error control fail the primary purpose and render them suboptimal.
CS–uniform hypothesis set
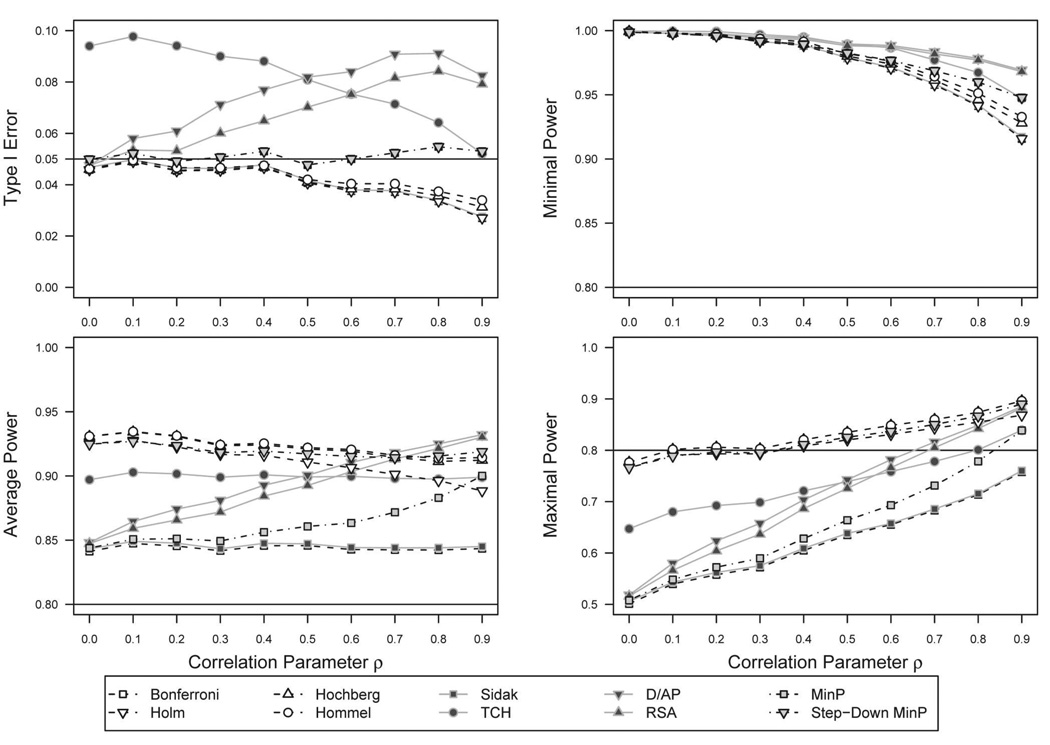
In Figure 2, we show the performance across CS correlation structures for the p value adjustment methods under the uniform hypothesis sets (four TNs for Type I error, four FNs for power). Type I error performance is shown in the upper left panel. The resampling-class methods demonstrated stable Type I error around α = .05 as the CS correlation ρ increased. The Bonferroni-class methods demonstrated a decreasing trend in Type I error with increasing correlation between outcomes. The Bonferroni and Holm (1979) methods showed the lowest Type I error, whereas the Hochberg (1988) and Hommel (1988) methods allowed more error but were still conservative when ρ exceeded 0.5. The Sidak method exhibited marginally higher Type I error than the Bonferroni method. The TCH method followed a decreasing, but elevated trend; in the case of independence, it demonstrated high Type I error with values nearly double the threshold α = .05. However, in the case of high correlation, ρ = 0.9, it was the only method that reasonably approached α = .05. The D/AP and RSA methods followed liberal nonmonotonic trends. These methods showed increasing Type I error up to around ρ = 0.6–0.7, after which the trends decreased.
Figure 2.
p value adjustment method performance across compound-symmetry correlation structures, Type I error, and power estimates for uniform hypothesis set. The upper left panel shows Type I error rates of the p value adjustment methods across increasing values of the compound-symmetry correlation parameter ρ. In this case, all M = 4 hypotheses are simulated to be true. Values near α = .05 are optimal. Values well above α = .05 indicate failure to protect Type I error at α. The remaining panels show different measures of power, where the four hypotheses are simulated to be false. Higher power is optimal, conditional on Type I error not exceeding α. A full color version of this figure is included in the supplemental materials online.
For average power, shown in the lower left panel, all the methods exhibited acceptable rates greater than 0.8. The Bonferroni and Sidak methods exhibited low, stable power near 0.85. The stepwise Bonferroni derivatives exhibited high power that decreased slowly with increasing correlation. The Hommel (1988) method was slightly more powerful than the Hochberg (1988) method, which was more powerful than the Holm (1979) method. The TCH method showed reasonably stable power around 0.9. The D/AP and RSA methods increased in average power as ρ increased and, at high correlation, were more powerful than the Bonferroni derivatives. However, as noted before, the power for the Sidak derivatives is irrelevant considering the Type I error rates well above α = .05. The minP method showed an increasing trend in average power with increasing correlation. The sd.minP method demonstrated an increase in power associated with a stepwise approach.
For minimal power, shown in the upper right panel, all methods were able to detect a difference between groups for at least one of four outcomes across all correlations with power greater than 0.9. The original Bonferroni and Sidak methods had the least power, followed by the Bonferroni derivatives, the resampling-class methods, and finally the Sidak derivatives.
For maximal power, shown in the lower right panel, all methods exhibited less power in comparison to the minimal and average power and demonstrated monotonic increasing trends with higher correlation with differing rates of change. The Bonferroni and Sidak methods again demonstrated the least power. The Bonferroni derivatives and the sd.minP performed generally well, ranging from just below 0.8 for low correlation and approaching 0.9 for high correlation. As before, the Holm (1979) method was less powerful than the Hochberg (1988) method, which was equivalent to the Hommel (1979) method, with the sd.minP method in between. Again, the TCH method followed the Sidak pattern in an elevated fashion. The D/AP and RSA methods demonstrated a steep rate of increase with increasing correlation, with power levels near Sidak with low correlation and power similar to the Bonferroni derivatives and the sd.minP method at high correlation.
CS–split hypothesis set
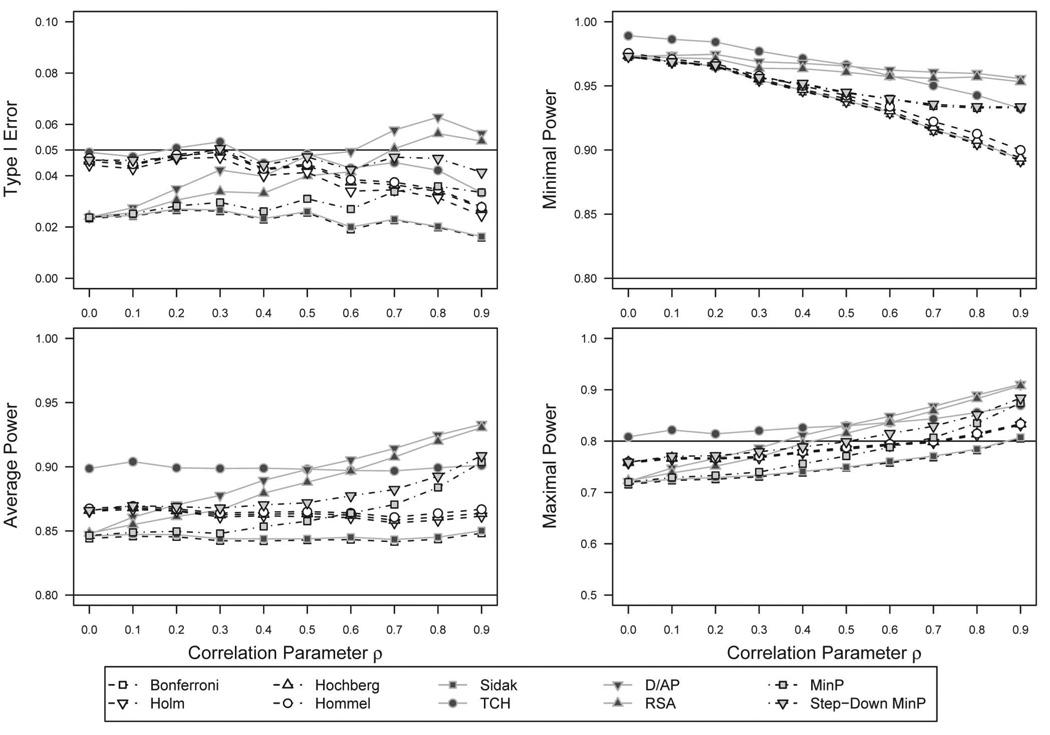
Figure 3 shows the results for the split hypothesis set across CS correlation structures. Similar relationships were found in comparison to the uniform hypothesis set, although the overall magnitudes decreased for all methods. Of note is the relative lack of decrease seen among stepwise methods, the Bonferroni derivatives and the sd.minP methods. The Type I error rates of the other methods were nearly halved in many instances. The D/AP and RSA methods exceeded α = .05 for high values of ρ.
Figure 3.
p value adjustment method performance across compound-symmetry correlation structures, Type I error, and power estimates for split hypothesis set. The upper left panel shows Type I error rates of the p value adjustment methods across increasing values of the CS correlation parameter ρ. In this case, all only two of the M = 4 hypotheses are simulated to be true. Values near α = .05 are optimal. Values well above α = .05 indicate failure to protect Type I error at α. The remaining panels show different measures of power, using the two hypotheses simulated to be false. Higher power is optimal, conditional on Type I error not exceeding α. A full color version of this figure is included in the supplemental materials online.
Compared with the uniform hypothesis set power estimates, the Bonferroni derivatives exhibited lower average power, whereas the other methods performed similarly. The sd.minP method also showed a decrease in average power, although it increased with correlation. For minimal power, all methods exhibited a small reduction in power, although less pronounced for the Sidak derivatives. In terms of maximal power, the results for the Bonferroni derivatives were similar to the uniform hypothesis set counterparts, and all other methods exhibited greater power. The Bonferroni and Sidak methods continued to be the most conservative, but the Sidak derivatives exhibited higher power than all other methods for CS correlation ρ > 0.3.
Discussion
The simulation results indicated that the Bonferroni and Sidak methods, although protecting Type I error, became increasingly conservative with high correlation between outcomes and were under-powered, particularly with regard to maximal power. The Bonferroni derivatives, although not improving the Type I error issue, notably improved average and maximal power. The single-step Sidak derivatives did not exhibit power similar to the stepwise methods. The average power of the D/AP and RSA methods increased with increasing correlation. However, these methods did not maintain acceptable Type I error. The resampling-class methods demonstrated consistent Type I error across the correlation structures and levels explored. The sd.minP method again demonstrated the advantage of a stepwise approach with similar power to the Bonferroni derivatives. Among methods examined, the Hochberg (1988), Hommel (1979), and sd.minP methods exhibited the best performance, with considerable power and reasonable Type I error protection. With higher outcome correlation, the sd.minP method demonstrated higher power, particularly in the split hypothesis experiments. Thus, for lower correlation between neuropsychological outcomes, that is, average ρ < 0.5, we recommend either the Hochberg or the Hommel methods for reasons of easy implementation and exact replicability. For higher correlation between neuropsychological outcomes, we recommend the sd.minP method for increased power.
However, we must note a caveat to this simple guideline. With the implementation of the SAS/STAT multtest procedure (SAS Institute Inc., 2002–2006), the equal-variance assumption was the only option for the test statistics used with the minP and sd.minP methods. When the equal-variance assumption is violated, using equal-variance t tests may yield inaccurate observed p values and inaccurate empirical minP null distributions, thus producing the conservative results shown in our sensitivity analysis.
Ideally, one might wish to use the sd.minP method without assuming equal variances for all outcomes, although to our knowledge current statistical software packages do not support this feature. Whereas the parametric methods are simple formulas that produce identical results across packages, the resampling-class methods may vary in their implementation from package to package, specifically with respect to the type of tests that may be conducted. If equality-of-variance tests are rejected for many outcomes, current software implementations may yield lower power. In this case, for average ρ ≥ 0.5, we prefer the Hochberg (1988) and Hommel (1979) methods. For the neuropsychological data examined in the sensitivity analysis, with high correlation between outcomes and many outcomes with unequal variances between groups, the Hochberg and Hommel methods are most appropriate.
Another important caveat with regard to the resampling-class methods is the number of Nboot samples used to generate the empirically derived null minimum p value distributions. Westfall and Young (1993) recommended at least 10,000. In practice, this may not be enough. One cannot estimate small p values with a reasonable amount of precision without enough samples to estimate the tails of the distribution. With too few resamples, repeated applications of these methods may yield different inferences. Although we used 100,000 for our sensitivity analysis, admittedly the smallest unadjusted p value could not have been precisely estimated with 100,000, although the adjusted counterpart was still quite below α = .05.
The D/AP and RSA methods, designed to incorporate correlation into the adjustment, proved insufficient in protecting Type I error. The average power of these methods was adequate, but maximal power was weak for low correlation between outcomes. Further research in this area may yield another function that overcomes these deficiencies.
More methods might have been considered in this investigation. Dunnett and Tamhane (1992) and Rom (1990) both developed stepwise procedures with the motivation of lowering Type II error. Both methods make strong distributional assumptions and require complicated, iterative calculation. Furthermore, neither method has been implemented in any statistical software. The resampling-class methods also include permutation methods, which yield similar results to bootstrap methods when both methods can be easily applied but are extremely complicated to apply in many analytical situations (Westfall & Young, 1993). Thus, we excluded these methods from consideration.
We chose to simulate only four outcomes to obtain a perspective of the performance of these methods. It is likely that the trends would simply become more pronounced and exaggerated with a higher number of outcomes, although this could be confirmed by another extensive simulation study.
The sensitivity analysis and simulation study were conducted in SAS and R because many of the methods used were built into the software and the remaining methods could be programmed with relative ease. SPSS and Stata, software preferred by some researchers, have a limited selection of methods available for analysis of variance–type comparisons, and none for multiple, two-sample tests as explored in this study (SPSS Inc., 2006; Stata Press, 2007). The Hochberg (1988) method could be programmed with relative ease in either package; in fact, it could be programmed in spreadsheet software. The Hommel (1979) and sd.minP methods, however, would be more complicated. Reprogramming these methods for SPSS or Stata would likely be less efficient than learning the comparatively few commands necessary to conduct the p value adjustments in SAS or R.
Currently, there exists no perfect adjustment method for multiple hypothesis testing with neuropsychological data. The sd.minP, Hochberg (1988), and Hommel (1979) methods demonstrated Type I error protection with good power, although new research may yield methods that surpass their performance.
Supplementary Material
Acknowledgments
This research was supported by the National Institute of Mental Health Grants T32 MH073451, P30 MH071944, and R01 MH072947 and National Institute on Aging Grant P01 AG020677. We thank Sanat Sarkar of Temple University for his input on this article.
Footnotes
Supplemental materials: http://dx.doi.org/10.1037/a0012850.supp
Contributor Information
Richard E. Blakesley, Department of Biostatistics, University of Pittsburgh
Sati Mazumdar, Department of Biostatistics, University of Pittsburgh, and Department of Psychiatry, University of Pittsburgh School of Medicine.
Mary Amanda Dew, Department of Psychiatry, University of Pittsburgh School of Medicine, and Departments of Epidemiology and Psychology, University of Pittsburgh.
Patricia R. Houck, Department of Psychiatry, University of Pittsburgh School of Medicine
Gong Tang, Department of Biostatistics, University of Pittsburgh.
Charles F. Reynolds, III, Department of Psychiatry, University of Pittsburgh School of Medicine.
Meryl A. Butters, Department of Psychiatry, University of Pittsburgh School of Medicine
References
- Butters MA, Whyte EM, Nebes RD, Begley AE, Dew MA, Mulsant BH, et al. The nature and determinants of neuropsychological functioning in late-life depression. Archives of General Psychiatry. 2004;61:587–595. doi: 10.1001/archpsyc.61.6.587. [DOI] [PubMed] [Google Scholar]
- Dudoit S, Shaffer JP, Boldrick JC. Multiple hypothesis testing in microarray experiments. Statistical Science. 2003;18:71–103. [Google Scholar]
- Dunnett CW, Tamhane AC. A step-up multiple test procedure. Journal of the American Statistical Association. 1992;87:162–170. [Google Scholar]
- Hochberg Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika. 1988;75:800–802. [Google Scholar]
- Hochberg Y, Benjamini Y. More powerful procedures for multiple significance testing. Statistics in Medicine. 1990;9:811–818. doi: 10.1002/sim.4780090710. [DOI] [PubMed] [Google Scholar]
- Holm S. A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics. 1979;6:65–70. [Google Scholar]
- Hommel G. A stagewise rejective multiple test procedure based on a modified Bonferroni test. Biometrika. 1988;75:383–386. [Google Scholar]
- Hommel G. A comparison of two modified Bonferroni procedures. Biometrika. 1989;76:624–625. [Google Scholar]
- Pocock SJ. Clinical trials with multiple outcomes: A statistical perspective on their design, analysis, and interpretation. Controlled Clinical Trials. 1997;18:530–545. doi: 10.1016/s0197-2456(97)00008-1. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. Vienna: R Foundation for Statistical Computing; 2006. R: A language and environment for statistical computing. Available at http://www.R-project.org. [Google Scholar]
- Rom DM. A sequentially rejective test procedure based on a modified Bonferroni inequality. Biometrika. 1990;77:663–665. [Google Scholar]
- Saltelli A, Chan K, Scott EM, editors. Sensitivity analysis: Gauging the worth of scientific models. New York: Wiley; 2000. [Google Scholar]
- Sankoh AJ, D’Agostino RB, Huque MF. Efficacy endpoint selection and multiplicity adjustment methods in clinical trials with inherent multiple endpoint issues. Statistics in Medicine. 2003;22:3133–3150. doi: 10.1002/sim.1557. [DOI] [PubMed] [Google Scholar]
- Sankoh AJ, Huque MF, Dubey SD. Some comments on frequently used multiple endpoint adjustment methods in clinical trials. Statistics in Medicine. 1997;16:2529–2542. doi: 10.1002/(sici)1097-0258(19971130)16:22<2529::aid-sim692>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- SAS Institute Inc. SA S OnlineDoc 9.1.3. Cary, NC: Author; 2002–2006. [Google Scholar]
- Sidak Z. Rectangular confidence regions for the means of multivariate normal distributions. Journal of the American Statistical Association. 1967;62:626–633. [Google Scholar]
- Simes RJ. An improved Bonferroni procedure for multiple tests of significance. Biometrika. 1986;73:751–754. [Google Scholar]
- SPSS Inc. SPSS base 1 5.0 user’s guide. Chicago: Author; 2006. [Google Scholar]
- Stata Press. Stata 10 base documentation set. College Station, TX: Author; 2007. [Google Scholar]
- Venables WN, Ripley BD. Modern applied statistics with S. 4th ed. New York: Springer; 2002. [Google Scholar]
- Verbeke G, Molenberghs G. Linear mixed models for longitudinal data. New York: Springer; 2001. [Google Scholar]
- Westfall PH, Young SS. Resampling-based multiple testing: Examples and methods for p-value adjustment. New York: Wiley; 1993. [Google Scholar]
- Wright SP. Adjusted P-values for simultaneous inference. Biometrics. 1992;48:1005–1013. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.