Runaway cultural niche construction

Abstract

Cultural niche construction is a uniquely potent source of selection on human populations, and a major cause of recent human evolution. Previous theoretical analyses have not, however, explored the local effects of cultural niche construction. Here, we use spatially explicit coevolutionary models to investigate how cultural processes could drive selection on human genes by modifying local resources. We show that cultural learning, expressed in local niche construction, can trigger a process with dynamics that resemble runaway sexual selection. Under a broad range of conditions, cultural niche-constructing practices generate selection for gene-based traits and hitchhike to fixation through the build up of statistical associations between practice and trait. This process can occur even when the cultural practice is costly, or is subject to counteracting transmission biases, or the genetic trait is selected against. Under some conditions a secondary hitchhiking occurs, through which genetic variants that enhance the capability for cultural learning are also favoured by similar dynamics. We suggest that runaway cultural niche construction could have played an important role in human evolution, helping to explain why humans are simultaneously the species with the largest relative brain size, the most potent capacity for niche construction and the greatest reliance on culture.

1. Introduction

In recent years, there has been increasing recognition of the significance of niche construction, the capacity of organisms to modify natural selection in their environment and thereby act as co-directors of their own, and other species', evolution [1,2]. Examples of niche construction include animals manufacturing nests, burrows and webs, and plants modifying nutrient cycles. The defining characteristic of niche construction is not a modification of the environment per se, but rather an organism-induced change in the selective environment; hence the term includes migration, dispersal and habitat selection, where organisms relocate in space and experience new conditions, as well as traits that have a negative effect on the constructor's fitness, such as habitat degradation [2].

Genetic and ecological models have demonstrated that niche construction can affect evolutionary outcomes, even without culture [2–6]. For instance, niche construction can fix genes that would otherwise be deleterious [3,4], allow the persistence of organisms in inhospitable environmental conditions that would otherwise lead to their extinction [6], and be favoured even when costly because of the benefits that will accrue to distant descendants [7]. However, mathematical models reveal that niche construction due to cultural processes can be even more potent than gene-based niche construction, and demonstrate that cultural niche construction can modify selection on human genes with resulting effects on evolutionary outcomes [2,8–11]. Indeed, human niche construction is informed by a uniquely potent and cumulative cultural knowledge base [2,12].

It is highly probable that human cultural niche construction has co-directed human evolution [8,10,13–15]. In the last 100 kyr, humans have spread from East Africa around the globe, experienced an ice age, begun to exploit agriculture, witnessed rapid increases in densities, domesticated hundreds of species of plants and animals, and, by keeping animals, experienced a new proximity to animal pathogens [15]. Each of these events represents a major transformation in human selection pressures, and all (except the ice age) have been self-imposed. Humans have modified selection, for instance, by dispersing into new environments with different climatic regimes, devising agricultural practices or domesticating livestock. Niche-construction theory leads to the expectation that gene–culture coevolution has been a general feature of human evolution [15].

This perspective is reinforced by analyses of data from the human genome, which have revealed numerous genes that have experienced recent positive selection, many of which exhibit functions that imply they are responses to human cultural practices [15–21]. For instance, several lines of evidence demonstrate that dairy farming created the selective environment that favoured the spread of alleles for adult lactose tolerance [22–26]. Similarly, Perry et al. [27] found that copy number of the salivary amylase gene (AMY1) is positively correlated with salivary amylase protein level and that individuals from populations with high-starch diets have, on average, more AMY1 copies than those with traditionally low-starch diets. Higher AMY1 copy numbers and protein levels are thought to improve the digestion of starchy foods, consumed at elevated levels by agricultural populations, and may buffer against the fitness-reducing effects of intestinal disease. The transition to novel food sources with the advent of agriculture would appear to have been a major source of selection on human genes, and several genes related to the metabolism of protein, carbohydrates, lipids and phosphates show signals of recent selection [16,17,21,28]. In turn, agriculture and the domestication of animals is known to have facilitated the spread of crowd diseases and zoonoses, generating selection for human genes that confer resistance to these diseases in regions where they are prevalent [16–18,20,29,30]. Cultural niche construction could also have selected for enhanced cognitive capabilities, and many of the alleles subject to recent selection are known to be expressed in the brain [15–17].

Estimates for the number of human genes subject to recent rapid evolution range from a few hundred to two thousand; Williamson et al. [21] conclude that as much as 10 per cent of the human genome may be affected by linkage to targets of positive selection. While, in the vast majority of cases, it is not known what phenotype was the target of the inferred selection, nor which environmental conditions favoured such phenotypes, human cultural practices remain primary candidates, and geneticists are increasingly considering culture as a source of selection on humans [31,32].

One of the best-researched cases is the haemoglobin S allele (HbS), famous as a textbook case of heterozygote advantage, since it provides protection against malaria in the heterozygote form. Durham [22] studied populations of Kwa-speaking agriculturalists from West Africa, who cut clearings in forests to grow crops, often yams. The removal of trees had the effect of inadvertently increasing the amount of standing water when it rained, which provided better breeding grounds for malaria-carrying mosquitoes, which intensified selection on HbS. The fact that adjacent populations whose agricultural practices are different do not show the same increase in allele frequency supports the conclusion that cultural practices can drive genetic evolution. Moreover, this example illustrates how it may be necessary for models to take account of the frequency of resources modified through human niche construction (in this case, the amount of standing water) if they are to capture coevolutionary dynamics accurately.

Human agricultural practices are tied to specific spatial locations, and the selective feedback on human genes resulting from such practices, whether related to diet, disease resistance or morphology, is likely to covary in space with the incidence of the practice. Accordingly, there is a need for spatially explicit models with which to better understand how some human cultural processes have interacted with human genes during recent human evolution, while simultaneously tracking the frequency of relevant resources [26]. While there has been extensive modelling of human gene–culture coevolution [15,33–39], thus far spatial effects have been comparatively neglected. However, the introduction of spatial structure and stochasticity in finite populations is known to affect evolutionary outcomes when compared with non-spatial models [40–42]. Moreover, spatially explicit models of gene-based niche construction have revealed that niche-constructing traits can drive themselves to fixation by creating statistical associations with the recipient traits they favour [5]. Niche-constructing alleles expressed in the modification of local resources transform environmental conditions to favour some genotypes, and provided mating and dispersal is local, the niche-constructing alleles can hitchhike across a landscape to fixation.

Here, we develop spatially explicit gene–culture coevolutionary models to explore the interaction between local cultural niche construction and genetic evolution. Our aim was to explore whether interactions between cultural traits and alleles mediated by niche construction can create the conditions under which runaway selection can lead to evolutionary outcomes that can overcome external natural selection. We therefore investigate whether, and under what circumstances, cultural niche-constructing practices can ‘run away’ with genetic variation, and to what extent this dynamic is affected by (i) cultural transmission biases operating against the niche-constructing trait, (ii) the cost of cultural niche construction, modelled as a viability deficit to the cultural practice, and (iii) a viability cost to the genotype favoured by cultural niche construction. We also consider (iv) whether genetic variation enhancing the capability for cultural niche construction can be favoured by this runaway dynamic. Our analysis concentrates on three questions:

1. Can a culturally transmitted niche-constructing practice become universal, even when costly, through statistical association with a genetic trait it favours?

2. Can cultural niche construction generate selection for costly genetic traits that confer improved ability to cope with, or exploit the products of, said niche construction (e.g. genes expressed in disease resistance, or an expensive digestive protein)?

3. Can cultural niche construction favour the secondary hitchhiking of costly capabilities at other loci which confer more powerful niche-constructing abilities on the bearer (e.g. bigger brains)?

2. Methods

Our model marries the spatially explicit individual-based methods of Silver & Di Paolo [5] with the gene–culture coevolutionary analysis of Laland et al. [8]. The model therefore draws on simpler, well-understood systems to provide a foundation for exploring these complex coevolutionary processes. We consider a finite population of diploid individuals. We focus initially on a single diallelic resource-dependent locus, A, with alleles A and a, and a single two-state cultural niche-constructing practice, E, with variants E and e, but add a further genetic locus, B, for later analyses. Following Silver & Di Paolo [5], individuals are arranged in an n × n square lattice with wrap-around (toroidal) boundaries. Each lattice point (i, j) is occupied by a single individual with phenogenotype {A_ij,E_ij} and has an associated, local environmental resource frequency {R_ij}. Each individual has eight nearest neighbours (its Moore neighbourhood). Alleles make a contribution to fitness that is in part a function of the local resource frequency. Resource frequencies are subject to change as a result of (i) the niche-constructing activities of individuals in the population and (ii) independent processes of depletion and renewal. An individual's capacity for niche construction depends on the cultural practice deployed, with E individuals exhibiting niche construction, and e individuals exhibiting no niche construction. As in Laland et al. [8], if p_t−1(E) is the frequency of the trait E in the population at time t−1, the amount of the resource, R, at time t is given by

2.1

Here, λ₁ is the coefficient of independent depletion; λ₂ is the coefficient of positive niche construction, corresponding to niche-constructing activity that increases R (we consider only positive niche construction here); and λ₃ is a coefficient of independent renewal. Following Silver & Di Paolo [5], a scalar version of this equation is applied at each lattice point. At any particular lattice point, p(E) takes one of the values {0, 1} corresponding to the two possible cultural states, respectively {e, E}. Local resource frequency is thus a function of independent processes of depletion and renewal, and of the cumulative effect of local niche-construction activity over preceding generations. Following Laland et al. [8], we assume that 0 < λ₁, λ₂, λ₃, λ₁ + λ₂ + λ₃ ≤ 1, so that the local resource frequency, R_ij, can take any real value between 0, corresponding to a complete absence of the resource, and 1, corresponding to resource ‘saturation’. Unless otherwise specified, these parameters were set to λ₁ = 0.7, λ₂ = 0.2 and λ₃ = 0.1 in the simulations we report here. These values mean that we assume a resource that depletes in the absence of niche construction to an equilibrium of λ₃/(1 − λ₁) = 1/3. For example, in the case of the aforementioned Kwa, the amount of standing water is a function of independent renewal (i.e. rainfall), independent depletion (e.g. evaporation, runoff, absorption) and niche-constructing activities over multiple generations (e.g. planting crops, which reduces absorption and thereby increases standing water). All variables and coefficients are dimensionless.

We allocate fitnesses to combinations of genotype and cultural practice, henceforth ‘phenogenotypes’, as specified in tables 1–3, which are tailored to addressing questions 1–3 above. Genotype fitnesses depend both on resource frequency and on selection from an external source. In all models, the baseline fitness of the three genotypes are based on Laland et al. [8] as follows:

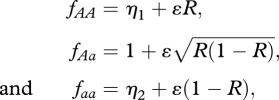2.2

where R = R_ij, the resource frequency at the individual's lattice point. The first terms in each of these fitness relations correspond to fixed fitness components, representing the effect of external selection operating at A. The second terms refer to the resource frequency-dependent components of selection, and it is these that are affected by niche construction. The coefficient of proportionality ɛ determines the strength (relative to external selection), and direction of resource frequency-dependent selection, with positive ɛ indicating that increased environmental resource levels will favour the A allele. We set ɛ = 0.3 in all the simulations we report here. A summary of all parameters used is given in table 4.

Table 1.

Phenogenotype fitness functions to explore the evolution of costly cultural niche construction (α is the selection coefficient operating on the cultural practice E).

	E	e
AA	w11 = α+ ɛR	w12 = 1 + ɛR
Aa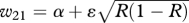
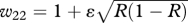aa	w31 = α+ ɛ(1 − R)	w32 = 1 + ɛ(1 − R)

Table 3.

Can niche construction favour the hitchhiking of costly capabilities at other loci? Here, R_t =λ₁R_t−1 + λ₂(z₁(1 + φ) + z₂(1 + φ/2) + z₃) + λ₃, where z₁–z₃ are the frequencies of BBE, BbE and bbE individuals, respectively.

	BB (β1)	Bb ((β1 + β2)/2)	bb (β2 = 1)
AA (η = 0.999)	w11 = β1 + ɛR	w12 = ((β1 + β2)/2) + ɛR	w13 = 1 + ɛR
Aa (1)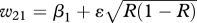
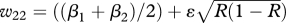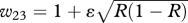aa (1)	w31 = β1 + ɛ(1 − R)	w32 = ((β1 + β2)/2) + ɛ(1 − R)	w33 = 1 + ɛ(1 − R)

Table 4.

Summary of terms.

term	explanation
E,e	alternative niche-constructing cultural practices
A,a	alleles at A locus
B,b	alleles at B locus
R	resource frequency
λ1	independent resource depletion
λ2	positive niche construction
λ3	independent resource renewal
p(E)	frequency of E cultural practice
γ	negative niche construction
ɛ	strength and direction of resource frequency dependence
α	selection coefficient acting on cultural practice
c0	probability e × e mating has E offspring
c1	probability e × E mating has E offspring
c2	probability E × e mating has E offspring
c3	probability E × E mating has E offspring
η1	AA fitness
η2	aa fitness
β1	BB fitness
β2	bb fitness
φ	degree to which B potentiates niche construction
f	probability of oblique transmission

Individuals mate with a randomly chosen neighbour (Moore neighbourhood), and offspring inherit their parents' genotypes in Mendelian proportions. Here we consider both vertical and oblique transmission of cultural traits. Vertical transmission occurs according to the parameters specified in table 5. Offspring (viability) fitness is determined with reference to the resource level at one (randomly selected) parent's location, under the assumption that newborn offspring develop in the same location as one of their parents. The probability of an offspring surviving is proportional to its fitness related to the minimum and maximum values of equation (2.2) given the selection coefficients in a given simulation and the limits of R (0,1). Offspring surviving to the dispersal stage are placed in a cell chosen at random from the eight cells in the neighbourhood of the parent with which the newborn develops, plus that parent's own cell, replacing the original occupant. These individuals are then considered adult and capable of reproduction. In this way fitter offspring may spread out to colonize neighbouring cells, while an effective carrying capacity equal to the total population size is maintained. Following Silver & Di Paolo [5], a generation is defined as n² consecutive random matings, so that there will be significant overlap between one generation and the next.

Table 5.

Probabilities of vertical cultural transmission of E and e given parental traits.

parental traits	probability of E offspring	probability of e offspring
E × E	c3	1 − c3
E × e	c2	1 − c2
e × E	c1	1 − c1
e × e	c0	1 − c0

We considered questions 1–3 in turn, in each case running a series of simulations to explore the behaviour of the system, using the parameters and fitness equations described in tables 1–3, respectively. For each set of parameter values we varied the starting frequencies of A and E independently from 0.1 to 0.9 in 0.1 increments, giving 81 different starting conditions, and ran 10 simulations at each one. Spatial models ran in a 60 × 60 toroidal grid, and non-spatial models had the same population size of 3600 individuals. Alleles were distributed randomly and independently of each other at the start of each simulation, such that genotype frequencies at the start of the simulation averaged Hardy–Weinberg proportions, and cultural traits were randomly distributed across individuals irrespective of genotype. Lattice points were assigned uniform randomly distributed starting resource values (R) between 0 and 1. For each analysis, we also ran non-spatial controls in which the ‘neighbourhoods' for mating and dispersal comprised the entire lattice so that individuals and resource locations were picked at random from the general population. All simulations ran until A (question 1), E (question 2) or A and E (question 3) became either fixed or extinct, or simulations reached 1000 generations.

1. Can a cultural niche-constructing practice drive itself to fixation, even when costly, through statistical association with a genetic trait it favours?

We consider a costly niche-constructing practice E (selection coefficient α < 1), which increases the amount of resource R in the environment and generates selection favouring allele A. Phenogenotype fitnesses are specified in table 1. Here we explore how a transmission bias for and against the cultural practice E (i.e. variation in c = c₁ = c₂ = {0.45, 0.5, 0.55}, c₀ = 0, c₃ = 1) and selection against E (α) affect the dynamics.

2. Can cultural niche construction generate selection for costly genetic traits?

We consider a costly genetic trait AA (selection coefficient η ≤ 1), which is favoured by the niche-constructing practice E (selection coefficient α = 1). Here, the increase in resource due to niche construction depends on the frequency of both A and E. The modified version of equation (2.1) used to update the resource level and the relevant phenogenotype fitness functions are specified in table 2. We explore how a transmission bias for and against the cultural practice E(c) and selection against the AA genotype (η) affect the dynamics.

Table 2.

Phenogenotype fitness functions to explore the evolution of a costly capability to exploit cultural niche construction. Here, R_t = λ₁R_t−1 + λ₂u + λ₃, and u is the frequency of AE.

genotype	fitness
AA	w11 = η+ ɛR
Aa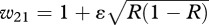
aa	w31 = 1 + ɛ(1 − R)

3. Can cultural niche construction favour the secondary hitchhiking of costly capabilities at other loci, expressed in more potent niche construction?

For this question we introduce a second genetic locus, B, with alleles B and b, where allele B enhances the rate at which niche constructors produce resource R. Homozygous BB individuals have selection coefficient β₁, those with bb have coefficient β₂, and heterozygotes (Bb) have (β₁+ β₂)/2. In individuals with the cultural trait E (selection coefficient α = 1), BB enhances niche construction by proportion 1 + ϕ, and Bb by proportion 1 + ϕ/2 (although the condition 0 ≤ R ≤ 1 was still applied). The modified version of equation (2.1) used to update the resource level and the relevant phenogenotype fitness functions are specified in table 3. We explore how a transmission bias for and against the cultural practice E(c) and selection against the B allele (β₁ < 1, β₂ = 1) affect the evolutionary dynamics.

3. Results

(a). Can a cultural niche-constructing practice drive itself to fixation, even when costly?

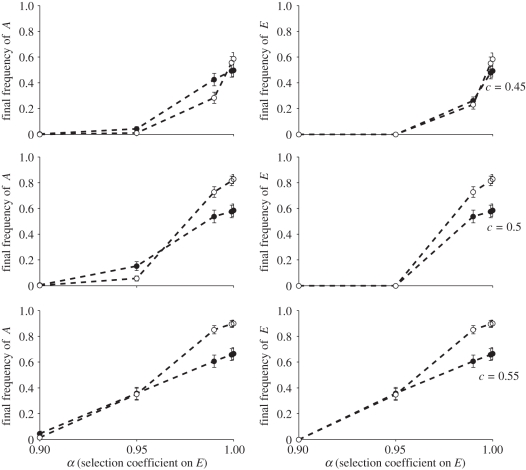
Across a broad range of conditions, cultural niche-constructing practices can generate selection for specific gene-based traits and hitchhike to elevated frequencies through the build up of statistical associations between practice and trait (figures 1–3). This is most apparent where there is little or no fitness cost to the cultural practice (figure 2, α ≈ 1), but is observed to a lesser degree even in the face of strong selection against E (e.g. a 5% disadvantage).

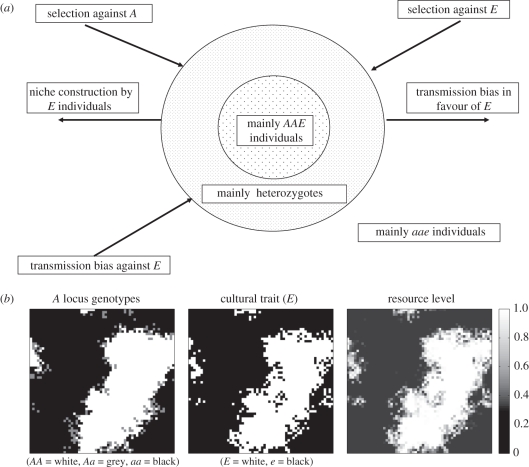
Figure 1.

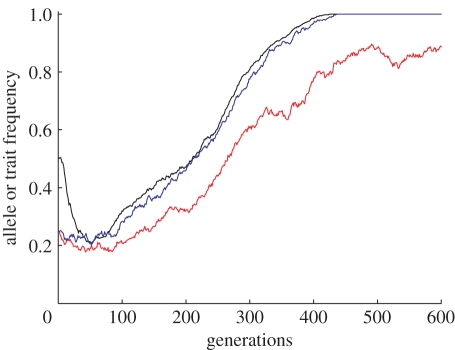
(a) Schematic of evolutionary forces acting on spatial clusters of individuals carrying linked cultural niche-construction traits and alleles favoured by niche construction. (b) Snapshot illustrating spatial clustering associations between A, E and R during a simulation run of the evolution of a costly capability to take advantage of cultural niche construction (selection against A allele, η = 0.95, no cultural transmission bias).

Figure 3.

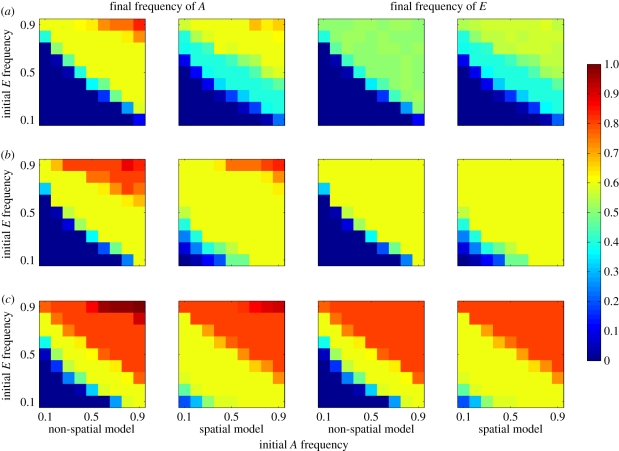
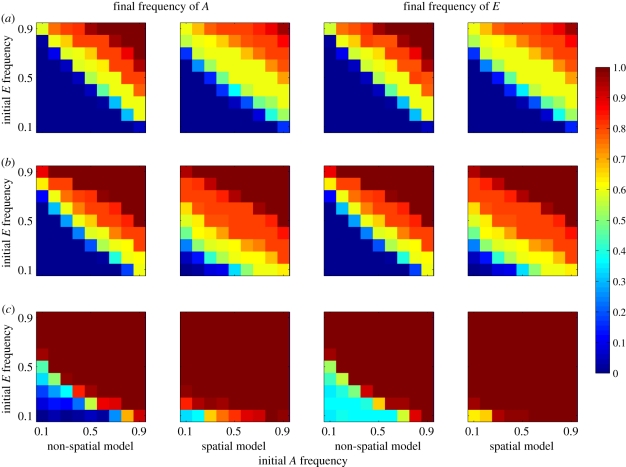
Effect of starting conditions on the evolution of costly cultural niche construction. Plots show end frequencies of A and E against their starting frequencies. Cell values are means over all levels of selection against E (α ={0.9, 0.95, 0.99, 0.999, 1}). (a) c = 0.45; (b) c = 0.5; (c) c = 0.55.

Figure 2.

Evolution of costly cultural niche construction. Plots show frequency of allele A favoured by higher resource levels and cultural niche-constructing trait E at the end of simulations run with varying levels of selection against, and cultural transmission bias with respect to, E (α and c parameters, respectively). Values are means over all starting conditions with respect to the initial frequencies of A and E and error bars show ±1 s.e. Open circles show results from simulations with local mating and dispersal, filled circles are from those with global interactions.

These dynamics occur because, initially by chance, clusters of niche constructors appear in specific regions of space, generating a local concentration of the resource R, which in turn generates selection that favours allele A. In the spatial model, individuals mate and reproduce locally. Under these circumstances, allele A becomes statistically associated with the niche-constructing practice E, while allele a becomes associated with e. This means that the selection on A generated by niche construction inadvertently favours E through hitchhiking. Provided the clusters of niche constructors reach a critical threshold size they will typically increase until the trait is fixed. This assortative mating does not occur in the non-spatial model, preventing E from being disproportionately favoured by selection on A.

The cluster size effect represents a balance of several processes (figure 1). The dynamics are similar to those observed in Silver & Di Paolo's [5] genetic niche construction spatial model, but here there is the additional complication of cultural transmission biases. To understand the process, it is helpful to envisage two concentric circles, the smallest encompassing the cluster. Because the niche construction leads to non-random associations between the alleles and cultural traits, inside the inner circle are mainly AAE individuals, while outside the outer circle are mainly aae individuals. Separating the two is a boundary layer dominated by heterozygotes. Newly born AAE individuals disperse into the boundary layer from the inner circle, while newly born aae individuals enter the boundary layer from the outer region. Because the outer circle is larger than the inner circle, other matters being equal, this dispersal will tend to act to reduce cluster size. The magnitude of this force diminishes with cluster size, since the relative size of the two circles approaches 1 as the cluster increases. Opposing this process is the niche construction of those boundary layer individuals exhibiting the E cultural practice. This niche construction generates conditions that favour the A allele, which is disproportionately found in E individuals. Natural selection and cultural transmission also play a role, by affecting phenogenotype fitness (figure 1). Provided the balance of these processes favours E over e within the boundary layer, then the clusters will increase in size.

We found that cultural niche construction could overcome moderate and sometimes even strong counter selection, and evolve to high frequency, especially when there was no transmission bias or where a transmission bias favoured the practice (c > 0.5) (figure 2). The similarity in outcome for both the A allele and the E cultural practice shows that strong associations are built up between them under most conditions. Generally, in spatially structured populations A and E both reached higher frequencies on average than in fully mixed scenarios, except when counter-acting natural or cultural selection was very strong. This difference was driven largely by spatial structure, enabling both trait and practice to become established and increase from lower initial frequencies (figure 3). When initial frequencies are very high or very low there are also differences between spatial and non-spatial model outcomes. These result from the possibility in spatial models that local gene frequencies can diverge significantly from population-level frequencies. This can have a buffering effect that acts to preserve low-frequency alleles in pockets of local abundance in situations where a lack of spatial structure would lead to extirpation of the allele. The exception to this trend occurred when a cultural transmission bias (i.e. c < 0.5) or extremely strong selection (i.e. α = 0.9) acted against the E trait. In this case, the outcomes in mixed and structured populations were very similar. While here we concentrate on the findings of a vertical cultural transmission model, we have also analysed a model with oblique transmission, in which individuals learn from their immediate neighbours. We found that the effects described above break down when oblique transmission is very potent (i.e. the probability of learning from a non-parent is greater than 0.8), but that the effects persist with moderate or low levels of oblique transmission.

(b). Can cultural niche construction generate selection for costly gene-based traits?

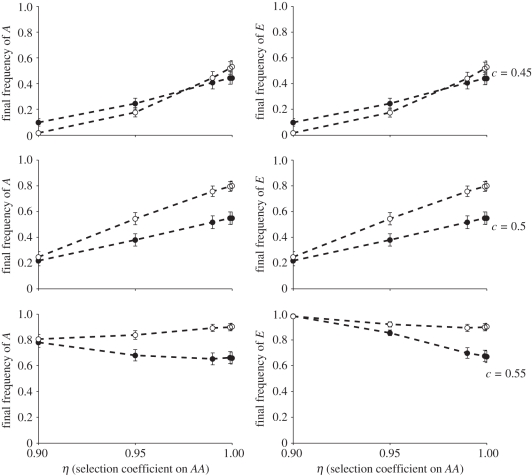
Here our results were very clear. Under almost all conditions a cultural niche-construction trait could drive a genetic trait to fixation, in spite of a significant viability deficit to the trait. The only exception occurred when a cultural transmission bias against the niche-constructing practice and a very strong viability deficit to the trait were both acting together. The aforementioned dynamics, resulting from the association of genetic trait and cultural practice, is sufficiently strong to overcome strong counter selection (e.g. more than 5% disadvantage). Even more striking is the observation that a modest cultural transmission bias favouring the practice can generate selection that takes extremely low fitness traits (e.g. more than 10% disadvantage) to fixation. That this is not dependent on spatially mediated hitchhiking is illustrated by the observation of the same process operating in non-spatial populations, and is consistent with earlier analyses of the impact of cultural niche construction [8]. The niche construction allows allele A to reach high frequencies when counter-selection was moderate to weak, and persist at non-negligible frequencies even in the face of potent counter-selection (figure 4). Only a moderate cultural transmission bias (i.e. c > 0.5) is required to strongly favour the niche-constructing practice so that both allele and cultural practice nearly always evolve to fixation even when initially quite rare (figure 5). Again, spatial structure facilitates the spread of these traits to higher frequencies than in mixed populations. We note in presenting these results that the values we chose for λ₁, λ₂, λ₃, and ɛ mean that the fitness functions defined in equation (2.2) produce an asymmetry with respect to that portion of fitness that relates to the level of R that favours the A allele (in the long-term presence of E, R → 1, so the second term of the fitness function for AA evaluates to ɛ while for aa in the long-term presence of e this evaluates to 2ɛ/3). Not surprisingly, altering the dynamics of the niche-constructing ecology via these parameters can alter the model outcomes such that the coevolution of A and E no longer occurs. We concentrated here on areas of the parameter space where these effects could occur, but the reader should bear in mind that there will be areas where it does not.

Figure 4.

Evolution of a costly capability to take advantage of cultural niche construction. Plots show frequency of allele A favoured by higher resource levels and cultural niche-constructing trait E at the end of simulations run with varying levels of selection against the homozygote AA (η = {0.9, 0.95, 0.99, 0.999, 1}), and cultural transmission bias with respect to E (c). Values are means over all starting conditions with respect to the initial frequencies of A and E and error bars show ±1 s.e. Open circles show results from simulations with local mating and dispersal, filled circles are from those with global interactions.

Figure 5.

Effect of starting conditions on the evolution of a costly capability to take advantage of cultural niche construction. Plots show end frequencies of A and E against their starting frequencies. Cell values are means over all levels of selection against A (η). (a) c = 0.45; (b) c = 0.5; (c) c = 0.55.

In terms of starting frequencies, the switch between those resulting in extinction of the trait and those resulting in fixation occurred over much smaller change in starting conditions than the previous analysis. Under some conditions, particularly when cultural transmission biases favour E, a change in the starting frequencies of either allele by 0.1 can shift the outcome from a high probability of extinction to a near-certainty of fixation, suggesting that factors such as drift, bottlenecks or founder effects could play a significant role in shifting populations from one state to another.

(c). Can cultural niche construction favour the secondary hitchhiking of costly capabilities at other loci, expressed in more potent niche construction?

Here a similar analysis produced more ambiguous results, with B only hitchhiking to higher frequency under much more restricted conditions. Across the bulk of conditions under which E hitchhikes, B does not. While A and E both reach high frequencies, and exhibited a similarity of outcome that showed they were highly associated, there was no indication that B had formed any association with either A or E. To the contrary, its outcomes were independent of the practice and the alleles at the other locus, and appeared largely to be affected only by selection at B, even for large values of ϕ (e.g. ϕ = 10), and no matter the strength of cultural transmission bias, c. These results occur in spite of the fact that, even with ϕ = 1, the effect of B on resource levels is dramatic.

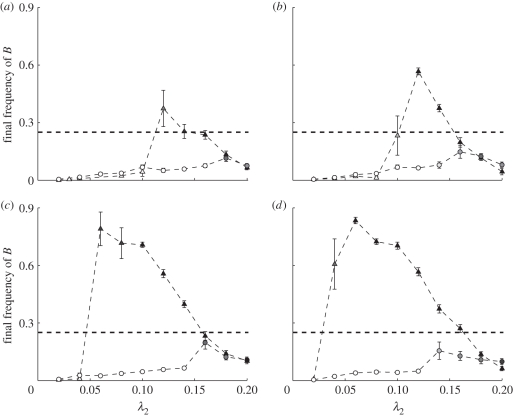
However, there is a restricted region of parameter space in which the secondary hitchhiking reliably occurs. It requires, perhaps counter-intuitively, a low coefficient of positive niche construction, λ₂. Figure 6 shows that B's hitchhiking lags behind the rapid and strong interaction between A and E; this is the characteristic pattern. There exists a window of low levels of positive niche construction, λ₂, under which secondary hitchhiking is apparent (figure 7), with values of λ₂ too high or too low failing to lead to increased frequencies of B. When λ₂ is too high then the niche construction of individuals with bb genotype and the E practice is already potent, and the resource R reaches saturation before enough time has passed for an association of alleles A and B to build up. Once A and E become fixed, the opportunity for B to hitchhike on them is lost. Conversely, when λ₂ is too low then the niche construction of E individuals with the bb genotype is too weak, so A and E simply never become established, and B cannot hitchhike. Only when niche construction is within the window illustrated in figure 7 are A's and E's spread to fixation sufficiently reliable and slow to allow linkages to build up between these and B. Once the association is established, typically in a confined spatial region, then the AABBE combination begins to expand. This effect was only observed in spatial models, and never in non-spatial ones. Spatial structure is absolutely essential for B's spread because the requisite mutual reinforcement of the A, E and B traits cannot happen if their effects are diluted and dispersed across a population.

Figure 6.

Time series of a single simulation run with λ₂ = 0.06, showing lagged hitchhiking of B allele even when selection acts against BB (β₁ = 0.99). Note that after A and E fix (typically at this point the resource, R, will also be saturated), B can no longer hitchhike and begins to show drift-like dynamics. Other parameters were cultural transmission bias, c = 0.5, selection on AA, η = 0.999, and selection on bb, β₂ = 1. Black line, A; red line, B; blue line, E.

Figure 7.

Effect of λ₂, the coefficient of positive niche construction, and ϕ, the strength of B's effect on niche construction, on the evolution of costly genes that potentiate niche construction. Plots show frequency of allele B at the end of simulation runs, with each point representing the mean (±1 s.e.) of 10 runs. Symbols are shaded according to the proportion of the 10 runs in which A and E both fixed (white = no runs fixed, black = all runs fixed). All other parameters were fixed—cultural transmission bias, c = 0.5, selection on AA, η = 0.999, selection on BB, β₁ = 0.99, selection on bb, β₂ = 1. Initial frequencies of E, A and B were set at 0.25, 0.5 and 0.25, respectively. Note the high levels of B at intermediate values of λ₂ for spatial models only. Triangles, spatial model; circles, non-spatial model; dashed lines, B starting frequency. (a) ϕ = 1; (b) ϕ = 2; (c) ϕ = 5; (d) φ = 10.

4. Discussion

We have used spatially explicit gene–culture coevolutionary models to investigate how cultural processes could drive bouts of selection on human genes through modifying local resource distributions. The principle point to emerge from our analysis is that under a broad range of conditions cultural niche-constructing practices can generate selection for specific gene-based traits and hitchhike to fixation through the build up of statistical associations between practice and trait. This is most apparent where the fitness cost of the cultural practice is low but is observed to a lesser degree even in the face of very strong counter-selection. Cultural niche construction could overcome moderate and even strong counter selection and evolve to high frequency, especially when there was no transmission bias or where a transmission bias favoured the practice.

These dynamics are most pronounced in the spatially explicit models because niche construction and spatial structure lead the genetic trait and cultural practice to become statistically associated. This means that the selection on genes generated by niche construction inadvertently favours the cultural niche-constructing practice itself through hitchhiking. Provided the clusters of niche constructors reach a critical threshold size they will typically increase until the trait is fixed. The dynamics are similar to those observed in Silver & Di Paolo's [5] genetic niche construction spatial model, but further complicated by cultural transmission biases. They are robust to moderate levels of oblique cultural transmission (here, learning from neighbours), although high levels of oblique transmission unsurprisingly make it harder to build up gene–culture correlations.

In essence, the dynamical process we describe closely resembles that of runaway sexual selection. Geneticist Fisher [43] proposed a positive feedback mechanism that could potentially explain the evolution of costly traits in animals that do not increase survival. Such traits were thought to be favoured because they increase the individual's attractiveness to the opposite sex. Subsequent analysis has established that if the preference reaches a sufficiently high frequency it can overcome a viability deficit to the trait and generate selection that will increase trait frequency. Since individuals with the trait mate assortatively with individuals with the preference, over time these characters become statistically associated, such that the selection on the trait leads to the preference hitchhiking to higher frequency [44,45]. The process is described as ‘runaway’ because over time it would facilitate the elaboration of both trait and preference.

Here the cultural niche-construction practice (E) is analogous to the mating preference which, provided it is of sufficiently high frequency, could generate a selective environment that favours the otherwise costly allele A. We find strong support for the hypothesis that cultural niche construction can generate selection for costly gene-based traits. The cultural niche-construction trait almost always drove the low viability genetic trait to fixation, with the only exception being where both natural selection and a transmission bias opposed the process. Population structure strengthens this effect because it promotes assortative mating leading to non-random associations between trait and practice. While here the process stops once the trait reaches fixation, the resulting uplift in the frequency of E is sufficient to significantly increase the chances of E becoming fixed. Niche-constructing cultural traits have effectively driven themselves to fixation. Note, our focus on a single diallelic locus is purely for mathematical convenience, and is designed to provide insight into the probable selection on any relevant genetic variation. In reality, human biological traits are likely to be influenced by multiple genes, and the runaway cultural niche-construction process we describe would potentially favour, and hitchhike on, any genetic variation that thrived in the resource rich environment. Moreover, genetic variation that enhances the cultural niche-constructing capability can also be caught up in this dynamic, opening up the possibility that both cultural practice and trait may experience repeated waves of selection, as is characteristic of runaway sexual selection. This process can help explain the evolution of certain costly biological traits in the human lineage, such as large brains, complex cognition or expensive digestive enzyme production. We note that alleles expressed in the nervous system, brain function and brain development are an over-represented category among classes of genes known to be subject to recent selection [16,17]. Molecular geneticists have not only identified numerous brain-expressed genes in the human genome (or, indeed, no longer in the human genome) that have been subject to recent selection, they have estimated the time depth of these changes, and they have mapped them onto gene-expression networks using molecular tools such as co-expression analysis [32]. Cultural niche construction is a prime candidate for the source of this selection [15], and the processes revealed by our analysis are potentially important candidate mechanisms.

Such considerations are further strengthened by our description of the conditions favouring secondary hitchhiking at other loci, whereby costly alleles are favoured simply because they amplify the niche-constructing effects of the cultural trait E. Two points stand out in these findings—firstly, that this secondary hitchhiking can only occur when the niche-constructing effect on resource dynamics is comparatively weak, and secondly that this can only occur in spatially structured populations.

The first limitation arises from the time lag between the initial favouring of the AAE complex and the subsequent hitchhiking of the B allele on its rising frequency. If, either because niche construction is too weak to favour allele A, or because niche construction is so effective that AAE fixes too rapidly and the resource R saturates, B cannot hitchhike. However, within this window of opportunity, weak but nonetheless effective niche-constructing capabilities generate selection for more potent niche-constructing capabilities, in a self-reinforcing dynamic.

We note that this restriction to the range of circumstances under which secondary hitchhiking occurs results directly from the assumption of our model that there is a fixed upper bound to R. One might argue that for many aspects of human niche construction this assumption might be relaxed. For example, agricultural revolutions have repeatedly produced massive increases in yields per unit area. If R was an unbounded resource, then it is possible to envisage how a prolonged upward dynamic of primary hitchhiking resulting from niche construction could produce broader conditions favourable to the secondary hitchhiking of enhanced niche-constructing capabilities. Nonetheless, most resources cannot rise without limit, so at some point an upper bound will be reached, and the opportunities for the evolution of more potent niche construction will diminish.

The second limitation, that secondary hitchhiking can only occur in spatially structured populations, is especially interesting because it appears to reflect so well the kind of agriculture- or technology-driven gene–culture coevolution discussed in the introduction. This spatial structure acts in two ways. Firstly, it generates a local concentration of the AAE complex, and secondly, it creates an advancing boundary zone of heterozygotes (figure 1), which is especially fertile ground for secondary hitchhiking. It is possible to envisage such zones occurring as waves of agricultural or technological innovation, through which cultural niche-constructing traits favour locally advantageous genotypes and in the process relentlessly drive their own advance, and perhaps even their own potency. In the non-spatial case, the dispersal of niche-constructing individuals across the shared resources of a population dilutes local resource concentrations, and means that statistical associations between the A and B alleles cannot build up.

Our findings suggest that runaway cultural niche construction could have played an important role in human evolution, both through driving specific gene–culture coevolutionary episodes, and through facilitating the evolution of an enhanced niche-constructing capability in the human lineage through secondary hitchhiking [15]. Note that the models we have presented here considered only moderate biases in cultural transmission (0.45 ≤ c ≤ 0.55), but such biases can be considerably stronger [33], and this may well increase the potency of cultural niche construction further. The B locus in our model can potentially serve to represent any genetic locus expressed in a costly biological trait that impacts the niche-constructing capability. Our consideration of this secondary hitchhiking was largely motivated by the possibility that the average effect of allele B might confer a larger brain or enhanced cognitive capability. The latter includes an improved cultural capability, for instance, a capacity for motor imitation, teaching or language. Accordingly, our analysis may help to explain the observations that humans are simultaneously the species with the largest relative brain size, the most potent capacity for niche construction, and the greatest reliance on culture. Furthermore, it has not escaped our attention that in spatially structured contexts such as those we address, the benefits of local niche construction could potentially accrue both to the constructor's own offspring and those of its neighbours. The potential for niche-construction theory to generate insights into the evolution of cooperation is an exciting area for future research [7,46,47].

It is apparent that cultural niche construction can lead to non-trivial alterations in evolutionary processes, especially in the case of spatially structured populations. We consider it highly probable that human cultural processes have driven evolutionary episodes in the human lineage, and our analysis may help understand current features of the human genome.