Before senescence: the evolutionary demography of ontogenesis

Abstract

The age-specific mortality curve for many species, including humans, is U-shaped: mortality declines with age in the developing cohort (ontogenescence) before increasing with age (senescence). The field of evolutionary demography has long focused on understanding the evolution of senescence while largely failing to address the evolution of ontogenescence. The current review is the first to gather the few available hypotheses addressing the evolution of ontogenescence, examine the basis and assumptions of each and ask what the phylogenetic extent of ontogenescence may be. Ontogenescence is among the most widespread of life-history traits, occurring in every population for which I have found sufficiently detailed data, in major groups throughout the eukaryotes, across many causes of death and many life-history types. Hypotheses seeking to explain ontogenescence include those based on kin selection, the acquisition of robustness, heterogeneous frailties and life-history optimization. I propose a further hypothesis, arguing that mortality drops with age because most transitions that could trigger the risks caused by genetic and developmental malfunctions are concentrated in early life. Of these hypotheses, only those that frame ontogenescence as an evolutionary by-product rather than an adaptation can explain the tremendous diversity of organisms and environments in which it occurs.

1. Introduction

The study of the evolution of senescence largely began with Sir Peter Medawar's lecture [1], ‘An unsolved problem of biology’. In it, he presents a human age-specific mortality curve, showing high rates of mortality among infants, minimum mortality at age 12 and an exponentially increasing death rate thereafter. This last portion he dubs senescence. He writes, ‘because there are clearly special reasons why baby animals should be more vulnerable… than their elders, I am proposing to neglect the arc of the curve of the course of mortality that lies before its minimum’. Explaining senescent portions of age-specific mortality curves remains the central focus of evolutionary demography [2–6]. Yet Medawar never enumerated what the clear special reasons for mortality's long initial decline may be. In the tradition he began, few attempts have been made to explain the evolution of death rates at ages prior to senescence.

As pointed out by Young [7], published age-specific survival curves for vertebrates ‘have mainly been segments of the life curve, usually with the anterior end missing [8]’. Many recent vertebrate [9,10] and invertebrate [11–17] examples confirm this; the focus on senescence is such that mortality before senescence is rarely mentioned. The ontogenetic decline in mortality risk is so understudied as to lack even a standard name. To facilitate discussion, I coin the term ‘ontogenescence’. Ontogenescence is a population-level phenomenon in which the death rate of each cohort tends to decrease with increasing age between conception and maturity. This pattern has been referred to simply as ‘juvenile mortality’, but this is a misnomer, as the period of ontogenescence begins well before the juvenile phase. Further, the phrase juvenile mortality conveys nothing about change in rates of mortality with age, simply that individuals are dying during the juvenile phase, conflating level of mortality with slope of mortality.

The pattern Medawar describes, of ontogenescence followed by senescence, is shared by all mammals for which good data exist (see compilations in [18–20]), a wide range of other biological organisms (discussed below) and at least some populations of organizational [21] and mechanical entities [22]. The problem of the evolution of senescence has, perhaps prematurely, been declared solved [23]. Yet, many basic questions regarding the evolution of ontogenescence have never been systematically asked. The most central of the unanswered questions is, why has natural selection led to (or failed to eliminate) ontogenescence? The force of selection against mortality is constant across pre-reproductive ages [24]. Dying before reproducing is generally maladaptive, and the most cited evolutionary explanations of senescence [1,24–27] fail to predict ontogenescence, or early-life mortality generally. An examination of disparate literatures reveals few developed hypotheses and no attempt to synthesize or compare them. Below, I review the evidence for ontogenescence in humans and other biological organisms and summarize the available hypotheses to explain the evolution of ontogenescence, proposing one novel mechanism. I then examine which of these hypotheses operate broadly enough to explain the pattern, and speculate on what sort of population might lack ontogenescence.

2. The pattern in humans

Our most detailed knowledge of ontogenescence comes from human populations, making us a useful starting place in specifying the pattern to be explained. Demographers have developed several mathematical models describing the shape of ontogenescence, summarized in the electronic supplementary material S1. The unifying factor in these models is an exponential (or faster than exponential) decline in mortality with age from birth. No human population lacking such a decline has been documented.

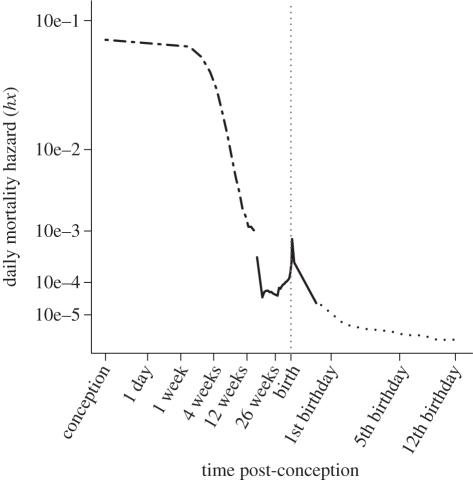
This pattern begins well before birth [28,29], with mortality risk extraordinarily high at the very beginning of pregnancy. Figure 1 describes daily mortality risk at each age from conception to 12 years after birth. The changing mortality risk is not monotonic, as there is a peak spanning those ages when births occur. However, the overall pattern is rapidly falling mortality risk coupled with a decrease in the rate of this fall. These data are averaged across maternal ages; risk of pregnancy loss is considerably higher in the youngest and the oldest mothers. Indeed, the fall in fertility between the ages of 20 and 40 is due largely to changes in risk of foetal loss rather than changes in fecundability, the capacity to initiate pregnancies [28,30]. Pregnancies are not easily detectable in their first week with current technology; our understanding of pregnancy initiation and loss in the first week depends upon models (electronic supplementary material, S2). Prenatal ontogenescence has often been linked to the proximate mechanism of chromosomally abnormal conceptuses spontaneously aborting. Postnatal ontogenescence is observed in statistics on most common proximate causes of death [31]; both are probably attributable to multiple interacting ultimate causes.

Figure 1.

Mortality hazard from conception to 12th birthday. Estimated mortality hazard from conception to 12th birthday for a composite of human populations. Both axes are root transformed for graphical convenience. The dotted grey line demarks the transition from foetal to infant mortality. Mortality hazard drops sharply with in utero development, beginning to rise around 26 weeks and reaching a local maximum with the number of deliveries. Mortality declines nearly monotonically for 12 years thereafter. Data are from three sources: foetal data from rural Bangladesh (dashed–dotted line [28]), late foetal and infant data from Norway 1967–1973 (solid line [90]) and childhood mortality data from Norway 1970 (dashed line [91]). A population effect can be seen in these data, but it is strongly outweighed by the age effect.

3. The pattern in other organisms

A huge range of organisms experience unsustainably high mortality near the beginning of life. Whether in the laboratory, on the farm or in the wild, many offspring do not make it to hatching, birth or germination. Mortality of the newly independent organisms is frightfully high, and as they mature, mortality declines until senescence sets in. While it took time and informed analysis to put to rest the contention that senescence does not occur in the wild [32–35], it requires no great effort to detect natural ontogenescence. The severity of the environment may influence the magnitude of the losses (e.g. [36,37]), and particular causes of death (e.g. siblicide [38] or juvenile migration [39]), and may drive mortality at one stage of development to exceed that at an earlier stage. Nevertheless, the general declining trend seems to be modified by, not caused by, unsuitable environments.

It is beyond the scope of one paper to examine ontogenescence for every species for which relevant data are available, but I will mention a few points. Ontogenescence is found in species that invest heavily in few offspring, such as African elephants, Loxodonta africana [40] and grey whales, Eschrichtius robustus [41], and those that produce large numbers of inexpensive offspring, such as asymptotically growing marine fishes [42,43]. Ontogenescence is known to occur in each major group of vertebrates [7,10,18,37,44–49]. We may hypothesize that while it is not unique to vertebrates, all vertebrate populations experience ontogenescence.

Ontogenescent mortality is detectable in insect populations [50], brown algae [51], red algae [52] and many green plants [53–57]. Benthic marine invertebrates including foraminifera, polychaetes, bivalves, gastropods, barnacles, ascidians, bryozoans and echinoderms generally lose more than 90 per cent of each cohort in short juvenile periods, with mortality highest early, in the planktonic phase and just after settlement [58–60]. Foraminifera are notable as the only single-celled organisms for which I have found published evidence for ontogenescence [59]. For most micro-organisms, we have little or no data on age-specific mortality, and many major gaps persist in our phylogenetic map of ontogenescence.

4. Explaining the pattern

While no field has focused its attention on the evolution of ontogenescence, several fields, including demography, sociobiology, population genetics and ecology have made forays into the subject. The isolated hypotheses they propose frame ontogenescence as an adaptation, a by-product, a maladaptive trait or as a process of selection in itself. Lacking direct evidence as to what drives the evolution of ontogenescence, we may evaluate each hypotheses on whether it can predict the breadth of the pattern.

(a). Ontogenescence as an adaptive trait

Ontogenescence may have arisen through selection for limiting the resources flawed offspring draw from kin [24]. If so, two actors may be seen to initiate the death, the offspring or the kin. The flawed offspring could initiate its own death, so as to avoid consuming the resources of its relatives. It seems more reasonable that parents should evaluate the viability of offspring and withdraw investments in the inviable as soon as possible [61]. Filial cannibalism, for example, is far more likely to be selectively advantageous when parents can selectively consume offspring of low quality [62]. In many teleost fish, risk of filial cannabalism is high, but declines with increasing offspring age [63].

Without specifying the actor, Lee [64] formalizes the argument that ontogenescence arises through the evolutionary response of age-specific mortality to patterns of familial transfers of resources. Under this model, an individual's mortality risk is determined by that individual's economic value (measured in expectations of inward and outward transfers of resources) to kin, with more valuable individuals less likely to die. Lee's model has been criticized as using the group as the unit of selection [65], as it makes no correction for the degree of relatedness between transferring kin. A subsequent microsimulation [66] modelling the population as single sex supported Lee's original conclusions, but the idea has yet to be modelled while accounting for the relatedness structures of sexually reproducing populations. Species providing parental care may be selected to quickly practise quality control, withdrawing care from suboptimal offspring, leading to high and decreasing mortality. This hypothesis cannot explain ontogenescence that continues past the age at which parental investment ceases (e.g. in marine invertebrates [67], or megapod birds [68, p.74]), and therefore is insufficient as a general explanation of ontogenescence.

(b). Ontogenescence as a by-product: the link to growth

Ontogenescent mortality, if not adaptive, may be framed as a by-product of selection. A theoretical model offered by Chu et al. [69] shows that both senescence and ontogenescence may arise through an optimal allocation of resources in the absence of parental care, if there is a trade-off between reproduction, current growth and current survival. If selection for growth is strong enough, a risky developmental pattern that increases growth rate but decreases protection against mortality may be favoured over a slower and more protected path. Biological evidence exists for such a trade-off in many species, often mediated through the trade-off between increased foraging and reduced predation risk [70–73]. Larger adult bicolour damselfish (Stegastes partitus) experience lower mortality, but juveniles that grow more quickly are more exposed to predators and less likely to survive to adulthood [74].

Without need to assume any trade-off, ontogenescent mortality may be a by-product of growth patterns. If mortality is strongly size dependent, it should decrease with age while the organism is growing, not because the early concentration of mortality is advantageous, but because it is unavoidable when individuals start out small and vulnerable [75]. This thinking underlies the linking of mortality with the von Bertalanffy model of somatic growth [76] (common in fisheries science [43,74]) and is not restricted to size dependence; if robustness to any sort of insult increases with age, mortality from that insult should decrease with age. Examples of this in humans can be found in pertussis (whooping cough), viral diarrhoeas and other infectious diseases that are extremely dangerous to infants but less so with increasing age. In addition to size and immunocompetence, developing individuals may accumulate status, knowledge, strength or resources, which serve to decrease their mortality risk. This acquired robustness hypothesis is perhaps what Medawar, an immunologist, saw as the clear special reason for ontogenescence [1].

(c). Removal of the least fit: ontogenescence as selection

Where biologists have thought of ontogenescence as deriving from selection, demographers have suggested it may in fact be a process of selection. Differences in frailty may derive from genetic differences, maternal effects or heterogeneous environments. Demographic frailty models [77] assume that there is some unobserved distribution of individual frailties that modify each individual's age-specific mortality risk. Vaupel & Yashin [78] show that where each individual's mortality hazard is age invariant, but frailties are heterogeneous, death rate can drop with age. They speculate that the ‘high initial rate of breakdown could be due to a group of lemons’, i.e. that ontogenescence is a selective process in which the frailest individuals die youngest.

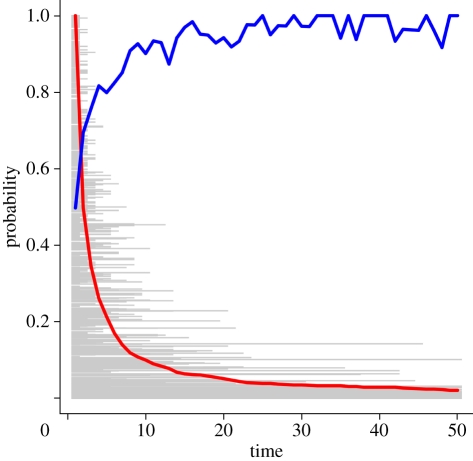
Figure 2 represents a simple microsimulation illustrating this process. Each of 1000 simulated individuals is randomly assigned a frailty from a uniform distribution between zero and one. In each time period, its probability of mortality is equal to its own frailty value, independent of its age. Initially, the mean frailty of the population is close to 0.5, but quickly drops as the frailer individuals die. Simultaneously, probability of survival through the time period increases because of the decreasing mean frailty. This leads to a decreasing rate of removal, and therefore a deceleration of ontogenescence. Similar results are achieved under any non-unitary frailty distribution and a wide range of individual age-specific mortality risks. Comparing the rates of decline in mortality between populations with different heterogeneities would be an excellent first test of this hypothesis.

Figure 2.

Simulated frailty-based ontogenescence. A simple simulation demonstrates how heterogeneous frailties can cause ontogenescence. The height of each grey line is the frailty of one individual, and the termination of that line is its age at death. Each of 1000 simulated individuals has a unique but time-constant frailty. As the frailer individuals die out, the proportion of survivors (l_x, red line) decreases, and the mean probability of remaining individuals surviving through the period (p_x, blue line) increases.

This frailty model of ontogenescence requires only that there is variation between individuals in risk of mortality, and that an individual's risk at one age is correlated with its risks at other ages. In this case, the question of why evolution allows for ontogenescence may be reduced to the question of why evolution allows for, or causes, heterogeneity in individual quality.

(d). Linking ontogenescence to the ontogenetic programme

Ontogenesis as a process is far more complex than constant individual risks or mere size dependence can account for. A vast diversity of developmental and genetic mechanisms must work correctly and in concert for the organism to be viable and developing at each size and stage from fertilization to reproductive adult. As the new organism undergoes its first cell division, its first invagination or takes its first breath, mechanisms it has never before used are tested for the first time. A mishap at any level of organization may make the organism fail any one of these tests and perish. Transitions in transcription, physiology or environment are dangerous because they present new tests the organism has not yet passed. While the logic underlying this transitional timing hypothesis is largely the same regardless of mechanism, I focus here on genetic mechanisms, as I believe them to be the least intuitively obvious, and for many organisms the most important.

As this hypothesis is to the best of my knowledge novel, I shall first explain by analogy, then describe in greater biological detail. Imagine that each of many copies of a complex piece of a computer code has had a random line deactivated, and each is to be tested for how long it takes to malfunction. Time-to-failure for each will depend on several factors, but one of these is the time elapsed before each line of the code is executed, giving the loss of function the opportunity to cause a failure. If the amount of code the program first executes in each time period is constant across periods, the malfunctions may also be uniformly distributed over time (non-ontogenescent failures). If however, most of the code is necessary for the program to boot-up, most of the failures would occur very early, and the rate of failures decreases with the rate of first executions (ontogenescent failures). A similar process may cause ontogenescence in those organisms for which the majority of genes must function properly for short-term survival.

Models of senescence employing age-of-action reasoning [79,80] tend to implicitly assume that mutations affecting probability of mortality at any age are as likely to arise as those affecting any other. Moorad & Promislow [81] point out that the violation of this assumption allows for a U-shaped mortality curve, even where the fitness effects of mortality decline monotonically with age, although their refutation of this assumption depends upon decreasing residual reproduction with age, and therefore applies only to reproductive-age individuals. Nevertheless, they are correct in that the assumption of age invariance is both biologically untenable and contrary to experimental evidence [82–84]. Invariance requires either that the ages at which each mutation influences fitness are independent of the ages at which the affected gene is expressed, or that the number of genes having their expression modulated at each age is constant across ages.

The first of these possibilities can be rejected. While some mutations cause changes in the age of onset of diseases (e.g. [85]), most de novo mutations with fitness effects are recessive losses of function [86,87], not modifications in age at function. Mortality owing to a loss of function will not be evenly distributed across all ages, but rather will tend to be concentrated in those ages when the relevant gene product is first required. Evidence for this can be seen in the fact that mortality owing to chromosomal abnormalities and congenital defects is concentrated shortly after conception and birth, not distributed evenly throughout life. This implies that rather than being uniformly distributed, the effects of deleterious mutations are largely timed based on the organism's normal timing of transcriptional transitions.

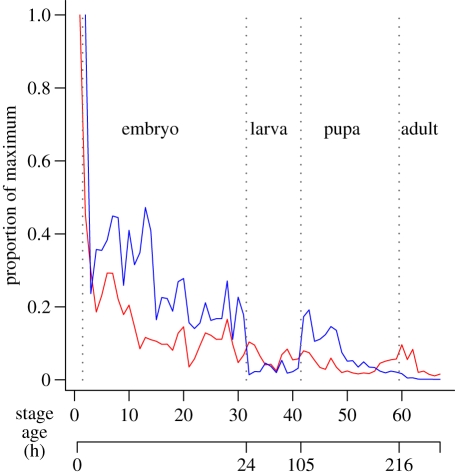
The second possibility, that these transcriptional transitions are uniformly distributed with age, can also be rejected. Figure 3 illustrates the age distribution of such events using the best full life-course genomic expression time series available from Drosophila melanogaster [88]. The two models presented, of mean rate of change in expression level between developmental stages, and of number of genes reaching new expression maxima at each stage, tell similar stories; both are strongly concentrated at the beginning of life. Stage or age-specific mortality for pre-adult Drosophila is not well characterized, so the mortality pattern cannot currently be compared with these functions. Such comparisons, between the distribution of transitions (genetic or physiological) and of deaths, would be powerful tests of the transitional timing hypothesis.

Figure 3.

Potential transcriptional triggers of mutational action by stage in Drosophila melanogaster. Changes in transcription may signal that the organism is employing its genome in developmentally novel ways, testing systems not previously used by the organism and potentially triggering mortality. Two measures of the rate of such change are plotted. The blue line is a mean of how severely individual genes are being up- or downregulated between adjacent stages. The red line indicates how many genes are being expressed at higher levels than they have at any previous stage. Time scale is linear within, but not between, life stages and the y-axis is scaled to the maximum value of each function. The peaks in transcriptional change early in the pupal phase suggest that risk is associated with many transitions, but both functions are highest in the earliest stages of embryonic development.

This transitional timing hypothesis requires heterogeneity, and mild assumptions about the genome of the organism, but not about the ecology of the organism. Given that most organisms require large portions of their expressed genome to survive any meaningful amount of time, mortality based on novel mutations should generally be ontogenescent. The ramifications of this type of age-dependent mutation rates reach beyond the study of ontogenescence; as one example, old-age mortality plateaus may be caused, at least in part, by the paucity of mutations having age-specific actions at those advanced ages.

(e). A broad pattern needs broad explanations

These several hypotheses are not mutually exclusive, but we may ask which operate broadly enough to explain the pattern. As ontogenescence is widespread across causes of death, taxa and life histories, the hypotheses requiring the fewest ecological assumptions can provisionally be assumed to have caused ontogenescence in many ancestral populations, and to serve in its maintenance. These are the frailty hypothesis, the transitional timing hypothesis and the acquisition of robustness hypothesis. These three may function simultaneously and synergistically. The growth trade-off hypothesis requires more complex assumptions about change over age in the force of selection for growth or the mortality risk associated with rapid growth. While it probably operates in many populations, it is not a general explanation. Selection for early termination of inviable young may alter the form of ontogenetic mortality, and in some taxa ontogenescence may be exapted for this function, but this reasoning is insufficient to explain the breadth of the pattern.

5. The non-ontogenescing organism

Just as some species apparently do not senesce [89], it is likely that there are others that do not ontogenescence. Given the hypotheses compiled here (table 1), we may speculate what such a population may look like. We seek an organism lacking parental care or internal development; otherwise parental withdrawal of investment from the inviable would probably lead to high and declining early mortality. Our organism should also lack any resource-driven trade-off between growth and mortality avoidance, or invest a constant portion of its resources in growth throughout its lifetime. Further, it should not face predation or other insults that growth and development could mediate. Its environment should not be geographically heterogeneous in risks. The population should lack heterogeneous frailties and variation in per-offspring investment. Finally, it should lack an early phase during which developmentally novel genetic and physiological mechanisms are concentrated.

Table 1.

Primary hypotheses for the evolutionary basis of ontogenescence.

hypothesis name	hypothesis: death rate decreases with age in developing cohorts because…
quality control hypothesis	… kin terminate potentially inviable individuals early so as to avoid bearing unnecessary costs.
growth trade-off hypothesis	… as individuals grow, they can decrease their relative need for continued growth and therefore accept fewer growth-enabling mortality risks.
robustness hypothesis	… as individuals develop, they acquire characteristics that increase their robustness to insults.
heterogeneous frailty hypothesis	… the frailest individuals die first, causing mean frailty to decline with age.
transitional timing hypothesis	… transcriptional, developmental and environmental transitions are dangerous, and these are concentrated early in life.

What organism could possibly meet these criteria? Anecdotal evidence suggests that laboratory populations of some species may lack ontogenescence when both genetic and environmental heterogeneity are close to absent, extrinsic risk is null, deleterious recessives do not affect the population and per-offspring investment is low.

In natural populations, these conditions will only be approximated in asexually reproducing populations. Where an asexually produced genome is a copy of the parental genome that has passed every necessary test, the one produced sexually is novel and therefore untested. This conjecture runs contrary to the common view of asexual reproduction as leading to high rates of inviability. I would argue that this view derives from cases of pathological asexual reproduction, where no reliable mechanism exists to remove deleterious mutations. In populations where asexual reproduction is facultative or cyclical, and possibly in cases of highly reliable DNA repair (e.g. bdelloid rotifers), asexual reproduction in certain environments may lead to a near-total absence of ontogenescence. If so, ontogenescent mortality may belong high on our list of the costs of sexual reproduction.

6. Conclusions

While many relevant datasets and theories exist, the lack of synthesis and of concentrated investigation has left the study of the evolution of ontogenescence very much ready for foundational work. The hypotheses and models sketched in this paper require refining, enumeration of predictions and synthesis. Informed reasoning suggests that ontogenescence is most likely to derive from the early winnowing of the frailest individuals, the acquisition of robustness by the survivors and the early concentration of dangerous transitions. It further suggests that life-history trade-offs play a role in shaping ontogenescence in many taxa but ontogenescence is not an adaptation and ontogenetic mortality is generally maladaptive. These conclusions remain speculative and debateable and additional hypotheses may yet be proposed. Many of the currently available hypotheses are amenable to comparative and experimental work; none have yet been directly tested.

While most scientists, policymakers and taxpayers are personally concerned with senescence, we are beyond the worst depredations of ontogenescence. Nevertheless, ontogenescence represents the tremendous wastage of life, not only human, but of our cultivars, livestock and wildlife. No estimate is available of the economic cost of ontogenescent death; it would surely be staggering. The conservation implications of early mortality in endangered species, in the wild and in breeding facilities, are tremendous. The medical, social, emotional and economic implications of foetal–infant mortality in humans are immense.

Further, ontogenescence is a tremendous hole in our understanding of evolution. It is among the most widespread and least studied of life-history traits. In many species, the majority of mortality occurs during ontogenescence; insofar as this mortality is associated with the chromosomal and genetic characteristics of the deceased, this is a remarkable process of natural selection occurring even in steady-state populations. The evolution of ontogenescence is deeply tied to that of reproductive strategies, menopause, sociality, senescence, transcription patterns and the ontogenetic programme. Studying ontogenescence requires far less time than studying senescence; the next few years may finally elucidate the clear special reasons why young organisms are so prone to die.

7. Methods for figures

Figure 1: Age-specific mortality hazard was calculated from a life table compiled from three sources. For ages from conception to 112 days post-conception, data are derived from a foetal mortality estimate by Holman & Wood [28], based on intensive pregnancy testing in rural Bangladesh. Two sources from Norway provided data for ages 14 weeks post-conception through first birthday [90] and from birth to 12th birthday [91]. From each of these sources, I calculated an l_x column (survivors at age x out of 10 000 conceptions), and calculated the hazard rate at each age as

Interval length varied between sources and ages. Each h_x value was plotted at the midpoint of the age interval for which it was calculated and the second derivative of the function is positive; this tended to slightly overestimate the hazard at each age.

Figure 2: Frailty microsimulation was performed in the open-source statistical programming language R. This code is available in electronic supplementary material, S3.

Figure 3: Gene expression levels for 4028 D. melanogaster genes at 67 developmental points were measured by Arbeitman et al. [88] using cDNA microarrays. Expression of each gene at each age was measured, then normalized on a log₂ scale, with zero being set equal to the level of expression of that gene in a pooled sample from all developmental stages. Developmental points included one for unfertilized eggs, 30 embryonic ages, 10 ages during the larval phase, 18 ages during metamorphosis and eight adults ages, up to 30 days post-eclosion.

From these published data, I calculated two functions relating to changes in gene expression with development. First, I calculated change in the expression level (on the log₂ scale) of each gene between each stage and the stage preceding it, divided this by the number of hours between the stages to get a rate of change and took the mean of the absolute values of these changes for each stage.

More formally, if gene j at stage i is expressed at a level equal to 2^L × r, where r is the reference level of expression for that gene, and t_i is the time between stages i − 1 and i,

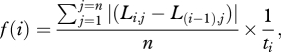where f(i), normalized to its own maximum, is the first function in figure 3.

Second, I calculated how many genes during each stage reached levels of expression equal to or greater than the maximum expression of that gene at all preceding stages. That is, g(i) equals the number of genes that in each stage meet the criterion that

where g(i), again normalized to its maximum, is the second function in figure 3.